Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 5, стр. 524-533

ВВЕДЕНИЕ

Исследования волн – периодических течений жидкостей, в которых дисперсионное соотношение задает связь между частотой и длиной волны или волновым числом, занимают важное место в физических науках об атмосфере, океане и прикладной гидродинамике в силу фундаментальности темы и важности практических приложений. Несмотря на более чем тысячелетнюю историю наблюдений и экспериментальных исследований и более чем трехсотлетний период активных усилий теоретиков, многие вопросы теории волн, эффектов нестационарности, нелинейности, диссипации, вопросы практических приложений нуждаются в уточнении. Традиционно, начиная с работ Эйлера, Лагранжа, Даламбера внимание уделяется изучению отдельных типов волн – гравитационных, звуковых, инерциальных в жидких или газообразных средах. Первоначально рассматривались гравитационные волны на поверхности актуально однородной жидкости, плотность которой одинакова в пространстве и неизменна во времени. Полученные результаты отражены в большом числе оригинальных и обзорных статей, обобщены в известных трактатах [1, 2]. По наблюдениям волновой картины перед и позади рыболовной лески на дрейфующей яхте, Томсон идентифицировал капиллярные волны [3], описание которых приводится в современных учебниках в практически неизменной оригинальной форме.

Постепенно появляющиеся примеры наблюдений заметного влияния даже слабых вариаций переменной плотности на свойства течений в атмосфере, в океане и в лаборатории стимулировали изучение волн в неоднородной жидкости, вначале – в двухслойной в работах Дж.Г. Стокса [4]. Анализируя эксперименты по моделированию перьевых облаков, Рэлей вывел уравнении и рассчитал предельную частоту бегущих внутренних волн в непрерывно стратифицированной жидкости [5]. Удивительным образом, глубокая статья Рэлея выпала из научного оборота и долгое время оставалась неизвестной широкому кругу исследователей. Только через сорок лет финский ученый В. Вяйсяля вновь вычислил частоту собственных колебаний непрерывно стратифицированной жидкости применительно к динамике разрабатываемых шаров-зондов [6], а через два года английский метеоролог Д. Брент определил ее значение при интерпретации спектров сигналов микробарографов [7].

Активные исследования влияния стратификации на волновые движения, которые стали формироваться в начале сороковых годов прошлого века в Германии [8], получили широкое развитие в конце шестидесятых годов прошлого века в Великобритании [9] и довольно скоро в других странах. Стали изучаться все основные свойства отдельных типов волновых движений – групповые и фазовые скорости [2, 10], эффекты рефракции [11], дифракции [12], интерференции, нелинейности [13] и в гидросфере, и в атмосфере [14].

Однако реальная картина морского волнения [15], как правило, нестационарного вследствие ветрового разгона, диссипативного затухания и нелинейного взаимодействия волн между собой, с неоднородными течениями и топографией, существенно отличается от идеализированной в современных теоретических построениях. Волны легко разрушаются с образованием пенных шапок, вытянутых по ветру сплошных струек и последовательностей капель (капельных струй) [16]. В свою очередь, волны меняют морфологию дна в море, реках и каналах [17]. Короткие капиллярные волны на склонах гравитационных волн, [18], меняют шероховатость контактной поверхности, определяющую взаимодействие океана и атмосферы (расчеты распространения капиллярных волн по сферической поверхности проведены в [19]). Визуализация капельных течений показывает сложность многомасштабной картины волнового переноса вещества, включающего образование вихрей, и тонких волокон [10].

В природных условиях в поле силы тяжести, подвижные среды – атмосфера и океан, естественно стратифицируются под действием сил плавучести при изменении температуры, солености и давления и допускают существование бегущих внутренних волн [5, 10]. Типичные значения периода (частоты) плавучести ${{T}_{b}} = 2\pi {\text{/}}N$ составляют 5–10 мин ($N\sim 0.01\;{{\operatorname{c} }^{{ - 1}}}$) в сезонном термоклине и 20–60 мин в годовом термоклине в океане ($N\sim 0.001\;{{\operatorname{c} }^{{ - 1}}}$) [20, 21] Во всех случаях отношение изменчивости плотности и ее вариаций в течении являются малыми, что позволяет представлять ее распределение в виде

функция $r\left( z \right)$ задает исходную стратификацию, а $s\left( {x,z,t} \right)$ – волновое возмущение плотности.

Научный и практический интерес представляет изучение свойств волн в жидкости со свободной поверхностью, по которой могут распространяться периодические гравитационно-капиллярные волны с учетом эффектов непрерывной стратификации, обеспечивающих существование внутренних волн.

МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Современное математическое описание течений жидкостей и газов базируется на полной системе фундаментальных уравнений неразрывности, переноса вещества (диффузии Фика), тепла (Фурье) и импульса (Навье-Стокса) [22]. Однако ключевые свойства различных типов волновых процессов, которые обычно изучаются в приближении невязкой жидкости [1, 2, 5, 10, 13], сохраняются в виде регулярной части решений задач в полной постановке. Следуя традиции, далее рассматривается задача о распространении периодических волн – поверхностных капиллярно-гравитационных и внутренних волн в невязкой экспоненциально стратифицированной жидкости, влиянием диссипативных факторов (эффектами вязкости, диффузии и теплопроводности), как и сжимаемостью жидкости, пренебрегается.

Рассмотрение проводится в декартовой системе координат Oxyz, в которой плоскость Oxy совпадает с равновесным уровнем жидкости $z = 0$, а ось Oz направлена вертикально вверх против направления действия сил тяжести g. Отклонение свободной поверхности от равновесного значения описывается функцией $z = \zeta \left( {x,y,t} \right)$. Невозмущенная несжимаемая жидкость характеризуется распределением плотности по глубине ${{\rho }_{0}}(z) = {{\rho }_{{00}}}r\left( z \right)$, которое описывается масштабом, $\Lambda = {{\left| {{\text{d}}{\kern 1pt} \ln {\kern 1pt} \rho /{\text{d}}z} \right|}^{{ - 1}}}$, частотой $N = \sqrt {g/\Lambda } \;{{с}^{{ - 1}}}$, периодом плавучести ${{T}_{b}} = 2\pi /N$, и коэффициентом поверхностного натяжения $\sigma $ или его нормированным на плотность значением $\gamma = \sigma {\text{/}}{{\rho }_{{00}}}$. Для упрощения записи обычно выбирается экспоненциальное распределение плотности, к которому может быть приведено произвольное гладкое распределение плотности с использованием преобразования масштабов, приведенного в [23].

Математическая формулировка задачи основана на предельно редуцированной системе фундаментальных уравнений в приближении Буссинеска [22], в которой уравнение состояния заменяет невозмущенное распределение плотности.

Здесь приняты обозначения: ${\mathbf{u}} = \sum\nolimits_i {{{u}_{i}}{{{\mathbf{e}}}_{i}}} $ – вектор скорости, $P$ – гидродинамическое давление. Рассмотрим задачу в плоской постановке, считая, что волновое движение не зависит от горизонтальной координаты $y$. В этом случае, принимая во внимание несжимаемость жидкости, можно ввести функцию тока $\psi $ такую, что: $u = {{\partial }_{z}}\psi $, а $w = - {{\partial }_{x}}\psi $ и в линейной постановке в приближении Буссинеска в случае экспоненциальной стратификации с масштабом $\Lambda $ системa (2) преобразуется в уравнение (подробный вывод приводится в приложении А):

Уравнение (3) дополняется кинематическим и динамическим граничными условиями на свободной поверхности жидкости. В линейном приближении после процедуры снесения граничных условий на невозмущенную поверхность $z = 0$ граничные условия принимают вид [2]:

С учетом (4) условие (5) приводится к следующему уравнению

Решение уравнений (3, 6) находится методами теории возмущений [25–27].

РЕШЕНИЕ ЗАДАЧИ В ПЕРВОМ ПРИБЛИЖЕНИИ ТЕОРИИ ВОЗМУЩЕНИЙ

Для поверхностных волн частота которых превышает частоту плавучести $\omega > N$ решение (6) ищется в виде:

Поскольку коэффициенты в уравнении (3) зависят от глубины z, решение вида (7) нужно понимать как коротковолновое ВКБ-приближение к задаче [26].

Подстановка (7) в (3) приводит к связи между горизонтальной и вертикальной компонентами волнового вектора ${{k}_{x}}$ и ${{k}_{z}}$:

Подставляя (7) в граничные условия (6) получим дисперсионное соотношение:

Используя (8) дисперсионное уравнение (9) преобразуется в:

В силу громоздкости выражений значения корней кубического уравнения (10) здесь не приводятся.

Для удобства дальнейшего анализа выражения (8) и (10) приводятся к в безразмерному виду с использованием естественных масштабов задачи – в качестве масштаба времени выбирается величина, обратная частоте плавучести ${{T}_{N}} = 1{\text{/}}N$, а масштаба длины – капиллярная постоянная $\delta _{g}^{\gamma } = \sqrt {{\gamma \mathord{\left/ {\vphantom {\gamma g}} \right. \kern-0em} g}} $. В качестве малого параметра выбирается отношение собственных масштабов задачи $\varepsilon = {{\delta _{g}^{\gamma }} \mathord{\left/ {\vphantom {{\delta _{g}^{\gamma }} \Lambda }} \right. \kern-0em} \Lambda }$. Тогда с ${{k}_{{x*}}} = {{k}_{x}}\delta _{g}^{\gamma }$ и ${{\omega }_{*}} = \omega {\text{/}}N$ формулы (8) и (10) принимают вид

Не все решения уравнения (12) имеют физический смысл. Для обеспечения затухания движения с глубиной необходимо выполнение условия $\operatorname{Re} \left( {{{k}_{z}}} \right) > 0$. Как показывает анализ, этому условию удовлетворяет только один корень. Представление корней дисперсионного уравнения и доказательство единственности физически реализуемого корня приводится в приложении Б.

В более привычном виде выражение для дисперсионного уравнения (10) приводится в форме зависимости частоты $\omega $ от волнового числа ${{k}_{z}}$

Рассмотрение показывает, что из всех значений выражения (13) условию физической реализации удовлетворяет только один корень, которому соответствуют верхние знаки. В отсутствии стратификации ($N \to 0$) (13) переходит в известное дисперсионное соотношение для капиллярно-гравитационных волн [1, 2]:

Традиционно дисперсионное уравнение представляют именно в таком виде, а не в форме (12). Поскольку частота волнового движения несет в себе энергетический смысл, она должна быть действительной и положительно определенной величиной. Волновое число, напротив, учитывающее ослабление волн с удалением от источника, может быть комплексным. Действительная часть компоненты ${{k}_{x}}$ и мнимая часть компоненты ${{k}_{z}}$ в этом случае характеризуют волновое движение, а мнимая часть компоненты ${{k}_{x}}$ и действительная часть компоненты ${{k}_{z}}$ описывают пространственное затухание волны. Выбор более адекватного представления базовых параметров бегущих волн нуждается в экспериментальном обосновании.

Если частота волны меньше частоты плавучести $\omega < N$, решение (6) можно искать в виде внутренних волн:

Подстановка (14) в (3) приводит к:

Подставляя (14) в граничные условия (6) получим дисперсионное соотношение:

которое с использованием (15) приводит к связи между амплитудами $\alpha $ и $\beta $: Здесь использованы обозначения ${{k}^{2}} = k_{x}^{2} + k_{z}^{2}$ – квадрат волнового числа, $\cos \theta = {\omega \mathord{\left/ {\vphantom {\omega N}} \right. \kern-0em} N}$ – безразмерный параметр, характеризующий отношение частоты волнового движения во внутренней волне к частоте плавучести. Угол $\theta $ характеризует направление распространения групповой скорости волны по отношению к вертикали или фазовой скорости – к горизонтали. Полученные соотношения описывают внутренние гравитационно-капиллярные волны, которые испытывают отражение от свободной поверхности. Из выражений (17) для коротких внутренних волн ($k\Lambda \gg 1$) следует, что что означает, согласно (14), отсутствие поверхностной волны: вся энергия, падающая на свободную поверхность, отражается и распространяется уже в виде отраженной волны. Энергия низкочастотных движений, вносимых на свободную поверхность атмосферными возмущениями, также переносится внутренними волнами в толщу жидкости, что обеспечивает низкую плотность энергии в спектральном диапазоне с периодом в интервале от нескольких минут до нескольких часов и длинами волн от нескольких сотен метров до нескольких сотен километров [24].

В теории однородной жидкости в теоретических построениях широко используется свойство потенциальности поверхностных волн [2]. В стратифицированной жидкости это свойство теряется вследствие действия механизма бароклинной генерации завихренности [2]. С учетом связи ротора скорости с функцией тока в двумерном течении [2]:

из (7) и (8) следует, что завихренность поверхностных волн в стратифицированном океане ненулевая и равна

Оценка у завихренности для внутренних волн следует из формул (14) и (15):

Рассмотрим амплитуды $A{{N}_{S}}_{ \pm }$ и $A{{N}_{{I \pm }}}$ в предельных случаях. Вблизи поверхности жидкости ($z \to 0$) выполняются переходы:

И для поверхностных и для внутренних волн выражение (22) при приближении частоты волнового движения к частоте плавучести неограниченно растет и в пределе достигает бесконечно больших значений. Поверхностные волны с очень большими частотами ($\omega \gg N$) обладают нулевой завихренностью (в этом случае выражение (22) для поверхностных волн устремляется к нулевому значению). Внутренние волны с малыми частотами ($\omega \ll N$) обладают конечной завихренностью (выражение (22) для внутренних волн в этом случае стремится к постоянному значению ${{A}_{ \pm }}$).

На глубине (при $z \to - \infty $) выполнятся переходы:

Таким образом, для поверхностных волн можно сделать вывод, что завихренность экспоненциально затухает с глубиной (см. выражение (20)), а внутренние волны на глубине обладают конечной завихренностью.

ПОСТРОЕНИЕ ДИСПЕРСИОННЫХ ЗАВИСИМОСТЕЙ

Расчеты показывают, полученные выражения в предельных переходах сводятся к общепринятым, однако, наблюдения и сравнения с экспериментом построения лучше выполнять в пространстве физически наблюдаемых величин – длины, частоты, групповой скорости волны. Для выполнения построений необходимо, в первую очередь, определить понятие модуля волнового вектора, поскольку остальные величины прямо или косвенно зависят от него. В двумерном случае модуль волнового вектора можно определить двумя способами:

Согласно наиболее общему определению волновой вектор – это градиент фазы волны. В выражении (22) учтены компоненты волнового вектора, отвечающие за затухание и за волновое движение, тогда как в выражении (23) компоненты, отвечающие за затухание, отсутствуют. Отличие в значениях величин (22) и (23) составляет $\sqrt 2 $ раз. Поскольку пространственное затухание не оказывает влияния на фазу волнового движения, более предпочтительным и физически обоснованным выглядит определение (23). В дальнейшем в этой работе мы будем придерживаться его.

В таком случае длина волны легко находится следующим образом:

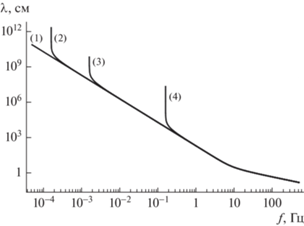
Подставляя дисперсионные соотношения в (24) получим зависимость длины волны от частоты волнового движения. Эта зависимость изображена на рис. 1 (здесь и далее все построения будут выполнены для жидкости с параметрами воды $\sigma = 72\,\,{\text{дин/см}}$, ${{\rho }_{{00}}} = 1\,\,{\text{г/с}}{{{\text{м}}}^{{\text{3}}}}$, $g = 981\,\,{\text{см/}}{{{\text{с}}}^{{\text{2}}}}$). Цифрой (1) обозначены зависимости для нестратифицированной жидкости ($N = 0\,\,{{{\text{с}}}^{{ - 1}}}$). Цифрой (2) обозначены зависимости для очень слабо стратифицированной жидкости ($N = 0.001\,\,{{{\text{с}}}^{{ - 1}}}$), что соответствует годовому термоклину в океане [20, 21]. Цифрой (3) обозначены зависимости для слабо стратифицированной жидкости (N $ = 0.01\,\,{{{\text{с}}}^{{ - 1}}}$). Такая ситуация свойственна сезонному термоклину в океане [20, 21]. Цифрой (4) обозначены зависимости для сильно стратифицированной жидкости ( $N = 1\,\,{{{\text{с}}}^{{ - 1}}}$). Такие значения воспроизводимы в лабораторных условиях для жидкости с сильной стратификацией.

Из рис. 1 видно, что различия в генерируемых длинах волн между жидкостью с очень слабой стратификацией и однородной жидкостью начинают проявляться на очень больших длинах волн (порядка ${{10}^{9}}$ см). При больших значениях стратификации различия проявляются для меньших длин волн.

Отдельный интерес представляет собой скорость распространения фазового фронта и скорость переноса энергии. Фазовая скорость волнового движения задается соотношением:

Групповая скорость волнового движения, характеризующая за перенос энергии волной, определяется как градиент частоты волнового движения в пространстве волновых чисел:

На рис. 2 представлены зависимости фазовой и групповой скоростей от частоты для жидкостей с разной стратификацией. Фазовые скорости обозначены на рисунке пунктирными линиями, групповые скорости – сплошными. Цифрами от (1) до (4) помечены графики зависимостей фазовых скоростей, а цифрам от (5) до (8) соответствуют графики зависимостей групповых скоростей при разных уровнях стратификации. Цифрами (1) и (8) обозначены зависимости для однородной жидкости ($N = 0\;\,{{{\text{с}}}^{{ - 1}}}$), (2) и (7) – для очень слабо стратифицированной жидкости ($N = 0.001\,\,{{{\text{с}}}^{{ - 1}}}$), (3) и (6) – для слабо стратифицированной жидкости ($N = 0.01\,\,{{{\text{с}}}^{{ - 1}}}$). Цифрами (4) и (5) обозначены зависимости для сильно стратифицированной жидкости ($N = 1\,\,{{{\text{с}}}^{{ - 1}}}$).

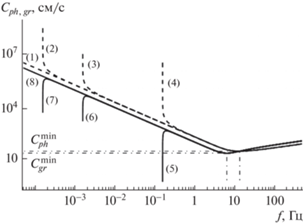
С увеличением частоты длина волны уменьшается. При достижении длиной волны значений, сопоставимых с масштабом стратификации $\Lambda $ (порядка ${{10}^{3}}\,\,{\text{см}}$ для сильно стратифицированной жидкости, зависимости для которой обозначены литерой (4) и (5), порядка ${{10}^{7}}\,\,{\text{см}}$ для слабо стратифицированной жидкости, зависимости для которой обозначены литерой (3) и (6) и порядка ${{10}^{9}}\,\,{\text{см}}$ для очень слабо стратифицированной жидкости, зависимости для которой обозначены литерой (2) и (7)) стратификация для волны перестает быть заметна и все кривые ведут себя так, как ведут себя как для однородной жидкости (кривые, обозначенные литерой (1) и (8)).

И фазовая и групповая скорости обладают экстремумом – минимумом, причем своего минимального значения фазовая скорость достигает при большей частоте, чем групповая. На больших частотах групповая скорость превышает фазовую. С уменьшением частоты обе скорости уменьшаются и при некотором значении сравниваются – скорость переноса фазы волны совпадает со скоростью переноса энергии группой волн. Дальнейшее уменьшение частоты приводит к еще одному примечательному значению – частоте, при которой наблюдается минимальное значение групповой скорости волнового движения.

С уменьшением частоты волнового движения увеличивается длина волны и становится заметно влияние стратификации: с приближением к частоте плавучести фазовая скорость неограниченно возрастает, а групповая скорость устремляется к нулю. Частота плавучести является в некотором роде критической частотой: в идеальной жидкости поверхностные волны с частотой меньше, чем частота плавучести не реализуются (см. приложение Б).

Для наблюдения удобнее строить зависимости фазовой и групповой скоростей не от частоты, а от длины волны. При построении зависимостей для идеальной нестратифицированной жидкости в [2] проводилась нормировка на длину волны, при которой достигается минимум фазовой скорости. Учитывая важность групповой скорости как показателя переноса энергии, предпочтительнее выглядит выбор длины волны ее минимального значения. В аналитическом виде это сделать довольно затруднительно. На рис. 3 представлены зависимости фазовой и групповой скорости от длины волны для жидкостей с разной стратификацией. Обозначения на рис. 3 соответствуют обозначениям, введенным на рис. 2. Литерами (9) и (10) помечены линии, отмечающие минимум фазовой и групповой скоростей соответственно.

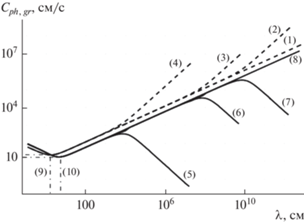
Из рис. 2 и 3 видно, что существует два характерных значения скорости: минимальное значение фазовой скорости $C_{{ph}}^{{\min }}$ и минимальное значение групповой скорости волн $C_{{gr}}^{{\min }}$.

Также интерес представляет значение частоты ${{f}_{ = }}$ (длины волны ${{\lambda }_{ = }}$), при которой фазовая и групповая скорость сравниваются. Для жидкости, для которой были выполнены построения ($\sigma = 72\,\,{\text{дин/см}}$, ${{\rho }_{{00}}} = 1\,\,{\text{г/с}}{{{\text{м}}}^{{\text{3}}}}$, $g = 981\,\,{\text{см/}}{{{\text{с}}}^{{\text{2}}}}$) эти особенные значения совпадают и для однородной и для стратифицированной жидкости. Своего минимального значения $C_{{ph}}^{{\min }} = 23.06\,\,{\text{см/с}}$ фазовая скорость достигает при значениях частоты $f_{{ph}}^{{\min }} = 13.5\,\,{\text{Гц}}$ и длины волны $\lambda _{{ph}}^{{\min }} = 1.7\,\,{\text{см}}$. Минимальная групповая скорость $C_{{gr}}^{{\min }} = 17.7\,\,{\text{см/с}}$ достигается при значениях частоты $f_{{gr}}^{{\min }} = 6.5\,\,{\text{Гц}}$ и длины волны $\lambda _{{gr}}^{{\min }} = 4.3\,\,{\text{см}}$. Интересно, что групповая и фазовая скорости сравниваются при характерном значении частоты ${{f}_{ = }} = f_{{ph}}^{{\min }} = 13.5\,\,{\text{Гц}}$ и длины волны ${{\lambda }_{ = }} = \lambda _{{{\text{ph}}}}^{{{\text{min}}}} = 1.7\,\,{\text{см}}$ и принимают значение $C_{{ph}}^{ = } = C_{{gr}}^{ = } = C_{{ph}}^{{\min }} = 23.06\,\,{\text{см/с}}$.

В эксперименте значительные отличия в скорости распространения фазового фронта и группы волн стоит ожидать на таких длинах волн, значения которых сопоставимы с масштабом стратификации $\Lambda $. С увеличением длины волны различия должны быть более заметны и существенны. При малых длинах волн по сравнению с масштабом стратификации последняя незаметна для волнового движения и в таких моделях жидкость можно считать однородной, что существенно упрощает расчеты.

ВЫВОДЫ

Проведен анализ распространения поверхностных волн в идеальной экспоненциально стратифицированной несжимаемой жидкости в плоской постановке в физически наблюдаемых переменных.

Показано, что при достижении длиной волны значений порядка масштаба стратификации жидкость ведет себя как однородная. С приближением частоты к частоте плавучести перенос энергии уменьшается: групповая скорость поверхностных волн стремится к нулю, а фазовая – к бесконечности.

В случае инфинитезимальных возмущений стратифицированной жидкости со свободной поверхностью получено: поверхностные и внутренние волны существуют в различных частотных областях. Геометрия распространения внутренних волн обеспечивает снижение интенсивности поверхностных возмущений с частотами, меньшими частоты плавучести.

Приложение А

В приближении Буссинеска второе уравнение системы (2) с учетом принятой функции распределения плотности (1) запишется следующим образом:

В линейном приближении уравнение (А.1) по компонентам запишется:

Стоит отметить, что в выражении (А.2) отсутствуют компоненты давления, отвечающие за гидростатическое давление столба жидкости постоянной плотности ${{\rho }_{{00}}}$. Запишем компоненты скорости через функцию тока $\psi $ и произведем дифференцирование верхнего уравнения системы (А.2) по координате z, а нижнего уравнения – по координате x:

Вычтем из верхнего уравнения нижнее и получим уравнение, связывающее функцию тока $\psi $ и возмущение плотности $s$:

Уравнение неразрывности с учетом принятых предположений и обозначений перепишется в виде:

С учетом введения функции тока:

уравнение неразрывности перепишется:

И в линейном приближении справедливо:

Продифференцируем уравнение (А.4) по времени, уравнение (А.8) – по переменной x и домножим последнее на g и сложим результаты:

Для случая экспоненциальной стратификации уравнение (А.9) можно записать в явном виде:

С точностью до принятых в работе обозначений уравнение (А.10) совпадает с уравнением (3) в основном тексте работы.

Кроме того, можно показать, что решение линеаризованной задачи (7), (14) обнуляет нелинейный член $\left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}}$ в уравнении Эйлера в системе (2). Действительно, подстановка и (7) и (14) в $\left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}}$ дает:

Следовательно, можно утверждать, что решение линеаризованной задачи удовлетворяет полной нелинейной системе (2) в данной постановке задачи.

Приложение Б

Первый корень дисперсионного уравнения (13) принимает вид:

Для поверхностных волн $\omega > 1$ выражение в знаменателе всегда положительно. Первое слагаемое в числителе отрицательно, а второе – положительно. Если пренебречь малыми слагаемыми, содержащими $\varepsilon $ (которые вносят положительный вклад), то получим выражение, совпадающее с аналогичным для идеальной однородной жидкости:

Сравнивая отрицательное и положительное слагаемые можно увидеть, что они равны друг другу только при $\omega = 1$. Учет стратификации жидкости приводит только к увеличению модулю положительного слагаемого.

Два оставшихся корня комплексно сопряженные и выглядят следующим образом:

Видно, что действительная часть комплексно сопряженных корней с точностью до множителя $ - \frac{1}{2}$ совпадает с первым корнем.

Условие физической реализации корней дисперсионных соотношений возникает из-за необходимости затухания движения с глубиной:

и существования компонент в волновом векторе, отвечающих за волновое движение: и/или

Условию (Б.4) удовлетворяет только корень (Б.1). Причем для поверхностных волн это условие выполняется как для волн с частотой больше частоты плавучести (в безразмерных переменных $\omega > 1$) так и для волн с частотой меньше частоты плавучести ($\omega < 1$).

Для поверхностных волн связь между компонентами ${{k}_{x}}$ и ${{k}_{z}}$ в безразмерном виде выглядит следующим образом:

и для волн с частотой больше частоты плавучести а для волн с частотой меньше частоты плавучести справедливо:

Для реальных жидкостей $\varepsilon \ll 1$ и если выполнить разложение в ряд по малому параметру $\varepsilon $ выражение (Б.1), то как минимум до слагаемых 20 порядка малости в компоненте волнового числа ${{k}_{z}}$ не обнаруживается мнимой составляющей. Исходя из выражений (Б.9) и условий физической реализации корней дисперсионного уравнения (Б.4) – (Б.6) можно утверждать, что для поверхностных волн физически реализуем только один корень (Б.1) в области частот больших, чем частота плавучести.