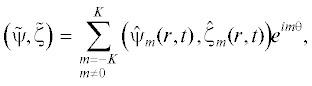Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 5, стр. 512-523
Хаотическая адвекция пассивной примеси в кольцевом баротропном струйном течении
В. П. Реутов a, *, Г. В. Рыбушкина a, **
a Институт прикладной физики РАН
603950 Нижний Новгород, ул. Ульянова 46, Россия
* E-mail: reutov@appl.sci-nnov.ru
** E-mail: ryb@appl.sci-nnov.ru
Поступила в редакцию 28.04.2022
После доработки 31.05.2022
Принята к публикации 09.06.2022
- EDN: YRCSLG
- DOI: 10.31857/S0002351522050108
Аннотация
Исследуется хаотическая адвекция пассивной примеси при возбуждении цепочек вихревых структур в кольцевых баротропных течениях со сложным двухструйным профилем скорости, моделирующих мезомасштабные зональные течения в океане и атмосфере Земли и в лабораторных экспериментах. Основное внимание уделено хаотической адвекции в режиме эйлеровского динамического хаоса. Описание генерации структур основывается на численном решении уравнений баротропного (квазидвумерного) течения с учетом внешнего трения и бета-эффекта. На стенках кольцевого канала ставятся условия непротекания и прилипания. Найдены критические значения параметров на пороге возникновения неустойчивости и изучен переход к эйлеровскому хаосу в двух струйных течениях со сложным профилем скорости. На основе вычисления конечно-временного ляпуновского показателя определены области кольцевого течения, в которых возникает лагранжев хаос (стохастическое перемешивание). Показано, что в результате расширения областей стохастического перемешивания при переходе в режим эйлеровского хаоса, возможно распространение изначально локализованной пассивной примеси по всему объему течения. Приведены оценки, подтверждающие возможность наблюдения рассмотренных эффектов в реальных условиях.
ВВЕДЕНИЕ
Исследование хаотической адвекции пассивной примеси в присутствии вихревых структур на фоне мезомасштабных сдвиговых течений в океане и атмосфере Земли остается одной из важных задач геофизической гидродинамики [1–5]. Хаотическая адвекция, связанная с генерацией цепочек вихревых структур, наблюдалась экспериментально в двумерном кольцевом течении [6]. Имеющиеся данные показывают, что в океане и погодном слое атмосферы возможны зональные течения со сложным многоструйным профилем скорости, осциллирующем в меридиональном направлении [7–10]. Согласно теореме Го (Kuo), необходимым условием неустойчивости идеального баротропного течения на бета-плоскости в линейном приближении является наличие точек с нулевым градиентом потенциальной завихренности [11–13]. Исследования перехода к турбулентности, проведенные в работах [14–18], показали, что при возбуждении цепочек структур в баротропных (квазидвумерных) течениях со сложным профилем скорости, имеющим несколько таких точек, возможно установление динамического хаоса при умеренных надкритичностях, достижимых в реальных условиях. Установлено, что на всех стадиях перехода к динамическому хаосу в баротропных течениях со сложным профилем скорости сохраняются квазистационарные цепочки структур с замкнутыми линиями тока, модуляция которых возрастает при увеличении надкритичности. При этом генерация дополнительных (по отношению к основной волне) спектральных компонент поля скорости приводит к образованию стохастических слоев в окрестности границ замкнутых линий тока и, соответственно, к хаотической адвекции пассивной примеси, обусловленной стохастическим перемешиванием частиц примеси [16]. Кроме того, образование стохастических слоев может сопровождаться поперечным к потоку (боковым) переносом жидких частиц. Это явление неоднократно исследовалось в приложении к океанскому течению Гольфстрим и другим меандрирующим струям [1, 2, 19].
В данной работе изучается хаотическая адвекция пассивной примеси при возбуждении цепочек вихревых структур в баротропных (квазидвумерных) кольцевых течениях со сложным двухструйным профилем скорости, моделирующих крупномасштабные зональные течения в океане и атмосфере Земли и в лабораторных экспериментах. Основное внимание уделено качественным особенностям хаотической адвекции в режиме динамического хаоса. В отличие от работы [18] изучается хаотическая адвекция пассивной примеси, локализованной в начальный момент времени. Описание генерации вихревых цепочек основывается на численном решении уравнений баротропной модели течения с учетом внешнего трения и бета-эффекта. На стенках кольцевого канала ставятся условия непротекания и прилипания. Один из профилей скорости совпадает с изученным в [16] при анализе перехода к хаосу в приближении плоскопараллельного течения, что позволяет сравнить возникновение динамического хаоса в плоскопараллельной и кольцевой моделях течения. Другой профиль скорости характеризуется более сильным разделением струй и более сильной неустойчивостью, что способствует развитию динамического хаоса при выраженном влиянии бета-эффекта. Анализ хаотической адвекции и распространения примеси в кольцевом течении проводится в рамках динамически согласованной модели, основанной на численном решении квазигеострофических уравнений в цилиндрических координатах. Обсуждение динамических моделей хаотической адвекции при возбуждении цепочек вихревых структур можно найти в работах [2, 14–18]. Для идентификации областей перемешивания используется метод, основанный на вычислении конечно-временного ляпуновского показателя [14], позволяющий выделить области лагранжева хаоса, которые характеризуются экспоненциальным “разбеганием” траекторий жидких частиц, переносящих пассивную примесь. Приводятся оценки, подтверждающие возможность реализации изучаемых явлений в натурных условиях и в лабораторном эксперименте.
ОСНОВНЫЕ УРАВНЕНИЯ И АППРОКСИМАЦИИ
Рассмотрим квазидвумерное (баротропное) течение в кольцевом канале между жесткими стенками в приближении бета-плоскости с учетом внешнего (донного) трения. Перейдем к безразмерным переменным, используя характерную скорость течения $U$ и пространственный масштаб радиального сдвига скорости $L$. Перейдем от декартовых координат $\left( {x,y} \right)$ к цилиндрическим координатам $\left( {r,\theta } \right)$, полагая $x = r{\kern 1pt} \cos {\kern 1pt} \theta $ и $у = r\sin \theta $. Кольцевой канал имеет серединный радиус ${{r}_{0}}$, а координаты стенок есть $r = {{r}_{0}} \pm b$, где $b$ – полуширина канала. Исходные уравнения запишем в цилиндрических координатах через безразмерную относительную завихренность $\zeta $ и функцию тока $\psi $ [12, 17]
(1)
$\begin{gathered} \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{r}\left( {\frac{{\partial \psi }}{{\partial \theta }}\frac{{\partial \zeta }}{{\partial r}} - \frac{{\partial \psi }}{{\partial r}}\frac{{\partial \zeta }}{{\partial \theta }}} \right) - \frac{\beta }{r}\frac{{\partial \psi }}{{\partial \theta }} = \\ = \,\, - \lambda \left( {\zeta - {{\zeta }_{0}}} \right) + {{{\text{R}}}^{{ - 1}}}\Delta \left( {\zeta - {{\zeta }_{0}}} \right),\,\,\,\,\Delta \psi = - \zeta , \\ \end{gathered} $Все переменные представим в виде суперпозиции средних и осциллирующих по $\theta $ с периодом $2\pi $ составляющих
(2)
$\begin{gathered} \zeta = \bar {\zeta }(r,t) + \tilde {\zeta },\,\,\,\,\psi = - \int {{{{\bar {v}}}_{\theta }}(r,t)dr} + \tilde {\psi }, \\ {{v}_{\theta }} = {{{\bar {v}}}_{\theta }}(r,t) - \frac{{\partial{ \tilde {\psi }}}}{{\partial r}}, \\ \end{gathered} $(4)
${{\left. {{{{\hat {\psi }}}_{m}}} \right|}_{{r = {{r}_{{_{0}}}} \pm b}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{{\hat {\psi }}}_{m}}}}{{\partial r}}} \right|}_{{r = {{r}_{{_{0}}}} \pm b}}} = 0,\,\,\,\,{{\left. {{{{\bar {v}}}_{\theta }}} \right|}_{{r = {{r}_{{_{0}}}} \pm b}}} = 0.$Рассмотрим квазидвумерное двухструйное течение в кольцевом канале с радиальным профилем азимутальной компоненты скорости вида
(5)
$\begin{gathered} {{v}_{0}}(r{\kern 1pt} ') = \frac{{f(r{\kern 1pt} ')f_{{\max }}^{{ - 1}} - \alpha }}{{1 - \alpha }}, \\ f(r{\kern 1pt} ')\, = \,{{a}_{1}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{\kappa }_{1}}\left( {r{\kern 1pt} ' - \,d\, - \,s} \right)} \right]\, + \,{{a}_{2}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{\kappa }_{2}}\left( {r{\kern 1pt} ' - \,d\, + \,s} \right)} \right], \\ \end{gathered} $Рис. 1.
Профили азимутальной скорости струйных течений P1 (а) и P2 (б) между стенками кольцевого канала $2.5 < r < 10.5$: 1 – равновесное течение, 2 – режим динамического хаоса при ${{R}_{c}} = 60$, $\beta = 0$, $\gamma = 3.39$ (а) и при ${{R}_{c}} = 60$, ${{\beta }_{c}} = 0.3$, $\gamma = 3.17$ (б).
ЛИНЕЙНАЯ ЗАДАЧА И ВЫЧИСЛЕНИЕ КОНЕЧНО-ВРЕМЕНОГО ЛЯПУНОВСКОГО ПОКАЗАТЕЛЯ
Решение линейной задачи на собственные значения проводилось по схеме, описанной в [15–18]. После линеаризации уравнений (1)–(4) на фоне равновесного профиля скорости (5) решение ищем в виде $(\tilde {\psi },\tilde {\zeta }) = ({{f}_{1}},{{f}_{2}})\exp (im\theta - i\omega \,t)$, где $m = 1,2,...$ – волновое число, $\omega $ – циклическая частота (${{f}_{{1,2}}}(r)$– комплексные функции). В данном случае $\Omega = \operatorname{Re} \omega {\text{/}}m$ есть азимутальная фазовая скорость пространственной гармоники с номером $m$, равная угловой частоте вращения цепочки структур, созданной этой гармоникой. Будем считать, что скорость струйного течения в максимуме профиля скорости $U$ увеличивается при постоянных значениях размерностных параметров $\beta {\kern 1pt} *{\kern 1pt} *$, $\lambda {\kern 1pt} *{\kern 1pt} *$ и $\nu $. Введем надкритичность течения $\gamma = U{\text{/}}{{U}_{c}}$, где ${{U}_{c}}$ – критическая скорость возникновения неустойчивости. В соответствии с принятыми нормировками изменение введенных выше безразмерных параметров связано соотношениями $\gamma = {{\lambda }_{c}}{\text{/}}\lambda = {{\beta }_{c}}{\text{/}}\beta = {\text{R/}}{{{\text{R}}}_{c}}$ (индексом $с$ отмечены критические значения на границе потери устойчивости). Исходя из заданных величин ${{\operatorname{R} }_{c}}$ и ${{\beta }_{c}}$, построим зависимость собственной частоты $\omega $ от волнового числа $m$ для наиболее неустойчивой моды течения в отсутствие внешнего трения ($\lambda = 0$). После этого в соответствии с известным свойством собственных значений в данной задаче [12, 13] найдем критическое волновое число ${{m}_{с}}$, при котором достигается максимальное значение инкремента данной моды, совпадающее с критическим значением безразмерного параметра внешнего трения: ${{\lambda }_{с}} = \mathop {\max }\limits_m \left[ {\operatorname{Im} \omega (m;{{{\text{R}}}_{c}},{{\beta }_{c}})} \right] = \operatorname{Im} \omega ({{m}_{с}}{\text{;}}{{{\text{R}}}_{c}},{{\beta }_{c}})$. Необходимые в дальнейшем результаты расчета критических значений ${{m}_{c}}$, ${{\lambda }_{c}}$ и $\operatorname{Re} \omega {\kern 1pt} {\kern 1pt} ({{m}_{c}})$ для течений равновесными профилями скорости P1 и P2 показаны в таблице 1. Как и в случае плоскопараллельной модели течения с профилем скорости P1, рассмотренной в [16], задано критическое значение числа Рейнольдса ${{{\text{R}}}_{c}} = 60$. Расчеты показали, что при ${\text{R}} > 60$ максимальный инкремент неустойчивости в отсутствие внешнего трения ($\lambda = 0$) слабо зависит от ${\text{R}}$ и близок к “невязкому” пределу.
Таблица 1.
Результаты вычисления критических параметров ${{m}_{c}}$, ${{\lambda }_{c}}$ и $\operatorname{Re} \omega {\kern 1pt} {\kern 1pt} ({{m}_{c}})$ для двух кольцевых баротропных течений с профилями скорости P1 и P2
| ${{{\text{R}}}_{c}}$ | ${{\beta }_{c}}$ | ${{m}_{c}}$ | ${{\lambda }_{c}}$ | $\operatorname{Re} \omega {\kern 1pt} {\kern 1pt} ({{m}_{c}})$ | |
|---|---|---|---|---|---|
| P1 | 60 | 0 | 6 | ${\text{0}}{\text{.1063}}$ | ${\text{0}}{\text{.3224}}$ |
| P1 | 60 | 0.1 | 6 | 0.09769 | 0.2667 |
| P2 | 60 | 0 | 9 | ${\text{0}}{\text{.1381}}$ | 0.4588 |
| P2 | 60 | 0.3 | 9 | ${\text{0}}{\text{.1096}}$ | ${\text{0}}{\text{.3193}}$ |
Видно, что уменьшение критического значения ${{\lambda }_{c}}$ для профиля P1 при переходе от $\beta = 0$ к ${{\beta }_{c}} = 0.1$ составляет приблизительно $8$%. В то же время, для профиля P2 переход от $\beta = 0$ к ${{\beta }_{c}} = 0.3$ демонстрирует существенное влияние $\beta $-эффекта на линейную неустойчивость. Отметим, что во всех примерах азимутальные фазовые скорости возбуждаемых волн $\Omega $ малы.
Для исследования нелинейного развития баротропной неустойчивости кольцевого течения уравнения (1) с граничными условиями прилипания и непротекания на стенках канала решались численно псевдоспектральным методом, описанным в [15–18]. Для вычисления спектров использовался алгоритм быстрого преобразования Фурье (FFT), который включал в себя 128 комплексных гармоник. Совместная система уравнений для комплексных амплитудных профилей гармоник ${{\hat {\psi }}_{m}}$, ${{\hat {\zeta }}_{m}}$ и азимутальной компоненты средней скорости ${{\bar {v}}_{\theta }}(r,t)$ с граничными условиями (4) приведена в [17]. Дискретизация по радиальному направлению содержала 240 равноотстоящих узлов. Для подавления эффектов алиасинга в усеченном разложении (3) полагалось $K = 42$ [17, 18]. Основные расчеты проводились для течений с двумя указанными выше равновесными профилями азимутальной скорости P1 и P2 в кольцевом канале с параметрами $b = 4$ и ${{r}_{0}} = 6.5$ при критическом значении числа Рейнольдса ${{{\text{R}}}_{c}} = 60$.
Как отмечалось во Введении, рождение дополнительных к основной волне спектральных компонент с различной фазовой скоростью и возникновение динамического хаоса при умеренных надкритичностях возможно в течениях со сложным профилем скорости, к которым относятся двухструйные течения, описанные в п. 1. Переход к динамическому хаосу изучался по той же схеме, которая использовалась в [15, 16] для плоскопараллельных баротропных течений и в [17, 18] для кольцевых течений. Как и в п. 1, в этих работах принималось, что единственным изменяемым параметром является скорость течения, связанная с надкритичностью $\gamma $. С учетом результатов линейной теории увеличение надкритичности $\gamma = {{\lambda }_{c}}{\text{/}}\lambda $ от порогового значения $\gamma = 1$ проводилось посредством скачкообразного уменьшения $\lambda $ шаг за шагом с малым декрементом $\Delta \lambda = 0.005$. После каждого шага связанные между собой безразмерные параметры $\gamma $, $\lambda $, $\beta $ и ${\text{R}}$ поддерживались постоянными в течение интервала времени $\Delta t = 2000$ вплоть до следующего шага. Выбор $\Delta t$ обеспечивал переход к новому установившемуся режиму генерации цепочек структур с замкнутыми линиями тока. Начальные условия после каждого скачка параметров соответсвовали значениям полей перед скачком с добавлением малых шумовых “затравок” [15]. В рамках данной схемы строились эволюционные диаграммы, описывающие эволюцию интегральных амлитуд гармоник азимутальной скорости ${{B}_{m}} = {{\left( {\int_{{{r}_{0}} - b}^{{{r}_{0}} + b} {{{{\left| {{{v}_{{\theta m}}}} \right|}}^{2}}} dr} \right)}^{{1/2}}}$, где $m$ – номер пространственной гармоники, ${{v}_{{\theta m}}} = - \partial {{\hat {\psi }}_{m}}(r,t){\text{/}}\partial r$ – амплитудные профили гармоник азимутальной скорости [17]. Такие диаграммы были построены для плоскопараллельных течений в [15, 16] и для кольцевых течений в [17, 18]. С помощью этих диаграмм, дополненных вычислением частотно-волновых спектров продольной скорости ${{v}_{\theta }}(r,\theta ,t)$ на фиксированных уровнях по $r$, выделялись основные режимы генерации волн и структур при переходе к динамическому хаосу. Расчеты показали, что как в плоскопараллельных, так и в кольцевых течениях на начальной стадии после потери устойчивости обычно возбуждается периодическая нелинейная волна, после чего происходит чередование мультигармонических режимов с дискретным частотно-волновым спектром, для которых характерно наличие гармоник с различными фазовыми скоростями. При переходах между ними обычно происходило уменьшение номера доминирующей гармоники спектра. Возникновение динамического хаоса характеризуется рождением квазисплошного частотно-волнового спектра (в котором расстояние по частоте между компонентами уменьшается с ростом длины реализации во времени). В зависимости от профиля скорости течения и его параметров существование эйлеровского хаоса возможно в ограниченной области по $\gamma $ (с последующим возобновлением мультигармонических режимов) либо во всей расчетной области по $\gamma $, размеры которой ограничены применимостью выбранной схемы численного решения. В данной работе описанные выше схемы исследования перехода к хаосу применяются к двухструйным течениям с профилями скорости P1 и P2.
Эффективным методом идентификации областей перемешивания и хаотической адвекции является вычисление пространственного распределения конечно-временного ляпуновского показателя (КВЛП), характеризующего экспоненциальное “разбегание” траекторий жидких частиц [14, 18]. Систему уравнений, описывающую кольцевое струйное течение, следует дополнить уравнениями движения жидких частиц, переносящих пассивную примесь. Это позволяет получить распределение КВЛП для всего течения. Уравнения движения частиц пассивной примеси в цилиндрических координатах $(r,\theta )$ имеют вид [17, 18]
(6)
$\frac{{dr}}{{dt}} = \frac{1}{r}\frac{{\partial{ \tilde {\psi }}}}{{\partial \theta }},\,\,\,\,\frac{{d\theta }}{{dt}} = \frac{1}{r}{{\bar {v}}_{\theta }}(r,t) - \frac{1}{r}\left( {\frac{{\partial{ \tilde {\psi }}}}{{\partial r}}} \right).$Производя варьирование траекторий жидких частиц в окрестности основных траекторий $\left[ {r(t),\,\theta (t)} \right]$, определенных уравнениями (6) при различных начальных условиях, получим следующую систему уравнений для вариации траектории по радиальному и азимутальному направлениям:
(7)
$\frac{{d\delta r}}{{dt}} = \left( { - \frac{1}{{{{r}^{2}}}}\frac{{\partial{ \tilde {\psi }}}}{{\partial \theta }} + \frac{1}{r}\frac{{{{\partial }^{2}}\tilde {\psi }}}{{\partial \theta \,\partial r}}} \right)\delta r + \frac{1}{r}\frac{{{{\partial }^{2}}\tilde {\psi }}}{{\partial {{\theta }^{2}}}}\delta \theta ,$(8)
$\begin{gathered} \frac{{d\delta \theta }}{{dt}} = \left( { - \frac{1}{{{{r}^{2}}}}{{{\bar {v}}}_{\theta }}(r,t) + \frac{1}{r}\frac{{\partial {{{\bar {v}}}_{\theta }}(r,t)}}{{\partial r}} + } \right. \\ \left. { + \,\,\frac{1}{{{{r}^{2}}}}\frac{{\partial{ \tilde {\psi }}}}{{\partial r}} - \frac{1}{r}\frac{{{{\partial }^{2}}\tilde {\psi }}}{{\partial {{r}^{2}}}}} \right)\delta r - \frac{1}{r}\left( {\frac{{{{\partial }^{2}}\tilde {\psi }}}{{\partial r\partial \theta }}} \right)\delta \theta . \\ \end{gathered} $Конечно-временной ляпуновский показатель $h$ определен выражением [14]
(9)
$h = \frac{1}{T}\ln \left[ {\frac{{\left| {\delta \vec {l}(T)} \right|}}{{\left| {\delta \vec {l}(0)} \right|}}} \right]\left( {\left| {\delta \vec {l}} \right| = \sqrt {{{{\left( {\delta r} \right)}}^{2}} + {{r}^{2}}{{{\left( {\delta \theta } \right)}}^{2}}} } \right),$Для анализа распространения частиц пассивной примеси, их начальное распределение задавалось в эллиптических областях, внешняя граница которых описывается уравнением
(10)
$\frac{{{{{\left( {\theta - {{\theta }_{0}}} \right)}}^{2}}}}{{\Delta {{\theta }^{2}}}} + \frac{{{{{\left( {r - {{r}_{0}}} \right)}}^{2}}}}{{\Delta {{r}^{2}}}} = 1,$ПЕРЕХОД К ХАОСУ И РАСПРОСТРАНЕНИЕ ПАССИВНОЙ ПРИМЕСИ
Расчеты, проведенные для кольцевого струйного течения с равновесным профилем скорости P1, показали, что при $\beta = 0$ в области $1 < \gamma < $ 1.89 возбуждается строго периодическая нелинейная волна с волновым числом $m = 6$ (значение ${{\lambda }_{c}}$ из Таблицы согласуется результатами численного решения). В интервале $1.89 < \gamma < 3.15$ получены два мультигармонических режима с дискретным частотно-волновым спектром и различными фазовыми скоростями пространственно-временных гармоник.
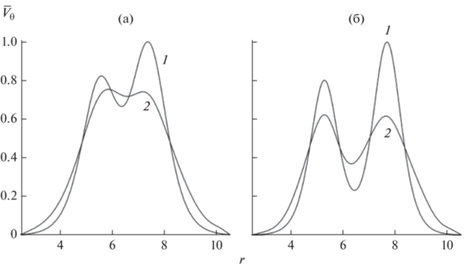
На рис. 2 показан мгновенный снимок линий тока и результаты вычисления КВЛП в мультигармоническом режиме, возникающем при $\gamma = $ 2.29. Как и в плоскопараллельном течении с равновесным профилем скорости P1, в кольцевом струйном течении с данным профилем скорости генерируются две цепочки структур с замкнутыми линиями тока, находящиеся на краях струи. Линии тока на рис. 2а показаны в системе отсчета внутренней (ближайшей к внутренней границе кольца) цепочки структур, имеющей угловую скорость $\Omega = 0.087$ с вращением против часовой стрелки. Следует отметить, что замкнутые линии тока внешней цепочки, которая имеет угловую скорость $\Omega = $0.047, оказываются немного “сжатыми” по радиальной координате по сравнению с их изображением в сопутствующей внешней цепочке системе отсчета. Число структур с замкнутыми линиями тока соответствует двум главным пикам в частотно-волновом спектре, построенном на окружности $r = 5.17$ (аналогично см. [17, 18]). Вычисление КВЛП проводилось путем решения уравнений (6) – (9) в лабораторной системе отсчета на сетке начальных координат частиц [$r(0)$, $\theta (0)$], содержащей $200 \times 200$ равноотстоящих узлов в сегменте кольцевого течения $ - 4 < r(0) - {{r}_{0}} < 4$, $ - \pi {\text{/}}4 < \theta (0) - {{\theta }_{*}} < \pi {\text{/}}4$ (${{\theta }_{*}}$ – азимутальный угол, определяющий ориентацию сегмента). Начальный момент $t = 0$ при вычислении КВЛП выбирался в установившемся режиме генерации цепочек. Распределение КВПЛ на рис. 2б, полученное на интервале $T = 500$, показано в цилиндрических координатах [$r(0)$, $\theta (0)$] в шкале градаций серого (белый цвет отображает максимальное значение, черный – минимальное). Распределение КВЛП имеет мозаичную структуру с хаотическим чередованием светлых и темных точек. Это позволяет предположить, что данное множество является квазифрактальным [20]. Узкие светлые области, содержащие максимальные значения КВЛП, опредедяют границы стохастических слоев, в которых происходит хаотическое перемешивание частиц примеси. Светлые области на рис. 2б показывают стохастические слои, окаймляющие границы замкнутых линий тока, как они выглядят в сопровождающих цепочки системах отсчета [14]. Показано, что функция распределения числа частиц с начальными координатами в узлах сетки по значениям соответствующего им показателя $f(h)$ [14, 18] имеет несимметричную колоколообразную форму с максимумом при $h \approx 0.023$ и спаданием по краям в два раза при $h \approx 0.013$ и $h \approx 0.026$. Фактически $f(h)$ характеризует частоту появления различных значений показателя в момент $t = T$.
Рис. 2.
Мгновенный снимок линий тока в системе отсчета “внутренней” цепочки структур (а) и распределение КВЛП при $T = 1000$ на сетке $200 \times 200$ точек в системе координат [$r(0)$, $\theta (0)$] (б) в струйном течении с профилем скорости P1 при ${{{\text{R}}}_{c}} = 60$, $\beta = 0$, $\gamma = 2.29$ (здесь и далее на рис. 3 и 4 тоновые изображения даны в градациях серого; $x$ и $у$ – декартовы координаты).
Чтобы описать эволюцию распределения пассивной примеси, уравнения движения частиц-трассеров (6) решались в лабораторной системе отсчета (переход в сопровождающую систему отсчета приводит к повороту мгновенного распределения частиц в целом). Результаты вычислений на временнных интервалах, близких к $T$, согласуются с полученными в [18] для реверсивной струи. Когда частицы-трассеры располагались в эллиптической области (10), покрывающей один из замкнутых контуров на рис. 2б, в хаотическом перемешивании учавствовали только частицы, близкие к внешней границе этой эллиптической области, тогда как основная масса частиц внутри нее оставалась неподвижной. В данном случае отсутсвует заметный поперечный к потоку (боковой) перенос частиц примеси, которому препятствует барьер, созданный примыкающим к границам замкнутых линий тока круговым течением [2, 18]. Расчеты подтвердили наличие автомодельных степенных законов зависимости среднего смещения частиц по азимутальной координате $\theta $ и его дисперсии от времени, характерных для аномального танспорта (аналогично см. [15–18]).
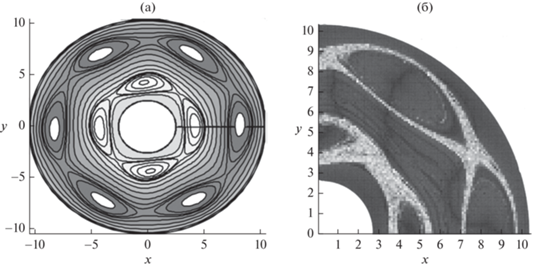
Эйлеровский динамический хаос возникает скачкообразно при $\gamma > 3.15$. На рис. 3а представлен мгновенный снимок линий тока, полученный в системе отсчета вращающейся с угловой скоростью внутренней цепочки в режиме динамического хаоса ($\gamma = 3.39$). Сравнение линий тока на рис. 2а и 3а показывает, что при увеличении надкритичности модуляция замкнутых линий тока возрастает. На внутренней цепочке можно видеть составные структуры, аналогичные рассмотренным в [17]. Угловые фазовые скорости внутренней и внешней цепочек имеют значения $\Omega = $0.086 и $\Omega = $0.043. При расчетах КВЛП в хаотическом режиме ($\gamma = $3.39) равномерная сетка с начальными координатами частиц [$r(0)$, $\theta (0)$] содержала $200 \times 400$ равноотстоящих узлов по $r(0)$ и $\theta (0)$, расположенных по всей окружности кольцевого канала. Как и на рис. 2б, распределение КВЛП на рис. 3б построено в цилиндрической системе координат [$r(0)$, $\theta (0)$]. Из рис. 3б видно, что область лагранжева хаоса охватывает не только внутреннюю цепочку структур с линиями тока, показанными на рис. 3а, но и прилегающее к границе замкнутых линий тока круговое течение. Этот результат согласуются с утверждением работы [14], согласно которому возникновение эйлеровского динамического хаоса происходит одновременно с проникновением лагранжева хаоса вовнутрь замкнутых линий тока. Аналогичный эффект отмечался в [18] для реверсивной струи. На внешней цепочке видны “провалы” КВЛП в центральной части замкнутых линий тока. Это можно объяснить более слабой нестационарностью внешней цепочки по сравнению с внутренней. Между цепочками находится темная кольцевая область с близкими к нулю значениями $h$, в которой перемешивание отсутствует. В данном случае функция распределения числа узлов сетки по значениям показателя $f(h)$ имеет максимум при $h \approx 0.015$ и спадает в два раза при $h \approx 0.0071$ и $h \approx 0.024$.
Рис. 3.
Мгновенный снимок линий тока в системе отсчета внутренней цепочки структур (а), распределение КВЛП при $T = 500$ на сетке $200 \times 400$ точек в системе координат [$r(0)$, $\theta (0)$] (б) и мгновенное распределение частиц-трассеров в режиме эйлеровского динамического хаоса (в) при ${{{\text{R}}}_{c}} = 60$, $\beta = 0$, $\gamma = $3.39. Темные эллиптические области на линиях тока показывают локализацию частиц-трассеров в начальный момент $t = 0$.

Образование обширных областей лагранжева хаоса приводит к качественным изменениям в распространении изначально локализованной пассивной примеси. Расчеты проводились в лабораторной системе отсчета для частиц-трассеров с начальными координатами в темных эллиптических областях, показанных на рис. 3а. На рис. 3в представлено мгновенное распределение частиц-трайсеров, полученное в конце интервала времени $T = 500$ при равномерном начальном распределении 7897 трассеров в каждой из эллиптических областей. Как видно из рис. 3в, трассеры равномерно заполняют область лагранжева хаоса, покрывающую внутреннюю цепочку на рис. 3б. Распределение частиц во внешней цепочке локализовано в окрестности границ замкнутых линий тока, что также согласуется с распределением КВЛП на рис. 3б. При этом наиболее значительно уменьшается число трассеров в узком внешнем слое эллиптической области вблизи границы замкнутых линий тока. На месте темной полосы в серединной части кольцевого канала на изображении КВЛП видна светлая кольцевая область, в которой частицы отсутствуют. Расчеты, проведенные с введением в поток одного из двух пятен примеси, отмеченных на рис. 2б, показали, что каждое из них определяет показанное на рис. 3в распределение примеси со своей стороны от границы этой полосы. Таким образом, полоса с близким к нулю КВЛП играет роль барьера, препятствующего распространению частиц примеси в поперечном к потоку направлении [1, 2, 18].
Полученные выше результаты по переходу к эйлеровскому динамическому хаосу в кольцевом течении с профилем скорости P1 при $\beta = 0$ можно сравнить с представленными в работе [16] для плоскопараллельной модели течения с таким же профилем скорости. Следует иметь в виду, что в плоской модели с периодическими граничными условиями число структур на периоде течения можно варьировать, тогда как в кольцевом течении оно однозначно определено решением нелинейной системы уравнений. В работе [16] число структур, возбуждаемых после превышения порога возникновения неустойчивости при $\beta = 0$, принималось равным 7, тогда как в кольцевом течении с профилем скорости P1 сначала возникает цепочка из 6-ти структур (см. табл. 1). Как видно из рис. 3а, в хаотическом режиме число одиночных структур с замкнутыми линиями тока в цепочках равно 5. Согласно [16], при $\beta = 0$ в плоскопараллельном течении динамический хаос возникает при переходе надкритичности через пороговое значение $\gamma = 1.81$, которое в 1.9 раза меньше указанного выше для течения в кольце. Таким образом, даже при близких периодах структур и одинаковых равновесных профилях скорости при переходе к кольцевому течению порог возникновения динамического хаоса сдвигается в сторону более высоких надкритичностей. В расчетах для плоского течения с профилем скорости P1 при $\beta = 0.4$ порог возникновения эйлеровского хаоса возрастал до $\gamma = 2.15$ [16]. В кольцевом течении с таким же профилем азимутальной скорости уже при $\beta = 0.1$ режим динамического хаоса не был обнаружен в интервале надкритичностей вполоть до ${{\gamma }_{{\max }}} = 6.0$. Поскольку в соответствии с Таблицей при $\beta = 0.1$ бета-эффект слабо влияет на линейную неустойчивость, можно сделать вывод, что при переходе от плоского течения к кольцевому усиливается стабилизирующее воздействие $\beta $-эффекта на переход к динамическому хаосу эйлеровских полей. Таким образом, неусточивость кольцевого течения с профилем скорости P1 оказывается слишком слабой для возникновения динамического хаоса при существенном влиянии бета-эффекта на линейную неустойчивость. В связи с этим был рассмотрен профиль скорости P2, который характеризуется более сильной неустойчивостью в отсутствие внешнего трения. Отметим, что в кольцевом течении с профилем скорости P1 даже при существенном воздействии бета-эффекта на линейную неустойчивость (например, при $\beta = 0.25$) были получены мультигармонические режимы, которые приводят к локализации лагранжева хаоса в окрестности границ замкнутых линий тока, как это показано на рис. 2б. В этом случае возможна азимутальная хаотическая адвекция (включая аномальную диффузию), однако вдоль цепочек переносятся только частицы узкого внешнего слоя эллиптического пятна пассивной примеси, покрывающего структуру с замкнутыми линиями тока (подобно тому, как это показано на рис. 3в).
Построение эволюционной диаграммы для амплитуд гармоник ${{B}_{m}}(t)$ и частотно-волновых спектров для струйного течения с профилем скорости P2 проводилось при $\beta = 0.3$. Как видно из Таблицы в данном случае бета-эффект оказывает существенное влияние на величину ${{\lambda }_{с}}$. Показано, что режим периодической нелинейной волны реализуется в интервале надкритичностей $1 < \gamma < $ < 2.0, после чего начинается чередование мультигармонических режимов. Динамический хаос эйлеровских полей возникает скачкообразно при $\gamma > 2.97$. Типичный мговенный снимок линий тока в режиме динамического хаоса ($\gamma = 3.17$) представлен на рис. 4а. Видно, что в системе отсчета внутренней цепочки структур с угловой частотой вращения $\Omega = 0.07$, возбуждаются три цепочки структур с замкнутыми линиями тока. Изучение динамики цепочек с помощью видеофильма показало, что все они демонстрируют квазипериодическое изменение в пространстве и во времени, однако наиболее нестабильной является промежуточная (расположенная в серединной части кольцевого канала) цепочка структур, которая периодически появляется в результате «вспучивания» круговой линии тока. Структуры быстро достигают максимального размера (этот момент показан на рис. 4а), после чего начинают изгибаться в направлении вращения внешней цепочки (на рис. 4а это направление по часовой стрелке). Цикл завершается слиянием структур с круговой линией тока в результате перемещения их центров в сторону уменьшения $r$. Рождение структур синхронизовано с внутренней цепочкой, а кратковременное азимутальное перемещение их центров – с внешней. Этим можно объяснить тот факт, что промежуточная цепочка хорошо видна в системе отсчета внутренней цепочки и сглаживается в системе отсчета внешней дорожки (имеющей угловую частоту $\Omega = 0.0275$).
Рис. 4.
Мгновенный снимок линий тока в системе отсчета внутренней цепочки структур (а), распределение КВЛП при $T = 1000$ на сетке $400 \times 500$ точек в системе координат [$r(0)$, $\theta (0)$] (б) и мгновенные распределения частиц-трассеров в режиме эйлеровского динамического хаоса, возникающие при локализации примеси в промежуточной (в) и внутренней цепочках структур (г) в струйном течении с профилем скорости P2 при ${{{\text{R}}}_{c}} = 60$, $\beta = 0.3$, $\gamma = 3.17$. Темные эллиптические области на линиях тока показывают начальную локализацию частиц-трассеров в начальный момент $t = 0$.

Распределение КВЛП в режиме динамического хаоса, рассчитанное с помощью формул (6)–(9) на равномерной сетке начальных значений координат частиц [$r(0)$, $\theta (0)$] с числом узлов $400 \times 500$, показано на рис. 4б (построение в цилиндрической системе координат [$r(0)$, $\theta (0)$]). Видно, что область лагранжева хаоса покрывает промежуточную цепочку структур и проникает в пространство между замкнутыми линиями тока внешней цепочки. Кроме того, кольцевая область лагранжева хаоса с более низкими значениями $h$ охватывает внутреннюю цепочку структур. В данном случае функция распределения числа узлов сетки по значениям показателя $f(h)$ имеет максимум при $h \approx 0.025$ и спадает в два раза при $h \approx 0.0085$ и $h \approx 0.034$. Расчеты распространения пассивной примеси проводились раздельно для двух равномерных распределений частиц-трассеров в эллиптических областях (10), расположенных во внешней и внутренней цепочках (они показаны темными пятнами на рис. 4а). На рис. 4в изображено мгновенное распределение частиц-трассеров, полученное при локализации эллиптической области с равномерным распределением 3970 частиц в промежуточной цепочке. Время движения трассеров совпадает с временным интервалом $T = 1000$, принятым при построении распределения КВЛП на рис. 4б. Видно, что распределение частиц имеет хаотический характер и почти полностью заполняет течение. Наиболее плотное кольцо частиц находится в серединной части кольцевого канала, где отмечается наибольшая концентрация высоких значений КВЛП. Более низкая концентрация частиц-трассеров наблюдается во внутренней и внешней цепочках. Частицы отсутствуют внутри замкнутых линий тока внешней цепочки, нестационарность которой наименее выражена. Отметим, что пустоты в распределении частиц повторяют форму границ замкнутых линий тока в системе отсчета, сопутствующей данной цепочке, что соответствует распределению КВЛП на рис. 4б. На рис. 4г представлено мгновенное распределение частиц-трассеров, которые в начальный момент находятся в эллиптической области, расположенной на замкнутых линиях тока внутренней цепочки и содержащей 5114 трассеров. В данном случае также происходит полное размывание пятна с распространением примеси по всему кольцевому течению, однако наибольшая плотность частиц наблюдается в кольцевой области, покрывающей внутреннюю цепочку. За пределами этой области оказывается относительно небольшое число частиц. Поскольку области лагранжева хаоса во внутренней и промежуточной цепочках не перекрываются, можно предположить, что прохождение примеси через разделяющую их границу возможно благодаря эффекту поперечного к потоку (бокового) переноса [2, 18]. Таким образом, результаты расчета мгновенного распределения частиц-трассеров, представленные на рис. 4в и 4г, согласуются с распределением КВЛП на рис. 4б.
Оценим возможность реализации перехода к динамическому хаосу и для лабораторного кольцевого течения с профилем скорости P1 в отсутствие $\beta $-эффекта, подразумевая создание этого течения МГД-методом [12, 13]. В качестве исходных параметров зададим ${{\operatorname{R} }_{c}} = 60$, $\beta = 0$, ${{\lambda }_{с}} = 0.1063$, $\nu = 0.01$ см2/с и размерностный серединный радиус кольца ${{r}_{0}}L = $ 14 см. Поскольку ${{r}_{0}} = 6.5$, находим пространственный масштаб $L = 2.15$ см, ширину канала $8L = $ 17.2 см и внутренний радиус кольца $({{r}_{0}} - 4)L = $ 5.38 см. Из формулы для числа Рейнольдса находим ${{U}_{с}} = \nu {{\operatorname{R} }_{c}}{\text{/}}L$ = = 0.28 см/c. Используя выражение для размерностного коэффициента внешнего трения [12, 13] $\lambda {\kern 1pt} *{\kern 1pt} * = 2\nu {\text{/}}{{H}^{2}}$, где $H$ – толщина жидкого слоя и формулу ${{\lambda }_{c}} = L\lambda {\kern 1pt} *{\kern 1pt} *{\text{/}}{{U}_{c}}$, получим толщину жидкого слоя $H = \sqrt {2\nu L{\text{/}}\left( {{{U}_{c}}{{\lambda }_{c}}} \right)} $ = 1.2 см. Рассмотренный выше режим динамического хаоса (см. рис. 3) возникает при $U = 3.39{{U}_{c}} = 0.95$ см/с. Текущая размерностная единица времени $L{\text{/}}U = 2.26$ с. Аномальный перенос в мультигармоническом режиме с линиями тока на рис. 2а и лагражевым хаосом на рис. 2б происходит при $U = 2.29{{U}_{c}} = 0.64$ см/с. Таким образом, оценки допускают возможность реализации режима динамического хаоса и сопутствующего ему распространения локализованной примеси в лабораторном течении.
Оценим возможность динамического хаоса и хаотической адвекции в кольцевом течении с профилем скорости P2 для погодного слоя земной атмосферы. Выберем размерностный радиус кольца из условия равенства длины соответствующей окружности $2\pi {{r}_{0}}L$ длине окружности на поверхности Земли $2\pi {{R}_{E}}\cos \varphi $, где ${{R}_{Е}}$ – радиус Земли, $\varphi $ – широта места. Отсюда находим пространственный масштаб нормировки сдвига скорости $L = $$\left( {{{R}_{E}}{\text{/}}{{r}_{0}}} \right)\cos {\kern 1pt} \varphi $. Полагая ${{R}_{Е}} = 6371$ км [11, 12], $\varphi = 67.5^\circ $, ${{r}_{0}} = 6.5$, получим $L = $ 375 км, ширину кольцевого канала $8L = $ 3000 км и внутренний радиус кольца $({{r}_{0}} - 4)L = $ 937.5 км. Исходя из принятого в расчетах ${{\beta }_{c}} = 0.3$, найдем критическую скорость ${{U}_{c}} = \beta {\kern 1pt} *{\kern 1pt} *{{L}^{2}}{\text{/}}{{\beta }_{c}} = 4.1$ м/с, где β** = $ = 2{{\Omega }_{0}}\cos (\varphi ){\text{/}}{{R}_{E}} = 2.29 \times {{10}^{{ - 11}}}\cos (\varphi )$ м–1 с–1 (Ω0 = ($ = 7.292 \times {{10}^{{ - 5}}}$ рад/c – угловая частота вращения Земли [11, 12]). Рассмотренный в данной работе хаотический режим (см. рис. 4) возможен при скорости течения $U = \gamma {{U}_{c}} \approx 13$ м/c и значении размерностного коэффициента внешнего трения $\lambda {\kern 1pt} *{\kern 1pt} * = {{U}_{c}}{{\lambda }_{c}}{\text{/}}L = 1.2 \times {{10}^{{ - 6}}}$ с–1. Размерностная единица времени в хаотическом режиме $L{\text{/}}\left( {\gamma {{U}_{c}}} \right) = 2.88 \times {{10}^{4}}$ c. Таким образом, приведенные оценки допускают возможность реализации рассмотренного течения в атмосфере.
ЗАКЛЮЧЕНИЕ
В данной работе изучена хаотическая адвекция локализованной пассивной примеси при переходе к динамическому хаосу в баротропных течениях с модельными двухструйными профилями скорости, порождающими цепочки волновых структур с замкнутыми линиями тока. В качестве индикатора областей лагранжева хаоса (стохастического перемешивания) использовано распределение конечно-временного показателя Ляпунова, построенное в системе начальных координат жидких частиц. Показано, что при одинаковом профиле скорости порог возникновения эйлеровского динамического хаоса в кольцевом течении сдвигается в сторону более высоких надкритичностей по сравнению с плоскопараллельной моделью. Кроме того, в этом случае обнаружено усиление стабилизирующего влияния бета-эффекта на возникновение эйлеровского хаоса.
В мультигармоническом режиме, предшествующем динамическому хаосу, области лагранжева хаоса и стохастические слои смешения локализуются в окрестности границ замкнутых линий тока, как эти границы видны в сопутствующих этим цепочкам системах отсчета. В данном случае только небольшая часть эллиптического пятна пассивной примеси распределяется по стохастическим слоям вдоль всей цепочки структур. Установлено, что качественные изменения в распространении пассивной примеси происходят в режиме эйлеровского динамического хаоса, переход к которому связан с образованием обширных областей лагранжева хаоса. Основной вывод состоит в том, что в режиме эйлеровского хаоса становится возможным распределение локализованной в начальный момент примеси по всему объему течения. Распространение примеси существенным образом зависит от профиля скорости. Так, для течения с профилем скорости P1 в отсутствие бета-эффекта получено равномерное распределение частиц-тассеров в кольцевой области, охватывающей внутреннюю цепочку структур, и распространение примеси в пределах узких стохастических слоев вдоль внешней цепочки. Показано, что возникновение эйлеровского хаоса в кольцевом течении с профилем скорости P2 при выраженном влиянии бета-эффекта приводит к образованию нестабильной промежуточной цепочки структур, в результате чего область лагранжева хаоса охватывает почти весь объем течения. В этом случае при локализации эллиптического пятна пассивной примеси в пределах промежуточной цепочки происходит почти равномерное распределение примеси по всему объему течения. Локализация примеси во внутренней цепочке структур приводит к ее равномерному распределению вдоль этой цепочки, за пределы которого проникает относительно небольшая часть частиц примеси. Представленные результаты могут быть использованы для интерпретации данных натурных наблюдений и анализа результатов вычислений в рамках комплексных прогностический моделей климата и распространения загрязнений, а также при постановке лабораторных экспериментов.
Работа профинансирована Министерством науки и высшего образования РФ в рамках государственного задания ИПФ РАН, проект № 0030-2021-0011.
Список литературы
Rogerson A.M., Miller P.D., Pratt L.J., Jones C.K.R.T. Lagrangian motion and fluid exchange in a barotropic meandering jet // J. Phys. Oceanogr. 1999. V. 29. P. 2635–2655.
Wiggins S. The dynamical system approach to Lagrangian transport in oceanic flows // Ann. Rev. Fluid Mech. 2005, V. 37. P. 295–328.
Del-Castillo-Negrete D. Asymmetric transport and non-Gaussian statistics of passive scalars in vortices in shear // Phys. Fluids A. 1998. V. 10. № 3. P. 576–594.
Кошель К.В., Пранц С.В. Хаотическая адвекция в океане. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2008. 360 с.
Aref H. et al. Frontiers of chaotic advection // Rev. Mod. Phys. 2017. V. 89. № 2. P. 025007. https://doi.org/10.1103/RevModPhys.89.025007
Solomon T.H., Weeks E.R., Swinney H.L. Chaotic advection in a twodimensional flow: Levy flights and anomalous diffusion // Physica D. 1994. V. 76. P. 70–84.
Vasavada A.R., Showman A.P. Jovian atmospheric dynamics: an update after Galileo and Cassini // Rep. Prog. Phys. 2005. V. 68. P. 1935–1996. https://doi.org/10.1088/0034-4885/68/8/r06
Young R.M.B., Read P.L., Wang Y. Simulating Jupiter’s weather layer. Part I: Jet spin-up in a dry atmosphere // Icarus. 2019. V. 326. P. 225–252. https://doi.org/10.1016/j.icarus.2018.12.005
Nakano H., Hasumi H.A series of zonal jets embedded in the broad zonal flows in the Pacific obtained in eddy-permitting ocean general circulation models // J. Phys. Oceanogr. 2005. V. 35(4). P. 474–488.
Maximenko N.A., Bang B., Sasaki H. Observational evidence of alternating zonal jets in the world ocean // Geophys. Res. Lett. 2005. V. 32. L12607. https://doi.org/10.1029/2005GL022728
Педлоски Дж. Геофизическая гидродинамика. Т. 2. Перевод с англ. М: Мир, 1984. 398 с.
Должанский Ф.В. Основы геофизической гидродинамики. М: Физматлит, 2011. 264 с.
Должанский Ф.В., Крымов В.А., Манин Д.Ю. Устойчивость и вихревые структуры квазидвумерных сдвиговых течений // УФН. 1990. Т. 160. № 7. С. 1–47.
Finn J.M., Del-Castillo-Negrete D. Lagrangian chaos and Eulerian chaos in shear flow dynamics // Chaos. 2001. V. 11. № 4. P. 816–832.
Reutov V.P., Rybushkina G.V. Anomalous transport of a passive scalar at the transition to dynamical chaos in a barotropic shear layer // Eur. J. Mech. /B Fluids. 2019, V. 74(3). P. 211–218. https://doi.org/10.1016/j.euromechflu.2018.11.017
Реутов В.П., Рыбушкина Г.В. Нестационарные цепочки волновых структур и аномальный перенос пассивной примеси в баротропном струйном течении // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 6. С. 201–210. https://doi.org/10.31857/S0002-3515556201-210
Reutov V.P., Rybushkina G.V. Transition to the dynamical chaos and anomalous transport of a passive scalar in the annular Kolmogorov flow // Phys. Fluids. 2020. V. 32. P. 106601. https://doi.org/10.1063/5.0023254
Reutov V.P., Rybushkina G.V. Dynamical chaos and lateral transport of a passive scalar in the annular reverse jet flow. Russian Journal of Nonlinear Dynamics. 2021. V. 17. № 3. P. 263–274. https://doi.org/10.20537/nd210302
Liu Y., Wilson C., Green M.A., Hughes C. W. Gulf Stream transport and mixing processes via coherent structure dynamics // Journal of Geophysical Research: Oceans. 2018. V. 123. https://doi.org/10.1002/2017JC013390
Будянский М.В., Пранц С.В., Улейский М.Ю. Хаотическая адвекция в меандрирующем струйном потоке // Нелинейная динамика. 2006. Т. 2. № 2. C. 165–180.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана