Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 5, стр. 504-511
Вертикальный перенос импульса внутренними волнами в сдвиговом потоке при учете турбулентной вязкости и диффузии
А. А. Слепышев *
Морской гидрофизический институт РАН
299011 Севастополь, ул. Капитанская, 2, Россия
* E-mail: slep55@mail.ru
Поступила в редакцию 10.02.2022
После доработки 29.04.2022
Принята к публикации 09.06.2022
- EDN: OSUVED
- DOI: 10.31857/S000235152205011X
Аннотация
В приближении Буссинеска рассматриваются свободные инерционно-гравитационные внутренние волны при учете турбулентной вязкости и диффузии в плоскопараллельном течении, перпендикулярном к направлению распространению волны. Для однородной стратификации и при постоянном сдвиге скорости течения аналитически решается краевая задача для амплитуды вертикальной скорости и находится дисперсионное соотношение. Мнимая часть частоты волны отрицательная, т.е. волна затухает. Определяются вертикальные волновые потоки импульса и скорость стоксова дрейфа частиц жидкости. Учет турбулентной вязкости и диффузии несколько увеличивает вертикальный волновой поток импульса, а скорость стоксова дрейфа, наоборот, уменьшает.
Вертикальный обмен в океане играет ключевую роль в функционировании экосистемы, поэтому исследования механизмов обмена является актуальной задачей. Традиционно процессы переноса по вертикали связывают с мелкомасштабной турбулентностью. Механизмы ее генерации самые разнообразные: обрушение поверхностных и внутренних волн, гидродинамическая неустойчивость течений и приливов, донное трение. Внутренние волны вследствие гидродинамической неустойчивости могут передавать энергию более мелкомасштабным внутренним волнам [1], которые, в свою очередь, вследствие нелинейных взаимодействий передают ее еще в более мелкие масштабы и в конце концов в турбулентность. Так реализуется каскадный механизм передачи энергии от внутренних волн в мелкомасштабную турбулентность. В натурном эксперименте это проявляется в присутствии пятен турбулентности в областях с пониженным числом Ричардсона, меньшим критического [1–5]. Однако турбулентность может поддерживаться внутренними волнами и при отсутствии гидродинамической неустойчивости за счет действия сдвига скорости течения [6]. Это более мягкий режим поддержания турбулентности без обрушения внутренних волн. Захват внутренних волн горизонтальными неоднородностями стратификации и течений приводит к фокусировке внутренних волн, амплитуда волны подрастает вплоть до проявления нелинейных эффектов и диссипации энергии в турбулентность [7]. Аналогичный эффект имеет место при захвате внутренних волн на шельфе, когда волна распространяется в область уменьшения глубины.
Плотностная стратификация в пикноклине сильно подавляет мелкомасштабную турбулентность, в то время как пикноклин является волноводом для внутренних волн. Поэтому актуальным является исследование вклада внутренних волн в вертикальный обмен. Нелинейные эффекты при распространении пакетов внутренних волн проявляются в генерации средних на временном масштабе волны течений [8, 9]. Вертикальная составляющая этих течений на переднем и заднем фронте пакета имеет разные знаки, поэтому интегрального вертикального переноса не происходит. В стратифицированной среде мелкомасштабная турбулентность имеет перемежаемый характер и можно говорить об “эффективном” коэффициенте турбулентного обмена.
Внутренние волны при учете турбулентной вязкости и диффузии затухают [10–13]. Вертикальные волновые потоки импульса $\overline {uw} $, $\overline {vw} $ при этом отличны от нуля [14]. При учете вращения Земли и среднего течения, у которого компонента скорости, перпендикулярная направлению распространения волны зависит от вертикальной координаты, вертикальные волновые потоки импульса отличны от нуля даже при отсутствии турбулентной вязкости и диффузии [15]. При этом мнимая часть частоты волны отлична от нуля и может быть как положительной, так и отрицательной в зависимости от частоты волны и номера моды [15]. В настоящей работе рассматривается влияние турбулентной вязкости и диффузии на эти эффекты. Для этого используется аналитически разрешимая модель однородной стратификации с постоянным сдвигом скорости течения и постоянными коэффициентами турбулентного обмена. Без учета турбулентной вязкости и диффузии ранее было получено в [16], что уравнение для амплитуды вертикальной скорости имеет комплексные коэффициенты, собственная функция комплексная, а частота волны действительная в случае, когда волна распространяется нормально к потоку. Вертикальные волновые потоки импульса отличны от нуля. Компонента скорости стоксова дрейфа, перпендикулярная направлению распространению волны также отлична от нуля [16]. Ниже будет рассматриваться влияние турбулентной вязкости и диффузии на эти эффекты, т.к. турбулентная вязкость и диффузия без учета среднего течения также приводит к вертикальному переносу импульса [14]. Поскольку коэффициенты горизонтального турбулентного обмена на три-четыре порядка больше коэффициентов вертикального турбулентного обмена, то последними пренебрегается.
Постановка задачи. Рассматриваются свободные инерционно-гравитационные внутренние волны на плоскопараллельном стратифицированном течении с вертикальным сдвигом скорости в безграничном бассейне постоянной глубины при учете горизонтальной турбулентной вязкости и диффузии. Коэффициенты горизонтальной турбулентной вязкости $K$ и диффузии $M$ предполагаются не зависящими от пространственных координат и времени. Горизонтальным изменением поля средней плотности и скорости течения на рассматриваемых масштабах пренебрегается. Скорость течения ${{V}_{0}}(z)$ зависит от вертикальной координаты. В линейном приближении решается краевая задача для амплитуды вертикальной скорости и находится дисперсионное соотношение. Во втором порядке по амплитуде волны определяются скорость стоксова дрейфа и вертикальные потоки импульса. Система уравнений гидродинамики в приближении Буссинеска для волновых возмущений имеет вид:
(1)
$\frac{{Du}}{{Dt}} - fv = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial x}} + K{{\Delta }_{h}}u,$(2)
$\frac{{Dv}}{{Dt}} + fu + w\frac{{d{{V}_{0}}}}{{dz}} = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial y}} + K{{\Delta }_{h}}v,$(3)
$\frac{{Dw}}{{Dt}} = - \frac{1}{{{{\rho }_{0}}(0)}}\frac{{\partial P}}{{\partial z}} - \frac{{g\rho }}{{{{\rho }_{0}}(0)}} + K{{\Delta }_{h}}w,$(5)
$\,\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}\, + \frac{{\partial w}}{{\partial z}} = 0,$Граничные условия на поверхности моря ($z = 0$) – условие “твeрдой крышки”, которое отфильтровывает внутренние волны от поверхностных волн [17] и отсутствие тангенциальных напряжений [15, 18]
(7)
$K\frac{{\partial w}}{{\partial x}} = 0,\,\,\,\,K\frac{{\partial w}}{{\partial y}} = 0,\,\,\,\,z = 0.$Граничные условия на дне – условие непротекания и отсутствие тангенциальных напряжений (условие “гладкого скольжения” [9]):
(9)
$K\frac{{\partial w}}{{\partial x}} = 0,\,\,\,\,K\frac{{\partial w}}{{\partial y}} = 0,\,\,\,\,z = - H,$Линейное приближение. Решения в линейном приближении представляются в виде:
(10)
$\begin{gathered} u_{1}^{{}} = {{u}_{{10}}}(z)A{{{\text{e}}}^{{i\theta }}} + {\text{c}}{\text{.c}}{\text{.,}}\,\,\,\,v_{1}^{{}} = {{v}_{{10}}}(z)A{{{\text{e}}}^{{i\theta }}} + {\text{c}}{\text{.c}}{\text{.}}, \\ {{w}_{1}} = {{w}_{{10}}}(z)A{{{\text{e}}}^{{i\theta }}} + {\text{c}}{\text{.c}}{\text{.}},\,\,\,\,{{P}_{1}} = {{P}_{{10}}}(z)A{{{\text{e}}}^{{i\theta }}} + {\text{c}}{\text{.c}}{\text{.}}, \\ {{\rho }_{1}} = {{\rho }_{{10}}}(z)A{{{\text{e}}}^{{i\theta }}} + {\text{c}}{\text{.c}}{\text{.}} \\ \end{gathered} $Подставляя (10) в систему (1)–(5) находим связь амплитудных функций ${{u}_{{10}}},\,\,{{v}_{{10}}},\,\,{{\rho }_{{10}}},\,\,{{P}_{{10}}}\,$ с ${{w}_{{10}}}$ в линейном приближении
(12)
$\begin{gathered} \frac{{{{P}_{{10}}}}}{{{{\rho }_{0}}(0)}} = \frac{i}{k}\left[ {\frac{{\left( {\omega + i{{k}^{2}}K} \right)}}{k}\frac{{d{{w}_{{10}}}}}{{dz}} + } \right. \\ + \,\,\left. {\frac{f}{{\omega + i{{k}^{2}}K}}\left( {i\frac{{d{{V}_{0}}}}{{dz}}{{w}_{{10}}} - \frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}}} \right)} \right], \\ \end{gathered} $(13)
$\begin{gathered} {{\rho }_{{10}}} = - \frac{i}{{\left( {\omega + i{{k}^{2}}M} \right)}}{{w}_{{10}}}\frac{{d{{\rho }_{0}}}}{{dz}}, \\ {{v}_{{10}}} = \frac{1}{{\left( {\omega + i{{k}^{2}}K} \right)}}\left( {\frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}} - i{{w}_{{10}}}\frac{{d{{V}_{0}}}}{{dz}}} \right). \\ \end{gathered} $Функция ${{w}_{{10}}}$ удовлетворяет уравнению
(14)
$\frac{{{{d}^{2}}{{w}_{{10}}}}}{{d{{z}^{2}}}} + a(z)\frac{{d{{w}_{{10}}}}}{{dz}} + b(z){{w}_{{10}}} = 0,$Граничные условия для ${{w}_{{10}}}$ следуют из (6), (8):
Граничные условия (7), (9) выполняются автоматически.
Нелинейные эффекты. Скорость стоксова дрейфа частиц жидкости определяется по формуле [19]:
(17)
${{{\mathbf{u}}}_{s}} = \overline {\left( {\int\limits_{\text{0}}^{\text{t}} {{\mathbf{u}}{\text{d}}\tau } \nabla } \right){\mathbf{u}}} $(18)
${{u}_{{\text{s}}}} = \frac{{{{A}_{1}}A_{1}^{*}}}{k}\left[ {\frac{1}{\omega }\frac{d}{{dz}}\left( {{{w}_{{10}}}\frac{{dw_{{10}}^{*}}}{{dz}}} \right) + {\text{c}}{\text{.c}}.} \right],$Поперечная к направлению распространения волны горизонтальная компонента скорости стоксова дрейфа определяется по формуле
(19)
$\begin{gathered} {{v}_{{\text{s}}}} = {{A}_{1}}A_{1}^{*}\frac{d}{{dz}} \times \\ \times \,\,\left[ {\frac{{{{w}_{{10}}}}}{{\omega \left( {\omega {\kern 1pt} * - i{{k}^{2}}K} \right)k}}\left( {if\frac{{dw_{{10}}^{*}}}{{dz}} - k\frac{{d{{V}_{0}}}}{{dz}}w_{{10}}^{*}} \right)} \right] + {\text{c}}{\text{.c}}{\text{.}} \\ \end{gathered} $Используя (10) найдем вертикальные волновые потоки импульса $\overline {uw} $ и $\overline {vw} $.
(20)
$\overline {uw} = \frac{i}{k}\left| {A_{1}^{2}} \right|\left( {w_{{10}}^{*}\frac{{dw_{{10}}^{{}}}}{{dz}} - w_{{10}}^{{}}\frac{{dw_{{10}}^{*}}}{{dz}}} \right),$(21)
$\overline {vw} = \frac{{w_{{10}}^{*}\left| {A_{1}^{2}} \right|}}{{\left( {\omega + i{{k}^{2}}K} \right)}}\left( {\frac{f}{k}\frac{{d{{w}_{{10}}}}}{{dz}} - i{{w}_{{10}}}\frac{{d{{V}_{0}}}}{{dz}}} \right) + {\text{c}}{\text{.c}}{\text{.}}$При учете горизонтальной турбулентной вязкости и диффузии волновые потоки импульса (20), (21) и поперечная к направлению распространения волны компонента скорости стоксова дрейфа (19) отличны от нуля.
Если турбулентную вязкость и диффузию не учитывать, то при $\frac{{d{{V}_{0}}}}{{dz}} \ne 0$ волновой поток импульса $\overline {uw} $ и поперечная к направлению распространения компонента скорости стоксова дрейфа ${{{v}}_{s}}$ при учете вращения Земли отличны от нуля. Поток импульса $\overline {vw} $ при этом отличен от нуля и при отсутствии течения, но при учете вращения Земли.
Если не учитывать ни вращение Земли, ни турбулентную вязкость и диффузию, то при $\frac{{d{{V}_{0}}}}{{dz}} \ne 0$ волновые потоки импульса (20), (21) нулевые, а поперечная к направлению распространения компонента скорости стоксова дрейфа Vs(19) отлична от нуля.
Нормирующий множитель $\left| {{{A}_{1}}} \right|$ находится по известной величине максимальной амплитуды вертикальных смещений. Для этого выразим вертикальное смещение $\zeta $, используя соотношение $\frac{{d\zeta }}{{dt}} = w$:
Отсюда следует
Результаты расчетов. Уравнение (14) допускает точное аналитическое решения для частного случая однородной стратификации и постоянного сдвига скорости, который мы и рассмотрим. В этом случае $N = {\text{const}}$, $\frac{{d{{V}_{0}}}}{{dz}} = {{V}_{{00}}} = {\text{const}}$, ${{V}_{0}}(z) = {{V}_{{00}}}(z + H)$, $H > 0$ Уравнение (14) упрощается к линейному однородному дифференциальному уравнению второго порядка с постоянными коэффициентами:
(22)
$\frac{{{{d}^{2}}{{w}_{{10}}}}}{{d{{z}^{2}}}} + i{{a}_{1}}\frac{{d{{w}_{{10}}}}}{{dz}} + {{b}_{1}}{{w}_{{10}}} = 0,$Решение краевой задачи (15), (16), (22) имеет вид:
(23)
$\begin{gathered} {{w}_{{10}}}(z) = {{e}^{{ - \frac{{i{{a}_{1}}z}}{2}}}} \times \\ \times \,\,\left[ {\exp \left( {iz\sqrt {\frac{{a_{1}^{2}}}{4} + {{b}_{1}}} } \right) - \exp \left( { - iz\sqrt {\frac{{a_{1}^{2}}}{4} + {{b}_{1}}} } \right)} \right]. \\ \end{gathered} $(24)
$\begin{gathered} {{k}^{2}}\left( {\omega + i{{k}^{2}}K} \right)\left[ {\frac{{{{N}^{2}}}}{{\omega + i{{k}^{2}}M}} - \left( {\omega + i{{k}^{2}}K} \right)} \right] \times \\ \times \,\,{{\left[ {{{{\left( {\omega + i{{k}^{2}}K} \right)}}^{2}} - {{f}^{2}}} \right]}^{{ - 1}}} + \\ + \,\,\frac{{{{f}^{2}}{{k}^{2}}V_{{00}}^{2}}}{4}{{\left[ {{{{\left( {\omega + i{{k}^{2}}K} \right)}}^{2}} - {{f}^{2}}} \right]}^{{ - 2}}} = {{\left( {\frac{{\pi n}}{H}} \right)}^{2}}, \\ \end{gathered} $(25)
$\begin{gathered} {{\omega }^{2}} = {{f}^{2}} - \\ - \,\,\frac{{{{f}^{2}}V_{{00}}^{2}}}{{2({{N}^{2}}\, - \,{{f}^{2}})\, - \,2\sqrt {{{{({{N}^{2}}\, - \,{{f}^{2}})}}^{2}}\, + \,{{f}^{2}}V_{{00}}^{2}\left( {1\, + \,\frac{{{{\pi }^{2}}{{n}^{2}}}}{{{{k}^{2}}{{H}^{2}}}}} \right)} }}. \\ \end{gathered} $При ${{V}_{{00}}} \to 0$ дисперсионное соотношение (25) переходит в известное соотношение для однородной стратификации [10, 17]:
Коэффициент горизонтальной диффузии $M$ зависит от масштаба явления по закону “4/3” [20, 21]:
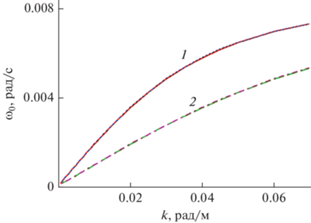
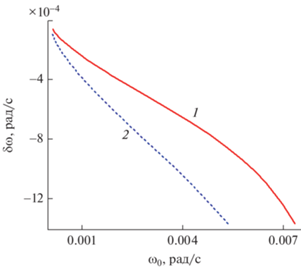
Здесь под масштабом $l$ подразумевается длина волны.Дисперсионное уравнение (24) решается численно для фиксированного волнового числа и номера моды. Находится действительная и мнимая часть частоты волны при $N = 5$ цикл/ч, $H = 70$ м, ${{V}_{{00}}} = 1{\text{/}}140$ с$^{{ - 1}}$, ${{C}_{1}} = 0.01\,\,{\text{с}}{{{\text{м}}}^{{{\text{2/3}}}}}{{{\text{с}}}^{{ - 1}}}$. Число Ричардсона ${\text{Ri}} = N{}^{2}/V_{{00}}^{2}$ равно 1.5. При турбулентном числе Прандтля ${{\Pr }_{T}} = 2$ из соотношения (7) работы [22] следует, что параметр анизотропии $R = 0.95$, что соответствует рассматриваемому случаю, когда горизонтальный масштаб турбулентности много больше вертикального [22]. Коэффициент турбулентной вязкости $K$ связан с коэффициентом турбулентной диффузии $M$ соотношением $K{\text{/}}M = {{\Pr }_{T}}$, отсюда $K = 2M$. Зависимость действительной части частоты ${{\omega }_{0}} = \operatorname{Re} (\omega )$ от волнового числа $k$ для первых двух мод показана на рис. 1. На этом же рисунке показаны дисперсионные кривые первых двух мод, когда турбулентная вязкость и диффузия не учитываются, т.е. при $K = M = 0$. Из рис. 1 следует, что учет турбулентной вязкости и диффузии на дисперсионные влияния практически не оказывает. Зависимость мнимой части частоты волны $\delta \omega = \operatorname{Im} (\omega )$ от волнового числа для первых двух мод показана на рис. 2. Мнимая часть частоты волны при учете турбулентной вязкости и диффузии отрицательная, т.е. волна затухает, а $\delta \omega $ – декремент затухания волны. У второй моды декремент затухания по модулю выше, чем у первой при фиксированной действительной части частоты волны.
Рис. 2.
Зависимость мнимой части частоты волны от действительной части частоты: 1 – первая мода, 2 – вторая мода.
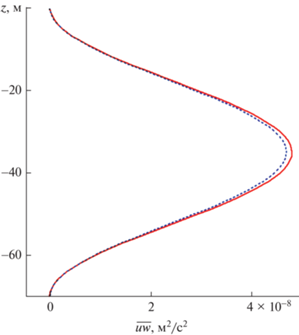
Сравнение волновых потоков импульса $\overline {uw} $ (20), $\overline {vw} $ (21) приводится на рис. 3 для внутренней волны низшей моды при $k = 0.01$ рад/м, ${{\zeta }_{{\max }}} = 0.5$ м. Волновой поток $\overline {vw} $ превышает по абсолютной величине поток $\overline {uw} $. На рис. 4 делается сопоставление волнового потока импульса $\overline {uw} $ (20) при учете (сплошная кривая) и без учета турбулентной вязкости и диффузии при одной и той же максимальной амплитуде волны низшей моды ${{\zeta }_{{\max }}} = 0.5$ м при $k = 0.01$ рад/м. Из рис. 4 следует, что при учете турбулентной вязкости и диффузии волновой поток $\overline {uw} $ больше.
Рис. 3.
Волновые вертикальные потоки импульса $\overline {uw} $ (1), $\overline {vw} $ (2) для первой моды внутренних волн.
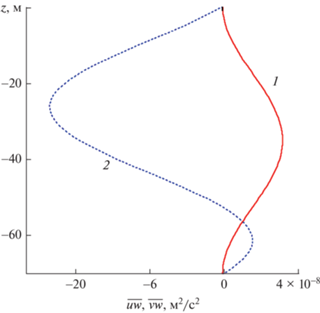
Рис. 4.
Профили вертикального потока импульса $\overline {uw} $ при учете турбулентной вязкости и диффузии и без их учета.
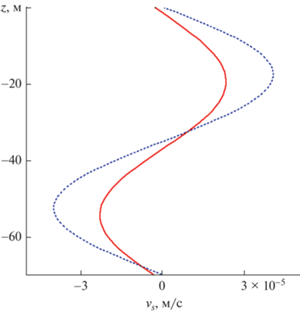
На рис. 5 делается сопоставление волнового потока импульса $\overline {vw} $ при учете (сплошная кривая) и без учета турбулентной вязкости и диффузии для низшей моды при $k = 0.01$ рад/м, ${{\zeta }_{{\max }}} = 0.5$ м. Волновой поток импульса $\overline {vw} $ при учете турбулентной вязкости и диффузии преобладает над потоком без их учета в верхнем 40-метровом слое. Глубже, наоборот, преобладает поток без учета турбулентной вязкости и диффузии.
Рис. 5.
Профили вертикального потока импульса $\overline {vw} $ при учете турбулентной вязкости и диффузии и без их учета.
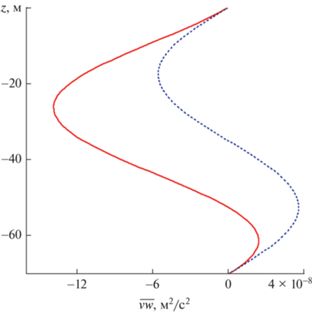
Вертикальные профили скорости стоксова дрейфа ${{u}_{s}}$ показаны на рис. 6 при учете турбулентной вязкости и диффузии (сплошная кривая) и без их учета для внутренних волн низшей моды при $k = 0.01$ рад/м. Из рис. 6 следует, что компонента скорости стоксова дрейфа ${{u}_{s}}$ практически не зависит от турбулентной вязкости и диффузии.
Рис. 6.
Вертикальные профили скорости стоксова дрейфа ${{u}_{s}}$ при учете и без учета турбулентной вязкости и диффузии.
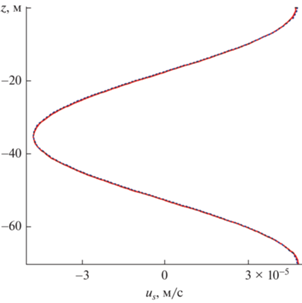
Вертикальные профили компоненты скорости стоксова дрейфа ${{v}_{s}}$ показаны на рис. 7 при учете турбулентной вязкости и диффузии (сплошная кривая) и без их учета. Сравнение компоненты скорости стоксова дрейфа ${{v}_{s}}$, поперечной к направлению распространения волны при учете и без учета турбулентной вязкости и диффузии показывает, что отличие очень слабое. Для исследования влияния турбулентной вязкости и диффузии на скорость стоксова дрейфа увеличим коэффициенты горизонтального турбулентного обмена в 5 раз, т.к. имеет смысл говорить об интервале значений коэффициентов обмена. Вертикальные профили компонент скорости стоксова дрейфа при учете (сплошная линия) и без учета турбулентной вязкости и диффузии показаны на рис. 8, 9. Из рис. 8 следует, что учет турбулентной вязкости и диффузии при увеличенных коэффициентах обмена несколько уменьшает максимумы модуля скорости стоксова дрейфа ${{u}_{s}}$. Вертикальные профили поперечной к направлению распространения волны компоненты скорости стоксова дрейфа ${{v}_{s}}$ при учете увеличенных коэффициентах турбулентного обмена и без их учета показаны на рис. 9. Сплошная линия соответствует случаю учета турбулентной вязкости и диффузии. Сравнение поперечной к направлению распространения волны компоненты скорости стоксова дрейфа ${{v}_{s}}$ при учете увеличенных коэффициентов турбулентного обмена и без их учета показывает, что учет турбулентной вязкости и диффузии уже более значительно уменьшает максимальные по модулю значения этой компоненты скорости, чем у ${{u}_{s}}$.
Рис. 7.
Вертикальные профили скорости стоксова дрейфа ${{v}_{s}}$ при учете и без учета турбулентной вязкости и диффузии.
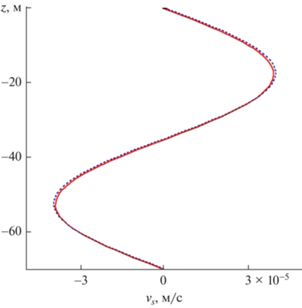
Рис. 8.
Вертикальные профили скорости стоксова дрейфа ${{u}_{s}}$ без учета и при учете турбулентной вязкости и диффузии при увеличенных коэффициентах обмена.
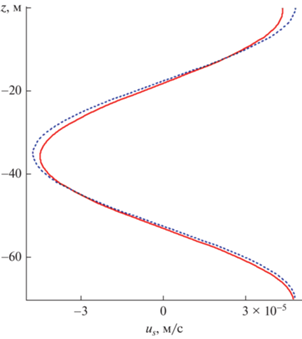
Рис. 9.
Вертикальные профили компоненты скорости стоксова дрейфа ${{v}_{s}}$ без учета и при учете турбулентной вязкости и диффузии при увеличенных коэффициентах обмена.
ВЫВОДЫ
1. У инерционно-гравитационных внутренних волн в сдвиговом потоке мнимая поправка к частоте при учете горизонтальной турбулентной вязкости и диффузии отрицательная, т.е. волна затухает.
2. Вертикальный волновой поток импульса $\overline {vw} $ у первой моды внутренних волн при учете горизонтальной турбулентной вязкости и диффузии превышает поток без их учета в верхнем 40-метровом слое, глубже, наоборот этот поток меньше потока без учета турбулентной вязкости и диффузии.
3. Вертикальный волновой поток импульса $\overline {uw} $ при учете турбулентной вязкости и диффузии превышает этот поток без их учета.
4. Турбулентная вязкость и диффузия слабо влияет на скорость стоксова дрейфа. Увеличение коэффициентов турбулентного обмена в пять раз приводит к тому, что продольная составляющая скорости стоксова дрейфа ${{u}_{s}}$ незначительно уменьшается, у поперечной компоненты скорости стоксова дрейфа ${{v}_{s}}$ уменьшение максимумов модуля скорости более значительное.
Работа выполнена в рамках государственного задания по теме: 0555-2021-0004 “Фундаментальные исследования океанологических процессов, определяющих состояние и эволюцию морской среды под влиянием естественных и антропогенных факторов, на основе методов наблюдения и моделирования” (шифр “Океанологические исследования”).
Список литературы
Пантелеев Н.А., Охотников И.Н., Слепышев А.А. Мелкомасштабная структура и динамика океана. Киев: Наук. думка, 1993. 195 с.
Самодуров А.С., Любицкий А.А., Пантелеев Н.А. Вклад опрокидывающихся внутренних волн в структурообразование, диссипацию энергии и вертикальную диффузию в океане // Морской гидрофизический журнал. 1994. № 3. С. 14–27.
Van Haren H., Gostiaux L., Morozov E., and Tarakanov R. Extremely long Kelvin-Helmholtz billow trains in the Romanche Fracture Zone // Geophysical Research Letters. 2014. V. 41. P. 8445–8451.
Holford J.M., Linden P.F. Turbulent mixing in a stratified fluid // Dynamics of atmosphere and oceans. 1999. V. 30. № 4. P. 173–198.
Ostrovskii A.G., Zatsepin A.G. Intense ventilation of the Black Sea pycnocline due to vertical turbulent exchange in the Rim Current area // Deep – Sea Res. 2016. V. 116. P. 1–13.
Ivanov A.V., Ostrovsky L.A.,Soustova I.A.,Thimring L.Sh. Interaction of internal waves and turbulent in the upper layer of the ocean // Dynamics of Atmosheres and Ocean. 1984. V. 3. № 7. P. 221–232.
Бадулин С.И., Цимринг Л.Ш., Шрира В.И. Захват и вертикальная фокусировка внутренних волн в пикноклине горизонтальными неоднородностями стратификации и течений // Докл. АН СССР. 1983. Т. 273. № 2. С. 459–463.
Борисенко Ю.Д., Воронович А.Г., Леонов А.И., Миропольский Ю.З. К теории нестационарных слабонелинейных внутренних волн в стратифицированной жидкости // Изв. АН СССР. Физика атмосферы и океана. I976. Т. 12. № 3. С. 293–301.
Grimshaw R. The modulation of an internal gravity wave packet and the resonance with the mean motion // Stud. In Appl. Math. 1977. V. 56. P. 241–266.
Ле Блон П., Майсек Л. Волны в океане. Москва: Мир, 1981. Ч. 1. 480 с. Ч. 2. 365 с.
LeBlond P.H. On damping of internal gravity waves in a continuously stratified ocean // Journal of Fluid Mechanics. 1966. V. 25. № 1. P. 121–142.
Островский Л.А., Соустова И.А. Верхний перемешанный слой как сток энергии внутренних волн // Океанология. 1979. Т. 19. № 6. С. 973–981.
Sukoriansk S. and Galperin B. An analytical theory of the buoyancy - Kolmogorov subrange transition in turbulent flows with stable stratification // Philosophical Transactions of the Royal Society. Series A. 2013. 371: 20120212. https://doi.org/10.1098/rsta.2012.0212
Слепышев А.А. Вертикальный перенос импульса внутренними волнами при учете турбулентной вязкости и диффузии // Изв. РАН. Физика атмосферы и океана. 2016. Т. 52. № 3. С. 342–350.
Slepyshev A.A. Vertical Transfer of Momentum by Inertia-Gravity InternalWaves on a Two-Dimensional Shear Flow // Physical Oceanography, [e-journal], 2021. V. 28. № 4. P. 445–459.
Слепышев А.А., Лактионова Н.В. Вертикальный перенос импульса внутренними волнами в сдвиговом потоке // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 6. С. 194–200.
Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. Ленинград: Гидрометеоиздат, 1981. 302 с.
Черкесов Л.В. Гидродинамика волн. Киев: Наук. думка, 1980. С. 222.
Longuet-Higgins M.S. On the transport of mass by time varying ocean current // Deep-Sea Research 1969. V. 16. № 5. P. 431–447.
Озмидов Р.В. Горизонтальная турбулентность и турбулентный обмен в океане. Москва: Наука, 1968. 200 с.
Боуден К. Физическая океанография прибрежных вод. Москва: Мир, 1988. С. 285.
Соустова И.А., Троицкая Ю.И. и др. Простое описание турбулентного переноса в стратифицированном сдвиговом потоке применительно к описанию термогидродинамики внутренних водоемов // Изв. РАН. Физика атмосферы и океана. 2020. Т. 56. № 6. С. 689–699.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана