1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 93, № 12, 2019

Журнал физической химии, 2019, T. 93, № 12, стр. 1894-1900

Моделирование работы микросепаратора с учетом изменения толщины слоя Штерна на поверхности пор электродов

Н. А. Тихонов a, *, М. Г. Токмачев a

a Московский государственный университет им. М.В. Ломоносова, Физический факультет
Москва, Россия

* E-mail: niktandr@yandex.ru

Поступила в редакцию 15.02.2019
После доработки 22.04.2019
Принята к публикации 24.04.2019

Полный текст (PDF)

Аннотация

На основе математического моделирования изучена динамика деионизации раствора электролита с помощью сорбции на аэрогельных электродах. Учитываются процессы переноса вещества потоком раствора, диффузии и сорбции в порах. Показано, что для корректного описания этих физических процессов необходимо учитывать изменение толщины слоя Штерна вблизи поверхности пор электрода при электродиффузии ионов внутрь пор. Рассчитано изменение толщины слоя Штерна, а также приведены примеры моделирования процесса деионизации в циклическом режиме при различных значениях физических параметров.

Ключевые слова: деионизация, аэрогельные электроды, слой Штерна, математическое моделирование

Метод емкостной деионизации водных растворов – это перспективный и наиболее экономичный метод опреснения воды, который заключается в прокачке водного раствора через электрохимическую ячейку между двумя пористыми электродами с высокоразвитой поверхностью, между которыми задается определенная разность потенциалов. В качестве электродов обычно используются углеродные электроды с высокой удельной поверхностью, на которых происходит адсорбция ионов и как следствие – деионизация воды [1–3].

По сравнению с обратным осмосом и дистилляцией, метод емкостной деионизации считается энергоэффективной технологией опреснения воды [4]. Это происходит главным образом потому, что в этом методе удаляются ионы соли из воды, в то время как другие технологии экстрагируют воду из раствора соли.

Имеется много различных экспериментальных исследований метода емкостной деионизации, их литературный обзор можно найти, например, в [1, 5–9]. В основном исследования направлены на изучение равновесия между концентрациями различных электролитов во внешней области аэрогелей и сорбцией их внутри аэрогеля, энергозатраты, а также возникающие в переменных режимах токи, характеризующие динамику деионизации [8–11].

Качественное объяснение механизма процесса базируется на представлении о том, что на поверхности пор при наличии напряжения создается двойной электрический слой [12]. Для формирования этого слоя происходит отбор ионов из раствора. Во многих работах теоретический подход по существу сводится к представлению аэрогельных электродов, как поверхности конденсатора большой емкости [11, 13–17] собирающего ионы из промежутка между электродами, по которому происходит движение раствора. Соответственно для описания процесса при этом используются так называемая одномерная модель пористых электродов. Таким способом обоснованно рассматривать и рассчитывать процесс деионизации, в том числе в циклическом режиме, если поры аэрогеля достаточно крупные и промежуток между электродами, по которому происходит перенос раствора, относительно широкий. В этом случае лимитирующей стадией процесса является перенос ионов внутри промежутка к поверхности электродов, а более тонкие явления внутри аэрогеля не существенны. В то же время, если поставить задачу определения параметров, при которых процесс деионизации наиболее эффективен, то ситуация меняется: диаметр пор следует уменьшать. Применение материалов, содержащих поры в виде нанотрубок, показало высокую способность к накоплению заряда [18]. Может меняться отношение толщины промежутка между электродами к толщине электродов и увеличиваться скорость пропускания раствора по промежутку. В этом случае лимитирующей стадией процесса деионизации будет являться диффузия ионов внутри электрода. Для определения оптимальных характеристик деионизатора необходимы модели, которые обеспечивают учет пространственного распределения заряда внутри электродов. Целью математического моделирования является не только описание имеющихся экспериментальных данных, но и предсказание процесса деионизации во всех подробностях.

Модель, где рассматривается перенос ионов не только по промежутку между электродами, но и внутри пористого аэрогеля, предложена в [19]. Это двумерная модель переноса вещества. В целом, она базируется на фундаментальных законах физики, однако ее слабым местом является описание связи заряда и концентрации ионов в поре.

Исследования процесса деионизации, проводимого в циклическом режиме, на основе математического моделирования, приведены в [20]. В этой работе изучается сдвиг равновесия концентраций ионов между каналом и порами, влияние на скорость диффузии в тонких порах сильно неоднородного электрического поля, решены вопросы, вызывающие трудность при расчетах. Построен алгоритм количественного расчета процесса. Результат перенесен на случай сорбента с разбросом формы пор. Недостатком модели, рассмотренной в [20], является то, что она не учитывает конечный размер ионов и не оценивает изменение слоя Штерна в процессе диффузии ионов в порах. Как показали дальнейшие исследования, это может приводить к неверным количественным результатам.

В настоящей работе учитывается влияние этих факторов при формулировке модели процесса и при получении количественных результатов. На основании математического моделирования рассчитывается толщина слоя Штерна и диффузного слоя Гуи-Чепмена, возникающих вблизи заряженной плоской поверхности, определяющих сорбционные характеристики пористых электродов. Приведены примеры расчета процесса деионизации в циклическом режиме при различных значениях физических параметров.

ФИЗИЧЕСКАЯ МОДЕЛЬ

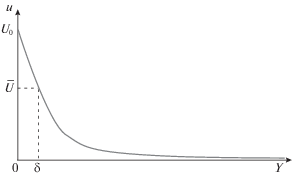
Принципиальная схема электрического деионизатора представлена на рис. 1.

Рис. 1.

Схема деионизатора (a). Схема поры в электроде в модельном представлении (б); 1 – поры сорбента, 2 – образующийся на поверхности пор слой Штерна, 3 – канал, 4 – скелет сорбента.

Пусть имеется плоский конденсатор, состоящий из двух металлических пластин длины ${{L}_{z}}$ (две крайние сплошные горизонтальные полоски на рис. 1a). На пластины нанесены слои толщины $H$ электропроводящего пористого вещества, образующие электроды. Само пористое вещество электродов, будем называть сорбентом. Между слоями расстояние $2L$. В дальнейшем пространство между электродами будем называть “каналом”.

В модельном рассмотрении будем поры представлять в виде тонких плоских щелей ширины $2R$ и глубины H, расположенных перпендикулярно пластинам, а скелет сорбента в виде пространства между порами, затемненного на рис. 1a. Будем считать ${{L}_{z}}$ порядка нескольких см, $L$ – нескольких мм, $H$ – долей мм, $R$ – десятков нм. (На рис. 1 соотношение $R$, $H$ и толщины слоя скелета между порами искажено. Поры и разделяющие их слои скелета изображены широкими для лучшей различимости.)

На вход в канал ($z = 0$) подается раствор электролита, концентрация которого поддерживается равной ${{C}_{0}}$. Будем считать ${{C}_{0}}$ величиной порядка долей моль/литр. Будем считать, что физические характеристики ионов разного знака, в том числе их коэффициенты диффузии, одинаковы. Тогда распределение концентраций ионов симметрично относительно середины канала и мы можем рассматривать происходящее только в одном слое сорбента.

Пусть первоначально пора заполнена электролитом с концентрацией ${{C}_{0}}$. При подаче напряжения между электродами обе стенки поры приобретают потенциал ${{U}_{0}}$, а внутри поры возникает переменный по пространству потенциал. Длина поры много больше ее ширины (примерно в 105 раз). В этих условиях будем пренебрегать градиентом поля вдоль поры по сравнению с градиентом в направлении $x$. Считаем электропроводимость сорбента достаточно высокой и учитываем малую толщину его слоя $H$ по сравнению с $L$. При этом время перераспределения зарядов по скелету сорбента много меньше характерного времени диффузии и переноса раствора по каналу. Поэтому считаем потенциал во всех точках скелета сорбента равным потенциалу пластины конденсатора, на которую он нанесен.

В циклическом режиме работа установки проходит через две стадии: стадия адсорбции, где вода опресняется, и стадия десорбции, где электроды регенерируются. Во время стадии адсорбции на два электрода накладывается разность потенциалов. Происходит деионизация проходящего раствора. После этого полярность электродов меняют местами или разность потенциалов уменьшают до нуля. При этом ионы покидают поры электрода, вымываются из ячейки, что приводит к выходу потока с высокой концентрацией соли.

Пусть в начальный момент, при $t = 0$ разность потенциалов между обкладками конденсатора равна 0, а затем на время ${{T}_{{{\text{sorp}}}}}$ ключ замыкается и разность потенциалов равна $\Phi $. Считаем $\Phi \approx 1.0$ В – меньше напряжения, при котором начинается гидролиз воды. Затем на время ${{T}_{{{\text{reg}}}}}$ ключ размыкается, поле между пластинами пропадает, и наступает стадия регенерации. В циклическом режиме этот процесс периодически повторяется. Наша задача состоит в том, чтобы составить модель, допускающую расчет процесса и построить зависимость количества собранного у поверхности вещества и концентрацию выходящего из канала раствора от времени при различных параметрах физической модели.

СЛОЙ ШТЕРНА ВБЛИЗИ ПОВЕРХНОСТИ СОРБЕНТА В ПОРЕ

Введем безразмерный потенциал

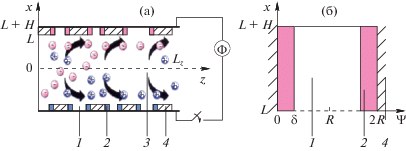
$u = {{q\varphi } \mathord{\left/ {\vphantom {{q\varphi } {(kT),}}} \right. \kern-0em} {(kT),}}$
где $\varphi $ – электрический потенциал, $q$ – заряд электрона, $k$ – постоянная Больцмана, а $T$ – температура раствора. Так как потенциал определяется с точностью до постоянной, то будем отсчитывать его от середины канала, тогда на самих пластинах
$u = {{U}_{0}} = \pm \frac{{q\Phi }}{{2kT}}.$
Энергия взаимодействия 1 моля ионов с обкладкой конденсатора будет равна $W = {{N}_{{Av}}}q\Phi {\text{/}}2 = $ $ = RT{{U}_{0}}$ ~ 50 кДж/моль, а энергия гидратации большинства ионов – порядка несколько сотен кДж/моль, поэтому ионы вблизи поверхности остаются в гидратированном состоянии.

Пусть концентрация раствора C0 = 0.01 моль/л. В состоянии равновесия, локальная концентрация ионов подчиняется закону Больцмана: локальная концентрация отрицательно заряженных ионов будет ${{C}^{ - }} = {{C}_{0}}{{e}^{u}}$, а положительно заряженных ионов – ${{C}^{ + }} = {{C}_{0}}{{e}^{{ - u}}}$. Предположим, что вблизи поверхности сорбента, также как и в остальном растворе, выполняется закон Больцмана. Тогда ${{\left. {{{C}^{ - }}} \right|}_{{y = 0}}} = {{C}_{0}}{{e}^{{{{U}_{0}}}}}$ ≅ $2.86 \times {{10}^{6}}\;{\text{моль/л}}$. Это значение превышает реализуемую концентрацию на несколько порядков. Следовательно, вблизи заряженной поверхности закон Больцмана не выполняется. Оценив радиус гидратированного иона как ${{r}_{0}} = 0.3\;{\text{нм}}$, можно найти концентрацию максимально упакованных гидратированных ионов: ${{C}_{{\max }}} = ((4{\text{/}}3) \times $ $ \times \;\pi r_{0}^{3}{{N}_{{Av}}}{{)}^{{ - 1}}}$ ≅ $14.7\;{\text{моль/л}}$. Эти гидратированные ионы, которые плотно прижаты друг к другу вблизи заряженной поверхности, изменяют толщину слоя Штерна относительно “исходного” слоя, который возник вблизи незаряженной поверхности из-за различных сорбционных эффектов. Исключая “исходный” слой из рассмотрения, мы будем называть упомянутое изменение слоя Штерна под воздействием разности потенциалов как “плотный” слой вблизи поверхности. Обозначим толщину этого слоя как $\delta $.

Для корректного описания изменения потенциала в поре необходимо учесть появление “плотного” слоя. В условиях равновесия потенциал определяется системой:

$\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} = {{\mu }^{2}}{{С}_{{\max }}},\quad {\text{для}}\quad y < \delta ;$
(1)
$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} = {{\mu }^{2}}{{C}_{0}}({{e}^{u}} - {{e}^{{ - u}}}),\quad {\text{для}}\quad y > \delta \\ {{\left. u \right|}_{{y = 0}}} = {{U}_{0}},\quad {{\left. {\frac{{\partial u}}{{\partial y}}} \right|}_{{y = R}}} = 0,\quad {{\left. u \right|}_{{\delta - 0}}} = {{\left. u \right|}_{{\delta + 0}}}, \\ \end{gathered} $
${{\left. {\frac{{\partial u}}{{\partial y}}{\kern 1pt} } \right|}_{{\delta - 0}}} = {{\left. {\frac{{\partial u}}{{\partial y}}{\kern 1pt} } \right|}_{{\delta + 0}}},\quad {{C}_{{\max }}} = {{C}_{0}}{{\left. {{{e}^{u}}} \right|}_{{y = \delta }}},$
где ${{\mu }^{2}} = \frac{{{{q}^{2}}{{N}_{{av}}}}}{{\varepsilon {{\varepsilon }_{0}}kT}} \cong 5.3 \times {{10}^{{18}}}\,{{{\text{м}}}^{{ - 2}}}\;{\text{мол}}{{{\text{ь}}}^{{ - 1}}}\;{\text{л}}$. Для ${{C}_{0}}{\text{/}}{{C}_{{\max }}} \ll 1$ и $R\mu \sqrt {{{C}_{0}}} \gg 1$, аналитически решая систему (1), получим оценку величины $\delta $:
$\delta \cong \sqrt {2{\text{/}}{{C}_{{\max }}}} [\sqrt {{{U}_{0}} - \ln ({{C}_{{\max }}}{\text{/}}{{C}_{0}}) + 1} - 1]{\text{/}}\mu $
Толщина “плотного” слоя $\delta $ выражается из условия:
$\bar {U} = u\left( \delta \right) = \ln \left( {{{C}_{{\max }}}{\text{/}}{{C}_{0}}} \right)$
Для указанных значений ${{C}_{0}}$ и $\Phi $ толщина “плотного” слоя $\delta $ мала, но сильно зависит от $\bar {U}$.

Качественное изменение потенциала в зависимости от расстояния до заряженной поверхности проиллюстрировано на рис. 2.

Рис. 2.

Изменение электрического потенциала в зависимости от расстояния до положительно заряженной стенки поры.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАБОТЫ ДЕИОНИЗАТОРА

Будем описывать процессы, происходящие в области $x > 0$, для $x < 0$ все симметрично.

Пренебрегаем диффузией вдоль канала по сравнению с переносом вещества потоком. Тогда уравнение переноса вещества в канале ($0 < x < L$) имеет вид:

(2)
$\frac{{\partial C}}{{\partial t}} + v\frac{{\partial C}}{{\partial z}} = {{D}_{{{\text{ex}}}}}\frac{{{{\partial }^{2}}C}}{{\partial {{x}^{2}}}}.$
Диффузия ионов из канала в поры происходит под действием градиента концентрации и градиента потенциала. Локальный диффузионный поток описывается уравнением Нернста–Планка. Непосредственно использовать это уравнение для расчета всего процесса сложно, вследствие того, что при $y \approx \delta $ градиент поля очень велик. Поэтому требуется чрезмерно большое количество узлов разностной сетки. В [20] показано, что эту трудность можно обойти, если оперировать понятием средней концентрации электролита $\overline С (x,z,t)$ в сечении поры и использовать величину $f$ (см. уравнение (3)), характеризующую отклонение средней концентрации в поре от равновесной. Здесь $\overline С $ понимается, как $\bar {C} = ({{\bar {C}}_{ + }} + {{\bar {C}}_{ - }}){\text{/}}2$, где ${{\bar {C}}_{ \pm }}$ средние по сечению $\left( {x = {\text{const}},\,\,\delta < y < R} \right)$ значения концентраций ионов. При этом подходе удается выделить расчет поля в отдельный блок и получить относительно простые уравнения для описания диффузии.

Действительно, перенос ионов вдоль поры происходит по всей ее толщине за исключением толщины слоя Штерна, т.е. в интервале $\delta < y < R$. Так как $R \gg H$, то можно пренебречь временем локального перераспределения ионов поперек поры и считать, что в области $\delta < y < R$ концентрации ионов соответствуют уравнению Больцмана: ${{C}^{ - }} = C{{e}^{u}}$, а ${{C}^{ + }} = C{{e}^{{ - u}}}$, где C некоторое значение, определяющее количество ионов. Это значение находится из условия баланса вещества:

$\bar {C}(R - \delta ) = \int\limits_\delta ^{{{R}_{{}}}} {\frac{{({{C}^{ + }} + {{C}^{ - }})}}{2}} dy = \int\limits_\delta ^{{{R}_{{}}}} {\widetilde C\frac{{{{e}^{u}} + {{e}^{{ - u}}}}}{2}} dy.$

Отсюда

$\widetilde C = \bar {C}2(R - \delta ){\text{/}}\int\limits_\delta ^{{{R}_{{}}}} {({{e}^{u}} + {{e}^{{ - u}}})} dy.$
Получаем соотношения, позволяющие рассчитать $u$ в сечении $(x = {\text{const}},$ $\delta < y < R)$ в зависимости от $\bar {C}$ и $\delta $:
(3)
$\begin{gathered} \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} = \mu \widetilde C({{e}^{u}} - {{e}^{{ - u}}}),\quad f = \frac{{\int\limits_\delta ^{{{R}_{{}}}} {({{e}^{u}} + {{e}^{{ - u}}})} dy}}{{2(R - \delta )}}, \\ \widetilde C = \frac{{\bar {C}}}{f}{{\left. {,\quad u} \right|}_{{y = \delta }}} = \ln ({{C}_{{\max }}}{\text{/}}\widetilde C),\quad {{\left. {\frac{{\partial u}}{{\partial r}}{\kern 1pt} } \right|}_{{y = R}}} = 0. \\ \end{gathered} $
Из (3) видно, что $f = f(\bar {C},R,\delta )$. Находим зависимости $f(\bar {C},R,\delta )$ и $\frac{{df(\bar {C},R,\delta )}}{{d\bar {C}}}$ для разных значений $\bar {C}$, $R$ и $\delta $. После этого переходим к описанию диффузии вдоль пор.

Плотность диффузионного потока вдоль поры описывается законом Нернста–Планка:

${{j}_{ \pm }} = - D\left( {\frac{{\partial {{C}_{ \pm }}}}{{\partial x}} \pm {{C}_{ \pm }}\frac{{\partial u}}{{\partial x}}} \right).$

Запишем это уравнение в виде:

${{j}_{ \pm }} = - D\frac{{\partial ({{e}^{{ \pm u}}}{{C}_{ \pm }})}}{{{{e}^{{ \pm u}}}}}.$
Поскольку ${{C}^{ \pm }} = (\bar {C}{\text{/}}f){{e}^{{ \pm u}}}$, то ${{j}_{ \pm }} = - D\frac{\partial }{{\partial x}}\left( {\frac{{\bar {C}}}{f}} \right){{e}^{{ \mp u}}}$.

Общий поток целевого компонента через сечение поры будет:

$\begin{gathered} J = \int\limits_\delta ^R {\left( {{{j}_{ + }} + {{j}_{ - }}} \right)} dy = - D\int\limits_\delta ^R {\frac{\partial }{{\partial x}}\left( {\frac{{\bar {C}}}{f}} \right)} ({{e}^{u}} + {{e}^{{ - u}}})dy = \\ = \, - {\kern 1pt} D\int\limits_\delta ^R {\left( {\frac{{(\partial{ \bar {C}}{\text{/}}\partial x)({{e}^{u}} + {{e}^{{ - u}}})}}{f}\, - \,\bar {C}\frac{{df}}{{d\overline C }}\frac{{\partial{ \bar {C}}}}{{\partial x}}\frac{{{{e}^{u}} + {{e}^{{ - u}}}}}{{{{f}^{2}}}}} \right)} dy\, = \\ = \; - {\kern 1pt} \left( {R - \delta } \right)D\frac{{\partial{ \bar {C}}}}{{\partial x}}\left( {1 - \frac{{\bar {C}}}{f}\frac{{df}}{{d\overline C }}} \right). \\ \end{gathered} $
Таким образом, находим поток в зависимости от концентрации $\bar {C}$ и ее производной $\partial{ \bar {C}}{\text{/}}\partial x$.

Если ${{\left. u \right|}_{\Sigma }} = 0$, то $f = 1$ и $J = - (R - \delta )D\frac{{\partial{ \bar {C}}}}{{\partial x}}$.

Поправка к коэффициенту диффузии, порожденная учетом градиента потенциала вдоль поры, будет

(4)
$F(\bar {C},R,\delta ) = 1 - \frac{{\bar {C}}}{f}\frac{{\partial f}}{{\partial{ \bar {C}}}},$
а условия связи концентрации ионов на границе канала и пор имеют вид
(5)
$\bar {C} = Cf(\bar {C},R,\delta )\quad {\text{при}}\quad x = L.$
Пусть $\eta $ – порозность электрода. Условия непрерывности потока вещества на границе канала и пор, будут:

(6)
$\begin{gathered} {{D}_{{{\text{ex}}}}}\frac{{\partial C}}{{\partial x}} = \eta {{D}_{{{\text{in}}}}}\left( {1 - \frac{\delta }{R}} \right)\frac{{\partial{ \bar {C}}}}{{\partial x}}F(\bar {C},R,\delta ) \\ {\text{при}}\quad x = L. \\ \end{gathered} $

Уравнение диффузии ионов вдоль поры сорбента, с учетом баланса вещества:

(7)
$\begin{gathered} {{C}_{{\max }}}\frac{{\partial \delta }}{{\partial t}} + (R - \delta )\frac{{\partial{ \bar {C}}}}{{\partial t}} = \\ = (R - \delta ){{D}_{{{\text{in}}}}}\frac{{{{\partial }^{2}}\bar {C}}}{{\partial {{x}^{2}}}}F(\bar {C},R,\delta ). \\ \end{gathered} $

Кинетическое условие для описания изменения толщины слоя Штерна в порах:

(8)
$\frac{{\partial \delta }}{{\partial t}} = \beta ({{\delta }_{{{\text{eq}}}}} - \delta ),$
где равновесная толщина “плотного” слоя ${{\delta }_{{{\text{eq}}}}}$ выражается формулой:
(9)
$\begin{gathered} {{\delta }_{{{\text{eq}}}}} = \left\{ \begin{gathered} \sqrt {\frac{2}{{{{C}_{{\max }}}}}} \frac{{\sqrt {\theta + 1} - 1}}{\mu },\quad {\text{если}}\quad \theta > 0, \hfill \\ 0,\quad {\text{если}}\quad \theta \leqslant 0, \hfill \\ \end{gathered} \right. \\ \vartheta = {{U}_{0}} - \ln \left( {\frac{{{{C}_{{\max }}}f(\bar {C},R,\delta )}}{{\bar {C}}}} \right). \\ \end{gathered} $
Дополнительные условия состоят из начальных, граничных и условий смены напряжения на электродах в каждом цикле длительностью (${{T}_{{{\text{sorp}}}}} + {{T}_{{{\text{reg}}}}}$):

(10)
$\begin{gathered} {{\left. C \right|}_{{t = 0}}} = {{\left. {\bar {C}{\kern 1pt} } \right|}_{{t = 0}}} = {{C}_{0}},\quad {{\left. {\delta {\kern 1pt} } \right|}_{{t = 0}}} = 0,\quad {{\left. C \right|}_{{z = 0}}} = {{C}_{0}}, \\ {{\left. {\frac{{\partial C}}{{\partial x}}{\kern 1pt} } \right|}_{{x = 0}}} = 0,\quad {{U}_{0}} > 0\quad {\text{при}}\quad 0 < t < {{T}_{{{\text{sorp}}}}}, \\ {{U}_{0}} = 0\quad {\text{при}}\quad {{T}_{{{\text{sorp}}}}} < t < {{T}_{{{\text{sorp}}}}} + {{T}_{{{\text{reg}}}}}. \\ \end{gathered} $

Уравнения (2)–(10) образуют полную математическую модель процесса.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ

Расчеты проводились в соответствие с представленной моделью. На рисунках приведены выходные кривые, полученные при моделировании для двух полных циклов. Каждый цикл состоит из этапа сорбции ионов из раствора и этапа регенерации электродов. Первый этап продолжается ${{T}_{{{\text{sorp}}}}}$. На этом этапе на электроды (см. описание физической модели и (10)) подается напряжение. Ионы из проходящего по каналу раствора диффундируют внутрь электрода и сорбируются на поверхности пор. При этом концентрация в канале и в том числе средняя по сечению канала концентрация на выходе ${{C}_{{{\text{out}}}}}(t)$ меньше входной концентрации ${{C}_{0}}$. По мере того, как у поверхности пор возрастает количество ионов, интенсивность процесса отбора ионов из раствора уменьшается. Если процесс сорбции продолжается достаточно долго, то нормированная выходная кривая ${{C}_{{{\text{out}}}}}{\text{/}}{{C}_{0}}$ приближается к единице. Величина $M = 2Lv\int_0^{{{T}_{{{\text{sorb}}}}}} {({{C}_{0}} - {{C}_{{{\text{out}}}}}(t))dt} $ характеризует количество сорбированных ионов на первом этапе.

На втором этапе цикла, в течение ${{T}_{{{\text{reg}}}}}$, в соответствие с (10), напряжение между электродами отсутствует. Ионы, собравшиеся ранее в порах на этапе сорбции с концентрацией большей ${{C}_{0}}$, диффундируют обратно в проточный канал, повышая в нем концентрацию по сравнению с входной. Поэтому ${{C}_{{{\text{out}}}}}{\text{/}}{{C}_{0}}$ становится больше единицы. Количество вышедшего из электрода в канал вещества может немного меняться в первых циклах, но примерно равно M.

Приведенные ниже графики соответствуют следующим значениям параметров: С0 = $ = 0.017\;{\text{моль/л}}$ (эта концентрация соответствует концентрации 1 г/л для хлорида натрия), ${{T}_{{{\text{sorp}}}}} = {{T}_{{{\text{reg}}}}} = 60\;{\text{мин}}$, $v = 0.03\;{{{\text{мм}}} \mathord{\left/ {\vphantom {{{\text{мм}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$, ${{L}_{z}} = 6\;{\text{см}}$, $L = 2.5\;{\text{мм}}$, ${{D}_{{{\text{ex}}}}} = 1.2 \times {{10}^{{ - 9}}}\;{{{\text{м}}}^{{\text{2}}}}{\text{/с}}$. ${{D}_{{{\text{in}}}}} = {{D}_{{{\text{ex}}}}}{\text{/}}3$ – коэффициент диффузии растворенного вещества в порах выбирался в 3 раза меньше, чем в канале, чтобы отразить тот факт, что в реальном сорбенте только 1/3 “щелей” направлена перпендикулярно оси канала. Следовательно, диффузия из канала во внутренние полости электрода при той же пористости идет в три раза медленнее.

Один полный цикл протекает в течение ${{T}_{{{\text{sorp}}}}} + {{T}_{{{\text{reg}}}}} = 120$ мин. На приведенных ниже рисунках показаны выходные кривые в течение 240 мин, то есть для двух циклов. Изломы кривых соответствуют моментам переключения напряжения на электродах.

Влияние глубины пор $H$ на количество сорбированного вещества (гидратированных ионов) на этапе сорбции и на выброс вещества из электродов в канал при регенерации

Как видно из рис. 3, в более глубоких порах оседает больше вещества, однако достаточно глубокие поры будут очень медленно очищаться в процессе регенерации. В связи с этим, с точки зрения экономической эффективности, глубину пор необходимо подбирать в зависимости от остальных параметров процесса.

Рис. 3.

Влияние глубины пор $H$ на динамику сорбции вещества и регенерации электродов; 1 – $H = 0.1\;{\text{мм}}$, 2 – $H = 0.5\;{\text{мм}}$, 3 – $H = 1\;{\text{мм}}$, 4 – $H = 2\;{\text{мм}}$. Кривые соответствуют $R = 80\;{\text{нм}}{\text{.}}$

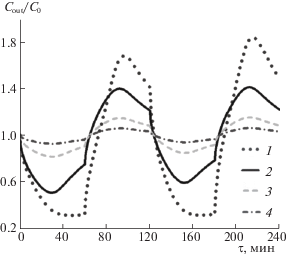
Влияние ширины пор $R$ на динамику процесса

Моделирование показало (рис. 4), что чем меньше ширина пор, тем заметно сильнее эффект емкостной деионизации раствора.

Рис. 4.

Влияние полуширины поры $R$ на динамику сорбции вещества и динамику регенерации электродов; 1 – $R = 10\;{\text{нм}}$, 2 – $R = 30\;{\text{нм}}$, 3 – $R = 80\;{\text{нм}}$, 4 – $R = 200\;{\text{нм}}$. Кривые соответствуют $H = 1\;{\text{мм}}{\text{.}}$

Аналогичным образом были рассмотрены зависимости выходных кривых от $v$, ${{L}_{z}}$, $L$.

Таким образом, в работе построена математическая модель процесса деионизации растворов с помощью сорбции на аэрогельных мелкопористых электродах. Модель учитывает условия равновесия, переноса и диффузии, а также конечный размер ионов.

Возникновение разности потенциалов между раствором в канале и порах приводит к сдвигу равновесия концентраций ионов в соответствие с законом Больцмана. Это определяет втягивание ионов в сорбент и создание распределенного слоя ионов у поверхности. Существенное влияние на сорбционные возможности аэрогеля играет толщина слоя Штерна на заряженной поверхности пор. Эта толщина меняется в процессе сорбции. В работе показан алгоритм ее расчета.

Приведены выходные кривые, полученные на аэрогельном деионизаторе в циклическом режиме, и проанализировано влияние некоторых параметров на эффективность процесса.

Список литературы

  1. Al Marzooqi F.A., Al Ghaferi A.A., Saadat I. et al. // Desalination. 2014. V. 342. P. 3.

  2. Volfkovich Yu.M., Mikhailn A.A., Rychagov A.Yu. et al. // Electrodes based on carbon nanomaterials: structure, properties and application to capacitive deionizationin static cells, Chapter in the book “Nanooptics, nanophotonics, nanostructures and their applications”, Springer International Publishing, 2018, pp. 127–146, DOI: 10.1007/978-3-319-91083-3_9.

  3. Вольфкович Ю.М., Рычагов А.Ю., Сосенкин В.Е. и др. // Электрохимия. 2014. Т. 50. № 11. С. 1222. https://doi.org/10.7868/S0424857014110127

  4. Porada S., Zhao R., van der Wal A. et al. // Progress in Materials Science. 2013. V. 58. № 8. P. 1388.

  5. Suss M.E., Porada S., Sun X. et al. // Energy & Environmental Science. 2015. V. 8. № 8. P. 2296.

  6. Anderson M.A., Cudero A.L., Palma J. // Electrochimica Acta. 2010. V. 55. № 12. P. 3845.

  7. Vol’fkovich Yu.M., Mikhalin A.A., Bograchev D.A. et al. // Elektrokhimiya, 2012. V.48. № 4. P. 467.

  8. Oren Y. // Desalination. 2008. V. 228. P. 10.

  9. Rasines G., Lavela P., Macнas C. et al. // J. Electroanalytical Chem. 2012. V. 671. P. 92.

  10. Marmanis D., Christoforidis A., Ouzounis K. et al. // Global NEST Journal. 2014. V. 16. № 4. P. 609.

  11. Iozzo D.A.B., Tong M., Wu G. et al. // J. Phys. Chem. C. 2015. V. 119. № 45. P. 25235.

  12. Kirby B.J. The Diffuse Structure of the Electrical Double Layer, www.kirbyresearch.com/index.cfm/wrap/textbook/microfluidicsnanofluidics.html.

  13. Yang K., Ying T., Yiacoumi S. et al. // Langmuir. 2001. V. 17. P. 1961.

  14. Rios Perez C.A., Demirer O.N., Clifton, R.L. et al. // J. Electrochem. Soc. 2013. V. 160. № 3. P. E13.

  15. Robinson D.B., Wu Ch. M., Jacobs B.W. // J. Electrochem. Soc. 2010. V. 157. № 8. P. A912.

  16. Honda K., Yoshimura M., Kawakita K. et al. // J. Electrochem. Soc. 2004. V. 151. № 4. P. A532.

  17. Hoyt N.C., Wainright J.W., Savinell R.F. // J. Electrochem. Soc. 2015. V. 162. № 4. P. A652.

  18. Niu C., Sichel E.K., Hoch R. et al. // Appl. Phys. Lett. 1997. V. 70. № 11. P. 1480.

  19. Hemmatifar A., Stadermann M., Santiago J.G. // J. Phys. Chem. C. 2015. V. 119. № 44. P. 24681.

  20. Tikhonov N.A. // J. Math. Chem. 2018. V. 56. P. 700.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал