1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 93, № 4, 2019

Журнал физической химии, 2019, T. 93, № 4, стр. 508-515

Самосогласованность расчета скоростей адсорбции–десорбции и изотермы адсорбции на шероховатой поверхности аэрозолей

Е. С. Зайцева a, Ю. К. Товбин a, b, *

a Государственный научный центр Российской Федерации “Научно-исследовательский физико-химический институт им. Л.Я. Карпова”
Москва, Россия

b Российская академия наук, Институт общей и неорганической химии им. Н.С. Курнакова
Москва, Россия

* E-mail: tovbin@nifhi.ru

Поступила в редакцию 04.07.2018

Полный текст (PDF)

Аннотация

Рассмотрено выполнение условия самосогласованности описания скоростей адсорбции и десорбции недиссоциирующихся молекул на шероховатой поверхности аэрозоля. Скорости рассчитаны с учетом взаимодействия ближайших соседей в квазихимическом приближении. Проанализированы четыре типа моделей, одна из которых описывает исходную распределенную неоднородную поверхность, а остальные три являются ее усреднениями: по числу монослоев (с переходом к однослойной неоднородной поверхности), и по типам центров адсорбции с разными константами Генри (с переходом на эффективный однородный монослой в полислойной переходной области), либо одновременно по числу монослоев и типам центров адсорбции (с переходом к однослойной однородной поверхности). Выделены типы моделей, для которых условие самосогласования выполняется строго, и для которых оно нарушено. Дано объяснение наблюдающихся рассогласований. Установлена зависимость степени рассогласования, если оно имеет место, от плотности газа в системе, энергии взаимодействия активированного комплекса и радиуса частиц адсорбента.

Ключевые слова: самосогласованность теории, теория абсолютных скоростей реакций, неидеальные реакционные системы, шероховатая поверхность, переходная область капля–пар, модель решеточного газа, квазихимическое приближение

Понятие самосогласованного описания динамики и равновесного состояния системы хорошо известно для идеальных реакционных систем – это закон действующих масс, который обоснован для идеальных газовой смеси и разбавленных растворов [1–4]. Он одинаково широко используется как в задачах химической кинетики, так и при исследовании равновесия. Его суть заключается в том, что при равенстве скоростей прямого и обратного направлений реакции должно получаться то же самое уравнение для равновесного распределения компонентов реакционной смеси, которое непосредственно следует из построения уравнения в равновесной теории. Идеальные реакционные системы всегда обладают этим свойством, так как теория имеет одночастичный характер, а скорости реакций не зависят от состояний соседей. Проблемы возникают при учете межчастичных взаимодействий, ответственных за неидеальное поведение реальных систем.

В работе [5] показано, что во всех элементарных стадиях, связанных с движением в ходе реакции тяжелых атомов и фрагментов молекул, необходимо использовать трактовку М.И. Темкина [6–8]. Она отвечает условию быстрой элементарной стадии реакции при практически неизменном состоянии окружения. Широко известный подход Г. Эйринга [9], использующего представления о коэффициенте активности активированного комплекса элементарной стадии, не является корректным для описания неидеальных реакционных систем, за исключением случая учета влияния электронной поляризации среды. В нем предполагается, что реакция идет медленно, и окружение может быть полностью уравновешено с состоянием активированного комплекса.

Напомним, что принцип самосогласованности был использован в работе Ленгмюра [10] при получении изотермы адсорбции из условия равенства скоростей адсорбции и десорбции и в работе [11] при получении уравнения БЭТ.

Важный фактор реальных реакционных систем, особенно гетерогенных, – учет неоднородности поверхности. С формальной точки зрения, в отсутствие латеральных взаимодействий каждый центр поверхности работает независимо, но в силу условия на равновесное распределение компонентов, находящихся на разных центрах неоднородной поверхности, между концентрациями компонентов существует взаимосвязь. Это приводит к сложным концентрационным зависимостям, по которым не всегда удается выявить наличие или отсутствие самосогласованности моделей. Тем не менее, фундаментальность данного принципа была заложена в работах Темкина по процессам на неоднородных поверхностях [7] и при высоких давлениях [8].

В данной работе рассмотрен процесс адсорбции–десорбции недиссоциирующихся молекул на шероховатой поверхности малого аэрозоля. Монослойная граница раздела фаз – очень сильная идеализация структуры поверхности. Реальная структура аэрозольных частиц во многом зависит от условий процесса их формирования [12–15]. Моделирование шероховатых поверхностей представляет собой сложную задачу [16–20]. В неизотермических условиях формирование новой фазы и ее поверхности описывается кинетическими уравнениями. Среди разных процессов была выделена ситуация, когда структуру поверхности можно описывать равновесными уравнениями, если считать, что в ходе резкого охлаждения капля быстро замораживается, сохраняя свою равновесную поверхностную структуру, которая у нее была до охлаждения [21]. Состояние поверхности капли определяется тепловой шероховатостью границы раздела пар–жидкость, вызванной изменением плотности вещества при переходе от жидкости к пару. Ширина переходной области κ зависит от температуры, от которой происходит резкое понижение температуры.

В рассматриваемой задаче учитываются латеральные взаимодействия между ближайшими соседями, а также как неидеальность системы, так и неоднородность поверхности. В таких условиях провести аналитическую проверку условия самосогласованности сложно, поэтому используется численный анализ.

С этой целью используется молекулярно-кинетическая теория для трех агрегатных состояний [18, 19, 22, 23], которая основана на базе многочастичных функций распределений, введенных Н.Н. Боголюбовым [24]. Она отражает дискретное пространственное распределение молекул на масштабе размера молекул, формируя ячейки, и континуальное описание распределения молекул внутри ячеек объемом ${{v}_{0}}$. Данный метод применим для вещества, находящегося в трех агрегатных состояниях, поэтому он единственный обеспечивает равноточное описание трех границ раздела фаз. Микроскопическая модель границы шероховатого раздела фаз была построена в работах [25] и использована для исследования степени заполнения разных центров адсорбции в зависимости от температуры и внешнего давления адсорбирующегося газа. Использована теория на базе модели решеточного газа в квазихимическом приближении, отражающем эффекты прямых корреляций взаимодействующих частиц [18, 19, 22, 23].

В задаче возникает две ситуации: самосогласованность при расчете равновесной шероховатой поверхности границы раздела фаз (при условии медленного протекания стадий адсорбции и десорбции) и самосогласованность при адсорбции иного газа на сформированную поверхность аэрозоля. Во втором случае важную роль играет процедура усреднения характеристик неоднородной поверхности. Здесь можно проследить влияние характера загрубления описания поверхности в зависимости от способа усреднения по разным монослоям и разным центрам адсорбции внутри каждого монослоя. Ситуация является типовой во многих экспериментальных задачах, когда точная информация о типе поверхности неизвестна, и модели могут строиться по-разному в зависимости от предполагаемых поверхностных структур.

В данной работе представлены следующие способы описания поверхности шероховатого аэрозоля: модель 1 – распределенная модель – имеет статистическое описание свойств поверхности по модели [21, 25, 26]; модель 2 – проводится усреднение по разным монослоям в предположении, что константы Генри узлов не зависят от их положения в разных монослоях (поверхность остается неоднородной, но однослойной); модель 3 – усреднение проводится по разным типам центров внутри монослоя (это загрубляет свойства центров внутри полислойной модели); модель 4 – усреднение проводится как по монослоям, так и по типам центров внутри монослоев (остается монослойная однородная поверхность с усредненным значением константы Генри).

В более общем случае можно было рассмотреть полностью распределенную модель с фиксацией координат узлов [18, 19, 23]. Самосогласованность такой модели доказана аналитически [19, 23]. Модель [21], в соответствии с целью работы, отражает частичное усреднение, так как в ней сделан переход к типам узлов вместо их номеров (или координат) в пространстве. Выражения для соответствующих элементарных стадий выписываются для конкретности для адсорбции (для десорбции уравнений строятся полноcтью аналогично [18, 19, 22]). При наличии самосогласования скорости десорбции совпадают со скоростью адсорбции, а при отсутствии самосогласования степень их расхождения одинакова.

Распределенная модель 1. В рассматриваемой версии распределенной модели шероховатой поверхности капли тип узла (q, {mqp}), доступного для адсорбции, определяется номером монослоя q, 1 ≤ q ≤ κ, и множеством чисел {mqp}, где p – номер соседних слоев, p = q, q ± 1, которые вместе характеризуют константу Генри (подробнее см. [21]). Обозначим соседний узел номером его монослоя h и множеством его пар соседей чисел {mhk}, т.е. узел задается через символы (h,{mhk}).

Вероятность встретить соседа типа (h,{mhk}) рядом с центральным узлом типа (q,{mqp}) выражается через функции распределения типов узлов $\Theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ и их пар $\Theta _{{qh}}^{{VV}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)$, введенными в [21]:

(1)
$d_{{qh}}^{{}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right) = \frac{{{{z}_{{qh}}}\Theta _{{qh}}^{{VV}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)}}{{\left( {{{z}_{{qh}}} - {{m}_{{qh}}}} \right)\Theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)}},$
где zqh – число соседних узлов из монослоя h у узла из монослоя q. Введенная вероятность (1) входит в выражение для функции неидеальности $S_{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ для скорости адсорбции одноузельной стадии, $U_{q}^{{VB}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$:
$\begin{gathered} U_{q}^{{VB}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right) = \hat {K}_{q}^{{VB}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)\theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)S_{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right), \\ S_{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right) = \prod\limits_{h = q - 1}^{q + 1} \times \\ \end{gathered} $
$ \times \;{{\left[ {\sum\limits_{\left\{ {{{m}_{{hk}}}} \right\}*} {{{d}_{{qh}}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)S_{{qh}}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)} } \right]}^{{{{z}_{{qh}}} - {{m}_{{qh}}}}}}{\kern 1pt} ,$
(2)
$\begin{gathered} S_{{qh}}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right) = \\ = \;\sum\limits_{j = B,V} {\theta _{{qh}}^{{Vj}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)\exp \left\{ {\beta \delta \varepsilon _{{}}^{{Vj}}} \right\}} {\text{/}}\theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right) = \\ \end{gathered} $
$ = \;1 + \sum\limits_{j = B} {\theta _{{qh}}^{{Vj}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right){{x}^{{Vj}}}} {\text{/}}\theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right),$
$\begin{gathered} {{x}^{{Vj}}} = \exp \left\{ {\beta \delta {{\varepsilon }^{{Vj}}}} \right\} - 1,{\text{ }}\delta {{\varepsilon }^{{Vj}}} = {{\varepsilon }^{{Vj*}}} - {{\varepsilon }^{{Vj}}} \\ = \;{{\varepsilon }^{{Vj*}}} = {{\alpha }_{\varepsilon }}{{\varepsilon }^{{Bj}}}, \\ \end{gathered} $
где $\hat {K}_{q}^{{VB}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ – константа скорости, $\theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ – локальная плотность заполнения узлов типа (q,{mqp}), $S_{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)$ – функция неидеальности, $\theta _{{qh}}^{{Vj}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)$ – вероятность встретить узлы типа (q,{mqp}) и (h,{mhk}) рядом, ${{\alpha }_{\varepsilon }}$ – параметр энергии взаимодействия активированного комплекса, 0 ≤ ${{\alpha }_{\varepsilon }}$ ≤ 1.5, ${{\varepsilon }^{{Bj}}}$ – энергия взаимодействия частицы B с частицей j.

Модель 2, усредненная по монослоям, с разделением типов по константе Генри. При данном усреднении различаются только узлы, имеющие различное значение константы Генри. Обозначим новый тип узлов в адсорбционном пространстве через ξ, а тип его соседа ς. Значения ξ и ς однозначно задают число частиц адсорбента А – mξ и mς соответственно в окружении соответствующих узлов. Тогда выражение для вероятности ${{d}_{{\xi \zeta }}}$ встретить рядом с узлом типа ξ соседний узел типа ς отличается от выражения (1) тем, что в числителе и знаменателе появляются суммы по типам узлов (q,{mqp}) и (h,{mhk}) из распределенной модели, удовлетворяющих определению типов ξ и ς из модели 2:

(3)
${{d}_{{\xi \zeta }}} = \frac{{\sum\limits_q {\sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}**} {\sum\limits_h {\sum\limits_{\left\{ {{{m}_{{hk}}}} \right\}**} {{{z}_{{qh}}}{\text{/}}\left( {{{z}_{{qh}}} - {{m}_{{qh}}}} \right)\Theta _{{qh}}^{{VV}}\left( {\left\{ {{{m}_{{qp}}}} \right\},\left\{ {{{m}_{{hk}}}} \right\}} \right)} } } } }}{{\sum\limits_q {\sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}**} {\Theta _{q}^{V}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)} } }},$
где вторая и четвертая суммы ведутся только по тем множествам {mqp}** и {mhk}**, которые дают равенства: $\sum\nolimits_p {{{m}_{{qp}}}} = {{m}_{\xi }}$ и $\sum\nolimits_k {{{m}_{{hk}}}} = {{m}_{\zeta }}$ соответственно.

Введенная вероятность ${{d}_{{\xi \zeta }}}$ входит в выражение для функции неидеальности $S_{\xi }^{V}$ для скорости адсорбции одноузельной стадии $U_{\xi }^{{VB}}$:

$U_{\xi }^{{VB}} = \hat {K}_{\xi }^{{VB}}\theta _{\xi }^{V}S_{\xi }^{V},$
где $\hat {K}_{\xi }^{{VB}}$ – константа скорости, $\theta _{\xi }^{V}$ – локальная плотность, $S_{\xi }^{V}$ – функция неидеальности:
(4)
$\begin{gathered} S_{\xi }^{V} = {{\left[ {\sum\limits_{{{m}_{\zeta }} = 0}^{z - 1} {{{d}_{{\xi \zeta }}}S_{{\xi \zeta }}^{V}} } \right]}^{{z - {{m}_{\xi }}}}},{\text{ }} \\ S_{{\xi \zeta }}^{V}\, = \,\sum\limits_{j = B,V} {\theta _{{\xi \zeta }}^{{Vj}}\exp \left\{ {\beta \delta \varepsilon _{{}}^{{Vj}}} \right\}} {\text{/}}\theta _{\xi }^{V}\, = \,1\, + \,\sum\limits_{j = B} {\theta _{{\xi \zeta }}^{{Vj}}{{x}^{{Vj}}}} {\text{/}}\theta _{\xi }^{V}. \\ \end{gathered} $
Здесь и ниже выписана только функция неидеальности $S_{\xi }^{V}$ для скорости адсорбции (2) вместо полного его выражения.

В следующих двух моделях узлы для каждого монослоя характеризуются усредненными значениями чисел частиц адсорбента А в окружении вакансии, в которую идет адсорбция. Таким образом, неоднородные узлы переходят в однородные с усредненной константой Генри, поэтому все вероятности встретить соседа данного типа рядом с центральным узлом данного типа обращаются в единицу.

Модель 3, усредненная по константе Генри внутри каждого монослоя. В данной модели шероховатой поверхности аэрозоля каждый тип узла, доступного для адсорбции, определяется только номером монослоя q, который однозначно задает множество частиц А в окружении узла по монослоям {${{\hat {m}}_{{qp}}}$}, усредненных по монослою q для каждого соседа p в отдельности:

(5)
${{\hat {m}}_{{qp}}} = \sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}} {{{m}_{{qp}}}{{\Theta }_{q}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)} {\text{/}}\sum\limits_q {\sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}} {{{\Theta }_{q}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)} } .$
Полученное значение ${{\hat {m}}_{{qp}}}$ входит в выражение для функции неидеальности $S_{q}^{V}$ для скорости адсорбции одноузельной стадии $U_{q}^{{VB}}$:
$U_{q}^{{VB}} = \hat {K}_{q}^{{VB}}\theta _{q}^{V}S_{q}^{V},$
где $\hat {K}_{q}^{{VB}}$ – константа скорости, $\theta _{q}^{V}$ – локальная плотность, $S_{q}^{V}$ – функция неидеальности:

(6)
$\begin{gathered} S_{q}^{V} = \prod\limits_{h = q - 1}^{q + 1} {{{{\left[ {S_{{qh}}^{V}} \right]}}^{{{{z}_{{qh}}} - {{{\hat {m}}}_{{qh}}}}}}} , \\ {\text{ }}S_{{qh}}^{V}\, = \,\sum\limits_{j = B,V} {\theta _{{qh}}^{{Vj}}\exp \left\{ {\beta \delta \varepsilon _{{}}^{{Vj}}} \right\}} {\text{/}}\theta _{q}^{V}\, = \,1\, + \,\sum\limits_{j = B} {\theta _{{qh}}^{{Vj}}{{x}^{{Vj}}}} {\text{/}}\theta _{q}^{V}. \\ \end{gathered} $

Полностью усредненная модель 4. Здесь все узлы, доступные для адсорбции, принадлежат одному типу и описываются общим значением $\hat {m}$ числа частиц А в окружении узла, усредненным по всему объему:

(7)
$\hat {m} = \sum\limits_q {\sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}} {{{\Theta }_{q}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)\sum\limits_h {{{m}_{{qh}}}} } } {\text{/}}\sum\limits_q {\sum\limits_{\left\{ {{{m}_{{qp}}}} \right\}} {{{\Theta }_{q}}\left( {\left\{ {{{m}_{{qp}}}} \right\}} \right)} } .$
Полученное значение $\hat {m}$ входит в выражение для функции неидеальности $S_{{}}^{V}$ для скорости адсорбции одноузельной стадии, $U_{{}}^{{VB}}$:
$U_{{}}^{{VB}} = \hat {K}_{{}}^{{VB}}\theta _{{}}^{V}S_{{}}^{V},$
где $\hat {K}_{{}}^{{VB}}$ – константа скорости, $\theta _{{}}^{V}$ – плотность заполнения узлов, $S_{{}}^{V}$ – функция неидеальности:

(8)
$\begin{gathered} {\text{ }}S_{{}}^{V} = {{\left[ {S_{{pair}}^{V}} \right]}^{{{{z}_{{}}} - \hat {m}}}},{\text{ }} \\ S_{{pair}}^{V}\, = \,\sum\limits_{j = B,V} {\theta _{{}}^{{Vj}}\exp \left\{ {\beta \delta \varepsilon _{{}}^{{Vj}}} \right\}} {\text{/}}\theta _{{}}^{V}\, = \,1\, + \,\sum\limits_{j = B} {\theta _{{}}^{{Vj}}{{x}^{{Vj}}}} {\text{/}}\theta _{{}}^{V}. \\ \end{gathered} $

Таким образом, в зависимости от введенного усреднения меняется вид функции неидеальности, которая входит в выражение для скорости адсорбции/десорбции единым образом для всех моделей.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

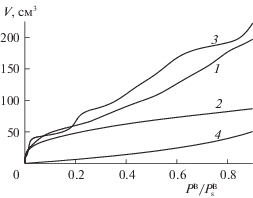
Изотермы. Проведение усреднений меняет вид изотерм по разным моделям (рис. 1). Для сравнения выбраны условия адсорбции азота на кремнеземе при 78 К (до области конденсации). Параметры расчета соответствуют эксперименту [27] (подробнее, см. [25, 26]). По оси ординат отложен объем V адсорбированного газа на одном моле адсорбента, по оси абсцисс – давление газа В (PB), нормированное на давление насыщенного пара ($P_{s}^{{\text{B}}}$). Область определения давления не доходит до области конденсации: 0 < ${{P}^{{\text{B}}}}{\text{/}}P_{s}^{{\text{B}}}$ < 0.9.

Рис. 1.

Изотермы адсорбции азота на кремнеземе. Номер кривой соответствует номеру модели.

Изотермы 2 и 4 по усредненным моделям лежат существенно ниже кривой 1 распределенной модели из-за грубости усреднения, не учитывающего реального характера неоднородности поверхности. Молекулы газа адсорбируются на поверхности адсорбента за счет взаимодействия с адсорбентом и за счет взаимодействия с уже адсорбированными молекулами. Модель 2 отражает первый фактор, определяющий константу Генри, без искажений, а окружение из свободных узлов полностью усредняется. Очевидно, что в пространстве, которое заполняется адсорбатом, (назовем его адсорбционным пространством) преобладают узлы, слабо связанные с адсорбентом и не контактирующие с ним, а, значит, плотность вещества в последних может повыситься по сравнению с плотностью газа только за счет межмолекулярного взаимодействия с адсорбатом. Следовательно, после усреднения окружение будет практически полностью состоять из подобных узлов, вероятность заполнения которых веществом немногим выше, чем в газе, а потому поле соседей будет слабым.

В итоге получаем, что модель 2 достаточно точно описывает состояние только адцентров с высокой степенью связи с адсорбентом. Данные узлы заполняются при малых давлениях, поэтому кривая 2 хорошо согласуется с кривой 1 в области малых давлений. Далее с повышением давления в модели 2 заполнение узлов с более слабой связью с адсорбентом и узлов, несоприкасающихся с адсорбентом, затруднено из-за слабого поля окружения, искаженного самим усреднением. Кривая 4 в силу двойного усреднения по окружению центральных узлов и по всему адсорбционному пространству приводит к резкому уменьшению эффективной константы Генри. Поэтому кривая 4 сильно отличается от кривой 1 во всей области давлений.

Изотерма для модели 3 лучше всего согласуется с изотермой 1. Причиной является то, что в данной модели более детально описывается окружение центрального узла с выделением соседей из монослоев выше, ниже и того же монослоя. Более того, косвенно в данной модели при разбиении узлов по типу также учитывается величина константы Генри, так как вероятность встретить узел с заданным числом контактов с адсорбентом зависит от плотности адсорбента, которая изменяется по монослоям.

Скорости адсорбции по разным моделям представлены на рис. 2. Скорости адсорбции UVB азота на кремнеземе показаны в зависимости от нормированного давления ${{P}^{{\text{B}}}}{\text{/}}P_{s}^{{\text{B}}}$.

Рис. 2.

Зависимости скорости адсорбции UVB азота на кремнеземе от нормированного давления ${{P}^{{\text{B}}}}{\text{/}}P_{s}^{{\text{B}}}$ при αε = 0 (а), 0.5 (б), 1 (в), 1.5 (г). Номера кривых соответствуют номерам моделей.

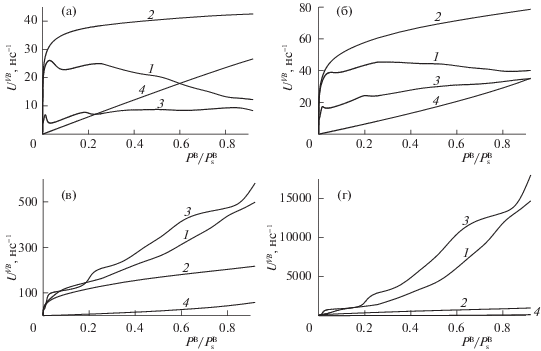
Из рис. 2 видно, что с результатами модели 1 (кривая 1) коррелируют только кривые модели 3, с увеличением давления имеющие схожее поведение с кривой 1. С увеличением параметра αε кривая 3 воспроизводит результаты кривой 1 не только качественно, но и количественно. Кривые 2 и 4 резко отличаются от свойств реальных неоднородных систем (кривые 1 и 3).

Скорость адсорбции в модели 1 может немонотонно меняться с ростом давления в зависимости от соотношения вкладов разных адцентров. Близкое поведение имеет и кривая модели 3. Она достаточно точно отражает неоднородность поверхности распределенной модели 1. Модель 4 описывает адсорбцию на плоской однородной поверхности – скорость такого процесса монотонно растет с ростом давления. Модель 2 делит типы по величине константы Генри, формируя плоскую неоднородную по силе потенциала поверхность: узлы с ненулевой константой Генри заполняются в первую очередь при небольшом увеличении давления от нуля, что дает резкое увеличение скорости адсорбции от нуля, затем идет монотонный рост скорости адсорбции как на кривой 4.

Скорости десорбции $U_{{}}^{{BV}}$ определяются по аналогичным уравнениям, что и скорости адсорбции $U_{{}}^{{VB}}$, для которых выражения выписаны выше. Так, в модели 4 скорость десорбции $U_{{}}^{{BV}}$ задается выражением: $U_{{}}^{{BV}} = \hat {K}_{{}}^{{BV}}\theta _{{}}^{B}S_{{}}^{B},$ где $\hat {K}_{{}}^{{BV}}$ – константа скорости, $\theta _{{}}^{B}$ – плотность вакансий, $S_{{}}^{B}$ – функция неидеальности:

${\text{ }}S_{{}}^{B} = {{\left[ {S_{{pair}}^{B}} \right]}^{{{{z}_{{}}} - \hat {m}}}},$
$\begin{gathered} S_{{pair}}^{B} = \sum\limits_{j = B,V} {\theta _{{}}^{{Bj}}\exp \left\{ {\beta \delta \varepsilon _{{}}^{{Bj}}} \right\}} {\text{/}}\theta _{{}}^{B} = \\ = \;1 + \sum\limits_{j = B} {\theta _{{}}^{{Bj}}{{x}^{{Bj}}}} {\text{/}}\theta _{{}}^{B}, \\ \end{gathered} $
${{x}^{{Bj}}} = \exp \left\{ {\beta \delta {{\varepsilon }^{{Bj}}}} \right\} - 1,$
$\delta {{\varepsilon }^{{Bj}}} = {{\varepsilon }^{{Bj*}}} - {{\varepsilon }^{{Bj}}} = {{\varepsilon }^{{Bj}}}\left( {{{\alpha }_{\varepsilon }} - 1} \right).$

Анализ значений $U_{{}}^{{BV}}$ и $U_{{}}^{{VB}}$ позволил сделать главные выводы работы: скорости десорбции в моделях 3 и 4 полностью совпадают с кривыми для скоростей адсорбции 3 и 4 соответственно на рис. 2. Это доказывает самосогласованность указанных двух моделей. В моделях 1 и 2 имеются отклонения между скоростями адсорбции и десорбции, из чего следует нарушение самосогласованности в данных моделях.

Нами исследованы зависимости степени расхождения скоростей адсорбции UVB и десорбции UBV от параметра αε, задающего энергию взаимодействия активированного комплекса, и от плотности газа В (рис. 3). Показаны зависимости скоростей для модели 1 (1, 2) и модели 2 (3, 4) от плотности газа B. Здесь область определения плотности газа соответствует области определения давления: 0 < ${{P}^{{\text{B}}}}{\text{/}}P_{s}^{{\text{B}}}$ < 0.9.

Рис. 3.

Зависимости скорости адсорбции UVB и скорости десорбции UBV азота на кремнеземе от плотности газа B при αε = 0 (а), 0.5 (б), 1 (в), 1.5 (г).

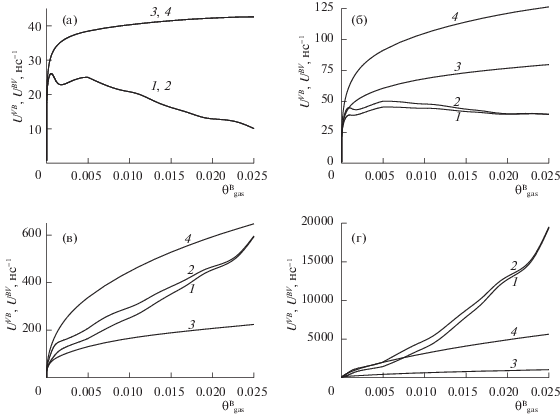
Когда αε = 0 (рис. 3а), отношение функций неидеальности прямой и обратной реакций становится тождественным функции неидеальности изотермы. Это следует из определения самих скоростей реакций и выполняется в рамках любых моделей. В результате получаем, что скорости адсорбции и десорбции совпадают для любой модели по определению, т.е. полностью совпадают кривые 1 и 2 модели 1 и кривые 3 и 4 модели 2. Согласно рис. 3б–3г, рассогласование в модели 1 невелико и практически не зависит от αε: кривые 1 и 2 лежат одинаково близко друг к другу. Рассогласование в модели 1 уменьшается с ростом плотности газа (с увеличением давления в системе). Рассогласование в модели 2 существенно: кривые 3 и 4 сильно отклоняются друг от друга. Различие между скоростями адсорбции (кривая 3) и десорбции (кривая 4) растет с ростом αε и плотности газа (с увеличением давления в системе). Характер кривых (монотонный и немонотонный) на рис. 3 повторяет характер соответствующих кривых 1 и 2 на рис. 2, так как плотность газа (абсциссы на рис. 3) изменяется монотонно с ростом давления газа (абсциссы на рис. 2).

Радиус аэрозоля. Данные рис. 1–3, относятся к фиксированному радиусу аэрозоля: R = 75 межмолекулярных расстояний. Данный радиус R наравне с температурой образования капли, которая впоследствии подвергается закалке, определяет межмолекулярные распределения частиц адсорбента в переходной области, а значит, изменяет показатели неоднородности поверхности.

Степень рассогласования рассмотрим для моделей 1 и 2 в зависимости от радиуса частиц аэрозоля R, который влияет на молекулярные распределения в переходной области адсорбента. На рис. 4 показаны зависимости скорости адсорбции UVB и скорости десорбции UBV азота на кремнеземе по моделям 1 и 2 от радиуса частиц адсорбента R, выраженного в числах межмолекулярных расстояний, при плотности газа B $\theta _{{{\text{gas}}}}^{{\text{B}}}$ = 0.01 (${{P}^{{\text{B}}}}{\text{/}}P_{s}^{{\text{B}}}$ = = 0.4794) и при αε = 0.5.

Рис. 4.

Зависимости (по моделям 1 (1, 2) и 2 (3, 4)) скорости адсорбции UVB (1, 3) и скорости десорбции UBV (2, 4) азота на кремнеземе от радиуса аэрозоля R.

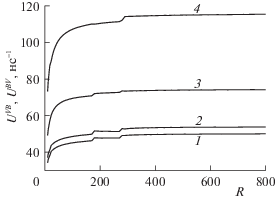
Данные рис. 4 демонстрируют, что рассогласование практически не зависит от величины R для обеих моделей 1 и 2: кривые 1 и 2 распределенной модели и кривые 3 и 4 усредненной одинаково удалены друг от друга вдоль всей области определения. В итоге получаем, что в модели 2 скорости адсорбции и десорбции отличаются в 2 раза. В модели 1 скорость десорбции на 10% больше скорости адсорбции.

Самосогласованность состояния капли. Сама переходная область капли, формирующаяся до ее закалки, описывается распределением плотности $\theta _{q}^{A}$ по монослоям q. Узлы из монослоя q характеризуются зависящими от радиуса капли R числами связей zqh(R) с узлами из монослоев h = q, q ± 1. Скорость конденсации запишется как $U_{q}^{{VB}} = \hat {K}_{q}^{{VB}}\theta _{q}^{V}S_{q}^{V},$ $S_{q}^{V} = \prod\nolimits_{h = q - 1}^{q + 1} {{{{\left[ {S_{{qh}}^{V}} \right]}}^{{{{z}_{{qh}}}(R)}}}} $. Так как переходная область строится по монослоям, то данный вид выражений повторяет выражения для скорости адсорбции в модели 3 за исключением того, что в числителе функции неидеальности $S_{q}^{V}$ отсутствует число частиц ${{\hat {m}}_{{qp}}}$, уменьшающее число свободных узлов в окружении центрального узла.

Для переходной области капли должно выполняться условие самосогласованности описания скоростей элементарных стадий в силу мультипликативной структуры функции неидеальности $S_{q}^{V}$. Выполнение данного условия было доказано аналитически в [5].

ОБСУЖДЕНИЕ РАСЧЕТОВ

Результаты расчетов показали, что с результатами распределенной модели 1 коррелируют только модель 3. Ее особенность состоит в том, что сама величина константы Генри формируется из энергетических вкладов соседних частиц аэрозоля, находящихся в окружающих слоях. Поэтому усреднение по этим константам более точно отражает неоднородность системы, чем просто усреднение по разным монослоям переходной области, как это происходит в моделях 2 и 4. Такая специфика налагает ограничения на выдвигаемые модели структуры поверхности для описания экспериментальных данных. Это показывает, что выбор модели структуры неоднородной системы должен контролироваться моделями разного уровня точности.

Численно подтверждена важность выражения функций неидеальности в виде произведений от конкретных типов соседних узлов (свойство мультипликативности). Строгое самосогласование выполняется для переходной области жидкость–пар на этапе формирования капли перед ее замораживанием. Аналогичная структура выражений функции неидеальности в модели 3 указывает на реализацию самосогласования в модели 3 (и как ее частный случай – модель 4). Наоборот, самосогласование нарушается, когда в функции неидеальности появляются суммы по конфигурациям соседнего узла, т.е. по способам окружения частицами адсорбента соседнего узла в моделях 1 и 2.

Результаты анализа нарушения условия самосогласованности показали, что в распределенной модели 1 степень рассогласования невелика (различие между получаемыми скоростями адсорбции и десорбции при малых плотностях составляет около 10%) и уменьшается с ростом плотности газа в системе, но не зависит от энергии взаимодействия активированного комплекса и радиуса частиц адсорбента R, а в модели 2 степень рассогласования более значительная (скорость адсорбции меньше скорости десорбции при малых плотностях в ~2 раза) и растет с ростом параметра αε и плотности газа, но не зависит от радиуса частиц адсорбента. Эти особенности моделей необходимо учитывать при работе с конкретными типами неоднородных поверхностей.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта № 18-03-00030а).

Список литературы

  1. Еремин Е.Н. Основы химической кинетики. М.: Высшая школа, 1976. 374 с.

  2. Никитин Е.Е. Теория элементарных атомно-молекулярных процессов в газах. М.: Химия, 1970. 456 с.

  3. Киреев В.А. Курс физической химии. М.: Химия, 1975. 773 с.

  4. Хаазе Р. Термодинамика необратимых процессов. М.: Мир, 1967. 544 с.

  5. Товбин Ю.К. // Журн. физ. химии. 2018. Т. 92. № 6. С. 929.

  6. Темкин М.И. // Там же. 1938. Т. 11. С. 169.

  7. Темкин М.И. // Там же. 1941. Т. 15. С. 296.

  8. Темкин М.И. // Там же. 1950. Т. 24. С. 1312.

  9. Эйринг 14. Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций. М.: Изд-во иностр. лит., 1948.

  10. Langmuir I. // J. Amer. Chem. Soc., 1916. V. 38. P. 2217.

  11. Fowler R.H. // Proc. Camb. Phil. Soc. 1935. V. 31. P. 260.

  12. Лодиз Р., Паркер Р. Рост монокристаллов / Пер. с англ. под ред. A. А. Чернова, А. Н. Лобачева. М.: Мир, 1974. 540 с.

  13. Чернов Ф.Ф., Гиваргизов E.И., Багдасаров Х.С., Демьянец Л.Н., Кузнецов В.А., Лобачев А.Н. Современная кристаллография Т. 3. 1980. 408 с.

  14. Мелихов И.В., Меркулова М.С. Сокристаллизация. М.: Химия, 1975. 280 с.

  15. Барре П. Кинетика гетерогенных процессов / Пер. с фр. под. ред. В. В. Болдырева. М.: Мир, 1976. 399 с.

  16. Saito Y., Muller-Krumbhaar H. // J. Chem. Phys. 1979. V. 70. P. 1078.

  17. Cherepanova T.A. // J. Cryst. Growth. 1981. V. 52. Part 1. P. 319.

  18. Товбин Ю.К. Тeория физико-химичeских процeссов на границe газ–твeрдоe тeло. М.: Наука, 1990. 288 с.

  19. Tovbin Yu.K. // Progress in Surface Science. 1990. V. 34. № 1–4. P. 1.

  20. Wu M.K. // Aerosol Science and Technology. 1996. V. 25. P. 392.

  21. Товбин Ю.К., Зайцева Е.С., Рабинович А.Б. // Журн. физ. химии. 2018. Т. 92. № 3. С. 473.

  22. Tovbin Yu.K. // Equiliblia and Dynamics of Gas Adsorption on Heterogeneous Solid Surfaces / W. Rudzinski, W. A. Steele, G. Zgrablich (Eds.), Amsterdam: Elsevier, 1997. P. 201.

  23. Товбин Ю.К. Молекулярная теория адсорбции в пористых телах. М.: Физматлит, 2012. 624 с.

  24. Боголюбов Н.Н. Проблемы динамической теории в статистической физике. М.: Гостехиздат, 1946. 94 с.

  25. Зайцева Е.С., Товбин Ю.К. // Там же. 2018. Т. 92. № 5. С. 816.

  26. Зайцева Е.С., Товбин Ю.К. // Физикохимия поверхности и защита материалов. 2018. Т. 54. № 4. С. пока нет оттиска. Protection of Metals and Physical Chemistry of Surfaces. 2018. V. 54. № 4. З. 557–564.

  27. Грег К., Синг К. Адсорбция. Удельная поверхность. Пористость. М.: Мир, 1984.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал