Журнал физической химии, 2019, T. 93, № 7, стр. 971-975

ПОСТАНОВКА ЗАДАЧИ

Применение классической теории обратимого цикла Карно к реальным объектам, преобразующим теплоту в квалифицированную энергию, приводит к значительному расхождению к.п.д. реального энергетического цикла с к.п.д. обратимого цикла Карно [1]

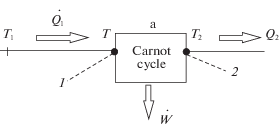
где ${{T}_{1}}$ и ${{T}_{2}}$ – абсолютные температуры, K, нагревателя и холодильника. Это расхождение связано с генерацией энтропии в реальных процессах.

Успешным приемом, позволившим получить столь же простое как формула (1) выражение для к.п.д. реального устройства, $\eta = 1 - \sqrt {\frac{{{{T}_{2}}}}{{{{T}_{1}}}}} $ [2], является принцип максимальной мощности А.И. Алиханова, сформулированный в 1956 г. применительно к крупномасштабным энергетическим установкам [3]. Согласно этому принципу реальный энергетический объект моделируется обратимым циклом Карно, на входе к которому поток тепла ${{\dot {Q}}_{1}}$ поступает из теплообменного устройства $a$, характеризуемого заданной температурой нагревателя ${{T}_{1}}$ и температурой $T$ на выходе из теплообменника (рис. 1).

Предполагается, что передача теплоты от теплообменника к циклу Карно протекает обратимым образом при температуре $T$, передача теплоты от цикла Карно к холодильнику протекает обратимым образом при температуре равной температуре холодильника ${{T}_{2}}$. Следовательно, обратимый цикл Карно в реальном устройстве функционирует между температурами $T$ и ${{T}_{2}}$, и его к.п.д. можно записать как

где ${{T}_{2}} < T < {{T}_{1}}$.

Теплообменник $a$ с заданным механизмом теплопереноса является необратимым устройством, генерирующим энтропию. Поток квалифицированной энергии $\dot {W}$, генерируемый циклом Карно, может быть представлен в виде произведения к.п.д. цикла Карно (2), являющегося возрастающей функцией $T$, и потока тепла ${{\dot {Q}}_{1}}$ из теплообменника к циклу Карно, являющегося убывающей функцией $T$,

В силу указной структуры формулы (3) $\dot {W}$ имеет максимум по $T$, и согласно принципу А.И. Алиханова температура $T$ определяется из условия

При этом к.п.д. реального процесса $\eta $ совпадает с к.п.д. внутреннего цикла Карно $\eta _{C}^{{({\text{in}})}}$ (2)

Однако $\eta < {{\eta }_{C}}$, где ${{\eta }_{C}} = 1 - \frac{{{{T}_{2}}}}{{{{T}_{1}}}}$ – к.п.д. воображаемого цикла Карно, непосредственно подключенного к источнику тепловой энергии. Замечательно, что при таком подходе важен тип теплопереноса в теплообменнике, в то же время такие детали, как коэффициент теплопроводности и геометрические параметры теплообменника являются несущественными.

Определим индекс механизма переноса теплоты как к.п.д. внутреннего цикла Карно (2), рассчитанный по температуре $T$, соответствующей максимальной мощности тепловой машины с данным механизмом теплопереноса. Индекс механизма теплопереноса позволяет ранжировать различные модели теплопереноса, такие как свободно-конвективный перенос (ламинарный и вихревой), молекулярный перенос (кондукция), перенос теплоты конденсацией пара и при некоторых дополнительных предположениях перенос теплоты излучением.

РАНЖИРОВАНИЕ МЕХАНИЗМОВ ПЕРЕНОСА ТЕПЛОТЫ

В общей теории явлений переноса поток теплоты ${{\dot {Q}}_{1}}$ описывают на основе безразмерного коэффициента теплоотдачи, или числа Нуссельта $Nu$ [4, 5]

Здесь $L$ – характерный размер области теплопереноса $a$, м; $\lambda $ – коэффициент теплопроводности области теплопереноса, Дж/(с м К), $\Delta T$ – движущая сила теплопереноса, К. Число Нуссельта зависит от физико-химических свойств теплоносителя и геометрии области теплопереноса [5, 6] где $C$ – безразмерная константа, ${{\alpha }_{V}}$ – коэффициент термического расширения теплоносителя, 1/К; $k$ – коэффициент температуропроводности теплоносителя, м²/с; $\nu $ – кинематическая вязкость теплоносителя, м²/с; $L$ – характерный размер области $a$, м; $g$ – ускорение силы тяжести, м/с². Показатель степени $n$ в формуле (7) назовем параметром Нуссельта.

В соответствии со схемой на рис. 1 в качестве движущей силы $\Delta T$ естественно принять величину $\left( {{{T}_{1}} - T} \right)$ и представить поток теплоты (6), (7) в виде

где $C_{n}^{*} = C\frac{\lambda }{L}{{\left( {{{\alpha }_{V}}\frac{{g{{L}^{3}}}}{{\nu k}}} \right)}^{n}}$ – размерная величина, Дж/(м² с К^–(n + 1)). Формула (8) представляет собой общее соотношение, возникающее при математическом моделировании процессов переноса теплоты веществом [5, 6].

В безразмерных величинах

индекс механизма теплопереноса (3) принимает вид

Используя формулы (4), (8) и безразмерные величины (9), преобразуем уравнение (5) в квадратное уравнение относительно безразмерной температуры $\theta $, соответствующей максимуму мощности тепловой машины с заданными параметром Нуссельта $n$ и параметром внешних условий $\chi = \frac{{{{T}_{2}}}}{{{{T}_{1}}}}$,

Нетрудно убедиться, что решение уравнения (11) имеет вид

Продифференцируем уравнение (11) по параметру $n$ при постоянном параметре внешних условий $\chi $. После преобразований получаем

Поскольку $0 < \chi < \theta < 1$, то нетрудно убедиться, что производная $\theta _{n}^{'}$ – отрицательная функция параметра Нуссельта $n$, и мы приходим к важному выводу – с увеличением параметра Нуссельта при фиксированном параметре внешних условий $\chi $ уменьшается температура $\theta $, соответствующая максимальному экстремальному значению мощности $\dot {W}$, и одновременно уменьшается индекс механизма теплопереноса (10). Этот вывод позволяет ранжировать механизмы теплопереноса по величине индекса.

Свободно конвективный перенос теплоты. При свободной конвекции параметр Нуссельта $n$ зависит от режима движения теплоносителя в области $a$. В практических задачах различают два режима движения – ламинарный и вихревой. В ламинарном режиме $n = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$; в вихревом режиме $n = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ [6]. Следовательно, при указанных значениях параметра $n$ эффективность механизма теплопереноса в режиме вихревой конвекции меньше эффективности механизма теплопереноса в режиме интенсивной ламинарной конвекции.

Кондуктивный теплоперенос. Кондуктивному теплопереносу соответствует параметр Нуссельта $n = 0$, описывающему режим линейной теплопроводности. Из (10) и (12) при $n = 0$ следует, что индекс механизма переноса теплоты кондукцией, по определению равный $\eta = 1 - \sqrt {{{{{T}_{2}}} \mathord{\left/ {\vphantom {{{{T}_{2}}} {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}} $¹¹, превосходит индекс переноса теплоты в режиме свободной конвекции, которым соответствуют параметры Нуссельта $n = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ и $n = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$. Это на первый взгляд несколько парадоксальный результат. Действительно, интенсивное перемешивание теплоносителя сближает температуры $T$ и ${{T}_{1}}$, уменьшая движущую силу теплопереноса. Из общей формулы (8) следует, что уменьшение потока теплоты тем значительнее, чем больше параметр Нуссельта. И хотя одновременно увеличивается к.п.д. цикла Карно (3), но первый фактор является преобладающим: при $T \to {{T}_{1}}$ имеем ${{\dot {Q}}_{1}} \to 0$, $\eta \to 1 - \frac{{{{T}_{2}}}}{{{{T}_{1}}}} = {\text{const}}$.

Перенос теплоты конденсацией сухого насыщенного пара. Поток насыщенного пара с температурой ${{T}_{1}}$, покидающий источник теплоты, конденсируется на поверхности цилиндрической трубы, поддерживая постоянную температуру поверхности $T < {{T}_{1}}$. Конденсируясь, пар передает единице поверхности трубы поток теплоты конденсации ${{\dot {Q}}_{1}}$, описывается формулой [6],

где $\tilde {C}$ – некоторая константа. Следовательно, параметр Нуссельта $n = - 0.25$ и индекс переноса теплоты конденсацией пара превосходит индексы переноса теплоты кондукцией и свободной конвекцией.

Перенос теплоты излучением. Различают два способа преобразования излучения в квалифицированную энергию: прямое преобразование (фотоэлемент) и преобразование через промежуточную стадию генерирования теплоты. В отличие от рассмотренных механизмов теплопереноса перенос теплоты излучением не связан с вещественным теплоносителем, поэтому приведенная ранее схема на рис. 1 нуждается в уточнении. Источник теплоты (излучатель) будем рассматривать как абсолютно черное тело с постоянной температурой ${{T}_{1}}$. Приемник излучения будем рассматривать как непрозрачное тело с поглощательной способностью $A$, излучательной способностью (степень черноты) $\varepsilon $ и температурой $T$. Параметры $A$ и $\varepsilon $ – безразмерные величины. Поток излучения от излучателя равен ${{\dot {J}}_{{{\text{in}}}}} = \alpha T_{1}^{4}$, где $\alpha $ – константа Стефана–Больцмана. Приемник излучения, поглощая поток излучения $\alpha AT_{1}^{4}$, частично преобразует его в поток теплоты ${{\dot {Q}}_{1}}$, передаваемый циклу Карно, и частично рассеивает в окружающую среду в виде собственного излучения ${{\dot {J}}_{{{\text{out}}}}} = \alpha \varepsilon {{T}^{4}}$. Поток теплоты ${{\dot {Q}}_{1}}$ преобразуется циклом Карно в поток работы $\dot {W}$ и тепловой поток ${{\dot {Q}}_{2}}$, рассеиваемый в окружающую среду (рис. 2).

Из квазистационарного уравнения баланса энергии для приемника излучения

следует, что тепловой поток ${{\dot {Q}}_{1}}$, поступающий из приемника излучения к циклу Карно, равен

Мощность $\dot {W}$ (4) с учетом формулы (15) принимает вид

Применив к выражению (16) принцип максимальной мощности Алиханова (5) и перейдя к безразмерным величинам (9), после некоторых преобразований получим алгебраическое уравнение пятой степени относительно безразмерной температуры $\theta = {T \mathord{\left/ {\vphantom {T {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}$

Параметр $E = {A \mathord{\left/ {\vphantom {A \varepsilon }} \right. \kern-0em} \varepsilon }$ равен отношению поглощательной и излучательной способностей приемника излучения цикла Карно.

Из определения индекса механизма теплопереноса (3) следует, что равенство температур $T$ на стадии получения теплоты циклом Карно при разных механизмах переноса теплоты соответствует равенству их индексов. В частности, если к.п.д. цикла Карно при кондуктивном теплопереносе равен к.п.д. цикла Карно при излучении, то безразмерная температура $\sqrt \chi $ является корнем уравнения (28). Подставим $\theta = \sqrt \chi $ в уравнение (28) и после некоторых преобразований получим соотношение

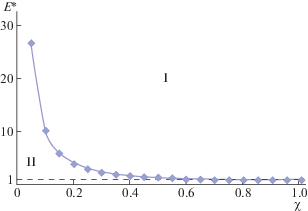
где $E* = {{E}^{{ - 1}}} = \frac{\varepsilon }{A}$. График функции $E{\kern 1pt} {\text{*}}(\chi )$ представлен на рис. 3.

Линия $E{\kern 1pt} {\text{*}}(\chi )$ является линией равенства индексов кондукции и излучения и разделяет плоскость $\left( {E{\text{*}},{\text{ }}\chi } \right)$ на две области: над линией ($\varepsilon > A$) всегда индекс переноса теплоты излучением превышает индекс переноса теплоты кондукцией, и, следовательно, превышает индексы свободно-конвективного переноса теплоты. Ниже линии ($\varepsilon < A$) индекс кондуктивного переноса теплоты меньше индекса переноса теплоты излучением. Таким образом, если приемник теплоты удовлетворяет условию $\varepsilon > A$, то при всех значениях параметра внешних условий $\chi = {{{{T}_{2}}} \mathord{\left/ {\vphantom {{{{T}_{2}}} {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}$ индекс переноса теплоты излучением превосходит индекс переноса теплоты кондукцией. Следовательно, для устройств максимальной мощности излучение как способ переноса теплоты к преобразующему устройству при $\varepsilon > A$ эффективнее кондукции и свободно конвективного теплопереноса.

Таким образом, предложен термодинамический метод ранжирования механизмов переноса теплоты. В качестве количественной оценки механизма теплопереноса введен индекс механизма теплопереноса, равный к.п.д. тепловой машины с данным механизмом теплопереноса при условии максимальной мощности. Показано, что величина индекса определяется суперпозицией двух факторов – движущей силой процесса теплопереноса и к.п.д. идеального цикла Карно. Проведено ранжирование нескольких механизмов переноса теплоты по величине индекса – излучение, конденсация сухого пара, кондукция, свободная конвекция ламинарная и вихревая. Показано, что для энергогенерирующих устройств максимальной мощности конденсация и излучение обладают наибольшими индексами среди других механизмов переноса теплоты.