Журнал физической химии, 2020, T. 94, № 12, стр. 1889-1898

УРАВНЕНИЯ МОДЕЛИ

В МРГ объем поры разбивается на отдельные элементарные ячейки со стороной, равной диаметру молекулы λ. Ячейкам присваивается порядковый номер  f  и координаты положения поперек (1 ≤ h ≤ H) и вдоль (1 ≤ q ≤ L) поры, где Н – ширина поры, L – длина транслируемого вдоль поры участка (координатам (h, q) отвечает порядковый номер f ). Внутри переходной области поры ячейка с номером f характеризуется числом связей ${{z}_{{fg}}}$ с соседними ячейками g из ближайшего окружения f, g ∈ G(f ) [13]. В работе использовалась примитивная кубическая решетка с координационным числом z = 6. По одной из осей пространства узлы транслируются как узлы одного типа, а по двум другим осям выделяется двумерный участок поры шириной H и длиной L с полным выделением узлов разного типа. Поэтому каждый узел f имеет два соседних узла того же типа z_ff = 2 и четыре соседних узла, различных по типу между собой и с центральным узлом f, z_fg = 1, g ≠ f.

Расчет изотермы адсорбции и локальных заполнений узлов разных групп, учитывающих энергетическую неоднородность узлов решетки и взаимодействия между ближайшими молекулами, обеспечивает решение системы уравнений:

где θ – степень заполнения объема пор при давлении Р; F_f – доля узлов f, $\sum\nolimits_f {{{F}_{f}}} = 1$; θ_f – мольная доля молекул в узлах f; a_f = $a_{f}^{0}$exp(βQ_f) – константа Генри молекул в узлах f, $a_{f}^{0}$ – предэкспоненциальный фактор, ${{Q}_{f}} = Q_{f}^{*}{\text{/}}{{\varepsilon }^{{{\text{AA}}}}}$ – потенциал поля стенки $Q_{f}^{*}$ в узле f, нормированный на ε_AA, ε_AA – параметр латерального взаимодействия ближайших соседей, β = (k_ВT)^–1, k_В – постоянная Больцмана, T – температура. Дополнительно учитываются следующие нормировочные соотношения для парных вероятностей $\theta _{{fg}}^{{ij}}$ нахождения частиц i и j на соседних узлах в слоях f и g: $\theta _{{fg}}^{{{\text{AA}}}}$ + $\theta _{{fg}}^{{{\text{AV}}}}$ = θ_f ≡ ≡ $\theta _{f}^{{\text{A}}}$ и $\theta _{{fg}}^{{{\text{VA}}}}$ + $\theta _{{fg}}^{{{\text{VV}}}}$ = $\theta _{f}^{{\text{V}}}$ = 1 – θ_f (символ V означает вакансию – свободный узел), а также $\theta _{f}^{{\text{A}}}$ + $\theta _{f}^{{\text{V}}}$ = 1.

Равновесное распределение частиц по всему множеству узлов {θ_f} и давление P находили итерационным методом Ньютона из системы уравнений (1), задавая θ при фиксированной T и прочих параметрах. Точность решения этой системы не менее чем 0.1%. Плотности сосуществующих газовой и жидкой фаз определяли с помощью построения Максвелла [22].

На основе найденных локальных распределений молекул свободная энергия F, относящаяся к сечению щелевидной или цилиндрической поры постоянного сечения, в квазихимическом приближении записывается как [19]:

где N – общее число узлов в рассматриваемом фрагменте поры; $\nu _{f}^{i}$ = –β^–1ln($a_{f}^{i}$P) – одночастичный вклад частицы сорта i, адсорбированной на узле f, в свободную энергию системы ($\nu _{f}^{{\text{V}}}$ = 0); символ k относится к одному из компонентов смеси – опорный сорт частиц, 1 ≤ k ≤ s, k ≠ i, s – номер последнего состояния занятости – вакансии. Конкретный номер символа k не играет роли – этот выбор может быть обусловлен удобством решения задачи.

Функция $M_{f}^{i}$ определяет вклад, вносимый частицами сорта i в свободную энергию системы для узла с номером f. Разность $M_{f}^{i}$ – $M_{f}^{{\text{V}}}$ определяет уравнение на локальную изотерму адсорбции (1).

УСЛОВИЯ РАСЧЕТА

Как и в работе [13], рассматривается равновесное распределение атомов аргона в парожидкостном равновесии внутри щелевидной поры шириной H и с заданным потенциалом стенок пор в первом монослое, примыкающем к стенке, ${{Q}_{h}}_{{ = 1}}$. В последующих монослоях вплоть до монослоя h* как $Q_{{2 \leqslant h \leqslant h}}^{*}$ = ${{Q}_{h}}_{{ = 1}}$/h³, где h* – монослой поры, до которого действует потенциал стенки поры включительно, $Q_{{h > h}}^{*}$ = 0 [6, 16–18]. Оба указанных параметра (Н и ${{Q}_{h}}_{{ = 1}}$) варьируются в широких дипазонах. Величина ${{Q}_{h}}_{{ = 1}}$ (в единицах параметра межчастичного взаимодействия адсорбата ε_AA) меняется от 9.24 (что соответствует графиту) до 0.2 (соответствует матрицам полимера) [6]. В частности, потенциал стенки в первом монослое ${{Q}_{h}}_{{ = 1}}$ = 5 соответствует пористой матрице силикагеля. Рассмотренный диапазон Н (в монослоях или в единицах параметра решетки, равного 1.12σ, где σ – параметр твердой сферы потенциала Леннард-Джонса) менялся от 10 до 5000 [13], но основное внимание уделяется области до 100 нм. Сопоставлялись области действия потенциала стенки до h* = 2 и 9. Температура в системе T = 126 K – относительно высокая температура, но вне критической области расслаивания аргона в объеме.

ЛОКАЛИЗАЦИЯ ГРАНИЦ ДВУХФАЗНОГО КОНТАКТА

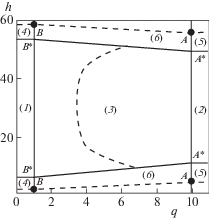
По молекулярным распределениям $\{ \theta _{f}^{{\text{A}}}\} $ флюида, полученным из системы (1) [13], находятся изолинии плотности, эквимолекулярные поверхности, области сосуществования двух и трех фаз, и рассчитываются все физико-химические свойства, в том числе и ПН на трех типах границ фаз: жидкость–пар, твердое тело–жидкость, твердое тело–пар. Анализ молекулярных распределений позволил выделить следующую типовую структуру фазовых состояний адсорбата внутри щелевидной поры. С учетом пленки адсорбата у стенок поры вся рассматриваемая область пространства внутри поры разбивается на следующие области (см. рис. 1): в центре поры 1) жидкость и 2) пар и 3) переходная область между ними жидкость–пар; у стенок поры переходная область 4) жидкость–твердое тело и 5) пар–твердое тело; и между ними область трех фаз 6) жидкость–пар–твердое тело. Выделение двухфазных областей осуществляется на основе значений ширины переходных областей жидкость – твердое тело κ_liq, пар – твердое тело κ_vap и жидкость – пар L, которые были подробно рассмотрены в [13].

На рис. 1 жирные линии ограничивают фазы (жидкость и пар) в поре от переходных областей между фазами. Пунктирные линии – эквимолекулярные поверхности раздела фаз; А* и В* – точки на пересечении с переходными областями границ областей пара и жидкости соответственно (эти точки соединены жирной линией). Отрезок АВ построен по эквимолекулярным границам пар–твердое тело и жидкость–твердое тело, проходящим через точки А и В соответственно.

Каждая из границ раздела характеризуется постоянным значением ширины переходной области, в которых имеется градиент плотности между соседними фазами: жидкость–пар, твердое–жидкость и твердое–пар. Критерием на выделение отдельных двухфазных областей является информация о постоянстве ширины переходных областей, рассчитываемая с заданной точностью [13]. Изменение величины ширины переходной области указывает на смещение вглубь трехфазного контакта. Интерполяция границ твердого тела с жидкостью (точка В* на рис. 1) к пару (точка А* на рис. 1) отделяет область жидкость–пар от области трех фаз жидкость–пар–твердое.

ПН МЕЖДУ ФАЗАМИ ТВЕРДОЕ–ПАР И ТВЕРДОЕ–ЖИДКОСТЬ

Наличие концентрационных профилей на границах раздела фаз формально позволяет рассчитать ПН на границах раздела твердое тело–мобильная фаза. Межфазное натяжение σ определяется разностью свободных энергий приповерхностной области Ω и свободной энергией в объеме раствора Ω₀ в большом каноническом ансамбле [20, 21, 26, 27]. Воспользуемся построениями работ [19, 24, 28] для связи профиля и ПН.

Обсуждаемая адсорбция расслаивающегося флюида в щелевидных порах в общем случае не является равновесной по отношению к состоянию стенки твердого адсорбента. В такой ситуации рассмотрим три варианта использования профиля для оценок ПН твердое тело–мобильная фаза. Это означает использование неравновесных аналогов величины ПН [29], которая выражается теми же самыми формулами через локальные унарные и парные ФР, что и в случае равновесной границы.

Для иллюстрации различий между строго равновесными и неравновесными концентрационными профилями на рис. 2 приведены профили плотности вблизи плоской границы раздел: кривая 1 – профиль плотностей в переходной области жидкость–пар при температуре, близкой к тройной точке; кривая 2 – профиль плотностей в переходной области твердое тело–пар при температуре, близкой к тройной точке; кривые 3 и 4 – профили плотностей в переходной области от стенки с потенциалом ${{Q}_{h}}_{{ = 1}}$ = 1 и 5 соответственно к пару при T = 126 K.

Концентрационные профили 1 и 2, построенные при равновесных условиях, имеют симметричный вид с большим градиентом плотности в центре переходной области и с пологими участками вблизи фаз. На кривой 4, построенной при неравновесных условиях, обусловленных большим потенциалом стенки ${{Q}_{h}}_{{ = 1}}$ = 5, отсутствует пологий участок на концентрационном профиле со стороны плотной фазы – вместо него участок с существенным градиентом плотности, идущим от стенки. Однако на кривой 3, построенной также при неравновесных условиях с потенциалом стенки ${{Q}_{h}}_{{ = 1}}$ = 1, снова имеется пологий участок со стороны плотной фазы, так как заданная величина ${{Q}_{h}}_{{ = 1}}$ = 1 воссоздает состояние системы при равновесии (потенциал стенки совпадает с энергией межмолекулярных взаимодействий).

Все три варианта расчета ПН с формальной строго равновесной точки зрения условны. В литературе очень часто допускается [14], что в рассматриваемой модели разделяющая поверхность находится между атомами твердого тела и первым монослоем флюида (обозначим его как первый вариант)

где A – площадь единичной поверхности; у функции $\mu _{{h,q}}^{{\text{V}}}$ индекс q = 1 для границы твердое тело–жидкость и q = L для границы твердое тело–пар. В этом случае весь профиль дает вклад в адсорбционный избыток, определяющий величину ПН.

Здесь и ниже, согласно [24, 27],

Второй вариант расчета ПН “твердое–флюид” относится к положению разделяющей поверхности как эквимолекулярной плоскости (эквимолекулярная поверхность лежит в монослое ρ_e) между центром поры и поверхностным адслоем (избыточным является второй монослой и далее). Такое определение следует из того факта, что плотность первого монослоя практически одинакова при сильном притяжении, и состояние данного монослоя берется для оценки состояния твердого тела:

Третий вариант представляет собой случай, когда твердое тело является равновесным по отношению к флюиду, и его характеристики получаются при решении задачи при другой температуре, а здесь его состояние заморожено. В этом случае первый монослой, в отличие от предыдущего, отнесен к избытку:

где $\mu _{0}^{{\text{V}}}$ – функция твердого тела, получаемая из отдельной задачи на изотерму состояния твердого тела (как соответствует кривой 4 на рис. 2).

Условие на положение эквимолекулярной поверхности на границе фаз жидкость–твердое тело и пар–твердое тело для второго варианта запишется:

и для третьего варианта запишется соответственно: где ${{\theta }_{0}}$ – плотность твердого тела.

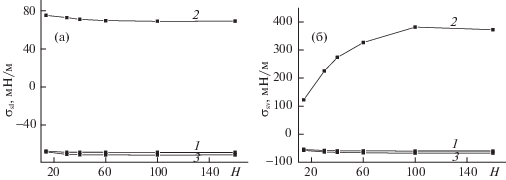
На рис. 3 представлены зависимости ПН аргона на границе жидкости (а) и пара (б) с твердым телом от потенциала стенки ${{Q}_{h}}_{{ = 1}}$ щелевидной поры, шириной H = 60 и h* = 9, при T = 126 K для трех типов фиксации границы: номера кривых 1–3 соотносятся с вариантами положения границы раздела фаз.

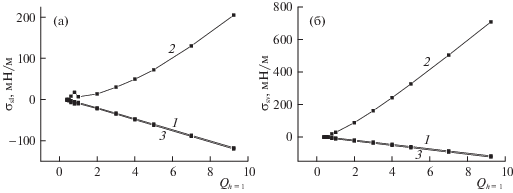
Согласно рис. 3, при больших ${{Q}_{h}}_{{ = 1}}$ ≥ 0.8 величина ПН твердое тело–пар больше по модулю ПН твердое тело–жидкость, а ниже ${{Q}_{h}}_{{ = 1}}$ = 0.8 величина ПН жидкость–твердое тело имеет максимум на кривой 2 (рис. 3а) и минимум на кривых 1 и 3 (рис. 3а) в зависимости от ${{Q}_{h}}_{{ = 1}}$, благодаря чему величина ПН жидкость–твердое тело становится больше по модулю ПН пар–твердое тело. Также из рис. 3 видно, что значения ПН твердое тело–пар и твердое тело–жидкость по первому и второму вариантам (кривые 1 и 3) отрицательны при любых ${{Q}_{h}}_{{ = 1}}$ и с убыванием ${{Q}_{h}}_{{ = 1}}$ уменьшаются по модулю.

Значения ПН твердое тело–жидкость по варианту 2 (кривая 2 на рис. 3а) положительны при любых ${{Q}_{h}}_{{ = 1}}$. С убыванием ${{Q}_{h}}_{{ = 1}}$ до ${{Q}_{h}}_{{ = 1}}$ = 2 ПН убывает, от ${{Q}_{h}}_{{ = 1}}$ = 2 до ${{Q}_{h}}_{{ = 1}}$ = 0.8 величина ПН возрастает и ниже ${{Q}_{h}}_{{ = 1}}$ = 0.8 ПН снова убывает. Величины ПН твердое тело–пар (кривая 2 на рис. 3б) положительны при больших и средних ${{Q}_{h}}_{{ = 1}}$, с уменьшением ${{Q}_{h}}_{{ = 1}}$ убывают вплоть до значения ${{Q}_{h}}_{{ = 1}}$ = 0.6, при котором ПН становится отрицательным, далее с убыванием ${{Q}_{h}}_{{ = 1}}$ ПН возрастает.

На рис. 4 представлены зависимости ПН аргона на границе жидкости (а) и пара (б) с твердым телом от ширины щелевидной поры H c потенциалом стенки ${{Q}_{h}}_{{ = 1}}$ = 5 и h* = 9 при T = 126 K для трех типов фиксации границы (номера кривых 1–3 указывают номера вариантов).

Согласно рис. 4а, ПН твердое тело–жидкость по всем вариантам (кривые 1–3) убывает с ростом H, слабо изменяясь при больших H. Как было показано в [13], с ростом H существенно возрастает плотность жидкости в поре, что уменьшает градиент плотности от жидкости к твердому телу и в результате уменьшает соответствующее ПН. На рис. 4б ПН твердое тело–пар по всем вариантам (кривые 1–3) растет по модулю с ростом H. Из-за большой области значений, которую занимает кривая 2, построенная по варианту 2, в котором первый монослой у стенки не дает вклада в избыточную свободную энергию при расчете ПН, по сравнению со слабым изменением значений на кривых 1 и 3 следует, что изменение ширины поры H сильнее всего влияет на внутренние монослои поры и слабее всего на первый (пристеночный) монослой. Однако в виду близости кривых 1 и 3 и схожести их качественного поведения следует, что вклад от первого монослоя является определяющим для конечного значения ПН твердое тело–пар.

Подробно соотношение между ПН твердое тело–жидкость и твердое тело–пар рассмотрено на рис. 5, где разница между этими значениями дана как функция от ${{Q}_{h}}_{{ = 1}}$ (рис. 5а) и H (рис. 5б) для трех вариантов расчета ПН (номера на кривых соответствуют вариантам ПН). Кривые по вариантам 1 и 3 показаны на основных полях, а кривая по второму варианту – на вставке. Рисунок 5 наглядно демонстрирует, что по первому и второму вариантам ПН твердое тело–пар больше ПН твердое тело–жидкость при любых ${{Q}_{h}}_{{ = 1}}$ и H, так как кривые 1 и 3 лежат полностью в области положительных значений. Согласно третьему варианту, преимущественно ПН твердое тело–пар меньше ПН твердое тело–жидкость в широких областях значений ${{Q}_{h}}_{{ = 1}}$ и H (кривая 2 лежит в области отрицательных значений), и только при малых ${{Q}_{h}}_{{ = 1}}$ < < 0.8 (рис. 5а) и H < 25 (рис. 5б) кривая 2 лежит в области положительных значений.

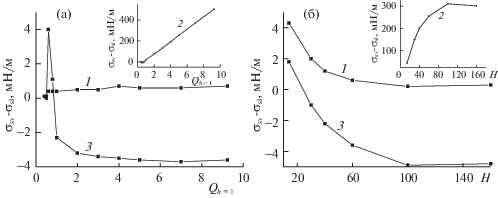
Согласно рис. 5, по всем вариантам с убыванием ${{Q}_{h}}_{{ = 1}}$ и H различие между ПН твердое тело–жидкость и ПН твердое тело–пар уменьшается, за исключением резкого скачка на кривой 3 рис. 5а при ${{Q}_{h}}_{{ = 1}}$ < 0.5. Но эта область относится к так называемым “несмачиваемым” ситуациям, для которой характерны разные особенности.

ГРАНИЦА РАЗДЕЛА МЕНИСКА ПАР–ЖИДКОСТЬ

Найденные профили для пара и жидкости служат граничными условиями для расчета двумерного распределения плотности между паровой и жидкой фазами внутри щелевидной поры. Именно между этими профилями (кривыми 1 и 2) находятся переходные области θ_q,h, формирующие двумерные неоднородные распределения молекул. Сами двумерные распределения находятся из системы уравнений на плотности, аналогичной системе уравнений (1), в которой номера узлов f и g заменены на двумерные символы в виде f = q, h [6]: ${{\theta }_{q}}_{{,h}}$ с двумя индексами номера вдоль нормали 2 ≤ q ≤ (L – 1), 1 ≤ h ≤ H, где (L – 2) – ширина переходной области вдоль линии раздела.

Одно из самых простых следствий рассматриваемой молекулярной теории – вывод о характере изменения формы поверхности натяжения и величины ПН на границе фаз. В узких порах область парожидкостного перехода, а следовательно, и поверхность натяжения имеет сложную форму, отличающуюся от традиционно предполагаемых цилиндрической (для щелевидных) и сферической (для цилиндрических пор). Формы переходной области и величины ПН зависят от локальных равновесных распределений (частиц адсорбата в порах), зависящих, в свою очередь, от размера пор, температуры, материала стенок пор и свойств адсорбата. Анизотропия локальных распределений частиц в порах служит причиной тому, что величина ПН и характеристики самой поверхности натяжения имеют ярко выраженный локальный характер.

Методика определения локального значения ПН σ(h). Уравнения для локальных вкладов свободной энергии (2) и (3) относятся к любым подсистемам неоднородно распределенного флюида. Определение локальных молекулярных распределений (1) позволяет рассчитать свободную энергию в узких порах и, установив положение поверхности раздела фаз, определить ПН. В порах постоянного сечения будем рассматривать узлы h, находящиеся вдоль оси  f  решеточной структуры параллельной стенкам поры [25]. Вдоль каждой оси переходная область имеет свою ширину, которая определяется аналогично эквимолекулярной разделяющей поверхности. Процедура поиска положения поверхности натяжения состоит в поиске узла h* переходной области вдоль оси f и его долей, относящихся к сосуществующим фазам. В результате для каждой оси ширина переходной области разбивается на две части, относящиеся к сосуществующим паровой и жидкостной фазам: κ(f ) = κ_п(f ) + κ_ж(f ), где κ_п,ж(f ) – ширина области, относящейся к паровой (жидкостной) фазе внутри переходной области. За границу раздела фаз принимается традиционная для термодинамики эквимолекулярная поверхность, которая строится на основе профилей плотностей $\{ \theta _{f}^{A}\} $ в переходной области щелевидной поры. Положение каждой точки ${{\rho }_{h}}$ эквимолекулярной поверхности определяется по материальному балансу в монослое h:

где ${{F}_{{q|h}}}$ – доля узлов q в монослое h, ${{\theta }_{{h,q}}}$ – плотность в ячейке с координатами (h, q).

При расчете локальной избыточной свободной энергии учитывается весь профиль локальных плотностей θ(h, q) вдоль каждой из осей решеточной структуры f, а также тот факт, что вдали от границы раздела локальные значения плотностей θ(f ) и свободной энергии F_п,ж(f ) являются переменными по сечению поры. Это приводит к пространственной зависимости локальной величины поверхностного натяжения σ(f ).

При построении площади локальной поверхности плоскости натяжения S(f ), относящей к ячейке h*(f ), в силу малости размеров ячейки и дискретности рассматриваемых величин плотности, свободной энергии и т.д., можно ограничиться кусочной аппроксимацией общей поверхности натяжения внутри каждой ячейки h*(f ), находящейся на границе пар–жидкость. В первом приближении аппроксимация поверхности может быть задана в виде математической плоскости, разделяющей объем ячейки на части, относящиеся к жидкой и паровой фазам [25]. Вторым приближением служит введение секущей поверхности второго порядка и т.д.

ПН рассчитывается с учетом ориентации сечения внутри ячейки [25]. Для этого точечное значение ПН в ячейке (h, q) нормировалось на площадь эквимолекулярной поверхности в ячейке (h, q), которая проходит в ней под углом, определяемым координатами соседних точек эквимолекулярной поверхности. На рис. 6 сравниваются профили локальных значений ПН жидкость–пар в монослоях h с корректировкой по углу наклона поверхности раздела в ячейке (кривая 1) и без (кривая 2) при ${{Q}_{h}}_{{ = 1}}$ = 5, H = 60, h* = 9 и T = 126 K.

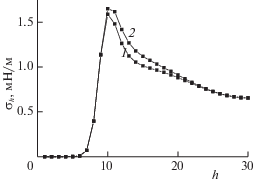
Согласно рис. 6, корректировка по углу наклона поверхности раздела в ячейке уменьшает величину ПН жидкость–пар (кривая 1 лежит ниже кривой 2). Существенное различие между кривыми 1 и 2 на рис. 6 имеется только при достаточном отдалении как от стенки поры, так и от центра поры (где поверхность раздела фаз проходит практически перпендикулярно стенкам пор, а поэтому корреляционный коэффициент будет равен единице).

В общем случае влияние уменьшения размера поры на уменьшение ПН проявляется через два фактора. Во-первых, уменьшается центральная область поры, ответственная за капиллярную конденсацию. Во-вторых, происходит уменьшение критической температуры, и различие между фиксированной температурой и критической уменьшается. Эффект уменьшения ПН жидкости по мере приближения к критической температуре хорошо известен [14, 27]. В результате скорость убывания величины ПН с уменьшением ширины или диаметра поры в узких порах должна быть выше, чем в объемной фазе. А так как с уменьшением размера поры капиллярная конденсация исчезает [6], то нижним пределом величины поверхностного натяжения является его нулевое значение.

Выражение для локального значения ПН σ_h в монослое h:

где ρ_h – положение эквимолекулярной границы в монослое h. Усредненное по ширине поры значение ПН жидкость–пар будет равно: где ${{F}_{h}}$ – доля узлов в монослое h от общего числа узлов в поре.

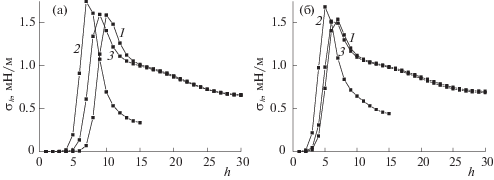
На рис. 7 представлены зависимости локального ПН (кривая 1) жидкость–пар аргона в центре щелевидной поры h = H/2 и усредненного по ширине щелевидной поры значения ПН жидкость–пар аргона (кривая 2) при h* = 9 и T = 126 K. На рис. 7а показаны зависимости от ширины поры H при ${{Q}_{h}}_{{ = 1}}$ = 5, на рис. 7б – зависимости от потенциала стенки ${{Q}_{h}}_{{ = 1}}$ при H = 60.

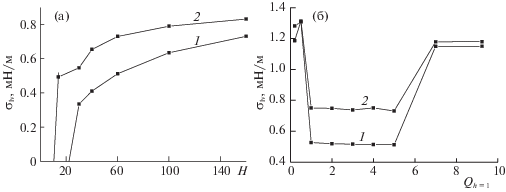
С ростом ширины поры H (рис. 7а) локальное значение ПН в центре поры (кривая 1) и среднее значение ПН (кривая 2) растут, при этом среднее значение ПН всегда больше значения ПН в центре поры вследствие возрастания локальных величин ПН с приближением монослоя к адсорбционной пленке. Как было показано в [13], с ростом ширины поры H сначала на “объемные” значения выходит ширина переходной области жидкость–пар L, затем плотности сосуществующих фаз и, наконец, величина ln(a₀P). Когда величина ln(a₀P) достигнет своего “объемного” значения, одновременно с ней при том же Н⁰ принимает “объемное” значение и ПН жидкость–пар.

С ростом потенциала стенки поры ${{Q}_{h}}_{{ = 1}}$ (рис. 7б) локальное значение ПН в центре поры (кривая 1) возрастает при малых ${{Q}_{h}}_{{ = 1}}$ < 0.6, когда имеется изгиб границы жидкость–пар в сторону жидкости (аналог капель в паре), затем при дальнейшем росте ${{Q}_{h}}_{{ = 1}}$ граница жидкость–пар приобретает изгиб в сторону пара (аналог пузырьков в жидкости), и ПН в центре резко убывает, и в области 0.6 < ${{Q}_{h}}_{{ = 1}}$ < < 7 убывает, после чего резко возрастает при больших ${{Q}_{h}}_{{ = 1}}$ вследствие сильных молекулярных перераспределений в результате сильного потенциала стенок пор. При этом усредненное по ширине поры ПН (кривая 2) имеет схожее поведение с ПН в центре поры (кривая 1), отклонения от которого обусловлены вкладами от монослоев вблизи адсорбционной пленки.

ПРОФИЛЬ ЛОКАЛЬНОГО ПН ЖИДКОСТЬ–ПАР ПОПЕРЕК ПОРЫ

На рис. 8 показаны профили локальных значений ПН жидкость–пар в щелевидной поре шириной H = 30 (кривая 2) и 60 (кривые 1, 3), потенциалом стенок ${{Q}_{h}}_{{ = 1}}$ = 2 (кривая 3) и 5 (кривые 1, 2) и дальнодействием потенциала стенок до h* = 2 (рис. 8б) и 9 (рис. 8а).

Согласно рис. 8, с ростом ширины поры H, потенциала стенок поры ${{Q}_{h}}_{{ = 1}}$ и дальнодействия потенциала стенок h* локальные значения ПН в адпленке (до максимума на кривых на рис. 8) уменьшаются, а в последующих монослоях (после максимума на кривых) локальные значения ПН наоборот увеличиваются. Так, кривая 1 с наибольшими H и ${{Q}_{h}}_{{ = 1}}$ на рис. 8а и 8б до своего максимума лежит ниже, а затем выше кривых 2 и 3. Так же, как и кривые на рис. 8а, построенные при h* = 9, до своего максимума лежат ниже, а затем выше аналогичных кривых на рис. 8б.

Уменьшение ширины поры с H = 60 (кривые 1) до H = 30 (кривые 2) почти вдвое уменьшает значение ПН в центре поры (правая крайняя точка на кривых). Изменение потенциала стенок пор ${{Q}_{h}}_{{ = 1}}$ и его дальнодействия h* практически не меняют значение ПН в центре поры: кривые 1 и 3 почти совпадают на правых концах как на рис. 8а, так и на рис. 8б. На всех кривых рис. 8 вблизи стенки, где крайне малый градиент плотности, локальные значения ПН обращаются в ноль. В промежуточной области между областью стенки (где градиент плотности практически отсутствует) и центральной областью поры (где имеется градиент плотности имеется только в двух направлениях между разными монослоями h) появляется максимум ПН за счет градиентов как вдоль монослоя h, так и относительно соседних монослоев h ± 1. Это дает дополнительный вклад в локальное ПН, увеличивая его.

ЗАКЛЮЧЕНИЕ

Выделение трех двухфазных границ флюида в щелевидной поре и их унифицированное описание, в том числе оценка ПН на границе двух фаз: жидкость–пар, твердое тело–жидкость и твердое тело–пар проводится на основе анализа молекулярных распределений флюида. Каждая из границ раздела характеризуется постоянным значением ширины переходной области. Изменение величины ширины переходной области указывает на смещение вглубь трехфазного контакта.

Рассмотрены три варианта расчета ПН адсорбат–адсорбент, отличающихся положением поверхности раздела фазы, на которой рассчитывается ПН: положение непосредственно на границе с твердым телом, положение на эквимолекулярной поверхности, относя состояние прилегающего монослоя к твердому телу к состоянию фазы или к вкладу в избыточную свободную энергию. Появление разных вариантов расчета обусловлено неравновесностью адсорбента, создающего внешнее поле для распределений адсорбата. Проведено сравнение значений между ПН твердое–жидкость и твердое–пар и сделаны оценки влияния на разницу этих величин параметров поры: ширины поры и потенциала стенок пор, для описанных трех вариантов. Получено, что ПН твердое–жидкость на порядок больше ПН жидкость–пар в центре поры, а ПН твердое–пар на два порядка больше той же величины.

Ранее было отмечено [6], что непрямое влияние стенок поры друг на друга через молекулярные распределения передается на значительно большие расстояния до одного–двух порядков по с равнению с прямым межмолекулярным взаимодействием молекул в поре (это меняет значения критических температур расслаивания в порах). Результаты расчетов молекулярных распределений на границе мениска пар–жидкость в поре подтверждают верхнюю границу этих оценок, и указывают, что для неоднородных распределений адсорбата на границе мениска, такое влияние распространяется на более широкие поры.

Построены размерные зависимости локальных значений ПН пар–жидкость по мере удаления локального участка границы от стенок поры: с приближением к стенке ПН меняется через максимум и у стенки ПН обращается в ноль. Нулевое значение ПН у стенки обосновано крайне малым градиентом плотности в адпленке, максимальные значения ПН в последующих монослоях связаны с наличием градиента плотности в двух направлениях в то время, как в монослоях в центре поры градиент плотности имеется только вдоль самой поры.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта № 18-03-00030а).