1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 94, № 4, 2020

Журнал физической химии, 2020, T. 94, № 4, стр. 521-527

Термодинамические функции в бинарной системе производное фуллерена C60–метионин–Н2О

К. Н. Семенов a, b, Н. А. Чарыков a, d, А. В. Куриленко a, В. А. Кескинов a, c, *, Ж. К. Шаймарданов c, Б. К. Шаймарданова c, Н. А. Куленова c, М. Ю. Матузенко a, В. В. Клепиков a

a Санкт-Петербургский государственный технологический институт (технический университет)
190013 Санкт-Петербург, Россия

b Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Россия

c Восточно-Казахстанский государственный технический университет им. Д. Серикбаева
Усть-Каменногорск, Казахстан

d Санкт-Петербургский государственный электротехнический университет “ЛЭТИ”
197376 Санкт-Петербург, Россия

* E-mail: keskinov@mail.ru

Поступила в редакцию 14.05.2019
После доработки 14.05.2019
Принята к публикации 15.06.2019

Полный текст (PDF)

Аннотация

Температура начала кристаллизации льда (∆Т) определена для бинарных водных растворов водорастворимого трис-аддукта легкого фуллерена с метионином: С60(C5H11NO2S)3 в температурном интервале 272.58–273.15 K. Установлено, что концентрация бис-аддукта в шкале мольной доли варьировалась в широком диапазоне x = 0.000–7.71 × 10–5 отн. ед. Температуры ликвидуса определены с помощью термометра Бекмана с линейным разрешением шкалы прибора ∆T/∆h ≈ 0.01 K/мм. Рассчитаны парциальные молярные избыточные функции для H2O. Для термодинамического описания подобных систем разработана оригинальная полуэмпирическая модель VD-AS, основанная на вириальном разложении молярной энергии Гиббса по мольным долям компонентов в растворе. С помощью модели VD-AS рассчитаны парциальные молярные функции и бис-аддукта. Рассчитана избыточная и полная средние молярные энергии Гиббса растворов и концентрационные области несмешиваемости. Сделан вывод, что модель VD-AS точно описывает процессы предрасслаивания или образования микрогетерогенной структуры.

Ключевые слова: криометрия, бис-аддукт фуллерена С60, метионин, термодинамическая модель

Статья является продолжением исследований, посвященных синтезу, идентификации и исследованию физико-химических и некоторых биологических свойств водорастворимых производных легких фуллеренов С60 и С70, таких как: сложные эфиры двухосновных карбоновых кислот (малонатов, оксалатов), полигидроксилированных форм (фуллеренолов), аддуктов с аминокислотами (aргинином, треонином, лизином, метионином и т.д.) [1–39 ]. В этих работах, в частности, изучались такие физико-химические свойства водных растворов производных легких фуллеренов, как концентрационные зависимости: объемных свойств (плотности, парциальных объемов компонентов и средних молярных объемов), рефракционных свойств (показателя преломления, удельной и молярной рефракции растворов и нанокластеров), явлений электропереноса (удельной и молярной электропроводности, водородного показателя, кажущихся степени и констант диссоциации), явлений ассоциации нанокластеров (размеров и типов ассоциатов, электрокинетических ζ-потенциалов), поверхностного натяжения и некоторых других.

Исследования поведения избыточных термодинамических функций (активностей, коэффициентов активности, избыточных энергий Гиббса (энтальпий, энтропий и т.п.), насколько известно авторам, практически не проводилось, за исключением нескольких оригинальных работ [40–43]. Этому имеется объяснение. Экспериментальное исследование подобных систем осложнено достаточно малой растворимостью последних (мольная доля нанокластеров в насыщенных растворах не превышает 0.001 отн. ед., что определяет низкую информативность наиболее точных и часто применяемых экспериментальных методов, например изопиестического. С точки зрения модельных построений, указанные системы ведут себя крайне необычно. Для них характерна иерархическая ассоциация с последовательным образованием ассоциатов первого, второго и, иногда, третьего порядка. Системы характеризуются гигантскими положительными отклонениями от идеальности, описать которые стандартными полуэмпирическими моделями (например, моделью Питцера для водных растворов электролитов [44, 45]) также не представляется возможным. В работах [40–43] на примере водных растворов водорастворимых производных легких фуллеренов проведены криометрические исследования, определены температуры начала кристаллизации льда, рассчитаны активности воды, а затем численным интегрированием уравнения Гиббса–Дюгема рассчитаны активности нанокластеров. В работах [40, 41] предложена оригинальная модель VD-AS (Virial Decomposition Asymmetric Model) для количественного описания подобных систем, и также рассчитаны концентрационные области диффузионной неустойчивости (микрогетерогенности) растворов.

Криометрические данные в бинарной системе С60(С5Н11NO2S)3–Н2О при 272.58–273.15 K

Понижение температур начала кристаллизации льда (∆T) была определена в системе трис-аддукт легкого фуллерена С60(С5Н11NO2S)3–Н2О при 272.58–273.15 K. Концентрации растворов (в мольных долях) варьировались в пределах Хnano-cluster = 0.000–7.71 × 10–5 отн. ед. Температуры ликвидуса определены с помощью термометра Бекмана с линейной разрешающей способностью ∆T/∆h ≈ 0.01 K/мм (h – высота поднятия Hg в капилляре). Криометрические данные ΔT(Хnano-cluster) представлены на рис. 1 и в табл. 1.

Рис. 1.

Концентрационная зависимость понижения температуры начала кристаллизации льда (температуры ликвидуса) (∆T) для бинарной системы: С60(С5Н11NO2S)3–H2O при 272.58–273.15 K. Стрелка демонстрирует ∆T для идеального раствора недиссоциирующего компонента (неэлектролита).

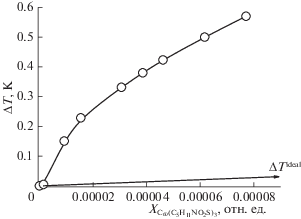
Таблица 1.  

Криометрические данные и избыточные термодинамические функции в бинарной системе трис-аддукт легкого фуллерена С60(С5Н11NO2S)3–Н2О при 272.58–273.15 K (М = 1167 г/моль). При расчетах использована модель VD-AS

${{X}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ × 105, отн. ед. ∆T (K), отн. ед. $ - \ln {{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ × 103, отн. ед. $ - \ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ ×103, отн. ед. $\ln \gamma _{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}^{{{\text{as}}}}$, отн. ед.
0.000 0.000 0.000 0.000 0.000
0.154 0.005 0.0556 0.0541 29.10
0.925 0.150 1.68 1.67 150.0
1.54 0.230 2.55 2.53 217.4
3.08 0.325 3.7 3.66 272.5
3.85 0.380 4.24 4.20 239.0
4.62 0.415 4.72 4.68 167.8
6.16 0.500 5.58 5.52 –100.1
7.71 0.570 6.37 6.29 –524.2

На рис. 1 видно, что зависимость $\Delta T({{X}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}})$ существенно нелинейна, сама система демонстрирует очень сильные положительные отклонения от идеальности, даже в случае очень разбавленных растворов. На рис. 1 также стрелкой представлено ∆T для идеального раствора недиссоциирующего компонента (неэлектролита) – ∆Тideal. В значения ∆Т превосходят ∆Тideal на один–два порядка.

Расчет избыточных термодинамических функций H2О в растворе

Для расчета активности воды нами использовано хорошо известное уравнение, получаемое из равенства химических потенциалов H2O в однокомпонентном льду и водном жидком растворе [40–43]:

(1)
$[--\Delta H_{{\text{W}}}^{{\text{f}}}\Delta T\,--\,\Delta {{C}_{P}}\Delta {{T}^{2}}]{\text{/}}[R(T_{0}^{{\text{f}}}\,--\,\Delta T)T_{0}^{{\text{f}}}]\, = \,\ln {{a}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}},$
где $H_{{\text{W}}}^{{\text{f}}}$ = 5990 Дж/моль, ∆CP = –38.893 Дж/(моль K), $T_{0}^{{\text{f}}}$ = 273.15 K теплота плавления, изменение теплоемкости при кристаллизации (в интервале температур 0.570 K величина практически постоянная) и температура плавления H2О, соответственно. Уравнение (1) получено в симметричной шкале нормировки для обоих компонентов раствора:
(2)
${{a}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}}({{Х}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}} = 1) = {{\gamma }_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}}({{Х}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}} = 1) = 1,$
(3)
$\begin{gathered} {{X}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}({{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}}}}_{{{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S}}{{{\text{)}}}_{{\text{3}}}}}} = 1) = \\ = {{\gamma }_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}({{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{2}}{\text{S)}}}}_{3}}}}} = 1) = 1, \\ \end{gathered} $
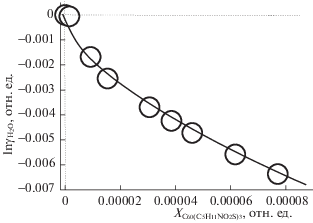
где Хi, ai, γi – мольная доля, активность и коэффициент активности i-го компонента. Расчетные данные $\ln [{{a}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{O}}}}}({{Х}_{{{\text{nano - cluster}}}}})]$ представлены на рис. 2 и в табл. 1.

Рис. 2.

Концентрационная зависимость логарифма активности Н2О ($\ln {{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$) для бинарной системы С60(С5Н11NO2S)3–H2O в интервале температур 272.58–273.15 K.

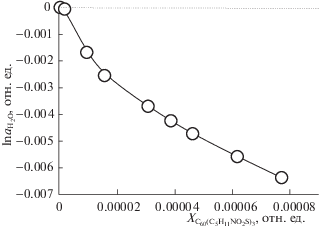
Ранее авторы [42, 43] рассчитывали концентрационные зависимости $\ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ и производных $d\ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$/dXnano-cluster (численно). Далее авторы [42, 43] получали зависимости dln γnano-cluster/Хnano-cluster, (согласно уравнению Гиббса–Дюгема), а затем также численным интегрированием рассчитывали зависимости ln γnano-cluster(Хnano-cluster). В результате, как и ожидалось, были получены гигантские положительные отклонения от идеальности: ln γnano-cluster ≈ n(100–101–102 отн. ед. Для изучаемой системы С60(С5Н11NO2S)3–H2O в области диффузионной стабильности растворов отмечен аналогичный результат (табл. 1 и ниже – рис. 3). Естественно, что для описания таких гигантских отклонений от идеальности оказались неприменимыми классические полуэмпирические модели растворов. Для этих целей авторами в [40, 41] была разработана оригинальная модель VD-AS, которая вполне успешно справилась с описанием водных растворов производных легких фуллеренов.

Рис. 3.

Концентрационная зависимость логарифма коэффициента активности Н2О ($\ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$) для бинарной системы С60(С5Н11NO2S)3–H2O в интервале температур 272.58–273.15 K (точки – экспериментальные данные, линия – расчет VD-AS).

Модель VD-AS

Полуэмпирическая модель VD-AS (Virial Decomposition Asymmetric Model) основана на вириальном разложении избыточной молярной энергии Гиббса раствора по мольным долям компонентов. Этот прием и ранее часто использовался при описании систем различной природы: растворов электролитов [44–47], расплавов неэлектролитов (полупроводников) [48–51], твердых растворов изовалентного замещения [52–54]. Если в подобном разложении ограничиться только одним членом (см. ниже) реализуется хорошо известная модель строго регулярных растворов – RSM. При учете температурной зависимости этого единственного вириального коэффициента модель RSM переходит в модель квазирегулярных растворов – QRSM. Если использовать третьи вириальные коэффициенты в разложении (см. ниже) реализуется модель субрегулярных растворов – SRSM. Наконец, при учете вклада неспецифических электростатических взаимодействий в избыточные функции раствора (согласно теории Дебая–Хюккеля) реализуется модель Питцера в различных вариантах.

Пусть: 1 – номер растворенного компонента (в нашем случае нанокластера), 2 – номер растворителя (H2O). Постулируем следующее уравнение:

(4)
$\begin{gathered} {{G}^{{{\text{ex}}}}}{\text{/}}RT = ({{n}_{1}} + {{n}_{2}}){{\Sigma }_{{i = 1}}}{{\Sigma }_{{j = 1}}}Х_{1}^{i}Х_{2}^{j}{\kern 1pt} *{\kern 1pt} {{\lambda }_{{ij}}} = \\ = ({{\Sigma }_{{i = 1}}}{{\Sigma }_{{j = 1}}}n_{1}^{i}n_{2}^{j}{\kern 1pt} *{\kern 1pt} {{\lambda }_{{ij}}}){\text{/}}{{({{n}_{1}} + {{n}_{2}})}^{{i + j--}}}^{1}, \\ \end{gathered} $
где Gex – молярная избыточная свободная энергия Гиббса, R = 8.31 Дж/K, T – температура (K), ni и Хi – число молей и мольная доля i-го компонента соответственно, λij – ij-й вириальный коэффициент в разложении Gex/RT по числам молей компонентов. Иными словами, λij естественно отождествляется с приведенной к RT, энергией специфического взаимодействия i частиц 1-го компонента и j частиц 2-го компонента. Если учесть огромную (на 2 порядка) разницу в массах компонентов (1-й тяжелее) и в их линейных размерах на 1 порядок (нанокластеры в нашем случае полые), становится ясным, что верхний предел суммирования по отношению к 1-му компоненту представляет собой небольшое натуральное число (не более 4–6), а по отношению ко 2-му компоненту больше на 1–2 порядка.

Рассчитаем теперь избыточные функции компонентов: lnγi:

(5.1)
$\begin{gathered} \ln {{\gamma }_{1}} = \partial ({{G}^{{{\text{ex}}}}}{\text{/}}RT){\text{/}}\partial {{n}_{1}} = \\ = {{\Sigma }_{{i = 1}}}{{\Sigma }_{{j = 1}}}[i--(i + j--1){{X}_{1}}]X_{1}^{{i - 1}}X_{2}^{j}{{\lambda }_{{ij}}}, \\ \end{gathered} $
(5.2)
$\begin{gathered} \ln {{\gamma }_{2}} = \partial ({{G}^{{{\text{ex}}}}}{\text{/}}RT){\text{/}}\partial {{n}_{2}} = \\ = {{\Sigma }_{{i = 1}}}{{\Sigma }_{{j = 1}}}[j--(i + j--1){{X}_{2}}]X_{1}^{i}X_{2}^{{j - 1}}{{\lambda }_{{ij}}}. \\ \end{gathered} $
В нашем случае мольные доли компонентов несопоставимы:
(6)
${{Х}_{2}} \gg {{X}_{1}},\quad {{Х}_{2}} > 0.999 \approx 1,\quad {{X}_{1}} \ll 1.$
Значит, уравнения (5.1), (5.2) могут быть упрощены:
(7.1)
$\ln {{\gamma }_{1}} \approx {{\Sigma }_{{i = 1}}}iX_{1}^{{i - 1}}{{\Sigma }_{{j = 1}}}{{\lambda }_{{ij}}},$
(7.2)
$\ln {{\gamma }_{2}} \approx {{\Sigma }_{{i = 1}}}(1 - i)X_{1}^{i}{{\Sigma }_{{j = 1}}}{{\lambda }_{{ij}}} = {{\Sigma }_{{i = 2}}}(1 - i)X_{1}^{i}{{\Sigma }_{{j = 1}}}{{\lambda }_{{ij}}}.$
Из систем (5.1), (5.2) и (7.1), (7.2) хорошо видно, что они термодинамически согласованы, т.е. подчиняются уравнению Гиббса–Дюгема при Т, Р = const:
(8.1)
${{X}_{1}}d\ln {{\gamma }_{1}} + {{X}_{2}}d\ln {{\gamma }_{2}} = 0.$
Или, исходя из уравнений (7.1), (7.2), получаем:
(8.2)
$\begin{gathered} {{X}_{1}}{{\Sigma }_{{i = 1}}}i(i - 1)X_{1}^{{i - 2}}{{\lambda }_{{ij}}}d{{X}_{1}} + \\ + \;{{\Sigma }_{{i = 1}}}(1 - i)iX_{1}^{{i - 1}}{{\lambda }_{{ij}}}d{{X}_{1}} = 0. \\ \end{gathered} $
Перепишем теперь уравнения (7.1), (7.2), обозначив Λi сумму вириальных коэффициентов:
(9)
${{\Sigma }_{{j = 1}}}{{\lambda }_{{ij}}} = {{\Lambda }_{i}}(Т).$
Таким образом, в условиях нашего рассмотрения:
(10.1)
$\ln {{\gamma }_{1}} \approx {{\Sigma }_{{i = 1}}}i{{\Lambda }_{i}}X_{1}^{{i - 1}},$
(10.2)
$\ln {{\gamma }_{2}} \approx {{\Sigma }_{{i = 1}}}(1 - i){{\Lambda }_{i}}X_{1}^{i} = {{\Sigma }_{{i = 2}}}(1 - i){{\Lambda }_{i}}X_{1}^{i}.$
Если Λ1 ≠ 0, то логарифмы предельных коэффициентов активности – $\ln \gamma _{i}^{0}$ = limitX1 → 0ln γi, соответствуют симметричной нормировке избыточных функций:
(11.1)
$\ln \gamma _{1}^{0} = {{\Lambda }_{1}} \ne 0,\quad {{\gamma }_{1}}({{Х}_{1}} \to 0) = \gamma _{1}^{0} \ne 1,$
(11.2)
$\ln \gamma _{2}^{0} = 0,\quad {{\gamma }_{2}}({{Х}_{1}} \to 0) = 1.$
В нашем случае несомненно более удобно воспользоваться ассиметричной нормировкой избыточных функций (для этого вполне достаточно выполнить единственное условие Λ1 = 0):
(12.1)
$\ln \gamma _{1}^{0} = 0,\quad {{\gamma }_{1}}({{Х}_{1}} \to 0) = \gamma _{1}^{0} = 1,$
(12.2)
$\ln \gamma _{2}^{0} = 0,\quad {{\gamma }_{2}}({{Х}_{1}} \to 0) = 1,$
(12.3)
$\ln \gamma _{1}^{{{\text{ass}}}} \approx {{\Sigma }_{{i = 2}}}i{{\Lambda }_{i}}X_{1}^{{i - 1}},$
(12.4)
$\ln \gamma _{2}^{{{\text{ass}}}} \approx {{\Sigma }_{{i = 2}}}(1 - i){{\Lambda }_{i}}X_{1}^{i},$
Впредь всегда будем пользоваться именно этой нормировкой.

Рассмотрим функцию Gmix/RT (приведенную к RT молярную энергию Гиббса смешения) и вторую производную от Gmix/RT, которая численно совпадает со второй производной от полной молярной свободной энергии Гиббса, отнесенной к RT – Gmix/RT

(13.1)
$\begin{gathered} {{G}^{{{\text{mix}}}}}{\text{/}}RT = {{X}_{1}}\ln {{X}_{1}} + {{X}_{2}}\ln {{X}_{2}} + \\ + \;{{X}_{1}}\ln {{\gamma }_{1}} + {{X}_{2}}\ln {{\gamma }_{2}}, \\ \end{gathered} $
(13.2)
$\begin{gathered} \partial [{{G}^{{{\text{mix}}}}}{\text{/}}RT]{\text{/}}\partial {{X}_{1}} = 1{\text{/}}{{X}_{1}} + 1{\text{/}}{{X}_{2}}--(\ln {{X}_{2}} + 1) + \\ + \;{{\Sigma }_{{i = 1}}}{{i}^{2}}{{\Lambda }_{i}}{{X}_{1}}{{^{{i - }}}^{1}} + {{\Sigma }_{{i = 2}}}(1 - i){{\Lambda }_{i}}[i(i - 1)X_{1}^{{i - 2}} - \\ --\;(i + 1)X_{1}^{{i - 1}}], \\ \end{gathered} $
(13.3)
${{\partial }^{2}}[{{G}^{{{\text{mix - ass}}}}}{\text{/}}RT]{\text{/}}\partial X_{1}^{2}\, \approx \,1{\text{/}}{{X}_{1}}\, + \,{{\Sigma }_{{i = 2}}}i(i\, - \,1){{\Lambda }_{i}}X_{1}^{{i - 2}}.$
Абсолютно аналогично можно рассчитать (приведенную к RT) первую производную от химического потенциала – μ1 или логарифма активности ln a1, соответственно:
(14)
$\begin{gathered} 1{\text{/}}RT(\partial {{\mu }_{1}}{\text{/}}\partial {{X}_{1}}) = (\partial \ln {{a}_{{\text{1}}}}{\text{/}}\partial {{X}_{1}}) \approx \\ \approx 1{\text{/}}{{X}_{1}} + {{\Sigma }_{{i = 2}}}i(i - 1){{\Lambda }_{i}}X_{1}^{{i = 2}}. \\ \end{gathered} $
Тогда уравнение потери диффузионной устойчивости раствором (или условие спинодального распада) примет вид:

(15)
$\begin{gathered} G_{{11}}^{{{\text{mix - ass}}}} = {{\partial }^{2}}[{{G}^{{{\text{mix - ass}}}}}{\text{/}}RT]{\text{/}}\partial X_{1}^{2} = \\ = (\partial \ln {{a}_{1}}{\text{/}}\partial {{X}_{1}}) \approx 1{\text{/}}{{X}_{1}} + {{\Sigma }_{{i = 2}}}i(i - 1){{\Lambda }_{i}}X_{1}^{{i - 2}} = 0. \\ \end{gathered} $

Применение модели VD-AS к описанию избыточных функций производных легких фуллеренов в системе С60(С5Н11NO2S)3–H2O. Области диффузионной неустойчивости

Предварительные расчеты показали, что трехчленной аппроксимации в модели VD-AS – (i.e. i = 2, 3, 4) вполне достаточно для достаточно точного описания избыточных функций в системе С60(С5Н11NO2S)3–H2O, как и ранее в иных подобных системах [42, 43]:

(16.1)
$\ln \gamma _{1}^{{{\text{ass}}}} \approx 2{{\Lambda }_{2}}{{X}_{1}} + 3{{\Lambda }_{3}}X_{1}^{2} + 4{{\Lambda }_{4}}X_{1}^{3},$
(16.2)
$\ln \gamma _{2}^{{{\text{ass}}}} \approx - {{\Lambda }_{2}}X_{1}^{2} - 2{{\Lambda }_{3}}X_{1}^{3} - 3{{\Lambda }_{4}}X_{1}^{4}.$
Тогда уравнение потери диффузионной стабильности (спинодали) принимает вид:
(16.3)
$12{{\Lambda }_{4}}X_{1}^{3} + 6{{\Lambda }_{3}}X_{1}^{2} + 2{{\Lambda }_{2}}{{X}_{1}} + 1 = 0.$
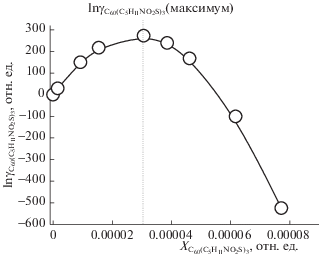
Уравнение легко разрешается относительно X1 (формула Кардано для кубического уравнения). Рассчитанные параметры VD-AS (отн. ед.): Λ2 = = 9.70 × 106, Λ3 = –1.15 × 1011, Λ4 = 1.71 × 1014, Xdiff-instab ≈ 3.10 × 10–5. Параметры модели (Λ2, Λ3, Λ4) были рассчитаны нами из зависимостей $\ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$(Х1) (см. табл. 1) по уравнению (16.2):
(17)
$\begin{gathered} \ln {{\gamma }_{2}} = \ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = \ln {{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}--\ln {{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = \\ = \ln {{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}--\ln (1--{{X}_{1}}). \\ \end{gathered} $
Формально огромные значения суммарных вириальных коэффициентов (Λ2, Λ3, Λ4) сотни членов, не являются неожиданными, поскольку они представляют собой суммы рядов, содержащих возможно сотни и более членов, отвечающих за приведенные энергии взаимодействия считанных молекул нанокластеров с огромным количеством молекул воды. Чтобы продемонстрировать адекватность модели VD-AS в приложении к рассматриваемой системе, приведем расчетные и экспериментальные данные по концентрационной зависимости $\ln {{\gamma }_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}({{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}})$ – рис. 3.

Далее, согласно уравнению (16.1), мы рассчитали концентрационные зависимости $\ln \gamma _{1}^{{{\text{ass}}}}$(Х1) (табл. 1 и рис. 4). Из рис. 4 видно, что зависимость $\ln \gamma _{1}^{{{\text{ass}}}}$(Х1) проходит через максимум при: Х1 ≈ 3 × 10–5 отн. ед. Установить положение максимума по уравнению (16.1) легко, решая квадратное уравнение:

(18)
$(1{\text{/}}2)d(\ln \gamma _{1}^{{{\text{ass}}}}{\text{/}}d{{X}_{1}}) = {{\Lambda }_{2}} + 3{{\Lambda }_{3}}{{X}_{1}} + 6{{\Lambda }_{4}}X_{1}^{2} = 0,$
или:

(19)
${{X}_{1}} = [--1.5{{\Lambda }_{3}} \pm {{(4.5\Lambda _{3}^{2} - 12{{\Lambda }_{2}}{{\Lambda }_{4}})}^{{1/2}}}]{\text{/}}{{\Lambda }_{2}}.$
Рис. 4.

Концентрационная зависимость логарифма коэффициента активности С60(С5Н11NO2S)3 для бинарной системы С60(С5Н11NO2S)3–H2O в интервале температур 272.58–273.15 K.

Согласно уравнению (16.3) определили границы диффузионной устойчивости – Xdiff-instab (табл. 2 и рис. 5), решая кубическое уравнение:

(20)
$F = 12{{\Lambda }_{4}}X_{1}^{3} + 6{{\Lambda }_{3}}X_{1}^{2} + 2{{\Lambda }_{2}}{{X}_{1}} + 1 = 0.$
Из табл. 2 видно, что уравнение (20) имеет один действительный корень в области изученных концентраций. Из этого факта можно сделать заключение, что, начиная с определенной концентрации: $X_{1}^{{{\text{diff}}}}$ ≈ 3.1 × 10–5 отн. ед. растворы нанокластера в воде начинают расслаиваться или возможно предрасслаиваться (см. ниже). На рис. 5 представлена концентрационная зависимость функции диффузионной неустойчивости: F = 12Λ4$X_{1}^{3}$ + 6Λ3$X_{1}^{2}$ + 2Λ2X1 + 1. Из рис. 5 видно, что функция F(X1) имеет пересечение с осью абсцисс, что отвечает потере диффузионной устойчивости.

Рис. 5.

Концентрационная зависимость функции диффузионной неустойчивости: F = 12Λ4$X_{1}^{3}$ + 6Λ3$X_{1}^{2}$ + + 2Λ2X1 + 1 для бинарной системы С60(С5Н11NO2S)3–H2O в интервале температур 272.58–273.15 K.

Процессы ассоциации в системах водорастворимое производное легкого фуллерена–Н2О изучались неоднократно методом динамического светорассеяния (см., в частности работы [22–24, 26, 40]). Установлено, что с ростом концентраций последовательно образуются из мономерных молекул ассоциаты первого порядка, из них – ассоциаты второго порядка и, наконец, из них – ассоциаты третьего порядка. В связи с этим представляется уместным, с точки зрения, факта потери раствором диффузионной устойчивости, с одной стороны, и линейных размеров превалирующих ассоциатов, с другой стороны, разделить концентрационный интервал на 4 зоны:

I. Первая зона при ${{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ → 0 (бесконечно разбавленный раствор), где присутствуют только мономеры с линейными размерами около 2 нм. Этой зоны мы в эксперименте не наблюдали ни в одной из изученных систем [22–24, 26, 40]. Растворы истинные и абсолютно стабильные.

II. Во второй зоне при ${{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ < < $Х_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}^{{{\text{diff - instab}}}}$ ≈ 3.1 × 10–5 отн. ед. в растворе образуются “малые ассоциаты” (с линеными размерами десятки – первые сотни нм). Растворы становятся наноколлоидными.

III. В третьей зоне при ${{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ ≈ ≈ $Х_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}^{{{\text{diff - instab}}}}$ ≈ 3.1 × 10–5 отн. ед. в добавление к “малым ассоциатам” в растворе появляются “большие ассоциаты” с линейными размерами последние сотни нм вплоть до 1 мкм. Растворы становятся микроколлоидными и начинают терять диффузионную устойчивость, т.е. предрасслаиваться.

В четвертой зоне при ${{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ > > $Х_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}^{{{\text{diff - instab}}}}$ или ${{Х}_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}}$ ≫ $Х_{{{{{\text{С}}}_{{{\text{60}}}}}{{{{\text{(}}{{{\text{С}}}_{{\text{5}}}}{{{\text{Н}}}_{{{\text{11}}}}}{\text{N}}{{{\text{O}}}_{{\text{2}}}}{\text{S)}}}}_{{\text{3}}}}}}^{{{\text{diff - instab}}}}$ появляются “суперассоциаты” с линейными размерами несколько мкм. Растворы быстро теряют диффузионную устойчивость, становятся реальными коллоидными или гетерогенными.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (коды проектов №№ 18-08-00143 А, 19-015-00469 А, 19-016-00003 А).

Список литературы

  1. Li J., Takeuchi A., Ozawa M. et al. // J. Chem. Soc. Chem. Commun. 1993. V. 23. P. 1784.

  2. Chiang L.Y., Bhonsle J.B., Wang L. et al. // Tetrahedron. 1996. V. 52. P. 4963.

  3. Chiang L.Y., Upasani R.B., Swirczewski J.W. // J. Am. Chem. Soc. 1992. V. 114. P. 10154.

  4. Meier M.S., Kiegiel J. // Org. Lett. 2001. V. 3. P. 1717.

  5. Szymanska L., Radecka H., Radecki J. et al. // Biosens. Bioelectron. 2001. V. 16. P. 911.

  6. Mirkov S.M., Djordjevic A.N., Andric N.L. et al. // Nitric Oxide. 2004. V. 11. P. 201.

  7. Kokubo K., Matsubayashi K., Tategaki H. et al. // ACS Nano. 2008. V. 2. № 2. P. 327.

  8. Yang J.M., He W., Ping H. et al. // Chinese. J. Chem. 2004. V. 22. № 9. P. 1008.

  9. Sheng W., Ping H., Jian_Min Z. et al. // Synthetic Communications. 2005. V. 35. № 13. P. 1803.

  10. Chiang Long Y. Fullerene Derivatives as Free_Radical Scavengers. US patent 5648523. July 15. 1997.

  11. Lamparth I., Hirsch A. // J. Chem. Soc. Chem. Commun. 1994. P. 1727.

  12. Liang Bing Gan, Chu Ping Luo // Chinese Chemical Letters .1994. V. 5. № 4. P. 275.

  13. Kotelnikova R.A., Kotelnikov A.I., Bogdanov G.N. et al. // FEBS Lett. 1996. V. 389. P. 111.

  14. Hu Z., Guan W., Wang W. et al. // Carbon. 2008. V. 46. P. 99.

  15. Kumar A., Rao M.V., Menon S.K. // Tetrahedron Lett. 2009. V. 50. P. 6526.

  16. Jiang G., Yin F., Duan J., Li G. // J. Mater. Sci: Mater. Med. 2015.V. 26. P. 1.

  17. Grigoriev V.V., Petrova L.N., Ivanova T.A. et al. // Biology Bull. 2011. V. 38. P. 125.

  18. Kotel’nikova R.A., Faingol’d I.I., Poletaeva D.A. et al. // Rus. Chem. Bull. 2011. V. 6. P. 1172.

  19. Leon A., Jalbout A.F., Basiuk V.A. // Chem. Phys. Lett. 2008. V. 452. P. 306.

  20. Hu Y.H., Ruckenstein E. // Mol. Struct. Theochem. 2008. V. 865. P. 94.

  21. Semenov K.N., Charykov N.A., Postnov V.N. et al. // Rus. Chem. Rev. 2016. V. 85. P. 38.

  22. Semenov K.N., Charykov N.A., Murin I.V. et al. // J. Molecular Liquids. 2015. V. 202. P. 50.

  23. Semenov K.N., Charykov N.A., Murin I.V. et al. // J. Molecular Liquids. 2015. V. 202. P. 1.

  24. Manyakina O.S., Semenov K.N., Charykov N.A. et al. // J. Molecular Liquids. 2015. V. 211. P. 487.

  25. Semenov K.N., Charykov N.A., Keskinov V.A. et al. // Rus. J. Phys. Chem. V. 85. № 6. P. 1009.

  26. Semenov K.N., Charykov N.A., Keskinov V.A. et al. // J. Chem. Eng. Data. 2011. V. 56. P. 230.

  27. Lushin A.I., Charykov N.A., Semenov K.N. et al. // Industrial and Engineering Chemical Research. 2013. V. 52. P. 14583.

  28. Semenov K.N., Charykov N.A., Keskinov V.A. et al. // Ibid. 2013. V. 52. P. 16095.

  29. Shestopalova A.A., Semenov K.N., Charykov N.A. et al. // J. Molecular Liquids. V. 211. 2015. P. 301.

  30. Semenov K.N., Postnov V.N., Charykov N.A. et al. // Rus. J. Appl.Chem. 2011. T. 84. № 1. P. 44.

  31. Semenov K.N., Letenko D.G., Charykov N.A. et al. // Ibid. 2010. V. 83. P. 1948.

  32. Семенов К.Н., Иванова Н.М., Чарыков Н.А. и др. // Журн. физ. химии. 2017. Т. 91. № 2. С. 318.

  33. Semenov K.N., Meshcheriakov A.A., Charykov N.A. et al. // RSC Advances. 2017. № 7. P. 15189.

  34. Noskov B.A., Timoshen K.A., Akentiev Al.V. et al. // Colloids and Surfaces A: Physicochemical and Engineering Aspects. 2017. V. 529. P. 1.

  35. Lelet M.I., Semenov K.N., Andrusenko El.V. et al. // J. Chem. Thermodynamics. 2017. V. 115. P. 7.

  36. Semenov K.N., Charykov N.A., Meshcheriakov A.A. et al. // J. Molecular Liquids. 2017. V. 242. P. 940.

  37. Semenov K.N., Andrusenko El.V., Charykov N.A. et al. // Progress in Solid State Chemistry. 2017. V. 47–48. P. 1.

  38. Serebryakov E.B., Semenov K.N., Stepanyuk I.V. et al. // J. Molecule Liquids. 2018. V. 256. P. 507.

  39. Yur'ev G.O., Lelet M.I., Pochkayeva E.A. et al. // J. Chem. Thermodynamics 2018. V. 127. P. 39.

  40. Charykov N.A., Semenov K.N., López En.R. et al. // J. Molecule Liquids. 2018. V. 256. P. 305.

  41. Safyannikov N.M., Charykov N.A., Garamova P.V. et al. // Nanosystems: Physics, Chemistry, Mathematics. 2018. V. 9. № 1. P. 46.

  42. Matuzenko M.Yu., Shestopalova A.A., Semenov K.N. et al. // Nanosystems: Physics, Chemistry, Mathematics. 2015. V. 6. № 5. P. 715.

  43. Matuzenko M.Yu., Tyurin D.P., Manyakina O.S. et al. // Ibid. 2015. V. 6. № 4. P. 704.

  44. Pitzer K.S. // J. Phys. Chem. 1973. V. 77. № 2. P. 268.

  45. Pitzer K.S., Kim J.J. // J. Amer. Chem. Soc. 1974. V. 96. № 18. P. 5701.

  46. Filippov V.K., Charykov N.A., Rumyantsev A.V. // Rep. Rus. Acad. Sciences. Seria: Physics-Chemistry. 1987. V. 296. № 3. P. 665.

  47. Чарыкова М.В., Чарыков Н.А. Термодинамическое моделирование процессов эвапоритовой седиментации. СПб.: Наука, 2003.

  48. Charykov N.A., Litvak A.M., Mikhailova M.P. et al. // Rus. Phys. and Tech. Semic. 1997. V. 31. № 4. P. 410.

  49. Litvak A.M., Charykov N.A. // Rus. J. Phys. Chem. 1990. V. 64. № 9. P. 2331.

  50. Litvak A.M., Moiseev K.D., Charykov N.A. et al. // Rus. Tech. Phys. Lett. 1990. V. 16. № 13. P. 41.

  51. Baranov A.N., Guseinov A.A., Litvak A.M. et al. // Ibid. 1990. V. 16. № 5. P. 33.

  52. Stringfellow G.B. J. Elecrctron. Mat. 1981. V. 10. № 5. P. 919–936.

  53. Stringfellow G.B. // J. Cryst. Growth. 1982. V. 58. P. 194.

  54. Litvak A.M., Charykov N.A. // Rus. J. Neorg. Chem. 1990. V. 35. № 12. P. 3059.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал