1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 95, № 2, 2021

Журнал физической химии, 2021, T. 95, № 2, стр. 231-237

Анализ размеров макромолекул альбумина в его водных растворах

Н. П. Маломуж a, А. В. Хорольский b, *

a Одесский национальный университет имени И.И. Мечникова
Одесса, Украина

b Полтавский национальный педагогический университет имени В.Г. Короленко
Полтава, Украина

* E-mail: khorolskiy.alexey@gmail.com

Поступила в редакцию 07.04.2020
После доработки 24.05.2020
Принята к публикации 25.05.2020

Полный текст (PDF)

Аннотация

Обсуждены изменения структуры и размеров макромолекул сывороточного альбумина человека и бычьего сывороточного альбумина в водных растворах в зависимости от температуры, концентрации и кислотно-щелочного баланса среды. Принято во внимание, что изменение гидродинамического радиуса макромолекулы служит одним из индикаторов структурных фазовых превращений глобулярных белков. Обсуждены методы определения радиусов макромолекул из данных по сдвиговой вязкости их растворов и данных по самодиффузии макромолекул в них. Произведено тщательное сравнение значений гидродинамического радиуса макромолекул альбумина, полученных указанными методами. Показана возможность на основании полученных данных сделать выводы о характере связности молекул воды с макромолекулами белков.

Ключевые слова: гидродинамический радиус макромолекул, сдвиговая вязкость растворов, самодиффузия макромолекул альбумина, ячеечный подход

Структура и свойства белков продолжают оставаться в центре внимания исследователей – медиков, химиков, физиков и т.п. Особенности изменения структуры белков при их растворении в воде и водных растворах – основные вопросы изучения для физиков. В этой работе мы остановимся на подобных превращениях, происходящих с макромолекулами альбумина – важнейшего компонента плазмы крови. В дальнейшем рассмотрим биомакромолекулы сывороточного альбумина человека и бычьего сывороточного альбумина.

Сывороточный альбумин человека (САЧ) состоит из 585 аминокислотных остатков, объединенных в одну макромолекулярную цепь с молекулярной массой 66.5 кДа [1]. В кристаллическом состоянии макромолекула САЧ свернута в компактную конформацию правильной треугольной призмы сердцевидной формы с размерами ~80 и ∼30 Å [2]. Бычий сывороточный альбумин (БСА) состоит из 583 остатков аминокислот, объединенных в макромолекулу с молекулярной массой 66.5 кДа и пространственной структурой, подобной структуре сывороточного альбумина человека [1, 3]. Аминокислотные последовательности САЧ и БСА идентичны на 75.52% [4].

Общепринятой является доменная структура САЧ и БСА. При физиологических значениях рН вторичная структура САЧ и БСА состоит из альфа-спиралей (50–68%) и бета-складок (16–18%), стабилизированных водородными связями, а также неупорядоченной части макромолекулярной цепи [1, 3, 5]. Благодаря 17 дисульфидным связям между цистеиновыми остатками альфа-спиралей образуется третичная структура указанных альбуминов: формируются три домена, каждый из которых образован субдоменами из трех альфа-спиралей, а гидрофобные взаимодействия между доменами определяют глобулярную структуру белков [1, 3].

Отличия в нуклеотидных последовательностях альбуминов приводят к некоторому изменению гидрофобности и конформационной подвижности макромолекулы САЧ по сравнению с макромолекулой БСА [4]. Одно из отличий строения САЧ от БСА – присутствие в макромолекулярной цепи БСА двух остатков триптофана (Trp134 и Trp213) и одного остатка триптофана в макромолекуле САЧ (Trp214) [1].

При растворении в воде, а также в водных и биологических растворах вследствие взаимодействия с водой жесткая конформация макромолекул альбумина должна нарушаться. В наибольшей степени это касается тех особенностей структуры альбумина, которые обусловлены кулоновскими силами. При растворении происходит небольшое перераспределение локально заряженных участков макромолекулы альбумина, что изменяет ее гидрофильные и гидрофобные свойства. Гидрофобность может быть причиной уплотнения макромолекул альбумина, т.е. уменьшения размеров макромолекулы, в то время как преобладание гидрофильных взаимодействий может способствовать преобразованию компактного доменного строения в квазилинейную структуру [1, 4]. Следовательно, и гидрофобные, и гидрофильные взаимодействия могут содействовать разрушению доменной структуры альбумина в растворе, которая присуща кристаллическому состоянию биомакромолекулы.

По сути дела, при растворении в воде происходят такие трансформации макромолекул альбумина, которые можно рассматривать как внутренний структурный фазовый переход. Преобразования структуры макромолекулы альбумина будут менять и структуру водного окружения. Одна из характеристик подобного фазового перехода – изменение размера макромолекулы.

Одним из индикаторов отмеченных структурных фазовых превращений служит изменение гидродинамического радиуса. Последний исследуется различными физико-химическими методами: фотонной корреляционной спектроскопией [6, 7], малоугловым рассеянием нейтронов [8, 9], атомно-силовой микроскопией [10], малоугловым рассеянием рентгеновских лучей [11], ЯМР-спектроскопией с импульсным градиентом магнитного поля [12], гель-проникающей хроматографией [13], капиллярной вискозиметрией [14].

Наше внимание сосредотачивается на методах, позволяющих определить радиус макромолекул альбумина как индикатор конформационных переходов с помощью значений сдвиговой вязкости растворов макромолекул и коэффициентов самодиффузии макромолекул в них. Эти методы позволяют: 1) исследовать изменение гидродинамического радиуса макромолекулы в зависимости от температуры, концентрации, кислотно-щелочного баланса (рН), наличия солей и природы буферных растворов; 2) анализировать динамику молекул растворителя, связанных межмолекулярными взаимодействиями с макромолекулой.

Чтобы дифференцировать эффекты температуры, концентрации и кислотно-щелочного баланса (рН) на внутреннюю структуру макромолекулы, проводится сравнение температурно-концентрационных зависимостей гидродинамического радиуса макромолекул альбуминов.

ОПРЕДЕЛЕНИЕ РАДИУСОВ МАКРОМОЛЕКУЛ ИЗ ДАННЫХ ПО СДВИГОВОЙ ВЯЗКОСТИ ИХ ВОДНЫХ РАСТВОРОВ

Исходным является соотношение между массовой ${{c}_{m}}$ и объемной $\varphi $ концентрациями раствора макромолекул:

(1)
$\varphi = \frac{{4\pi {{R}^{3}}{{c}_{m}}\rho {{N}_{{\text{A}}}}}}{{3M}},$
где $R$ – радиус примесной частицы, $\rho $ – плотность раствора, ${{N}_{{\text{A}}}}$ – постоянная Авогадро, $M$ – молекулярная масса вещества. Отсюда следует, что эффективный радиус макромолекулы определяется соотношением:
(2)
$R = \gamma {{\varphi }^{{1.3}}},\quad \gamma = d{{(\rho {{c}_{m}})}^{{ - 1/3}}},\quad d = \sqrt[3]{{\frac{{3M}}{{4\pi {{N}_{{\text{A}}}}}}}},$
в котором массовая плотность определяется линейной комбинацией:
(3)
$\rho = {{\rho }_{w}}(1 - {{c}_{m}}) + {{\rho }_{{alb}}}{{c}_{{m,}}}$
где ${{\rho }_{w}}$ – массовая плотность воды, а ${{\rho }_{{alb}}}$ – массовая плотность сухого альбумина. Для макромолекул альбумина ${{d}_{{alb}}} = 2.98 \times {{10}^{{ - 8}}}$ кг1/3.

В разбавленных растворах макромолекулы приближенно можно считать сферическими частицами. В этом предположении усредненную вязкость раствора $\bar {\eta }$ можно оценивать по теории Бэтчелора [15], которая приводит к формуле:

(4)
$\begin{gathered} \bar {\eta } = {{\eta }_{0}}(1 + {{a}_{1}}\varphi + {{a}_{2}}{{\varphi }^{2}} + \ldots ), \\ {{a}_{1}} = 2.5,\quad {{a}_{2}} = 5.2, \\ \end{gathered} $
где ${{\eta }_{0}}$ – вязкость растворителя (воды). В линейном по $\varphi $ приближении формула (4), как и должно быть, совпадает с формулой Эйнштейна [16]. Отметим, что квадратичный по $\varphi $ вклад в (4) обусловлен гидродинамическими взаимодействиями между макрочастицами. Из уравнения (4), переписанного в виде:
${{a}_{1}}\varphi + {{a}_{2}}{{\varphi }^{2}} + \ldots = \lambda ,$
где $\lambda = \frac{{\bar {\eta }}}{{{{\eta }_{0}}}} - 1$, следует, что $\varphi (\lambda )$ при $\lambda \ll 1$ представляется рядом по степеням $\lambda $:
(5)
$\begin{gathered} \varphi (\lambda ) = {{b}_{1}}\lambda + {{b}_{2}}{{\lambda }^{2}} + \ldots , \\ {{b}_{1}} = \frac{1}{{{{a}_{1}}}} = 0.4,\quad {{b}_{2}} = \frac{{{{a}_{2}}}}{{a_{1}^{3}}} = - 0.3328. \\ \end{gathered} $
Подставляя полученные таким путем значения $\varphi $ в (2), находим:
(6)
${{R}_{\eta }} = \gamma {{({{b}_{1}}\lambda )}^{{1/3}}}\left[ {1 + \frac{{{{b}_{2}}}}{{3{{b}_{1}}}}\lambda - \frac{1}{9}{{{\left( {\frac{{{{b}_{2}}}}{{{{b}_{1}}}}} \right)}}^{2}}{{\lambda }^{2}} + \ldots } \right].$
Формула Бэтчелора оказывается применимой вплоть до объемных концентраций $\varphi \leqslant 0.2$, что соответствует отношению вязкостей: $\bar {\eta }{\text{/}}{{\eta }_{0}} < 1.5$. К сожалению, дальнейшее обобщение метода Бэтчелора сталкивается со значительными трудностями при нахождении членов ряда теории возмущений более высокого порядка, нахождении суммы ряда и даже в решении вопроса о его сходимости.

При $\varphi > 0.2$ прогресс в определении эффективных радиусов макромолекул связан с использованием ячеечных моделей [17], в которых учитывается, что гидродинамические возмущения, вызываемые примесными частицами, локализуются, главным образом, внутри сферической ячейки, которая окружает частицу. Также считается, что на границе ячейки нормальная составляющая скорости возмущения и тангенциальные составляющие напряжений равны нулю, что эквивалентно отсутствию трения на внешней поверхности ячейки [17]. Среди различных версий ячеечных подходов мы отдаем предпочтение версии [17, 18], в которой соседние макромолекулы возмущают гидродинамическое поле вращающейся частицы. В этом случае свойства симметрии затравочного и возмущенного гидродинамических полей используются максимально полно. В работах [17, 18] показано, что вязкость разбавленных растворов макромолекул определяется формулой:

(7)
$\bar {\eta } = {{\eta }_{0}}\frac{{\psi (1 - \psi )}}{{\psi (1 - \psi ) + 1 - \sqrt {1 + 2{{\psi }^{2}}(1 - \psi )} }},$
где $\psi = {{({{R}_{0}}{\text{/}}R)}^{3}}$, R0 – радиус макромолекулы и R – радиус ячейки. Таким образом, задача определения средней вязкости раствора макромолекул сводится к установлению взаимосвязи между параметром модели $\psi = {{({{R}_{0}}{\text{/}}R)}^{3}}$ и величиной удельного объема:
(8)
$\varphi = {{V}_{0}}{\text{/}}V,$
измеряемого экспериментально, где V0 – суммарный объем, занимаемый макромолекулами, V – объем системы. Формула (7) позволяет описать поведение вязкости разбавленных растворов макромолекул вплоть до значений объемной концентрации частиц $\varphi \leqslant 0.5$, что фактически совпадает с плотностью раствора, соответствующей непосредственному контакту всех ближайших соседей [17, 18]. Важно отметить, что при концентрациях $\varphi \leqslant 0.2$ формулы (7) и (4) полностью эквивалентны друг другу (это обстоятельство следует непосредственно из построения (7)).

Уравнение (7) применяется нами для определения эффективной объемной концентрации $\varphi $:

(9)
${{\bar {\eta }}_{{\exp }}} = {{\eta }_{{(7)}}}(\varphi ).$
Эффективный радиус макромолекул находится непосредственно по формуле (2). Независимый способ определения эффективных радиусов макромолекул связан с коэффициентом их самодиффузии.

ОЦЕНКА РАДИУСОВ МАКРОМОЛЕКУЛ ИЗ ДАННЫХ О КОЭФФИЦИЕНТЕ САМОДИФФУЗИИ МАКРОМОЛЕКУЛ В РАСТВОРЕ

Характер зависимости коэффициента самодиффузии от объемной концентрации $\varphi $ обычно представляется в виде:

(10)
${{D}_{S}} = {{D}_{0}}\left( {1 + f(\varphi )} \right),$
напоминающем формулу (4) для сдвиговой вязкости, где D0 – коэффициент самодиффузии примесной макромолекулы в предельно разбавленном растворе:
(11)
${{D}_{0}} = \frac{{{{k}_{{\text{B}}}}T}}{{6\pi {{\eta }_{0}}{{R}_{0}}}}.$
В соответствии с (11), радиус ${{R}_{0}}$ изолированной макромолекулы принимается равным:
${{R}_{0}} = \frac{{{{k}_{{\text{B}}}}T}}{{6\pi {{\eta }_{0}}{{D}_{0}}}}$.
С другой стороны, коэффициент самодиффузии ${{D}_{S}}$ примесной макромолекулы можно представить в виде:
(12)
${{D}_{S}} = \frac{{{{k}_{{\text{B}}}}T}}{{6\pi {{\eta }_{0}}{{R}_{D}}}},$
где ${{R}_{D}}$ имеет смысл эффективного радиуса макромолекулы. Для его нахождения в общем случае представляем ${{R}_{D}}$ в виде: ${{R}_{D}} = {{R}_{0}} + \delta R \equiv {{R}_{0}}(1 + u)$. Тогда
(13)
${{D}_{S}} = {{D}_{0}}\frac{1}{{1 + u}},$
и
(14)
$\varphi = {{\varphi }_{0}}(c){{(1 + u)}^{3}},$
где ${{\varphi }_{0}}(c) = {{({{R}_{0}}{\text{/}}\gamma )}^{3}}$. Подставляя (13) и (14) в (10), получаем следующее уравнение для определения $u$:
(15)
$\frac{1}{{1 + u}} = 1 + f({{\varphi }_{0}}{{(1 + u)}^{3}}).$
Если $\varphi \ll 1$ для решения (15) можно использовать теорию возмущений. В этом случае
(16)
$\delta R = {{R}_{0}}\left[ { - {{a}_{1}}\varphi + (a_{1}^{2} - {{a}_{2}}){{\varphi }^{2}} + \ldots } \right],$
где

(17)
${{a}_{1}} = {{\left. {\frac{{\partial f(\varphi )}}{{\partial \varphi }}} \right|}_{0}},\quad {{a}_{2}} = \frac{1}{2}{{\left. {\frac{{{{\partial }^{2}}f(\varphi )}}{{\partial {{\varphi }^{2}}}}} \right|}_{0}},\; \ldots $

ЭФФЕКТИВНЫЕ РАДИУСЫ МАКРОМОЛЕКУЛ БЫЧЬЕГО СЫВОРОТОЧНОГО АЛЬБУМИНА

Для получения эффективных радиусов макромолекул БСА нами используются экспериментальные значения сдвиговой вязкости в их водных растворах, полученные в [19]. С использованием формул (7)–(9) и (2) ячеечного подхода, получены температурные и концентрационные зависимости эффективного радиуса макромолекул. Поверхности эффективных радиусов макромолекул БСА в интервале концентраций 2.0–20.0 мас. % ($\varphi = (0.05{\kern 1pt} \div {\kern 1pt} 0.49)$) и температур 278–318 K при постоянном значении рН 5.0 (что соответствует окрестности изоэлектрической точки БСА) представлены на рис. 1.

Рис. 1.

Температурно-концентрационные зависимости эффективных радиусов макромолекул бычьего сывороточного альбумина при рН 5.2 [19].

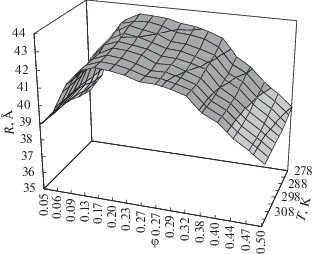
Как видим, при всех исследованных температурах концентрационные зависимости эффективного радиуса $R_{\eta }^{{{\text{(БСА)}}}}$ макромолекул БСА существенно немонотонны. При концентрациях ∼5 мас. % ($\varphi \approx 0.17$) величины $R_{\eta }^{{{\text{(БСА)}}}}$ принимают максимальные значения и достаточно быстро спадают в обе стороны от максимума. При концентрациях, больших 10 мас. % ($\varphi \approx 0.32$), концентрационные зависимости квазилинейны.

Наблюдаемый концентрационный максимум зависимости эффективных радиусов $R_{\eta }^{{{\text{(БСА)}}}}$ соответствует изолированным макромолекулам, так как переход от изолированных макромолекул к макромолекулам с перекрывающимися опушками происходит при $c* \approx $ 7 мас.% ($\varphi \approx 0.23$) [20, 21]. Положение максимума эффективного радиуса $R_{\eta }^{{{\text{(БСА)}}}}$ находится в физиологическом интервале концентраций альбумина (35–55 г/л) в плазме крови [19] и соответствует наибольшей площади поверхности макромолекулы. В свою очередь это обеспечивает максимальный доступ к центрам связывания альбумина для выполнения одной из главных его функций – транспортной [1].

Сравним размеры макромолекул БСА, полученных нами из анализа сдвиговой вязкости их водных растворов, с имеющимися литературными данными. В работе [22] методом динамического рассеяния света для разбавленных водных растворов БСА (температура $T = 298$ K, кислотно-щелочной баланс pH 5.0, концентрация ионов I = = 0.15 M) определен коэффициент самодиффузии ${{D}_{S}} = (6.14 \pm 0.03) \times {{10}^{{ - 11}}}$ м2/с, который, в соответствии с (12), приводит к $R_{D}^{{{\text{(БСА)}}}} = (39.92 \pm 0.03)$ Å. Это значение практически совпадает с $R_{\eta }^{{{\text{(БСА)}}}} = (39.90 \pm 0.05)$ Å, полученным нами из анализа вязкости при $c = 2.14$ мас. % ($\varphi = 0.06$), $T = 298$ K, рH 5.2. Подчеркнем, что значение pH растворов в обоих сравниваемых случаях находится вблизи изоэлектрической точки растворов БСА.

Метод динамического рассеяния света для определения значений коэффициента самодиффузии макромолекул альбумина используется также в работе [23]. При $c = 1$ мас. % ($\varphi = 0.024$), $T = 296$ K, рН 5.0 и I = 0.023 M гидродинамический радиус оказывается равным: $R_{D}^{{{\text{(БСА)}}}} = 37.9$ Å. Это значение также хорошо коррелирует с полученным из анализа рис. 2, если соответствующую кривую экстраполировать к значениям концентрации ∼1 мас. % ($\varphi = 0.024$).

Рис. 2.

Концентрационная зависимость эффективных радиусов БСА в водном растворе при $T = 298$ K и pH 5.2 [19].

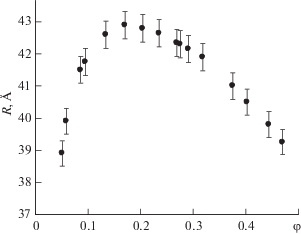
В работе [24] методом диффузии через пористые диафрагмы для разбавленных водных растворов БСА ($c = 2.79$ мас. % ($\varphi = 0.08$), Т = 298 K, рH 4.7) получен коэффициент самодиффузии, используя который и формулу (12), рассчитаем: $R_{D}^{{{\text{(БСА)}}}} = 36.9$ Å. Это значение несколько меньше величины гидродинамического радиуса $R_{\eta }^{{{\text{(БСА)}}}} = $ = (41.50 ± 0.05) Å, полученного нами из анализа вязкости водного раствора БСА со свойствами с = 2.79 мас. % ($\varphi = 0.08$), Т = 298 K, рH 5.2. Здесь некоторое расхождение величин гидродинамических радиусов макромолекул БСА можно связать с несоответствием кислотно-щелочных балансов (pH) растворов и присутствием ионов солей в растворах работы [24].

В работе [25] на основе вискозиметрических данных для предельно разбавленных растворов БСА с использованием обобщенной формулы Эйнштейна для макромолекул вытянутой формы [26] получена эффективная длина большой полуоси сфероида вращения: $R_{\eta }^{{{\text{(БСА)}}}} = 41.5$ Å.

Сравнение величин эффективных радиусов макромолекул БАС, рассчитанных из данных о вязкости ${{R}_{\eta }}$, согласно формуле (7), и данных о коэффициенте самодиффузии ${{R}_{D}}$, согласно формуле (12), приведено в табл. 1. В скобках указаны свойства раствора – температура Т, показатель кислотно-щелочного баланса рН и концентрация ионов (I, М) в растворе.

Таблица 1.  

Сравнение величин эффективных радиусов макромолекул БАС, рассчитанных из данных о вязкости (${{R}_{\eta }}$) и о коэффициенте самодиффузии (${{R}_{D}}$)

с, мас. % $\varphi $ ${{R}_{\eta }}(T,\;{\text{pH}},\;I)$, Å ${{R}_{D}}(T,\;{\text{pH}},\;I)$, Å
1.00 0.024 35.6 (296 K, 5.2, 0 ) 37.9 (296 K, 5.0, 0.023)
2.14 0.06 39.90 (298 K, 5.2, 0 ) 39.92 (298 K, 5.0, 0.15)
2.79 0.08 41.5 (298 K, 5.2, 0 ) 36.9 (298 K, 4.7, 0.1)
40.3 (298 K, 4.7, 0.1)*

* Расчет с использованием поправок по формулам (16), (17).

Таким образом, полученные нами результаты хорошо коррелируют с литературными данными. Кроме того, корректировка значений гидродинамического радиуса макромолекул альбумина по формулам (16), (17) позволяет добиваться практически полной согласованности данных, полученных на основе сдвиговой вязкости и самодиффузии. Некоторая неоднозначность сравнения радиусов макромолекулы определяется несоответствием рН раствора и присутствием ионов солей, к которым чувствительна структура альбумина.

ЭФФЕКТИВНЫЕ РАДИУСЫ МАКРОМОЛЕКУЛ СЫВОРОТОЧНОГО АЛЬБУМИНА ЧЕЛОВЕКА

Для получения температурных и концентрационных зависимостей эффективных радиусов макромолекул САЧ нами используются формулы (7)–(9) и (2) ячеечного подхода и экспериментальные значения сдвиговой вязкости в работе [27]. Поверхность эффективных радиусов макромолекул САЧ как функция температуры в интервале 278–318 K и концентрации в диапазоне 0.82–18.2 мас. % ($\varphi = (0.03{\kern 1pt} \div {\kern 1pt} 0.48)$) для значения рН 7.0 представлена на рис. 3.

Рис. 3.

Температурно-концентрационные зависимости эффективных радиусов макромолекул сывороточного альбумина человека при рН 7.0 [27].

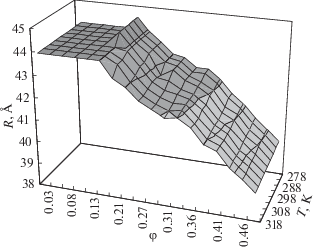
В работе [27] показано, что во всем температурном интервале можно выделить три области концентраций: 1) 0.82–3.65 мас. % ($\varphi = (0.03{\kern 1pt} \div {\kern 1pt} 0.14)$), где эффективные радиусы сывороточного альбумина человека остаются неизменными; 2) 4.6–9.45 мас. % ($\varphi = (0.18{\kern 1pt} \div {\kern 1pt} 0.31)$), где эффективные радиусы альбумина в водном растворе уменьшаются и 3) 10.2–18.2 мас. % ($\varphi = (0.33{\kern 1pt} \div {\kern 1pt} 0.48)$), где эффективные радиусы макромолекул альбумина с ростом концентрации линейно уменьшаются, причем угол наклона слабо зависит от температуры (рис. 4).

Рис. 4.

Концентрационная зависимость эффективных радиусов макромолекул САЧ вдоль изотерм при pH 7.0 [27].

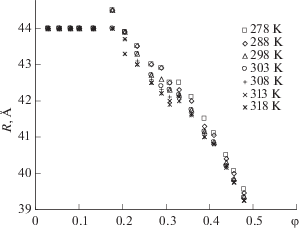
В работе [27] построены зависимости концентрации от температуры $C = {{\left. {f(T)} \right|}_{{R = {\text{const}}}}}$, при которых радиус макромолекулы САЧ остается неизменным. Кривая, которой отвечает $R_{\eta }^{{{\text{(САЧ)}}}} = $ $ = (42.53 \pm 0.05)$ Å в концентрационном диапазоне 7.0–10.0 мас. % ($\varphi = 0.21{\kern 1pt} \div {\kern 1pt} 0.28$), имеет два минимума при температурах ${{T}_{{\min 1}}} = 298 \pm 1$ K и ${{T}_{{\min 2}}} = 314 \pm 1$ K и один максимум при температуре ${{T}_{{\max }}} = 303 \pm 1$ K. При этом температурный интервал между локальными минимумами соответствует границам существования теплокровных организмов [27]. В работе [28] изменение конформации альбумина в температурном интервале 293–338 K связывают с динамическим фазовым переходом, происходящим в воде при ∼315 K (42°С). При росте концентрации САЧ возрастает роль взаимодействий воды с макромолекулами альбумина. Конформационную динамику альбумина авторы работы [29] связывают с изменением свойств воды, происходящим в физиологическом диапазоне температур.

Сравним размеры макромолекул САЧ, полученных нами из анализа сдвиговой вязкости их водных растворов, с имеющимися литературными данными. В работе [9] методом малоуглового рассеяния нейтронов исследованы разбавленные водные растворы САЧ (I = 0.15 M): результаты свидетельствуют в пользу вероятности конформации САЧ в виде несимметричного сплющенного эллипсоида радиусом 42.5 Å, что хорошо коррелирует с нашими результатами.

В работах [29, 30] методами фотонной корреляционной спектроскопии и молекулярной динамики в разбавленных водных растворов САЧ (с = 0.1 мас. % ($\varphi = 0.004$), T = 298–323 K, (0.075 М < $ < I < $ 0.225 М)) показана независимость величины гидродинамического радиуса $R_{D}^{{{\text{(САЧ)}}}} = 50 \pm 3$ Å от температуры, что хорошо коррелирует с полученными нами результатами для концентраций $\varphi < 0.15$ (см. рис. 4). Некоторое расхождение наших результатов $R_{\eta }^{{{\text{(САЧ)}}}} = 44$ Å для макромолекул САЧ с величиной $R_{D}^{{{\text{(САЧ)}}}} = 50 \pm 3$ Å в работе [29] можно связать с присутствием в последних растворах ионов хлорида натрия.

В работах [6, 31] представлены несколько меньшие значения гидродинамического радиуса $R_{D}^{{{\text{(САЧ)}}}} = (30.5 \pm 0.5)$ Å, полученные методом динамического рассеяния света для разбавленных водных растворов САЧ (с = 0.5–2 мас. % ($\varphi = 0.018{\kern 1pt} \div {\kern 1pt} 0.074$), T = 298 K, pH 7). Эти величины гидродинамических радиусов макромолекул САЧ сопоставимы с радиусами инерции макромолекул САЧ, полученными методом малоуглового рассеяния нейтронов [11]. В работе [6] отмечается независимость величины гидродинамического радиуса от концентрации для разбавленных растворов САЧ, что характерно и для построенной нами температурно-концентрационной зависимости в области разбавленных растворов САЧ ($\varphi < 0.15$).

Таким образом, полученные нами результаты сопоставимы с литературными данными. Как и выше, сравнение радиусов макромолекулы затрудняется несоответствием значений рН раствора и присутствием ионов солей, к которым чувствительна структура альбумина.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Проанализированы изменения структуры и размеров макромолекул САЧ и БСА в водных растворах в зависимости от температуры, концентрации и кислотно-щелочного баланса (рН) среды. Специальное внимание уделено сравнению значений гидродинамического радиуса, полученных из данных о самодиффузии макромолекул и из данных по сдвиговой вязкости водных растворов макромолекул. Важность этих вопросов определяется необходимостью аккуратного учета влияния воды на структуру белков.

Определение радиусов макромолекул из данных по сдвиговой вязкости их растворов с помощью ячеечных подходов оказывается одним из самых простых и эффективных методов. Важной особенностью используемого нами ячеечного подхода [17, 18] является то, что при $\varphi < 0.2$ он приводит к результатам, в точности совпадающим с полученными методами Эйнштейна [16] и Бэтчелора [15]. Он дополняет и уточняет картину особенностей динамики биомакромолекул в водных растворах, полученных другими методами.

Подчеркнем, что анализ размеров макромолекул, полученных различными методами, чрезвычайно важен для изучения изменений структуры макромолекулярных клубков вследствие их взаимодействия с водой при растворении в ней, а также при учете взаимодействия между опушками различных клубков, особенно при их перекрытии, и взаимодействия с ионами кислот и щелочей, растворенных в воде.

Список литературы

  1. Peters Jr.T. All About Albumin: Biochemistry, Genetics, and Medical Applications. Academic Press, 1996. 432 p.

  2. He X.M., Carter D.C. // Nature. 1992. V. 358 (6383). P. 209.https://doi.org/10.1038/358209a0

  3. Majorek K.A., Porebski P.J., Dayal A. et al. // Molecular Immunology. 2012. V. 52. P. 174.https://doi.org/10.1016/j.molimm.2012.05.011

  4. Akdogan Y., Reichenwallner J., Hinderberger D. // PLoS ONE. 2012. V. 7 (9). P. e45681.https://doi.org/10.1371/journal.pone.0045681

  5. Carter D.C., Ho J.X. // Adv. Protein Chem. 1994. V. 45. P. 153.https://doi.org/10.1016/s0065-3233(08)60640-3

  6. Luik A.I., Naboka Yu.N., Mogilevich S.E. et al. // Spectrochim. Acta. A Mol. Biomol. Spectrosc. 1998. V. 54. № 10. P. 1503.https://doi.org/10.1016/s1386-1425(98)00171-1

  7. Maslova M.N., Zaritskiy A.R., Chaykov L.L. // Biophysical J. 2014. V. 106. № 2. P. 457a.https://doi.org/10.1016/j.bpj.2013.11.2595

  8. Sjöberg B., Mortensen K. // Biophys. Chemist. 1994. V. 52. P. 131.https://doi.org/10.1016/0301-4622(94)00089-1

  9. Киселев М.А., Грызунов Ю.А., Добрецов Г.Е. и др. // Биофизика. 2001. Т. 46. № 3. С. 423.

  10. Chicea D., Chicea R., Chicea L.M. // Rom. Reports Phys. 2013. V. 65. № 1. P. 178.

  11. Olivieril J.R., Craievich A.F. // Eur. Biophys. J. 1995. V. 24. P. 77.https://doi.org/10.1007/bf00211402

  12. Wilkins D.K., Grimshaw S.B., Receveur V. et al. // Biochemistry. 1999. V. 38. P. 16424.https://doi.org/10.1021/bi991765q

  13. Qian J., Tang Q., Cronin B. et al. // J. Chromatogr. A. 2008. V. 1194. № 1. P. 48.https://doi.org/10.1016/j.chroma.2008.01.040

  14. Monkos K. // Biochimica et Biophysica Acta. 2004. V. 1700. № 1. P. 27.https://doi.org/10.1016/j.bbapap.2004.03.006

  15. Batchelor G.K. An Introduction to Fluid Dynamics. Cambridge University Press, 1967. 615 p.

  16. Einstein A. // Ann. Phys. 1906. V. 19. P. 289.https://doi.org/10.1002/andp.19063240204

  17. Malomuzh N.P., Orlov E.V. // Ukr. J. Phys. 2005. V. 50. № 6. P. 618.

  18. Orlov E.V. // Colloid J. 2010. V. 72. P. 820.https://doi.org/10.1134/S1061933X1006013X

  19. Khorolskyi O.V., Moskalenko Yu.D. // Ukr. J. Phys. 2020. V. 65. № 1. P. 41.https://doi.org/10.15407/ujpe65.1.41

  20. Khorolskyi O.V. // Ibid. 2018. V. 63. № 2. P. 144.https://doi.org/10.15407/ujpe63.2.144

  21. Malomuzh N.P., Bulavin L.A., Gotsulskyi V.Ya. et al. // Ibid. 2020. V. 65. № 2. P. 151.https://doi.org/10.15407/ujpe65.2.151

  22. Yadav S., Shire S.J., Kalonia D.S. // Pharm. Res. 2011. V. 28. № 8. P. 1973.https://doi.org/10.1007/s11095-011-0424-7

  23. Gaigalas A.K., Hubbard J.B., McCurley M. et al. // J. Phys. Chem. 1992. V. 96. P. 2355.https://doi.org/10.1021/j100184a063

  24. Keller K.H., Canales E.R., Yum S.I. // Ibid. 1971. V. 75. P. 379.https://doi.org/10.1021/j100673a015

  25. Jachimska B., Pajor A. // Bioelectrochemistry. 2012. V. 87. P. 138.https://doi.org/10.1016/j.bioelechem.2011.09.004

  26. Brenner H. // J. Multiphase Flow. 1974. V. 1. P. 195.https://doi.org/10.1016/0301-9322(74)90018-4

  27. Khorolskyi O.V. // Ukr. J. Phys. 2019. V. 64. № 4. P. 287.https://doi.org/10.15407/ujpe64.4.287

  28. Bardik V., Gotsulskii V., Pavlov E. et al. // J. Mol. Liq. 2012. V. 176. P. 60.https://doi.org/10.1016/j.molliq.2012.09.012

  29. Atamas N., Bardik V., Bannikova A. et al. // Ibid. 2017. V. 235. P. 17.https://doi.org/10.1016/j.molliq.2017.01.017

  30. Atamas N., Bardik V.Y., Komisarenko S. et al. // Atti Accad. Pelorit. Pericol. Cl. Sci. Fis. Mat. Nat. 2019. V. 97. № S2. P. A16.https://doi.org/10.1478/AAPP.97S2A16

  31. Hushcha T.O., Luik A.I., Naboka Y.N. // Talanta. 2000. V. 53. № 1. P. 29.https://doi.org/10.1016/s0039-9140(00)00454-9

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал