Журнал физической химии, 2021, T. 95, № 7, стр. 1118-1123

При термодинамической интерпретации эффективности процессов разделения важное значение приобретает термодинамическое обоснование и расчет функций, определяющих работу разделения [1–7]. Максимальная полезная работа при заданных температуре и давлении равна убыли энергии Гиббса термодинамической системы [8, 9]. Процесс распределения разделяемых компонентов между двумя фазами (жидкость–жидкость, жидкость–сорбент) рассматривается обычно как изобарно-изотермический [10, 11]. В [12] представлен расчет изменения энергии Гиббса в системах фракционной экстракции при разделении пары компонентов (А и В) исходной (перерабатываемой в каскаде [13–15]) смеси. Цель настоящей работы состоит в распространении предложенного подхода на смеси, содержащей более чем одну пару разделяемых компонентов [7].

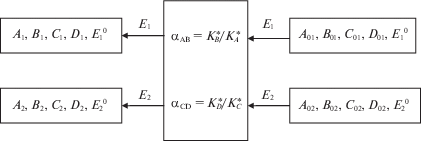
Рассмотрим в качестве примера процесс разделения компонентов A, B, C и D многокомпонентной смеси, содержащей две выбранные пары AB и CD, в распределительной системе (см. рис. 1) в условиях независимого распределения разделяемых компонентов между двумя несмешивающимися растворителями – экстрагентами E₁ и E₂. При использовании взаимонерастворимых экстрагентов в количествах $E_{1}^{0}$ и $E_{2}^{0}$ молей в систему с одной стороны подаются два бесконечно разбавленных раствора, содержащих разделяемые компоненты в количествах A₀₁, B₀₁, C₀₁, D₀₁ и A₀₂, B₀₂, C₀₂, D₀₂ молей, а с другой стороны выводятся два аналогичных раствора, содержащих A₁, B₁, C₁, D₁ и A₂, B₂, C₂, D₂ молей разделяемых компонентов. Данная система представляет собой ступень каскада, подобного описанному в [7, 13–15]. Эффект однократного разделения выбранных пар AB и CD охарактеризуем, как это принято в общей теории процессов разделения [1, 16], коэффициентами разделения α и эффективными коэффициентами разделения β:

Отсюда Здесь α_CD > α_AB [7], 1 < β < α [16] и Обозначения p и q широко используются в жидкостной экстракции [13]. Смысл этих обозначений следует из соотношений: где ε – факторы экстракции [13] и k – факторы хроматографического удерживания [11, 17] компонентов A, B, C и D.

Термодинамические коэффициенты распределения [10, 11]

Далее будем постулировать и где F – воображаемый компонент [17] (k_D > k_B > > k_F > k_A > k_C) и Постулируемые равенства наблюдаются, например [17, 18], при хроматографическом разделении веществ гомологического ряда. Для A, B, C и D, подбирая экстрагенты и условия разделения, возможно, как и в случае отдельного разделения пар AB и CD [13], установить, по крайней мере, в принципе Эти равенства отвечают симметричному разделению [13]. При симметричном разделении получают наилучшие результаты [13].

Для рассматриваемой системы (см. рис. 1) принимаем [10, 12]

Оптимальным условиям разделения при экстракции отвечают соотношения [12, 13, 16]: которые характеризуют также симметричное разделение молекулярных и изотопных смесей в общей теории процессов разделения (β_AB = $\alpha _{{{\text{AB}}}}^{{1/2}}$, β_CD = $\alpha _{{{\text{CD}}}}^{{1/2}}$ [1, 16]).

Термодинамический эффект разделения заключается в изменении свободной энергии системы и энтропии смешения [4, 5, 19]. Энергия Гиббса системы (рис. 1) в начальном состоянии [10, 20]

где химический потенциал $\mu _{i}^{j}$ для бесконечно разбавленных растворов [11, 21–24]. Здесь R – газовая постоянная, Т – абсолютная температура, где $\gamma _{i}^{{0j}}$ – коэффициенты активности при бесконечном разбавлении [11, 13, 22, 24].

Энергия Гиббса в конечном состоянии (состояние равновесия [20, с. 150])

Здесь Из равенства химических потенциалов при равновесии по данным [11, 13] Изменение энергии Гиббса (конечная величина [4]) где [23] Для членов одного гомологического ряда [17] и характерна линейная зависимость логарифма коэффициента активности γ⁰ от числа атомов углерода [24].

Записанные соотношения для ∆G можно получить по аналогии с данными [12], используя предыдущие уравнения и применяя для предельно разбавленных растворов формулы:

При отдельном разделении пар AB и CD имеем [12]: Убыль энергии Гиббса, отвечающая оптимальным условиям проведения процесса разделения, следует, соответственно [12], из уравнения где q_AB = A₀+ B₀, q_CD = C₀+ D₀, При α < 1.5 имеем f(α) ≈ 0.25 [12], поэтому для тонкого разделения [1], когда α – 1 ≪ 1, можно принять Здесь W характеризует приращение ценности смеси и максимальную разделительную способность системы при отдельном разделении пар AB и CD [1, 5, 6, 25]. Название “работа разделения” для W = q(α – 1)/ 8 предложено Юри в 1939 г. [1, 5]. Таким образом, установлена связь между изменением энергии Гиббса экстракционной системы и фундаментальными понятиями общей теории процессов разделения. Эти понятия имеют большое значение [6], так как позволяют дать сравнительную оценку эффективности процессов разделения [2, 5, 7].

Из проведенного расчета и полученных уравнений следует, что ∆G = G_K– G_Н < 0. Если ∆G < 0, то с точки зрения химической термодинамики процесс является самопроизвольным и способным [8, 9] совершить обратимую работу W_T = = ‒∆G, где ∆G – изменение энергии Гиббса, вычисленное при полной неравновесности процесса. Эта функция обладает свойством термодинамической аддитивности и в рассмотренном примере разделения многокомпонентной смеси, состоящей из выбранных пар AB и CD, представляет собой сумму работ W_T,AB = –∆G_AB и W_T,CD = = –∆G_CD отдельного разделения указанных пар [7]. Таким образом, подтверждено предполагаемое ранее [7] свойство термодинамической аддитивности работы разделения.