Журнал физической химии, 2022, T. 96, № 10, стр. 1428-1435

Аппроксимация термодинамических свойств твердого диборида урана моделями CALPHAD третьего поколения

А. Л. Восков^a, *

^a Московский государственный университет имени М.В. Ломоносова, Химический факультет
Москва, Россия

Поступила в редакцию 27.12.2021
После доработки 27.12.2021
Принята к публикации 10.01.2022

EDN: NLEWZN
DOI: 10.31857/S0044453722100326

Аннотация

Получены выражения для энергии Гиббса твердого диборида урана UB₂ для T = 0–2300 K в системе отсчета “standard element reference”. Установлено, что они описывают экспериментальные данные по теплоемкости и теплосодержанию во всем интервале температур единой зависимостью. Показано, что взвешенная сумма функций Эйнштейна без полиномиального вклада приближенно воспроизводит предельное поведение теплоемкости при T = 1–5 K. Также предложена упрощенная зависимость для энергии Гиббса с шестью параметрами, пригодная для использования при T = 200–2000 K.

Ключевые слова: диборид урана, теплоемкость, теплосодержание, функции Эйнштейна, энергия Гиббса, энтальпия, CALPHAD

Диборид урана UB₂ представляет интерес как компонент перспективных ядерных топлив, устойчивых к авариям (accident tolerant fuels) [1], и изучение его термодинамических свойств важно как для оптимизации условий их получения, так и для предсказания фазовых и химических равновесий с его участием. Термодинамическая модель двойной системы уран–бор [2] позволяет получить фазовую диаграмму, а также свойства всех существующих в ней бинарных соединений: UB₂, UB₄ и UB₁₂. Она относится к моделям CALPHAD второго поколения, т.е. пригодна только для T ≥ 298.15 K и основана на полиномиальных функциях. Возможная альтернатива – модели CALPHAD третьего поколения, впервые предложенные в 1995 г. [3]. В них для аппроксимации изобарной теплоемкости C_p используются функции Эйнштейна или Дебая, что обеспечивает их применимость вплоть до 0 K и возможность экстраполяции в области как низких, так и высоких температур. В дальнейшем Ворониным и Куценком [4] и Якобсом и др. [5] было независимо предложено использовать взвешенную сумму нескольких функций Эйнштейна, что позволило достичь высокой точности аппроксимации теплоемкости сложных веществ в широком интервале температур. Впоследствии эта модель была дополнена полиномиальной частью в [6] и использовалась для аппроксимации теплоемкостей графита и алмаза.

Для твердого диборида урана UB₂ имеются экспериментальные данные по изобарной теплоемкости C_p [7] и теплосодержанию H_T – H_298.15 [8, 9], покрывающие температурный интервал 1.1–2300 K. Их краткий перечень представлен в табл. 1. Все они были получены для образцов состава UB_1.979. Для перехода к термодинамическим функциям стехиометрического UB₂ использовался множитель 3/2.979 ≈ 1.007, предложенный авторами [7]. В этой же работе были рекомендованные следующие значения термодинамических функций UB₂ при T = 298.15 K, полученные из экспериментальных данных по теплоемкости: $S_{{298.15}}^{ \circ } = 55.51 \pm 0.11$ Дж/(моль К), $H_{{298.15}}^{ \circ } - H_{0}^{ \circ } = 8880 \pm 17$ Дж/моль, $C_{{p,298.15}}^{ \circ }\, = \,55.76\, \pm $ $ \pm \;0.11$ Дж/(моль К).

Таблица 1.

Имеющиеся экспериментальные данные по теплоемкостям и теплосодержаниям UB₂

T, K	Тип данных	Число точек	Метод измерения	Источник
1.1–20.6	C_p	41	изопериболическая калориметрия	[7]
7.4–348	C_p	55	адиабатическая калориметрия	[7]
579–1486	H_T – H_298.15	18	дроп-калориметрия	[8]*
1303–2300	H_T – H_298.15	11	дроп-калориметрия	[9]*

* Экспериментальные данные по теплосодержанию H_T – H_298.15, пересчитанные на стехиометрический состав UB₂, были взяты из [2].

Энтальпия образования диборида урана ${{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }({\text{U}}{{{\text{B}}}_{2}}) = - 164.43 \pm 17$ кДж/моль (–39.3 ± ± 4.0 ккал/моль) [7] была получена сжиганием образца UB₂ в калориметрической бомбе в атмосфере фтора с использованием литературных данных по энтальпиям образования UF₆ и BF₃.

Помимо экспериментальных данных приводится также температурная зависимость энергии Гиббса для UB₂ для T = 298.15–2300 K [2] в системе отсчета “standard element reference”. Она выглядит следующим образом, формулы даны в пересчете на U_1/3B_2/3:

(1)

$\begin{gathered} G(T)--{{H}_{{{\text{SER}}}}},\;{\text{Дж/моль}} = --63\,972.50 + \\ + \;137.55038T--22.286574T\ln T-- \\ - \;5.157738 \times {{10}^{{ - 3}}}{{T}^{2}} + 0.39417 \times {{10}^{{ - 6}}}{{T}^{3}} + \\ + \;310\,100{\text{/}}T\quad (298.15\;{\text{K}} < T < 1600\;{\text{K}}), \\ \end{gathered} $

(2)

$\begin{gathered} G(T)--{{H}_{{{\text{SER}}}}},\;{\text{Дж/моль}} = --344\,980.46 + \\ + \;2063.58552T--283.582964T\ln T + \\ + \;106.066517 \times {{10}^{{ - 3}}}{{T}^{2}}--8.73248 \times {{10}^{{ - 6}}}{{T}^{3}} + \\ + \;58\,632\,007{\text{/}}T\quad (1600\;{\text{K}} < T < 2300\;{\text{K}}), \\ \end{gathered} $

где H_SER – уровень отсчета, т.е. энтальпия образования простых веществ (стабильные аллотропные модификации) при T = 298.15 K и p = 1 бар. Обобщенное выражение G_T – H_SER для индивидуального соединения выглядит следующим образом:

(3)

${{G}_{T}} - {{H}_{{{\text{SER}}}}} = ({{H}_{T}} - {{H}_{{298.15}}} + {{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }) - T{{S}_{T}},$

где ${{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }$ – стандартная энтальпия образования соединения. Для UB₂ использовалось ее значение, полученное в [7] (см. выше). Недостатки этой полиномиальной модели – использование двух разных зависимостей для T = = 298.15–1600 K и T > 1600 K, а также непригодность для расчета C_p при T < 298.15 K. Значение энтропии $S_{{298.15}}^{ \circ } = 54.525~$ Дж/(моль К) использовалось в готовом виде (т.е. оно не может быть получено из полиномиальной зависимости C_p(T)).

В литературе не описаны термодинамические модели, позволяющие рассчитывать изобарную теплоемкость UB₂ при T = 0–298.15 K. Авторы [7] предложили следующую аппроксимацию низкотемпературной C_p для T < 4.2 K:

(4)

$\begin{gathered} {{C}_{p}},\;{\text{мДж/}}({\text{моль}}\;{\text{К}}) = (9.40 \pm 0.01)T + \\ + \;(3.18 \pm 0.14) \times {{10}^{{--2}}}{{T}^{3}}. \\ \end{gathered} $

В этой же работе была предложена аппроксимация аномалии теплоемкости твердого UB₂ при T = 40–100 K двухуровневой моделью Шоттки. К сожалению, эти две модели не перекрывают весь температурный интервал 0–298.15 K и не могут использоваться для расчета $S_{{298.15}}^{ \circ }$. Хотя в [7] для этих целей экспериментальные теплоемкости аппроксимировались полиномиальными зависимостями, сами зависимости не приводятся.

Цель данной работы – получение температурных зависимостей энергии Гиббса твердого диборида урана UB₂, основанных на моделях CALPHAD третьего поколения и имеющихся экспериментальных данных по изобарной теплоемкости, теплосодержанию и энтальпии образования.

МЕТОДИКА РАСЧЕТОВ

В данной работе экспериментальные данные по теплоемкости и теплосодержанию аппроксимировались моделью, включающей в себя взвешенную суммой функций Эйнштейна и полиномиальный вклад:

(5)

$\begin{gathered} {{C}_{p}}(T,\vec {\alpha },\vec {\theta },{{a}_{1}},{{a}_{2}}) = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{C}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) + \\ + \;R{{a}_{1}}\left( {\frac{T}{{{{T}_{0}}}}} \right) + R{{a}_{2}}{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}^{4}}, \\ \end{gathered} $

(6)

$\frac{{{{C}_{{\text{E}}}}(x)}}{R} = \frac{{3{{x}^{2}}{{e}^{x}}}}{{{{{({{e}^{x}} - 1)}}^{2}}}},$

где T₀ = 298.15 K, R – универсальная газовая постоянная, m – число функций Эйнштейна, ${{\alpha }_{i}}$, ${{\theta }_{i}}$, a₁ и a₂ – параметры модели. Эта модель предложена авторами [6] и получена добавлением полиномиальной части к модели изобарной теплоемкости на основе взвешенной суммы функций Эйнштейна, предложенной Ворониным и Куценком [4]. Полиномиальная часть уравнения (5) отличается от используемого в [6] выражения AT + + BT⁴ безразмерностью коэффициентов a₁ и a₂.

Выражения для энтропии и теплосодержания могут быть получены интегрированием уравнения (6) и выглядят следующим образом:

(7)

$\begin{gathered} S(T,\vec {\alpha },\vec {\theta },{{a}_{1}},{{a}_{2}}) = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{S}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) + \\ + \;R{{a}_{1}}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{R{{a}_{2}}}}{4}{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}^{4}}, \\ \end{gathered} $

(8)

$\frac{{{{S}_{{\text{E}}}}(x)}}{R} = 3\left( {\frac{x}{{{{e}^{x}} - 1}} - \ln (1 - {{e}^{{ - x}}})} \right),$

(9)

$\begin{gathered} H(T,\vec {\alpha },\vec {\theta },{{a}_{1}},{{a}_{2}}) - {{H}_{0}} = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{H}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) + \\ + \;RT\left( {\frac{{{{a}_{1}}}}{2}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{{{a}_{2}}}}{5}{{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}}^{4}}} \right), \\ \end{gathered} $

(10)

$\frac{{{{H}_{{\text{E}}}}(x)}}{{RT}} = \frac{{3x}}{{{{e}^{x}} - 1}}.$

Подстановкой уравнений (7)–(10) в уравнение (3) можно получить выражение для энергии Гиббса в системе отсчета “standard element reference”:

(11)

$\begin{gathered} G(T,\vec {\alpha },\vec {\theta },{{a}_{1}},{{a}_{2}}) - {{H}_{{{\text{SER}}}}} = {{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ } - \\ - \;({{H}_{{298.15}}} - {{H}_{0}}) + \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{G}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) - \\ - \;RT\left( {\frac{{{{a}_{1}}}}{2}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{{{a}_{2}}}}{{20}}{{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}}^{4}}} \right), \\ \end{gathered} $

(12)

$\frac{{{{G}_{{\text{E}}}}(x)}}{{RT}} = \frac{{{{H}_{{\text{E}}}}(x)}}{{RT}} - \frac{{{{S}_{{\text{E}}}}(x)}}{R} = 3\ln (1 - {{e}^{{ - x}}}).$

Для аппроксимации экспериментальных данных использовались четыре варианта описанной выше модели.

1. Модель без полиномиальной части (т.е. в уравнениях (5), (7), (9) и (11) ${{a}_{1}} = {{a}_{2}} = 0$), параметры которой были получены с использованием всех экспериментальных данных из табл. 1. Далее будет обозначаться как Ein.

2. Модель EinLT без полиномиальной части, при оптимизации ее параметров использовались только данные из интервала T = 0–1486 K.

3. Модель EinPoly с полиномиальной частью (т.е. ${{a}_{1}} \ne 0$ и ${{a}_{2}} \ne 0$), основанная на тех же данных, что и модель Ein.

4. Упрощенная модель с двумя функциями Эйнштейна и полиномиальной частью (Ein2), основанная на данных при T = 200–2300 K, а также на полученных из модели Ein значениях $S_{{298.15}}^{ \circ }$ и $H_{{298.15}}^{ \circ } - H_{0}^{ \circ }$.

Значения параметров моделей оптимизировались нелинейным методом наименьших квадратов, реализованным в программе CpFit [10]. Для первых трех моделей использовалась целевая функция, основанная на взвешенной сумме квадратов относительных отклонений:

(13)

$\begin{gathered} RSS = \mathop \sum \limits_{k~ = ~1}^{{{n}_{C}}} \,\omega _{{C,k}}^{2}{{\left( {\frac{{C_{p}^{{{\text{calc}}}}({{T}_{k}}) - C_{{p,k}}^{{{\text{expt}}}}}}{{C_{{p,k}}^{{{\text{expt}}}}}}} \right)}^{2}} + \\ + \;\mathop \sum \limits_{k~ = ~1}^{{{n}_{H}}} \,\omega _{{H,k}}^{2}{{\left( {\frac{{{{\Delta }}{{H}^{{{\text{calc}}}}}({{T}_{k}}) - {{\Delta }}H_{k}^{{{\text{expt}}}}}}{{{{\Delta }}H_{k}^{{{\text{expt}}}}}}} \right)}^{2}}, \\ \end{gathered} $

где индексы calc и expt относятся к расчетным и экспериментальным значениям, ω_С и ω_H – статистические веса для изобарных теплоемкостей и теплосодержаний соответственно, ω_С = 1 для T ≥ ≥ 5 K и ω_С = 0.25 для T < 5 K. В случае же ω_H во всех моделях, кроме Ein2, использовались единичные статистические веса ω_H = 1, а в модели Ein2 – ω_H = 1 и ω_H = 0.1 для точек из [8] (T = 479–1486 K) и [9] (T = 1303–2300 K) соответственно. Для упрощенной модели Ein2 с двумя функциями Эйнштейна и полиномиальной частью использовались экспериментальные данные исключительно для T > 100 K. Воспроизводимость значений $S_{{298.15}}^{ \circ }$ и $H_{{298.15}}^{ \circ } - H_{0}^{ \circ }$ обеспечивалась введением в целевую функцию двух дополнительных слагаемых, т.е. использованием новой целевой функции RSS₂:

(14)

$\begin{gathered} RS{{S}_{2}} = RSS + {{10}^{4}}{{\left( {\frac{{S_{{298.15}}^{{ \circ ,{\text{calc}}}} - S_{{298.15}}^{{ \circ ,{\text{ref}}}}}}{{S_{{298.15}}^{{ \circ ,{\text{ref}}}}}}} \right)}^{2}} + \\ + \;{{10}^{4}}{{\left( {\frac{{{{\Delta }}{{H}^{{ \circ ,{\text{calc}}}}} - {{\Delta }}{{H}^{{ \circ ,{\text{ref}}}}}}}{{{{\Delta }}{{H}^{{ \circ ,{\text{ref}}}}}}}} \right)}^{2}}, \\ \end{gathered} $

где RSS – описываемая уравнением (13) целевая функция, а надстрочные индексы calc и ref относятся к величинам, полученным из моделей Ein2 и Ein соответственно. Также при оптимизации параметров модели Ein2 использовалось дополнительное условие $\sum\nolimits_i^{} {{{\alpha }_{i}}} = {{N}_{{{\text{atoms}}}}}$ = 3, реализованное в программе CpFit путем следующей замены переменных:

(15)

$\left\{ \begin{gathered} {{\alpha }_{1}} = (1 - {{\xi }_{1}}){{N}_{{{\text{atoms}}}}}, \hfill \\ {{\alpha }_{2}} = {{\xi }_{1}}{{N}_{{{\text{atoms}}}}}, \hfill \\ \end{gathered} \right.$

где ${{\xi }_{1}} \in \left[ {0;\,\,1} \right]$ – оптимизируемый параметр, а ${{N}_{{{\text{atoms}}}}} = 3$.

Для оценки точности аппроксимации экспериментальных данных использовались две величины: стандартное отклонение и нормированное абсолютное медианное отклонение. Они рассчитываются следующим образом для абсолютных и относительных отклонений:

(16)

$\begin{gathered} s(\delta Y) = \sqrt {\frac{{\sum\limits_{i~ = ~1}^n {{{{(Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}})}}^{2}}} }}{n}} ; \\ s(\varepsilon Y) = \sqrt {\mathop \sum \limits_{i~ = ~1}^n \,{{n}^{{ - 1}}}{{{\left( {\frac{{Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}}}}{{Y_{i}^{{{\text{expt}}}}}}} \right)}}^{2}}} ; \\ \end{gathered} $

(17)

$\begin{gathered} {{s}_{{{\text{MAD}}}}}(\delta Y) = \frac{{\operatorname{median} ~\left| {Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}}} \right|}}{{{{{{\Phi }}}^{{ - 1}}}(0.75)}}; \\ {{s}_{{{\text{MAD}}}}}(\varepsilon Y) = \frac{{\operatorname{median} ~\left| {\frac{{Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}}}}{{Y_{i}^{{{\text{expt}}}}}}} \right|}}{{{{{{\Phi }}}^{{ - 1}}}(0.75)}}, \\ \end{gathered} $

где $Y$ – изобарная теплоемкость C_p или теплосодержание ${{H}_{T}} - {{H}_{{298.15}}}$, ${{{{\Phi }}}^{{ - 1}}}(x)$ – обратная интегральная функция распределения для стандартного нормального распределения, $1{\text{/}}{{{{\Phi }}}^{{ - 1}}}(0.75) \approx $ $ \approx 1.483$. Более подробное описание этих оценок точностью аппроксимации, в т.ч. обоснование использования нормирующего множителя 1.483, даны в одной из предыдущих публикаций по использованию программы CpFit для составления баз данных [11].

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Полученные наборы параметров для уравнений (5)–(12) представлены в табл. 2. Для упрощенной модели Ein2 были получены следующие значения параметров:

(18)

$\begin{gathered} {{\alpha }_{1}} = 1.96081,\quad {{\alpha }_{2}} = 1.03919, \\ {{\theta }_{1}}{\text{/K}} = 855.158,\quad {{\theta }_{2}}{\text{/K}} = 181.689, \\ {{a}_{1}} = 0.609182,\quad {{a}_{2}} = 1.88976 \times {{10}^{{ - 5}}}. \\ \end{gathered} $

Таблица 2.

Оптимизированные параметры моделей α_i, θ_i, a₁, a₂ для взвешенной суммы функций Эйнштейна с полиномиальным термом и без него (см. уравнения (5), (7), (9), (11))

Параметр	Модель
Параметр	Ein	EinLT	EinPoly
α₁	248.427 ± 460	0.753366 ± 0.080	1.36636 ± 0.33
θ₁, K	20583.0 ± 4800	2566.79 ± 360	1054.84 ± 86
α₂	0.748971 ± 0.081	1.98150 ± 0.094	0.918373 ± 0.33
θ₂, K	2525.86 ± 360	865.288 ± 45	622.662 ± 64
α₃	1.98367 ± 0.092	0.295821 ± 0.12	0.903728 ± 0.0099
θ₃, K	861.749 ± 46	411.299 ± 93	179.195 ± 2.1
α₄	0.287805 ± 0.11	0.900898 ± 0.027	0.0695765 ± 0.012
θ₄, K	405.253 ± 96	175.593 ± 2.2	98.1887 ± 4.2
10³α₅	899.380 ± 29	61.9041 ± 11	2.42919 ± 0.40
θ₅, K	175.441 ± 3.4	90.8470 ± 4.8	34.2918 ± 2.2
10³α₆	61.4672 ± 12	5.8325 ± 0.58	0
θ₆, K	90.6821 ± 5.1	33.0569 ± 2.8	0
10³α₇	5.8178 ± 0.60	1.5352 ± 0.24	0
θ₇, K	33.0007 ± 2.9	11.846 ± 1.6	0
10³α₈	1.5315 ± 0.25	0.74844 ± 0.11	0
θ₈, K	11.8263 ± 1.6	3.0199 ± 0.43	0
10³α₉	0.74745 ± 0.11	0	0
θ₉, K	3.01636 ± 0.45	0	0
a₁	0	0	0.345204 ± 0.0035
a₂	0	0	(9.1395 ± 1.3) × 10^–4
$\sum\nolimits_i^{} {{{\alpha }_{i}}} $	252.4	4.002	3.260

В табл. 3 и 4 приведена точность аппроксимации экспериментальных данных по изобарной теплоемкости [7] и теплосодержанию [8, 9] различными термодинамическими моделями: как полученными в данной работе, так и взятой из [1]. В случае данных [7] два температурных диапазона соответствуют выборкам, полученных методами изопериболической и адиабатической калориметрии (см. табл. 1).

Таблица 3.

Точность аппроксимации экспериментальных данных по теплоемкости из [7] (см. табл. 1) разными моделями

Модель	T, K	$100s(\varepsilon {{C}_{p}})$	$100{{s}_{{{\text{MAD}}}}}(\varepsilon {{C}_{p}})$	$s(\delta {{C}_{p}})$, Дж/(моль К)	${{s}_{{{\text{MAD}}}}}(\delta {{C}_{p}})$, Дж/(моль К)
Ein	1.1–20.6	0.56	0.76	8.8 × 10^–4	2.3 × 10^–4
	7.4–348	0.58	0.28	0.079	0.031
EinLT	1.1–20.6	0.56	0.78	8.9 × 10^–4	2.3 × 10^–4
	7.4–348	0.58	0.28	0.078	0.032
EinPoly	1.1–20.6	0.78	1.0	8.9 × 10^–4	3.2 × 10^–4
	7.4–348	0.58	0.23	0.048	0.037
Ein2	200–348	0.23	0.28	0.11	0.15
Poly	298–348	1.1	1.1	0.63	0.65

Таблица 4.

Точность аппроксимации экспериментальных данных по теплосодержанию из [8, 9] (см. табл. 1) разными моделями

Модель	T, K	$~100s(\varepsilon {{\Delta }}H)$	$100{{s}_{{{\text{MAD}}}}}(\varepsilon {{\Delta }}H)$	$s(\delta {{\Delta }}H)$, кДж/моль	${{s}_{{{\text{MAD}}}}}(\delta {{\Delta }}H)$, кДж/моль
Ein	579–1486	0.22	0.23	0.13	0.15
	1303–2300	0.42	0.55	0.51	0.64
EinLT	579–1486	0.22	0.23	0.14	0.13
	1303–2300	3.6	1.0	6.5	1.1
EinPoly	579–1486	0.40	0.50	0.24	0.29
	1303–2300	0.94	0.91	1.4	1.2
Ein2	579–1486	0.29	0.27	0.16	0.16
	1303–2300	1.5	0.82	2.7	1.2
Poly	579–1486	0.26	0.17	0.087	0.12
	1303–2300	0.57	0.27	0.72	0.39

На рис. 1 и 2 показаны результаты аппроксимации экспериментальных данных по изобарной теплоемкости и теплосодержанию. Температурные зависимости C_p и H_T – H_298.15 изображены на рис. 1а и 2а, а соответствующие им диаграммы рассеяния – на рис. 1б и 2б.

Рис. 1.

Результаты аппроксимации экспериментальных значений изобарной теплоемкости UB₂: a – зависимости C_p от T; б – зависимости относительных отклонений $\varepsilon {{C}_{p}} = 100(C_{p}^{{{\text{expt}}}} - C_{p}^{{{\text{calc}}}}){\text{/}}C_{p}^{{{\text{expt}}}}$ от T. Линии: сплошная, штрих, штрих-пунктир и пунктир – модели Ein, EinPoly, Ein2 и Poly соответственно. Точки – экспериментальные значения C_p из [7]: круги – изопериболическая калориметрия, треугольники – адиабатическая калориметрия.

Рис. 2.

Результаты аппроксимации экспериментальных значений теплосодержания UB₂: a – зависимость ${{\Delta }}H = ({{H}_{T}} - {{H}_{{{{T}_{0}}}}}){\text{/}}(T - {{T}_{0}})$ от T, T₀ = 298.15 K; б – зависимость относительных отклонений 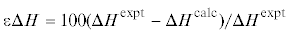от T. Линии: толстая сплошная, тонкая сплошная, штрих, штрих-пунктир и пунктир – модели Ein, EinLT, EinPoly, Ein2 и Poly соответственно. Точки – полученные дроп-калориметрией экспериментальные данные: ромбы – из [8], квадраты – из [9].

Все исходные данные и полученные параметры моделей в виде файлов для программы CpFit, а также программы на языке GNU Octave для построения графиков и таблиц, доступны как Mendeley Data Set, см. https://doi.org/10.17632/3vkpz6nfff.1

Из полученных в данной работе моделей наиболее точной оказалась модель Ein с 9 функциями Эйнштейна и без полиномиальной части с 18 оптимизируемыми параметрами, причем в ней $\sum\nolimits_i^{} {{{\alpha }_{i}}} \gg {{N}_{{{\text{atoms}}}}} = 3$. Это связано с тем, что без полинома разность C_p – C_V, ангармонизм колебаний решетки и рост C_p перед плавлением аппроксимируются функциями Эйнштейна со значениями ${{\alpha }_{i}}$ и ${{\theta }_{i}}$, не имеющими явного физического смысла. Подобное уже наблюдалось ранее для диоксида урана UO₂ [10].

Добавление полиномиальной части в модель EinPoly позволило добиться приближенного выполнения условия $\sum\nolimits_i^{} {{{\alpha }_{i}}} \approx {{N}_{{{\text{atoms}}}}}$ для UB₂, а также уменьшить число функций Эйнштейна до 5 (а количество параметров модели – до 12, см. табл. 2). Оно также улучшает предельное поведение модели при T < 1 K (см. рис. 1а). При этом у моделей Ein и EinPoly сопоставимая точность во всем температурном интервале T = 1–2300 K, а различия при T < 1 K не оказывают значимого влияния на значения $S_{{298.15}}^{ \circ }$ и ${{H}_{T}} - {{H}_{{298.15}}}$. В случае модели EinLT приближенное выполнение условия $\sum\nolimits_i^{} {{{\alpha }_{i}}} \approx {{N}_{{{\text{atoms}}}}} = 3$ было достигнуто иначе, а именно исключением данных по теплосодержанию с T > 1486 K. Это позволило уменьшить количество функций Эйнштейна до 8 (а число параметров – до 16) и привело к снижению точности аппроксимации экспериментальных значений H_T – H_298.15 из [8] (T = 1303–2300 K).

Полученные в данной работе модели Ein, EinLT и EinPoly описывают теплоемкость UB₂ точнее, чем имеющаяся в литературе полиномиальная модель [2], и не уступают ей в точности аппроксимации теплосодержаний, но при этом первые две требуют больше оптимизируемых параметров. Полиномиальная модель из [2] включает всего 12 параметров: по 6 на каждый температурный интервал (см. уравнения (1), (2)). Для проверки возможности уменьшить их число в данной работе была построена упрощенная модель Ein2 с шестью параметрами, включающая две функции Эйнштейна и полиномиальную часть. Ее точность сопоставима с моделями Ein, EinLT и EinPoly при T = 200–2000 K при меньшем числе параметров. При выходе за этот диапазон ее точность ощутимо ухудшается (см. рис. 1, 2 ), но выдаваемые ей значения остаются физически корректными.

Табулированные значения термодинамических функций твердого диборида урана UB₂ для T = 1–2300 K приведены в табл. 5. Они рассчитаны с помощью модели Ein, т.е. модели на основе взвешенной функции Эйнштейна без полиномиальной части, так как она оказалась точнее остальных, в том числе описанной в [2] полиномиальной модели. Значения $C_{{p,298.15}}^{ \circ }$, $S_{{298.15}}^{ \circ }$ и ${{H}_{T}} - {{H}_{{298.15}}}$, полученные из всех четырех построенных в данной работе моделей, совпадают в пределах их доверительных интервалов. Они также согласуются с данными [7].

Таблица 5.

Термодинамические функции диборида урана UB₂, рассчитанные на основе модели Ein (см. уравнения (5), (7), (9), (11) и их параметры в табл. 2)

T, K	${{C}_{p}}$, Дж/(моль К)	$S$, Дж/(моль К)	$H - {{H}_{0}}$, Дж/моль	$G - {{H}_{{{\text{SER}}}}}$, Дж/моль
1	9.2 × 10^–3	3.8 × 10^–3	2.9 × 10^–3	–173 315
5	0.051	0.043	0.12	–173 315
10	0.13	0.10	0.56	–173 316
20	0.79	0.33	4.16	–173 317
50	10.30	4.32	157.13	–173 374
100	21.89	15.47	994.40	–173 867
150	31.03	26.04	2313.5	–174 907
200	40.62	36.29	4106.3	–176 466
250	49.10	46.29	6355.8	–178 532
298.15	55.72 ± 0.16	55.53 ± 0.10	8885.1 ± 17	–180 985
300	55.94	55.87	8988.4	–181 089
350	61.40	64.92	11 926.9	–184 111
400	65.83	73.42	15 111.3	–187 571
500	72.68	88.89	22 055.4	–195 703
600	77.77	102.6	29 589.6	–205 291
700	81.67	114.9	37 569.9	–216 177
800	84.71	126.0	45 895.1	–228 232
900	87.09	136.1	54 489.7	–241 347
1000	88.99	145.4	63 297.2	–255 431
1100	90.52	154.0	72 274.8	–270 405
1200	91.79	161.9	81 391.8	–286 204
1300	92.94	169.3	90 628.6	–302 768
1400	94.11	176.2	99 979.9	–320 047
1500	95.53	182.8	109 459	–337 999
1600	97.48	189.0	119 103	–356 589
1700	100.3	195.0	128 985	–375 788
1800	104.5	200.8	139 214	–395 579
1900	110.5	206.6	149 945	–415 951
2000	118.7	212.5	161 380	–436 905
2100	129.7	218.5	173 772	–458 454
2200	143.8	224.9	187 417	–480 621
2300	161.6	231.6	202 657	–503 443

Таким образом, термодинамические модели на основе взвешенной суммы функций Эйнштейна позволяют аппроксимировать экспериментальные данные по теплоемкости и теплосодержанию твердого диборида урана во всем интервале температур (1–2300 K). Добавление полиномиальной части вида AT + BT⁴ в зависимость C_p(T) не повышает точность аппроксимации, но уменьшает число параметров модели, позволяет добиться приблизительного выполнения соотношения $\sum\nolimits_{i~ = ~1}^m {{{\alpha }_{i}}} = {{N}_{{{\text{atoms}}}}}$, а также улучшает предельное поведение функции C_p(T) при T → 0 K. Упрощенная термодинамическая модель с двумя функциями Эйнштейна и полиномиальной частью пригодна для использования при T = 200–2000 K, дает физически корректные значения теплоемкости при экстраполяции в области высоких и низких температур, а также точные значения $C_{{p,298.15}}^{ \circ }$, $S_{{298.15}}^{ \circ }$ и ${{H}_{T}} - {{H}_{{298.15}}}$. Ее преимущества по сравнению с полиномиальной моделью авторов [2] – в 2 раза меньше параметров, отсутствие кусочно заданных функций, а также физически корректное поведение при экстраполяции в область низких температур.

Список литературы

Turner J., Middleburgh S., Abram T. // J. Nucl. Mater. 2020. V. 529. ID 151891. https://doi.org/10.1016/j.jnucmat.2019.151891
Chevalier P.Y., Fischer E. // J. Nucl. Mater. 2001. V. 288. № 2. P. 100. https://doi.org/10.1016/S0022-3115(00)00713-3
Chase M.W., Ansara I., Dinsdale A. et al. // Calphad. 1995. V. 19. № 4. P. 437. https://doi.org/10.1016/0364-5916(96)00002-8
Voronin G.F., Kutsenok I.B. // J. Chem. Eng. Data. 2013. V. 58. № 7. P. 2083. https://doi.org/10.1021/je400316m
Jacobs M.H.G., Schmid-Fetzer R., van den Berg A.P. // Phys. Chem. Minerals. 2013. V 40. № 3. P. 207. https://doi.org/10.1007/s00269-012-0562-4
Bigdeli S., Chen Q., Selleby M. // J. Phase Equilib. Diffus. 2018. V. 39. № 6. P. 832. https://doi.org/10.1007/s11669-018-0679-3
Flotow H.E., Osborne D.W., O’Hare P.A.G. et al. // J. Chem. Phys. 1969. V. 51. № 2. P. 583. https://doi.org/10.1063/1.1672038
Fredrickson D.R., Barnes R.D., Chasanov M.G. et al. // High Temp. Sci. 1969. V. 1. P. 373.
Fredrickson D.R., Barnes R.D., Chasanov M.G. // High Temp. Sci. 1970. V. 2. P. 299.
Voskov A.L., Kutsenok I.B., Voronin G.F. // Calphad. 2018. V. 61. P. 50. https://doi.org/10.1016/j.calphad.2018.02.001
Voskov A.L., Voronin G.F., Kutsenok I.B., Kozin N.Yu. // Calphad. 2019. V. 66. ID 101623. https://doi.org/10.1016/j.calphad.2019.04.008

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал