Физика металлов и металловедение, 2019, T. 120, № 11, стр. 1136-1142
Оптическое поглощение композита на основе биметаллических наночастиц. Классический подход
А. В. Коротун a, *, А. А. Коваль a, В. И. Рева a, И. Н. Титов b
a Национальный университет “Запорожская политехника”
69063 Запорожье, ул. Жуковского, 64, Украина
b UAD Systems
69002 Запорожье, ул. Александровская, 84, Украина
* E-mail: andko@zntu.edu.ua
Поступила в редакцию 14.03.2019
После доработки 02.04.2019
Принята к публикации 09.04.2019
Аннотация
С использованием теории Максвелл–Гарнетт проанализировано поглощение электромагнитного излучения композитом на основе биметаллических наночастиц со структурой типа “ядро–оболочка”. Получены выражения для действительной и мнимой частей диэлектрической функции двухслойной частицы в предельных случаях “толстой” и “тонкой” оболочек. Установлено, что наличие двух металлов в составе включений приводит к расщеплению максимумов и минимумов на частотных зависимостях диэлектрической функции и коэффициента поглощения нанокомпозита. Рассчитаны частотные зависимости действительной и мнимой частей диэлектрической функции и коэффициента поглощения композита с биметаллическими наночастицами разных металлов. Обнаружено существенное влияние на оптические свойства композита как геометрических характеристик частиц-включений, так и их состава.
ВВЕДЕНИЕ
Уровень развития нанотехнологий, достигнутый в последние десятилетия, привел к усовершенствованию методов синтеза наночастиц [1–4]. При этом на их оптические свойства влияет не только изменение размеров и формы частиц, но и вариация их внутренней структуры и состава. Особый интерес среди подобных объектов вызывают биметаллические наносистемы [5–14]. Это обусловлено дополнительными возможностями по управлению оптическими свойствами материала на их основе, в частности, частотной полосой поглощения при изменении морфологии наночастиц. Такое изменение соответствует варьированию структуры биметаллических наночастиц от неупорядоченного сплава до слоистых структур типа “ядро–оболочка” ($A@B$) [15–17], в которых металл $A$ (ядро) находится в оболочке металла $B.$
Одним из наиболее важных оптических свойств биметаллических наночастиц, имеющих широкое практическое применение, является наличие широкой полосы поглощения в видимой области спектра, происхождение которой связано с существованием поверхностных плазмонов. Положением и шириной плазмонного резонанса в биметаллической наночастице можно управлять при помощи соответствующего выбора ее состава и размеров (радиуса ядра и толщины оболочки). Последнее имеет первостепенное значение в связи с их возможными применениями в качестве светостабильных цветовых фильтров [18], поляризаторов [19], оптических датчиков [2, 8], для биологической маркировки и поверхностного комбинационного рассеянии [20].
Существенный интерес вызывает изучение оптических свойств композитов на основе таких наночастиц, поскольку последние находят широкое применение в науке и технике. В частности, металлические наночастицы наносят на поверхности для изменения отражательной способности материала, используют для оптической записи информации [21], а также в биосенсорике и геномике [22] для визуализации клеточных структур [23].
Целью данной работы является исследование и анализ оптического поглощения композитов на основе биметаллических наночастиц.
ОСНОВНЫЕ СООТНОШЕНИЯ
Рассмотрим композит, состоящий из диэлектрика (матрицы) с проницаемостью ${{\epsilon }_{{\text{m}}}}$ и сферических металлических включений радиусом $r,$ покрытых слоем другого металла толщиной $t$ (рис. 1). При исследовании оптических свойств подобных гетерогенных систем используют разнообразные теории эффективной среды [24–26]. В случае разреженного композита ($\beta \ll 1,$ где $\beta $ – объемное содержание включений) комплексная диэлектрическая функция задается соотношением Максвелл–Гарнетт:
(1)
${{\epsilon }_{{{\text{eff}}}}} = {{\epsilon }_{{\text{m}}}}\left[ {1 + \frac{{3\beta \left( {{{\epsilon }_{{{\text{core}} - {\text{shell}}}}} - {{\epsilon }_{{\text{m}}}}} \right)}}{{2{{\epsilon }_{{\text{m}}}} + {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}}}} \right],$(2)
${{\epsilon }_{{{\text{core}} - {\text{shell}}}}} = {{\epsilon }_{{{\text{shell}}}}}\frac{{2{{Q}^{3}}\left( {{{\epsilon }_{{{\text{core}}}}} - {{\epsilon }_{{{\text{shell}}}}}} \right) + \left( {2{{\epsilon }_{{{\text{shell}}}}} + {{\epsilon }_{{{\text{core}}}}}} \right)}}{{\left( {2{{\epsilon }_{{{\text{shell}}}}} + {{\epsilon }_{{{\text{core}}}}}} \right) - {{Q}^{3}}\left( {{{\epsilon }_{{{\text{core}}}}} - {{\epsilon }_{{{\text{shell}}}}}} \right)}},$Диэлектрическая функция металлических ядра и оболочки описывается выражениями Друде:
(3)
$\begin{gathered} {{\epsilon }_{{{\text{core}}}}}\left( \omega \right) = \epsilon _{{{\text{core}}}}^{{\text{I}}}\left( \omega \right) + \operatorname{i} \epsilon _{{{\text{core}}}}^{{{\text{II}}}}\left( \omega \right) = \\ = \epsilon _{{\text{c}}}^{\infty } - \frac{{\omega _{{p,{\text{c}}}}^{2}\tau _{{\text{c}}}^{2}}}{{1 + {{\omega }^{2}}\tau _{{\text{c}}}^{2}}} + \operatorname{i} \frac{{\omega _{{p,{\text{c}}}}^{2}{{\tau }_{{\text{c}}}}}}{{\omega \left( {1 + {{\omega }^{2}}\tau _{{\text{c}}}^{2}} \right)}}; \\ \end{gathered} $(4)
$\begin{gathered} {{\epsilon }_{{{\text{shell}}}}}\left( \omega \right) = \epsilon _{{{\text{shell}}}}^{{\text{I}}}\left( \omega \right) + \operatorname{i} \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\left( \omega \right) = \\ = \epsilon _{{\text{s}}}^{\infty } - \frac{{\omega _{{p,{\text{s}}}}^{2}\tau _{{\text{s}}}^{2}}}{{1 + {{\omega }^{2}}\tau _{{\text{s}}}^{2}}} + \operatorname{i} \frac{{\omega _{{p,{\text{s}}}}^{2}{{\tau }_{{\text{s}}}}}}{{\omega \left( {1 + {{\omega }^{2}}\tau _{{\text{s}}}^{2}} \right)}}. \\ \end{gathered} $Подставляя формулы (3), (4) в (2) и разделяя действительную и мнимую части, получим
(5)
$\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}} = \frac{{\operatorname{Re} \Lambda }}{\Xi };\,\,\,\,\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}} = \frac{{\operatorname{Im} \Lambda }}{\Xi },$(6)
$\operatorname{Re} \Lambda = \epsilon _{{{\text{shell}}}}^{{\text{I}}}G\left( {\alpha ,\phi ,\gamma ,\delta } \right) + \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}{{Q}^{3}}\varsigma ;$(7)
$\operatorname{Im} \Lambda = \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}G\left( {\alpha ,\phi ,\gamma ,\delta } \right) + \epsilon _{{{\text{shell}}}}^{{\text{I}}}{{Q}^{3}}\varsigma ;$(8)
$\Xi = {{\left[ {\alpha - {{Q}^{3}}\gamma } \right]}^{2}} + {{\left[ {\phi - {{Q}^{3}}\delta } \right]}^{2}}$(9)
$\begin{gathered} \alpha \equiv 2\epsilon _{{{\text{shell}}}}^{{\text{I}}} + \epsilon _{{{\text{core}}}}^{{\text{I}}};\,\,\,\,\phi \equiv 2\epsilon _{{{\text{shell}}}}^{{{\text{II}}}} + \epsilon _{{{\text{core}}}}^{{{\text{II}}}}; \\ \gamma \equiv \epsilon _{{{\text{core}}}}^{{\text{I}}} - \epsilon _{{{\text{shell}}}}^{{\text{I}}};\,\,\,\,\delta \equiv \epsilon _{{{\text{core}}}}^{{{\text{II}}}} - \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}; \\ \varsigma \equiv 4\epsilon _{{{\text{shell}}}}^{{\text{I}}}\epsilon _{{{\text{shell}}}}^{{{\text{II}}}} - 2\epsilon _{{{\text{core}}}}^{{\text{I}}}\epsilon _{{{\text{core}}}}^{{{\text{II}}}} + \\ + \,\,5\epsilon _{{{\text{shell}}}}^{{\text{I}}}\epsilon _{{{\text{core}}}}^{{{\text{II}}}} - 7\epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\epsilon _{{{\text{core}}}}^{{\text{I}}}; \\ G\left( {\alpha ,\phi ,\gamma ,\delta } \right) \equiv {{\alpha }^{2}} - {{\phi }^{2}} + {{Q}^{3}}\left[ {\alpha \gamma - \phi \delta } \right] - \\ - \,\,2{{Q}^{6}}\left[ {{{\gamma }^{2}} - {{\delta }^{2}}} \right]. \\ \end{gathered} $Рассмотрим некоторые предельные случаи.
1. Толстая оболочка ($q \to 1,$ $Q \to 0$)
(10)
$\operatorname{Re} \Lambda = \epsilon _{{{\text{shell}}}}^{{\text{I}}}\left\{ {{{\alpha }^{2}} - {{\phi }^{2}}} \right\};$(11)
$\operatorname{Im} \Lambda = \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\left\{ {{{\alpha }^{2}} - {{\phi }^{2}}} \right\};$2. Тонкая оболочка ($q \to 0,$ $Q = 1 - q$). Тогда
(13)
$\begin{gathered} {{Q}^{3}} = {{\left( {1 - q} \right)}^{3}} \cong 1 - 3q; \\ {{Q}^{6}} = {{\left( {1 - q} \right)}^{6}} \cong 1 - 6q. \\ \end{gathered} $Подставляя в (6)–(8) разложения (13), получим
(14)
$\operatorname{Re} \Lambda = 5\epsilon _{{{\text{shell}}}}^{{\text{I}}}\kappa - \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\varsigma + 3q\left[ {\epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\varsigma + 3\epsilon _{{{\text{shell}}}}^{{\text{I}}}\mu } \right];$(15)
$\operatorname{Im} \Lambda = 5\epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\kappa + \epsilon _{{{\text{shell}}}}^{{\text{I}}}\varsigma + 3q\left[ { - \epsilon _{{{\text{shell}}}}^{{\text{I}}}\varsigma + 3\epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\mu } \right];$(16)
$\begin{gathered} \Xi = \left[ {{{{\left( {\alpha - \gamma } \right)}}^{2}} + {{{\left( {\phi - \delta } \right)}}^{2}}} \right]\,\, \times \\ \times \,\,\left[ {1 + 6q\frac{{\alpha \gamma + \varphi \delta - {{\gamma }^{2}} - {{\delta }^{2}}}}{{{{{\left( {\alpha - \gamma } \right)}}^{2}} + {{{\left( {\phi - \delta } \right)}}^{2}}}}} \right], \\ \end{gathered} $(17)
$\begin{gathered} \kappa \equiv \epsilon _{{{\text{shell}}}}^{{\text{I}}}\epsilon _{{{\text{core}}}}^{{\text{I}}} - \epsilon _{{{\text{shell}}}}^{{{\text{II}}}}\epsilon _{{{\text{core}}}}^{{{\text{II}}}}; \\ \mu \equiv \epsilon _{{{\text{core}}}}^{{{\text{I}}\,2}} - \epsilon _{{{\text{core}}}}^{{{\text{II}}\,2}} + 2\left( {\epsilon _{{{\text{shell}}}}^{{{\text{I}}\,2}} - \epsilon _{{{\text{shell}}}}^{{{\text{II}}\,2}}} \right) - 3\kappa . \\ \end{gathered} $Соотношение для расчета коэффициента поглощения имеет вид
(18)
$\begin{gathered} \eta \left( \omega \right) = \frac{{2\omega }}{{c\sqrt {{{\epsilon }_{{\text{m}}}}} }} \times \\ \times \,\,\sqrt {\frac{{ - \operatorname{Re} {{\epsilon }_{{{\text{eff}}}}} + \sqrt {{{{\left( {\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}} \right)}}^{2}} + {{{\left( {\operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}} \right)}}^{2}}} }}{2}} , \\ \end{gathered} $(19)
$\begin{gathered} \operatorname{Re} {{\epsilon }_{{{\text{eff}}}}} = {{\epsilon }_{{\text{m}}}}\left[ {1{{ + }_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}^{{^{{^{{^{{}}}}}}}}} \right. \\ + \,\,\left. {\frac{{3\operatorname{Re} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\operatorname{Re} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\, + \,2{{\epsilon }_{{\text{m}}}}} \right)\, + \,{{{\left( {\operatorname{Im} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}} \right)}}^{2}}}}{{{{{\left( {\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}} + 2{{\epsilon }_{{\text{m}}}}} \right)}}^{2}}\, + \,{{{\left( {\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}} \right)}}^{2}}}}\beta } \right]; \\ \operatorname{Im} {{\epsilon }_{{{\text{eff}}}}} = 3\beta {{\epsilon }_{{\text{m}}}}{\kern 1pt} \times \\ \times \,\,\frac{{\operatorname{Im} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left[ {\left( {\operatorname{Re} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\, + \,2{{\epsilon }_{{\text{m}}}}} \right)\, - \,\operatorname{Im} {\kern 1pt} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}} \right]}}{{{{{\left( {\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}} + 2{{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}} \right)}}^{2}}}}. \\ \end{gathered} $Известно, что величина времени релаксации может значительно различаться благодаря наличию примесей и дефектов структуры в образцах. Однако основной причиной такого различия в металлических наночастицах являются размерные эффекты. Так, когда характерные размеры наночастицы становятся меньше длины свободного пробега электронов в $3D$-металле, кроме рассеяния электронов на фононах, примесях и прочих дефектах необходимо учитывать рассеяние на границах наночастиц. В этом случае в формулы (3) и (4) для диэлектрических функций металлических ядра и оболочки вместо $\tau $ будет входить эффективное время релаксации ${{\tau }_{{{\text{eff}}}}},$ зависящее от характерного среднего радиуса металлических включений и частоты падающей электромагнитной волны [24]
(20)
$\frac{1}{{\tau _{{{\text{eff}}}}^{{{\text{c}}\left( {\text{s}} \right)}}}} = \frac{1}{{\tau _{{{\text{bulk}}}}^{{{\text{c}}\left( {\text{s}} \right)}}}} + {{\mathcal{A}}_{{{\text{c}}\left( {\text{s}} \right)}}}\left( {\omega ,r} \right)\frac{{{v}_{{\text{F}}}^{{{\text{c}}\left( {\text{s}} \right)}}}}{{{{r}_{{{\text{c}}\left( {\text{s}} \right)}}}}},$В рамках кинетического подхода, развитого в работах [28] при описании процессов рассеяния на поверхности и в объеме сферических металлических наночастиц, степень потери когерентности определяется выражением
(21)
$\begin{gathered} {{\mathcal{A}}_{{{\text{c}}\left( {\text{s}} \right)}}}\left( {\omega ,r} \right) = \frac{1}{4}{{\left( {\frac{{{{\omega }_{{p,{\text{c}}\left( {\text{s}} \right)}}}}}{\omega }} \right)}^{2}} \times \\ \times \,\,\left[ {1 - \frac{{2\nu _{s}^{{{\text{c}}\left( {\text{s}} \right)}}}}{\omega }\sin \frac{\omega }{{\nu _{s}^{{{\text{c}}\left( {\text{s}} \right)}}}} + \frac{{2\nu {{{_{s}^{{{\text{c}}\left( {\text{s}} \right)}}}}^{2}}}}{{{{\omega }^{2}}}}\left( {1 - \cos \frac{\omega }{{\nu _{s}^{{{\text{c}}\left( {\text{s}} \right)}}}}} \right)} \right], \\ \end{gathered} $Отметим, что в случае наночастиц в вакууме при частотах $\omega \to {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}$ и ${{\nu }_{s}} \ll \omega $ из (21) получаем хорошо известный результат $\mathcal{A} = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}$ [28] и тогда можно записать
(22)
$\frac{1}{{\tau _{{{\text{eff}}}}^{{{\text{c}}\left( {\text{s}} \right)}}}} = \frac{1}{{\tau _{{{\text{bulk}}}}^{{{\text{c}}\left( {\text{s}} \right)}}}} + \frac{3}{4}\frac{{{v}_{{\text{F}}}^{{{\text{c}}\left( {\text{s}} \right)}}}}{{{{r}_{{{\text{c}}\left( {\text{s}} \right)}}}}}.$Выражения (20), (21) используются для получения частотных зависимостей диэлектрических функций биметаллических наночастиц и композита, а также коэффициента поглощения композита.
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ И ОБСУЖДЕНИЕ
Вычисления были проведены для наночастиц ${\text{Ag}}@{\text{Au,}}$ ${\text{Au}}@{\text{Ag}}$ и ${\text{Cu}}@{\text{Ag}}$ в тефлоне (${{\epsilon }_{{\text{m}}}} = 2,3$), параметры которых приведены в табл. 1 (${{a}_{0}}$ – боровский радиус, ${{r}_{s}}$ – среднее расстояние между электронами; $\bar {n} = {3 \mathord{\left/ {\vphantom {3 {4\pi r_{s}^{3}}}} \right. \kern-0em} {4\pi r_{s}^{3}}}$ – концентрация электронов).
Таблица 1.
Параметры металлов
| Металл | Cu | Au | Ag |
|---|---|---|---|
| ${{{{r}_{s}}} \mathord{\left/ {\vphantom {{{{r}_{s}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ [29] | 2.11 | 3.01 | 3.02 |
| ${{m{\text{*}}} \mathord{\left/ {\vphantom {{m{\text{*}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$ [30] | 1.49 | 0.99 | 0.96 |
| ${{\epsilon }^{\infty }}$ [31] | 12.03 | 9.84 | 3.7 |
| ${{\tau }_{{{\text{bulk}}}}},$ фс [29] | 27 | 29 | 40 |
На рис. 2 и 3 приведены кривые частотной зависимости действительной и мнимой частей диэлектрических функций сферических биметаллических наночастиц различного состава с разными радиусами ядра и толщиной оболочки. Отметим, что функция $\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\hbar \omega } \right)$ является знакопеременной и имеет один максимум и два минимума в различных частях спектра (кроме случая частиц ${\text{Ag}}@{\text{Au}}$ и ${\text{Cu}}@{\text{Ag}}$ с $t = 1$ нм), в то время как функция $\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\hbar \omega } \right) > 0$ во всем рассматриваемом диапазоне частот, причем количество экстремумов для нее существенно больше, чем для $\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\hbar \omega } \right).$ При относительно малых частотах на кривых частотных зависимостей действительной и мнимой частей заметны мелкомасштабные осцилляции, амплитуда которых больше в случае $\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}.$ Наличие подобных осцилляций обусловлено классическими размерными эффектами, возникающими вследствие близости размера наночастицы и длины волны падающего излучения из данного спектрального диапазона. Кроме того, на кривых $\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\hbar \omega } \right)$ и $\operatorname{Im} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}\left( {\hbar \omega } \right)$ наблюдаются расщепления минимумов и максимумов, что объясняется поглощением и рассеянием электромагнитных волн как в ядре, так и в оболочке. Изменение характера расположения кривых 1–3 на рис. 2а и 2б при изменении архитектуры наночастицы ${\text{Ag}}@{\text{Au}}$ на “обратную” структуру ${\text{Au}}@{\text{Ag}}$ связано с увеличением вклада межзонных переходов в $\epsilon _{{{\text{shell}}}}^{{{\text{II}}}},$ а соответственно и в $\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}$ в области частот $\hbar \omega \simeq 2$ эВ.
Рис. 2.
Частотные зависимости $\operatorname{Re} {{\epsilon }_{{{\text{core}} - {\text{shell}}}}}$ для ${\text{Ag}}@{\text{Au}}$ (а), ${\text{Au}}@{\text{Ag}}$ (б) и ${\text{Cu}}@{\text{Ag}}$ (в) с радиусом ядра 10 нм и различной толщиной оболочки: 1 – $t = 1$; 2 – $t = 5$; 3 – $t = 10$ нм.

Рис. 3.
Зависимости мнимой части ${{\epsilon }_{{{\text{core}} - {\text{shell}}}}}$ для частиц ${\text{Ag}}@{\text{Au:}}$ (а) при постоянном радиусе ядра 10 нм и различной толщине оболочки; (б) при постоянной толщине оболочки 10 нм и различном радиусе ядер.
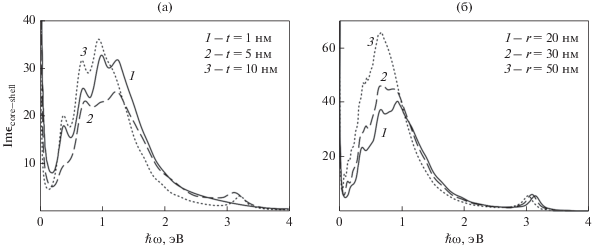
Частотные зависимости действительной и мнимой частей эффективной диэлектрической функции нанокомпозита с биметаллическими наночастицами разного состава с разными радиусами ядер и толщинами оболочек приведены на рис. 4, 5. Кривые $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right)$ как в случае включений ${\text{Ag}}@{\text{Au}}$ (рис. 4а), так и в случае ${\text{Cu}}@{\text{Ag}}$ (рис. 4б) имеют по два максимума и минимума, что объясняется наличием в составе наночастиц двух металлов. Следует отметить, что расстояние между минимумами и максимумами $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}$ меньше в случае включений ${\text{Ag}}@{\text{Au,}}$ поскольку объемные концентрации электронов, определяющие оптические константы для этих металлов, близки. По аналогии с вышеописанным, кривые $\operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right)$ в случае металлических включений обоих типов имеют два максимума (рис. 5), характер расположения которых такой же, как и для кривых $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right).$
Рис. 4.
Частотные зависимости действительной части эффективной диэлектрической функции композита с частицами ${\text{Ag}}@{\text{Au}}$ (а) и ${\text{Cu}}@{\text{Ag}}$ (б) в тефлоне с $\beta = 0.05{\text{:}}$ 1 – $r = 20$, $t = 10$; 2 – $r = 50$, $t = 5$ нм.
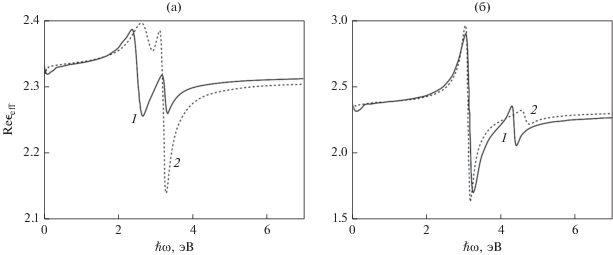
Рис. 5.
Частотные зависимости мнимой части эффективной диэлектрической функции композита с частицами ${\text{Ag}}@{\text{Au}}$ (а) и ${\text{Cu}}@{\text{Ag}}$ (б) в тефлоне с $\beta = 0.05{\text{:}}$ 1 – $r = 20$, $t = 10$; 2 – $r = 50$, $t = 5$ нм.

Кривые частотной зависимостей коэффициента поглощения композита с биметаллическими наночастицами изображены на рис. 6. Зависимости $\eta \left( {\hbar \omega } \right)$ и $\operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right)$ качественное подобны, поскольку $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right) \ll \operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right)$ кроме области $\omega \approx {{\omega }_{{\max }}},$ где ${{\omega }_{{\max }}}$ – частота, соответствующая наибольшему максимуму действительной части эффективной диэлектрической функции. Кроме того, расположение максимумов коэффициента поглощения такое же, как и для мнимой части эффективной диэлектрической функции, а отличие расстояний между пиками вызвано той же причиной, что и в случае экстремумов функций $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right)$ и $\operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right).$
Рис. 6.
Частотные зависимости коэффициента поглощения композита с частицами ${\text{Ag}}@{\text{Au}}$ (а) и ${\text{Cu}}@{\text{Ag}}$ (б) в тефлоне с $\beta = 0.05{\text{:}}$ 1 – $r = 20$, $t = 10$; 2 – $r = 50$, $t = 5$ нм.

Следует отметить, что на рис. 4–6 кривые 1 соответствуют биметаллическим частицам с “толстой” оболочкой, а кривые 2 – с “тонкой”. Расстояние между экстремумами $\operatorname{Re} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right),$ $\operatorname{Im} {{\epsilon }_{{{\text{eff}}}}}\left( {\hbar \omega } \right),$ $\eta \left( {\hbar \omega } \right)$ больше для композитов с частицами , имеющими “толстую” оболочку. В случае композита с частицами ${\text{Cu}}@{\text{Ag}}$ ситуация противоположная, что связано с существенным влиянием компоненты, описывающей вклад ионного остова, на частотные зависимости действительной и мнимой частей диэлектрической функции и коэффициента поглощения композита. Таким образом, изменяя радиус частицы-включения и толщины оболочки можно регулировать положение экстремумов оптических характеристик металл-диэлектрического композита.
ЗАКЛЮЧЕНИЕ
В работе получены и проанализированы частотные зависимости действительной и мнимой частей диэлектрической функции биметаллических наночастиц со структурой типа “ядро–оболочка”, а также действительной и мнимой частей эффективной диэлектрической функции и коэффициента поглощения композитов с малым содержанием биметаллических включений, когда справедлива теория Максвелл–Гарнетт.
Установлено наличие расщепления минимумов и максимумов действительной и мнимой частей диэлектрической функции биметаллических наночастиц, вызванного поглощением и рассеянием электромагнитного излучения ядром и оболочкой частицы-включения.
Показано, что наличие в составе частицы-включения двух металлов приводит к существованию двух максимумов и минимумов на частотных зависимостях действительной части эффективной диэлектрической функции композита и двух максимумов на аналогичных зависимостях мнимой части диэлектрической функции и коэффициента поглощения.
Продемонстрировано, что для композитов с включениями ${\text{Ag}}@{\text{Au}}$ расстояния между экстремумами действительной и мнимой частей диэлектрической функции и коэффициента поглощения меньше, чем в случае композитов с включениями ${\text{Cu}}@{\text{Ag,}}$ что объясняется близкими значениями среднего расстояния между электронами для золота и серебра и отличием этой характеристики у меди.
Выяснено, что, варьируя геометрические характеристики биметаллических частиц-включений, можно эффективно управлять оптическими параметрами композита, содержащего указанную металлическую фракцию.
Список литературы
Haug J., Kruth H., Dubiel M., Hofmeister H., Haas S., Tatchev D., Hoell A. ASAXS study on the formation of core–shell Ag/Au nanoparticles in glass // Nanotechnology. 2009. V. 20. id. 505705.
Deng J., Du J., Wang Y., Tu Y., Di J. Synthesis of ultrathin silver shell on gold core for reducing substrate effect of LSPR sensor // Electrochem. Commun. 2011. V. 13. P. 1517–1520.
Lu L., Burkey G., Halaciuga I., Goia D.V. Core–shell gold/silver nanoparticles: Synthesis and optical properties // J. Colloid Interface Sci. 2013. V. 392. P. 90–95.
Dong P., Lin Y., Deng J., Di J. Ultrathin Gold-Shell Coated Silver Nanoparticles onto a Glass Platform for Improvement of Plasmonic Sensors // ACS Appl. Mater. Interfaces. 2013. V. 5. P. 2392–2399.
Moskovits M., Srnová-Šloufová I., Vlčková B. Bimetallic Ag–Au nanoparticles: Extracting meaningful optical constants from the surface-plasmon extinction spectrum // J. Chem. Phys. 2002. V. 116. P. 10 435–10 446.
Belotelov V.I., Carotenuto G., Nicolais L., Pepe G.P., Zvezdin A.K. Optical characterization of the polymer embedded alloyed bimetallic nanoparticles // Eur. Phys. J. B. 2005. V. 45. P. 317–324.
Belotelov V.I., Carotenuto G., Nicolais L., Longo A., Pepe G.P., Perlo P., Zvezdin A.K. Online monitoring of alloyed bimetallic nanoparticle formation by optical spectroscopy // J. Appl. Phys. 2006. V. 99. P. 044304 (9).
Fu Q., Zhang D.G., Yi M.F., Wang X.X., Chen Y.K., Wang P., Ming H. Effect of shell thickness on a Au–Ag core–shell nanorods-based plasmonic nano-sensor // J. Opt. 2012. V. 14. P. 085001 (6).
Singh R., Soni R.K. Plasmonics properties of trimetallic Al@Al2O3@Ag@Au and Al@Al2O3@AuAg nanostructures // Appl. Phys. A. 2014. V. 116. Is. 3. P. 955–967.
Zhu J., Li J.-J., Zhao J.-W. Tuning the plasmon band number of aluminum nanorod within the ultraviolet-visible region by gold coating // Phys. Plasmas 2014. V. 21. P. 112108 (6).
Saliminasab M., Shirzaditabar F.,·Moradian R. Electromagnetic field amplification in Al/Ag spherical nanostructures // Appl. Phys. A. 2018. V. 124. P. 870 (9).
Valizade-Shahmirzadi N., Pakizeh T. Optical characterization of broad plasmon resonances of Pd/Pt nanoparticles // Mater. Res. Express 2018. V. 5. id. 045038.
Sompech S., Thaomola S., Chingsungnoen A., Dasri T. Theoretical calculation of optical absorption property of Cu@Ag core–shell composite nanoparticle // Mater. Res. Express. 2019. V. 6. id. 026201.
Скиданенко А.В., Авакян Л.А., Козинкина Е.А., Бугаев Л.А. Влияние внутреннего строения биметаллических наночастиц на оптические свойства материала AuAg/стекло // ФТТ. 2019. Т. 61. № 1. С. 115–122.
Chaudhuri R.G., Paria S. Core/Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications // Chem. Rev. 2012. V. 112. P. 2373–2433.
Guterman V., Belenov S., Pakharev A., Min M., Tabachkova N., Mikheykina E., Vysochina L., Lastovina T. Pt-M/C (M = Cu, Ag) electrocatalysts with an inhomogeneous distribution of metals in the nanoparticles // Int. J. Hydrogen Energy. 2016. V. 41. P. 1609–1626.
Dang-Bao T., Pla D., Favier I., Gomez M. Bimetallic Nanoparticles in Alternative Solvents for Catalytic Purposes // Catalysis. 2017. V. 7. P. 207.
De León A.G., Dirix Y., Staedler Y., Feldman K., Hähner G., Caseri W.R., Smith P. Method for Fabricating Pixelated, Multicolor Polarizing Films // Appl. Opt. 2000. V. 39. P. 4847–4851.
Lu A.H., Lu G.H., Kessinger A.M., Foss C.A. Dichroic Thin Layer Films Prepared from Alkanethiol-Coated Gold Nanoparticles // J. Phys. Chem. B. 1997. V. 101 (45). P. 9139–9142.
Eberhardt W. Clusters as new materials // Sur. Sci. 2002. V. 500. P. 242–270.
Qu S., Du C., Song Y., Wang Y., Gao Y., Liu S., Li Y., Zhu D. Optical nonlinearities and optical limiting properties in gold nanoparticles protected by ligands // Chem. Phys. Lett. 2002. V. 356. P. 403–408.
Stuart D.A., Haes A.J., Yonzon C.R., Hicks E.M., Van Duyne R.P. Biological applications of localised surface plasmonic phenomenae // IEEE Proc. Nanobiotechnol. 2005. V. 152. P. 13–32.
Rosi N.L., Mirkin C.A. Nanostructures in biodiagnostics // Chem. Rev. 2005. V. 105. P. 1547–1562.
Kreibig U., Vollmer M. Optical Properties of Metal Clusters. Berlin: Springer, 1995. 527 p.
Виноградов А.П. Электродинамика композитных материалов. М.: Эдиториал УРСС, 2001. 208 с.
Bohren C.F., Huffman D.R. Absorption and scattering of light by small particles. John Wiley & Sons, 2008. 530 p.
Bан де Хюлст Г. Рассеяние света малыми частицами. М.: ИИЛ, 1961. 536 с.
Grigorchuk N.I., Tomchuk P.M. Optical and transport properties of spheroidal metal nanoparticles with account for the surface effect // Phys. Rev. B. 2011. V. 84. № 8. id. 085448.
Ашкрофт Н., Мермин Н. Физика твердого тела. М.: Мир, 1979. Т. 1. 400 с.
Johnson P.B., Christy R.W. Optical constants of the noble metals // Phys. Rev. B. 1972. V. 12. № 6. P. 4370–4379.
Sönnichsen C. Plasmons in metal nanostructures, Ph.D. thesis, Munchen, 2001. 134 p.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение



