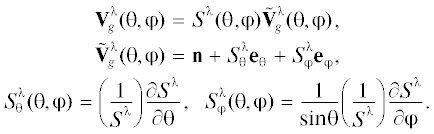1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 120, № 11, 2019

Физика металлов и металловедение, 2019, T. 120, № 11, стр. 1129-1135

Влияние анизотропии упругой энергии на электрон-фононное увлечение и температурные зависимости термоэдс в кристаллах калия при низких температурах

И. И. Кулеев a, *, И. Г. Кулеев a

a Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия

* E-mail: kuleev@imp.uran.ru

Поступила в редакцию 14.03.2019
После доработки 28.05.2019
Принята к публикации 03.06.2019

Полный текст (PDF)

Аннотация

Исследовано влияние анизотропии упругой энергии на электрон-фононное увлечение и термоэлектрические явления в кристаллах калия. Рассчитаны температурные зависимости теплопроводности, термоэдс и вкладов в них от фононов различных поляризаций. Результаты расчета согласованы с экспериментальными данными путем вариации константы электрон-фононного взаимодействия для квазипоперечных фононов. Установлено, что вклад медленных квазипоперечных фононов в термоэдс увлечения объемных кристаллов калия на порядок величины превышает вклад квазипродольных фононов. Определены максимальные величины термоэдс увлечения в совершенных кристаллах калия. Показано, что они не зависят от значений констант электрон-фононного взаимодействия, а определяются упругими модулями второго порядка и концентрацией электронов.

Ключевые слова: щелочные металлы, упругая энергия, термоэдс, электрон-фононное увлечение, квазипоперечные фононы, решеточная теплопроводность

ВВЕДЕНИЕ

В [1–4] были измерены термоэлектрические эффекты в щелочных металлах при низких температурах, определена решеточная теплопроводность, а также проанализировано влияние электрон-фононного увлечения на термоэдс. Полученные результаты, как и термоэдс увлечения в других металлах, интерпретировали в модели изотропной среды [1–5]. В этой модели только продольные фононы могут взаимодействовать с электронами и участвовать в электрон-фононном увлечении [6–9]. Целью настоящей работы является исследование влияния анизотропии упругой энергии на электрон-фононное увлечение в щелочных металлах при низких температурах. Анизотропия спектра фононов приводит к неколлинеарности групповых и фазовых скоростей фононов и к анизотропии фононного транспорта [10]. Кроме того, в упругоанизотропных кристаллах распространяются квазипоперечные фононы, которые имеют отличную от нуля продольную компоненту [11, 12] и в рамках стандартной теории потенциала деформации могут участвовать в электрон-фононном увлечении [6–9]. Поэтому, в отличие от модели изотропной среды, необходимо учитывать вклады всех колебательных мод в электрон-фононное увлечение. Наиболее подходящими кристаллами для анализа этих эффектов являются щелочные металлы Li, Na, K, для которых спектр электронов проводимости считается изотропным. Они обладают кубической симметрией и максимальными параметрами анизотропии упругой энергии k – 1 (k – 1 = (с12 + 2с44 – с11)/(с11 – с44), сij – упругие модули второго порядка), которые в значительной степени определяют отклонения направлений групповых и фазовых скоростей фононов и, соответственно, фокусировку фононов (табл. 1). В связи с этим продольная компонента квазипоперечных фононов также имеет максимальное значение, существенно превосходящее величины для полупроводниковых кристаллов (см. табл. 1). Однако кристаллы Li и Na при температурах ниже 36 К испытывают мартенситный переход из оцк в гпу и при более низких температурах представляют двухфазную систему. Поэтому основное внимание уделено исследованию термоэдс увлечения в кристаллах калия.

Таблица 1.  

Упругие модули второго порядка сij (1012 дин/см2), плотность ρ (г/см3), параметр анизотропии k – 1 для кристаллов HgSe:Fe и Si, K, Li, Na

Соединение с11 с12 с44 ρ k – 1 $\left\langle {{{{({\mathbf{e}}_{{}}^{L}{\mathbf{n}})}}^{2}}} \right\rangle $ $\left\langle {{{{({\mathbf{e}}_{{}}^{{t1}}{\mathbf{n}})}}^{2}}} \right\rangle $ $\left\langle {{{{({\mathbf{e}}_{{}}^{{t2}}{\mathbf{n}})}}^{2}}} \right\rangle $
HgSe:Fe 0.69 0.51 0.23 8.26 0.61 0.99 6.7 × 10–4 7.0 × 10–3
Si 1.677 0.65 0.804 2.33 0.67 0.99 7.5 × 10–4 7.9 × 10–3
K 0.0457 0.0374 0.0263 0.91 2.284 0.965 0.0028 0.0323
Li 0.148 0.125 0.108 0.55 4.825 0.942 0.0044 0.0536
Na 0.0615 0.0469 0.0592 1.01 45.13 0.902 0.0069 0.0908

В [13] мы главным образом ограничились исследованием влияния фокусировки фононов на анизотропию термоэдс увлечения в кристаллах калия. Рассмотрена возможность реализации режима кнудсеновское течение фононного газа в монокристаллических нанопластинках калия при низких температурах. Показано, что этот режим реализуется при уменьшении толщины пластинок до D < 10–5 см, когда граничное рассеяние в кристаллах калия становится доминирующим механизмом релаксации фононов. Анализ вкладов различных мод в термоэдс увлечения и решеточную теплопроводность кристаллов калия показал, что медленные квазипоперечные фононы вносят преобладающий вклад в электрон-фононное увлечение, на порядок величины превышающий вклад продольных фононов [13]. Очевидно, что модель изотропной среды не является корректной для описания электрон-фононного увлечения в металлах. Необходимо учитывать влияние анизотропии упругой энергии на спектр и вектора поляризации фононов. В настоящей работе мы рассчитали температурные зависимости решеточной теплопроводности и термоэдс увлечения для кристаллов калия и согласовали результаты расчета с экспериментальными данными [1, 4]. Анализ вкладов квазипродольных и квазипоперечных фононов в температурные зависимости теплопроводности и термоэдс увлечения показал, что результаты расчета могут быть согласованы с экспериментальными данными только в предположении, что константа деформационного взаимодействия поперечных фононов с электронами E0t в два раза превышает ее значение для продольных фононов. Аналитически рассчитан предел, определяющий максимальные значения термоэдс увлечения в кристаллах калия без дислокаций. Определены максимальные значения термоэдс увлечения в совершенных кристаллах калия. Показано, что они определяются исключительно упругими модулями второго порядка и не зависят от значений констант электрон-фононного взаимодействия. Ниже мы ограничимся учетом только анизотропии, связанной с подсистемой фононов.

ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ФОНОНОВ В КРИСТАЛЛАХ КАЛИЯ

В щелочных металлах подсистема электронов является сильно вырожденной. В этом случае благодаря законам сохранения энергии и импульса в электрон-фононных взаимодействиях могут участвовать только электроны, находящиеся в пределах теплового размытия поверхности ферми.

Поэтому для них при температурах, гораздо меньших температуры Дебая основной вклад в релаксацию электронов будут вносить длинноволновые фононы с волновым вектором q $ \ll $ qD (qD – дебаевский волновой) [6–9]. В связи с этим для описания фононов мы воспользуемся моделью анизотропного континуума [11, 12]. В этой модели спектр фононов с поляризацией λ представим в виде ${\omega }_{q}^{{\lambda }}$ = ${{S}^{{\lambda }}}({\theta },{\varphi })q.$ фазовая скорость ${{S}^{{\lambda }}}(\theta ,{\varphi })$ зависит от угловых переменных θ и φ вектора q. В системе координат по ребрам куба она определена в работе [12]. Индекс поляризации L соответствует продольным фононам, t1 и t2 – “быстрой” и “медленной” поперечным колебательным модам, соответственно. векторы поляризации фононов определяются выражениями [12]:

(1)
$\begin{gathered} e_{j}^{\lambda } = \frac{1}{{{{A}_{\lambda }}}}\left\{ {\frac{{{{n}_{j}}}}{{\psi _{j}^{\lambda }}}} \right\},\,\,\,\,{{A}_{\lambda }} = \pm \sqrt {\sum\limits_j {\frac{{n_{j}^{2}}}{{{{{\left( {\psi _{j}^{\lambda }} \right)}}^{2}}}}} } ; \\ ({{{\mathbf{e}}}^{\lambda }}{\mathbf{n}}) = \frac{1}{{{{A}_{\lambda }}}}\sum\limits_j {\frac{{n_{j}^{2}}}{{\psi _{j}^{\lambda }}}} ,\,\,\,\,\psi _{j}^{\lambda } = \frac{1}{3} + {{z}_{\lambda }} + (k - 1)n_{j}^{2}; \\ k = {{({{c}_{{12}}} + {{c}_{{44}}})} \mathord{\left/ {\vphantom {{({{c}_{{12}}} + {{c}_{{44}}})} {({{c}_{{11}}} - {{c}_{{44}}})}}} \right. \kern-0em} {({{c}_{{11}}} - {{c}_{{44}}})}}, \\ \end{gathered} $
где сij – упругие модули второго порядка, n = q/q =  = (sin θ сos φ, sin θ sin φ, сos θ) – единичный волновой вектор фонона, ${{z}_{{\lambda }}}$ – корни уравнения Кристоффеля, определяющие спектр и вектора поляризации (см. подробнее [10]). Значения модулей упругости второго порядка при T = 4.2 К взяты из работы [14]. Как видно из табл. 1, средние величины$\left\langle {{{{({{{\mathbf{e}}}^{{t2}}}{\mathbf{n}})}}^{2}}} \right\rangle ,$ входящие в константу электрон-фононного взаимодействия при переходе от кристаллов Si к калию и натрию, увеличиваются в четыре и одиннадцать раз, соответственно. Это приводит к значительному увеличению вклада квазипоперечных мод в электрон-фононное увлечение.

Направления переноса энергии и фокусировка фононов определяются групповыми скоростями фононов, которые могут быть представлены в виде [10]:

(2)

Здесь eθ = (cos θ cos φ, cos θ sin φ, –sin θ), eφ = (–sinφ, cosφ, 0), а вектор n определен выше. Вектора n, eθ и eφ образуют взаимно ортогональную тройку единичных векторов. Параметры анизотропии k – 1 в щелочных кристаллах значительно превышают значения для Si и HgSe:Fe (табл. 1). Поэтому фокусировка фононов в кристаллах калия существенно отличается от полупроводниковых кристаллов (см. подробнее [15]).

ВЛИЯНИЕ АНИЗОТРОПИИ УПРУГОЙ ЭНЕРГИИ НА ТЕРМОЭДС УВЛЕЧЕНИЯ В МЕТАЛЛАХ

Впервые влияние анизотропии упругой энергии кристалла на спектр, векторы поляризации и фокусировку фононов при анализе термоэдс увлечения проводниках с вырожденной статистикой носителей тока учтено в работе [16]. Для этого была решена система кинетических уравнений для неравновесных электронной f(k, r) и фононной Nλ(q, r) функций распределения в линейном приближении по внешним возмущениям, обусловленным действием электрического поля (E = {Ex, 0, 0}) и градиента температуры ∇T = (∇хT, 0, 0). Отметим, что такие эффекты, как термоэдс и теплопроводность находят из условия равенства нулю полного тока через образец. В этом случае средняя скорость упорядоченного движения электронов в любом физически малом объеме образца равна нулю. Поэтому перенормировку термоэдс за счет взаимного увлечения электронов и фононов мы не рассматриваем. В этом случае градиент температуры приводит к стационарному потоку фононов от горячего конца образца к холодному, и передача импульса упорядоченного движения фононов к электронам в значительной степени определяет величину полной термоэдс при низких температурах. В результате термоэдс может быть представлена в виде аддитивной суммы диффузионного вклада и термоэдс электрон-фононного увлечения: $\alpha $ = ${{\alpha }_{{{\text{dif}}}}} + {{\alpha }_{{{\text{drag}}}}}.$ Диффузионная термоэдс определяется известным выражением [6–9]:

(3)
$\begin{gathered} {{\alpha }_{{{\text{dif}}}}} = \frac{{{{k}_{{\text{B}}}}}}{e}\left( {\frac{{{{\pi }^{2}}{{k}_{{\text{B}}}}T}}{{3{{\varepsilon }_{{\text{F}}}}}}} \right){{A}_{{{\text{dif}}}}}, \\ {{A}_{{{\text{dif}}}}} = \frac{{{{\varepsilon }_{{\text{F}}}}d}}{{d\varepsilon }}{{\left[ {\ln \left( {\frac{{{{k}^{3}}(\varepsilon )\tau (\varepsilon )}}{{m(\varepsilon )}}} \right)} \right]}_{{\varepsilon = {{\varepsilon }_{{\text{F}}}}}}}. \\ \end{gathered} $
Здесь ${{k}_{{\text{B}}}}$ – постоянная Больцмана, Т – температура, εF – энергия Ферми. Полное время релаксации электронов ${\tau }({{{\varepsilon }}_{k}})$ = ${{\left[ {{{{\nu }}_{{{\text{ei}}}}}({{{\varepsilon }}_{k}}) + {{{\nu }}_{{{\text{eph}}}}}({{{\varepsilon }}_{k}})} \right]}^{{ - 1}}},$ где νеi(k) – скорость релаксации электронов на примесях [8, 9], νеph(k) – скорость релаксации электрона на фононах в модели анизотропного континуума [25 ] :
(4)
$\begin{gathered} {{\nu }_{{{\text{eph}}}}}({{\varepsilon }_{k}}) = \frac{m}{{8{{\pi }^{2}}{{\hbar }^{3}}{{{\left( k \right)}}^{3}}}}\sum\limits_ \pm {\int\limits_0^{2k \pm {{q}_{0}}} {{{{(Z_{q}^{\lambda })}}^{5}}dZ_{q}^{\lambda }} } , \\ \int\limits_0^{2\pi } {d{{\varphi }_{q}}} {{\left| {C\left. {_{0}^{\lambda }} \right|} \right.}^{2}}{{\left( {{{q}_{{T\lambda }}}} \right)}^{5}}N_{{q\lambda }}^{0}(N_{{q\lambda }}^{0} + 1)\Phi _{\lambda }^{ \pm }({{\varepsilon }_{k}},q), \\ \Phi _{\lambda }^{ \pm }({{\varepsilon }_{k}},q) = \pm \left[ {\frac{{{{f}_{0}}\left( {{{\varepsilon }_{k}} \pm \hbar \omega _{q}^{\lambda }} \right) - {{f}_{0}}({{\varepsilon }_{k}})}}{{{{f}_{0}}(1 - {{f}_{0}})}}} \right]\left[ {1 \mp \frac{{q_{0}^{\lambda }(\theta ,\varphi )}}{q}} \right], \\ q_{T}^{\lambda } = \frac{{{{k}_{{\text{B}}}}T}}{{\hbar {{S}^{\lambda }}(\theta ,\varphi )}},\,\,\,\,Z_{q}^{\lambda } = \frac{{\hbar \omega _{q}^{\lambda }}}{{{{k}_{{\text{B}}}}T}}, \\ q_{0}^{\lambda }(\theta ,\varphi ) = \frac{{2{{m}_{e}}S_{0}^{\lambda }(\theta ,\varphi )}}{\hbar }, \\ \end{gathered} $
где $N_{{q{\lambda }}}^{0}$ – функция Планка, ${{\left. {\left| {C_{q}^{{\lambda }}({\theta },{\varphi })} \right.} \right|}^{2}}$ = ${{\left( {C_{0}^{{\lambda }}({\theta },{\varphi })} \right)}^{2}}q,$ ${{\left( {C_{0}^{{\lambda }}({\theta },{\varphi })} \right)}^{2}}$ = E0λ – константа деформационного потенциала, для щелочных металлов [6].

Детали расчета термоэдс увлечения приведены в [13, 16], поэтому их здесь мы не воспроизводим, а ограничимся конечным выражением, затем конкретизируем некоторые детали для металлов. В отличие от ранее опубликованных [17, 18], релаксацию импульса фононов в неравновесной электрон-фононной системе мы учитываем, не ограничиваясь линейным приближением по параметру неупругости $Z_{q}^{{\lambda }}.$ В [1–4] исследования термоэдс и решеточной теплопроводности проводили на кристаллах калия с концентрацией электронов ${{n}_{e}} = 1.4 \times {{10}^{{22}}}$ см–3, ${{k}_{{\text{F}}}} = 0.75 \times {{10}^{8}}$ см–1, эффективной массой ${{m}_{F}} \cong 1.1{{m}_{0}}$ (${{m}_{0}}$ – масса свободного электрона) и энергией Ферми ${{{\varepsilon }}_{{\text{F}}}} = 2.12\,\,{\text{эВ,}}$ $\rho \cong 0.91 \times {{10}^{8}}\,\,{\text{г}} \cdot {\text{с}}{{{\text{м}}}^{{ - {\text{3}}}}},$ ${{E}_{{0\lambda }}} \cong \left( {2{\text{/}}3} \right){{\varepsilon }_{F}} = 1.41\,\,{\text{эВ}}{\text{.}}$ Из значений фазовых скоростей ($S_{L}^{{[100]}}$ = 2.24 × 105 см/с и $S_{t}^{{[100]}} = 1.7 \times {{10}^{5}}\,\,{\text{см/с}}$) следует, что величина q0 на три порядка меньше, чем 2kF. Поэтому в термоэдс увлечения можно пренебречь добавкой $ \pm q_{0}^{\lambda }$ по сравнению с $2{{k}_{{\text{F}}}}$ и объединить члены, соответствующие испусканию и поглощению фононов. Тогда получим [13, 16]:

(5)
$\begin{gathered} {{\alpha }_{{{\text{drag}}}}} = \frac{{{{k}_{{\text{B}}}}}}{e}\sum\limits_\lambda {\left( {\frac{3}{{4\pi }}} \right)\int {d{{\Omega }_{q}}} } \int\limits_0^{{{T_{F}^{\lambda }({\theta },{\varphi })} \mathord{\left/ {\vphantom {{T_{F}^{\lambda }({\theta },{\varphi })} T}} \right. \kern-0em} T}} {{{{\left( {Z_{q}^{\lambda }} \right)}}^{4}}{\text{th}}\left( {{{Z_{q}^{\lambda }} \mathord{\left/ {\vphantom {{Z_{q}^{\lambda }} 2}} \right. \kern-0em} 2}} \right)dZ_{q}^{\lambda } \times } \\ \times \,\,\left( {\frac{{\nu _{{{\text{eph}}0}}^{\lambda }({{k}_{F}},q_{T}^{\lambda })}}{{\nu _{{{\text{ph}}}}^{{\lambda }}(q)}}} \right)\left( {\frac{{T_{{\delta }}^{\lambda }}}{T}} \right)\left\{ {\tilde {V}_{{g3}}^{\lambda }n_{{q3}}^{{}}} \right\}, \\ T_{{_{\delta }}}^{\lambda } = {{\left( {2{{m}_{{\text{F}}}}{{{\left( {{{S}^{\lambda }}(\theta ,\varphi )} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {2{{m}_{{\text{F}}}}{{{\left( {{{S}^{\lambda }}(\theta ,\varphi )} \right)}}^{2}}} \right)} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}. \\ \end{gathered} $

Здесь $\tilde {V}_{{g3}}^{\lambda }$ и $n_{{q3}}^{{}}$ – проекции групповой скорости и единичного волнового вектора фонона на направление градиента температур, $\nu _{{{\text{eph}}0}}^{\lambda }({{k}_{{\text{F}}}},\,\,q_{T}^{\lambda })$ – скорость релаксации электрона с импульсом ${{k}_{{\text{F}}}}$ на тепловом фононе с импульсом $q_{T}^{\lambda }$:

(6)
$\begin{gathered} \nu _{{{\text{eph}}0}}^{\lambda }({{k}_{F}},q_{T}^{\lambda }) = \frac{{m({{\varepsilon }_{{\text{F}}}}){{{(C_{0}^{\lambda })}}^{2}}}}{{2\pi {{\hbar }^{3}}k_{{_{F}}}^{3}}}{{\left( {q_{T}^{\lambda }} \right)}^{5}}N_{{q\lambda }}^{0}(N_{{q\lambda }}^{0} + 1), \\ q_{T}^{\lambda } = \frac{{{{k}_{{\text{B}}}}T}}{{\hbar {{S}^{\lambda }}(\theta ,\varphi )}},\,\,\,\,Z_{q}^{\lambda } = \frac{q}{{q_{T}^{\lambda }}} = \frac{{\hbar \omega _{q}^{\lambda }}}{{{{k}_{{\text{B}}}}T}}. \\ \end{gathered} $

В выражении (5) верхний предел интегрирования определяется отношением ${{T_{F}^{\lambda }(\theta ,\varphi )} \mathord{\left/ {\vphantom {{T_{F}^{\lambda }(\theta ,\varphi )} T}} \right. \kern-0em} T}$ = = ${{2\hbar {{k}_{{\text{F}}}}{{S}^{\lambda }}(\theta ,\varphi )} \mathord{\left/ {\vphantom {{2\hbar {{k}_{{\text{F}}}}{{S}^{\lambda }}(\theta ,\varphi )} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}.$ Поскольку величины $T_{{\text{F}}}^{\lambda }(\theta ,\varphi )$ имеют порядок 102 К ($T_{{\text{F}}}^{{[100]L}}$ = 258 К и $T_{{\text{F}}}^{{[100]t}}$ = = 196 К), то при температурах порядка 1–3 К мы можем распространить верхний предел интегрирования до бесконечности.

Для дальнейших оценок и анализа температурных зависимостей термоэдс в калии мы учтем актуальные в низкотемпературной области механизмы релаксации фононов: рассеяние на границах образца, дислокациях, электронах и дефектах (изотопическом беспорядке). Для этих механизмов скорость релаксации может быть представлена в виде

(7)
$\begin{gathered} \nu _{{{\text{ph}}}}^{\lambda }(q,\theta ,\varphi ) = \nu _{{{\text{phB}}}}^{\lambda }(\theta ,\varphi ) + \frac{{{{k}_{{\text{B}}}}T}}{\hbar }Z_{q}^{\lambda }\left[ {\nu _{{{\text{phd}}}}^{{ * \lambda }}(\theta ,\varphi ) + } \right. \\ \left. { + \,\,\nu _{{{\text{phe}}}}^{{ * \lambda }}(\theta ,\varphi )} \right] + \nu _{{{\text{phi}}}}^{{\lambda }}(q,\theta ,\varphi ). \\ \end{gathered} $

Здесь $\nu _{{{\text{phB}}}}^{\lambda }(\theta ,\varphi )$ – скорость релаксации фононов на границах (см. [10]), $\nu _{{{\text{phd}}}}^{{ * \lambda }}(\theta ,\varphi ) = A{{b}^{2}}{{N}_{d}},$ $\nu _{{{\text{phe}}}}^{{ * \lambda }}(\theta ,\varphi )$ ≅ ≅ $\frac{{m_{F}^{2}}}{{{{\hbar }^{4}}}}\frac{{E_{{0\lambda }}^{2}}}{{2\pi {{S}^{\lambda }}(\theta ,\varphi )\rho }}{{\left( {{{{\mathbf{e}}}^{\lambda }}(\theta ,\varphi ){\mathbf{n}}{\text{ }}} \right)}^{2}}$ – безразмерные величины. Согласно [4], $A \approx 1,$ b ≈ 4.5 × 10–8 см – вектор Бюргерса, Nd = 1011 см–2 ⋅ ${{\tilde {N}}_{d}}.$ Приведенная концентрация дислокаций ${{\tilde {N}}_{d}}$ является подгоночным параметром для образцов с различной степенью деформации. Для приведенных выше параметров калия находим:

(8)
$\begin{gathered} \nu _{{{\text{phd}}}}^{{ * \lambda }}(\theta ,\varphi ) \cong 2.03 \times {{10}^{{ - 4}}}{{{\tilde {N}}}_{d}}, \\ \nu _{{{\text{phe}}}}^{{ * \lambda }}(\theta ,\varphi ) \cong \frac{{6.59 \times {{{10}}^{{ - 4}}}}}{{{{{\tilde {S}}}^{\lambda }}(\theta ,\varphi )}}{{\left( {{{{\mathbf{e}}}^{\lambda }}(\theta ,\varphi ){\mathbf{n}}{\text{ }}} \right)}^{2}}, \\ {{{\tilde {S}}}^{\lambda }}(\theta ,\varphi = {{S}^{\lambda }}(\theta ,\varphi ) \times {{10}^{{ - 6}}}. \\ \end{gathered} $

Для скорости релаксации фононов на изотопическом беспорядке имеем [15, 20, 21]:

(9)
${{\nu }_{{{\text{iso}}}}} \cong {{A}_{{{\text{iso}}}}}{{\left( {TZ_{q}^{\lambda }} \right)}^{4}},\,\,\,\,{{A}_{{{\text{iso}}}}} = \frac{{g{{V}_{0}}}}{{12\pi }}{{\left( {{{{{k}_{{\text{B}}}}} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}} \hbar }} \right. \kern-0em} \hbar }} \right)}^{4}}\left\langle {{{{\left( {S_{0}^{\lambda }} \right)}}^{{ - 3}}}} \right\rangle .$

Здесь V0 – объем, приходящийся на один атом, g =1.64 × 10–4 – фактор изотопического беспорядка. Для константы Aiso в калии получим: Aiso = 2.85 × × 104 с–1 К–1. Как видно из (5)–(8), при понижении температуры роль рассеяния на дислокациях и электронах уменьшается. В случае, когда доминирует граничное рассеяние фононов, термоэдс увлечения будет следовать зависимости ${{\alpha }_{{{\text{drag}}}}} \approx В{{T}^{4}},$ а при доминирующей роли рассеяния на дислокациях и электронах ${{\alpha }_{{{\text{drag}}}}} \approx С{{T}^{3}}.$

ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ ТЕРМОЭДС УВЛЕЧЕНИЯ И РЕШЕТОЧНОЙ ТЕПЛОПРОВОДНОСТИ В КРИСТАЛЛАХ КАЛИЯ

Из анализа температурных зависимостей теплопроводности [15] следует, что доминирующими механизмами релаксации фононов в калии при низких температурах 1–3 К являются рассеяние на электронах и дислокациях. В пользу этих механизмов рассеяния указывают температурные зависимости теплопроводности $\kappa (T) \approx {{T}^{{\delta }}},$ где показатель ${{\delta }_{{\exp }}}\sim 1.6 - 2.4,$ и для большинства образцов он близок к двум [4]. Согласно оценкам [15], вклад изотопического рассеяния в полное теплосопротивление при Т = 2 К составлял менее 1.5%, а при учете дополнительного рассеяния на примесях с концентрацией 300 ррм этот вклад не превышает 3% [15], а рассеяние на границах – порядка 1%. В работах [13, 15] мы рассчитали температурные зависимости решеточной теплопроводности образцов К4 и К5 с деформациями ε ≈ 0.05 и ε ≈ 0.1 в интервале 1.5–3 К и согласовали результаты расчета с данными эксперимента [4]. В расчетах использована скорость релаксации фононов (7) с константой деформационного потенциала одинаковой для фононов различных поляризаций ${{E}_{{0\lambda }}} \cong \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}} \right){{\varepsilon }_{F}}$ = 1.41 эВ. Приведенная концентрация дислокаций ${{\tilde {N}}_{d}}$ использована в качестве подгоночного параметра. Для образцов К4 с деформациями ε ≈ 0.05 и ε ≈ 0.1 значения ${{\tilde {N}}_{d}}$ равны 0.3 и 0.55, для К5 с ε ≈ 0.053 и ε ≈ 0.027 значения ${{\tilde {N}}_{d}}$ равны 0.33 и 0.17 соответственно (см. [15]). Как видно из рис. 3 работы [13], результаты расчета хорошо согласуются с экспериментальными данными.

Для этих механизмов релаксации из выражений (5)–(7) термоэдс увлечения может быть представлена в аналитическом виде:

(10)
$\begin{gathered} {{\alpha }_{{{\text{drag}}}}}(Т) \approx B{{T}^{3}},\,\,\,\,\,B = \sum\limits_\lambda {{{B}_{\lambda }} = } \frac{{{{k}_{{\text{B}}}}}}{e} \times \\ \times \,\,\sum\limits_\lambda {\left( {\frac{{{{{\left( {{{m}_{F}}} \right)}}^{2}}E_{{0\lambda }}^{2}}}{{4{{{\left( \pi \right)}}^{4}}\rho {{\hbar }^{3}}{{n}_{{e0}}}}}} \right)\int {d{{\Omega }_{q}}} } {{\left( {\frac{{{{k}_{{\text{B}}}}}}{{\hbar {{S}^{\lambda }}(\theta ,\varphi )}}} \right)}^{3}} \times \\ \times \,\,\left( {\frac{{{{{\left( {{{{\mathbf{e}}}^{\lambda }}(\theta ,\varphi ){\mathbf{n}}{\text{ }}} \right)}}^{2}}\left\{ {\tilde {V}_{{g3}}^{\lambda }{{n}_{{q3}}}} \right\}}}{{\left[ {\nu _{{{\text{phd}}}}^{{ * \lambda }}(\theta ,\varphi ) + \nu _{{{\text{phe}}}}^{{ * \lambda }}(\theta ,\varphi )} \right]{{S}^{\lambda }}(\theta ,\varphi )}}} \right); \\ {{J}_{3}} = \left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right)\int\limits_0^\infty {{{{{{\left( {Z_{q}^{\lambda }} \right)}}^{3}}{\text{th}}\left( {{{Z_{q}^{\lambda }} \mathord{\left/ {\vphantom {{Z_{q}^{\lambda }} 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{{{{\left( {Z_{q}^{\lambda }} \right)}}^{3}}{\text{th}}\left( {{{Z_{q}^{\lambda }} \mathord{\left/ {\vphantom {{Z_{q}^{\lambda }} 2}} \right. \kern-0em} 2}} \right)} {{{{\left( {{\text{sh}}({{{{Z}_{q}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}} 2}} \right. \kern-0em} 2})} \right)}}^{2}}dZ_{q}^{\lambda }}}} \right. \kern-0em} {{{{\left( {{\text{sh}}({{{{Z}_{q}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}} 2}} \right. \kern-0em} 2})} \right)}}^{2}}dZ_{q}^{\lambda }}}} = 6.1 \\ \end{gathered} $

Однако расчетные значения термоэдс увлечения при тех же параметрах ${{E}_{{0\lambda }}} \cong \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}} \right){{\varepsilon }_{F}}$ = 1.41 эВ и ${{\tilde {N}}_{d}}$ оказались меньше экспериментальных данных при Т = 2 К почти в два раза. Анализ вкладов квазипродольных и квазипоперечных фононов в термоэдс увлечения кристаллов калия, проведенный в [15], показал, что вклад медленных квазипоперечных фононов, который ранее не учитывали (см. [1–5]), оказался на порядок величины больше вклада продольных фононов: для образца К5 с деформацией $\varepsilon \cong 0.05$ вклад медленной квазипоперечной моды составляет 86%, тогда как вклады $\alpha _{{{\text{drag}}}}^{L}$ и $\alpha _{{{\text{drag}}}}^{{t1}}$ – 8 и 6% [13]. Очевидно, что подгонка результатов расчета может быть осуществлена только за счет увеличения константы деформационного взаимодействия поперечных фононов с электронами ${{E}_{{0t}}}.$ По-видимому, имеется дополнительный механизм влияния сдвиговых деформаций на энергию электронов проводимости. Кстати, на это в свое время указывал Займан в классической монографии [6]. Поэтому мы провели одновременную подгонку температурных зависимостей теплопроводности и термоэдс при вариации константы деформационного потенциала ${{E}_{{0t2}}} = {{E}_{{0t1}}} = {{E}_{{0t}}}$ при фиксированном значении ${{E}_{{0L}}}$ ≅ 1.41 эВ. В результате были определены значения ${{E}_{{0t}}}$ ≅ 2.81 эВ и подгоночные параметры ${{\tilde {N}}_{d}}.$ Как видно из рис. 1 и 2, результаты расчета теплопроводности и термоэдс хорошо согласуются с экспериментальными данными.

Рис. 1.

Температурные зависимости теплопроводности образцов калия с прямоугольным сечением D × μD = 0.15 × 0.5 см2 (μ = 3.3) и длиной L = 3.8 см с деформациями: для К4 ε ≈ 0.1 и ε ≈ 0.05 (кривые 1 и 2) и К5 с ε ≈ 0.053 и ε ≈ 0.027 (кривые 1а и 2а), значения ${{\tilde {N}}_{d}}$ приведены в табл. 3. Точки – экспериментальные значения [4].

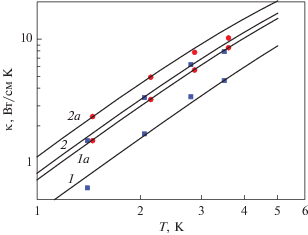
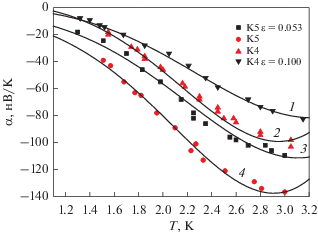
Рис. 2.

Температурная зависимость термоэдс: для К4 ε ≈ 0.1 ${{\tilde {N}}_{d}}$ = 0.4 и ε ≈ 0 (кривые 1 и 2) и К5 с ε ≈ 0.053 ${{\tilde {N}}_{d}}$ = 0.14 и ε ≈ 0 (кривые 3 и 4). Символы – экспериментальные значения [4].

Ранее при анализе термоэдс щелочных металлов в [1–4] использована эмпирическая формула (см. формулу (4.18) в [5]):

(11)
$\alpha = АT + В{{T}^{3}} + С\exp ({{ - \theta {\text{*}}} \mathord{\left/ {\vphantom {{ - \theta {\text{*}}} T}} \right. \kern-0em} T}).$

Здесь первый член соответствует вкладу диффузионной термоэдс (см. формулу (3)), второй член – вклад нормальных процессов электрон-фононного рассеяния в термоэдс увлечения (${{\alpha }_{{{\text{drag}}}}}(Т) \approx B{{T}^{3}}$), третий член определяет вклад процессов электрон-фононного переброса. В работе [4] все коэффициенты А, B, С и θ* являлись подгоночными параметрами при сопоставлении выражения (11) с экспериментальными данными. Для значений, приведенных в табл. 2, получено хорошее согласие с экспериментальными данными (см. [4] табл. 1 и рис. 4). Ниже мы рассчитаем коэффициент B и покажем, что параметры, приведенные в табл. 2, не является корректными. Во-первых, для процессов электрон-фононного переброса температура θ* не должна варьироваться от образца к образцу, поскольку она определяется фононным спектром. Ее общепринятое значение 20–22 К (см. [5, 19]), поэтому для нее мы взяли θ* = 20 К.

Таблица 2.  

Значения параметров A, B, C и θ* для образцов калия из работы [4]

Образец ε A, нВ/К2 B, нВ/К4 C, нВ/К θ*, К
K5 ε = 0.053 5 –10 2.5 × 104 15.2
K5 ε = 0 –0.5 –12.2 3 × 104 15.2
K4 ε = 0.1 7 –7.3 1.9 × 104 15.9
K4 ε = 0 9 –9.4 2.6 × 104 15.9

В нашей теории для определения полной термоэдс подгоночными параметрами являются коэффициенты А и С. Коэффициент В рассчитывали по формулам (10) и расчет проверяли согласно (5)–(9). Результаты нашей подгонки приведены в табл. 3. Как видно из рис. 2, использование этих значений позволяет согласовать величины полной термоэдс с экспериментальными данными [4]. Естественно, что увеличение концентрации дислокаций приводит к уменьшению термоэдс увлечения, и максимальное значение коэффициент В достигается при ${{\tilde {N}}_{d}} = 0.$ Этот случай особенно интересен, поскольку коэффициент ${{B}_{{\max }}}$ определяет значения термоэдс увлечения, которые могут быть достигнуты для совершенных кристаллов калия без дислокаций. Они уже не зависят от значений констант электрон-фононного взаимодействия $E_{{0\lambda }}^{2}$и факторов ${{\left( {{{{\mathbf{e}}}^{\lambda }}(\theta ,\varphi ){\mathbf{n}}{\text{ }}} \right)}^{2}},$ а определяются исключительно упругими модулями второго порядка и концентрацией электронов:

(12)
$\begin{gathered} {{B}_{{max}}} = {{J}_{3}}\frac{{{{k}_{B}}}}{e}\sum\limits_\lambda {\left( {\frac{1}{{2{{{\left( \pi \right)}}^{3}}{{n}_{{e0}}}}}} \right){{{\left( {\frac{{{{k}_{B}}}}{{hS_{{^{{[100]}}}}^{\lambda }}}} \right)}}^{3}}\int {d{{\Omega }_{q}}} } \times \\ \times \,\,\left( {\frac{{\left\{ {\tilde {V}_{{g3}}^{\lambda }{{n}_{{q3}}}} \right\}}}{{{{{\left( {{{{\tilde {S}}}^{\lambda }}(\theta ,\varphi )} \right)}}^{3}}}}} \right),\,\,\,\,{{{\tilde {S}}}^{\lambda }}(\theta ,\varphi = \frac{{{{S}^{\lambda }}(\theta ,\varphi )}}{{S_{{^{{[100]}}}}^{\lambda }(\theta ,\varphi )}}. \\ \end{gathered} $
Таблица 3.  

Значения параметров ${{\tilde {N}}_{d}},$ A, B, C и θ* для образцов калия K4 и K5 с различной концентрацией дислокаций

Образец $E_{{0L}}^{{}} \cong {{1.41}_{{}}}{\text{эВ}}$$E_{{0t}}^{{}} \cong {{2.81}_{{}}}{\text{эВ}}$
${{\tilde {N}}_{d}}$ A, нВ/К2 B, нВ/К4 C, нВ/К θ*, К
K5 ε = 0.053 0.139 –5 –6.13 5.5 × 104 20
K5 ε = 0.027 0.06   –6.78   20
K5 ε = 0 0 –9 –8.33 9 × 104 20
K4 ε = 0.1 0.4 2 –5.04 4 × 104 20
K4 ε = 0.05 0.11   –6.33   20
K4 ε = 0 0 7.8 –8.33 8 × 104 20

Непосредственный расчет для калия дает ${{B}_{{\max }}} \cong - 8.3,$ очевидно, что при учете дислокаций $\left| B \right| < \left| {{{B}_{{\max }}}} \right|$ ≅ 8.3. Из сравнения табл. 2 и 3 видно, что значения подгоночных параметров В, выбранных в [4] для образцов калия К4 В = –9.4 и К5 В = –10 и –12.2, заметно меньше параметра ${{B}_{{\max }}}.$ Таким образом, подгонка результатов эксперимента, выполненная в работе [4], является некорректной. Именно этот факт послужил основанием для нашего анализа роли квазипоперечных фононов в термоэдс увлечения. В этом пределе вклады медленной и быстрой квазипоперечных мод в ${{\alpha }_{{{\text{drag}}}}}$ составляют 80 и 16%, тогда как вклад продольных фононов – всего 4%. А соотношение коэффициентов В для различных мод имеет вид ${{B}_{{t2}}}:{{B}_{{t1}}}:{{B}_{L}}$ = 20 : 4 : 1.

Можно надеяться, что наш метод окажется полезным для оценок максимальных значений термоэдс увлечения в других щелочных и благородных металлах.

ЗАКЛЮЧЕНИЕ

Исследовано влияние анизотропии упругой энергии на температурные зависимости теплопроводности и термоэдс увлечения в кристаллах калия при низких температурах. Основные результаты можно сформулировать следующим образом.

1. Анализ вкладов квазипродольных и квазипоперечных фононов в термоэдс увлечения объемных кристаллов калия показал, что для образцов с дислокациями, исследованных в [4], вклад медленных квазипоперечных фононов, который ранее не учитывали, оказался на порядок величины больше вклада продольных фононов. Для объемных кристаллов калия без дислокаций, когда доминирующий вклад в релаксацию фононов вносит рассеяние на электронах, суммарный вклад квазипоперечных фононов достигает 96%, тогда как вклад продольных фононов – всего 4%.

2. Анализ вкладов колебательных мод в термоэдс увлечения показал, что результаты расчета могут быть согласованы с экспериментальными данными только в предположении, что константа деформационного взаимодействия поперечных фононов с электронами $E_{{0t}}^{{}}$ в два раза превышает ее значение для продольных фононов.

3. Определены максимальные значения термоэдс увлечения при низких температурах в кристаллах калия без дислокаций. Показано, что они определяются исключительно упругими модулями второго порядка и не зависят от значений констант электрон-фононного взаимодействия.

Проведенный анализ свидетельствует, что модель изотропной среды не может дать адекватного описания электрон-фононного увлечения в металлах. Необходимо учитывать вклады всех мод в термоэдс увлечения.

Работа выполнена в рамках государственного задания МИНОБРНАУКИ России (тема “Функция” АААА-А19-119012990095-0).

Список литературы

  1. MacDonald D.K.C., Pearson W.B., Templeton I.M. Thermo-Electricity at Low Temperatures. VIII. Thermo-Electricity of the Alkali Metals Below 2 K // Proc. R. Soc. Lond. A. 1960. V. 256. P. 334.

  2. Guenault A.M., MacDonald D.K.C. Electron and phonon scattering thermoelectricity in potassium and alloys at very low temperatures // Proc. R. Soc. Lond. A. 1961. V. 264. P. 41.

  3. Stinson M.R., Fletcher R., Leavens C.R. Thermomagnetic and thermoelectric properties of potassium // Phys. Rev. B. 1979. V. 20. P. 3970–3990.

  4. Fletcher R. Scattering of phonons by dislocations in potassium // Phys. Rev. B. 1987. V. 36. P. 3042–3051.

  5. Blatt F.J., Schroeder P.A., Foiles C.L., Greig D. Thermoelectric power of metals. N.Y. and London: Plenum press. 1976.

  6. Займан Дж. Электроны и фононы. М.: Изд-во ИЛ, 1962.

  7. Блатт Ф. Физика электронной проводимости в твердых телах. М.: Изд-во ИЛ, 1971.

  8. Гуревич Л.Э. Термоэлектрические свойства проводников.I // ЖЭТФ. 1946. Т. 16. С. 193; Термомагнитные и гальваномагнитные свойства проводников // ЖЭТФ. 1946. Т. 16. С. 416.

  9. Herring C. Theory of the Thermoelectric Power of Semiconductors // Phys. Rev. 1954. V. 96. P. 1163.

  10. Кулеев И.Г., Кулеев И.И., Бахарев С.М., Устинов В.В. Фокусировка фононов и фононный транспорт в монокристаллических наноструктурах. Екатеринбург: “Изд-во УМЦ УПИ”, 2018. 256 с.

  11. Федоров Ф.И. Теория упругих волн в кристаллах. М.: Наука, 1965. 388 с.

  12. Кулеев И.Г., Кулеев И.И. Упругие волны в кубических кристаллах с положительной и отрицательной анизотропией модулей упругости второго порядка // ФТТ. 2007. Т. 49. № 3. С. 422–429.

  13. Кулеев И.И., Кулеев И.Г. Роль квазипродольных и квазипоперечных фононов в термоэдс увлечения кристаллов калия при низких температурах // ЖЭТФ. 2019. 155. Т. 6. С. 56–70.

  14. Truel B., Elbaum C., Chick B.B. Ultrasonic methods in solid state physics. Academic Press, N.Y.−London. 1969.

  15. Кулеев И.И., Кулеев И.Г. Фокусировка фононов и анизотропия решеточной теплопроводности кристаллов калия при низких температурах // ФММ. 2018. Т. 119. С. 1141–1147.

  16. Кулеев И.Г., Кулеев И.И., Бахарев С.М., Устинов В.В. Фокусировка фононов и электрон-фононное увлечение в полупроводниковых кристаллах с вырожденной статистикой носителей тока // ЖЭТФ. 2016. Т. 150. С. 567–585.

  17. Гуревич Л.Э., Коренблит И.Я. Влияние увлечения электронов фононами и их взаимного увлечения накинетические коэффициенты полуметаллов // ФТТ. 1964. Т. 6. С. 856–863.

  18. Mahan G.D., Lindsay L., Broido D.A. The Seebeck coefficient and phonon drag in silicon // J. Appl. Phys. 2014. V. 116. P. 245102.

  19. Ekin J.W., Maxfield B.W. Electrical Resistivity of Potassium from 1 to 25° K // Phys. Rev. B. 1971. V. 4. P. 4215–4225.

  20. Жернов А.П., Инюшкин А.В. Изотопические эффекты в твердых телах. РНЦ “Курчатовский Институт”, М., 2001, 216 с.

  21. Klemens P.G. The scattering of low-frequency lattice waves by static imperfections // Proceedings of the Physical Society. Section A. 1955. V. 68. № 12. P. 1113–1128.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал