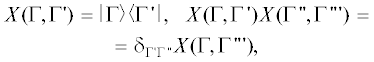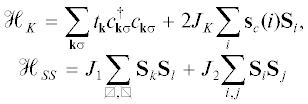Физика металлов и металловедение, 2019, T. 120, № 6, стр. 563-600
Современная физика конденсированного состояния: сильные корреляции и квантовая топология
В. Ю. Ирхин a, *, Ю. Н. Скрябин a
a Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С Ковалевской, 18, Россия
* E-mail: Valentin.Irkhin@imp.uran.ru
Поступила в редакцию 04.12.2018
После доработки 14.12.2018
Принята к публикации 09.01.2019
Аннотация
Темой обзора является применение новых идей необычных квантовых состояний к физике конденсированного состояния, в особенности твердого тела, в контексте современной теории поля. Проведено сопоставление с классическими работами по многоэлектронной теории, включая формализм многоэлектронных операторов. Обсуждаются принципиально многочастичная природа основного состояния, индивидуальные и коллективные возбуждения и квантовые флуктуации в рассматриваемых системах, а также квантовые фазовые переходы с упором на топологические аспекты и с учетом эффектов фрустрации. Рассмотрены вариационные подходы и представления вспомогательных частиц, соответствующие приближения среднего поля и теория калибровочных полей, проблема конфайнмента–деконфайнмента, нарушение картины ферми-жидкости и экзотические неферми-жидкостные состояния. Дан обзор современной теории запутанных топологических состояний, формирования спиновой жидкости, струн и струнных сетей.
1. Введение
1.1. Квантовые фазы и понятие квантовой топологии
1.2. Квантовые фазовые переходы
2. Развитие представлений и методов многоэлектронной теории
2.1. Вторичное квантование: фермионы и многоэлектронные операторы
2.2. Вариационные подходы
2.3. Представления вспомогательных частиц
2.4. $t - J$-модель и $s - d$-обменная модель с сильными корреляциями
3. Ферми-жидкость и неферми-жидкостные фазы
3.1. Теория среднего поля и калибровочные поля.
3.2. Конфайнмент и деконфайнмент
3.3. Дираковские фермионы и алгебраическая спиновая жидкость
3.4. Модель фазовых струн
3.5. Фрустрации в решетках Кондо
3.6. Фракционализованная ферми-жидкость
4. Теория квантовых фазовых переходов. Спиновая жидкость и топологический порядок
4.1. Деконфайнментная квантовая критичность
4.2. Хиггсова критичность
4.3. Квантовые фазовые переходы и некогерентные состояния в проводящих магнетиках
4.4. Сверхпроводимость и топологический порядок
5. Решеточные калибровочные теории и струны
5.1. Конденсация струнных сетей
5.2. Тензорные сети
6. Заключение
1. ВВЕДЕНИЕ
Нобелевская премия 2016 г. была присуждена за теоретические открытия топологических фазовых переходов и топологических фаз материи, за работы, сделанные в 1970–80-х гг., которые “раскрыли секреты экзотической материи”. За время, истекшее после пионерских работ Д. Халдейна, М. Костерлица и Д. Таулеса, был достигнут значительный прогресс в физике конденсированного состояния, связанный с применением новых, существенно квантовых топологических концепций. Сюда относятся топологические фазы вещества, в том числе защищенные симметрией, спиновые жидкости, экзотические возбуждения, струны, тензорные сети… Эти достижения были связаны с работой нескольких групп исследователей: Андерсона [1, 2], Вена [3–6], Сачдева [7], Коулмена [8]… Большой вклад здесь внесли и современные российские ученые – А.М. Поляков и А.Ю. Китаев.
1.1 Квантовые фазы и понятие квантовой топологии
Кратко остановимся на формальных математических определениях и подходах. Как известно из современной математики [9], топологическая теория поля и теория узлов тесно связаны. Действительно, интуитивно понятно, что топологическое запутывание ассоциируется с запутыванием (entanglement) квантовых состояний (в частности, это дает красивую аналогию с фейнмановским интегралом по траекториям). Таким образом, с практической точки зрения квантовая топология оказывается тесно связанной с проблемой квантовых вычислений [10].
Соответственно, была предложена математическая основа для классификации топологических фаз: каждая из них связана с математическим объектом, известным как “тензорная категория” [11, 12], который удовлетворяет некоторым алгебраическим уравнениям. Этот объект характеризует различные топологические фазы и определяет универсальные свойства квазичастичных возбуждений, как и аппарат обычных групп симметрии в теории Ландау. Таким образом, математическая структура тензорных категорий вместе с физической картиной струнной конденсации обеспечивают общую теорию топологических фаз.
Данный подход также предоставляет точно решаемые модели и волновые функции основного состояния для каждой из топологических фаз. Это локальные бозонные (или спиновые) модели, которые реализуют все дискретные калибровочные теории в любой размерности и теории Черна–Саймонса (в размерности 2 + 1). Топологический порядок характеризуется устойчивым вырождением основного состояния (квантовое состояние стабилизируется топологическими инвариантами) и нетривиальной статистикой частиц. В отличие от ситуации нарушения симметрии, возникающие (emergent) частицы в топологически упорядоченных состояниях включают калибровочные бозоны, а также фермионы либо энионы (частицы с дробной статистикой), которые могут возникать как коллективные возбуждения чисто бозонных моделей.
С точки зрения физики, квантовые фазы вещества являются фазами материи при нуле температур и соответствуют основным состояниям квантового гамильтониана системы [7]. В этом смысле изоляторы, магнетики и сверхпроводники существуют при нулевой температуре $T$ и являются примерами квантовых фаз.
После открытия дробного квантового эффекта Холла [13] и высокотемпературной сверхпроводимости (ВТСП) [14] было осознано, что существует новый тип порядка – топологический (элементарные возбуждения с энергетической щелью) или квантовый порядок (в более общем случае бесщелевых возбуждений). С тех пор изучение и классификация новых типов порядка в конденсированных средах стало весьма интенсивной областью исследования.
Согласно [4], возможна следующая классификация. Если квантовое состояние имеет щелевой спектр, то соответствующий квантовый порядок будет называться топологическим порядком. Низкоэнергетическая эффективная теория топологически упорядоченного состояния будет топологической квантовой теорией поля (TQFT [15]). Второй класс квантовых порядков соответствует ферми-жидкостям или свободным фермионным системам; при этом различные квантовые порядки классифицируются согласно топологии поверхности Ферми [16]. Третий, самый интересный класс квантового порядка описывается в терминах конденсации струнных сетей [12]. Такие состояния имеют некоторое сходство с обычной ситуацией нарушенной симметрии при конденсации отдельных частиц: они аналогичны бозе-конденсированным состояниям, но конденсат формируется из протяженных объектов. Коллективные возбуждения в струнном конденсате не являются обычными скалярными бозонами, – колебания замкнутых струн порождают калибровочные бозоны, а при разрыве струн их концы могут давать фермионы.
Таким образом, квантовая топология, рассматривающая внутренние степени свободы, может быть переформулирована на теоретико-полевом языке замкнутых струн, которые построены из локальных спинов либо псевдоспинов (кубитов – понятие, широко используемое в квантовых вычислениях). В свою очередь, от этих струн можно перейти к представлению“электрических” и “магнитных” калибровочных полей [17].
Само название “топологический порядок” исторически заимствовано из низкоэнергетической эффективной теории киральных спиновых состояний в TQFT [15]. Термин “топологический” здесь означает дальнодействующее запутывание, и поэтому он относится к квантовой топологии [5], – необходимо его отличать от обычной классической топологии, оперирующей с вихрями в сверхтекучей жидкости, различием между сферой и тором и т.д.
Киральное спиновое состояние как особый тип квантового состояния было предложено в 1987 г. для объяснения высокотемпературной сверхпроводимости [18, 19]. В отличие от известных в то время квантовых состояний, оно содержит новые экзотические частицы – спиноны и голоны – в состоянии деконфайнмента и соответствует стабильной фазе при нулевой температуре. Сначала, в предположении справедливости теории нарушенной симметрии Ландау, киральное состояние рассматривалось как состояние, которое нарушает симметрии обращения времени и четности, но сохраняет симметрию относительно вращения спинов и трансляций. Однако было быстро обнаружено, что существует множество различных киральных состояний, которые имеют ту же самую симметрию. Таким образом, одной симметрии недостаточно, чтобы характеризовать такие состояния. Это означает, что они представляют новый тип порядка, который и был назван топологическим порядком.
С макроскопической точки зрения топологический порядок характеризуется сильным вырождением основного состояния и неабелевыми геометрическими фазами [20]. С микроскопической же точки зрения топологический порядок определяется состоянием квантовой спиновой жидкости (QSL – quantum spin liquid) с щелевым энергетическим спектром [21, 22], которое не может быть представлено произведением одночастичных собственных состояний, если не рассматривать фазовых переходов с закрытием энергетической щели. Такие QSL проявляют дальнодействующее запутывание (entanglement), которое и есть внутренняя природа топологического порядка [23–25].
Формирование корреляций в топологических системах весьма необычно. Обычных “силовых” корреляций (предвестников дальнего порядка) здесь нет, но возникают особые, обусловленные топологией образца. При этом основное состояние вырождено, но не в силу симметрии, а благодаря топологическим характеристикам. Так, система “чувствует” сворачивание в тор, радикальным может оказаться влияние одной особой (выколотой) точки [26]…
1.2. Квантовые фазовые переходы
Традиционно считалось, что феноменологическая теория фазовых переходов Ландау [27, 28] может описать все возможные фазы вещества и фазовые переходы. Казалось, что все непрерывные фазовые переходы ассоциируются с нарушенной симметрией в рамках так называемого подхода Ландау–Гинзбурга–Вильсона. Долгое время была уверенность, что теория нарушенной симметрии Ландау также описывает все возможные квантовые фазы и непрерывные квантовые фазовые переходы (quantum phase transitions, QPT) между ними, т.е. фазовые переходы при $T = 0.$
В отличие от классических фазовых переходов, QPT учитывают флуктуации параметра порядка во мнимом времени. Отличительной чертой QPT является наличие нуль-температурной квантовой критической точки, разделяющей квантово-упорядоченную и квантово-разупорядоченную фазы на фазовой диаграмме температура–параметр (константа связи, давление, концентрация и т.д.), описывающий близость к квантовой критической точке. При конечной T эти фазы разделены квантовой критической областью, ограниченной линиями кроссоверов, сходящимися в критическую точку. Наличие такой области на фазовой диаграмме приводит ко многим необычным явлениям, в частности, к образованию неферми-жидкости в металлических системах.
В частности, были предложены так называемые проективные группы. Как известно, симметрия обычных упорядоченных фаз позволяет классифицировать их по 230 пространственным группам (в трех измерениях), а также приводит к появлению коллективных бесщелевых возбуждений – голдстоуновских бозонов. Проективные группы симметрии (Projective symmetry groups, PSG) для квантовых порядков имеет аналогичные приложения, позволяя классифицировать более 100 различных двумерных Z2-спиновых жидкостей, причем все они имеют одинаковую обычную симметрию [5]. Проективная группа симметрии также может приводить к возникновению бесщелевых калибровочных бозонов и фермионов. В методе PSG волновые функции не конкретизируются, а классифицируются по симметрии путем анализа с помощью локальных унитарных преобразований. Преобразования соответствующей ренормгруппы позволяют уловить простую суть возникающих сложных явлений. Метод PSG позволяет определить фазовые диаграммы, включающие фазы как с дальним, так и с ближним топологическим порядком и запутыванием. Кроме того, в теории топологических систем могут быть использованы термины и аналогии из теории информации и электрических цепей, а также нейронных сетей [29, 30].
После открытия ВТСП появилась надежда, что экзотические сильнокоррелированные состояния и квантовые спиновые жидкости могут играть решающую роль в ее понимании [1]. В таких состояниях возможно разделение спина и заряда: электрон распадается на две квазичастицы — спинон (спин 1/2, заряд 0) и голон (спин 0, заряд $e$). Бозе-конденсация голонов приводит к сверхпроводимости, и этот ее новый механизм объясняет бурный интерес к изучению различных спиновых жидкостей.
Однако, несмотря на определенные успехи, теория фаз с нарушенной симметрией не может объяснить существование QSL в основном состоянии из-за конфайнмента (взаимного удержания) спинонов и голонов, обусловленного возникающим калибровочным полем [31]. Действительно, было обнаружено (см., напр., [32]), что в U(1)-калибровочной теории основное состояние является либо антиферромагнитным, либо сверхпроводящим, либо ферми-жидкостью – все эти фазы находятся в состоянии конфайнмента.
Тем не менее на фазовой диаграмме высокотемпературных сверхпроводников при конечных температурах могут существовать области (“псевдощелевые” фазы), где фермионы и бозоны находятся в состоянии деконфайнмента. Следует отметить, что здесь фермионы и бозоны не могут рассматриваться как свободные из-за их сильного взаимодействия с калибровочным полем. В основном состоянии область деконфайнмента, как правило, редуцируется в “деконфайнментную” квантовую критическую точку [33, 34]. С этой точкой связан ряд важных физических явлений, включая разделение спиновых и зарядовых степеней свободы электрона.
В настоящем обзоре будут рассмотрены как феноменологические подходы в квантовой топологии, так и микроскопические модели для систем с сильными корреляциями. Мы постараемся проследить связи современных концепций, использующих последние достижения квантовойтеории поля, с классическими представлениями многоэлектронной теории, начатой в работах Шубина и Вонсовского, Гутцвиллера, Хаббарда и других авторов.
2. РАЗВИТИЕ ПРЕДСТАВЛЕНИЙ И МЕТОДОВ МНОГОЭЛЕКТРОННОЙ ТЕОРИИ
Первые успехи теории металлов в 20-е–30-е гг. ХХ века были связаны с созданием квантовой механики и открытием статистики Ферми. В рамках приближения свободных электронов, а затем одноэлектронной зонной теории — в работах Паули, Блоха, Вильсона, Пайерлса, Зоммерфельда – было дано объяснение парамагнетизма, поведения теплоемкости и кинетических свойств [35]. Однако для описания ферромагнетизма и ряда других явлений (например, перехода металл–изолятор) эти представления оказались недостаточными. С другой стороны, попытки использовать для магнитных металлов модель Дирака–Гейзенберга, основанную на атомной картине локализованных спинов, также не дали хороших результатов (в частности, она была не в состоянии объяснить дробные значения магнитных моментов). Таким образом, потребовался определенный синтез многоэлектронной модели Гейзенберга и одноэлектронной зонной модели.
В 1934 г. была предложена полярная модель Шубина и Вонсовского [36, 37], а в 1946 г. – $s - d$ обменная модель. Обе эти модели сыграли исключительно важную роль в теоретическом описании $d$- и $f$-металлов и их соединений. Дальнейшее развитие многоэлектронных подходов в основном пошло по направлениям диаграммных методов и феноменологической теории ферми-жидкости Ландау.
Новый импульс многоэлектронной теории кристалла придали идеи Хаббарда [38, 39], выделившего в своей модели наиболее существенную часть кулоновского взаимодействия – сильное отталкивание электронов на одном узле $U$. В случае невырожденной зоны ее гамильтониан запишется как
(1)
$\mathcal{H} = \sum\limits_{ij\sigma } {{{t}_{{ij}}}c_{{i\sigma }}^{\dag }{{c}_{{j\sigma }}}} + U\sum\limits_i {c_{{i \uparrow }}^{\dag }{{c}_{{i \uparrow }}}c_{{i \downarrow }}^{\dag }{{c}_{{i \downarrow }}}} ,$В своей лекции “Многочастичная физика: незаконченная революция” [8] П. Коулмен говорит о трех эрах физики конденсированного состояния: первых успехах после открытия квантовой механики (свободные фермионы), многочастичной физике середины ХХ века (использование теории возмущений и фейнмановской диаграммной техники, начало изучения коллективных явлений) и современной эре физики сильнокоррелированной материи – исследования “экзотических” систем, в которых коллективные явления выходят на первый план.
В настоящее время активно обсуждается роль квантовых корреляций, где на первый план выходят топологическое вырождение, приводящее к радикальному усложнению основного состояния системы.
2.1. Вторичное квантование: фермионы и многоэлектронные операторы
При переходе к стандартному представлению вторичного квантования [40] волновые функции кристалла $\Psi ({{x}_{1}} \ldots {{x}_{N}})$ ($x = \{ {{{\mathbf{r}}}_{i}}{{s}_{i}}\} ,$ ${{s}_{i}}$ – спиновые координаты) выбираются в виде линейных комбинаций слэтеровских определителей. Они составляются из одноэлектронных волновых функций ${{\psi }_{\lambda }}(x)$ ($\lambda = \{ \nu \gamma \} ,$ $\nu $ – индексы ячеек в решетке, а $\gamma $ – одноэлектронные наборы квантовых чисел):
(2)
$\begin{gathered} \Psi ({{x}_{1}} \ldots {{x}_{N}}) = \sum\limits_{{{\lambda }_{1}} \ldots {{\lambda }_{N}}} {f({{\lambda }_{1}} \ldots {{\lambda }_{N}})} {{(N!)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\sum\limits_P {{{{( - 1)}}^{P}}} P\prod\limits_i {{{\psi }_{{{{\lambda }_{i}}}}}({{x}_{i}})} , \\ \end{gathered} $(3)
$\Psi ({{x}_{1}} \ldots {{x}_{N}}) = \sum\limits_{\{ {{n}_{\lambda }}\} } {f( \ldots {{n}_{\lambda }} \ldots )} {{\Psi }_{{\{ {{n}_{\lambda }}\} }}}({{x}_{1}} \ldots {{x}_{N}}).$Тогда f(…nλ…) играет роль новой волновой функции. Одноэлектронные операторы рождения и уничтожения Ферми определяются следующим образом:
(4)
$\begin{gathered} {{c}_{\lambda }}f( \ldots {{n}_{\lambda }} \ldots ) = {{( - 1)}^{{{{\eta }_{\lambda }}}}}{{n}_{\lambda }}f( \ldots {{n}_{\lambda }} - 1 \ldots ), \\ c_{\lambda }^{\dag }f( \ldots {{n}_{\lambda }} \ldots ) = {{( - 1)}^{{{{\eta }_{\lambda }}}}}(1 - {{n}_{\lambda }})f( \ldots {{n}_{\lambda }} + 1 \ldots ), \\ \end{gathered} $Следует отметить, что само введение одноэлектронных операторов, ставшее для нас привычным, является весьма нетривиальным шагом. Альтернативно операторы фермионов в решеточных (псевдо) спиновых моделях могут быть сконструированы из операторов псевдоспина [3]:
(произведение идет по узлам решетки, упорядоченным определенным образом по контуру), что обобщает преобразование Йордана–Вигнера для одномерной цепочки на решетки высших размерностей. Таким образом, фермион предстает как существенно многочастичное и нелокальное образование. Это дает другое направление развития теории многочастичных систем, связанное со струнной картиной, использующей язык кубитов (см. разд. 5).Теперь обобщим метод вторичного квантования, вводя квантовые числа электронных групп $\Lambda = \{ \nu \Gamma \} ,$ $\Gamma $ – многоэлектронные (MЭ) уровни. В частности, можно объединить электроны на каждом узле в решетке ($\Lambda = \{ \nu \Gamma \} ,$ ${{\Gamma }_{i}}$ – MЭ уровни), получая
(6)
$\Psi ({{x}_{1}} \ldots {{x}_{N}}) = \sum\limits_{\{ {{N}_{\lambda }}\} } {f( \ldots {{N}_{\lambda }} \ldots )} {{\Psi }_{{\{ {{N}_{\lambda }}\} }}}({{x}_{1}} \ldots {{x}_{N}}).$В случае атомной конфигурации эквивалентных электронов ${{l}^{n}}$ MЭ-волновая функция электронной группы определяется рекуррентным соотношением (см. [41]):
(7)
$\begin{gathered} {{\Psi }_{{{{\Gamma }_{n}}}}}({{x}_{1}} \ldots {{x}_{N}}) = \\ = \sum\limits_{{{\Gamma }_{{n - 1}}},\gamma } {G_{{{{\Gamma }_{{n - 1}}}}}^{{{{\Gamma }_{n}}}}} C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}}{{\Psi }_{{{{\Gamma }_{{n - 1}}}}}}({{x}_{1}} \ldots {{x}_{{n - 1}}}){{\psi }_{\gamma }}({{x}_{n}}), \\ \end{gathered} $(8)
$C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}} \equiv C_{{{{L}_{{n - 1}}}{{M}_{{n - 1}}},lm}}^{{{{L}_{n}}{{M}_{n}}}}C_{{{{S}_{{n - 1}}}{{\mu }_{{n - 1}}},\tfrac{1}{2}\sigma }}^{{{{S}_{n}}{{\mu }_{n}}}},$(9)
$\begin{gathered} {{\Psi }_{{{{\Gamma }_{n}}}}}({{x}_{1}} \ldots {{x}_{n}}) = {{n}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\sum\limits_{i,{{\Gamma }_{{n - 1}}},\gamma } {{{{( - 1)}}^{{n - i}}}} C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}} \times \\ \times \,\,{{\Psi }_{{{{\Gamma }_{{n - 1}}}}}}({{x}_{1}} \ldots {{x}_{{i - 1}}},{{x}_{{i - 1}}} \ldots {{x}_{{n - 1}}}){{\psi }_{\gamma }}({{x}_{i}}) \\ \end{gathered} $По аналогии с (7), (9) можно ввести МЭ-операторы рождения для электронных групп [42]. Для эквивалентных электронов
(10)
$A_{{{{\Gamma }_{n}}}}^{\dag } = {{n}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\sum\limits_{{{\Gamma }_{{n - 1}}},\gamma } {G_{{{{\Gamma }_{{n - 1}}}}}^{{{{\Gamma }_{n}}}}} C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}}a_{\gamma }^{\dag }A_{{{{\Gamma }_{{n - 1}}}}}^{\dag }.$При добавлении электрона из другой оболочки
(11)
$A_{{{{\Gamma }_{n}}}}^{\dag } = \sum\limits_{{{\Gamma }_{{n - 1}}},\gamma } {C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}}} a_{\gamma }^{\dag }A_{{{{\Gamma }_{{n - 1}}}}}^{\dag }.$Операторы (10), (11) удобны только для работы с конфигурациями с фиксированным числом электронов. Чтобы избежать проблем “неортогональности” при различных n, следует ввести проекционные множители [43, 44]:
(12)
$\tilde {A}_{\Gamma }^{\dag } = A_{\Gamma }^{\dag }\prod\limits_\gamma {(1 - {{{\hat {n}}}_{\gamma }})} .$Формально произведение в (12) идет по всем допустимым одноэлектронным состояниям γ. Однако из-за тождества $c_{\gamma }^{\dag }{{\hat {n}}_{\gamma }} = 0$ достаточно сохранить только те γ, которые не входят в соответствующие произведения операторов в ${{A}_{\Gamma }}.$ Вводя MЭ-операторы, которые зависят от всех одноэлектронных квантовых чисел (как занятых, так и свободных состояний), мы делаем следующий шаг в квантово-полевом описании после обычного вторичного квантования. Таким образом, можно прийти к представлению MЭ-чисел заполнения ${{N}_{\Gamma }} = \tilde {A}_{\Gamma }^{\dag }{{\tilde {A}}_{\Gamma }}$ на данном узле.
Теперь мы можем вести обобщенные проекционные операторы $X$-операторы Хаббарда [39]:
которые переводят состояние $\Gamma {\text{'}}$ в состояние Γ. где $\left| \Gamma \right\rangle $ – точные собственные состояния гамильтониана. В простейшем случае s-электронов $\gamma = \sigma = \pm ( \uparrow , \downarrow ),$ $\Gamma = 0,\sigma ,2$ и $\left| 0 \right\rangle $ – свободное состояние (дырка), а $\left| 2 \right\rangle $ – дважды занятое синглетное состояние на узле (двойка).Произвольный оператор $\hat {O},$ действующий на электроны на данном узле i, выражается через X-операторы:
(15)
$\hat {O} = \sum\limits_{\Gamma \Gamma {\text{'}}} {\left\langle \Gamma \right|\hat {O}\left| {\Gamma {\text{'}}} \right\rangle } X(\Gamma ,\Gamma ').$Тогда, находя матричные элементы одноэлектронных ферми-операторов из (10), получаем представление [45]:
(16)
$c_{\gamma }^{\dag } = \sum\limits_n {{{n}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \sum\limits_{{{\Gamma }_{n}}{{\Gamma }_{{n - 1}}}} {G_{{{{\Gamma }_{{n - 1}}}}}^{{{{\Gamma }_{n}}}}C_{{{{\Gamma }_{{n - 1}}},\gamma }}^{{{{\Gamma }_{n}}}}} X({{\Gamma }_{n}},{{\Gamma }_{{n - 1}}}).$В частности, для s-электронов
В действительности МЭ-состояния вообще можно трактовать как первичные, получающиеся при решении полной МЭ-задачи, а не строить из одноэлектронных состояний (как было сделано выше на примере атомного подхода). При этом важную роль играет нелокальность, а природа коллективных состояний может быть очень сложной и включать дальнодействие.
Существование нетривиальных многочастичных состояний подтверждается обобщенной теоремой Либа–Шульца–Маттиса [46]. Она утверждает, что в системе с полуцелым спином на ячейку и глобальной U(1)-симметрией спектр возбуждения в термодинамическом пределе не может одновременно подчиняться двум требованиям: (а) основное состояние единственно и (б) существует конечная щель для всех возбуждений. Это означает, что щелевое состояние с ненарушенной симметрией должно иметь вырождение основного состояния, которое по своей природе является топологическим.
При увеличении силы корреляций в МЭ-системах происходит смена статистики элементарных возбуждений с зонной на атомную, которая проявляется как корреляционное хаббардовское расщепление и переход металл–изолятор (для наполовину заполненной зоны). Это превращение сопровождается формированием локальных магнитных моментов [47] и изменением числа состояний под поверхностью Ферми, если таковая вообще имеются (см. разд. 3.6).
Как указал Андерсон [48], образование хаббардовских подзон связано с катастрофой ортогональности, в результате которой исчезает квазичастичный вычет и нарушается картина ферми-жидкости Ландау. Исчезновение вычета означает, что добавление одной частицы в систему вызывает глобальное изменение ее состояния, что характерно для МЭ-систем. В такой ситуации, в частности, можно ожидать формирования экзотических частиц и состояния типа спиновой жидкости. Все эти вопросы будут обсуждаться ниже.
2.2. Вариационные подходы
Чтобы работать с МЭ-состояниями, на протяжении многих лет развивались различные приближенные методы. В работах Шубина и Вонсовского было использовано простейшее квазиклассическое приближение [36, 49]. Оно по существу состоит в замене Х-операторов c-числовыми функциями, определяющими амплитуду вероятности пребывания узла в состоянии однократно занятого узла, двойки или дырки:
(18)
$\begin{gathered} {{X}_{i}}( + ,0) \to \varphi _{i}^{ * }{{\Psi }_{i}},{{X}_{i}}(2, - ) \to \Phi _{i}^{ * }{{\psi }_{i}}, \\ {{X}_{i}}(2,0) \to \Phi _{i}^{ * }{{\Psi }_{i}} \\ \end{gathered} $(19)
$\begin{gathered} \phi = \prod\limits_i {[\varphi _{i}^{ * }{{X}_{i}}( + ,0)} + \psi _{i}^{ * }{{X}_{i}}( - ,0) + \\ + \,\,\Phi _{i}^{ * }{{X}_{i}}(2,0) + \Psi _{i}^{ * }]\left| 0 \right\rangle . \\ \end{gathered} $Она смешивает возбуждения бозевского и фермиевского типа, а потому не удовлетворяет принципу Паули. Тем не менее квазиклассическое приближение позволяет грубо описать переход металл–изолятор, что и было проделано впоследствии рядом авторов (см. обзор [49]). Так, в работе Карона и Пратта [50] было даже рассмотрено среднее поле для фермионов, так что фактически на с-числа заменялись не Х-операторы, а обычные фермиевские операторы.
Предвосхищая работы Хаббарда, уравнения квазиклассического приближения дают изменение ширины энергетической полосы, а также относительного расположения различных полос в зависимости от числа двоек и магнитного момента.
Более строгим и последовательным оказался вариационный метод Гутцвиллера, см. [51]. Соответствующая волновая функция может быть записана как
(20)
$\Psi = \prod\limits_i {[1 - (1 - {{{\hat {n}}}_{{i \uparrow }}}{{{\hat {n}}}_{{i \downarrow }}})]\left| {{{\psi }_{0}}} \right\rangle } ,$Другой вариант вариационного подхода, учитывающий дальнодействие, дает экситонный подход, в котором рассматривается конденсация электрон-дырочных или электрон-электронных пар [52, 53]. Проще всего он может быть проиллюстрирован на описании сверхпроводимости. Стандартная волновая функция БКШ записывается как
(21)
$\left| {{{\Psi }_{0}}} \right\rangle = \prod\limits_{\mathbf{k}} {({{u}_{{\mathbf{k}}}} + {{v}_{{\mathbf{k}}}}c_{{{\mathbf{k}} \uparrow }}^{\dag }c_{{ - {\mathbf{k}} \downarrow }}^{\dag })} \left| 0 \right\rangle $(22)
$\left| {{{\Psi }_{0}}} \right\rangle = {{\left[ {\sum\limits_{\mathbf{k}} {{{\phi }_{{\mathbf{k}}}}c_{{{\mathbf{k}} \uparrow }}^{\dag }c_{{ - {\mathbf{k}} \downarrow }}^{\dag }} } \right]}^{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}\left| 0 \right\rangle ,$(23)
$\left| {{{\Psi }_{0}}} \right\rangle = {{\left[ {\sum\limits_{\mathbf{k}} {{{\phi }_{{\mathbf{k}}}}c_{{{\mathbf{k}} + {\mathbf{Q}} \downarrow }}^{\dag }{{c}_{{{\mathbf{k}} \uparrow }}}} } \right]}^{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}\left| F \right\rangle ,$Аналогичное описание дальнего порядка в антиферромагнетике может быть дано в рамках модели Гейзенберга с помощью функции $\left| {{{\Psi }_{0}}} \right\rangle = {{(S_{{\mathbf{Q}}}^{ + })}^{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}\left| F \right\rangle $ [56].
Вариационное описание состояния резонирующих валентных связей (RVB – resonating valence bond), сочетающее упомянутые выше подходы, было развито Андерсоном [1]. В случае половинного заполнения зоны здесь может быть использована пробная функция
где ${{P}_{G}} = \prod\nolimits_i {(1 - {{{\hat {n}}}_{{i \uparrow }}}{{{\hat {n}}}_{{i \downarrow }}})} $ – проекционный оператор Гутцвиллера в пределе сильных корреляций, полностью устраняющий дважды занятые состояния на узле. Поскольку $\phi ({\mathbf{k}}) = {{{{v}_{{\mathbf{k}}}}} \mathord{\left/ {\vphantom {{{{v}_{{\mathbf{k}}}}} {{{u}_{{\mathbf{k}}}}}}} \right. \kern-0em} {{{u}_{{\mathbf{k}}}}}} \simeq {\text{sign}}({{t}_{{\mathbf{k}}}} - {{E}_{F}})$ (${{t}_{{\mathbf{k}}}}$ – зонная энергия), функция (24) может быть записана и в виде(25)
$\left| {{{\Psi }_{0}}} \right\rangle = \prod\limits_{k < {{k}_{F}}} {c_{{{\mathbf{k}} \uparrow }}^{\dag }c_{{ - {\mathbf{k}} \downarrow }}^{\dag }} \left| 0 \right\rangle .$Именно под действием проектора функция БКШ, описывающая сверхпроводящее состояние, превращается в состояние RVB – появляется поверхность Ферми, поскольку коэффициенты преобразования Боголюбова принимают значения 0 и 1. Таким образом, функция основного состояния должна строиться именно на МЭ-возбуждениях. Однако, как будет проиллюстрировано в разд. 3.1, на практике часто работают с особой функцией среднего поля, а правило сумм на узле может быть учтено через топологические вихревые возбуждения. Частный выбор функции $\phi ({\mathbf{k}})$ (например, в приближении ближайших соседей) позволяет учесть особое короткодействующее спаривание (образование синглетов).
Неелевское состояние обладает дальним порядком и бесконечным вырождением основного состояния, что приводит к появлению голдстоуновских мод – магнонов. С другой стороны, состояние RVB является невырожденным синглетным состоянием с ближним антиферромагнитным порядком. Возникновение подрешеток может быть описано как декогеренция (нарушение квантовой когерентности в синглетном состоянии) [57].
Согласно подходу [32], пробная функция для половинного заполнения в случае антиферромагнетика может быть записана в виде
(26)
$\left| {{{\Psi }_{0}}} \right\rangle = {{P}_{G}}{{\left[ {\sum\limits_{\mathbf{k}} {({{A}_{{\mathbf{k}}}}a_{{{\mathbf{k}} \uparrow }}^{\dag }a_{{ - {\mathbf{k}} \downarrow }}^{\dag } + {{B}_{{\mathbf{k}}}}b_{{{\mathbf{k}} \uparrow }}^{\dag }b_{{ - {\mathbf{k}} \downarrow }}^{\dag }} )} \right]}^{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}\left| 0 \right\rangle ,$Волновую функцию (24) также можно записать через многоэлектронные Х-операторы [1]:
(27)
$\left| {{{\Psi }_{0}}} \right\rangle = \prod\limits_{\mathbf{k}} {} ({{u}_{{\mathbf{k}}}} + {{v}_{{\mathbf{k}}}}X_{{\mathbf{k}}}^{{ + 0}}X_{{ - {\mathbf{k}}}}^{{ - 0}}\left| 0 \right\rangle ).$Идеи экситонного конденсата были также применены к системам с промежуточной валентностью типа SmB6 и SmS в рамках двухзонных моделей Фаликова–Кимбалла с гибридизацией или решетки Андерсона [58]. В зависимости от значений параметров в этих задачах могут возникать экситоны большого и малого радиуса.
В последнее время такие подходы к проблеме промежуточной валентности развивались и на современном языке экзотических частиц – спинонов и голонов [59, 60]. Согласно [59], нейтральный фермионный композитный экситон формируется как связанное состояние электрона проводимости и голона.
2.3. Представления вспомогательных частиц
Непосредственная работа с многоэлектронными Х-операторами затруднительна (в частности, отсутствуют обычные разложения теории возмущений и диаграммная техника, хотя могут быть использованы формальные разложения по обратному координационному числу ${1 \mathord{\left/ {\vphantom {1 z}} \right. \kern-0em} z}$ [44]). Поэтому часто используются их представления через вспомогательные (“auxiliary”, “slave” – слейв) бозевские и фермиевские операторы.
Исходя из конкретной физической задачи и ситуации, используются различные версии таких представлений. В связи с теорией двумерных высокотемпературных сверхпроводников, Андерсон [1] предложил представление
(28)
$c_{{i\sigma }}^{\dag } = f_{{i\sigma }}^{\dag }{{e}_{i}} + \sigma d_{i}^{\dag }{{f}_{{i - \sigma }}}.$Выражение (28) соответствует разбиению одноэлектронного оператора на два многоэлектронных Х-оператора (17), т.е. формированию хаббардовских подзон. Здесь $f_{{i\sigma }}^{\dag }$ – операторы рождения для нейтральных фермионов (спинонов), $e_{i}^{\dag },$ $d_{i}^{\dag }$ – операторы рождения для заряженных бесспиновых бозонов. Физический смысл таких возбуждений можно объяснить следующим образом. Рассмотрим решетку с одним электроном на узле с сильным хаббардовским отталкиванием, так что каждый узел нейтрален. В основном состоянии RVB каждый узел принимает участие в одной связи. Когда связь нарушается, появляются два неспаренных узла, которые обладают спинами, равными 1/2. Соответствующие возбуждения (спиноны) не заряжены. Вместе с тем, пустой узел (дырка) в системе несет заряд, но не спин. Такая картина описывает состояние спиновой жидкости, где имеет место разделение спиновых и зарядовых степеней свободы электрона и существенную роль играют калибровочные поля.
В работе [61] было предложено расширение физического пространства через введение четырех бозонов ${{p}_{{i\sigma }}},$ ${{e}_{i}},$ ${{d}_{i}},$ которые осуществляют проектирование на однократно занятые состояния, дырки и двойки соответственно. В результате гамильтониан Хаббарда принимает вид
(29)
$\mathcal{H} = \sum\limits_{ij\sigma } {{{t}_{{ij}}}f_{{i\sigma }}^{\dag }} {{f}_{{j\sigma }}}z_{{i\sigma }}^{\dag }{{z}_{{j\sigma }}} + U\sum\limits_i {d_{i}^{\dag }{{d}_{i}}} ,$(30)
$\begin{gathered} z_{{i\sigma }}^{\dag } = {{(1 - e_{i}^{\dag }{{e}_{i}} - p_{{i - \sigma }}^{\dag }{{p}_{{i - \sigma }}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,(p_{{i\sigma }}^{\dag }{{e}_{i}} + d_{i}^{\dag }{{p}_{{i - \sigma }}}){{(1 - d_{i}^{\dag }{{d}_{i}} - p_{{i\sigma }}^{\dag }{{p}_{{i\sigma }}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $Здесь имеется определенный произвол; дополнительные операторные множители имеют собственные значения 1 в физическом подпространстве, но при расцеплении позволяют перейти к пределу свободных электронов, что важно для построения теории среднего поля. Это представление позволило качественно воспроизвести ряд прежних результатов (например, как и квазиклассическое приближение (18), получить описание перехода металл–изолятор [62]). Теория среднего поля для представления бозонов Котляра–Рукенштейна (29) дает результаты, идентичные теории Гутцвиллера в пределе бесконечного координационного числа. В рамках этого представления может быть рассмотрено и магнитное упорядочение [63].
Существует также вращательно-инвариантная версия [64]:
(31)
$c_{{i\sigma }}^{\dag } = \sum\limits_{\sigma {\text{'}}} {f_{{i\sigma }}^{\dag }z_{{i\sigma \sigma {\text{'}}}}^{\dag }} ,\,\,\,\,{{\hat {z}}_{i}} = e_{i}^{\dag }{{\hat {L}}_{i}}{{M}_{i}}{{\hat {R}}_{i}}{{\hat {p}}_{i}} + \hat {\tilde {p}}_{i}^{\dag }{{\hat {L}}_{i}}{{M}_{i}}{{\hat {R}}_{{\hat {i}}}}{{d}_{i}},$Отметим также представление вспомогательных роторов (slave rotor) [66]
(32)
$c_{{i\sigma }}^{\dag } = f_{{i\sigma }}^{\dag }{{b}_{i}} = f_{{i\sigma }}^{\dag }exp(i{{\theta }_{i}}),$В работе [70] было предложено представление, содержащее два сорта фермиевских операторов – голонов ei и дублонов di, которые соответствуют дыркам и двойкам:
(33)
$\begin{gathered} {{X}_{i}}( + ,0) = {{e}_{i}}(1 - d_{i}^{\dag }{{d}_{i}})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} + s_{i}^{z}), \\ {{X}_{i}}( - ,0) = {{e}_{i}}(1 - d_{i}^{\dag }{{d}_{i}})s_{i}^{ - }, \\ X(2, - ) = d_{i}^{\dag }(1 - d_{i}^{\dag }{{d}_{i}})s_{i}^{ + }, \\ X(2, + ) = d_{i}^{\dag }(1 - d_{i}^{\dag }{{d}_{i}})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} + s_{i}^{z}). \\ \end{gathered} $При этом операторы физических спинов связаны с псевдоспиновыми операторами $s_{i}^{\alpha }$ соотношением ${{{\mathbf{S}}}_{i}} = {{{\mathbf{s}}}_{i}}(1 - d_{i}^{\dag }{{d}_{i}} - e_{i}^{\dag }{{e}_{i}}).$ Ранее рассматривались различные частные случаи этого представления, соответствующие пределу больших U ($t{\text{--}}J$-модели, см. обзор [71]).
В дальнейшем были предложены также суперсимметричные представления [72].
2.4. t–J-модель и s–d-обменная модель с сильными корреляциями
При рассмотрении сильнокоррелированных соединений, например, медь-кислородных высокотемпературных сверхпроводников, широко используется t–J-модель (модель Хаббарда с $U \to \infty $ и учетом гейзенберговского обмена). Ее гамильтониан в МЭ представлении имеет вид
(34)
$\mathcal{H} = - \sum\limits_{ij\sigma } {{{t}_{{ij}}}} {{X}_{i}}(0,\sigma ){{X}_{j}}(\sigma ,0) + \sum\limits_{ij} {{{J}_{{ij}}}} {{{\mathbf{S}}}_{i}}{{{\mathbf{S}}}_{j}}.$При выводе t–J-модели из модели Хаббарда с большим U устранение двоек каноническим преобразованием [73] приводит к андерсоновскому антиферромагнитному сверхобмену $J = {{ - 2{{t}^{2}}} \mathord{\left/ {\vphantom {{ - 2{{t}^{2}}} U}} \right. \kern-0em} U};$ впрочем, иногда удобно считать J независимой переменной. В простой модели (34) возникает богатая фазовая диаграмма, включающая спиральные магнитные структуры и неоднородные состояния (см. обзор [71]).
По утверждению Андерсона [74], t–J-гамильтониан – не просто удобная альтернатива модели Хаббарда; он отражает физический факт, что низкоэнергетические состояния находятся в подпространстве, которое является переполненным и описывается одной полосой электронных состояний, поскольку антисвязанные состояния двоек из верхней части зоны выброшены. Не существует такого сходящегося пертурбативного метода, который бы связал низкоэнергетические состояния с первоначальной зоной модели Хаббарда, поскольку они существуют в гильбертовых пространствах разных размерностей.
Первопринципной моделью для описания купратов является трехзонная p–d-модель
(35)
$\begin{gathered} \mathcal{H} = \sum\limits_{{\mathbf{k}}a\sigma } {\left[ {\varepsilon p_{{{\mathbf{k}}a\sigma }}^{\dag }{{p}_{{{\mathbf{k}}a\sigma }}} + \Delta d_{{{\mathbf{k}}\sigma }}^{\dag }{{d}_{{{\mathbf{k}}\sigma }}} + {{V}_{{\mathbf{k}}}}(p_{{{\mathbf{k}}\sigma }}^{\dag }{{d}_{{{\mathbf{k}}\sigma }}} + h.c.)} \right]} + \\ + \,\,U\sum\limits_i {d_{{i \uparrow }}^{\dag }{{d}_{{i \uparrow }}}d_{{i \downarrow }}^{\dag }{{d}_{{i \downarrow }}}} , \\ \end{gathered} $При $\left| {{{V}_{{pd}}}} \right| \ll \varepsilon - \Delta $ (большая щель для переноса заряда) гамильтониан (35) снова сводится каноническим преобразованием к $t - J$-модели с ${{t}_{{{\text{ef}}}}} = {{V_{{pd}}^{2}} \mathord{\left/ {\vphantom {{V_{{pd}}^{2}} {(\varepsilon }}} \right. \kern-0em} {(\varepsilon }} - \Delta ).$ Интересно, что $t - J$-модель, полученная из однозонной модели Хаббарда, также формально сводится к аналогичной структуре в представлении (30) со вспомогательными, а не физическими частицами ${{p}_{i}}.$ Таким образом, модель Хаббарда и модель (35) могут рассматриваться параллельным образом [75].
Модель (34) описывает взаимодействие носителей тока с локальными моментами. Для того чтобы продемонстрировать явно разделение этих степеней свободы, укажем на ее эквивалентность $s - d$-обменной модели с параметром обмена $\left| I \right| \to \infty .$ Действительно, после перехода к МЭ-представлению гамильтониан последней запишется в виде [76, 77]
(36)
$\mathcal{H} = \sum\limits_{ij\sigma } {{{t}_{{ij}}}g_{{i\sigma \alpha }}^{\dag }{{g}_{{j\sigma \alpha }}}} + {{\mathcal{H}}_{d}},\,\,\,\,\alpha = {\text{sign}}I,$(37)
$\begin{gathered} g_{{i\sigma \alpha }}^{\dag } = \sum\limits_M {\{ [S + \sigma \alpha M} + {{{{(1 + \alpha )} \mathord{\left/ {\vphantom {{(1 + \alpha )} 2}} \right. \kern-0em} 2}]} \mathord{\left/ {\vphantom {{{{(1 + \alpha )} \mathord{\left/ {\vphantom {{(1 + \alpha )} 2}} \right. \kern-0em} 2}]} {(2S}}} \right. \kern-0em} {(2S}} + \,1){{\} }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,{{X}_{i}}\left( {M + \frac{\sigma }{2},\alpha ;M} \right). \\ \end{gathered} $Модель (36) соответствует случаю, когда носители тока не принадлежат той же энергетической зоне, где формируются магнитные моменты. Такая ситуация имеет место в некоторых магнитных полупроводниках и изоляторах. Однако легко видеть, что при $S = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ α = – гамильтониан (36) совпадает с (34), причем ${{t}_{{ij}}}$ заменяется в (36) на $2{{t}_{{ij}}}$ (множитель 2 возникает из-за эквивалентности перескоков электронов с обоими противоположными спинами в модели Хаббарда).
Гамильтониан (36) может быть выражен через фермиевские операторы и операторы локализованных спинов. Используя (13), (11), можно выделить операторы электронов проводимости из X-операторов:
(38)
$g_{{i\sigma \alpha }}^{\dag } = \sum\limits_{\sigma {\text{'}}} {c_{{i\sigma {\text{'}}}}^{\dag }(1 - {{n}_{{i, - \sigma {\text{'}}}}})} \left[ {{{P}_{\alpha }}{{\delta }_{{\sigma \sigma {\text{'}}}}} + \frac{\alpha }{{2S + 1}}({{{\mathbf{S}}}_{i}}{{{\mathbf{\sigma }}}_{{\sigma {\text{'}}\sigma }}})} \right],$Далее, использование свойств матриц Паули дает
(40)
$\begin{gathered} \mathcal{H} = \sum\limits_{ij\sigma \sigma {\text{'}}} {{{t}_{{ij}}}} \left\{ {\left[ {P_{\alpha }^{2} + \frac{{{{{\mathbf{S}}}_{i}}{{{\mathbf{S}}}_{j}}}}{{{{{(2S + 1)}}^{2}}}}} \right]} \right.{{\delta }_{{\sigma \sigma {\text{'}}}}} + \\ + \,\,\frac{\alpha }{{{{{(2S + 1)}}^{2}}}}{{P}_{\alpha }}({{{\mathbf{S}}}_{i}} + {{{\mathbf{S}}}_{j}}){{\sigma }_{{\sigma \sigma {\text{'}}}}} + \\ + \,\,\left. {\frac{i}{{{{{(2S + 1)}}^{2}}}}{{\sigma }_{{\sigma \sigma {\text{'}}}}}[{{{\mathbf{S}}}_{i}} \times {{{\mathbf{S}}}_{j}}]} \right\}c_{{i\sigma }}^{\dag }(1 - {{{\hat {n}}}_{{i, - \sigma }}}) \times \\ \times \,\,(1 - {{{\hat {n}}}_{{j, - \sigma {\text{'}}}}}){{c}_{{j\sigma {\text{'}}}}} + {{\mathcal{H}}_{d}}. \\ \end{gathered} $Для спиновых операторов имеем
(41)
${{{\mathbf{S}}}_{i}} = \frac{1}{2}\sum\limits_{\sigma \sigma {\text{'}}} {a_{{i\sigma }}^{\dag }} {{\sigma }_{{\sigma \sigma {\text{'}}}}}{{a}_{{i\sigma {\text{'}}}}},$Представление гамильтониана (40) (разумеется, оно справедливо и в $t - J$-модели) было получено в [43, 44]. В дальнейшем оно было использовано для построения особой теории среднего поля в применении к фазовой диаграмме ВТСП-купратов как “новая формулировка $t - J$-модели” [78]. В теории среднего поля для $t - J$-модели этих авторов электронный спектральный вес происходит из двух зон: низкоэнергетической спинонной полосы и высокоэнергетической электронной зоны. Спектральный вес от спинонной зоны представляет собой острый когерентный пик. Широкий спектральный вес от электронной зоны соответствует некогерентному фону.
При рассмотрении спектра купратов возникает нодально-антинодальная дихотомия [32]: природа спектра различна на разных участках поверхности Ферми. Спектр является бесщелевым вблизи нодальных точек $({{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2},{{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2})$ (где возбуждения описываютсякак дираковские фермионы, см. разд. 3.3) и щелевым вблизи антинодальной точки $(0,\pi )$. Вблизи нодальной точки возникает сильное гибридизационное перемешивание между спинонами и электронами (допонами в терминологии [78]), а вблизи антинодальной точки смешивание отсутствует. По существу описанная картина близка к гибридизационной двухзонной модели решеток Кондо, где локализованные и коллективизированные состояния исходно разделены, но смешиваются в приближении среднего поля для вспомогательных f-псевдофермионов, так что последние принимают участие в формировании поверхности Ферми [79] (см. также раздел 3.5).
Таким образом, использование концепции двухзонной модели помогает получить физическую картину экзотических состояний сильно коррелированных систем.
Члены, содержащие векторные произведения, описывают анизотропное рассеяние электронов и могут быть важны при рассмотрении кинетических явлений в узких зонах, например аномального эффекта Холла. Гамильтониан (40) может быть полезен при исследовании состояний с аномальными “киральными” параметрами порядка, которые исследовались в рамках двумерной модели Гейзенберга и $t - J$-модели (см., напр., [80]).
3. ФЕРМИ-ЖИДКОСТЬ И НЕФЕРМИ-ЖИДКОСТНЫЕ ФАЗЫ
Концепция ферми-жидкости предполагает взаимно однозначное соответствие низкоэнергетических состояний между рассматриваемой взаимодействующей системой и системой невзаимодействующих электронов. Это подразумевает, в частности, существование только квазичастичных возбуждений с зарядом $ \pm e$ и спином 1/2. Отсюда следует существование поверхности Ферми, определяемой полюсами одночастичной функции Грина при энергии $E = 0.$ Эта поверхность Ферми подчиняется теореме Латтинджера, т.е. окружает объем импульсного пространства, определяемый полной плотностью электронов.
Нарушение ферми-жидкостного поведения при низких температурах может иметь различные источники. В чистых системах эффекты взаимодействия могут давать стабильные неферми-жидкостные фазы. Один из сценариев состоит в том, что низкоэнергетические возбуждения приобретают квантовые числа, отличные от обычных электронов или дырок, что приводит к необычным низкотемпературным свойства. В размерности $d = 1$ такое поведение носит общий характер и хорошо понято (латтинджеровские жидкости с разделением спина и заряда). Аналогичное разделение ожидается в спиновых жидкостях в более высоких размерностях.
В случае полузаполненной полосы при уменьшении кулоновского отталкивания моттовский изолятор переходит в металл. Вблизи этого перехода металлическое состояние будет сильно коррелированным, включая хаббардовские подзоны и локальные моменты, которые подвержены фрустрации. Совместное действие этих факторов может приводить к значительно уменьшенной шкале когерентности, а следовательно к тяжелофермионному поведению. Для рассмотрения перехода металл–диэлектрик удобно использовать роторное представление (32) электронного оператора уничтожения как произведение заряженного бозона ${{b}_{i}}$ и нейтрального фермиона со спином (спинона) ${{f}_{{i\sigma }}}$ [81, 82]. При нечетном заполнении зоны система бесспиновых бозонов переходит с увеличением хаббардовского параметра U в сверхтекучий моттовский изолятор. В приближении среднего поля спиноны являются свободными (невзаимодействующими), несмотря на сильные корреляции в электронной системе. Если бозон ${{b}_{i}}$ конденсируется, т.е. $\left\langle b \right\rangle \ne 0,$ мы получаем фазу ферми-жидкости физических электронов: при замене b на его $c$-числовое среднее $\left\langle b \right\rangle $ фермионы ${{f}_{\sigma }}$ приобретают те же квантовые числа, что и исходные электроны, так что их ферми-поверхность описывает обычный металл. Если бозон является щелевым и, следовательно, несконденсирован, образуется спин-жидкостной изолятор Мотта, в котором выживает поверхность Ферми нейтральных фермионных возбуждений (спинонов). Изолятор Мотта для бозонов также является диэлектрическим состоянием для электронов с щелью для всех заряженных возбуждений, и происходит непрерывный переход к изолятору с “призрачной” (ghost) поверхностью Ферми спинонов.
Аналогичный сценарий перехода металл–изолятор может быть рассмотрен в представлении бозонов Котляра–Рукенштейна (30) [62, 83]. При этом, когда $\left\langle b \right\rangle \ne 0$ или мало (квазичастичный вычет мал), недостающий спектральный вес определяется флуктуациями – некогерентным вкладом хаббардовских подзон [83].
Помимо уменьшения взаимодействия, еще один способ превратить фрустрированный изолятор Мотта в металл – допирование. При малых уровнях допирования имеются локальные моменты, и, следовательно, важными могут быть эффекты фрустрации. Поэтому был высказан ряд идей о возникновении необычных металлических фаз с неферми-жидкостным поведением; в частности, такой металл может быть фракционализованным состоянием со спинонными и голонными возбуждениями (раздел 3.6).
Можно предположить, что вдали от половинного заполнения зоны, особенно при малых плотностях электронов, возникает ферми-жидкостное состояние, поскольку акты рассеяния частиц становятся редкими, так что эффекты даже сильного кулоновского взаимодействия U слабы. Однако ситуация не столь проста. Действительно, согласно спектральному представлению функций Грина, имеем для числа двоек, определяющего локальный момент [47]:
(42)
$\begin{gathered} {{N}_{2}} = \left\langle {c_{{i \uparrow }}^{\dag }{{c}_{{i \uparrow }}}c_{{i \downarrow }}^{\dag }{{c}_{{i \downarrow }}}} \right\rangle = \\ = - \frac{1}{{\pi U}}\int {{\text{Im}}} \sum\limits_{\mathbf{k}} {\frac{{{{\Sigma }_{{\mathbf{k}}}}(E)}}{{E - {{t}_{{\mathbf{k}}}}}}} f(E)dE. \\ \end{gathered} $Поскольку собственная энергия ${{\Sigma }_{{\mathbf{k}}}}(E)$ конечна в пределе $U \to \infty $ (в частности, в Т-матричном приближении Канамори), ${{N}_{2}}$ ведет себя как ${1 \mathord{\left/ {\vphantom {1 U}} \right. \kern-0em} U}.$ Тогда теорема Гелмана–Фейнмана ${{N}_{2}} = {{\partial{ \mathcal{E}}} \mathord{\left/ {\vphantom {{\partial{ \mathcal{E}}} {\partial U}}} \right. \kern-0em} {\partial U}}$ дает расходимость энергии основного состояния $\mathcal{E}\,:$
Эта расходимость указывает на неадекватность одноэлектронной картины ферми-жидкости при больших U и формирование хаббардовских подзон. С другой стороны, расчет в многоэлектронном представление Х-операторов [47] дает правильную асимптотику ${{N}_{2}} \sim {1 \mathord{\left/ {\vphantom {1 {{{U}^{2}}}}} \right. \kern-0em} {{{U}^{2}}}}.$ Верный результат получается и в представлении бозонов Котляра–Рукенштейна (29).
Авторы [84] предложили феноменологическое представление для одноэлектронной функции Грина, которая удовлетворяет теореме Латтинджера по-другому: электронная плотность связана не с объемом поверхности Ферми, а с числом особенностей логарифма функции Грина при нулевой энергии. Таким образом, учитываются как обычные полюса, так и нули функции Грина (т.е. квазичастичные полюса электронной собственной энергии); последняя поверхность называется латтинджеровской.
Из феноменологической формы функции Грина получаются дисперсия квазичастиц и спектральный вес, характеризующие когерентную часть одноэлектронной функции Грина. При этом существует критическая концентрация дырок, выше которой спин-жидкостная аномальная собственная энергия исчезает. Как следствие, существует квантовая критическая точка, которая разделяет две топологически различные фазы. Ниже критической плотности дырок $G({\mathbf{k}},0)$ характеризуется сосуществующими поверхностью Латтинджера и дырочными карманами ферми-поверхности, а выше ее имеется только замкнутая поверхность Ферми, как в теории Ландау.
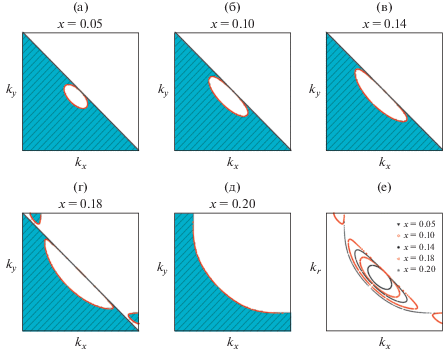
Как показано на рис. 1, в узком диапазоне $x \lesssim {{x}_{c}}$ возникает новый набор электронных ферми-карманов вблизи седловых точек, вне латтинджеровской поверхность нулей. Эти карманы сливаются с дырочными карманами внутри поверхности Латтинджера при $x = {{x}_{c}},$ чтобы образовать единую поверхности Ферми. Таким образом, имеется два близко расположенных топологических изменения: переход типа Лифшица, при котором форма ферми-поверхность полюсов претерпевает топологические изменения, и квантовая критическая точка $x = {{x}_{c}},$ связанная с открытием одночастичной щели при возникновении RVB-спиновой жидкости для $x < {{x}_{c}},$ что ведет к образованию поверхности Латтинджера.
Рис. 1.
Эволюция поверхности Ферми с концентрацией дырок $x$ в модели [84]. В затененной области $G({\mathbf{k}},0) > 0.$ Толстые линии на (а)–(г) являются линиями нулей Латтинджера; вблизи критического допирования ${{x}_{c}} = 0.18$ (г) имеется дополнительный электронный карман.
Форма функции Грина [84] близка к результату [85], полученному на основе слейв-бозонной средней теории поля в $t - J$-модели. В этом подходе спиноны и голоны взаимодействуют друг с другом через калибровочное поле, а для описания калибровочных флуктуаций вводится феноменологическое притяжение между ними, который является константой в некотором диапазоне расстояний. Такое притяжение и приводит к связыванию спинона и голона, а следовательно к квазичастичному полюсу собственной энергии.
3.1. Теория среднего поля и калибровочные поля
Обсудим картину спиновой жидкости в рамках представления (28). Для наполовину заполненной зоны присутствуют только спинонные возбуждения с кинетической энергией порядка $\left| J \right|.$ При допировании системы дырками возникают носители заряда, которые описываются операторами голонов. Таким образом, возникает состояние спиновой жидкости с подавленным дальним магнитным порядком. При этом в простейшем бесщелевом варианте теории RVB в чисто спиновых (недопированных) системах появляются малый энергетический масштаб J и большой линейный член в удельной теплоемкости с $\gamma \sim {1 \mathord{\left/ {\vphantom {1 {\left| J \right|}}} \right. \kern-0em} {\left| J \right|}},$ связанный с существованием ферми-поверхности спинонов [1].
При дальнейшем развитии теории было предложен другой вариант теории RVB, в котором на поверхности Ферми возникает щель, так что образуется структура типа d-волны с максимумом щели вблизи $(0,\pi );$ это согласуется с фотоэмиссионными экспериментами (см. [2]). Были развиты и более сложные версии теории RVB, которые используют топологическое рассмотрение и аналогии с дробным квантовым эффектом Холла (см., напр., [86]). Эти идеи привели к необычным и красивым результатам. В частности, спиноны могут подчиняться дробной статистике, т.е. волновая функция системы приобретает комплексный коэффициент при перестановке двух квазичастиц.
Рассмотрим приближение среднего поля в $t - J$-модели в представлении вспомогательных бозонов $c_{{i\sigma }}^{\dag } \to {{X}_{i}}(\sigma 0) = f_{{i\sigma }}^{\dag }{{b}_{i}},$ соответствующее теории U(1). Здесь можно ввести спаривания
(44)
${{\chi }_{{ij}}} = \sum\limits_\sigma {\left\langle {f_{{i\sigma }}^{\dag }{{f}_{{j\sigma }}}} \right\rangle } ,\,\,\,\,{{\Delta }_{{ij}}} = \left\langle {{{f}_{{i \uparrow }}}{{f}_{{j \downarrow }}} - {{f}_{{i \downarrow }}}{{f}_{{i \uparrow }}}} \right\rangle .$В однородной RVB-фазе (uRVB) ${{\chi }_{{ij}}} = \chi $ для всех связей и вещественно, а щель ${{\Delta }_{{ij}}} = 0,$ так что спектр f-фермионов имеет вид ${{E}_{{\mathbf{k}}}} = - 2J\chi (cos{{k}_{x}} + cos{{k}_{y}}).$ Однако имеются фазы с более низкой энергией, включая d-волновой сверхпроводник. Фазовая диаграмма с учетом последнего состояния показана на рис. 2.
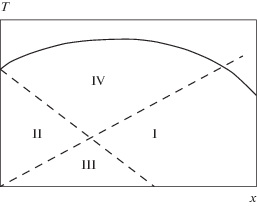
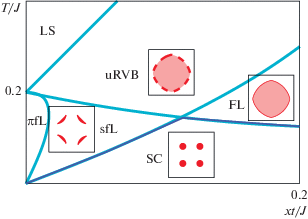
Рис. 2.
Схематическая фазовая диаграмма теории среднего поля U(1). Сплошная линия обозначает начало однородного состояния RVB $(\chi \ne 0),$ штриховая линия – возникновение фермионного спаривания $(\Delta \ne 0),$ а штрих из начала координат – бозе-конденсацию в подходе среднего поля $(b \ne 0).$ Возникает четыре области: (I) ферми-жидкость с $\chi \ne 0,$ $b \ne 0;$ (II) состояние спиновой щели с $\chi \ne 0,$ $\Delta \ne 0;$ (III) d-волновой сверхпроводник с $\chi \ne 0,$ $\Delta \ne 0,$ $b \ne 0$ и (IV) странный металл с $\chi \ne 0$ [87].
Следует еще раз отметить, что описание ферми-жидкостной фазы в $t - J$-модели является в некотором смысле внутренне противоречивым, поскольку часть состояний уже исключена благодаря проектированию на однократно занятые состояния. В этом смысле более последователен подход, учитывающий формирование двоек и включающий оба вспомогательных бозона e и d в рамках представлений (28) либо (29). Последнее представление позволяет также учесть формирование верхней и нижней хаббардовской подзоны как некогерентного вклада – связанного состояния спинона и голона [83].
Более сложные спин-жидкостные фазы получаются при учете SU(2)-инвариантности $t - J$-гамильтониана, что позволяет устранить ряд трудностей теории U(1) [32]. SU(2) слейв-бозонная теория, описывающая допированные спиновые жидкости, включает два SU(2)-дублета ${{\psi }_{i}}$ и ${{h}_{i}}$ с двумя бозонными полями ${{b}_{{1i}}}$ и ${{b}_{{2i}}}$ со спином 0, которые формируют SU(2)-синглеты. Тогда имеем представление электронного оператора
(45)
$\begin{gathered} {{c}_{{ \uparrow i}}} \to \frac{1}{{\sqrt 2 }}h_{i}^{\dag }{{\psi }_{i}} = \frac{1}{{\sqrt 2 }}\left( {b_{{1i}}^{\dag }{{f}_{{ \uparrow i}}} + b_{{2i}}^{\dag }f_{{ \downarrow i}}^{\dag }} \right); \\ {{c}_{{ \downarrow i}}} \to \frac{1}{{\sqrt 2 }}h_{i}^{\dag }\mathop {\bar {\psi }}\nolimits_i = \frac{1}{{\sqrt 2 }}\left( {b_{{1i}}^{\dag }{{f}_{{ \downarrow i}}} - b_{{2i}}^{\dag }f_{{ \uparrow i}}^{\dag }} \right). \\ \end{gathered} $В состоянии sfL (staggered flux liquid) получаем
Эта фаза имеет дираковский линейный спектр в точках $({{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2},{{ \pm \pi } \mathord{\left/ {\vphantom {{ \pm \pi } 2}} \right. \kern-0em} 2}).$ В фазе $\pi $fL
Помимо этих двух бесщелевых фаз, может возникать также щелевое Z2-состояние.
Фазовая диаграмма в SU(2) слэйв-бозонной теории допированного моттовского изолятора показана на рис. 3. Эта теория также не свободна от трудностей. В частности, площадь поверхности Ферми приближается к $1 - x$ очень медленно с ростом допирования x и понижением температуры.
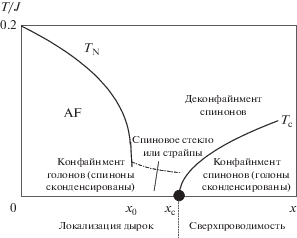
Рис. 3.
SU(2)-фазовая диаграмма среднего поля для ${t \mathord{\left/ {\vphantom {t J}} \right. \kern-0em} J} = 1$ [87]. Показаны поверхность Ферми, дуги Ферми или точки Ферми в различных фазах.
Интуитивная картина спиновой жидкости с симметрией SU(2) как раз дается андерсоновским состоянием RVB, которое включает синглетное спаривание спинов и формирование квантовой суперпозиции многих различных пар, т.е. различные димерные покрытия решетки, причем симметрия гамильтониана сохраняется. Эта картина включает дробные возбуждения, поскольку разрушение димера приводит к двум возбуждениям с независимой динамикой: получающиеся мономеры представляют собой объекты, несущие заряд 0 и спин 1/2, то есть спиноны. В спиновой жидкости Z2 они связаны с возникающими Z2 возбуждениями, которые представляют собой Z2-вихри (или потоки), называемые визонами (см. также раздел 5.1).
Волновая функция $\left| {{{\Psi }_{{{\text{MF}}({{\chi }_{{ij}}})}}}} \right\rangle $ гамильтониана среднего поля
(46)
$\begin{gathered} {{\mathcal{H}}_{\begin{gathered} {\text{MF}} \hfill \\ \end{gathered} }} = J\sum\limits_{ij\sigma } {({{\chi }_{{ij}}}f_{{i\sigma }}^{\dag }{{f}_{{j\sigma }}} + h.c.)} + \\ + \,\,\sum\limits_{i\sigma } {{{a}_{0}}} (f_{{i\sigma }}^{\dag }{{f}_{{i\sigma }}} - 1) \\ \end{gathered} $(47)
${{\Psi }_{{{\text{spin}}}}}({{\chi }_{{ij}}},\{ {{\sigma }_{i}}\} ) = \left\langle {{{0}_{f}}\left| {\prod\limits_i {{{f}_{{i{{\sigma }_{i}}}}}} } \right|{{\Psi }_{{{\text{MF}}}}}({{\chi }_{{ij}}})} \right\rangle ,$(48)
${{\Psi }_{{{\text{spin}}}}}({{a}_{{ij}}}) = \left\langle {{{0}_{f}}\left| {\prod\limits_i {{{f}_{{i{{\sigma }_{i}}}}}} } \right|{{\Psi }_{{{\text{MF}}}}}({{{\bar {\chi }}}_{{ij}}}exp(i{{a}_{{ij}}}))} \right\rangle ,$Обсудим топологическую природу квазичастичных возбуждений и калибровочного поля в киральном спиновом состоянии [3, 32]. Простейшее возбуждение в приближении среднего поля может быть получено путем добавления спинона в зону проводимости. Однако это возбуждение еще не является физическим, поскольку спинон в зоне проводимости нарушает ограничение $\sum\nolimits_\sigma {f_{{i\sigma }}^{\dag }{{f}_{{i\sigma }}}} = 1.$ Дополнительную плотность спинонов можно устранить, вводя вихревой поток калибровочного поля
Поэтому физические квазичастицы в киральном спиновом состоянии являются спинонами, одетыми π-вихрем. Одетые спиноны несут спин 1/2, поскольку вихрь не может индуцировать произвольные спиновые квантовые числа. Однако спинон, который несет единичный заряд калибровочного поля, имеет дробную статистику, будучи связанным состоянием зарядаи вихря.
В целом теория среднего поля оказывается чрезвычайно богатой. В рамках калибровочной теории возможно возникновение большого числа спиновых жидкостей – как щелевых, так и бесщелевых. Кроме спин-бозонного представления, описывающего фазу деконфайнмента с бесщелевыми спинонами, может быть использовано спин-фермионное представление, которое однако описывает только щелевые фазы [3].
3.2. Конфайнмент и деконфайнмент
Формально представление (28) справедливо всегда, однако в реальности картина спинонов и голонов может реализоваться лишь при определенных условиях (например, в точно решаемых моделях типа Китаева [88, 89]). Здесь принципиален вопрос о конфайнменте и деконфайнменте [3, 32]. В фазе конфайнмента вся картина спиновой жидкости разрушается при учете флуктуационных эффектов вследствие взаимодействия спинона с калибровочным бозоном: размножаются топологические дефекты, описываемые соответствующими гомотопическими группами [26]. В результате спиноны взаимодействуют друг с другом через линейно возрастающий с расстоянием потенциал, а для бозонов имеется большая энергетическая щель, так что все эти экзотические частицы никак не проявляются в низкоэнергетическом спектре. В итоге спиноны снова “склеиваются” с бозонами в обычные электроны и мы возвращаемся к тривиальному состоянию обычной ферми-жидкости – эффективной одночастичной теории. Таким образом,используемый сложный формализм согласуется с привычными физическими представлениями одноэлектронной теории [3].
Взаимодействие калибровочных полей на классическом уровне не приводит к конфайнменту. Однако, если мы выйдем за пределы классического приближения и рассмотрим взаимодействие между калибровочными флуктуациями, картина полностью изменится. В размерности 2 + 1 такое взаимодействие трансформирует потенциал $glnR$ в линейный, независимо от константы связи g. Таким образом, среднеполевые SU(2)-состояния с щелевыми фермионами нестабильны, а теории среднего поля нельзя доверять.
Иная картина возникает в фазе деконфайнмента (бесщелевой топологической фазе). Здесь топологические дефекты отсутствуют, калибровочное поле некомпактно, сохраняются поток электрического поля и топологический заряд. В результате спиноны и калибровочные бозоны являются хорошо определенными частицами, возникают струны электрического потока и топологический порядок (струнные сети), что означает многочастичное квантовое запутывание.
Взаимодействия и механизмы, ведущие к деконфайнменту, могут быть разными: фрустрации обменных параметров, эффект Кондо (подавление магнитных моментов электронами проводимости), туннелирование, псевдоспины… Часто их описание можно свести к эффективной изотропной или анизотропной модели Гейзенберга [90].
В качестве параметра порядка для перехода конфайнмент–деконфайнмент можно использовать петлю Вильсона (см. [32]). Она связана с калибровочным потенциалом $V(R)$ между двумя статическими калибровочными зарядами $ \pm q$ с противоположным знаком, помещенными на расстояние R как $W(C) = exp[ - V(R)T],$ причем петля C состоит из путей длины T по времени направления и длины R вдоль пространственного направления. Существует два типа поведения $W(C)\,:$ закон площади с $W(C) \sim exp[ - \alpha RT]$ и закон периметра с $W(C) \sim exp[ - \beta (R + T)],$ где α и β являются константами. В первом случае потенциал $V(R)$ линейно возрастает в R, и, следовательно, два калибровочных заряда не могут быть свободны. Поэтому он соответствует конфайнменту в то время как второй случай – деконфайнменту.
Компактная квантовая электродинамика (чистая калибровочная модель) в размерности 2 + 1 конфайнментна при сколь угодно малой константе связи из-за возникновения инстантонов [91]. При этом инстантон ведет себя как положительный магнитный заряд, а антиинстантон – как отрицательный. Кулоновский газ в 2 + 1 измерениях всегда находится в фазе экранирования: кулоновское взаимодействие становится короткодействующим из-за экранирования заряда облаком окружающих противоположных зарядов заряд. Поэтому энергия рождения инстантона конечна и освобождаются магнитные заряды, которые разупорядочивают калибровочное поле, что приводит к закону площадей и конфайнменту. Однако конфайнмент может исчезать выше некоторой температуры перехода.
При наличии материальных полей вопрос о конфайнменте еще более усложняется. Пары частиц-античастиц могут возбуждаться из вакуума, экранируя статические заряды. При конечных температура переход к деконфайнменту заменяется постепенным кроссовером в плазменную фазу. Поэтому можно ожидать, что слейв-бозонная теория среднего поля без конфайнмента описывает физику на промежуточной энергетической шкале, хотя основное состояние является конфайнментным (антиферромагнитным, сверхпроводящим, либо ферми-жидкостным). Примером может служить “деконфайнментное” псевдощелевое состояние, обсуждаемое для ВТСП-систем, которое существует только при конечных температурах и описывается фермионами и бозонами, связанными с некомпактными калибровочными полями.
Еще один способ получения фазы деконфайнмента – выход в высшие измерения. В размерности 3 + 1 бесщелевые U(1)-флуктуации не создают конфайнментных взаимодействий. В размерности 4 + 1 и выше даже неабелева калибровочная теории может быть в фазе деконфайнмента. Таким образом, можно построить бозонные модели на кубической решетке, которые имеют бесщелевые фотоны – U(1)-калибровочные бозоны [32].
Явление деконфайнмента в последнее время активно изучается в расчетах квантовым методом Монте-Карло для специфических моделей типа Китаева, включающих фрустрацию [92]; эти расчеты достаточно надежны, поскольку, в отличие от стандартных фермионных задач, проблема знака отсутствует. Картина деконфайнмента может быть достаточно сложной: вовлеченными в него оказываются не все частицы. Размер спинонов получается достаточно большим – сравнимым с размером их связанного состояния, что отличается от “классического” RVB с короткими связями.
Деконфайнмент в двумерных системах также исследуется экспериментально для металлоорганических соединений с квадратной решеткой. Он проявляется как возникновение спинонов в высокоэнергетическом спектре возбуждений даже в отсутствие фрустраций [93]. При удалении от соответствующего аномального волнового вектора эти дробные частицы связываются, образуя обычные магноны.
3.3. Дираковские фермионы и алгебраическая спиновая жидкость
Существует еще один путь к деконфайнментному состоянию – взаимодействие компактного калибровочного поля U(1) с бесщелевыми фермионами, в частности с дираковскими, возникающим в фазе sfL. В этом случае коррелированное металлическое состояние представляет собой полуметалл, содержащий бесщелевые электронные возбуждения только в изолированных фермиевских точках зоны Бриллюэна, что и определяет особую топологию проблемы [16]. Эти точки суть поверхность Ферми электронов. Такая модель может быть применима к ВТСП-купратам [32] либо двухслойному графену [94].
Поскольку состояния вблизи ферми-точек имеют дираковский спектр, проблема может быть проанализирована в рамках соответствующего релятивистского формализма. Низкоэнергетическое действие для нейтральных дираковских спинонов $\Psi $ в изоляторной фазе имеет структуру
(49)
$S = \int {{{d}^{3}}x} \sum\limits_\mu {\sum\limits_{\sigma = 1}^N {{{{\bar {\Psi }}}_{\sigma }}} } ({{\partial }_{\mu }} - i{{a}_{\mu }}){{\gamma }_{\mu }}{{\Psi }_{\sigma }},$В зависимости от деталей решетки, ${{a}_{\mu }}$ может быть калибровочным полем типа U(1) или SU(2). Для большого количества “цветов” N (определяемого числом точек Дирака в зоне Бриллюэна) действие ${{S}_{D}}$ описывает конформную теорию поля (CFT). Таким образом, мы имеем масштабно-инвариантное квантовое состояние с сильным взаимодействием и степенным спектром для всех возбуждений, причем хорошо определенные квазичастицы отсутствуют. Это состояние именуется как алгебраическая спиновая жидкость (см. [32, 82 ]).
Итак, бесщелевые возбуждения, несущие калибровочные заряды, могут экранировать калибровочное взаимодействие, делая его менее конфайнментным [32]. В отличие от истинных деконфайнментных фаз, где невзаимодействующие квазичастицы становятся свободными при низких энергиях, здесь деконфайнмент означает только то, что бесщелевые заряженные частицы остаются бесщелевыми, но не вполне свободны. Соответствующие бесщелевые спиновые жидкости получаются из фазы экзотической жидкости sfL и uRVB.
На уровне среднего поля электронная функция Грина состояния uRVB в координатном пространстве является произведением фермионной и бозонной функции Грина, а в импульсно-частотном представлении – их сверткой. Спектральная функция состоит из уширенного квазичастичного пика с весом порядка допинга и некогерентного фона. При допировании фазы uRVB возникает состояние странного металла с большой поверхностью Ферми, так что картина изолированных спинонных дираковских точек оказывается несколько измененной [32].
Среднеполевая фаза sfL приводит к бесщелевой U(1) спиновой жидкости. Она дает пример алгебраической спиновой жидкости, в которой корреляционные функции имеют разрезы вместо полюсов, а спиновые корреляции убывают по алгебраическому степенному закону. лые показатели и всегда содержат разрез ветви без каких-либо полюсов. Для других широко известных бесщелевых состояний, таких как твердые вещества, сверхтекучие жидкости, ферми-жидкости и т.д., бесщелевые возбуждения всегда описываются свободными бозонами или свободными фермионами. Единственным исключением является одномерная латтинджеровская жидкость; алгебраическую спиновую жидкость можно рассматривать как ее обобщение за пределами одного измерения. Важно, что алгебраическая спиновая жидкость является фазой материи, а не только возникает в критической точке между двумя фазами.
Ферми-жидкостная фаза включает бозонную конденсацию, которая восстанавливает квазичастичную картину. Поэтому низкоэнергетические возбуждения в этой фазе описываются электронно-подобными квазичастицами, и эта фаза соответствует ферми-жидкости электронов.
Динамика для калибровочного поля U(1) возникает из-за экранирования бозонами и фермионами, причем и те, и другие несут калибровочный заряд. В случае малого допирования можно учитывать только экранирование фермионами. После интегрирования по $\Psi $ в (49) эффективная статистическая сумма для калибровочного поля U(1) имеет вид [95]
(50)
$\begin{gathered} Z = \int {D{{a}_{\mu }}} exp\left( { - \frac{1}{2}\int {\frac{{{{d}^{3}}q}}{{{{{(2\pi )}}^{3}}}}} {{a}_{\mu }}(q){{\Pi }_{{\mu \nu }}}{{a}_{\nu }}( - q)} \right), \\ {{\Pi }_{{\mu \nu }}} = \frac{N}{8}\sqrt {{{q}^{2}}} \left( {{{\delta }_{{\mu \nu }}} - \frac{{{{q}_{\mu }}{{q}_{\nu }}}}{{{{q}^{2}}}}} \right). \\ \end{gathered} $Поляризуемость Π делает калибровочную связь ${{a}_{\mu }}{{j}^{\mu }}$ (${{j}^{\mu }}$ – ток) маргинальным возмущением в фиксированной точке свободных фермионов.
Рассмотрим электронную функцию Грина. В первом порядке в ${1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}$ было получено
(51)
$\begin{gathered} G(x) = {{\left\langle {{{b}^{\dag }}(x)b(0)} \right\rangle }_{0}} \times \\ \times \,\,\left\langle {f(x){{f}^{\dag }}(0)exp\left( {i\int\limits_0^x {dx \cdot a} } \right)} \right\rangle , \\ \end{gathered} $(52)
$G(x) \propto {{({{x}^{2}})}^{{{{ - (2 - \alpha )} \mathord{\left/ {\vphantom {{ - (2 - \alpha )} 2}} \right. \kern-0em} 2}}}}$3.4. Модель фазовых струн
Поскольку при наличии проекторов Хаббарда статистика Ферми–Дирака неприменима, Венг предложил “статистику фазовых струн”, описывающую процесс допирования в $t - J$-модели [96–98]. Вся фермионная знаковая структура на простых решетках для полузаполненной зоны в моттовском изоляторе полностью приводима (устранима), так как проблема взаимодействующих электронов превращается в проблему взаимодействия локализованных спинов. Когда решетка фрустрирована, спиновая задача может по-прежнему включать проблему знака, что затрудняет расчеты типа Монте-Карло, но характер спина в моттовском состоянии подразумевает локализацию, так что электроны становятся различимыми.
Инжектированная дырка остается стабильной из-за конфайнмента спинонов и голонов полем фазового сдвига, несмотря на то, что фон представляет собой спинон-голонное море. Точный деконфайнмент возникает только в пределе нулевого допинга, когда дырка теряет свою целостность и распадается на голон и спинон. ними, где “щелевой” эффект усиливается далее микроскопическое разделение фаз при низкой температуре. При допировании моттовского изолятора дырками возникает неприводимая знаковая структура, но при низком допинге эта структура должна быть очень разреженной по сравнению с эквивалентной системой свободных фермионов с той же плотностью.
Простой способ сформулировать статистику Венга – систематически посчитать неприводимые знаки на языке мировых линий [98]. Для невзаимодействующего ферми-газа эмпирические знаки входят в статсумму как
(53)
${{Z}_{{{\text{FG}}}}} = \sum\limits_c {{{{( - 1)}}^{{{{N}_{{{\text{ex}}[c]}}}}}}{{Z}_{0}}[c]} ,$(54)
${{Z}_{{t - J}}} = \sum\limits_c {{{{( - 1)}}^{{N_{{{\text{ex}}}}^{h}\left[ c \right] + N_{h}^{ \downarrow }\left[ c \right]}}}} \mathcal{Z}\left[ c \right].$Сумма теперь идет по конфигурациям мировых линий спиновых частиц (“спинонов”) и дырок. Относительно друг друга дырки ведут себя как фермионы, а $N_{{{\text{ex}}}}^{h}\left[ c \right]$ подсчитывает обмены в конфигурации c. Спиноны здесь представляют собой бозоны с твердой сердцевиной (спины вверх рассматриваются как фон). Новый аспект статистики Венга заключается в том, что знаковая структура определяется четностью числа дырочно-спинонных столкновений, связанных с конкретной конфигурацией мировых линий.
Формально, спроектированный оператор уничтожения электронов записывается в слейв-фермионном представлении, причем явно учитывается знаковый множитель ${{( - \sigma )}^{j}}\,:$ ${{c}_{{j\sigma }}} = {{( - \sigma )}^{j}}f_{j}^{\dag }{{b}_{{j\sigma }}},$ где $f_{j}^{\dag }$ – фермионный голон, а для спиновой системы используются швингеровские бозоны $b_{{j\sigma }}^{\dag }.$ Из-за знакового множителя межспиновый суперобмен приобретает общий отрицательный знак, поэтому волновая функция основного состояния чисто спиновой системы при половинном заполнении не имеет узлов.
Венг предложил еще одну формулировку, которая строго эквивалентна представлению мировых линий. Она включает бозонные операторы $h_{{i\sigma }}^{\dag }$ и ${{b}_{{i\sigma }}}$ для “голонов” и “спинонов”, удовлетворяющие ограничению $h_{i}^{\dag }{{h}_{i}} + \sum\nolimits_\sigma {b_{{i\sigma }}^{\dag }{{b}_{{i\sigma }}}} = 1,$ которое может интерпретироваться на псевдоспиновом языке. Используя формализм калибровочных полей, можно записать спроектированный электронный оператор как
(55)
${{c}_{{i\sigma }}} = h_{i}^{\dag }{{b}_{{i\sigma }}}exp\left( {\frac{1}{2}\left[ {\Phi _{i}^{s} - \Phi _{i}^{0} - \sigma \Phi _{i}^{h}} \right]} \right){{(\sigma )}^{{{{N}_{h}}}}}{{( - \sigma )}^{i}},$Согласно работе [100], антиферромагнитная и сверхпроводящая фазы в картине Венга дуальны: в первой голоны находятся в конфайнменте, а спиноны в деконфайнменте, во второй – наоборот. Эти две фазы разделены новой фазой – так называемым бозе-изолятором, где и голоны, и спиноны деконфайнментны.
3.5. Фрустрации и спиновая жидкость в решетках Кондо
За счет подавления (экранирования) магнитного момента эффект Кондо может приводить к возникновению экзотических состояний – тяжелой ферми-жидкости или спиновой жидкости. Выигрыш в энергии немагнитного состояния по сравнению с однозонной моделью Хаббарда или моделью Гейзенберга определяется температурой Кондо ${{T}_{{\text{K}}}}$ [101]. В свою очередь, тенденция к состоянию спиновой жидкости (образование RVB-синглетов) дает дополнительный выигрыш для кондовского состояния по сравнению с магнитоупорядоченными фазами.
Для описания основного состояния кондо-решетки в режиме сильной связи было разработано специальное приближение среднего поля, которое использует псевдофермионное представление для операторов локализованных спинов $S = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ В рамках этого приближения Коулмен и Андрей [101], учитывая SU(2)-симметрию в формализме континуального интеграла, рассмотрели формирование состояния спиновой жидкости в двумерной ситуации. Затем это приближение было применено к случаю ферро- и антиферромагнитного упорядочения [79, 102, 103 ]. При этом смешивание между локальными моментами и электронами проводимости может быть представлено через вспомогательный бозон ${{b}_{i}} \sim \sum\nolimits_\sigma {c_{{i\sigma }}^{\dag }{{f}_{{i\sigma }}}} .$ Его конденсация и означает формирование тяжелой ферми-жидкости: в области, где электронные состояния имеют преимущественно f-характер, зона является почти плоской.
Рис. 4.
Фазовая диаграмма модели фазовых струн при малом допировании [99]. Дуальная топологическая калибровочная структура определяет различные фазы посредством конфайнмента-деконфайнмента.
Роль фрустраций в решетках Кондо была детально исследована в работе [104]. Как видно из рис. 5, кондовское экранирование уменьшает величину локального момента, уменьшая тем самым критическое значение ${{Q}_{c}},$ необходимое для формирования спиновой жидкости. Граница антиферромагнитной фазы простирается от $K = {{K}_{c}}$ на кондовской оси до $Q = {{Q}_{c}}$ на оси фрустраций. При больших $Q$ и малых $K$ реализуется спин-жидкостной металл с локализованными f-электронами и малой поверхностью Ферми, а при больших $K$ возникает тяжелая ферми-жидкость с большой ферми-поверхностью и делокализованными f-электронами. Поскольку объем ферми-поверхности сохраняется, она не может плавно эволюционировать от малой до большой, поэтому спин-жидкостной металл и тяжелая ферми-жидкость должны быть разделены квантовым фазовым переходом при нулевой температуре.
Рис. 5.
Схематическая диаграмма решетки в Кондо-пространстве параметров квантовой фрустрации $Q$ и $K = {{{{T}_{{\text{K}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{K}}}}} {{{J}_{{\text{H}}}}}}} \right. \kern-0em} {{{J}_{{\text{H}}}}}}$ (${{J}_{{\text{H}}}}$ – гейзенберговское взаимодействие) [104]. Переход между малой и большой поверхностью Ферми может также происходить через промежуточную фазу “странного металла”.
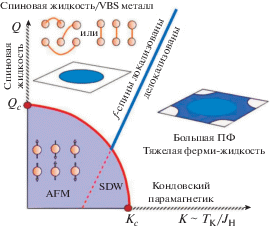
В [104] также был рассмотрен простой пример фрустрированной спиновой модели – решеточная модель Шастри–Сазерленда–Кондо, гамильтониан которой имеет вид ${{\mathcal{H}}_{{SSK}}} = {{\mathcal{H}}_{K}} + {{\mathcal{H}}_{{SS}}},$ причем слагаемые
содержат кондовское и гейзенберговское взаимодействия. Здесь означает сумму по плакетам с чередующимися диагональными связями. Отношение диагонального
взаимодействия к взаимодействию ближайших соседей $Q = {{{{J}_{1}}} \mathord{\left/ {\vphantom {{{{J}_{1}}} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}}$ играет роль параметра фрустрации.
означает сумму по плакетам с чередующимися диагональными связями. Отношение диагонального
взаимодействия к взаимодействию ближайших соседей $Q = {{{{J}_{1}}} \mathord{\left/ {\vphantom {{{{J}_{1}}} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}}$ играет роль параметра фрустрации.
Решетка Шастри–Сазерленда имеет то преимущество, что основное состояние при большой фрустрации является состоянием валентной связи со спиновыми синглетами, расположенными по диагональным связям, и четко определенной волновой функции. В отличие от других типов спиновой жидкости, можно показать, что это димерное состояние является точным основным состоянием модели при условии ${{J}_{1}} \gtrsim 2{{J}_{2}}.$
3.6. Фракционализованная ферми-жидкость
Еще один сценарий формирования нефермиевской жидкости был назван фракционализованной ферми-жидкостью FL*. В такой фазе заряженные возбуждения имеют обычные квантовые числа (заряд $ \pm e$ и спин 1/2), но они сосуществуют с дополнительными дробными степенями свободы. Важно отметить, что эта фаза имеет поверхность Ферми (ПФ) с объемом, нарушающим теорему Латтинджера.
В работах Сачдева и др. [103, 105] концепция фракционализованной ферми-жидкости была введена первоначально для $s{\text{--}}d(f)$-обменной модели (решетки Кондо). В фазе FL* отсутствует кондовское спаривание, т.е. конденсация хиггсовского бозона b ($\left\langle {{{b}_{i}}} \right\rangle = \left\langle {f_{i}^{\dag }{{c}_{i}}} \right\rangle = 0$), однако существует аномальное среднее RVB-типа ${{\chi }_{{ij}}} = \left\langle {f_{i}^{\dag }{{f}_{j}}} \right\rangle .$ Таким образом, локализованные моменты не принимают участие в формировании ПФ (они образуют отдельную спинонную ферми-поверхность), но адиабатически связаны со спиновой жидкостью, описываемой калибровочной теорией и обладающей соответствующими экзотическими возбуждениями в фазе деконфайнмента. В пространственных размерностях $d \geqslant 2$ стабильна спиновая жидкость типа Z2, а при $d \geqslant 3$ существует спиновая жидкость U(1). В этой фазе коэффициент электронной теплоемкости ${C \mathord{\left/ {\vphantom {C T}} \right. \kern-0em} T}$ логарифмически расходится. На фоне такого состояния может возникать магнитная неустойчивость для спинонной ПФ – металлическое магнитное состояние волны спиновой плотности SDW*, которое может характеризоваться малым моментом.
Упомянем трудности теории: в работе [103] пришлось искусственно ввести поле, стабилизирующее ненасыщенное состояние с малым моментом. В работе [106] такого введения удалось избежать, и в численных расчетах было получено состояние, где эффект Кондо сосуществует с антиферромагнетизмом, однако спин-жидкостной параметр порядка исчезает при переходе к малой ПФ. Отметим, что в простом ренормгрупповом рассмотрении квантовых фазовых переходов в магнитных решеток Кондо может возникать промежуточная область с неферми-жикостным поведением и частично подавленными магнитными моментами [79].
В последующих работах [105] фаза FL* как основное состояние уже рассматривалась только в квантовой критической точке, а за ее пределами – как неустойчивая относительно фазы с локальными моментами (см. разд. 4.1).
В дальнейшем, следуя идее Рибейро и Вена [78] о возникновении двух гибридизованных подсистем (спинонов и допонов) в $t - J$-модели (разд. 2.5), представление о фракционализованной ферми-жидкости было обобщено на однозонную модель Хаббарда [107, 108 ]. При этом в антиферромагнитной и спин-жидкостной (неупорядоченной) фазах спиноны описываются как швингеровские бозоны, а в ферми-жидкостной фазе – как фермионы (см. (41)).
Изменение статистики спинонов происходит в точке квантового фазового перехода между двумя конфайнментными фазами – магнитной и фазой с большой ПФ. Описание такого перехода требует дальнейших исследований. Здесь могут оказаться полезными суперсимметричные представления (см., напр., [72]). Упомянем также полностью фракционализованное представление электрона, где он разделяется на квазичастицы, несущие его спин и заряд, а также майорановские фермионы, несущие статистику Ферми [109].
При сравнении рис. 6 и 7 интересно отметить, что в отличие от модели Хаббарда, где кулоновское взаимодействие приводит к разрушению ферми-жидкостного состояния (формированию хаббардовских подзон с малой ПФ), эффект $s - d$-обмена противоположен: с ростом $s - d$-обменного параметра возникает тяжелая ферми-жидкость и большая ПФ. Причина состоит в том, что эти взаимодействия ведут к разным типам спаривания электронов и спинонов – диагональному и недиагональному (гибридизационному).
Представление швингеровских бозонов может быть введено не только в $t - J$-модели [108], но и в антиферромагнитной фазе спин-фермионной модели – модификации однозонной модели Хаббарда с конечным взаимодействием [107], что позволяет говорить ореализации в последней состояния необычной ферми-жидкости FL*.
Спин-фермионная модель [110], используемая при интерполяционном описании коллективизированного магнетизма (ее аналогии с $s - d$-обменной моделью обсуждаются в [111]), также позволяет разделить спиновые и электронные степени свободы.
Механизм перехода и описание квантовой критической точки между фазами FL и FL* обсуждается в работе [105] (рис. 6). Когда мы движемся к фазе FL* в пределах фазы FL, две поверхности Ферми с ${{k}_{{{\text{F}}1}}}$ и ${{k}_{{{\text{F}}2}}}$ ведут себя по-разному. ПФ с ${{k}_{{{\text{F}}1}}}$ эволюционирует в ПФ c ${{k}_{{{\text{F}} * }}}$ – в состояние FL* и остается “холодной” вблизи квантовой критической точки: сильного рассеяния этих квазичастиц нет, а квазичастичный вычет электронов при переходе остается конечным. Напротив, ПФ с ${{k}_{{{\text{F}}2}}}$ становится “горячей”: время жизни квазичастиц сокращается, а вычет уменьшается и в конечном счете исчезает в квантовой критической точке, так что динамика квазичастиц проявляет неферми-жидкостное поведение. Это аномальное поведение распространяется на всю горячую ПФ, в отличие от изолированных “горячих точек”, которые появляются в теории волн спиновой плотности.
Рис. 6.
Ферми-жидкостные фазы модели решетки Кондо [107]. В состоянии FL* спиновая жидкость локальных $f$-моментов отделена от малой ПФ $c$-электронов проводимости, которая не подчиняется обычной теореме Латтинджера.
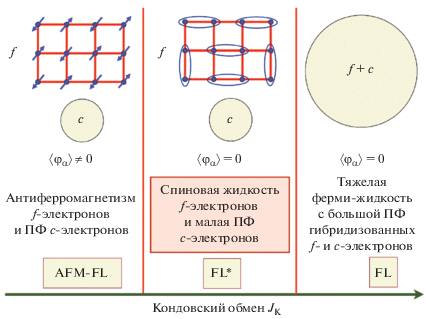
Рис. 7.
Фазовая диаграмма основного состояния модели Хаббарда согласно [107], ${{\varphi }_{\alpha }}$ – параметр антиферромагнитного порядка. В фазе AFM-FL удвоение элементарной ячейки АФМ порядком гарантирует выполнение теоремы Латтинджера. Фаза FL* не имеет антиферромагнитного порядка ($\left\langle {{{\varphi }_{\alpha }}} \right\rangle = 0$), однако наследует малые карманы ПФ от фазы с $\left\langle {{{\varphi }_{\alpha }}} \right\rangle \ne 0,$ причем теорема Латтинджера не выполняется.
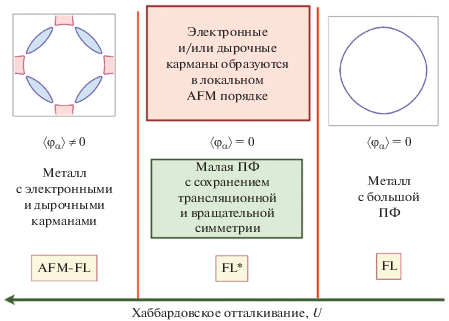
Рис. 8.
Состояние FL* с холодной ПФ и импульсом Ферми $k_{{\text{F}}}^{ * }.$ Фермионы f, образующие спиновую жидкость, схематически представлены пунктирной линией – a. Состояние FL, которое подчиняется обычной теореме Латтинджера, но имеет две ПФ – б.
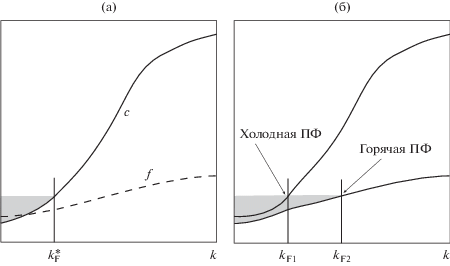
В состоянии FL* имеются дополнительные низкоэнергетические возбуждения локальных моментов, которые дают добавочный топологический вклад в изменение импульса кристалла. Действительно, действие вихревого потока аналогично преобразованию Либа–Шульца–Маттиса [46], так что спин-жидкостное состояние в размерности $d = 2$ приобретает это изменение импульса. Обычно объем поверхности Ферми определяется общим числом электронов в системе. Однако имеется общий топологический анализ [112], основанный на “протаскивании” кванта потока (благодаря циклическим граничным условиям система рассматривается как тор, в контурах которого возникает кристаллический импульс, что аналогично появлению силы Фарадея с изменением потока) и глобальной калибровочной симметрии U(1) (сохранение заряда). Из него следует, что существование немагнитного состояния FL* с другим объемом ПФ разрешено, если мы допускаем глобальные топологические возбуждения. Такие возбуждения естественно возникают в калибровочных теориях для FL*-состояния. Таким образом, нарушение теоремы Латтинджера должно сопровождаться топологическим порядком [103]. Следовательно, формирование малой ПФ, хаббардовского расщепления (отметим, что теорема Ошикавы [112] справедлива и для изолятора) и состояния с неупорядоченными локальными моментами можно связать с топологическим порядком в состоянии спиновой жидкости.
В многозонной системе существует возможность для парциального перехода Мотта между двумя металлическими фазами, где поверхность Ферми претерпевает квантованное изменение. В простейшем случае одна подполоса (или орбиталь) меняет свой характер с металлического на моттовский, в то время как другие полосы остаются металлическими (орбитально-селективный переход Мотта, см. [113]).
Будучи стабильной в низкотемпературном пределе, парциальная фаза Мотта нарушает теорему Латтинджера и, следовательно, является неферми-жидкостным металлом. Согласно концепции Сачдева, это и есть фракционализованная ферми-жидкость (FL*), а переход между FL и FL* является орбитально-селективным переходом Мотта.
Парциальный переход Мотта был получен из численных результатов для допированной однозонной хаббардовской модели купратных сверхпроводников. Это поведение, по-видимому, является импульсно-селективным, т.е. некоторые области в пространстве импульсов ведут подобно ферми-жидкости, а другие – как моттовский изолятор.
4. ТЕОРИЯ КВАНТОВЫХ ФАЗОВЫХ ПЕРЕХОДОВ. СПИНОВАЯ ЖИДКОСТЬ И ТОПОЛОГИЧЕСКИЙ ПОРЯДОК
С точки зрения квантовых фазовых переходов, особый интерес представляют фрустрированные магнитные системы, в которых дальний порядок подавлен (наиболее простой пример здесь – треугольная решетка, где согласно численным расчетам имеется конечная область деконфайнмента, обусловленная фрустрацией). При учете квантовых флуктуаций в них могут реализоваться состояния с локальными моментами без нарушения симметрии – вплоть до самых низких температур существует только ближний порядок. В случае половинного заполнения зоны эти системы могут демонстрировать переход металл–изолятор в парамагнитной фазе.
Такие квантовые спиновые жидкости (QSL) заметно отличаются от их классических аналогов по ряду позиций [113]. Квантовые колебания обычно устраняют сильное вырождение основного состояния фрустрированных систем за счет квантового туннелирования, что приводит к единственному основному состоянию (с точностью до глобальных преобразований симметрии или топологического вырождения). QSL – термодинамически стабильные фазы вещества, характеризующиеся динамическими калибровочными полями и топологическим порядком. Это подразумевает существование дробных возбуждений, связанных с калибровочным полем. Несмотря на такую связь, дробные возбуждения асимптотически свободны (деконфайнмент). Волновые функции в QSL могут характеризоваться дальнодействующим запутыванием. При этом QSL следует отличать от “тривиальных” квантовых парамагнетиков без топологического порядка и фракционализации (например, синглетные магнетики типа TlCuCl3, где связываются в пары спины 1/2).
4.1. Деконфайнментная квантовая критичность
Обратимся теперь к вопросу о том, как подход калибровочной теории может быть применен к проблеме высокотемпературной сверхпроводимости. В основном состоянии последняя возникает при допировании моттовского изолятора, когда антиферромагнитный порядок пропадает, причем при температурах выше точки сверхпроводящего перехода нормальное состояние описывается псевдощелевой картиной. Чтобы увязать одновременное исчезновение магнитного порядка с возникновением псевдощелевого поведения и сверхпроводимости, был предложен подход, позволяющий описать появление сначала немагнитного моттовского изолятора при нулевом допинге (спиновая жидкость), который при допировании превращается в сверхпроводник (см. рис. 9).
Рис. 9.
(а) Схема нуль-температурной фазовой диаграммы, показывающая маршрут между антиферромагнитным изолятором Мотта и d-волновым сверхпроводником как функцию допирования х. Вертикальная ось помечена параметром g, который означает меру фрустрации спиновой системы в изоляторной фазе. AF – антиферромагнитное упорядоченное состояние, SL – изоляторная спиновая жидкость, которая получеается путем увеличения фрустрации – a. То же, что на (a), но как функция химического потенциала – б.
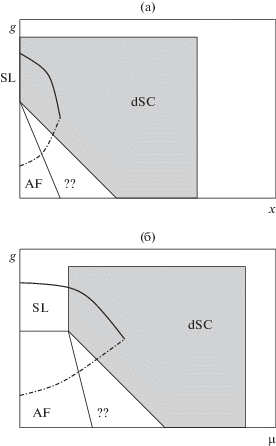
Рассмотрим некоторое спин-жидкостное моттовское состояние. При изменении химического потенциала в нем произойдет нуль-температурный моттовский фазовый переход, обусловленный не изменением взаимодействия, а допированием. Квантовая критическая точка будет определять поведение системы в конечном интервале параметров. Линии кроссоверов, возникающих вблизи этого перехода, показаны на рис. 10.
Рис. 10.
Схематическая фазовая диаграмма для индуцированного допированием перехода Мотта между спин-жидкостным изолятором и $d$-волновым сверхпроводником. Полужирная линия – путь, принятый системой c плотностью дырок $x$, которая имеет сверхпроводящее основное состояние. Область, обозначенная FS, представляет собой флуктуационный режим сверхпроводящего перехода. QC является квантовой критической областью, связанной с критической точкой Мотта. Эта область может быть сопоставлена с высокотемпературной псевдощелевой фазой.
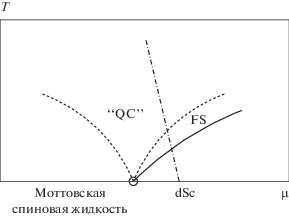
Интересно отметить, что роторное представление также позволяет описать промежуточную псевдощелевую фазу, давая переход к металлическому состоянию только при конечной концентрации дырок [69]. Похожую картину дает и модель фазовых струн (раздел 3.4), а также вычисления в представлении МЭ Х-операторов (некогерентные состояния при малом допировании) [65].
Среди возможных кандидатов на спин-жидкостное состояние в литературе упоминаются димерная фаза (валентно-связанное состояние, VBS), Z2 и U(1) спиновые жидкости. Поскольку наиболее вероятно, что трансляционно-инвариантное спин-жидкостное состояние можетпри допировании привести к $d$-волновой сверхпроводимости с нодальными квазичастицами, наиболее подходящей является фаза U(1) [32]. Более того, даже если физическая система не обладает стабильным состоянием U(1) спиновой жидкости, последняя может существовать как критическое состояние, разделяющее антиферромагнитную фазу и Z2 спиновую жидкость, что способствует возникновению псевдощелевой и сверхпроводящей фаз [114].
Простейшей ситуацией, выходящей за рамки теории Ландау, оказывается QPT при нулевой температуре, когда между различными квантовыми фазами с нарушенными симметриями в квантовой критической точке происходит переход, запрещенный по Ландау. Примером является фрустрированный антиферромагнетик [33, 34], где деконфайнментная квантовая критическая точка разделяет упорядоченные фазы с нарушенными вращательной и трансляционной симметрией. Для таких точек лучшим отправным пунктом при описании критического поведения является не обычный параметр порядка, а набор дробных возбуждений, которые специфичны для критической точки, но не присутствуют ни в одной из фаз рядом с ней. Более того, существует дополнительная топологическая структура, присутствующая в критической точке и связанная с топологическим законом сохранения. Дополнительную сохраняющуюся величину удобно интерпретировать как полный поток калибровочного поля, возникающего в критической точке. Он сохраняется только асимптотически — при низких энергиях в квантовой критической точке. Этот закон сохранения обеспечивает резкое различие между деконфайнментными и обычными критическими точками.
В континуальном пределе топологический поток определяется как
Известно, что компактная U(1)-калибровочная теория в 2 + 1-мерном пространстве-времени допускает наличие точечных дефектов (монополей), которые меняют топологический заряд (число скирмионов). Следуя [115], рассмотрим траектории двумерной ренормализационной группы с управляющим параметром s и параметром ${{\lambda }_{4}},$ описывающим эффективность монополей (monopole fugacity); они показаны на рис. 11.
Рис. 11.
Траектории ренормализационной группы для антиферромагнетика со спином $S = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ и квадратной решеткой.
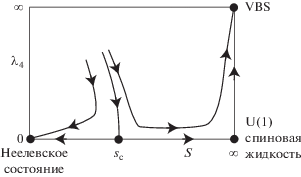
На линии ${{\lambda }_{4}} = 0$ расположена нестабильная неподвижная точка $s = {{s}_{c}},$ отделяющая линии ренормгрупповых траекторий в направлении магнитоупорядоченного неелевского состояния от линий в направлении парамагнитной спиновой жидкости с бесщелевым U(1)-фотоном и щелевыми спинонными возбуждениями.
Обратимся теперь к случаю ${{\lambda }_{4}} \ne 0.$ При малых s величина ${{\lambda }_{4}}$ оказывается несущественной (иррелевантной) для неподвижной точки ${{\lambda }_{4}} = 0,$ ${{s}_{c}} = 0.$ Однако для $s > {{s}_{c}}$ траектории отклоняются и притягиваются в сторону больших значений ${{\lambda }_{4}}.$ Это связано с тем, что параметр ${{\lambda }_{4}}$ становится опасно релевантным возмущением для неподвижной точки при больших s, описывающей спин-жидкостную фазу. Вблизи ${{s}_{c}}$ значение ${{\lambda }_{4}}$ очень мало на масштабах порядка корреляционной длины ${{\xi }_{{{\text{spin}}}}},$ но оно становится порядка единицы и более на втором масштабе длины, который обозначается как ${{\xi }_{{{\text{RVB}}}}}.$ Тогда мы имеем связь ${{\xi }_{{{\text{RVB}}}}} \sim \xi _{{{\text{spin}}}}^{\lambda },$ где $\lambda > 1,$ поэтому ${{\xi }_{{{\text{RVB}}}}} \gg {{\xi }_{{{\text{spin}}}}}.$
Второй пример деконфайнментной квантовой критической точки представляет собой QPT в тяжелой ферми-жидкости; рассмотрим ее неустойчивости, следуя [105] (рис. 12). В изоляторных магнетиках существует прямой переход второго рода между неелевским состоянием и состоянием с другим порядком – валентно-связанным твердым состоянием (VBS). Его можно рассматривать как аналог прямого перехода между тяжелой ферми-жидкостью и металлом с локальными магнитными моментами (LMM), где происходит потеря “кондовского” порядка одновременно с появлением магнитного. Действительно, неелевское состояние и состояние FL (решетка Кондо) являются устойчивыми хиггсовскими фазами компактной U(1)-калибровочной теории. Они нестабильны относительно “деконфайнментного” перехода в U(1)-спиновую жидкость и фазу FL* соответственно. Однако такие деконфайнментные фазы являются довольно лабильными состояниями вещества и могут быть неустойчивым по отношению к конфайнментным фазам с обычным порядком – например, неустойчивость U(1)-спиновой жидкости к переходу в VBS. Естественно рассмотреть неустойчивость состояния FL* по отношению к состоянию с LMM, но таким образом, чтобы квантовая критичность оставалась деконфайнментной. В изоляторных магнетиках переход между двумя конкурирующими порядками (неелевским и VBS) происходит не как функция некоторого параметра настройки, а динамически, как функция масштаба длины-времени. Действительно, в парамагнетике потеря корреляций Нееля происходит на одном масштабе ξ, тогда как пиннинг VBS-порядка появляется на гораздо большем масштабе ${{\xi }_{{{\text{VBS}}}}},$ который расходится как степень $\xi $. Аналогично, прямой переход второго рода между конкурирующими порядком Кондо в FL и магнитным порядком в металле с локальнымимоментами возможен, но требует по крайней мере двух расходящихся масштабов длины-времени в квантовой критической точке, причем деконфайнмент обнаруживается только на более коротких масштабах.
Рис. 12.
Фазовая диаграмма вблизи квантового перехода между ферми-жидкостью FL и состоянием с локальными моментами LMM [105]. Две различные энергетические шкалы приводят к двум отличающимися критическим показателям, согласно которым точка Нееля ${{T}_{N}}$ и температура когерентности ${{T}_{{{\text{coh}}}}}$ (или $T_{{{\text{coh}}}}^{ * }$) приближаются к квантовой критической точке.
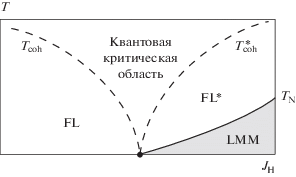
4.2. Хиггсова критичность
Как обсуждалось выше, начиная с работы [103] переходы между ферми-жидкостью и неферми-жидкостными состояниями обсуждаются в терминах хиггсовского бозона b. Как и в теории элементарных частиц, такой формализм удобен при описании нарушенных симметрий.
В фазе Хиггса калибровочное поле в кулоновском газе (разд. 3.2) станоаится щелевым по механизму Андерсона–Хиггса, так что для заряда $q = 1$ фаза Хиггса и конфайнментные фазы плавно связаны друг с другом. Ситуация резко отличается при $q = 2,$ т.е. когда поле бозонов соответствует спариванию, например, в сверхпроводнике. В этом случае может существовать граница между конфайнментной и хиггсовской фазами, так что последняя (фаза спаривания) деконфайнментна и имеет остаточную калибровочную симметрию Z2, поэтому параметр порядка инвариантен при изменении знака зарядов $q = 1,$ составляющих пару [32].
Следуя [116], обсудим эволюцию фазы U(1)–FL* с ее малой поверхностью Ферми к обычной “большой” ПФ при сильном допировании. Существует обычный путь преобразования, связанный с исчезновением антиферромагнитного порядка. Это переход между двумя состояниями ферми-жидкости, который описывает стандартная теория Герца–Миллиса [117, 118].
Простая SU(2)-теория поля [116], допускает конденсаты двух бозонных полей: калибровочного бозона $R$ и хиггсовского бозона ${{H}^{a}}.$ Соответствующие фазы получают путем изменения управляющих параметров s и g (рис. 13) и обозначаются по их конденсатам.
Рис. 13.
Схема металлических фаз по теории [116] в координатах обратная константа связи ${1 \mathord{\left/ {\vphantom {1 g}} \right. \kern-0em} g}$ – параметр хиггсовской критичности s. Только фаза А имеет нарушенную глобальную симметрию, связанную с наличием дальнего антиферромагнитного (AFM) порядка. Обычные ферми-жидкостные фазы сверху претерпевают переход от малых к большим поверхностям Ферми, сопровождаемый потерей AFM-порядка. Пунктирная стрелка – прямой маршрут между этими фазами, который может дать описание купратов с электронным допированием. Стрелка вокруг точки M – маршрут с увеличением дырочного допирования. Фаза U(1)-FL* спускается из фазы U(1) ACL и имеет малую поверхность ферми-электронов из-за наличия топологического порядка, тогда как фаза A выше нее имеет “малую” ПФ электронов из‑за нарушения трансляционной симметрии.
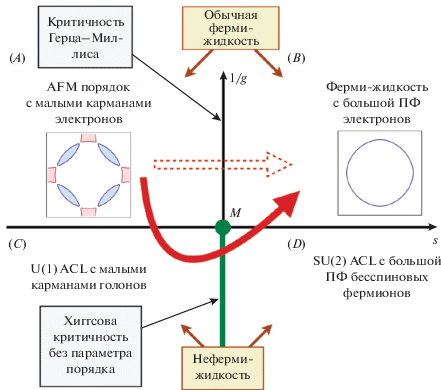
1) Фаза Хиггса, обозначенная как (A) на рис. 13, где обе симметрии SU(2)spin и SU(2)gauge нарушены, что приводит к $\left\langle R \right\rangle \ne 0,$ $\left\langle {{{H}^{a}}} \right\rangle \ne 0.$ Здесь калибровочные возбуждения-фотоны являются щелевыми. Эта фаза описывает AFM-металл, где большая поверхность Ферми реконструируется в дырочные и электронные карманы из-за конденсации бозона ${{H}^{a}}$ вдоль вектора неелевского параметра порядка n.
2) Конфайнментная фаза SU(2), обозначенная как (B) на рис. 13. Симметрия SU(2)spin здесь не нарушена. Мы имеем $\left\langle R \right\rangle \ne 0,$ $\left\langle {{{H}^{a}}} \right\rangle = 0,$ что необходимо для сохранения спиновой вращательной инвариантности, так как ${\mathbf{n}} = 0.$ Это обычная ферми-жидкость с большой ПФ.
3) В фазе Хиггса (C) симметрия SU(2)gauge нарушена, а SU(2)spin – нет, что ведет к $\left\langle R \right\rangle = 0,$ $\left\langle {{{H}^{a}}} \right\rangle \ne 0.$ Это означает развитые локальные AFM-флуктуации без какого-либо дальнего порядка. Если выбрать ${{H}^{a}}$ вдоль направления (0,0,1), проведя калибровочное преобразование, симметрия U(1)-подгруппы SU(2)gauge не нарушается, так что калибровочный ${{A}^{z}}$-фотон остается бесщелевым. Таким образом, эта фаза описывает U(1)-алгебраическую зарядовую жидкость (ACL), или голонный металл [119]. Однако из-за выраженного локально AFM-порядка ПФ реконструируется в карманы голонов ${{\psi }_{p}},$ которые минимально связаны с калибровочным полем U(1). В зависимости от температуры может происходить непрерывный кроссовер из U(1) ACL в U(1) FL* (или “голон-дырочный” металл), где некоторые из голонов (${{\psi }_{ \pm }}$) начинают формировать связанные состояния с щелевыми спинонами.
Рис. 14.
Фазовая диаграмма для купратов, основанная на теории критичности Хиггса. Алгебраические зарядовые жидкости (ACL) обладают ферми-поверхностями бесспиновых $\psi $-фермионов, несущих электромагнитный заряд: в SU(2) ACL-поверхность Ферми большая и связана с SU(2) калибровочным полем, тогда как в U(1) ACL-поверхность Ферми малая и связана с калибровочным полем U(1). Ферми-жидкость FL* опускается из U(1) ACL при связывании $\psi $-фермионов с нейтральными спинонами. d-BDW – волна плотности связей, SC – d-волновой сверхпроводник,
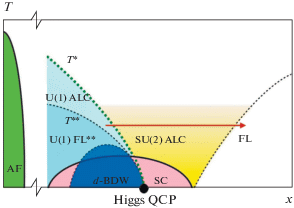
4) Последняя фаза (D) имеет полную симметрию, так что ни одно из полей не сконденсировано: $\left\langle R \right\rangle = \left\langle {{{H}^{a}}} \right\rangle = 0.$ В отличие от U(1) ACL, где только ${{A}^{z}}$-фотон был бесщелевым, в этой фазе имеется триплет бесщелевых SU(2)-фотонов, связанных с большой ПФ. Эта фаза может быть описана как SU(2) алгебраическая зарядовая жидкость. При достаточно низких температурах она неустойчива по отношению к сверхпроводимости.
Сравнение вычислений электронной функции Грина в топологически упорядоченной хиггсовской фазе SU(2) калибровочной теории флуктуирующего антиферромагнетизма на квадратной решетке с результатами первопринципных расчетах в динамической теории среднего поля (DMFT) и квантовом методе Монте-Карло проведено в работе [120].
4.3. Фазовые переходы и некогерентные состояния в проводящих магнетиках
В проводящих магнетиках при изменении параметров взаимодействия возникают дополнительные квантовые фазовые переходы по сравнению с моделью Гейзенберга – появление магнитного упорядочения в основном состоянии, качественное изменение поведения магнитногомомента и т.д. В пределе сильных корреляций такие переходы не описываются простыми подходами типа Стонера или Герца–Миллиса [117, 118]. В частности, в ферромагнетике может происходить переход из насыщенной в ненасыщенную фазу. В насыщенном (полуметаллическом) состоянии поверхность Ферми исчезает для одной из проекций спина, так что этот переход может считаться топологическим. Отметим, что строгое доказательство теоремы Нагаока о насыщенном ферромагнитном основном состоянии модели Хаббарда с бесконечным U имеет топологический характер; теория фазовых струн Венга в $t - J$-модели может рассматриваться как обобщение этого подходана случай конечных J.
Состояния со спином вниз в модели Хаббарда в насыщенном ферромагнетике дают самый простой пример неквазичастичных состояний. Формально в пределе $U = \infty $ удобно факторизовать оператор Хаббарда ${{X}_{i}}( - ,0) = {{X}_{i}}( - , + ){{X}_{i}}( + ,0),$ что аналогично разделению голона и спинона. Тогда вычисление дает [65]
(57)
$\begin{gathered} {{\left\langle {\left\langle {\left. {{{X}_{{\mathbf{k}}}}( - ,0)} \right|{{X}_{{ - {\mathbf{k}}}}}(0, - )} \right\rangle } \right\rangle }_{E}} = {{\left\{ {E - {{t}_{{\mathbf{k}}}} + {{{\left[ {G_{{{\mathbf{k}} \downarrow }}^{0}(E)} \right]}}^{{ - 1}}}} \right\}}^{{ - 1}}}, \\ G_{{{\mathbf{k}} \downarrow }}^{0}(E) = \sum\limits_{\mathbf{q}} {\frac{{{{n}_{{{\mathbf{k}} + {\mathbf{q}}}}}}}{{E - {{t}_{{{\mathbf{k}} + {\mathbf{q}}}}} + {{\omega }_{{\mathbf{q}}}}}}} , \\ \end{gathered} $Интересно, что исторически понятие спинонов было введено Андерсоном в связи с проблемой спиновой поляризации в ферромагнитных металлах [121] (см. также [122]). Спинонными были названы некогерентные вклады в электронную спектральную плотность, обусловленные взаимодействием с магнонами. Соответствующий формализм описания сильного зонного ферромагнетизма, основанный на тождестве Уорда, был разработан в работах Эдвардса и Герца [123]. Он был также применен для описания перехода металл–изолятор в парамагнитной фазе и трактовки неферми-жидкостного состояния [124]. Парамагнитное состояние с неупорядоченными магнитными моментами, полученное в [124] в аналогичном приближении, может быть отождествлено с андерсоновским состоянием RVB.
Дальнейшее развитие теории неустойчивости ферромагнетизма связано с анализом трехчастичных вкладов [125].
В $t - J$ модели антиферромагнетика большая часть состояний является некогерентной, хотя для конечных J состояния вблизи дна зоны образуют узкую когерентную полосу с малым вычетом порядка $\left| {{J \mathord{\left/ {\vphantom {J t}} \right. \kern-0em} t}} \right| \ll 1$ и тяжелой массой $ \sim \left| {{t \mathord{\left/ {\vphantom {t J}} \right. \kern-0em} J}} \right|$ [126].
Конкуренция ферро- и антиферромагнетизма при допировании моттовского изолятора приводит к переходам первого рода, формированию неоднородных состояний и спиральных магнитных структур (рис. 15). Соответствующие вычисления в обобщенном приближении Хартри–Фока и при учете корреляций в методе вспомогательных бозонов Котляра–Рукенштейна были проведены в работах [63, 127, 128 ]. При этом возникают различные антиферромагнитные фазы, в том числе характеризующиеся малым вычетом [128]. Методы типа Хартри-Фока переоценивают устойчивость магнитных фаз, в то время как учет корреляций позволяет успешно описать парамагнитную фазу при больших U, т.е. фазу типа спиновой жидкости [63].
Рис. 15.
Магнитная фазовая диаграмма основного состояния двумерной модели Хаббарда в рамках приближения Хартри–Фока (а) и при учете корреляций (б) для квадратной решетки при концентрации электронов $n < 1$ [63]. Спиральные фазы обозначены в соответствии с формой их волнового вектора. Жирные линии обозначают фазовые переходы второго рода. Штриховка показывает области фазового расслоения, пунктирные линии – границы между различными парами фаз. Сплошные линии соответствуют границам между однородной фазой и областями фазового расслоения, ${{{\mathbf{Q}}}_{{{\text{AFM}}}}} = (\pi ,\pi ),$ PM и FM – пара- и ферромагнитная фазы.
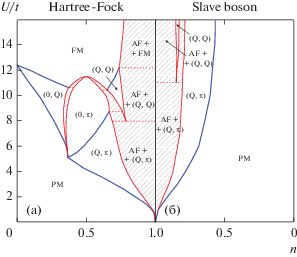
4.4. Сверхпроводимость и топологический порядок
Экспериментальное открытие сверхпроводящего порядка Камерлинг–Оннесом исторически привело к теории нарушенной симметрии, однако последовательное квантовое топологическое рассмотрение усложняет эту картину. В действительности сверхпроводимость может быть описана теорией Гинзбурга–Ландау с динамическим U(1)-калибровочным полем [5]. Конденсация электронной пары зарядов $2e$ нарушает калибровочную теорию U(1) до калибровочной теории Z2 при низких энергиях. Последняя является эффективной теорией топологического порядка Z2, так что реальный сверхпроводник имеет именно такой топологический порядок. Часто сверхпроводимость описывается теорией Гинзбурга–Ландау без динамического калибровочного поля U(1); вместо него рассматривается нарушенная симметрия U(1) [4]. Однако реальные сверхпроводники в электромагнитном калибровочном поле не являются состояниями с нарушенной симметрией, а представляют собой топологически упорядоченные состояния [129, 130]. Решающее значение здесь имеет теорема Элицура [131] о невозможности существования калибровочно-инвариантного локального параметра порядка для состояния в электромагнитном калибровочном поле.
Сам по себе сверхпроводящий порядок в поле не есть порядок, нарушающий симметрию, но является топологическим порядком, который выходит за рамки теории симметрии Ландау (хотя, разумеется, без поля эта теория дает полное описание); по иронии судьбы, именно он был обнаружен в 1911 году. При условии, что калибровочное U(1)-электромагнитное поле является динамическим, сверхпроводник имеет струнные возбуждения, характеризующие топологический порядок, – петли потока ${{hc} \mathord{\left/ {\vphantom {{hc} {2e}}} \right. \kern-0em} {2e}}.$
Оказывается, что разрушение сверхпроводящего порядка происходит за счет обычного механизма Березинского–Костерлица–Таулеса, включающего размножение топологических вихрей. В спиновой жидкости инстантоны, разрушающие топологический порядок, иррелевантны. Тогда U(1)-калибровочный поток является сохраняющейся величиной, и мы имеем деконфайнментное состояние.
Теория флуктуаций фазы в двух измерениях хорошо описывается подходом Березинского–Костерлица–Таулеса (БКТ), поэтому разрушение сверхпроводящего порядка идет по обычному механизму БКТ – за счет распространения вихрей и теплового “развязывания” пар вихрь-антивихрь.
Одним из следствий феноменологического подхода Гинзбурга–Ландау является конкуренция между переходом БКТ для фермионного спаривания и конденсацией бозонов. Поэтому линии фазового перехода для фермионного спаривания и бозонная конденсация на фазовой диаграмме становятся линиями кроссовера, и только сверхпроводящий переход остается реальным БКТ-переходом.
Во внешнем электромагнитнои поле вихри выталкиваются. Это поле при конденсации приобретает массу (отсюда возникает эффект Мейсснера), симметрия U(1) понижается до Z2 (т.е. возникает спиновая жидкость). Таким образом, в поле механизм Ландау нарушения симметрии, который имеет место в сверхтекучести, не работает – возникает топологический переход.
Теперь обратимся к вихревым структурам в сверхпроводящем состоянии. Самая интригующая проблема здесь – квантование магнитного потока. Поскольку бозон имеет заряд e, в то время как фермионная пара – 2e, вопрос состоит в том, может ли вихрь ${{hc} \mathord{\left/ {\vphantom {{hc} e}} \right. \kern-0em} e}$ быть более стабильным, чем обычный вихрь ${{hc} \mathord{\left/ {\vphantom {{hc} {2e}}} \right. \kern-0em} {2e}}.$ Как оказывается, вихрь типа B с квантованием потока ${{hc} \mathord{\left/ {\vphantom {{hc} e}} \right. \kern-0em} e}$ будет иметь более низкую энергию, чем вихри ${{hc} \mathord{\left/ {\vphantom {{hc} {2e}}} \right. \kern-0em} {2e}},$ особенно при низком допировании. Этот вывод является общей особенностью калибровочной теории U(1). Однако ${{hc} \mathord{\left/ {\vphantom {{hc} e}} \right. \kern-0em} e}$-вихри естественно объясняются в SU(2) теории с двумя бозонами [32].
Статистика Венга приводит к изменению скрытой топологической структуры по сравнению с ферми-жидкостным БКШ-сверхпроводником: сверхпроводник представляет собой конденсат бозонов с зарядом e и на первый взгляд кажется, что вихри несут поток ${{hc} \mathord{\left/ {\vphantom {{hc} e}} \right. \kern-0em} e}.$ Однако, если рассмотреть влияние взаимной статистики Черна-Саймонса на топологию сверхпроводника, голон с зарядом e приобретает скачок фазы $\pi $ при обходе изолированного спинона. Таким образом, связывание спинона с вихрем приводит к уменьшению кванта потока вдвое до значения ${{hc} \mathord{\left/ {\vphantom {{hc} {2e}}} \right. \kern-0em} {2e}},$ как и для обычного конденсата куперовских пар [96, 98].
5. РЕШЕТОЧНЫЕ КАЛИБРОВОЧНЫЕ ТЕОРИИ И СТРУНЫ
В теории поля часто используется переход к решеточным моделям, включающим дискретность пространства и времени. Такой переход является еще более естественным в квантовой теории твердого тела при использовании мнимого времени $t = i\tau ,$ поэтому ряд трудностей калибровочной теории разрешается легче. В пределе нулевой температуры временной интервал становится бесконечным, так что возникает дополнительное пространственное измерение.
Физическое пространство состояний абелевой решеточной калибровочной теории состоит из замкнутых петель электрического потока. Обсудим их происхождение, следуя обзору [17]. Удобно использовать гамильтонов подход в приближении непрерывного времени. Рассмотрим действие с анизотропными связями
(58)
$S = {{\beta }_{\tau }}\sum\limits_{nk} {[1 - cos{{\theta }_{{0k}}}(n)]} - \beta \sum\limits_{n,ik} {cos{{\theta }_{{ik}}}(n)} ,$(59)
$\mathcal{H} = ({{{{a}^{3}}} \mathord{\left/ {\vphantom {{{{a}^{3}}} 2}} \right. \kern-0em} 2})\sum\limits_{nk} {E_{k}^{2}({\mathbf{n}})} - ({1 \mathord{\left/ {\vphantom {1 {{{g}^{2}}a}}} \right. \kern-0em} {{{g}^{2}}a}})\sum\limits_{n,ik} {cos{{\theta }_{{ik}}}({\mathbf{n}})} .$После разложения в непрерывном пределе имеем
(60)
$\mathcal{H} = ({{{{a}^{3}}} \mathord{\left/ {\vphantom {{{{a}^{3}}} 2}} \right. \kern-0em} 2})\sum\limits_{nk} {[E_{k}^{2}({\mathbf{n}}) - B_{k}^{2}({\mathbf{n}})]} ,$Физическое пространство состояний является локально калибровочно-инвариантным и удовлетворяет закону Гаусса. Поэтому допустимы только замкнутые петли электрического потока: теория не имеет источников или стоков. При сильной связи важен только электрический член в уравнении (59), причем энергия замкнутой петли потока пропорциональна ее длине. Магнитный член в (59) позволяет петлям флуктуировать, но всегда оставляет их замкнутыми.
Потоки электрического заряда соответствуют потенциальной энергии, магнитная часть – кинетической. Сохранение потока в топологической фазе означает сохранение заряда, а следовательно наличие бозонов. Линии электрического потока определяют струны (strings; либо, в другой терминологии – петли, loops). Детали струнной картины определяются величиной константы взаимодействия g. Для электрического поля константа связи равна ${{g}^{2}},$ а для магнитного – ${1 \mathord{\left/ {\vphantom {1 {{{g}^{2}}}}} \right. \kern-0em} {{{g}^{2}}}}.$ Поэтому при больших g доминирует потенциальная энергия, замкнутые петли электрического потока стягиваются, их мало. Напротив, при малых g (в слабой связи) доминирует кинетическая энергия, роль которой играет магнитное поле, так что петли легко возбуждаются, их много.
А.М. Поляков установил глубокие соответствия решеточных калибровочных теорий в трех и четырех измерениях двумерным спиновым системам [132]. Двумерные O(n) гейзенберговские спиновые системы допускают точное решение в континуальном пределе для $n \geqslant 3.$ Причина этого заключается в том, что эти теории имеют ”скрытую симметрию”, что приводит к бесконечному числу законов сохранения. В двух измерениях эти законы сохранения запрещают образование частиц в процессах рассеяния. Такие законы сохранения не могут существовать в нетривиальных четырехмерных теориях. Однако Поляков предположил, что существует нетривиальное обобщение законов сохранения на неабелевы калибровочные поля в четырех измерениях, что может привести к замкнутому решению. Поляков рассмотрел неабелевы калибровочные теории как киральные поля, определенные на замкнутых петлях в реальном пространстве-времени. Абелеву решеточную калибровочную теорию можно рассматривать аналогичным образом – физическое пространство состояний теории состоит из замкнутых петель электрического потока.
Перечислим еще раз исходные модели, в которых есть слабые калибровочные взаимодействия и возможен деконфайнмент, а также возникают калибровочный бозон и фермионы:
1. Решеточная Z2-теория, которая в твердом теле дуальна модели Изинга, имеющей классические фазовые переходы. Она предсказывает квантовые фазовые переходы.
2. Абелева O(1) модель, которая в непрерывном пределе соответствует максвелловой теории электромагнитного поля.
3. Неабелева SU(2) модель, которой в твердом теле соответствует модель Гейзенберга.
В первых двух моделях возможен переход от конфайнмента к деконфайнменту, они могут быть использованы для описания спиновой жидкости. В третьей модели имеет место асимптотическая свобода, фазы деконфайнмента нет.
В Z2-спиновой жидкости и решеточной абелевой O(1)-модели возникают струны, которые, в свою очередь, образуют сети – жидкость струнных сетей. В зависимости от силы связи, в фазе возникает много или мало петель, они будут маленькими или большими. Струны могут колебаться. Колебания струнной жидкости описываются векторным полем, перпендикулярным направлению распространения волн, что аналогично теории Максвелла для распространения света. Таким образом, появляются калибровочные поля – бозоны, которые являются единственными возбуждениями в случае замкнутых струн. В квантовой электродинамике этим колебаниям струнной жидкости соответствуют бесщелевые фотоны. Если разорвать струну, возникают фермионы – ее оборванные концы. Они могут быть отождествлены с электронами, поскольку их взаимодействие с деформацией струнной сети описывается уравнениями электрон-фотонного взаимодействия [3].
Случайное возникновение (“вспыхивание”) монополей (см. разд. 3.2) приводит к конфайнменту фермионов; это аналогично взаимодействию кварков через мезоны в квантовой хромодинамике.
Фермионы возникают как дефекты квантовой дальнодействующей запутанности (entanglement), даже если исходная модель – чисто бозонная. Предыдущие подходы позволяли получить фермионы в моделях бозонного поля лишь для U(1) калибровочного поля в размерности пространства 2 + 1. В подходе же квантовой запутанности фермионы и бозоны одновременно получаются для любой размерности и калибровочной группы.
В обычной физике конденсированного состояния бозонное поле возникает в результате коллективных колебаний атомов: это фононы в твердом теле (две поперечные и одна продольная мода) и продольные волны сжатия в жидкости (одна мода). Коллективные колебания протяженных объектов (струн), составляющих среду в случае нашей сильно коррелированной системы, могут приводить к возникновению калибровочных бозонов (даже фотонов!) [3]. Более того, фермионы могут также появиться в результате коллективных колебанийквантовой жидкости, состоящей из протяженных объектов более сложной природы.
Чтобы избежать теоретико-полевого рассмотрения сплошной среды, обычно вводятся решеточные калибровочные теории, где поля включаются по связям, что соответствует дуальной решетке [17]. Эти поля эквивалентны электромагнитному полю и, согласно [3], порождают петли – калибровочные бозоны в фазе деконфайнмента. При разрыве петель образуются фермионы, которые можно рассматривать как связанные состояния кванта потока поля и заряженной частицы.
Китаев [88, 89] предложил точно решаемую модель, которая подтверждает результаты слейв-бозоннной теории относительно деконфайнмента. Квазичастицы в этой модели несут электрические и магнитные заряды соответствующей калибровочной группы.
В подходе Вена [4] используется представление кубитов – простейших элементов квантовой информации. В отличие от подхода слейв-бозонов, здесь первичными элементами являются псевдоспины, расположенные не в узлах, а на связях решетки. Свойства электромагнитного поля оказываются обусловленными сложной организацией кубитов – нетривиальным топологическим порядком. Если в основном состоянии (вакууме) все кубиты находятся в простейшем “ферромагнитном” состоянии со спином вверх, то состояние с несколькими перевернутыми спинами описывает пространство с несколькими бозе-частицами нулевого спина, которым соответствует скалярное поле. Однако такой простой подход сталкивается с рядом проблем и требует дальнейшего развития. В действительности вакуум должен иметь гораздо более сложное строение.
Наблюдаемые элементарные частицы могут возникать только из нетривиального кубитного эфира, запутанного на больших расстояниях, так что материя состоит из запутанных кубитов. Многообразие свойств материи определяется топологической сложностью организации ее степеней свободы, а не исходным многообразием полей. В этой картине материю можно отождествить с информацией.
Обсуждаемые решеточные теории не являются локальными бозонными моделями, так как в решеточных калибровочных теориях струны неразрывны. Из теории струнных сетей следует, что язык струн на самом деле не обязателен: кубиты сами способны генерировать калибровочные поля, подчиняющиеся уравнениям типа Максвелла или Янга-Миллса. Таким образом, калибровочная симметрия не имеет принципиального значения для калибровочной теории: решеточная калибровочная теория всегда будет воспроизводить калибровочное взаимодействие при низких энергиях. Поскольку калибровочное поле может получаться из локальных моделей кубита без калибровочной симметрии, картина струн превращается в картину дальнодействующей запутанности, а калибровочные поля становятся ее флуктуациями. Струнная сеть есть способ описания закономерностей такой системы [4].
5.1. Конденсация струнных сетей
В дополнение к полевой теории струн необходима физическая картина, которая разъясняет, как возникают топологические фазы из микроскопических степеней свободы. В работе [12] эти вопросы рассмотрены для широкого класса “удвоенных” топологических фаз, которые описываются суммой двух топологических квантово-полевых теорий с противоположными киральностями. Физически они характеризуются четностью и инвариантностью относительно обращения времени.
Как обсуждалось выше, локальные энергетические ограничения могут приводить микроскопические степени свободы к организации в эффективные протяженные объекты – струнные сети. Если кинетическая энергия этих струнных сетях велики, то они могут конденсироваться, давая начало топологическим фазам. Конденсация струнных сетей обеспечивает естественный физический механизм для возникновения топологических фаз в реальных системах конденсированных сред.
С простейшими кубитами на связях, образующих дуальную решетку, мы имеем дело в Z2 решеточной калибровочной теории. Соответствующий гамильтониан модели Китаева запишется в виде [12, 82]
(61)
$\mathcal{H} = - U\sum\limits_i {\prod\limits_{\left\langle {ij} \right\rangle } {\sigma _{{\left\langle {ij} \right\rangle }}^{x}} } - t\sum\limits_p {\prod\limits_{\left\langle {ij} \right\rangle \in p} {\sigma _{{\left\langle {ij} \right\rangle }}^{z}} } ,$В единственном невырожденном основном состоянии мы имеем для всех связей и плакетов ${{A}_{i}} = \prod\nolimits_{\left\langle {ij} \right\rangle } {\sigma _{{\left\langle {ij} \right\rangle }}^{x}} = 1,$ ${{F}_{p}} = \prod\nolimits_{\left\langle {ij} \right\rangle \in p} {\sigma _{{\left\langle {ij} \right\rangle }}^{z}} = 1$ (при этом важно, что $[{{A}_{i}},{{A}_{j}}]$ = $[{{F}_{p}},{{F}_{{p{\text{'}}}}}]$ $[{{A}_{i}},{{F}_{p}}] = 0$). Таким образом, спиновая жидкость является суперпозицией всех конфигураций замкнутых струн с равными положительными коэффициентами.
Спинонное возбужденное состояние в данном формализме является нарушенной связью в базисе $\sigma _{{\left\langle {ij} \right\rangle }}^{z}.$ Поскольку здесь нет сохраняющегося спинового квантового числа, спинон не несет спина, но меняет локальную обменную энергию; в Z2-калибровочной теории спинон несет соответствующий электрический заряд. Состояние спинона имеет собственные значения ${{A}_{i}} = - 1$ и ${{A}_{j}} = 1$ для всех $j \ne 1.$ При этом ${{F}_{p}} = 1$ на всех плакетах, так что спинон является суперпозицией всех конфигураций струн на решетке с единственным свободным концом на узле i.
Визон имеет дополнительную структуру: для него ${{F}_{p}} = - 1$ на одном плакете p и ${{F}_{{p{\text{'}}}}} = 1$ для всех $p{\text{'}} \ne p,$ однако ${{A}_{i}} = 1$ для всех узлов i. Волновая функция по-прежнему является суперпозицией всех конфигураций замкнутых струн, как и в основном состоянии.
Гамильтониан (61) по форме напоминает гамильтониан Хаббарда (1). Первый член в (61) – “электрическая энергия” порядка U, которая является натяжением струны, в то время как “магнитная энергия” порядка t – кинетическая энергия струны. Поэтому данный микроскопический гамильтониан эффективно описывает динамику струн.
Конфайнментная фаза соответствует большой электрической энергии и, следовательно, большому натяжению струны $U \gg t.$ Таким образом, основное состояние представляет собой вакуумную конфигурацию с несколькими небольшими струнами. Деконфайнментная фаза соответствует большой магнитной энергии и, следовательно, большой кинетической энергии, описывая квантовую жидкость больших струн – суперпозицию многих струнных конфигураций, струнный конденсат. Большие струнные сети имеют типичный размер порядка размера системы, заполняя все пространство (см. рис. 16). Переход между этими состояниями напоминает переход Мотта–Хаббарда.
Рис. 16.
Схематическая фазовая диаграмма для гамильтониана струнных сетей (61). Когда ${t \mathord{\left/ {\vphantom {t U}} \right. \kern-0em} U}$ (отношение кинетической энергии к натяжение струны) мало, система находится в нормальной фазе, основное состояние есть вакуум с малым числом сетей. Когда ${t \mathord{\left/ {\vphantom {t U}} \right. \kern-0em} U}$ велико, большие флуктуирующие струнные сети конденсируются. Таким образом, ожидается фазовый переход между двумя состояниями при некотором ${t \mathord{\left/ {\vphantom {t U}} \right. \kern-0em} U}$ порядка единицы.
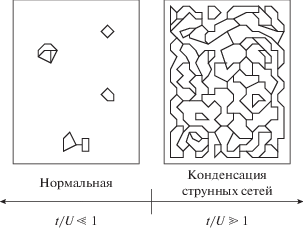
Хотя эти выводы получены в простейшей калибровочной теории – на решетке ${{Z}_{2}},$ подобная, но более сложная картина существует для других деконфайнментных калибровочных теорий.
В модели U(1) рассматриваются кубиты с N целыми уровнями (типами связей), в модели SU(2) возможны полуцелые значения (рис. 17). На каждом узле размещается квант потока, так и возникают струнные сети. Таким образом, топологические фазы возникают при конденсации струнных сетей аналогично тому, как традиционные упорядоченные фазы возникают через конденсацию частиц.
Рис. 17.
Типичные конфигурации струнных сетей в дуальной формулировке (a) ${{Z}_{2}},$ (б) U(1) и (в) SU(2) калибровочной теории [12]. В случае (a) конфигурации состоят из замкнутых (непересекающихся) петель. В случае (б) это ориентированные графы с ребрами, помеченными целыми числами. Они подчиняются правилам ветвления ${{E}_{1}} + {{E}_{2}} + {{E}_{3}} = 0$ для любых трех ребер, встречающихся в точке. В случае (в) сети состоят из (неориентированных) графов с ребрами, помеченными полуцелыми числами ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},1,{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},....$
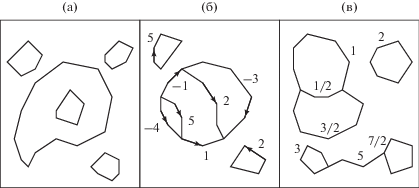
Следует подчеркнуть, что объединение калибровочных бозонов и фермионов струнными сетями существенно отличается от теории суперструн для калибровочных бозонов и фермионов. В теории струнных сетей внутрисетевые калибровочные бозоны и фермионы происходят из кубитов, которые формируют пространство, а “струнная сеть” – это просто модель кубитов, название, которое указывает, как кубиты организованы в основном состоянии. При этом калибровочные бозоны суть волны коллективных флуктуаций струнных сетей, а фермион соответствует концу струны. Напротив, в теории суперструн калибровочные бозоны и фермионы непосредственно происходят из струн, соответствуя их мелким кусочкам. Различные колебания этих кусочков струн приводят к разного рода частицам. Фермионы в теории суперструн получаются “вручную” путем введения грассмановых полей.
5.2. Тензорные сети
Новый язык в теории конденсированного состояния дают тензорные сети (Tensor Networks, TN) [3, 29 ]. В частности, он позволяет описать процессы запутывания и возникновения квантовых топологических состояний. Здесь за основу берется система квантовых псевдоспинов, а волновая функция системы описывается сетью связанных тензоров. Можно сказать, что такой тензор является “управляющей ДНК” для волновой функции: последняя конструируется из фундаментальных блоков-кусков квантового состояния по достаточно простым правилам [29]. В рамках этого метода удается описать широкий класс бозонных, фермионных и спиновых систем с различной размерностью, симметрией и граничными условиями, а также фазовые переходы в них.
Размерность гильбертова пространства, описывающего все связи в многочастичной системе, огромна: она экспоненциально велика по числу частиц (которое само очень велико, порядка числа Авогадро – 1023). К счастью, размерность пространства релевантных состояний в ряде случаев может быть уменьшена. Так, большинство гамильтонианов (в том числе, в теории твердого тела) являются локальными, – например, взаимодействие имеется только между ближайшими соседями. Оказывается, что для низкоэнергетических состояний таких гамильтонианов с щелевым спектром энтропия запутывания двух систем определяется не объемом, а площадью границы (здесь возникает аналогия с голографической моделью вселенной и теорией черных дыр, согласно которым вся информация закодирована на внешней поверхности). Это рассмотрение накладывает ограничение и на физически допустимый вид низкоэнергетических состояний. Более того, при эволюции квантовой многочастичной системы, описываемой локальным гамильтонианом, подавляющее большинство состояний оказывается реально недостижимыми.
Тензорная сеть (TN) – это набор тензоров, в котором некоторые (или даже все) индексы свернуты согласно некоторому правилу (эта операция называется сверткой TN). В результате получается новый тензор с несколькими открытыми индексами. При этом полное числоопераций, необходимых для получения окончательного результата для TN, существенно зависит от порядка свертки индексов. Формализм TN позволяет разбить волновую функцию многочастичного состояния на малые фрагменты.
Следуя обзору [29], рассмотрим квантовую систему из N частиц, степени свободы каждой из которых можно описать p различными состояниями (например, для системы типа квантовой модели Гейзенберга со спином 1/2 имеем $p = 2,$ так что каждая частица представляет собой двухуровневую систему или кубит). Для такой системы любую волновую функцию |Ψ❭, описывающую ее физические свойства, можно записать в виде
(62)
$\left| \Psi \right\rangle = \sum\limits_{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}} {{{C}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}}} \left| {{{i}_{1}}} \right\rangle \otimes \left| {{{i}_{2}}} \right\rangle \otimes \cdots \otimes \left| {{{i}_{N}}} \right\rangle $Простой пример (рис. 18а) – состояние Матричного Произведения (Matrix Product States, MPS) с периодическими граничными условиями. Здесь количество параметров составляет O(NpD2), где открытые индексы в TN принимают p значений, а остальные – D значений. Тогда свертка TN дает тензор ранга N, и, следовательно, ${{p}^{N}}$ коэффициентов. Однако эти коэффициенты не являются независимыми, а получаются из свертки данной TN и поэтому имеют некую структуру.
Рис. 18.
Разложение в тензорные сети тензора $C$ через (a) MPS с периодическими граничными условиями, (б) PEPS с открытым граничным условием и (в) произвольную тензорная сеть.
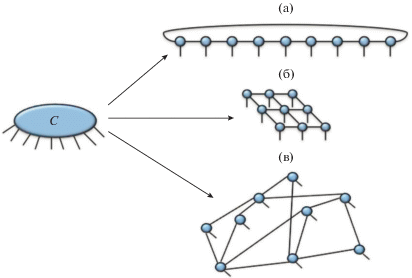
Состояние MPS имеет конечную корреляционную длину тогда и только тогда, когда наибольшее собственное значение ее двойного тензора невырождено. Состояние тензорного произведения (TP) является естественным обобщением состояния MPS на случай двух и большего числа измерений за счет размещения на каждом узле решетки тензоров высших ранга (вместо матриц). Оно также удовлетворяет закону площадей для запутанности. С другой стороны, оно описывает не только состояния с ближней запутанностью, но и топологически упорядоченные состояния с дальней запутанностью.
Замена тензора C на TN предполагает появление дополнительных степеней свободы в системе, которые отвечают за “склеивания” различных блоков нашей ДНК. Эти новые степени свободы обозначаются индексами, соединяющими тензоры в сеть. Такие индексы называются индексами связи и имеют важный физический смысл: они представляют структуру многочастичной запутанности в квантовом состоянии $\left| \Psi \right\rangle ,$ а число их различных значений является количественной мерой квантовых корреляций в волновой функции. Соответствующее максимальное значение D – размерность связи тензорной сети (или внутренняя размерность состояния MPS).
Поясним, как запутанность соотносится с индексом связи. Пусть мы имеем TN-состояние с размерностью связи D для всех индексов (рис. 19). Этот пример TN-состояния называется Проецированным Запутанным Парным Состоянием (Projected Entangled Pair State, PEPS). Оценим для этого состояния энтропию запутанности в случае линейного блока длины L. Введем совокупный индекс всех индексов TN $\bar {\alpha } = \{ {{\alpha }_{1}}{{\alpha }_{2}}...{{\alpha }_{{4L}}}\} .$ Если индексы ${{\alpha }_{i}}$ принимают D значений, $\bar {\alpha }$ может меняться до ${{D}^{{4L}}}.$ Тогда в терминах состояний внутренней и внешней части блока имеем
(63)
$\left| \Psi \right\rangle = \sum\limits_{\bar {\alpha } = 1}^{{{D}^{{4L}}}} {\left| {{\text{in}}(\bar {\alpha })} \right\rangle } \otimes \left| {{\text{out}}(\bar {\alpha })} \right\rangle .$Рис. 19.
Состояния $\left| {{\text{in}}(\bar {\alpha })} \right\rangle $ и $\left| {{\text{out}}(\bar {\alpha })} \right\rangle $ для блоков PEPS 4 × 4 и 6 × 6.
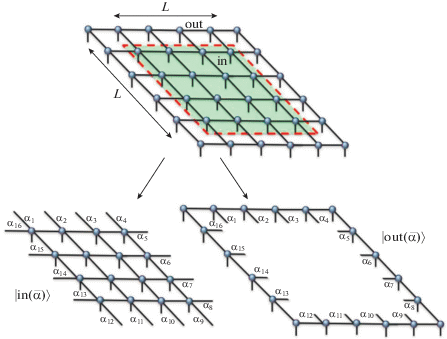
Редуцированная матрица плотности внутренней части запишется как
(64)
$\begin{gathered} {{\rho }_{{{\text{in}}}}} = \sum\limits_{\bar {\alpha },\bar {\alpha }{\text{'}}} {{{X}_{{\bar {\alpha }\bar {\alpha }{\text{'}}}}}} \left| {{\text{in}}(\bar {\alpha })} \right\rangle \left\langle {{\text{in(}}\bar {\alpha }{\text{'}})} \right|, \\ {{X}_{{\bar {\alpha }\bar {\alpha }{\text{'}}}}} \equiv \left\langle {\left. {{\text{out}}(\bar {\alpha }{\text{'}})} \right|{\text{out}}(\bar {\alpha })} \right\rangle , \\ \end{gathered} $MPS – это TN-состояния, которые описывают одномерные системы. В них имеется один тензор для каждого узла в системе многих тел. Соединительные индексы связей, которые склеивают эти тензоры, принимают D значений, а открытые индексы, соответствующие физическим степеням свободы локальных гильбертовых пространств, – p значений. Состояния PEPS (естественное обобщение MPS) позволяют описать случай более высоких пространственных измерений. На рис. 20 показано PEPS для квадратной решетки 4 × 4.
Рис. 20.
$4 \times 4$PEPS-состояния: (a) открытые граничные условия, (б) периодические граничные условия.
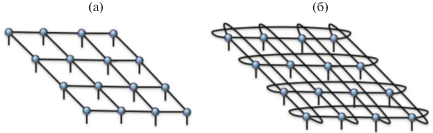
Для того чтобы вычислить ожидаемую величину локальных наблюдаемых в состоянии тензорного произведения, мы должны уметь свертывать двухмерные тензорные сети, что в общем случае не является простой и эффективной процедурой. Однако с этой целью были разработаны приближенные методы, применяемые в квантовых вычислениях [30].
6. ЗАКЛЮЧЕНИЕ
Современная теория конденсированного состояния для систем с сильными корреляциями оперирует существенно многоэлектронными состояниями. В таких системах МЭ-операторы и функции (разд. 2.2) оказываются первичными, а одноэлектронные операторы, в отличие от стандартной процедуры вторичного квантования, возникают при разрыве МЭ-струны. Наглядный пример здесь – андерсоновское состояние RVB, где электрон разделяется на спинон и голон (частицы, формально возникающие из представления МЭ оператора, разд. 2.4). Эти частицы возникают при разрыве связанной валентной пары, а исходно есть только полная волновая функция кристалла.
В отличие от обычной квантовой теории поля с одной стороны и классической топологии с другой, квантовая топология оперирует целыми пространствами многоэлектронных операторов, причем форма и запись последних оказывается неоднозначной (примером служит представление Котляра–Рукенштейна (29) и введение хиггсова поля [116]). Каждый МЭ-оператор представляет собой сложный динамический комплекс: в нем как из семени прорастают различные операторные произведения – процессы рекомбинации МЭ-состояний. Таким образом описываются многочисленные квантовые фазы, которым соответствуют различные спектры возбуждений и физические модели – теории среднего поля, а флуктуации описываются калибровочными полями, определяющими устойчивость этих фаз.
Картина квантовой дальней запутанности (entanglement) меняет наши представления о структуре пространства-времени и корреляции, делая последнюю нелокальной; это существенно связано с топологическими свойствами системы (см. статью [10], где подробно обсуждается обобщенный формализм фейнмановского интеграла по траекториям, описывающий топологию пространства-времени).
Ситуация напоминает эффект Эйнштейна–Подольского–Розена, в котором имеют место непричинные квантовые корреляции на бесконечно большом расстоянии. Дополнительным фактором, способствующим квантовой когерентности, являются топологические инварианты, которые стабилизируют квантовое состояние (в обычных макроскопических системах типа кота Шредингера слабые внешние воздействия приводят к декогеренции таких состояний).
Новое описание на языке коллективных возбуждений протяженных структур – струнных сетей – позволяет единым образом ввести как калибровочные бозоны, так и фермионные частицы [3, 4]. Напротив, классическая геометрическая точка зрения (расслоенные пространства) может привести только к калибровочным взаимодействиям, так что квантовая запутанность открывает новую главу в физике.
В теории конденсированного состояния возможны языки спинов, бозонов или квантов информации – кубитов (простейшее псевдоспиновое представление последних – занятый или пустой узел решетки либо два направления стрелки). Согласно [4], на глубоком уровне материю можно рассматривать как совокупность кубитов. Такое пространство является динамической средой, оно есть океан кубитов, “кубитный эфир”. Тогда материя, т.е. элементарные частицы суть возбуждения – волны, вихри, “пузырьки” и другие дефекты в этом эфире. При этом, согласно формулам квантовой физики и теории относительности, устанавливается эквивалентность массы, энергии, частоты, информации (энтропии).
В топологических подходах основное состояние рассматривается в рамках непертурбативного подхода. Основное состояние в упорядоченных фазах обычно описать не слишком трудно. Оно, как правило, устроено несложно и характеризуется слабой связью и голдстоуновскими возбуждениями. Наиболее интересной является как раз проблема описания “парамагнитного” (формально неупорядоченного) состояния, структура которого (в том числе топологическая, включая ряд спиновых жидкостей) может быть в реальности очень сложной, причем принципиальное значение имеют эффекты фрустрации. В обсуждаемых проблемах мы сталкиваемся с поиском основного состояния системы, которое сформировано квантовыми флуктуациями и обладает большим топологическим вырождением (простейшим примером является синглетное основное состояние гейзенберговского антиферромагнетика, разд. 2.3). Фундаментально важен вопрос об энтропии такого состояния и содержащейся в нем информации, которая может быть колоссальной. Ведь жидкостное состояние – совокупность (суперпозиция) всех возможных положений узлов, а в жидкости струн все положения сами являются матрицами или вмещают тензоры. В такой системе естественно возникает дальнодействующее запутывание.
Топологические фазы, как и любые квантовые системы, обладают огромным пространством состояний, а добавление одного элемента существенно меняет состояние всей системы (например, андерсоновская катастрофа ортогональности [2, 48]).
Топологический порядок и запутывание приводят к ряду новых состояний квантовой материи и физических явлений, таких как дробный заряд, дробная и неабелева статистики… Если мы сможем реализовать квантовую жидкость ориентированных струн в реальных материалах, это позволит нам создать искусственные элементарные частицы, искусственный мир в искусственном вакууме [3, 4]. Эта тематика также подводит нас к философским вопросам о нелокальности и коллективной квантовой природе сознания [133], проблемам виртуальной реальности и т.д. Имеется и возможность применения концепции экзотических топологических состояний к проблеме передачи и хранения информации в живой материи (здесь возникают аналогии со структурой ДНК, см., напр., [29] и обзор [134]).
Хотя теория суперструн в применении к физике элементарных частиц и космологии встретилась с серьезными трудностями [135], аналогичные струнные подходы оказываются весьма полезными в физике конденсированного состояния. В этом контексте разными авторами предлагаются различные струнные концепции [3, 97]. Здесь возникают глубокие связи с квантовой электродинамикой [17] и хромодинамикой [136, 137], причем удобным оказывается формализм электрической и магнитной составляющих калибровочного поля. Помимо физики элементарных частиц, в настоящее время широко используются формальные методы, объединяющие теорию топологических состояний с теорией гравитации и структуры вселенной, в том числе голографические модели (AdS/CFT теория) [138, 139]. Оказывается, что теория петлевой квантовой гравитации может быть переформулирована в терминах определенного типа струнной сети, где струны помечены положительными целыми числами. Таким образом, конденсация струнных сетей в спиновой модели может привести к гравитации [6].
Современная картина спектра возбуждений в конденсированных средах дает новый взгляд и на ряд давних проблем физики твердого тела, в частности на проблему коллективизированного магнетизма и особенно описания парамагнитного состояния – как сильно коррелированных, так и обычных систем. Его природа оказывается крайне сложной: она включает сложную топологию и огромную скрытую информацию. Топология оказывается существенной и при описании корреляционного (хаббардовского) расщепления спектра в многоэлектронных системах (см. разд. 3.6).
Что касается практических применений, формализм тензорных сетей находит применение в квантовых нейронных сетях [30], а топологические фазы в линейных и плоских структурах и даже трехмерных материалах могут быть использованы в новых поколениях электроники и потенциально в квантовых компьютерах.
Работа выполнена в рамках государственного задания ФАНО России (тема “Поток” № AAAA-A18-118020190112-8 и тема “Квант” № AAAA-A18-118020190095-4). Раздел 4 подготовлен при поддержке Российского Научного Фонда (проект 17-12-01207).
Список литературы
Anderson P.W. The resonating valence bond state in La2CuO4 and superconductivity // Science. 1987. V. 235. Issue 4793. P. 1196–1198.
Anderson P.W. Personal history of my engagement with cuprate superconductivity, 1986–2010 // Int. J. Mod. Phys. B. 2011. V. 25. № 1. P. 1–39.
Wen X.G. Quantum Field Theory of Many-Body Systems – From the Origin of Sound to an Origin of Light and Electrons. Oxford University Press, 2004.
Zeng B. et al. Quantum information meets quantum matter, from quantum entanglement to topological phase in many-body systems. In the Springer Book Series – Quantum Information Science and Technology in press // arXiv preprint arXiv:1508.02595. 2015.
Wen X.G. Zoo of quantum-topological phases of matter // Rev. Mod. Phys. 2017. V. 89. № 4. P. 41004.
Levin M.A., Wen X.G. Photons and electrons as emergent phenomena // Rev. Mod. Phys. 2005. V. 77. № 3. P. 871–880.
Sachdev S. Quantum Phase Transitions. Massachusetts: Harvard University, 2011.
Coleman P. Many Body Physics: Unfinished Revolution // Annales Henri Poincaré. 2003. V. 4. Issue 2. Suppl. P. 559–580.
Turaev V.G. Quantum Invariants of Knots and 3-Manifolds. Berlin–New York: W. de Gruyter, 1994.
Kauffman L.H. Quantum topology and quantum computing // Proc. of Symposia in Appl. Mathematics. 2002. V. 58. P. 273–304.
Kassel C. Quantum Groups. New York: Springer-Verlag, 1995.
Levin M.A., Wen X.G. String-net condensation: A physical mechanism for topological phases // Phys. Rev. B. 2005. V. 71. P. 045110.
Tsui D.C., Stormer H.L., Gossard A.C. Two-dimensional magnetotransport in the extreme quantum limit // Phys. Rev. Lett. 1982. V. 48. P. 1559–1562.
Bednorz J.G., Müeller K.A. Possible high ${{T}_{c}}$ superconductivity in the barium-lanthanum-copper-oxygen system // Z. Phys. B. 1986. V. 64. Issue 2. P. 189–193.
Witten E. Quantum field theory and the Jones polynomial // Comm. Math. Phys. 1989. V. 121. P. 351–399.
Воловик Г.Е. Экзотические переходы Лифшица в топологической материи // УФН. 2018. Т. 188. № 1. С. 95–105.
Kogut J.B. Introduction to lattice gauge theory and spin systems // Rev. Mod. Phys. 1979. V. 51. № 4. P. 659–713.
Kalmeyer V., Laughlin R.B. Equivalence of the resonating-valence-bond and fractional quantum Hall states // Phys. Rev. Lett. 1987. V. 59. P. 2095–2098.
Wen X.G., Wilczek F., Zee A. Chiral spin states and superconductivity // Phys. Rev. B. 1989. V. 39. P. 11 413–11 423.
Wen X.G. Topological orders in rigid states // Int. J. Mod. Phys. B. 1990. V. 4. P. 239–271.
Zeng B., Wen X.G. Gapped quantum liquids and topological order, stochastic local transformations and emergence of unitarity // Phys. Rev. B. 2015. V. 91. P. 125 121.
Swingle B., McGreevy J. Renormalization group constructions of topological quantum liquids and beyond // Phys. Rev. B. 2016. V. 93. P. 045127.
Kitaev A., Preskill J. Topological entanglement entropy // Phys. Rev. Lett. 2006. V. 96. P. 110404.
Levin M., Wen X.G. Detecting topological order in a ground state wave function // Phys. Rev. Lett. 2006. V. 96. P. 110405.
Chen X., Gu Z.C., Wen X.G. Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order // Phys. Rev. B. 2010. V. 82. P. 155138.
Mermin N.D. The topological theory of defects in ordered media // Rev. Mod. Phys. 1979. V. 51. № 3. P. 591–648.
Landau L.D. Theory of phase transformations I // Phys. Z. Sowjetunion. 1937. V. 11. P. 26.
Гинзбург В.Л., Ландау Л.Д. К теории сверхпроводимости // ЖЭТФ. 1950. Т. 20. С. 1064–1082.
Orús R. A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States // Annals of Physics. 2014. V. 349. P. 117–158.
Deng D.L., Li X., Das Sarma S. Quantum Entanglement in Neural Network States // Phys. Rev. X. 2017. V. 7. P. 021021.
Baskaran G., Anderson P.W. Gauge theory of high-temperature superconductors and strongly correlated Fermi systems // Phys. Rev. B. 1988. V. 37. P. 580–583.
Lee P.A., Nagaosa N., Wen X.G. Doping a Mott insulator: Physics of high-temperature superconductivity // Rev. Mod. Phys. 2006. V. 78. № 1. P. 17–85.
Senthil T. et al. Deconfined quantum critical points // Science. 2004. V. 303. Issue 5663. P. 1490–1494.
Senthil T. et al. Quantum criticality beyond the Landau-Ginzburg-Wilson paradigm // Phys. Rev. B. 2004. V. 70. P. 144407.
Бете Г., Зоммерфельд A. Электронная теория металлов: Пер. с нем. Л.-М.: ОНТИ НКТП СССР, Гостехиздат, 1938.
Schubin S., Wonsowsky S. On the electron theory of metals // Proc. Roy. Soc. A. 1934. V. 145. P. 159.
Шубин С.П. Избранные труды по теоретической физике. Свердловск: УрО АН СССР, 1991.
Hubbard J. Electron correlations in narrow energy bands // Proc. Roy. Soc. A. 1963. V. 276. № 1365. P. 238–257.
Hubbard J. Electron correlations in narrow energy bands. III. The atomic representation // Proc. Roy. Soc. A. 1965. V. 285. № 1403. P. 542–560.
Боголюбов Н.Н. Лекции по квантовой статистике. Избранные труды, т. 2. Киев: Наукова думка, 1970.
Собельман И.И. Введение в теорию атомных спектров. М.: Физматгиз, 1963.
Ирхин Ю.П. Теория обменного взаимодействия для случая нескольких магнитных электронов на атом // ЖЭТФ. 1966. Т. 50. № 2. С. 379–394.
Ирхин В.Ю., Ирхин Ю.П. Представление хаббардовских операторов в многоэлектронных моделях с реальными атомными конфигурациями // ФММ. 1993. Т. 76. № 6. С. 49–60.
Irkhin V.Yu., Irkhin Yu.P. Many-electron operator approach in the solid state theory // Phys. Stat. Sol. (b). 1994. V. 183. P. 9–58.
Джадд В.Р. Вторичное квантование и атомная спектроскопия: Пер. с англ. М.: Мир, 1970.
Lieb E.H., Schultz T.D., Mattis D.C. Two soluble models of an antiferromagnetic chain // Annals of Physics. 1961. V. 16. Issue 3. P. 407–466.
Auslender M.I., Irkhin V.Yu., Katsnelson M.I. Itinerant electron ferromagnetism in narrow energy bands // J. Phys. C: Solid State Phys. 1988. V. 21. № 32. P. 5521–5538.
Anderson P.W. Hidden Fermi liquid: The secret of high-${{T}_{c}}$ cuprates // Phys. Rev. B. 2008. V. 78. P. 174505.
Вонсовский С.В., Кацнельсон М.И., Трефилов А.В. Локализованное и делокализованное поведение электронов в металлах // ФММ. 1993. Т. 76. № 4. С. 3–93.
Caron L.G., Pratt G.W., Jr Correlation and magnetic effects in narrow energy bands. II // Rev. Mod. Phys. 1968. V. 40. № 4. P. 802–806.
Vollhardt D. Normal 3He: an almost localized Fermi liquid // Rev. Mod. Phys. 1984. V. 56. №1. P. 99–120.
Katsnelson M.I., Vonsovskii S.V. Possible effect of exciton condensation on properties of ferromagnetic metals // J. Magn. Magn. Mater. 1980. V. 15–18. P. 275–276.
Vonsovsky S.V., Irkhin V.Yu., Katsnelson M.I. Exciton approach to the description of the antiferromagnetic ground state in the Heisenberg and Hubbard model // J. Magn. Magn. Mater. 1986. V. 58. Issues 3–4. P. 309–312.
Irkhin V.Yu., Katsnelson M.I. On the ground-state wavefunction of a superconductor in the BCS model // Phys. Lett. A. 1984. V. 104. Issue 3. P. 163–165.
Katsnelson M.I., Irkhin V.Yu. Metal-insulator transition and antiferromagnetism in the ground state of the Hubbard model // J. Phys C: Solid State Phys. 1984. V. 17. № 24. P. 4291–4308.
Irkhin V.Yu., Katsnelson M.I. On the description of the antiferromagnetism without anomalous averages // Z. Phys. B. 1986. V. 62. Issue 2. P. 201–205.
Donker H.C., De Raedt H., Katsnelson M.I. Decoherence wave in magnetic systems and creation of Neel antiferromagnetic state by measurement // Phys. Rev. B. 2016. V. 93. P. 184426.
Ирхин В.Ю., Кацнельсон М.И. Theory of intermediate-valence semiconductors // ЖЭТФ. 1986. Т. 90. № 3. С. 1080–1091.
Chowdhury D., Sodemann I., Senthil T. Mixed-valence insulators with neutral Fermi surfaces // Nature Communications. 2018. V. 9. P. 1766.
Hohenadler M., Assaad F.F. Fractionalized Metal in a Falicov-Kimball Model // Phys. Rev. Lett. 2018. V. 121. P. 086601.
Kotliar G., Ruckenstein A.E. New Functional Integral Approach to Strongly Correlated Fermi Systems: The Gutzwiller Approximation as a Saddle Point // Phys. Rev. Lett. 1986. V. 57. P. 1362–1365.
Lavagna M. Functional-integral approach to strongly correlated Fermi systems: Quantum fluctuations beyond the Gutzwiller approximation // Phys. Rev. B. 1990. V. 41. P. 142–148.
Igoshev P.A. et al. Spiral magnetism in the single-band Hubbard model: the Hartree–Fock and slave-boson approaches // J. Phys.: Condens. Matter. 2015. V. 27. P. 446 002.
Frésard R., Wölfle P. Unified slave boson representation of spin and charge degrees of freedom for strongly correlated Fermi systems // Int. J. Mod. Phys. B. 1992. V. 6. P. 685–704.
Irkhin V.Yu., Katsnelson M.I. Ground state and electron-magnon interaction in an itinerant-electron ferromagnet: half-metallic ferromagnets // J. Phys.: Condens. Matter. 1990. V. 2. P. 7151–7171.
Florens S., Georges A. Slave-rotor mean field theories of strongly correlated systems and the Mott transition in finite dimensions // Phys. Rev. B. 2004. V. 70. P. 035 114.
Zhao E., Paramekanti A. Self-consistent slave rotor mean-field theory for strongly correlated systems // Phys. Rev. B. 2007. V. 76. P. 195101.
Kim K.S. Bandwidth-control versus doping-control Mott transition in the Hubbard model // Phys. Rev. B. 2006. V. 74. P. 115122.
Kim K.S. How to control pairing fluctuations: SU(2) slave-rotor gauge theory of the Hubbard model // Phys. Rev. B. 2007. V. 75. P. 245105.
Wang Y.R. Exact representation of the large-U Hubbard model and its application // Phys. Rev. B. 1995. V. 51. P. 234–239.
Изюмов Ю.А. Сильно коррелированные электроны: t–J-модель // УФН. 1997. Т. 167. № 5. С. 465–497.
Pépin C., Lavagna M. Supersymmetric Approach to Heavy–Fermion Systems // Z. Phys. B. 1996. V. 103. Issue 2. P. 259–261.
Zou Z., Anderson P.W. Neutral fermions, charge-$e$ boson excitations in the resonating-valence-bond state and superconductivity in La2CuO4-based compounds // Phys. Rev. B. 1988. V. 37. P. 627–630.
Anderson P.W., Casey P.A. Transport anomalies of the strange metal: Resolution by hidden Fermi liquid theory // Phys. Rev. B. 2009. V. 80. P. 094508.
Castellani C. et al. Collective excitations, photoemission spectra, and optical gaps in strongly correlated Fermi systems // Phys. Rev. Lett. 1992. V. 69. P. 2009–2012.
Ирхин В.Ю., Кацнельсон М.И. Спиновые волны в узкозонных ферромагнитных полупроводниках // ЖЭТФ. 1985. Т. 88. № 2. С. 522–531.
Irkhin V.Yu., Katsnelson M.I. Spin waves in narrow band ferromagnets // J. Phys. C: Solid State Phys. 1985. V. 18. № 21. P. 4173–4188.
Ribeiro T.C., Wen X.G. Doped carrier formulation and mean-field theory of the
 model // Phys. Rev. B. 2006. V. 74. P. 155113.
model // Phys. Rev. B. 2006. V. 74. P. 155113.
Ирхин В.Ю. Необычный магнетизм решеток Кондо // УФН. 2017. Т. 187. № 8. С. 801–816.
Narikiyo O., Kuboki K., Fukuyama H. Anyons in Extended t–J Model // J. Phys. Soc. Japan. 1990. V. 59. № 7. P. 2443–2456.
Senthil T. Critical Fermi surfaces and non-Fermi liquid metals // Phys. Rev. B. 2008. V. 78. P. 035103.
Sachdev S. Exotic phases and quantum phase transitions: model systems and experiments. Rapporteur talk at the 24th Solvay Conference on Physics, Quantum Theory of Condensed Matter, Brussels, Oct 2008; arXiv preprint arXiv:0901.4103.
Raimondi R., Castellani C. Lower and upper Hubbard bands: A slave-boson treatment // Phys. Rev. B. 1993. V. 48. P. 11453(R).
Yang K.Y., Rice T.M., Zhang F.C. Phenomenological theory of the pseudogap state // Phys. Rev. B. 2006. V. 73. P. 174501.
Ng T.K. Spinon-holon binding in t–J model // Phys. Rev. B. 2005. V. 71. P. 172509.
Изюмов Ю.А., Кацнельсон М.И., Скрябин Ю.Н. Магнетизм коллективизированных электронов. М.: Наука, 1994.
Wen X.G., Lee P.A. Theory of Underdoped Cuprates // Phys. Rev. Lett. 1996. V. 76. P. 503–506.
Kitaev A.Y. Fault-tolerant quantum computation by anyons // Annals of Physics. 2003. V. 303. Issue 1. P. 2–30.
Kitaev A.Y. Anyons in an exactly solved model and beyond // Annals of Physics. 2006. V. 321. Issue 1. P. 2–111.
Irkhin V.Yu., Katsnelson M.I. RVB-type states in systems with charge and spin degrees of freedom: Sm3Se4, Y1 –xSexMn2 etc // Phys. Lett. A. 1990. V. 150. Issue 1. P. 47–50.
Polyakov A.M. Gauge fields and strings. London: Harwood Academic, 1987.
Tang Y., Sandvik A.W. Confinement and Deconfinement of Spinons in Two Dimensions // Phys. Rev. Lett. 2013. V. 110. P. 217213.
Piazza B.D. et al. Fractional excitations in the square-lattice quantum antiferromagnet // Nature Physics. 2015. V. 11. P. 62–68.
Ирхин В.Ю., Скрябин Ю.Н. Точки Дирака, спиноны и спиновая жидкость в “повернутом” двухслойном графене // Письма в ЖЭТФ. 2018. Т. 107. № 10. С. 684–688.
Kim D.H., Lee P.A. Theory of Spin Excitations in Undoped and Underdoped Cuprates // Annals of Physics. 1999. V. 272. P. 130–164.
Weng Z.Y. Phase string theory for doped antiferromagnets // Int. J. Mod. Phys. B. 2007. V. 21. № 6. P. 773–827.
Weng Z.Y. Mott physics, sign structure, ground state wavefunction, and high-Tc superconductivity // Front. Phys. 2011. V. 6. № 4. P. 370–378.
Zaanen Z., Overbosch B.J. Mottness collapse and statistical quantum criticality // Phil. Trans. R. Soc. A. 2011. V. 369. P. 1599–1625.
Weng Z.Y. Understanding high ${{T}_{c}}$ superconductivity // Proceedings of the International Symposium on Frontiers of Science, Ed. H.-T. Nieh, World Scientific, Singapore, 2003, p. 109; arXiv:cond-mat/0304261.
Ye P. et al. Electron fractionalization and unconventional order parameters of the t–J model // Nuclear Physics B. 2012. V. 854. P. 815–840.
Coleman P., Andrei N. Kondo-stabilised spin liquids and heavy fermion superconductivity // J. Phys.: Condens. Matter. 1989. V. 1. P. 4057–4080.
Irkhin V.Yu., Katsnelson M.I. Kondo effect, spin dynamics and magnetism in anomalous rare earth and actinide compounds II. The problem of ground state // Z. Phys. B. 1991. V. 82. Issue 1. P. 77–85.
Senthil T., Vojta M., Sachdev S. Weak magnetism and non-Fermi liquids near heavy-fermion critical points // Phys. Rev. B. 2004. V. 69. P. 035 111.
Coleman P., Nevidomskyy A.H. Frustration and the Kondo effect in heavy fermion materials // J. Low Temp. Phys. 2010. V. 161. Issue 1–2. P. 182–232.
Senthil T., Sachdev S., Vojta M. Quantum phase transitions out of the heavy Fermi liquid // Physica B. 2005. V. 359–361. P. 9–16.
Isaev L., Vekhter I. Heavy antiferromagnetic phases in Kondo lattices // Phys. Rev. Lett. 2013. V. 110. P. 026 403.
Sachdev S., Metlitski M.A., Punk M. Antiferromagnetism in metals: from the cuprate superconductors to the heavy fermion materials // J. Phys.: Cond. Mat. 2012. V. 24. P. 294 205.
Punk M., Sachdev S. Fermi surface reconstruction in hole-doped t–J models without long-range antiferromagnetic order // Phys. Rev. B. 2012. V. 85. P. 195 123.
Xu C., Sachdev S. Majorana liquids: the complete fractionalization of the electron // Phys. Rev. Lett. 2010. V. 105. P. 057 201.
Abanov Ar., Chubukov A.V., Schmalian J. Quantum-critical theory of the spin-fermion model and its application to cuprates: Normal state analysis // Adv. Phys. 2003. V. 52. № 3. P. 119–218.
Katanin A.A., Irkhin V.Yu. Spectral functions of two-dimensional systems with coupling of electrons to collective or localized spin degrees of freedom // Phys. Rev. B. 2008. V. 77. P. 115129.
Oshikawa M. Topological Approach to Luttinger’s Theorem and the Fermi Surface of a Kondo Lattice // Phys. Rev. Lett. 2000. V. 84. P. 3370–3373.
Vojta M. Frustration and quantum criticality // Rep. Prog. Phys. 2018. V. 81. P. 064501.
Senthil T., Lee P.A. Cuprates as doped U(1) spin liquids // Phys. Rev. B. 2005. V. 71. P. 174515.
Senthil T. et al. Deconfined criticality critically defined // J. Phys. Soc. Japan. 2005. V. 74. Issue Suppl. P. 1–9.
Chowdhury D., Sachdev S. Higgs criticality in a two-dimensional metal // Phys. Rev. B. 2015. V. 91. P. 115 123.
Hertz J.A. Quantum critical phenomena // Phys. Rev. B. 1976. V. 14. P. 1165–1184.
Millis A.J. Effect of nonzero temperature on quantum critical points in itinerant fermion systems // Phys. Rev. B. 1993. V. 48. P. 7183–7196.
Kaul R.K., Kim Y.B., Sachdev S., Senthil T. Algebraic charge liquids // Nature Physics. 2008. V. 4. P. 28.
Scheurer M.S. et al. Topological order in the pseudogap metal // Proc. National Academy of Sciences. 2018. V. 115. P. E3665; arXiv preprint arXiv: 1711.09925.
Anderson P.W. Polarization of photoelectrons from ferromagnetic metals // Phil. Mag. 1971. V. 24. P. 203–211.
Corrias M. Electron correlations in itinerant strong ferromagnetism // J. Phys. F: Met. Phys. 1975. V. 5. P. L31–L34.
Edwards D.M., Hertz J.A. Electron-magnon interactions in itinerant ferromagnetism. II. Strong ferromagnetism // J. Phys. F. 1973. V. 3. P. 2191–2205.
Edwards D.M., Hertz J.A. Fermi liquid behaviour breakdown // Physica B. 1990. V. 163. P. 527–529.
Igarashi J. Three Body Problem in Transition Metals – Application to Nickel // J. Phys. Soc. Japan. 1983. V. 52. № 8. P. 2827–2837.
Kane C.L., Lee P.A., Read N. Motion of a single hole in a quantum antiferromagnet // Phys. Rev. B. 1989. V. 39. P. 6880–6897.
Igoshev P.A. et al. Incommensurate magnetic order and phase separation in the two-dimensional Hubbard model with nearest- and next-nearest-neighbor hopping // Phys. Rev. B. 2010. V. 81. P. 094407.
Igoshev P.A. et al. Magnetic phase transitions and unusual antiferromagnetic states in the Hubbard model // J. Magn. Magn. Mater. 2018. V. 459. P. 311–316.
Wen X.G. Mean-field theory of spin-liquid states with finite energy gap and topological orders // Phys. Rev. B. 1991. V. 44. P. 2664–2672.
Hansson T.H., Oganesyan V., Sondhi S.L. Superconductors are topologically ordered // Annals of Physics. 2004. V. 313. Issue 2. P. 497–538.
Elitzur S. Impossibility of spontaneously breaking local symmetries // Phys. Rev. D. 1975. V. 12. P. 3978–3982.
Polyakov A.M. String representations and hidden symmetries for gauge fields // Phys. Lett. B. 1979. V. 82. № 2. P. 247–250.
Менский М.Б. Концепция сознания в контексте квантовой механики // УФН. 2005. Т. 175. № 4. С. 413–435.
Irkhin V.Yu., Nikiforov V.N. Quantum effects and magnetism in the spatially distributed DNA molecules // J. Magn. Magn. Mater. 2018. V. 459. P. 345–349.
Смолин Л. Неприятности с физикой: взлет теории струн, упадок науки и что за этим следует. London: Penguin Book, 2007.
Kogut J.B. The lattice gauge theory approach to quantum chromodynamics // Rev. Mod. Phys. 1983. V. 55. № 3. P. 775–836.
Thomson A., Sachdev S. Fermionic Spinon Theory of Square Lattice Spin Liquids near the Neel State // Phys. Rev. X. 2018. V. 8. P. 011012.
Hartnoll S.A., Lucas A., Sachdev S. Holographic quantum matter. Cambridge, Massachusetts: MIT Press, 2018; arXiv preprint arXiv:1612.07324.
Sachdev S. What can gauge-gravity duality teach us about condensed matter physics? // Annual Review of Condensed Matter Physics. 2012. V. 3. P. 9; arXiv preprint arXiv:1108.1197.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение