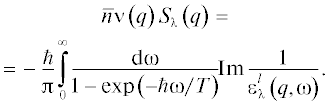1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 121, № 2, 2020

Физика металлов и металловедение, 2020, T. 121, № 2, стр. 122-127

О термодинамике электронной жидкости

В. Б. Бобров *

Объединенный институт высоких температур РАН
125412 Москва, ул. Ижорская, 13, стр. 2, Россия

* E-mail: vic5907@mail.ru

Поступила в редакцию 03.06.2019
После доработки 18.06.2019
Принята к публикации 28.06.2019

Полный текст (PDF)

Аннотация

С использованием теоремы вириала и уравнения движения для одночастичной функции Грина получены явные точные выражения для термодинамических функций электронной жидкости через одночастичную функцию Грина, а также сформулированы условия самосогласования для этих функций.

Ключевые слова: электронная жидкость, термодинамические функции, теорема вириала, одночастичная функция Грина

ВВЕДЕНИЕ

При исследовании металлического состояния, которое характеризуется слабым взаимодействием между электронами проводимости и ионами, в качестве исходного приближения широко применяется модель электронной жидкости (ЭЖ) (однокомпонентной электронной плазмы), которая представляет собой квантовую систему электронов, находящихся в компенсирующем фоне ионов [1–3]. Модель ЭЖ имеет существенное значение и при исследовании металлических кластеров (см., напр., [4]). В последние годы интерес к изучению этой модельной системы возрос в связи с возможностями численного моделирования и результатами исследований так называемой warm dense matter (теплого плотного вещества, см. подробнее [5‒10] и цитированную там литературу).

Сложности в теоретическом рассмотрении свойств ЭЖ обусловлены необходимостью одновременного учета коллективных эффектов, прежде всего экранирования кулоновского взаимодействия, и квантового описания, включая эффекты тождественности электронов [1–3]. Принципиальная возможность разрешения возникающих проблем основана на использовании различных вариантов диаграммной техники теории возмущений по кулоновскому взаимодействию электронов, разработанных в рамках методов квантовой теории поля (см., напр., [11, 12]). В этом случае основополагающим объектом является одночастичная функция Грина (ОФГ), что обусловлено возможностью представления термодинамического потенциала для ЭЖ как функционала ОФГ. На этой основе может быть построена динамическая вариационная процедура Латтинжера–Уорда [13] и Каданова–Бейма [14]. Однако явный вид подобных функционалов может быть представлен только в виде бесконечного функционального ряда теории возмущений по кулоновскому взаимодействию электронов (см. подробнее [15, 16]). Тем самым возникает традиционная проблема “обрыва” такого ряда, т.е. обоснования методов последовательного приближенного вычисления как ОФГ, так и термодинамических функций ЭЖ. В этой ситуации особое значение приобретают точные соотношения между функциями Грина (ФГ) и термодинамическим потенциалом ЭЖ вне рамок теории возмущений.

ТЕРМОДИНАМИЧЕСКИЙ ПОТЕНЦИАЛ И ТЕОРЕМА ВИРИАЛА

Рассмотрим пространственно однородную и изотропную систему точечных электронов с массой $m$ и спином $s = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ которая занимает объем $V$ и характеризуется гамильтонианом

(1)
$\begin{gathered} \hat {H} = {{{\hat {H}}}_{0}} + \hat {U},\,\,\,\,{{{\hat {H}}}_{0}} = \sum\limits_p {{{{\varepsilon }}_{0}}} \left( p \right)\hat {a}_{p}^{ + }{{{\hat {a}}}_{p}}, \\ \hat {U} = \frac{1}{{2V}}\sum\limits_{p,k,q \ne 0} {\nu \left( q \right)} \hat {a}_{p}^{ + }\hat {a}_{{k + q}}^{ + }{{{\hat {a}}}_{k}}{{{\hat {a}}}_{{p + q}}}, \\ {{{\varepsilon }}_{0}}\left( p \right) = {{\hbar }^{2}}{{{{{\mathbf{p}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\mathbf{p}}}^{2}}} {2m.}}} \right. \kern-0em} {2m.}} \\ \end{gathered} $

Здесь и далее ${{\hat {H}}_{0}}$ – гамильтониан невзаимодействующих электронов, $\hat {U}$ – гамильтониан кулоновского взаимодействия электронов,

(2)
$p \equiv \left( {{\mathbf{p}},{{{\sigma }}_{1}}} \right),\,\,\,\,k \equiv \left( {{\mathbf{k}},{{{\sigma }}_{2}}} \right),\,\,\,\,\,q \equiv {\mathbf{q}},$

$\hat {a}_{p}^{ + }$ и ${{\hat {a}}_{p}}$ – соответственно, операторы рождения и уничтожения электронов в состоянии, которое характеризуется импульсом $\hbar {\mathbf{p}}$ и проекцией спина ${{{\sigma }}_{1}},$ ${{{\sigma }}_{1}},{{{\sigma }}_{2}} = - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},~ + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2};$ $\nu \left( q \right) = 4{{\pi {{e}^{2}}} \mathord{\left/ {\vphantom {{\pi {{e}^{2}}} {{{q}^{2}}}}} \right. \kern-0em} {{{q}^{2}}}}$ – фурье-компонента потенциала кулоновского взаимодействия электронов $\varphi \left( r \right){\text{:}}$

(3)
$\nu \left( q \right) = \smallint {{{\text{d}}}^{3}}r{\text{exp}}\left( { - {\text{i}}{\mathbf{q}} \cdot {\mathbf{r}}} \right){\varphi }\left( {\left| {\mathbf{r}} \right|} \right),\,\,\,\,{\varphi }\left( r \right) = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} r}} \right. \kern-0em} r}.$

Термодинамический потенциал ${\Omega }\left( {V,T,{\mu }} \right)$ для ЭЖ при температуре $T$ (в энергетических единицах) равен

(4)
${\Omega }\left( {V,T,{\mu }} \right) = - T\ln {\text{Trexp}}\left( { - {{\left( {\hat {H} - {\mu }\hat {N}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {H} - {\mu }\hat {N}} \right)} T}} \right. \kern-0em} T}} \right),~$
где ${\mu }~$ – химический потенциал, $\hat {N} = \sum\nolimits_p {\hat {a}_{p}^{ + }{{{\hat {a}}}_{p}}} $ – оператор полного числа электронов в рассматриваемой системе.

Как было отмечено выше, термодинамический потенциал ${\Omega }\left( {V,T,{\mu }} \right),$ который полностью определяет термодинамические свойства ЭЖ, является функционалом ОФГ $g\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right){\text{:}}$ ${\Omega } = {\Omega }\left[ g \right]$ [11–14]. Здесь и далее

(5)
$\begin{gathered} g\left( {\hat {A},\hat {B};{\text{i}}{{{\omega }}_{n}}} \right) \equiv \\ \equiv \,\, - \frac{1}{2}\int\limits_{ - {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}}^{{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}} d \tau {\text{exp}}\left( {{\text{i}}{{{\omega }}_{n}}{\tau }} \right)\left\langle {{{{\hat {T}}}_{{\tau }}}\left( {\hat {A}\left( {\tau } \right)\hat {B}\left( 0 \right)} \right)} \right\rangle , \\ \end{gathered} $
(6)
$\hat {A}\left( {\tau } \right) = {\text{exp}}\left( {\left( {\hat {H} - {\mu }\hat {N}} \right){\tau }} \right)\hat {A}{\text{exp}}\left( { - \left( {\hat {H} - {\mu }\hat {N}} \right){\tau }} \right),~$

${{\hat {T}}_{{\tau }}}~$ – оператор ${\tau } - $ упорядочения, угловые скобки обозначают усреднение с большим каноническим распределением Гиббса (см. (4)), ωn = (2n + + 1)πT где $n$ – целое число, включая нуль [11].

Соотношения (4)–(6) имеют смысл только после перехода к термодинамическому пределу ${\text{Li}}{{{\text{m}}}_{T}}:~~V \to \infty ,$ $\left\langle {\hat {N}} \right\rangle \to \infty ,$ $\bar {n} = {{\left\langle {\hat {N}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\hat {N}} \right\rangle } V}} \right. \kern-0em} V} = {\text{const}}$ [17]. В результате соотношение (4) принимает вид

(7)
$P\left( {T,{\mu }} \right) = - {\text{Li}}{{{\text{m}}}_{T}}{\Omega }{{\left( {V,T,{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {V,T,{\mu }} \right)} V}} \right. \kern-0em} V},$
где $P\left( {T,{\mu }} \right)$ – давление в ЭЖ, которая характеризуется средней плотностью числа частиц $\bar {n}{\text{:}}$

(8)
$\bar {n}\left( {T,{\mu }} \right) = {\text{Li}}{{{\text{m}}}_{T}}\frac{1}{V}~\sum\limits_p f \left( p \right) = \sum\limits_\sigma {\int {\frac{{{{{\text{d}}}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } f\left( {{\mathbf{p}},\sigma } \right),$

$f\left( {{\mathbf{p}},\sigma } \right) = \left\langle {\hat {a}_{{{\mathbf{p}},\sigma }}^{ + }{{{\hat {a}}}_{{{\mathbf{p}},\sigma }}}} \right\rangle $ – точная одночастичная функция распределения по импульсам $\hbar {\mathbf{p}}$ и проекциям спина σ, которая в приближении идеального газа соответствует распределению Ферми–Дирака.

С другой стороны, согласно теореме вириала, которая имеет место для любого из распределений Гиббса (см. [17, 18] и цитированную там литературу), справедливо равенство

(9)
$P\left( {T,{\mu }} \right) = \frac{{2\left\langle k \right\rangle }}{3} - {\text{Li}}{{{\text{m}}}_{T}}\frac{{\left\langle {{\mathbf{r}} \cdot {{\nabla }_{{\mathbf{r}}}}{\varphi }\left( {\left| {\mathbf{r}} \right|} \right)} \right\rangle }}{{3V}},$
где $\left\langle k \right\rangle $ – средняя кинетическая энергия электронов, приходящаяся на единицу занимаемого ею объема $V{\text{:}}$

(10)
$\begin{gathered} \left\langle k \right\rangle = {\text{Li}}{{{\text{m}}}_{T}}\frac{1}{V}~\sum\limits_p {{{{\varepsilon }}_{0}}} \left( p \right)f\left( p \right) = \\ = \sum\limits_\sigma {\int {\frac{{{{{\text{d}}}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } {{{\varepsilon }}_{0}}\left( p \right)f\left( {{\mathbf{p}},\sigma } \right), \\ \end{gathered} $

а величина $\left\langle {{\mathbf{r}} \cdot {{\nabla }_{{\mathbf{r}}}}{\varphi }\left( {\left| {\mathbf{r}} \right|} \right)} \right\rangle $ является вириалом для потенциальной энергии,

(11)
${\text{Li}}{{{\text{m}}}_{T}}\frac{1}{V}\left\langle {{\mathbf{r}} \cdot {{\nabla }_{{\mathbf{r}}}}{\varphi }\left( r \right)} \right\rangle = \frac{1}{2}{{\bar {n}}^{2}}\int {{{{\text{d}}}^{3}}r} \left( {{\mathbf{r}} \cdot {{\nabla }_{{\mathbf{r}}}}{\varphi }\left( r \right)} \right){{g}_{2}}\left( r \right).$

Здесь ${{g}_{2}}\left( r \right)$ – точная парная корреляционная функция. Учитывая в (11) явный вид потенциала кулоновского взаимодействия электронов ${\varphi }\left( r \right)$ (3), нетрудно убедиться, что в ЭЖ

(12)
$\begin{gathered} {\text{Li}}{{{\text{m}}}_{T}}\frac{1}{V}\left\langle {{\mathbf{r}} \cdot {{\nabla }_{{\mathbf{r}}}}{\varphi }\left( r \right)} \right\rangle = - \left\langle u \right\rangle , \\ \left\langle u \right\rangle = \frac{1}{2}~\sum\limits_{p,k,q \ne 0} \nu \left( q \right)\left\langle {\hat {a}_{p}^{ + }\hat {a}_{{k + q}}^{ + }{{{\hat {a}}}_{k}}{{{\hat {a}}}_{{p + q}}}} \right\rangle , \\ \end{gathered} $
где $\left\langle u \right\rangle $ – средняя потенциальная энергия кулоновского взаимодействия электронов, приходящаяся на единицу занимаемого ею объема $V$ (см. (1)).

Таким образом, согласно теореме вириала для определения термодинамических функций ЭЖ достаточно вычислить среднюю кинетическую и среднюю потенциальную энергии.

ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И ОДНОЧАСТИЧНАЯ ФУНКЦИЯ ГРИНА

Чтобы упростить дальнейшее рассмотрение, используем спектральное представление для ОФГ (см. подробнее [11])

(13)
$g\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right) = \frac{1}{{\pi }}\int\limits_{ - \infty }^\infty {dE} \frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{E - {\text{i}}{{{\omega }}_{n}}}},$
где ${{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)$ – запаздывающая ОФГ, которая является аналитической функцией в верхней полуплоскости комплексных значений $E,$

(14)
$\begin{gathered} {{G}^{R}}\left( {\hat {A},\hat {B};E} \right) = \\ = \,\, - \frac{{\text{i}}}{\hbar }\int\limits_0^\infty {dt} {\text{exp}}\left( {i{{Et} \mathord{\left/ {\vphantom {{Et} \hbar }} \right. \kern-0em} \hbar }} \right)\left\langle {{{{\left[ {\hat {A}\left( t \right),\hat {B}\left( 0 \right)} \right]}}_{ + }}} \right\rangle . \\ \end{gathered} $
(15)
$\begin{gathered} \hat {A}\left( t \right) = {\text{exp}}\left( {{\text{i}}\left( {\hat {H} - \mu \hat {N}} \right)t{\text{/}}\hbar } \right) \times \\ \times \,\,\hat {A}{\text{exp}}\left( { - {\text{i}}\left( {\hat {H} - \mu \hat {N}} \right)t{\text{/}}\hbar } \right),\,\,\,\,{{\left[ {\hat {A},\hat {B}} \right]}_{ \pm }} \equiv \hat {A}\hat {B} \pm \hat {B}\hat {A}. \\ \end{gathered} $

При этом [19, 20]:

(16)
$\left\langle {\hat {B}\hat {A}} \right\rangle = \frac{1}{\pi }\int\limits_{ - \infty }^\infty {\frac{{{\text{Im}}{{G}^{R}}\left( {\hat {A},\hat {B};E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}} dE;$
(17)
$\begin{gathered} E{{G}^{R}}\left( {\hat {A},\hat {B};E} \right) = \\ = \,\,\left\langle {{{{\left[ {\hat {A},\hat {B}} \right]}}_{ + }}} \right\rangle + {{G}^{R}}\left( {{{{\left[ {\hat {A},\hat {H} - {\mu }\hat {N}} \right]}}_{ - }},\hat {B};E} \right). \\ \end{gathered} $

Из (16), (17), учитывая (1), (13)–(17), а также коммутационные соотношения для операторов $\hat {a}_{p}^{ + }$ и ${{\hat {a}}_{p}},$ получаем [21]:

(18)
$f\left( p \right) = \left\langle {\hat {a}_{p}^{ + }{{{\hat {a}}}_{p}}} \right\rangle = \frac{1}{{\pi }}\int\limits_{ - \infty }^\infty {dE} \frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}},$
(19)
$\begin{gathered} \left( {E - {{{\varepsilon }}_{0}}\left( p \right) + {\mu }} \right){{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right) = \\ = 1 + \frac{1}{V}\mathop \sum \limits_{,k,q} \nu \left( q \right){{G}^{R}}\left( {\hat {a}_{{k + q}}^{ + }{{{\hat {a}}}_{k}}{{{\hat {a}}}_{{p + q}}},\hat {a}_{p}^{ + };E} \right), \\ \end{gathered} $
(20)
$\begin{gathered} \left\langle {\hat {a}_{p}^{ + }\hat {a}_{{k + q}}^{ + }{{{\hat {a}}}_{k}}{{{\hat {a}}}_{{p + q}}}} \right\rangle = \\ = \,\,\frac{1}{{\pi }}\int\limits_{ - \infty }^\infty {dE} \frac{{{\text{Im}}{{G}^{R}}\left( {\hat {a}_{{k + q}}^{ + }{{{\hat {a}}}_{k}}{{{\hat {a}}}_{{p + q}}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}. \\ \end{gathered} $

Из (19), (20) с учетом (12) непосредственно следует, что

(21)
$\begin{gathered} \left\langle u \right\rangle = \sum\limits_\sigma {\int {\frac{{{{d}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } \int\limits_{ - \infty }^\infty {\frac{{dE}}{{2{\pi }}}} \left( {E - {{{\varepsilon }}_{0}}\left( p \right) + {\mu }} \right) \times \\ \times \,\,\frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}.{\text{\;}} \\ \end{gathered} $

Другими словами, в ЭЖ для вычисления как средней кинетической, так и средней потенциальной энергии достаточно ОФГ [12]. Подставляя (18), (21) в (9)–(12), находим

(22)
$\begin{gathered} P\left( {T,{\mu }} \right) = \frac{1}{3}~\sum\limits_\sigma {\int {\frac{{{{d}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } \times \\ \times \,\,\mathop \smallint \limits_{ - \infty }^\infty \frac{{dE}}{{2{\pi }}}\left( {E + 3{{{\varepsilon }}_{0}}\left( p \right) + {\mu }} \right)\frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}. \\ \end{gathered} $

Таким образом, согласно (22) задача определения термодинамических свойств ЭЖ сводится к вычислению ОФГ.

Обратим внимание, что возможность установления точного соотношения (22), связывающего давление и ОФГ в ЭЖ, является прямым следствием кулоновского взаимодействия между электронами. Только в этом случае вириал для потенциальной энергии (11) в термодинамическом пределе равен средней потенциальной энергии взаимодействия электронов (см. (12)). Для произвольного парного взаимодействия между частицами термодинамические функции однокомпонентной системы определяются двухчастичной ФГ [21].

Отметим также, что для вычисления термодинамического потенциала в рамках теории возмущений по межэлектронному взаимодействию обычно используется совершенно иная процедура. Гамильтониан ЭЖ записывается в виде (см. (1))

(23)
$\hat {H}\left( {\lambda } \right) = {{\hat {H}}_{0}} + {\lambda }\hat {U},$
где ${\lambda }$ – некоторый безразмерный непрерывный параметр. Тогда из (4), (23) непосредственно следует

(24)
(25)
$\begin{gathered} \left\langle {{{{\hat {A}}}_{{\lambda }}}} \right\rangle = {{Z}^{{ - 1}}}\left( {\lambda } \right){\text{Trexp}}\left\{ {\left( { - {{\left( {\hat {H}\left( {\lambda } \right) - {\mu }\hat {N}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {H}\left( {\lambda } \right) - {\mu }\hat {N}} \right)} T}} \right. \kern-0em} T}} \right)\hat {A}} \right\}, \\ Z\left( {\lambda } \right) = {\text{Trexp}}\left( { - {{\left( {\hat {H}\left( {\lambda } \right) - {\mu }\hat {N}} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {H}\left( {\lambda } \right) - {\mu }\hat {N}} \right)} T}} \right. \kern-0em} T}} \right). \\ \end{gathered} $

Здесь ${{{\Omega }}_{0}}\left( {V,T,{\mu }} \right)$ – термодинамический потенциал для идеального газа электронов. В свою очередь, величина ${{\left\langle {\hat {U}} \right\rangle }_{{\lambda }}}$ в (24) определяется точным соотношением (см. (11–13))

(26)
$\begin{gathered} \frac{{{{{\left\langle {\hat {U}} \right\rangle }}_{{\lambda }}}}}{V} = \frac{1}{2}\bar {n}\int {\frac{{{{{\text{d}}}^{3}}q}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} \nu \left( q \right)\left\{ {{{S}_{{\lambda }}}\left( q \right) - 1} \right\},\,\,{{S}_{{\lambda }}}\left( q \right) = 1 + \\ + \,\,\bar {n}\int {{{{\text{d}}}^{3}}} r{\text{exp}}\left( { - {\text{i}}{\mathbf{q}} \cdot {\mathbf{r}}} \right)\left\{ {{{g}_{2}}\left( {r;{\lambda }} \right) - 1} \right\}. \\ \end{gathered} $

Для вычисления статического структурного фактора ${{S}_{{\lambda }}}\left( q \right)$ для ЭЖ с гамильтонианом (23) используется его связь с продольной диэлектрической проницаемостью ${\varepsilon }_{{\lambda }}^{l}\left( {q,{\omega }} \right)$ (см. подробнее [1–3]):

(27)

Это означает, что в рамках традиционного подхода определение термодинамических свойств ЭЖ непосредственно связано с вычислением продольной диэлектрической проницаемости, что является чрезвычайно сложной задачей при учете межэлектронного взаимодействия [1–3].

В свою очередь, для вычисления ОФГ обычно используется уравнение Дайсона

(28)
$\begin{gathered} g\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right) = ~{{g}_{0}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right) + \\ + \,\,{{g}_{0}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right)\Sigma \left( {p,{\text{i}}{{{\omega }}_{n}}} \right)~g\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right), \\ \end{gathered} $
где ${{g}_{0}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right) = {{\left\{ {{\text{i}}{{{\omega }}_{n}} - {{\varepsilon }_{0}}\left( p \right) + {\mu }} \right\}}^{{ - 1}}}$ – ОФГ для идеального газа электронов, $\Sigma \left( {p,{\text{i}}{{{\omega }}_{n}}} \right)$ – так называемая собственно-энергетическая функция или массовый оператор (см. подробнее [11, 12]).

При вычислении ОФГ именно для функции $\Sigma \left( {p,{\text{i}}{{{\omega }}_{n}}} \right)$ традиционно используется то или иное приближение в рамках теории возмущений по межэлектронному взаимодействию. При этом уравнение (28) рассматривается как алгебраическое:

(29)
$\begin{gathered} g\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };{\text{i}}{{{\omega }}_{n}}} \right) = \\ = \,\,{{\left\{ {{\text{i}}{{{\omega }}_{n}} - {{{\varepsilon }}_{0}}\left( p \right) + {\mu } - \Sigma \left( {p,{\text{i}}{{{\omega }}_{n}}} \right)} \right\}}^{{ - 1}}}. \\ \end{gathered} $

Однако следует иметь в виду, что уравнение Дайсона является следствием процедуры частичного суммирования диаграмм определенного вида (класса). Такая процедура широко используется в квантовой теории поля и является основой функциональных методов в теории возмущений. С этой точки зрения собственно-энергетическая функция является функционалом ОФГ, а уравнение Дайсона (28) – функциональным, а не алгебраическим уравнением. Именно это обстоятельство служит одним из оснований для утверждения о том, что термодинамический потенциал ЭЖ является функционалом ОФГ (см. подробнее [13–16]). При установлении явного вида соответствующих функционалов возникает традиционная проблема “обрыва” функциональных рядов теории возмущений. Другими словами, необходимо установить требования для выбора тех или иных приближений для ОФГ.

С этой целью обратим внимание, что согласно (1), (10), (12), (18), (21) средняя (внутренняя) энергия ЭЖ ${{{\varepsilon }}_{V}} = \left\langle k \right\rangle + \left\langle u \right\rangle ,$ приходящаяся на единицу объема, равна

(30)
$\begin{gathered} {{{\varepsilon }}_{V}} = {\text{Li}}{{{\text{m}}}_{T}}{{\left\langle {\hat {H}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\hat {H}} \right\rangle } V}} \right. \kern-0em} V} = \\ = \sum\limits_\sigma {\int {\frac{{{{d}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } \int\limits_{ - \infty }^\infty {\frac{{dE}}{{2{\pi }}}} \left( {E + {{{\varepsilon }}_{0}}\left( p \right) + {\mu }} \right) \\ \times \,\,\frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}. \\ \end{gathered} $

Учитывая далее основное термодинамическое равенство (см., например, [22])

(31)
${{{\varepsilon }}_{V}} = T{{s}_{V}} - P + {\mu }\bar {n},$

нетрудно убедиться, что удельная энтропия ЭЖ ${{s}_{V}},$ приходящаяся на единицу объема, также определяется через ОФГ при заданной температуре $T$ и химическом потенциале μ:

(32)
$\begin{gathered} {{s}_{V}} = \frac{1}{{3T}}\sum\limits_\sigma {\int {\frac{{{{d}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } \int\limits_{ - \infty }^\infty {\frac{{dE}}{{\pi }}} \left( {2E + 3{{{\varepsilon }}_{0}}\left( p \right) - {\mu }} \right) \times \\ \times \,\,\frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}}.{\text{\;}} \\ \end{gathered} $

Таким образом, в рамках большого канонического распределения Гиббса термодинамические свойства ЭЖ могут быть определены на основе ОФГ вне рамок теории возмущений. Этот результат находится в согласии с полученным в рамках теории возмущений по межчастичному взаимодействию утверждением Латтинджера и Уорда [13], что термодинамический потенциал Гиббса для однокомпонентной системы является функционалом ОФГ. Явный вид такого функционала может быть установлен только в рамках теории возмущений, хотя предпринимаются попытки решить эту проблему в рамках термодинамически самосогласованных приближений (см. [23, 24] и цитированную там литературу).

УСЛОВИЯ САМОСОГЛАСОВАНИЯ

В связи с этим учтем, что целью вычисления ОФГ является ее последующее использование для определения термодинамических функций ЭЖ. Поэтому вполне естественно предположить, что искомое условие самосогласования непосредственно связано с термодинамическими соотношениями.

Действительно, как следует из проведенного рассмотрения выбранного приближения для ОФГ ${{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)$ достаточно, чтобы согласованно определить давление $P\left( {T,{\mu }} \right)$ (22), плотность числа электронов $\bar {n}\left( {T,{\mu }} \right)$ (8), (18), а также удельную внутреннюю энергию ${{{\varepsilon }}_{V}}\left( {T,{\mu }} \right)$ (30) и энтропию ${{s}_{V}}\left( {T,{\mu }} \right)$ (32).

С другой стороны, согласно законам термодинамики давление $P\left( {T,{\mu }} \right)$ должно удовлетворять дифференциальному соотношению [25]

(33)
$dP\left( {T,{\mu }} \right) = {{s}_{V}}\left( {T,{\mu }} \right)dT + \bar {n}\left( {T,{\mu }} \right)d{\mu },$

из которого непосредственно следует

(34)
$\begin{gathered} {{s}_{V}}\left( {T,{\mu }} \right) = {{\left( {\partial P{{\left( {T,{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {T,{\mu }} \right)} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{{\mu }}}, \\ \bar {n}\left( {T,{\mu }} \right) = {{\left( {\partial P{{\left( {T,{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {T,{\mu }} \right)} {\partial {\mu }}}} \right. \kern-0em} {\partial {\mu }}}} \right)}_{T}}. \\ \end{gathered} $

Таким образом, функции $P\left( {T,{\mu }} \right),$ $\bar {n}\left( {T,{\mu }} \right),$ ${{s}_{V}}\left( {T,{\mu }} \right),$ найденные по выбранному приближению для ОФГ ${{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right),$ должны удовлетворять соотношениям (34). Если это условие самосогласования не выполняется, то соответствующее приближение для ОФГ является некорректным.

Подчеркнем, что представленные выше результаты, устанавливающие связь между термодинамическими функциями ЭЖ и ОФГ, справедливы вне рамок теории возмущений по межэлектронному взаимодействию и имеют место исключительно для кулоновского потенциала взаимодействия.

Эти результаты корректны только после перехода к термодинамическому пределу. По этой причине они не могут быть получены из формального разложения для ОФГ (см. (14), (15)) по собственным волновым функциям гамильтониана ЭЖ (1) в макроскопическом, но конечном объеме V.

В частности, для идеального электронного газа, для которого

(35)
${\text{Im}}G_{0}^{R}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right) = {\pi \delta }\left( {E - {{{\varepsilon }}_{0}}\left( p \right) + {\mu }} \right),$

справедливость соответствующих результатов может быть показана только после перехода к термодинамическому пределу, когда давление ${{P}_{0}}\left( {T,{\mu }} \right)$ представимо в виде (см. подробнее [25])

(36)
$\begin{gathered} {{P}_{0}}\left( {T,{\mu }} \right) = \frac{2}{3}{{{\varepsilon }}_{0}}\left( {T,{\mu }} \right) = {{T}^{{5{\text{/}}2}}}{\Phi }\left( {{\mu \mathord{\left/ {\vphantom {\mu T}} \right. \kern-0em} T}} \right), \\ {\Phi }\left( {\alpha } \right) = \frac{{2\sqrt 2 {{m}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{3{{{\pi }}^{2}}{{\hbar }^{3}}}}\int\limits_0^\infty {\frac{{dx{{x}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{\text{exp}}\left( {x - {\alpha }} \right) + 1}}.} \\ \end{gathered} $

ЗАКЛЮЧЕНИЕ

В отличие от традиционного подхода (23)–(27), который основан на применении теории возмущений по межэлектронному взаимодействию при вычислении термодинамического потенциала ЭЖ, представленные выше результаты позволяют основное внимание уделить вопросу о самосогласованном вычислении ОФГ.

При этом возникает вопрос о связи с результатами феноменологической теории Силина для вырожденной ЭЖ [26], обобщающей теорию ферми-жидкости Ландау [27] с учетом дальнодействующего характера кулоновского взаимодействия между электронами.

Согласно теории Ландау–Силина, в нормальной ферми-жидкости роль частиц выполняют квазичастицы (элементарные возбуждения), обладающие определенной энергией. При этом их число равно числу исходных частиц (электронов). Кроме того, предполагается, что взаимодействие квазичастиц может быть описано с помощью самосогласованного поля окружающих частиц так, что энергия рассматриваемой системы является функционалом от функции распределения квазичастиц. Такие предположения имеют место только в пределе сильного вырождения, когда $T \ll {\mu }{\text{.}}$

В рамках формализма ФГ это означает, что полюса ОФГ в окрестности поверхности Ферми определяют энергетический спектр квазичастиц (см. (35)). На этой основе может быть найдена корреляционная функция Ландау, определяющая функционал для энергии ЭЖ (см., напр., [11]). Однако остается проблема вычисления коэффициентов разложения для корреляционной функции Ландау, что требует реализации определенной процедуры самосогласования (см. подробнее [28]). Это тем более актуально для равновесной ЭЖ, так как экспериментальное подтверждение теории Ландау–Силина в основном имеет место в отношении неравновесных свойств металлов, прежде всего, их электромагнитных характеристик [29].

С этой точки зрения, несомненный интерес представляет применение теории Ландау–Силина в формализме ФГ для анализа полученных выше результатов в пределе сильного вырождения. В этом случае, в частности, соотношение (31) принимает вид

(37)
$\begin{gathered} {{{\varepsilon }}_{V}}\left( {T \to 0,{\mu }} \right) + P\left( {T \to 0,{\mu }} \right) - \\ - \,\,{\mu }\bar {n}\left( {T \to 0,{\mu }} \right) = 0, \\ \end{gathered} $
где переход к пределу $T \to 0$ следует понимать в смысле $T \ll {\mu }{\text{.}}$

Следовательно, в вырожденной ЭЖ, для описания которой применима теория Ландау–Силина, условие самосогласования для энтропии (34) заменяется предельным равенством (см. (32))

(38)
$\begin{gathered} \mathop {\lim }\limits_{T \to 0{\text{\;}}} \sum\limits_\sigma {\int {\frac{{{{d}^{3}}p}}{{{{{\left( {2{\pi }} \right)}}^{3}}}}} } \mathop \smallint \limits_{ - \infty }^\infty \frac{{dE}}{{\pi }}\left( {2E + 3{{{\varepsilon }}_{0}}\left( p \right) - {\mu }} \right) \times \\ \times \,\,\frac{{{\text{Im}}{{G}^{R}}\left( {{{{\hat {a}}}_{p}},\hat {a}_{p}^{ + };E} \right)}}{{{\text{exp}}\left( {E{\text{/}}T} \right) + 1}} = 0. \\ \end{gathered} $

С другой стороны, положения феноменологической теории Ландау–Силина не могут быть использованы при рассмотрении warm dense matter [5–10]. В этой ситуации представленные выше выражения для термодинамических функций ЭЖ, полученные через точную ОФГ, имеют преимущество по сравнению с традиционным подходом (23)–(27). Это преимущество заключается в наличии условий самосогласования (34).

Дальнейшее развитие полученных выше результатов связано с построением самосогласованных приближений для ФГ в рамках предложенной в [20] схемы с использованием правил сумм для моментов ОФГ (см. подробнее [30]). Результаты использования этого подхода будут представлены в отдельной публикации.

Автор признателен С.А. Тригеру за полезные обсуждения.

Настоящая работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 19-08-00238-а).

Список литературы

  1. Ichimaru S. Strongly coupled plasmas: high-density classical plasmas and degenerate electron liquids // Rev. Mod. Phys. 1982. V. 54. № 4. P. 1017–1059.

  2. Коваленко Н.П., Красный Ю.П., Тригер С.А. Статистическая теория жидких металлов. М.: Наука, 1990. 204 с.

  3. Giuliani G., Vignale G. Quantum theory of the electron liquid. Cambridge: Cambridge. Univ. Press, 2005. 798 p.

  4. Погосов В.В., Рева В.И. К расчету энергий диссоциации, когезии, образовании вакансии, прилипания электронов и потенциала ионизации малых металлических кластеров, содержащих моновакансию // ФММ. 2017. Т. 118. № 9. С. 871–882.

  5. Brown E., Clark B., DuBois J., Ceperley D. Path-integral Monte Carlo simulation of the warm dense homogeneous electron gas // Phys. Rev. Lett. 2013. V. 110. № 14. P. 146405 (1–5).

  6. Baguet L., Delyon F., Bernu B., Holzmann M. Hartree-Fock ground state phase diagram of jellium // Phys. Rev. Lett. 2013. V. 111. № 16. P. 166402 (1–5).

  7. Pavlyukh Y., Uimonen A.-M., Stefanucci G., van Leeuwen R. Vertex corrections for positive-definite spectral functions of simple metals // Phys. Rev. Lett. 2016. V. 117. № 20. 206402 (1–6).

  8. McClain J., Lischner J., Watson Th., Matthews D.A., Ronca E., Louie S.G., Berkelbach T.C., Chan G.K.-L. Spectral functions of the uniform electron gas via coupled-cluster theory and comparison to the GW and related approximations // Phys. Rev. B. 2016. V. 93. № 23. P. 235139 (1–6).

  9. Valenzuela J.C., Krauland C., Mariscal D., Krasheninnikov I., Niemann C., Ma T., Mabey P., Gregori G., Wiewior P., Covington A.M., Beg F.N. Measurement of temperature and density using non-collective X-ray Thomson scattering in pulsed power produced warm dense plasmas // Scient. Rep. 2018. V. 8. P. 8432 (1–8).

  10. Dornheim T., Groth S., Bonitz M. The uniform electron gas at warm dense matter conditions // Phys. Rep. 2018. V. 744. P. 1–86.

  11. Абрикосов А.А., Горьков Л.П., Дзялошинский И.Е. Методы квантовой теории поля в статистической физике. М.: ГИФМЛ, 1962. 444 с.

  12. Kadanoff L.P., Baym G. Quantum statistical mechanics. Green’s function methods in equilibrium and nonequilibrium problems. New York: Benjamin, 1962. 203 p.

  13. Luttinger J.M., Ward J.C. Ground-state energy of a many-fermion system. II // Phys. Rev. 1960. V. 118. № 5. P. 1417–1427.

  14. Baym G., Kadanoff L.P. Conservation laws and correlation functions // Phys. Rev. 1961. V. 124. № 2. P. 287–299.

  15. Kotliar G., Savrasov S.Y., Haule K., Oudovenko V.S., Parcollet O., Marianetti C.A. Electronic structure calculations with dynamical mean-field theory // Rev. Mod. Phys. 2006. V. 78. № 3. P. 865–951.

  16. Blöchl P.E., Pruschke T., Potthoff M. Density-matrix functionals from Green’s functions // Phys. Rev. B. 2013. V. 88. № 20. P. 205139 (1–14).

  17. Зубарев Д.Н. Неравновесная статистическая термодинамика. М.: Наука, 1971. 416 с.

  18. Bobrov V.B., Trigger S.A., Zagorodny A. Virial theorem, one-particle density matrix, and equilibrium condition in an external field // Phys. Rev. A. 2010. V. 82. № 4. P. 044105 (1–4).

  19. Зубарев Д.Н. Двухвременные функции Грина в статистической физике // УФН. 1960. Т. 71. № 1. С. 71–116.

  20. Озрин В.Д. Цепочка уравнений для двухвременных температурных функций Грина // ТМФ. 1970. Т. 4. № 1. С. 66–75.

  21. Бобров В.Б. Термодинамика квантового газа и двухчастичная функция Грина // Письма в ЖЭТФ. 2017. Т. 106. № 6. С. 365–367.

  22. Balescu R. Equilibrium and nonequilibrium statistical mechanics. New York-London: Wiley, 1975. 756 p.

  23. Potthoff M., Aichhorn M., Dahnken C. Variational cluster approach to correlated electron systems in low dimensions // Phys. Rev. Lett. 2003. V. 91. № 20. P. 206402 (1–4).

  24. Potthoff M., Balzer M. Self-energy-functional theory for systems of interacting electrons with disorder // Phys. Rev. B. 2007. V. 75. № 12. P. 125112 (1–22).

  25. Ландау Л.Д., Лифшиц Е.М. Статистическая физика, часть 1. М.: Наука, 1976. 584 с.

  26. Силин В.П. К теории вырожденной электронной жидкости // ЖЭТФ. 1957. Т. 33. № 2. С. 495–500.

  27. Ландау Л.Д. Теория ферми-жидкости // ЖЭТФ. 1956. Т. 30. № 6. С. 1058–1064.

  28. Baym G., Pethick C. Landau Fermi-liquid theory: concepts and applications. Weinheim: Wiley-VCH, 1991. 216 p.

  29. Кондратьев А.С., Кучма А.Е. Электронная жидкость нормальных металлов. Ленинград: Изд-во Ленинградского ун-та, 1980. 200 с.

  30. Vogt M., Zimmermann R., Needs R.J. Spectral moments in the homogeneous electron gas // Phys. Rev. B. 2004. V. 69. № 4. P. 045113 (1–10).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал