Физика металлов и металловедение, 2021, T. 122, № 12, стр. 1257-1260

Влияние диффузии на возникновение перколяционного кластера в магнетиках с прямым обменом

В. И. Белоконь^a, *, О. И. Дьяченко^a, Р. В. Лапенков^a

^a Дальневосточный федеральный университет
690922 Приморский край, Владивосток, о. Русский, п. Аякс, 10, Россия

Поступила в редакцию 05.05.2021
После доработки 18.08.2021
Принята к публикации 23.08.2021

DOI: 10.31857/S0015323021120020

Аннотация

В рамках теории случайных полей исследуется влияние диффузии взаимодействующих, обладающих магнитным моментом ионов по узлам кристаллической решетки на процесс магнитного упорядочения. При этом возможно появление перколяционного кластера в условиях, при которых он не появился в случае неподвижных ионов. Это практически означает возникновение локальных областей повышенной концентрации “ферромагнитных” ионов. Приводятся графики зависимости температуры Кюри от концентрации $T = {{T}_{{\text{C}}}}\left( p \right)$ для числа ближайших соседей $z = 4$ и $z = 6$ в случае “замороженных” и подвижных ионов.

Ключевые слова: диффузия, теория случайных полей взаимодействия, температура Кюри, магнетики

ВВЕДЕНИЕ

Современное производство активно использует сплавы на основе ферромагнитной матрицы (Fe, Co, Ni). Большую роль в формировании их структуры и физико-механических свойств играет диффузия. Кроме того, диффузия является основой многих широко используемых технологий, например, азотирования стали, диффузионной сварки, спекания порошков [1, 2].

Известно, что магнитное упорядочение в системе распределенных по узлам кристаллической решетки взаимодействующих, обладающих магнитным моментом ионов возникает при появлении бесконечного (перколяционного) кластера, т.е. при достижении ими некоторой критической концентрации ${{p}_{{\text{c}}}},$ соответствующей перколяционному порогу. В свою очередь, этот порог вычисляется при условии случайного распределения ионов по узлам кристаллической решетки и их “замороженного” состояния в этих узлах. Нам представляется, что в случае перемещения ионов по узлам за счет диффузии возможно появление перколяционного кластера при $p < {{p}_{{\text{c}}}}.$ В природе подобные процессы происходят, например, в горных породах, содержащих титаномагнетит [3]. В данной работе предпринята попытка рассмотреть такую возможность в рамках теории случайных полей взаимодействия.

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ В СЛУЧАЕ “ЗАМОРОЖЕННЫХ” ИОНОВ

Предложенный нами метод случайных полей взаимодействия [4–6], предполагает расчет плотности распределения случайного поля H созданного остальными моментами ${{m}_{k}}$ системы, на помещенном в начале координат магнитном моменте ${{m}_{0}}.$ В отсутствие внешнего поля, гамильтониан обменного взаимодействия имеет вид:

(1)

$\begin{gathered} H = - \sum\limits_{k > j} {{{J}_{{kj{\text{\;}}}}}{{m}_{k}}{{m}_{j}}} = \\ = \,\, - \sum\limits_k {{{m}_{k}}} \sum\limits_j {{{J}_{{kj{\text{\;}}}}}{{m}_{j}}} = - \sum\limits_k {{{m}_{k}}{{H}_{k}}} , \\ \end{gathered} $

где ${{J}_{{kj~}}}$ – обменный интеграл, ${{H}_{k}}$ – молекулярное (эффективное) поле.

Последовательность расчета плотности распределения случайного поля $H$ состоит в следующем:

1. При известном условии распределения магнитных моментов ${{m}_{k}}$ по координатам, величине и направлению, условная плотность вероятности представляет из себя $\delta $-функцию:

(2)

$\delta \left( {H - \sum\limits_k {{{\varphi }_{k}}\left( {{{m}_{k}},{{r}_{k}}} \right)} } \right),$

где ${{\varphi }_{k}}$ – поле, создаваемое в начале координат магнитным моментом ${{m}_{k}},$ расположенным в точке ${{r}_{k}}.$

2. Плотность распределения W(H) получается суммированием по всем возможным функциям распределения магнитных моментов ${{{{\Phi }}}_{k}}{\text{:}}$

(3)

$\begin{gathered} W\left( H \right) = \iint {\delta \left( {H - \sum\limits_k {{{\varphi }_{k}}\left( {{{m}_{k}},~{{r}_{k}}} \right)} } \right)} \times \\ \times \,\,\prod\limits_k {{{{{\Phi }}}_{k}}\left( {{{m}_{k}},~{{r}_{k}}} \right){{{\text{d}}}^{3}}{{m}_{k}}{{{\text{d}}}^{3}}{{r}_{k}}} .~ \\ \end{gathered} $

В свою очередь ${{{{\Phi }}}_{k}}\left( {{{m}_{k}},{{r}_{k}}} \right) = f\left( {{{r}_{k}}} \right)\tau \left( {{{m}_{k}}} \right),$ поскольку распределение по координатам $f\left( {{{r}_{k}}} \right)$ и магнитным моментам $\tau \left( {{{m}_{k}}} \right)$ независимы.

3. Для кристаллических магнетиков распределение по координатам:

(4)

$f\left( {{{r}_{k}}} \right) = \delta \left( {{{r}_{k}} - {{r}_{{k,0}}}} \right),$

где ${{r}_{{k,0}}}$ – координаты узлов кристаллической решетки.

В рамках модели Изинга распределение по магнитным моментам:

(5)

$\begin{gathered} {{\tau }_{k}}\left( {{{m}_{k}}} \right){\text{d}}{{m}_{k}}{\text{d}}{{{{\theta }}}_{k}} = \left[ {{{\alpha }_{k}}\delta \left( {{{{{\theta }}}_{k}}} \right) + {{\beta }_{k}}\delta \left( {{{{{\theta }}}_{k}} - \pi } \right)} \right] \times \\ \times \,\,\left[ {\left( {1 - p} \right)\delta \left( {{{m}_{k}}} \right) + p\delta \left( {{{m}_{k}} - {{m}_{0}}} \right)} \right]{\text{d}}{{m}_{k}}{\text{d}}{{{{\theta }}}_{k}}, \\ \end{gathered} $

где ${{\theta }_{k}}$ – угол между осью ${{O}_{z}}$ и ${{m}_{k}},$ ${{\alpha }_{k}}$ – относительная вероятность для спина иметь направление “вверх” (${{\theta }_{k}} = 0$), ${{\beta }_{k}}$ – относительная вероятность для положения “вниз” (${{\theta }_{k}} = \pi $), $p$ – концентрация взаимодействующих (“ферромагнитных”) ионов, все такие ионы имеют одинаковые по величине магнитные моменты ${{m}_{0}}.$

В поле ${{H}_{k}}$ на ионе с номером $k$ равновесные значения ${{\alpha }_{k}}$ и ${{\beta }_{k}}$ определяются как

(6)

$\begin{gathered} {{\alpha }_{k}} = \frac{{\exp \left( {\frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right)}}{{\exp \left( {\frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right) + \exp \left( { - \frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right)}}, \\ {{\beta }_{k}} = \frac{{\exp \left( { - \frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right)}}{{\exp \left( {\frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right) + \exp \left( { - \frac{{i{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right)}}. \\ \end{gathered} $

Термодинамически среднее значение магнитного момента

(7)

$\left\langle {{{m}_{0}}} \right\rangle = {{m}_{0}}{\text{th}}\left[ {\frac{{{\text{\;}}{{m}_{0}}{{H}_{k}}}}{{kT}}} \right].$

4. Характеристическая функция

$A\left( \rho \right) = \int {W\left( H \right)\exp \left( {i\rho H} \right)dH} $ при этом выражается следующим образом:

(8)

$\begin{gathered} A\left( \rho \right) = \prod\limits_k {[(1 - p) + p({{\alpha }_{k}}\exp [i\rho {{\varphi }_{k}}] + } \\ + \,\,{{\beta }_{k}}\exp [ - i\rho {{\varphi }_{k}}])]. \\ \end{gathered} $

Здесь учтено, что смена направления ${{m}_{k}}$ приводит к смене знака ${{\varphi }_{k}}.$

5. При термодинамическом и конфигурационном усреднении:

(9)

$\begin{gathered} \ln \left[ {A\left( \rho \right)} \right] = \sum\limits_k {\ln [\left( {1 - p} \right) + } \\ + \,\,p\left( {\left\langle \alpha \right\rangle \exp [i\rho {{\varphi }_{k}}] + \left\langle \beta \right\rangle \exp [ - i\rho {{\varphi }_{k}}]} \right)], \\ \end{gathered} $

где $\left\langle \alpha \right\rangle $ и $\left\langle \beta \right\rangle $ – термодинамически и конфигурационно усредненные значения ${{\alpha }_{k}}$ и ${{\beta }_{k}}.$

Разлагая в ряд $\exp \left[ {i\rho {{\varphi }_{k}}} \right],$ $\exp \left[ { - i\rho {{\varphi }_{k}}} \right]$ и $\ln \left[ {A\left( \rho \right)} \right]$ до ${{\rho }^{2}}$ можно получить выражение:

(10)

$\begin{gathered} A\left( \rho \right) \approx i{\text{\;}}\rho \left( {\left\langle \alpha \right\rangle - \left\langle \beta \right\rangle } \right)p\sum\limits_k {{{\varphi }_{k}}} - \\ - \,\,\frac{1}{{2!}}{{\rho }^{2}}\left[ {1 - {{{\left( {\left\langle \alpha \right\rangle - \left\langle \beta \right\rangle } \right)}}^{2}}p} \right]p\sum\limits_k {\varphi _{k}^{2}} . \\ \end{gathered} $

Функция распределения случайных полей $W\left( H \right)$ оказывается “размазанной” $\delta $-функцией вида:

(11)

$W\left( H \right) = \frac{1}{{\sqrt \pi B}}\exp \left[ {\frac{{ - {{{\left( {H - {{H}_{0}}M} \right)}}^{2}}}}{{{{B}^{2}}}}} \right],$

с моментами распределения:

(12)

${{H}_{0}} = ~p\sum\limits_k {{{\varphi }_{k}}} ,$

(13)

${{B}^{2}} = 2p\left[ {1 - {{{\left( {\left\langle \alpha \right\rangle {\text{\;}} - \left\langle \beta \right\rangle } \right)}}^{2}}p} \right]\sum\limits_k {\varphi _{k}^{2}} ,$

где $M = \left\langle \alpha \right\rangle - \left\langle \beta \right\rangle ~$ – относительный магнитный момент, термодинамически и конфигурационно усредненный.

(14)

$M = \int {{\text{th}}\left[ {\frac{{{{m}_{0}}H}}{{k~T}}} \right]W\left( H \right)dH} .$

Если $B \to 0,$ то $W\left( H \right) \to \delta \left( {H - M~{{H}_{0}}} \right)$ и соотношение (14) соответствует теории молекулярного поля.

Существенное упрощение полученных соотношений состоит в замене $W\left( {H,~M} \right),$ представляющей из себя “размазанную” $\delta $-функцию, функцией вида:

(15)

$\tilde {W}\left( H \right) = \left\{ {\begin{array}{*{20}{c}} {0,~ - B + M{{H}_{0}} > H,~B + M{{H}_{0}} < H} \\ {\frac{1}{{2B}},~ - B + M{{H}_{0}} \leqslant H \leqslant B + M{{H}_{0}}.} \end{array}} \right.$

В этом случае

(16)

$M = \frac{1}{{2B}}\int\limits_{ - B}^B {{\text{th}}\left[ {\frac{{{{m}_{0}}\left( {H + M{{H}_{0}}} \right)}}{{kT}}} \right]dH} ,$

и легко показать, что при $M \ll 1,$

(17)

${{M}^{2}} = \frac{{3\left( {\frac{{{{H}_{0}}}}{{\text{B}}}{\text{th}}\left[ {\frac{{{{m}_{0}}B}}{{kT}}} \right] - 1} \right)}}{{\frac{{{{H}_{0}}}}{{\text{B}}}{{{\left( {\frac{{{{m}_{0}}{{H}_{0}}}}{{kT}}} \right)}}^{2}}\left[ {{\text{th}}\left[ {\frac{{{{m}_{0}}B}}{{kT}}} \right] - {\text{t}}{{{\text{h}}}^{3}}\left[ {\frac{{{{m}_{0}}B}}{{kT}}} \right]} \right]}}{\text{.}}$

Откуда следует, что числитель в выражении (16) должен быть больше нуля. Тогда:

(18)

$\frac{{{{H}_{0}}}}{{\text{B}}}{\text{th}}\left[ {\frac{{{{m}_{0}}B}}{{k{{T}_{{\text{C}}}}}}} \right] = 1,$

где ${{Т}_{{\text{C}}}}$ – точка Кюри. В данной модели эта величина принята как безразмерная (m₀ = 1, k = 1).

Если $\frac{{{{H}_{0}}}}{B} < 1,$ $M = 0$ при любой температуре и дальний порядок невозможен.

Для случая взаимодействия только ближайших соседей ${{H}_{0}} = pzJ,$ ${{B}^{2}} = 2pz{{J}^{2}}.$ Здесь $z$ – число ближайших соседей, $J$ – эффективное (обменное) поле, создаваемое ионом. При $p < {{p}_{{\text{c}}}} = \frac{2}{z}$ упорядочение отсутствует. При этом ${{p}_{{\text{c}}}}$ близки к известным критическим концентрациям, соответствующим теории протекания, что оправдывает использование принятых приближений [7].

ВЛИЯНИЕ ДИФФУЗИИ

В случае подвижных ионов, способных обмениваться местами с примесными, не взаимодействующими атомами, все узлы решетки эквивалентны. При этом большая статистическая сумма для отдельного узла:

(19)

$Z = 1 + \lambda \exp \left[ {\frac{{{{m}_{0}}H}}{{kT}}} \right] + \lambda \exp \left[ { - \frac{{{{m}_{0}}H}}{{kT}}} \right],$

где $\lambda = \exp \left[ {\frac{\mu }{T}} \right],$ $\mu $ – химический потенциал.

Тогда ${{\bar {\alpha }}} = \frac{{\lambda ~\exp \left[ {\frac{{{{m}_{0}}H}}{{kT}}} \right]}}{Z}$ – вероятность обнаружить магнитный момент, ориентированный “вверх”, ${{\bar {\beta }}} = \frac{{\lambda \exp \left[ { - \frac{{{{m}_{0}}H}}{{kT}}} \right]}}{Z}$ – вероятность обнаружить магнитный момент, ориентированный “вниз”, ${{\bar {\gamma }}} = \frac{1}{Z}$ – вероятность того, что магнитный момент отсутствует, узел занят примесным атомом.

Термодинамическое среднее значение относительного магнитного момента:

(20)

${{\bar {\alpha }}} - {{\bar {\beta }}} = \frac{{2\lambda {\text{sh}}\left[ {\frac{{{{m}_{0}}H}}{{kT}}} \right]}}{{1 + 2\lambda {\text{ch}}\left[ {\frac{{{{m}_{0}}H}}{{kT}}} \right]}},$

если концентрация $p = 1,$ то ${{\bar {\alpha }}} - {{\bar {\beta }}} = {\text{th}}~\left[ {\frac{{{{m}_{0}}H}}{{k~T}}} \right].$

При вычислении характеристической функции необходимо учесть эквивалентность всех узлов. Соответственно, (см. (9))

(21)

$\begin{gathered} \ln \left[ {A\left( \rho \right)} \right] = \\ = \,\,\sum\limits_k {\ln \left[ {\left\langle \alpha \right\rangle \exp \left[ {i\rho {{\varphi }_{k}}} \right] + \left\langle \beta \right\rangle \exp \left[ { - i\rho {{\varphi }_{k}}} \right] + \left\langle \gamma \right\rangle } \right]} . \\ \end{gathered} $

Как и в формуле (9), мы перешли к термодинамически и конфигурационно усредненным значениям.

Соответственно, так как $\left\langle {{\alpha }} \right\rangle + \left\langle {{\beta }} \right\rangle + \left\langle {{\gamma }} \right\rangle = 1,$

(22)

$\begin{gathered} {\text{то}}\,\,\ln \left[ {A\left( \rho \right)} \right] = \sum\limits_k {\ln \left[ {1 + i\rho \left( {\left\langle \alpha \right\rangle - \left\langle \beta \right\rangle } \right)\sum\limits_k {{{\varphi }_{k}}} - } \right.} \\ \left. { - \,\,\frac{1}{2}{{\rho }^{2}}\left[ {\left( {\left\langle \alpha \right\rangle + \left\langle \beta \right\rangle } \right) - {{{\left( {\left\langle \alpha \right\rangle - \left\langle \beta \right\rangle } \right)}}^{2}}} \right]\sum\limits_k {\varphi _{k}^{2}} } \right]. \\ \end{gathered} $

Мы снова приходим к функции

(23)

$W\left( H \right) = \frac{1}{{\sqrt \pi B}}\exp \left[ {\frac{{ - {{{\left( {H - \left( {\left\langle \alpha \right\rangle {\text{\;}} - \left\langle \beta \right\rangle } \right){{H}_{0}}} \right)}}^{2}}}}{{{{B}^{2}}}}} \right],$

где

(24)

$\begin{gathered} {{H}_{0}} = \sum\limits_k {{{\varphi }_{k}}} , \\ {{B}^{2}} = 2p\left[ {\left( {\left\langle \alpha \right\rangle + \left\langle \beta \right\rangle } \right) - {{{\left( {\left\langle \alpha \right\rangle - \left\langle \beta \right\rangle } \right)}}^{2}}} \right]\sum\limits_k {\varphi _{k}^{2}} . \\ \end{gathered} $

Если $\left\langle {{\gamma }} \right\rangle \to 0,$ $\left\langle {{\alpha }} \right\rangle + \left\langle {{\beta }} \right\rangle = 1$ и мы имеем формулу (10) при $p = 1.$ В нашем случае

$\left\langle {{\alpha }} \right\rangle + \left\langle {{\beta }} \right\rangle = p.$

Соответственно, вместо формулы (16) мы будем иметь:

(25)

$M = \frac{1}{{2B}}\int\limits_{ - B}^B {\frac{{2\lambda {\text{sh}}\left[ {\frac{{{{m}_{0}}(H + M{{H}_{0}})}}{{kT}}} \right]}}{{1 + 2\lambda {\text{ch}}\left[ {\frac{{{{m}_{0}}(H + M{{H}_{0}})}}{{kT}}} \right]}}dH} .$

При этом вблизи ${{T}_{{\text{C}}}},$ при $M = 0$

(26)

$\begin{gathered} \left\langle {\frac{p}{{1 - p}}} \right\rangle = \left\langle {\frac{{\alpha + \beta }}{\gamma }} \right\rangle = \frac{1}{{2B}}\int\limits_{ - B}^B {2\lambda {\text{ch}}\left[ {\frac{{{{m}_{0}}H}}{{kT}}} \right]dH} = \\ = \frac{{2\lambda }}{{2B}}\frac{{kT}}{{{{m}_{0}}}}{\text{2\;sh}}\left[ {\frac{{{{m}_{0}}B}}{{kT}}} \right] = \frac{p}{{1 - p}}, \\ \end{gathered} $

так как средние значения $p$ при смене мест “ферромагнитных” ионов сохраняются.

Отсюда

(27)

$2\lambda {\text{sh}}\left[ {\frac{{{{m}_{0}}B}}{{kT}}} \right] = \frac{p}{{1 - p}}\frac{{{{m}_{0}}B}}{{kT}}.$

В дальнейшем для упрощения формул положим ${{m}_{0}} = 1,$ $k = 1,$ обменный интеграл $J = 1$ и рассмотрим случай взаимодействия ближайших соседей.

Разлагая уравнение (25) в ряд по малому параметру $\frac{{M{{H}_{0}}}}{T},$ для определения температуры Кюри получим выражение, аналогичное (18):

(28)

$\frac{{{{H}_{0}}}}{B}\frac{{2\lambda {\text{sh}}\left[ {\frac{B}{{{{T}_{{\text{C}}}}}}} \right]}}{{1 + 2\lambda {\text{ch}}\left[ {\frac{B}{{{{T}_{{\text{C}}}}}}} \right]}} - 1 = 0,$

где $2\lambda {\text{sh}}\left[ {\frac{B}{T}} \right] = \frac{p}{{1 - p}}\frac{B}{T}.$

Окончательно, для определения T_C имеем:

(29)

$\frac{{{{H}_{0}}}}{B}\frac{{\frac{p}{{1 - p}}\frac{B}{{{{T}_{{\text{C}}}}}}}}{{1 + \frac{p}{{1 - p}}\frac{B}{{{{T}_{{\text{C}}}}}}{\text{\;cth}}\left[ {\frac{B}{{{{T}_{{\text{C}}}}}}} \right]}} = 1,$

где ${{H}_{0}} = z,$ ${{B}^{2}} = 2pz.$

На рис. 1 приведены графики зависимости T = = T_C(p) для $z = 4$ в случае “замороженных” ионов (формула (18)) (сплошная линия) и подвижных ионов (формула (29)) (штриховая линия).

Рис. 1.

Графики зависимости $T = {{T}_{{\text{C}}}}(p)$ для $z = 4$ в случае “замороженных” ионов (формула (18)) (сплошная линия) и подвижных ионов (формула (29)) (штриховая линия).

На рис. 2 приведены графики зависимости T = = T_C(p) для $z = 6$ в случае “замороженных” ионов (формула (18)) (сплошная линия) и подвижных ионов (формула (29)) (штриховая линия).

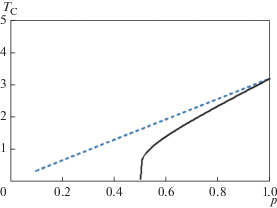
Рис. 2.

Графики зависимости $T = {{T}_{{\text{C}}}}(p)$ для $z = 6$ в случае “замороженных” ионов (формула (18)) (сплошная линия) и подвижных ионов (формула (29)) (штриховая линия).

Как видно, возможность диффузионной перестройки взаимодействующих ионов приводит к появлению отличного от нуля магнитного момента, то есть к возникновению перколяционного кластера при $p < {{p}_{{\text{c}}}}.$ Это практически означает появление локальных областей повышенной концентрации “ферромагнитных” ионов при сохранении $p < {{p}_{{\text{c}}}}$ в среднем.

ЗАКЛЮЧЕНИЕ

Таким образом, метод случайных полей взаимодействия довольно точно предсказывает критические концентрации, ниже которых не может быть установлен дальний порядок и появится перколяционный кластер.

В рамках теории случайных полей взаимодействия проведено исследование влияния диффузии взаимодействующих, обладающих магнитным моментом ионов по узлам кристаллической решетки на процесс магнитного упорядочения. Установлено, что возможность диффузионной перестройки взаимодействующих ионов приводит к появлению отличного от нуля магнитного момента, то есть к возникновению перколяционного кластера.

Работа выполнена при финансовой поддержке государственного задания Министерства образования и науки Российской Федерации № 0657-2020-0005.

Список литературы

Anton Schneider, Chu-Chun Fu, Frederic Soisson, Cyrille Barreteau. Atomic Diffusion in α-iron across the Curie Point: An Efficient and Transferable Ab Initio–Based Modeling Approach // Phys. Rev. Letters. 2020. V. 124. P. 215901.
Котина Н.М., Жевалёв О.Ю., Куц Л.Е. Влияние диффузионной сварки на свойства магнитных материалов // Вопр. электротехнологии. 2014. Т. 4(5). С. 63–65.
Батлер Р.Ф. Палеомагнетизм: от магнитных доменов до геологических террейнов. СПб, 1998. 288 с.
Belokon V., Semkin S. Random field method in the theory of ferromagnetism of binary alloys // J. Experiment. Theoret. Phys. 1993. V. 104(5). P. 3784.
Белоконь В.И., Дьяченко О.И., Лапенков Р.В., Чибиряк Е.В. Многообразие видов магнитного упорядочения: метод случайных полей обменного взаимодействия // Физика металлов и металловедение. 2020. Т. 121. № 8. С. 802–806.
Belokon V., Trofimov A., Dyachenko O. Oguchis method and random interaction fields method: Investigation of properties of ferromagnetic materials // J. Magn. Magn. Mater. 2019. V. 471. P. 501–503.
Efros A.L. Physics and Geometry of disorder. M.: Science, 1982.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал