1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 122, № 4, 2021

Физика металлов и металловедение, 2021, T. 122, № 4, стр. 446-452

Нестационарное энергетическое распределение каскада выбитых атомов в твердом теле с учетом их энергии связи

Е. В. Метелкин a, *, М. В. Лебедева a

a Российский химико-технологический университет им. Д.И. Менделеева
125047 Москва, Миусская площадь, 9, Россия

* E-mail: sitech47@mail.ru

Поступила в редакцию 01.09.2020
После доработки 24.11.2020
Принята к публикации 25.11.2020

Полный текст (PDF)

Аннотация

На основе решения кинетического уравнения Больцмана получено приближенное выражение для функции распределения, описывающей нестационарное энергетическое распределение каскада движущихся атомов. Развитие каскада рассматривается в материалах, состоящих из одинаковых атомов с учетом энергии связи атомов в узлах решетки (εd). Предполагается, что рассеяние движущихся атомов является упругим и сферически симметричным в системе центра инерции, а сечение взаимодействия обратно пропорционально скорости. На основе полученного решения проведен анализ влияния энергии связи атомов на функцию распределения и связанные с ней величины. В предельном случае εd = 0 полученное приближенное решение хорошо согласуется с точным решением соответствующей задачи.

Ключевые слова: кинетическое уравнение, столкновения, каскад атомов, сечение взаимодействия

ВВЕДЕНИЕ

При проектировании и создании ядерных реакторов и термоядерных установок возникает задача выбора для них радиационно-стойких материалов, поскольку в процессе эксплуатации их корпуса и отдельные элементы подвергаются длительному воздействию радиации. Именно радиационная стойкость материала во многом определяет время жизни установок и многие другие их физические характеристики.

При облучении различных материалов быстрыми частицами (в частности нейтронами) атомы кристаллической решетки, которым налетающая частица сообщает энергию, большую энергии связи, вылетают из своих равновесных положений. В дальнейшем столкновения движущихся атомов с атомами, расположенными в узлах решетки, приводят к образованию следующих поколений выбитых атомов. В результате возникает так называемый каскад движущихся атомов. Развитие каскадов в твердом теле приводит к образованию комплекса точечных дефектов (вакансий и междоузельных атомов, кластеров и т.д.), определяющих степень повреждения материала и его дальнейшие физические свойства [1–5].

Описание развития каскадов представляет собой достаточно сложную задачу. В связи с этим для ее решения в большинстве случаев с успехом используется компьютерное моделирование. Существует три основных метода, используемых для моделирования поведения атомов в каскаде смещений: метод бинарной аппроксимации столкновений, метод молекулярной динамики и кинетический метод Монте-Карло [2, 6–9].

Однако, аналитические решения соответствующей задачи для линейного уравнения Больцмана, несмотря на то, что они существуют в исключительных случаях, также представляют значительный интерес. Это связано с тем, что аналитические решения дают наглядное представление о протекающем процессе и его особенностях. Кроме того, эти результаты могут быть использованы для тестирования достаточно сложных численных расчетов.

Аналитическое описание каскадов атомных столкновений в твердом теле и их особенностей было представлено в целом ряде работ [10–21]. В [10] с помощью построенной модельной индикатрисы рассеяния было получено приближенное стационарное энергетическое распределение каскада движущихся атомов для произвольных потенциалов межатомного взаимодействия. В работах [11, 12] анализировалась возможность образования субкаскадов – ряда неперекрывающихся между собой областей, в процессе развития каскада атомных столкновений. Оценка пороговой энергии образования субкаскадов была проведена в [13].

В работе [14] была разработана теоретическая модель для исследования образования каскадов и субкаскадов атомных столкновений в облучаемых твердых телах, основанная на использовании линейного кинетического уравнения Больцмана. На основе расширенного толкования понятия первично выбитый атом (ПВА) в [14] был сформулирован критерий для определения пороговой энергии образования субкаскадов в твердом теле и получены формулы для определения средних размеров субкаскадов и их числа в зависимости от энергии ПВА. На основе результатов, представленных в [14], в работе [15] были проведены численные расчеты для конкретных материалов, согласующиеся с экспериментальными данными.

Кроме этого, представления, развитые в [14], в работе [16] были использованы для вычисления стационарного энергетического распределения релятивистских электронов, замедляющихся в веществе за счет ионизационных потерь, с учетом размножения электронов. Использование результатов из [14] в работе [17] позволило на основе решения кинетического уравнения Больцмана определить функцию распределения по энергии каскада движущихся атомов при степенном потенциале взаимодействия (U ~ 1/r n [18]) с учетом энергии связи атомов в узлах решетки.

В работах [19, 20] было получено точное решение кинетического уравнения Больцмана, описывающее нестационарное энергетическое распределение каскада движущихся атомов с учетом их размножения. Предполагалось, что материал состоит из одинаковых атомов, рассеяние движущихся атомов является упругим и сферически симметричным в системе центра инерции, а энергия связи атомов в узлах решетки не учитывалась (εd = 0). В [19] предполагалось, что сечение рассеяния обратно пропорционально скорости (Σ = = Σ0/v; Σ0 = const), а в [20] оно полагалось постоянной величиной (Σ = const). В работе [21] в тех же предположениях (εd = 0; Σ = const) с использованием P1 и транспортного приближений было получено нестационарное пространственно-энергетическое распределение каскада выбитых атомов.

В настоящей работе на основе приближенного метода решения кинетического уравнения Больцмана определяется нестационарное энергетическое распределение каскада движущихся атомов с учетом их энергии связи в узлах решетки. Рассеяние движущихся атомов считается упругим и сферически симметричным в системе центра инерции. Для простоты и наглядности расчетов полагается, что сечение рассеяния обратно пропорционально скорости.

Полученное решение при εd = 0 хорошо согласуется с точным решением аналогичной задачи (см. [19]). Это решение позволяет оценить энергетический диапазон влияния учета энергии связи на функцию распределения.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим распространение каскада выбитых атомов в твердом теле, состоящем из одинаковых атомов. Кинетическое уравнение Больцмана, описывающее этот процесс, имеет следующий вид [10, 22]:

(1)
$\begin{gathered} \frac{1}{v}\frac{{\partial {\Phi }\left( {E,t} \right)}}{{\partial t}} + \Sigma \left( E \right){\Phi }\left( {E,t} \right) = \int\limits_E^{{{E}_{0}}} {dE{\kern 1pt} '{\text{P}}} \left( {E{\kern 1pt} ' \to E} \right) \times \\ \times \,\,\Sigma \left( {E{\kern 1pt} '} \right){\Phi }\left( {E{\kern 1pt} ',t} \right) + \int\limits_{E + {{{\varepsilon }}_{d}}}^{{{E}_{0}}} {dE{\kern 1pt} '{\text{P}}} \left( {E{\kern 1pt} ' \to E{\kern 1pt} ' - E - {{\varepsilon }_{d}}} \right) \times \\ \times \,\,\Sigma \left( {E{\kern 1pt} '} \right){\Phi }\left( {E{\kern 1pt} ',t} \right) + {{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)\delta \left( t \right), \\ \end{gathered} $
где $f(E,t)dE$ – число атомов с энергией $E$ в интервале $dE$ в момент времени t в единице объема; ${\Phi }\left( {E,t} \right) = {v}f\left( {E,t} \right)$ – поток движущихся атомов; ${v}$ – их скорость; P(E ' → Ε) = Σ(E ' → E)/Σ(E ') – индикатриса рассеяния (вероятность того, что движущийся атом с энергией $E'$ в результате рассеяния перейдет в единичный интервал энергий вблизи значения $E$); ${\Sigma }\left( {E{\kern 1pt} ' \to E} \right)$ и ${\Sigma }\left( {E{\kern 1pt} '} \right)$ – дифференциальное и полное макроскопические сечения рассеяния атомов;$~$δ(x) – дельта-функция Дирака; ${{E}_{0}}$ – начальная энергия движущихся атомов; ${{N}_{0}}$ – полное число атомов, испущенных в единицу объема; ${{\varepsilon }_{d}}$ – энергия связи атомов в узлах решетки.

Первый интеграл, стоящий в правой части кинетического уравнения (1), описывает переход движущегося атома с энергией E ' в состояние с энергией E. Второй интеграл описывает образование выбитого атома с энергией E, когда движущийся атом перешел в состояние с энергией $\left( {E{\kern 1pt} ' - E - {{\varepsilon }_{d}}} \right).$

Выше отмечалось, что точное решение уравнения (1) было получено в работах [19, 20] для упругого, сферически симметричного рассеяния в системе центра инерции без учета энергии связи атомов в узлах решетки (${{\varepsilon }_{d}} = 0$).

В данной работе мы также будем считать, что рассеяние движущихся атомов на покоящихся является сферически симметричным в системе центра инерции и описывается индикатрисой рассеяния, имеющей следующий вид [22]:

(2)
${\text{P}}\left( {E{\kern 1pt} ' \to E} \right) = {1 \mathord{\left/ {\vphantom {1 {E{\kern 1pt} '}}} \right. \kern-0em} {E{\kern 1pt} '}}.$

Для учета энергии связи уравнение (1) запишем в более простом виде, удобном для дальнейшего решения [23]:

(3)
$\begin{gathered} \frac{1}{v}\frac{{\partial {\Phi }\left( {E,t} \right)}}{{\partial t}} + \left[ {{\Sigma }\left( E \right) + {\delta \Sigma }} \right]{\Phi }\left( {E,t} \right) = \\ = \int\limits_E^{{{E}_{0}}} {dE{\kern 1pt} '{\text{P}}} \left( {E{\kern 1pt} ' \to E} \right)\left[ {{\Sigma }\left( {E{\kern 1pt} '} \right) + {\delta \Sigma }} \right]{\Phi }\left( {E{\kern 1pt} ',t} \right) + \\ + \,\,\int\limits_E^{{{E}_{0}}} {dE{\kern 1pt} '{\text{P}}} \left( {E{\kern 1pt} ' \to E{\kern 1pt} ' - E} \right){\Sigma }\left( {E{\kern 1pt} '} \right){\Phi }\left( {E{\kern 1pt} ',t} \right) + \\ + \,\,{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)\delta \left( t \right).{\text{\;}} \\ \end{gathered} $

Величину δΣ найдем, следуя [23], из соотношения

(4)
$\frac{d}{{dt}}E\left( t \right) = - {{\varepsilon }_{d}}\frac{d}{{dt}}N\left( t \right),$
где

(5)
$N\left( t \right) = \int\limits_0^{{{E}_{0}}} {dE{\text{\;}}f\left( {E,t} \right)} ;\,\,\,\,E\left( t \right) = \int\limits_0^{{{E}_{0}}} {dEEf\left( E \right)} .$

Используя (2)–(4), получим

(6)
$\delta {\Sigma } = \frac{{2{{\varepsilon }_{d}}}}{E}{\Sigma }\left( E \right).$

Корректность использования уравнения (3) и соотношения (4) была подробно проанализирована в работах [10, 24]. Там было показано, что в этом случае учитываются соударения, сопровождающиеся передачей энергии, большей ${{\varepsilon }_{d}}.$ Кроме этого, в этих работах было представлено уравнение, аналогичное (3), и позволяющее более точно учесть наличие энергии связи, но являющееся значительно более сложным для аналитического решения.

Учитывая (2) и (6), уравнение (3) можно представить в следующем виде:

(7)
$\begin{gathered} \frac{1}{{v{\Sigma }}}\frac{{\partial {\Psi }\left( {E,t} \right)}}{{\partial t}} + \left( {1 + \frac{{2{{\varepsilon }_{d}}}}{E}} \right){\Psi }\left( {E,t} \right) = \\ = 2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} '}}{{E{\kern 1pt} '}}} \left( {1 + \frac{{{{\varepsilon }_{d}}}}{{E{\kern 1pt} '}}} \right){\Psi }\left( {E{\kern 1pt} ',t} \right) + {{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)\delta \left( t \right), \\ \end{gathered} $
где ${\Psi }\left( {E,t} \right) = {\Sigma }\left( E \right){\Phi }\left( {E,t} \right)$ – плотность соударений.

РЕШЕНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ

Применяя к обеим частям уравнения (7) преобразование Лапласа по времени [25]

(8)
${\tilde {\Psi }}\left( {E,p} \right) = \int\limits_0^\infty {\exp \left( { - pt} \right){\Psi }\left( {E,t} \right)dt} ,$
получим:

(9)
$\begin{gathered} \left( {\frac{p}{{v{\Sigma }}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{E}} \right){\tilde {\Psi }}\left( {E,p} \right) = \\ = 2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} '}}{{E{\kern 1pt} '}}} \left( {1 + \frac{{{{\varepsilon }_{d}}}}{{E{\kern 1pt} '}}} \right)\,{\tilde {\Psi }}\left( {E{\kern 1pt} ',p} \right) + ~{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right). \\ \end{gathered} $

Выделим в решении уравнения (9) нерассеянное излучение

(10)
${\tilde {\Psi }}\left( {E,p} \right) = {{{\tilde {\Psi }}}_{0}}\left( {E,p} \right) + \frac{{{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)}}{{\left( {\frac{p}{{v{\Sigma }}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{E}} \right)}}.$

Подставив (10) в (9), найдем уравнение для функции ${{{\tilde {\Psi }}}_{0}}\left( {E,p} \right){\text{:}}$

(11)
$\begin{gathered} \left( {\frac{p}{{v{\Sigma }}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{E}} \right){{{{\tilde {\Psi }}}}_{0}}\left( {E,p} \right) = \\ = \,2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} '}}{{E{\kern 1pt} '}}} \left( {1 + \frac{{{{\varepsilon }_{d}}}}{{E{\kern 1pt} '}}} \right){{{{\tilde {\Psi }}}}_{0}}\left( {E{\kern 1pt} ',p} \right) + \,\,\frac{{2{{N}_{0}}\left( {1 + \frac{{{{\varepsilon }_{d}}}}{{{{E}_{0}}}}} \right)}}{{{{E}_{0}}\left( {\frac{p}{{{{v}_{0}}{\Sigma }\left( {{{E}_{0}}} \right)}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{{{{E}_{0}}}}} \right)}}. \\ \end{gathered} $

Будем далее для простоты расчетов полагать, что

(12)
${\Sigma } = {{{{{\Sigma }}_{0}}} \mathord{\left/ {\vphantom {{{{{\Sigma }}_{0}}} v}} \right. \kern-0em} v};\,\,\,\,{{{\Sigma }}_{0}} = {\text{const}}.$

Используя (12) и дифференцируя (11) по энергии получим дифференциальное уравнение для функции ${{{\tilde {\Psi }}}_{0}}\left( {E,p} \right){\text{:}}$

(13)
$\frac{d}{{dE}}{{{\tilde {\Psi }}}_{0}}\left( {E,p} \right) = - \frac{{2{{{{\tilde {\Psi }}}}_{0}}\left( {E,p} \right)}}{{E\left( {\frac{p}{{{{{\Sigma }}_{0}}}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{E}} \right)}}.$

Начальное условие для уравнения (13) легко определить из (11):

(14)
${{{\tilde {\Psi }}}_{0}}\left( {{{E}_{0}},p} \right) = \frac{{2{{N}_{0}}\left( {1 + \frac{{{{\varepsilon }_{d}}}}{{{{E}_{0}}}}} \right)}}{{{{E}_{0}}{{{\left( {\frac{p}{{{{{\Sigma }}_{0}}}} + 1 + \frac{{2{{\varepsilon }_{d}}}}{{{{E}_{0}}}}} \right)}}^{2}}}}.$

Решая уравнение (13) с учетом (14), для образа Лапласа функции распределения получим:

(15)
$\begin{gathered} \tilde {f}\left( {E,p} \right) = \frac{{{\tilde {\Psi }}\left( {E,p} \right)}}{{{{{\Sigma }}_{0}}}} = \frac{{2{{N}_{0}}{{{\Sigma }}_{0}}\left( {1 + \frac{{{{\varepsilon }_{d}}}}{{{{E}_{0}}}}} \right)}}{{{{E}_{0}}{{{\left( {p + {{{\Sigma }}_{0}} + \frac{{2{{\varepsilon }_{d}}{{{\Sigma }}_{0}}}}{{{{E}_{0}}}}} \right)}}^{2}}}} \times \\ \times \,\,{{\left( {\frac{{{{E}_{0}} + \frac{{2{{\varepsilon }_{d}}{{{\Sigma }}_{0}}}}{{\left( {p + {{{\Sigma }}_{0}}} \right)}}}}{{E + \frac{{2{{\varepsilon }_{d}}{{{\Sigma }}_{0}}}}{{\left( {p + {{{\Sigma }}_{0}}} \right)}}}}} \right)}^{{\frac{{2{{{\Sigma }}_{0}}}}{{\left( {p + {{{\Sigma }}_{0}}} \right)}}}}} + \frac{{{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)}}{{\left( {p + {{{\Sigma }}_{0}} + \frac{{2{{\varepsilon }_{d}}{{{\Sigma }}_{0}}}}{{{{E}_{0}}}}} \right)}}. \\ \end{gathered} $

Очевидно, что при ${{\varepsilon }_{d}} = 0$ выражение (15) совпадает с точным решением соответствующей задачи (см. в [19] формулу (12)), поскольку при этом условии и сделанных предположениях совпадают уравнения (1) и (7).

Вычисление оригинала функции распределения $\left( {f\left( {E,t} \right)} \right),$ используя формулу (15), является достаточно сложной задачей. В связи с этим для функции распределения (первое слагаемое в (15)) выберем следующее приближенное выражение

(16)
$f\left( {E,t} \right) = A\left( E \right){{t}^{{b\left( E \right)}}}{\text{exp}}\left[ { - c\left( E \right)t} \right],$
где параметры $A\left( E \right),$ $b\left( E \right),$ $c\left( E \right)$ легко определяются через временные моменты (см. напр. [22])

(17)
$\left\langle {{{t}^{n}}\left( E \right)} \right\rangle = {{\int\limits_0^{{{E}_{0}}} {dt~{{t}^{n}}~f\left( {E,t} \right)} } \mathord{\left/ {\vphantom {{\int\limits_0^{{{E}_{0}}} {dt~{{t}^{n}}~f\left( {E,t} \right)} } {\int\limits_0^{{{E}_{0}}} {dt~f\left( {E,t} \right)} }}} \right. \kern-0em} {\int\limits_0^{{{E}_{0}}} {dt~f\left( {E,t} \right)} }}\,\,(n = 1,~2..).$

Используя (16), (17), найдем:

(18)
$\begin{gathered} A\left( E \right) = \frac{{\tilde {f}\left( {E,p = 0} \right)c{{{\left( E \right)}}^{{b\left( E \right) + 1}}}}}{{{\Gamma }\left[ {b\left( E \right) + 1} \right]}}; \\ b\left( E \right) = \frac{{{{{\left\langle {t\left( E \right)} \right\rangle }}^{2}}}}{{\left\langle {{{t}^{2}}\left( E \right)} \right\rangle - {{{\left\langle {t\left( E \right)} \right\rangle }}^{2}}}} - 1; \\ c\left( E \right) = \frac{{\left\langle {t\left( E \right)} \right\rangle }}{{\left\langle {{{t}^{2}}\left( E \right)} \right\rangle - {{{\left\langle {t\left( E \right)} \right\rangle }}^{2}}}}, \\ \end{gathered} $
где Γ(x) – гамма-функция [26].

Из выражения (16) следует, что наиболее вероятное время замедления равно.

(19)
${{t}_{m}}\left( E \right) = \frac{{b\left( E \right)}}{{c\left( E \right)}} = \frac{{2{{{\left\langle {t\left( E \right)} \right\rangle }}^{2}} - \left\langle {{{t}^{2}}\left( E \right)} \right\rangle }}{{\left\langle {t\left( E \right)} \right\rangle }}.$

Соответствующие временные моменты, используя (15), можно вычислить следующим образом:

(20)
$\left\langle {{{t}^{n}}\left( E \right)} \right\rangle = {{\left( { - 1} \right)}^{n}}{{\left\{ {\frac{{\left[ {\frac{{{{\partial }^{n}}}}{{\partial {{p}^{n}}}}\tilde {f}\left( {E,p} \right)} \right]}}{{\tilde {f}\left( {E,p} \right)}}} \right\}}_{{p = 0}}}.~$

Используя (15), (20), найдем:

(21)
$\begin{gathered} \tilde {f}\left( {E,p = 0} \right) = \frac{{2{{N}_{0}}{{E}_{0}}}}{{{{{\Sigma }}_{0}}{{{\left( {E + 2{{\varepsilon }_{d}}} \right)}}^{2}}}}; \\ \left\langle {t\left( E \right)} \right\rangle = \frac{2}{{{{{\Sigma }}_{0}}}}\left[ {1 + \ln \left( {\frac{{{{E}_{0}}}}{{E + 2{{\varepsilon }_{d}}}}} \right) - \frac{{2{{\varepsilon }_{d}}\left( {{{E}_{0}} - E} \right)}}{{{{E}_{0}}\left( {E + 2{{\varepsilon }_{d}}} \right)}}} \right]; \\ \left\langle {{{t}^{2}}\left( E \right)} \right\rangle = \frac{6}{{{\Sigma }_{0}^{2}}}\left\{ {\begin{array}{*{20}{c}} {1 + 2{\text{ln}}\left( {\frac{{{{E}_{0}}}}{{E + 2{{\varepsilon }_{d}}}}} \right) - } \\ { - \frac{{4{{\varepsilon }_{d}}\left( {{{E}_{0}} - E} \right)}}{{{{E}_{0}}\left( {E + 2{{\varepsilon }_{d}}} \right)}} - \frac{{4\varepsilon _{d}^{2}{{{\left( {{{E}_{0}} - E} \right)}}^{2}}}}{{3E_{0}^{2}{{{\left( {E + 2{{\varepsilon }_{d}}} \right)}}^{2}}}} + } \\ { + \frac{2}{3}{{{\left[ {{\text{ln}}\left( {\frac{{{{E}_{0}}}}{{E + 2{{\varepsilon }_{d}}}}} \right) - \frac{{2{{\varepsilon }_{d}}\left( {{{E}_{0}} - E} \right)}}{{{{E}_{0}}\left( {E + 2{{\varepsilon }_{d}}} \right)}}} \right]}}^{2}}} \end{array}} \right\}. \\ \end{gathered} $

Заметим, что в выражениях (21), мы пренебрегали членами порядка ${{{{\varepsilon }_{d}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{d}}} {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}},$ много меньшими единицы.

Таким образом, окончательно функцию распределения (16) (рассеянное излучение) можно представить в следующем безразмерном виде:

(22)
$\begin{gathered} f{\kern 1pt} '\left( {E,\tau } \right) = \frac{{f\left( {E,t} \right){{E}_{0}}}}{{{{N}_{0}}}} = 2{{\left( {\frac{{{{E}_{0}}}}{{E + 2{{\varepsilon }_{d}}}}} \right)}^{2}} \times \\ \times \,\,~\frac{{{{{\left[ {c{\kern 1pt} '\left( E \right)} \right]}}^{{b\left( E \right) + 1}}}}}{{{\Gamma }\left[ {b\left( E \right) + 1} \right]}}{{\tau }^{{b\left( E \right)}}}{\text{exp}}\left[ { - c{\kern 1pt} '\left( E \right)\tau } \right], \\ \end{gathered} $
где $\tau = {{{\Sigma }}_{0}}t$ – безразмерное время; $c{\kern 1pt} '\left( E \right) = {{c\left( E \right)} \mathord{\left/ {\vphantom {{c\left( E \right)} {{{{\Sigma }}_{0}}}}} \right. \kern-0em} {{{{\Sigma }}_{0}}}}.$

АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

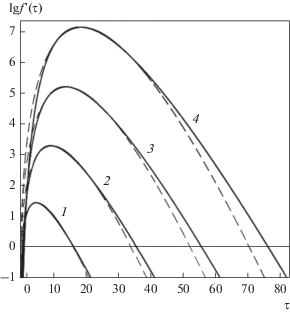
Оценим точность представления функции распределения в виде (16). На рис. 1 представлены зависимости функции распределения $\left( {f{\kern 1pt} '\left( {E,\tau } \right)} \right)$ от безразмерного времени $\tau {\text{\;}}$ для различных значений безразмерной энергии $\varepsilon = {E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}},$ построенные по формуле (22) при ${{\varepsilon }_{d}} = 0$ и по формуле (26) из [19], являющейся точным решением соответствующей задачи. Из рисунка видно, что функция (22) с хорошей точностью описывает точное решение задачи. Следует отметить, что время достижения максимума и значение функции (22) в максимуме на несколько процентов отличаются от соответствующих значений при точном решении (см. в [19] формулы (27), (28)).

Рис. 1.

Зависимости функции распределения от времени при различных значениях энергии ($\varepsilon = {E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}};$ 1 – ε = 10–1; 2 – ε = 10–2; 3 – ε = 10–3; 4 – ε = 10–4), построенные по точной формуле (штриховые линии) и по приближенной (сплошные линии).

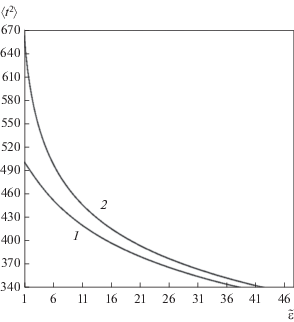
Учет энергии связи (${{\varepsilon }_{d}}$) приводит к уменьшению среднего времени замедления и среднего квадрата этой величины, что представлено на рис. 2 и 3. (кривые построены по формулам (21)). Это обстоятельство связано, очевидно, с тем, что при учете энергии связи образуется меньше выбитых атомов, поскольку учитываются потери энергии на выбивание атомов из узлов решетки. Напомним, что при ${{\varepsilon }_{d}} = 0$ число выбитых атомов возрастает не ограничено [19].

Рис. 2.

Зависимость среднего времени замедления $\left( {{{{\Sigma }}_{0}}\left\langle t \right\rangle } \right)$ от безразмерной энергии $\tilde {\varepsilon } = {E \mathord{\left/ {\vphantom {E {{{\varepsilon }_{d}}}}} \right. \kern-0em} {{{\varepsilon }_{d}}}}$ (1 – с учетом ${{\varepsilon }_{d}};$ 2 – без учета ${{\varepsilon }_{d}}$).

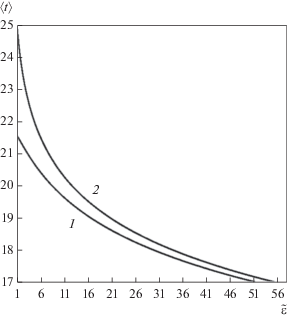
Рис. 3.

Зависимость среднего квадрата времени замедления $\left( {{\Sigma }_{0}^{2}\left\langle {{{t}^{2}}} \right\rangle } \right)$ от безразмерной энергии $\tilde {\varepsilon } = {E \mathord{\left/ {\vphantom {E {{{\varepsilon }_{d}}}}} \right. \kern-0em} {{{\varepsilon }_{d}}}}$ (1 – с учетом ${{\varepsilon }_{d}};$ 2 – без учета ${{\varepsilon }_{d}}$).

На рис. 4 показаны зависимости функции распределения от времени ($f{\kern 1pt} '\left( \tau \right)$), построенные по формуле (22) для различных значений безразмерной энергии $\tilde {\varepsilon } = {E \mathord{\left/ {\vphantom {E {{{\varepsilon }_{d}}}}} \right. \kern-0em} {{{\varepsilon }_{d}}}}$ при учете (штриховые линии) и без учета (сплошные линии) энергии связи атомов. При расчетах полагалось, что ${{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{\varepsilon }_{d}}}}} \right. \kern-0em} {{{\varepsilon }_{d}}}} = {{10}^{5}}.$

Рис. 4.

Зависимости функции распределения от времени, построенные по формуле (22), при различных значениях безразмерной энергии ($\tilde {\varepsilon } = {E \mathord{\left/ {\vphantom {E {{{\varepsilon }_{d}}}}} \right. \kern-0em} {{{\varepsilon }_{d}}}};$ 1 – $\tilde {\varepsilon }$ = = 25; 2 – $\tilde {\varepsilon }$ = 15; 3 – $\tilde {\varepsilon }$ = 5; 4 – $\tilde {\varepsilon }~$ = 1), при учете (штриховые линии) и без учета (сплошные линии) энергии связи.

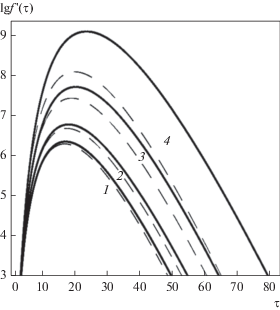
Из представленных результатов видно, что при учете энергии связи функция распределения достигает максимума при меньших значениях времени (см. рис. 4), и ее значение в максимуме существенно меньше. Это обусловлено, очевидно, тем, что при учете энергии связи количество выбитых атомов конечно, а в противном случае оно неограниченно возрастает. Однако с увеличением энергии эти различия становятся все менее и менее существенными, и при $E \geqslant 25{{\varepsilon }_{d}}~~$практически исчезают. Последнее обстоятельство уточняет область применимости точных результатов, полученных в работах [19–21].

Найдем каскадную функцию $v\left( {{{E}_{0}}} \right),$ представляющую собой полное число атомов решетки, выбитых одним первичным атомом с энергией ${{E}_{0}}.$ В нашем случае она будет определяться следующим выражением (см. [10, 24]):

(23)
$v\left( {{{E}_{0}}} \right) = \frac{1}{{{{N}_{0}}}}\int\limits_{{{{\varepsilon }}_{d}}}^{{{E}_{0}}} {{{{\Sigma }}_{0}}\tilde {f}} \left( {E,p = 0} \right)dE.$

Используя (23) и (21) и пренебрегая членами порядка ${{{{\varepsilon }_{d}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{d}}} {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}},$ много меньшими единицы, найдем:

(24)
$v\left( {{{E}_{0}}} \right) = \frac{{2{{E}_{0}}}}{{3{{\varepsilon }_{d}}}}.$

Это значение несколько превосходит известный результат Кинчина–Пиза (см. в [2]), поскольку мы не учитывали соударения с передачей атомам решетки энергии, меньшей ${{\varepsilon }_{d}}$ (подробный анализ приведен в [10, 24]).

ЗАКЛЮЧЕНИЕ

В настоящей работе получено приближенное аналитическое решение кинетического уравнения Больцмана, описывающее нестационарное энергетическое распределение каскада движущихся атомов в твердом теле при учете энергии связи атомов в узлах решетки (${{\varepsilon }_{d}}$). Предполагалось, что тело состоит из одинаковых атомов, рассеяние является сферически симметричным в системе центра инерции, а сечение взаимодействия обратно пропорционально скорости (см. (12)).

На основе полученного решения проведен анализ влияния энергии связи на функцию распределения и связанные с ней величины: среднее время замедления, средний квадрат этой величины (см. рис. 2–4). В предельном случае ${{\varepsilon }_{d}} = 0$ полученное приближенное решение хорошо согласуется с точным решением соответствующей задачи из [19] (см. рис. 1).

Показано, что учет энергии связи атомов в узлах решетки начнет оказывать влияние на функцию распределения при энергиях меньших $ \approx {\kern 1pt} 25{{\varepsilon }_{d}}.$ Это позволяет уточнить область применения точных решений уравнения Больцмана полученных в [19–21] при ${{\varepsilon }_{d}} = 0.$

Список литературы

  1. Лейман К. Взаимодействие излучения с твердым телом и образование элементарных дефектов. М.: Атомиздат, 1979. 297 с.

  2. Вас Гэри С. Основы радиационного материаловедения. Металлы и сплавы. М.: ТЕХНОСФЕРА, 2014. 992 с.

  3. Портных И.А., Козлов А.В. Рост вакансионных пор на начальной стадии нестационарного распухания // ФММ. 2018. Т. 119. № 6. С. 636–644.

  4. Васильев Л.С., Ломаев С.Л. Избыточный объем материалов с дислокациями // ФММ. 2019. Т. 120. № 7. С. 771–777.

  5. Исинбаев А.Р., Портных И.А., Козлов А.В. Влияние радиационной пористости, формирующейся в аустенитной стали при нелинейном облучении, на концентрацию собственных точечных дефектов // ФММ. 2020. Т. 121. № 1. С. 99–104.

  6. Воскобойников Р.Е. Радиационные дефекты в алюминии. Моделирование первичных повреждений в каскадах смещений в объеме материала // ФММ. 2019. Т. 120. № 1. С. 3–10.

  7. Воскобойников Р.Е. Радиационные дефекты в алюминии. Моделирование первичных повреждений в каскадах смещений на поверхности // ФММ. 2019. Т. 120. № 1. С. 11–17.

  8. Воскобойников Р.Е. Моделирование каскадов смещений на поверхности никеля методом молекулярной динамики // ФММ. 2020. Т. 121. № 1. С. 10–17.

  9. Воскобойников Р.Е. Моделирование первичных радиационных повреждений в никеле // ФММ. 2020. Т. 121. № 1. С. 18–24.

  10. Ryazanov A.I., Metelkin E.V. Concerning the theory of radiation cascades of atomic collisions in a solid with an arbitrary interatomic interaction potential // Radiation Effects and Defects in Solids. 1980. V. 52. № 1–2. P. 15–23.

  11. Sato Y., Kojimo S., Yoshiie T., Kiritani M. Criterion of subcascade formation in metals from atomic collision calculation // J. Nuclear Mater. 1991. № 179–181. P. 901–904.

  12. Sato Y., Yoshiie T., Kiritani M. Binary collision calculation of subcascade structure and its correspondence to observe subcascade defects in 14 MeV neutron irradiated copper // J. Nuclear Mater. 1992. № 191–194. P. 1101–1104.

  13. Метелкин Е.В., Рязанов А.И. Пороговая энергия образования субкаскадов // Атомная энергия. 1997. Т. 83. В. 3. С. 183–189.

  14. Метелкин Е.В., Рязанов А.И., Семенов Е.В. Разработка новых теоретических моделей для исследования образования каскадов и субкаскадов атомных столкновений в облучаемых твердых телах // Журн. экспериментальной и теоретич. физики. 2008. Т. 134. В. 3(9). С. 469–480.

  15. Ryazanov A.I., Metelkin E.V., Semenov E.V. Modeling of cascade and sub-cascade formation at high PKA energies in irradiated fusion structural materials // J. Nuclear Mater. 2009. № 386–388. P. 132–134.

  16. Метелкин Е.В., Лебедева М.В., Черняев А.В. Энергетическое распределение релятивистских электронов, замедляющихся в веществе // Атомная энергия. 2018. Т. 125. В. 3. С. 184–186.

  17. Aleksandrov A.A, Akatev V.A., Metelkin E.V., Barycheva E.J. Develop a Model to Study the Energy Distribution of Cascades of Atomic Collisions // Herald of the Bauman Moscow State Technical University, Series Natural Sciences. 2019. № 1. P. 27–36

  18. Lindhard J., Vibeke Nielsen, Scharff M. Approximation Method in Classical Scattering by Screened Coulomb Fields // Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddelelser. 1968. V. 36. № 10. P. 1–32.

  19. Метелкин Е.В., Манвелов А.Н., Пономарев А.Я., Шмырев В.И. Модель развития каскада выбитых атомов в твердом теле // ФММ. 2019. Т. 120. № 8. С. 892–896.

  20. Aleksandrov A.A., Akatev V.A., Metelkin E.V., Barycheva E.J. Investigation of the Nonstationary Energy Distribution of an Atomic Collision Cascad // Herald of the Bauman Moscow State Technical University, Series Natural Sciences. 2019. № 6. P. 40–49.

  21. Метелкин Е.В., Акатьев В.А., Шмырев В.И., Барышева Е.Ю. Нестационарное пространственно-энергетическое распределение каскада выбитых атомов в твердом теле // Журн. экспериментальной и теоретич. физики. 2019. Т. 156. В. 3(9). С. 387–395.

  22. Исаков А.И., Казарновский М.В., Медведев Ю.А., Метелкин Е.В. Нестационарное замедление нейтронов. Основные закономерности и некоторые приложения. М.: Наука, 1984. 264 с.

  23. Ахиезер А.И., Ахиезер И.А. К кинетической теории каскада столкновений в твердом теле. ХФТИ, 1975. Препринт 75–24. 35 с.

  24. Рязанов А.И., Метелкин Е.В. К теории образования точечных дефектов в радиационном каскаде столкновений атомов с произвольным потенциалом взаимодействия. ИАЭ, 1979. Препринт 3223. 35 с.

  25. Бейтман Г., Эрдейи А. Таблицы интегральных преобразований. Т. 1. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. 343с.

  26. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал