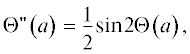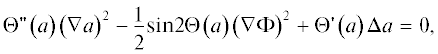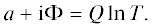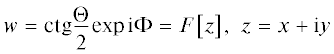Физика металлов и металловедение, 2021, T. 122, № 5, стр. 455-459

Новые типы трехмерных вихрей в модели Гейзенберга

А. Б. Борисов^a, *, Д. В. Долгих^a

^a Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия

Поступила в редакцию 27.10.2020
После доработки 01.12.2020
Принята к публикации 19.01.2021

DOI: 10.31857/S0015323021050028

Аннотация

Рассматривается модель Гейзенберга для изотропного магнетика. Для соответствующих уравнений применяется подстановка, которая сводит их к уравнениям с более простой геометрической интерпретацией. Одно из решений последних описывает новую магнитную структуру, которая представляет собой две прямолинейные пересекающиеся вихревые нити, меняющие топологический заряд после пересечения.

Ключевые слова: вихри, вихревые структуры, модель Гейзенберга, изотропный магнетик

ВВЕДЕНИЕ

Среди различных структур в исследуемых магнитных средах, в последнее десятилетие наблюдается повышенный интерес к изучению вихревых структур. Важную роль вихрей при описании магнитных топологических фазовых переходов отмечали многие исследователи (см., напр., [1–5]). Такие возбуждения представляют не только академический интерес. Предсказанные два десятилетия назад [6, 7] вихри в киральных магнетиках (киральные скирмионы) могут найти важное применение в беговой памяти [8–10]. К настоящему времени двумерные вихри в ферро- и антиферромагнетиках достаточно подробно изучены [6, 7, 11–15]. Отметим, что, несмотря на многолетнее изучение вихрей в “больших” (bulk) образцах, трехмерные вихревые структуры теоретически и зкспериментально мало изучены. Однако в последнее время появилась новая экмпериментальная техника – внеосевая электронная голография [16], которая позволяет исследовать трехмерные локализованные структуры. Недавно выяснилось, что предсказанные в [5, 6] двумерные киральные скирмионы имеют трехмерную структуру [17]. К настоящему времени из трехмерных структур теоретически описаны только магнонные капли [10], магнитные “ежи” и спиральные структуры [18]. Поэтому важное значение приобретает изучение трехмерных структур аналитическими методами.

Такие методы применимы, как правило, к моделям с высокой степенью симметрии. Хотя применимость аналитических методов ограничена, их научная значимость не вызывает сомнений. Они позволяют достаточно полно исследовать структуру ядер нелинейных образований и качественно учесть влияние других взаимодествий, не входящих в первоначальную модель. Кроме того, точные решения являются “затравочными” функциями при компьютерном моделировании минимизации плотности энергии, включающем магнитные поля, энергию анизотропии и т.д. Вихревые структуры в ферромагнетике формируются в основном обменным взаимодействием (модель Гейзенберга), и цель настояшей работы – найти трехмерные вихри в этой модели.

В этой работе мы обсуждаем новые типы трехмерных вихревых структур в модели Гейзенберга. Статья спланирована следующим образом. В первом параграфе в уравнениях изотропного магнетика мы используем подстановку, которая приводит модель к уравнению маятника и четырем уравнениям с простой геометрической интерпретацией. Последние редуцируются к двум уравнениям для комплексной функции $S\left( {x,y,z} \right).$ Мы находим общее решение этих уравнений, зависящее от произвольной функции. Простейшее решение этих уравнений мы обсуждаем во втором параграфе. Показано, что оно описывает новую магнитную структуру, которая представляет две прямолинейные пересекающиеся вихревые нити, меняющие топологический заряд после пересечения. В конце параграфа обсуждается экспериментальная реализация найденных структур.

1. УПРОЩЕНИЕ УРАВНЕНИЙ МОДЕЛИ ГЕЙЗЕНБЕРГА

Модель Гейзенберга основана на применении гамильтониана H обменного взаимодействия

$H = \sum\limits_{i{\text{ > }}j} {{{J}_{{ij}}}{{S}_{i}}{{S}_{j}}} ,$

где суммирование ведется по всем парам различных {i, j} узлов кристалла, в которых находятся ионы со спинами S_i и S_j, константы J_ij характеризуют обменное взаимодействие между этими ионами. С учетом изотропного обменного взаимодействияв между ближайшими соседями в континуальном пределе плотность гамильтониана ферромагнетика имеет простой вид:

(1)

$H = J~\nabla S~\nabla S{\kern 1pt} .$

Для ферромагнитной модели Гейзенберга J > 0 и J < 0 для антиферромагнитной модели [19]. Отметим, что разложение (1) учитывает только квадратичные слагаемые по градиентам спина. В общем слачае для описания даже обменного взаимодействия в некоторых системах нужно учитывать в (1) слагаемые более высокого порядка по $\nabla S{\text{,}}$ включая биквадратичные для спина $S \geqslant 1.$ Кроме того, мы исследуем далее случай нулевого магнитного поля, когда основное состояние модели Гейзенберга есть однородно намагниченный ферромагнетик без каких либо структур.

Тогда трехмерные уравнения Ландау–Лифшица можно записать в виде

(2)

$\left[ {n \times \left( {\partial _{x}^{2} + \partial _{y}^{2} + \partial _{z}^{2}~} \right)n} \right] = 0,\,\,\,\,{{n}^{2}} = 1,$

где n – единичный вектор намагниченности S = = M₀n, M₀ — спонтанная намагниченность. Здесь и далее ${{\Delta }} = \partial _{x}^{2} + \partial _{y}^{2} + \partial _{z}^{2}$ – трехмерный оператор Лапласа. Вектор n параметризуется полями ${{\Theta ,}}$ ${{\Phi :}}$

$n = \left( {\cos {{\Phi }}\sin {{\Theta }},\sin {{\Phi }}\sin {{\Theta }},\cos {{\Theta }}} \right).$

В этих переменных уравнения (2) переходят в систему нелинейных дифференциальных уравнений:

(3)

${{\Delta \Theta }} = \frac{1}{2}{{\left( {\nabla {{\Phi }}} \right)}^{2}}\sin 2{{\Theta ,}}\,\,\,\,\nabla \left[ {\left( {\nabla {{\Phi }}} \right){{{\sin }}^{2}}{{\Theta }}~} \right] = 0.$

Уравнение (2) инвариантно относительно группы $SO\left( 3 \right) \times SO\left( {3n} \right)$ спиновых и пространственных вращений. Такая симметрия позволяет найти широкий класс точных решений. Аналитическое решение уравнения (2) возможно лишь в определенных классах решений. Для выделения одного из них нужно обобщить процедуру, предложенную в [18], и положить поле ${{\Theta }}$ локально зависящим от вспомогательного поля ${{\Theta }} = {{\Theta }}\left( {a\left[ {x,y,z} \right]} \right).$ Тогда непосредственными вычислениями нетрудно убедиться, что из уравнений:

(4)

(5)

${{\Delta }}a = {{\Delta \Phi }} = 0,\,\,\,{{\left( {\nabla a} \right)}^{2}} = {{\left( {\nabla {{\Phi }}} \right)}^{2}},\,\,\,\nabla a\nabla {{\Phi }} = 0$

следуют уравнения (3). Действительно, после подстановки ${{\Theta }} = {{\Theta }}\left( {a\left[ {x,y,z} \right]} \right)$ первое уравнение в (3) переходит в

откуда и следует уравнение (4). Второе уравнение в (3) после подстановки приводится к виду

$2\cos {{\Theta }}~{{\Theta }}{\kern 1pt} {\text{'}}\left( a \right)\left( {\nabla a~\nabla {{\Phi }}} \right) + \sin {{\Theta }}~{{\Delta \Phi }} = 0.$

Tакие подстановки, как увидим далее, приводят к широкому классу точных решений неинтегрируемой модели (2).

Отметим, что уравнения (5) имеют простую геометрическую интерпретацию. Они описывают две пересекающие в каждой точке поверхности $a\left( {x,y,z} \right) = 0,$ ${{\Phi }}\left( {x,y,z} \right) = 0,$ нормали к которым, $\nabla a$ и $\nabla {{\Phi }}$ соответственно, имеют единичную длину, ортогональны и бездивергентны:

$\nabla \nabla a = 0,\,\,\,\,\nabla \nabla {{\Phi }} = 0.$

Перейдем к решению уравнений (4), (5). Введем комплексное поле $S = a + i{{\Phi }}$ и распишем (5) в виде системы из двух уравнений для поля S:

(6)

$\left( {\nabla S} \right)\left( {\nabla S} \right) = 0;$

(7)

${{\Delta }}S = 0.$

Эта система обладает замечательным свойством инвариантности к произвольным заменам поля S, которые мы будем использовать в дальнейшем. Нетрудно проверить, что если поле $S$ является решением этой системы, то и произвольная функция $\tilde {S} = F\left( S \right)$ также будет ее решением. Для решения системы (6), (7) используем процедуру, предложенную в [18]. Введем новое комплексное поле $T\left( {x,y,z} \right)$ соотношением

(8)

${{S}_{{,y}}}\left( {x,y,z} \right) = T\left( {x,y,z} \right){{S}_{{,z}}}\left( {x,y,z} \right).$

Здесь подстрочный индекс обозначает диффиренцирование по соответствующей переменной

${{S}_{{,y}}}\left( {x,y,z} \right) = \frac{{\partial S\left( {x,y,z} \right)}}{{\partial y}}$

и т.д. Подстановка (8) в (6) определяет ${{S}_{{,x}}}\left( {x,y,z} \right){\text{:}}$

(9)

${{S}_{{,x}}}\left( {x,y,z} \right) = {\text{i}}\sqrt {1 + {{T}^{2}}\left( {x,y,z} \right)} {{S}_{{,z}}}\left( {x,y,z} \right).$

Условие совместности (8), (9) дает нелинейное уравнение для поля T:

${{T}_{{,z}}} + T{{T}_{{,y}}} + {\text{i}}\sqrt {1 + {{T}^{2}}} {{T}_{{,x}}} = 0.$

Из теории дифференциальных уравнений первого порядка в частных производных следует, что поле $T$ определяется неявным уравнением

(10)

$G\left[ {{{H}_{1}},{{H}_{2}},{{H}_{3}}} \right] = 0,$

где величины ${{H}_{1}},$ ${{H}_{2}},$ ${{H}_{3}}$ суть интегралы характеристической системы уравнений для координат $x\left( t \right),$ $y\left( t \right),$ $z\left( t \right){\text{:}}$

$\begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}z\left[ t \right] = 1,\,\,\,\,\frac{{\text{d}}}{{{\text{d}}t}}y\left[ t \right] = T\left[ {x,y,z} \right], \\ \frac{{\text{d}}}{{{\text{d}}t}}x\left[ t \right] = {\text{i}}\sqrt {1 + {{T}^{2}}\left[ {x,y,z} \right]} ,\,\,\,\,\frac{{\text{d}}}{{{\text{d}}t}}T\left[ {x,y,z} \right] = 0. \\ \end{gathered} $

Интегралы имеют вид:

(11)

$\begin{gathered} {{H}_{1}} = T\left[ {x,y,z} \right],\,\,\,\,{{H}_{2}} = T\left[ {x,y,z} \right]z - y, \\ {{H}_{3}} = - {\text{i}}~\sqrt {1 + {{T}^{2}}\left[ {x,y,z} \right]} z + x. \\ \end{gathered} $

Из этого обширного класса решений (10), (11) выберем одно с функцией $G$ в виде

$G = {\text{i\;}}{{{\text{H}}}_{1}}{{H}_{2}} + {{H}_{3}}\sqrt {1 + H_{1}^{2}.} $

Тогда поле T удовлетворяет уравнению

$ - {\text{i}}\left( {z + yT} \right) + x\sqrt {1 + {{T}^{2}}} = 0$

и, следовательно.

(12)

$T = \frac{{ - yz + {\text{i}}x\sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} }}{{{{x}^{2}} + {{y}^{2}}}}.$

Оказывается, что поле (12) удовлетворяет не только уравнению (6), но и уравнению (7) (с заменой $S \to T$). Тогда согласно разбиению

С параметром Q, принимающим целочисленные значения, мы находим явный вид полей a, ${{\Phi :}}$

(13)

$\begin{gathered} {{\Phi }} = Q~{\text{arctg}}\left[ {\frac{{x\sqrt {{{x}^{2}} + {{y}^{2}} + {{z}^{2}}} }}{{ - yz}}} \right]; \\ a = Q\ln \frac{{\sqrt {{{x}^{2}} + {{z}^{2}}~} }}{{\sqrt {{{x}^{2}} + {{y}^{2}}} }}~, \\ \end{gathered} $

которые, как нетрудно убедиться прямыми вычислениями, удовлетворяют уравнениям (5).

Выберем в качестве ${{\Theta }}\left( {a\left( {x,y,z} \right)} \right)$ решение уравнения (4) в виде решетки солитонов:

(14)

$\cos {{\Theta }} = {\text{sn}}~\left[ {\frac{a}{k},k} \right],\,\,\,\,0 < k < 1.$

При $k = 1$ выражение (14) упрощается:

(15)

${{\Theta }} = 2~{\text{arctg}}~\left[ {\exp ( - a)} \right].$

Проанализируем далее формулы (13), (15) новой структуры в изотропном магнетике.

2. АНАЛИЗ ВИХРЕВОЙ СТРУКТУРЫ

Отметим вначале, что подстановка (4), (5) и система (6), (7) являются обобщением теории инстантонов [20] в двумерном случае для изотропного магнетика. Широкий класс решений, найденных в [20], описывается простой формулой:

с аналитической функцией F. В двумерном случае уравнения (6), (7) тождественно удовлетворяются при $S = S\left( z \right),$ и связь с полем w согласно (15) определяется простым соотношением

$w = {\text{exp}}\left( S \right).$

Несмотря на внешнюю простоту, выражение для поля ${{\Phi }}$ (13) имеет богатую трехмерную вихревую структуру. Исследованные ранее [6, 7, 11, 12] двумерные вихри представляли прямолинейную нить с зависимостью ${{\Phi }} = {{\Phi }}\left( \varphi \right)$ и ${{\Theta }} = {{\Theta }}\left( r \right)$ в полярной системе координат $\left( {r,\varphi } \right).$ Формула (13) описывает две пересекающиеся вихревые нити. Одна – прямолинейная вихревая нить, расположена на оси $Oz$ и в полярной системе координат ($x = r\cos \varphi ,$ $y = ~r\sin \varphi $) в плоскости $z = {\text{const}}$ имеет вид

(16)

${{\Phi }}\left( {r,z,\varphi } \right) = Q~{\text{arctg}}\left( {\frac{{\sqrt {{{r}^{2}} + {{z}^{2}}} }}{{ - z}}{\text{ctg}}~\varphi } \right)$

с топологическим зарядом

$q = \frac{1}{{2\pi }}\oint\limits_{{\gamma }} {\nabla {{\Phi d}}{\mathbf{r}}} ,$

равным $Q~{\text{sign}}\left( z \right).$ Здесь $\gamma $ – произвольный замкнутый контур в плоскости $z = {\text{const,}}$ охватывающий центр вихря. Интегрирование производится против часовой стрелки. Наиболее простой вид формула (16) имеет вблизи центра вихря ($r = 0$):

${{\Phi }}\left( {r,z,\varphi } \right) \to {\text{sign}}\left( z \right)~Q\left( {\varphi - \frac{\pi }{2}} \right)$

и описывает вихрь при $z > 0$ и антивихрь при $z < 0$ с топологическими зарядами $ \pm Q$ соответственно. Из граничных условий:

$\begin{gathered} {{\Phi }} \to \pm \frac{{Q\pi }}{2}\,\,\,\,\left( {x \to \pm \infty } \right), \\ {{\Phi }} \to \pm \frac{Q}{2}{\text{arctg}}\left( {\frac{x}{{ - z}}} \right)\,\,\,\,\left( {y \to \pm \infty } \right) \\ \end{gathered} $

и численного эксперимента следует, что (13) описывает две доменные границы с неэкспоненциальным поведением на бесконечности. Центры этих доменных границ (геометрическое место точек с максимальным значением производной) совпадает соответственно с осями $x = 0$ и $y = 0.$ Такое образование вихрей пересечением доменных границ детально исследовано для модели sin-Gordon в работах [21, 22].

Структура вихрей более наглядна в распределении векторного поля

$Z = \left( {\cos {{\Phi }},\sin {{\Phi }}} \right).$

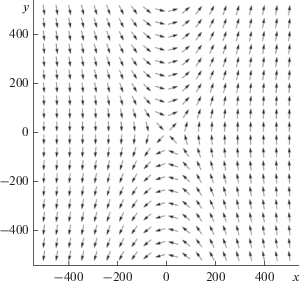
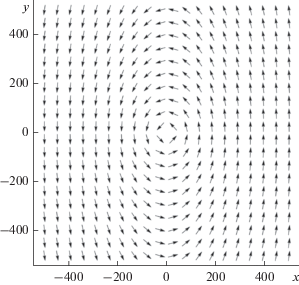
Это поле в плоскости $z = - 100$ и $z = 100$ изображено на рис. 1 и 2 соответственно. Из рис. 1 видно, что при постоянном значении $y$ вектор Z вращается от ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ до ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ против часовой стрелки при y < 0 и по часовой стрелке при y > 0, поэтому после пересечения доменных границ они меняют знак. Выражение (13) не определено при $x = 0,$ $z = 0,$ поэтому в плоскости $y = {\text{const}}$ оно описывает вторую прямолинейную вихревую нить. В системе координат $z = {{r}_{1}}\sin \varphi ,$ $x = {{r}_{1}}\cos \varphi $ вихревая структура, описываемая выражением

${{\Phi }}\left( {{{r}_{1}},y,\varphi } \right) = - Q~{\text{arcctg}}\frac{{{\text{tg}}~\varphi y}}{{\sqrt {r_{1}^{2} + {{y}^{2}}} }},$

Рис. 1.

Распределение вектора Z в плоскости $z = - 100.$

Рис. 2.

Распределение вектора Z в плоскости $z = 100.$

представляет собой вихрь (при $y > 0$) с топологическим зарядом Q и антивихрь (при $y < 0$) с тем же зарядом, который также образуется пересечением доменных границ.

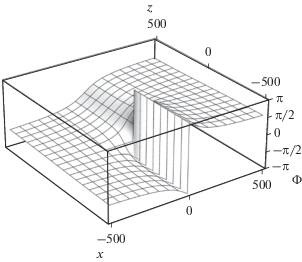
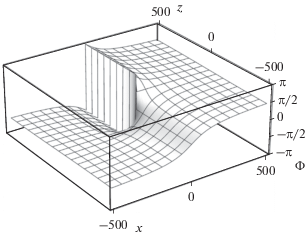
Вихревая структура изображена на рис. 3, 4, на которых ясно видны скачки поля ${{\Phi }}$ на $ - 2\pi $ (рис. 3, $y = - 100$) и $2\pi $ (рис. 4, $y = 100$).

Рис. 3.

Вихревая структура поля ${{\Phi }}$ в плоскости $xOz$ при $y = - 100.$

Рис. 4.

Вихревая структура поля ${{\Phi }}$ в плоскости $xOz$ при $y = 100.$

Структура поля ${{\Theta }}$ при $k = 1$ в стандартной полярной системе

${{\Theta }} = 2{\text{arcctg}}{{\left( {\frac{{\sqrt {{{z}^{2}} + {{r}^{2}}{{{\cos }}^{2}}\varphi } }}{r}} \right)}^{Q}}$

зависит от трех пространственных переменных.

Хотя при $z \to \pm \infty $ поле ${{\Theta }}$ стремится к основному состоянию (${{\Theta }} \to 0$), при $r \to \infty $ азимутальный угол зависит от полярного угла $\varphi {\text{:}}$

${{\Theta }} \to 2{\text{arctg}}\left[ {{{{\left| {\sec \varphi } \right|}}^{Q}}} \right]\,\,\,\,{\text{при}}\,\,\,\,r \to \infty .$

Поэтому поле n (2) имеет следующие асимптотики: оно не сингулярно в начале координат и

(17)

$\begin{gathered} n \to \left( {0,0,Q} \right)\,\,\,{\text{при}}\,\,\,z \to \pm \infty , \\ n \to \left( {0,Q\frac{{2\cos \varphi }}{{1 + {{{\cos }}^{2}}\varphi }}, - Q\frac{{{{{\sin }}^{2}}{\text{\;}}\varphi }}{{1 + {{{\cos }}^{2}}\varphi }}} \right)\,\,\,{\text{при}}\,\,\,r \to \infty , \\ n \to \left( {0,0,Q} \right)\,\,\,{\text{при}}\,\,\,r \to 0. \\ \end{gathered} $

Плотность энергии модели Гейзенберга

$e = \frac{1}{2}\left[ {{{{\left( {\nabla {{\Theta }}} \right)}}^{2}} + {{{\left( {\nabla {{\Phi }}} \right)}}^{2}}{{{\sin }}^{2}}{{\Theta }}} \right]JM_{0}^{2}$

при ограничениях (4), (5) имеет простой вид

$e = {\text{c}}{{{\text{h}}}^{{ - 2}}}a{{\left( {\nabla ~a} \right)}^{2}}~JM_{0}^{2}$

и полная энергия $E$ пропорциональна размеру системы L:

$E = \int {e~{{{\text{d}}}^{3}}r} = 8\pi LJM_{0}^{2}.$

Эта энергия существенно ниже энергии двумерного вихря [11, 12] в легкоплоскостном ферромагнетике, которая на один атомный слой пропорциональна ${\text{ln}}~\left[ {{L \mathord{\left/ {\vphantom {L {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right]$ (${{r}_{0}}$ – порядок постоянной решетки).

Предсказанные вихревые структуры могут зарождаться в цилиндре с поверхностной анизотропией термическими флуктуациями или переменным магнитным полем. При этом на боковых поверхностях намагниченность принимает вид (17).

Авторы благодарны Ф.Н. Рыбакову за обсуждение и полезные замечания.

Работа выполнена в рамках государственного задания Минобрнауки России (тема “Квант”, № АААА-А18-118020190095-4).

Список литературы

Nonlinearity in condensed matter, edited by Bishop A.R., Ecke R., Gubernatis S. Berlin: Springer, 1993. 276 p.
Nonlinear coherent structures in physics and biology, edited by Spatchek K.H., Mertens F.G. N.Y.: Plenum, 1994. 484 p.
Kosterlitz J.M., Thouless D.J. Ordering, metastability and phase transitions in two-dimensional systems // J. Phys. C: Solid State Phys. 1973. V. 6. P. 1181–1203.
Kosterlitz J.M. The critical properties of the two–dimensional XY model. // J. Phys. C: Solid State Phys. 1974. V. 7. P. 1046–1060.
Fluctuation phenomena: Disorder and nonlinearity, edited by Bishop A.R., Jimenez S., Vazquez L. Singapore: World Scientific, 1995. 244 p.
Богданов А.Н., Яблонский Д.А. Термодинамические устойчивые “вихри” в магнитоупорядоченных кристаллах. Смешанное состояние магнетиков // ЖЭТФ. 1989. Т. 95. С. 178–182.
Ivanov B.A., Stephanovich V.A., Zhmudskii, A.A. Magnetic vortices (the microscopic analogs of magnetic bubbles) // J. Magn. Magn. Mater. 1990. V. 88. P. 116–120.
Kiselev N.S. Bogdanov A.N., Schäfer R., Röler U.K. Chiral skyrmions in thin magnetic films: new objects for magnetic storage technologies // J. Phys. D: Appl. Phys. 2011. V. 44. № 39. P. 392001.
Parkin S., Yang S.-H. Memory on the racetrack // Nat. Nanotech. 2015. V. 10. P. 195–198.
Fert A., Cros V., Sampaio J. Skyrmions on the track // Nat. Nanotech. 2013. V. 8. P.152–156.
Косевич А.М., Иванов Б.А., Ковалев А.С. Нелинейные волны намагниченности. Динамические и топологические солитоны. Киев: Наукова думка, 1983. 192 с.
Kosevich A.M., Ivanov B.A., Kovalev A.S. Magnetic Solitons // Physics Reports. 1990. V. 194. № 3–4. P. 117–238.
Иванов Б.А., Колежук А.К. Солитоны в низкоразмерных антиферромагнетиках (обзор) // ФНТ. 1995. Т. 21. № 4. С. 355–389.
Borisov A.B., Kiselev V.V. Two–dimensional solution of the Landau–Lifshits equation // Physics Letters A. 1985. V. 107. № 4. P. 161–163.
Борисов А.Б., Киселев В.В. Нелинейные волны, солитоны и локализованные структуры в магнетиках. Т.2. Екатеринбург: УрО РАН, 2011. 416 с.
Midgley P.A., Dunin-Borkowski R.E. Electron tomography and holography in materials science // Nat.Mater. 2009. V. 4. P. 271–280.
Rybakov F.N., Borisov A.B., Bogdanov A.N. Three–dimensional skyrmion states in thin films of cubic helimagnets // Phys. Rev. B. 2013. V. 87. 094424.
Борисов А.Б. Трехмерные спиральные структуры в ферромагнетике // Письма ЖЭТФ. 2002. Т. 76. № 2.
Муртазаев А.К., Кассан-Оглы Ф.А., Рамазанов М.К., Муртазаев К.Ш. Исследование фазовых переходов в антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке методом Монте-Карло // ФММ. 2020. № 4. С. 346–351.
Белавин А.А., Поляков А.М. Метастабильные состояния двумерного изотропного ферромагнетика // Письма в ЖЭТФ. 1975. Т. 22. № 10. С. 500–506.
Borisov A.B., Tankeyev A.P., Shagalov A.G. et al. Multi-vortex-like solutions of the sine-Gordon equation // Phys.Lett.A. 1985. V. 111. № 1–2. P. 15–18.
Борисов А.Б., Танкеев А.П. Шагалов А.Г. Вихри и двумерные солитоны в легколоскоcтных магнетиках // ФММ. 1985. Т. 60. № 3. С. 467–479.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал