1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 122, № 5, 2021

Физика металлов и металловедение, 2021, T. 122, № 5, стр. 460-465

Фазовая диаграмма антиферромагнитной модели Поттса с числом состояний спина q = 4 на гексагональной решетке

А. К. Муртазаев b, *, М. К. Мазагаева a, М. К. Рамазанов a, М. А. Магомедов a

a Институт физики ДНЦ РАН
367003 Махачкала, ул. М. Ярагского, 94, Россия

b Дагестанский федеральный исследовательский центр РАН
367000 Махачкала, ул. М. Гаджиева, 45, Россия

* E-mail: sheikh77@mail.ru

Поступила в редакцию 10.12.2020
После доработки 18.01.2021
Принята к публикации 21.01.2021

Полный текст (PDF)

Аннотация

На основе алгоритма Ванга–Ландау метода Монте-Карло выполнены исследования магнитных структур основного состояния, фазовых переходов и термодинамических свойств двумерной антиферромагнитной модели Поттса с числом состояний спина q = 4 на гексагональной решетке с взаимодействиями ближайших J1 и следующих за ближайшими J2 соседей. Исследования проведены для соотношений обменных взаимодействий в диапазоне 0.0 ≤ r = |J2/J1| ≤ 1.0. Построена фазовая диаграмма зависимости критической температуры от величины взаимодействия следующих за ближайшими соседей. Проведен анализ характера фазовых переходов. Установлено, что в интервале 0.1 ≤ r ≤ 1.0 наблюдается фазовый переход первого рода, а при значении r = 0.0 в системе отсутствует фазовый переход и наблюдается сильное вырождение основного состояния.

Ключевые слова: модель Поттса, метод Монте-Карло, фазовый переход, фазовая диаграмма

ВВЕДЕНИЕ

При количественном описании фазовых переходов (ФП) и критических явлений в современной физике конденсированных сред используются различные решеточные модели. С помощью теоретических методов на простых решеточных моделях удается решить большое количество задач, имеющих широкие перспективы для практического применения [1–3]. Для изучения физических свойств магнитных материалов широко используют модели Изинга, Гейзенберга, Поттса и др. Эти модели также описывают большой класс реальных физических систем: слоистые магнетики, пленки жидкого гелия, сверхпроводящие пленки, адсорбированные пленки и др. [1, 4, 5].

На сегодняшний день, классические модели Изинга и Гейзенберга достаточно хорошо изучены и многие их свойства известны [6–10]. Иначе обстоит дело с моделью Поттса. В последние годы исследованию спиновых систем, описываемых моделью Поттса было посвящено значительное число работ [4, 11–15], в которых были получены ответы на многие вопросы. В работах [11–18] представлены результаты, полученные для двумерной модели Поттса с числом состояний спина q = 2, q = 3 и q = 4 на разных типах решеток. Результаты, представленные в этих работах, показывают, что многие физические свойства модели Поттса зависят от величины взаимодействия следующих за ближайшими соседей, числа состояний спина q и от геометрии решетки. В частности, изменение величины взаимодействия следующих за ближайшими соседей в модели Поттса может привести к вырождению основного состояния, к смене ФП и возникновению фрустраций [12, 13, 18].

В данной работе нами проводится исследование двумерной антиферромагнитной модели Поттса с числом состояний спина q = 4 на гексагональной решетке с учетом антиферромагнитных обменных взаимодействий следующих за ближайшими соседей. Интерес к этой модели обусловлен следующими основными причинами.

Во-первых, вопрос связанный с типом ФП для модели Поттса с q = 4 до сих пор является дискуссионным, так как значение q = 4 является граничным значением интервала 2 ≤ q ≤ 4, где наблюдается ФП второго рода и области значений q > 4, в котором наблюдается ФП первого рода [14].

Во-вторых, природа ФП и термодинамические свойства для рассматриваемой модели при различных значениях величины взаимодействия следующих за ближайшими соседей до сих пор не изучены.

В-третьих, учет обменных взаимодействий следующих за ближайшими соседей в исследуемой модели может привести к появлению новых магнитных структур.

В связи с этим, в данной работе нами проводится исследование этой модели в широком интервале значений величины взаимодействия следующих за ближайшими соседей. Исследование рассматриваемой модели на основе современных методов и идей позволит получить ответ на ряд вопросов, связанных с ФП и термодинамическими свойствами низкоразмерных систем с конкурирующими обменными взаимодействиями.

МОДЕЛЬ И МЕТОД ИССЛЕДОВАНИЯ

Гамильтониан модели Поттса с числом состояний спина q = 4 с учетом взаимодействий ближайших и следующих за ближайшими соседей может быть представлен в следующем виде [19, 20]:

(1)
$H = - {{J}_{1}}\sum\limits_{i,j} {\cos {{\theta }_{{i,j}}}} - {{J}_{2}}\sum\limits_{i,k} {\cos {{\theta }_{{i,k}}}} ,$
где J1 и J2 параметры обменных антиферромагнитных (J1 < 0 и J2 < 0) взаимодействий соответственно для ближайших и следующих за ближайшими соседей, θi, j, θi,k – углы между взаимодействующими спинами Si – Sj и Si – Sk. Направления спинов задается таким образом, чтобы выполнялось равенство:

(2)
$\begin{gathered} {{\theta }_{{i,j}}} = \left\{ {\begin{array}{*{20}{c}} {0,}&{{\text{если}}}&{{{S}_{i}} = {{S}_{j}}} \\ {109.47^\circ ,}&{{\text{если}}}&{{{S}_{i}} \ne {{S}_{j}}} \end{array}} \right., \\ {\text{Cos}}{{\theta }_{{i,j}}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{\text{если}}}&{{{S}_{i}} = {{S}_{j}}} \\ { - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3},}&{{\text{если}}}&{{{S}_{i}} \ne {{S}_{j}}} \end{array}} \right.. \\ \end{gathered} $

r = |J2/J1| – величина взаимодействия следующих за ближайшими соседей. В данной работе рассматривается интервал значений 0.0 ≤ r ≤ 1.0.

В настоящее время такие системы на основе микроскопических гамильтонианов успешно изучаются на основе метода Монте-Карло (МК) [21–24]. В последнее время разработано много новых вариантов алгоритмов метода МК. Одним из наиболее эффективных для исследования подобных систем является алгоритм Ванга–Ландау метода МК [25], особенно в низкотемпературной области. Поэтому нами, в данном исследовании был использован этот алгоритм.

В стандартный алгоритм Ванга–Ландау нами были внесены дополнения, которые позволяют выяснить магнитную структуру основного состояния системы. Более подробно алгоритм Ванга–Ландау изложен в работе [13]. Данный алгоритм позволяет рассчитать значения термодинамических параметров при любой температуре. В частности, внутреннюю энергию U, свободную энергию F, теплоемкость C и энтропию S можно вычислить, используя следующие выражения:

(3)
$U(T) = \frac{{\sum\limits_E {Eg(E){{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}}}}} }}{{\sum\limits_E {g(E){{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}}}}} }} \equiv {{\left\langle E \right\rangle }_{T}},$
(4)
$F\left( T \right) = - {{k}_{B}}T\ln \left( {\sum\limits_E {g\left( E \right){{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}}}}} } \right),$
(5)
$C = \left( {\frac{{{{{\left( {{{\left| {{{J}_{1}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{J}_{1}}} \right|} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}^{2}}}}{N}} \right)\left( {\left\langle {{{U}^{2}}} \right\rangle - {{{\left\langle U \right\rangle }}^{2}}} \right),$
(6)
$S\left( T \right) = \frac{{U\left( T \right) - F\left( T \right)}}{T},$
где N – число частиц, T – температура (температура дана в единицах |J1|/kB), (U является нормированной величиной).

Для анализа характера ФП нами был использован гистограммный метод анализа данных метода МК [25, 26]. Расчеты проводились для систем с периодическими граничными условиями и линейными размерами 3/4 × L × L = N, L = 12–96.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

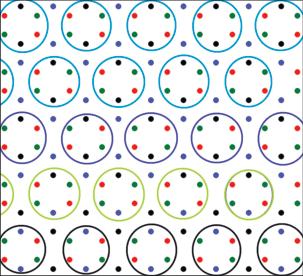
На рис. 1 и 2 представлены магнитные структуры основного состояния для значений r = 0.0 и 0.8. На этих рисунках спины обозначены кружками разных цветов. Спины, обозначенные кружками одинакового цвета, имеют одинаковое направление. Как видно на рис. 1 при r = 0.0 в данной модели магнитное упорядочение отсутствует.

Рис. 1.

Магнитная структура основного состояния для значения r = 0.0.

Рис. 2.

Магнитная структура основного состояния для значения r = 0.8.

Для значения r = 0.8 в системе обнаружено частичное упорядочение (рис. 2). Такая же картина наблюдается во всем диапазоне 0.1 ≤ r ≤ 1.0.

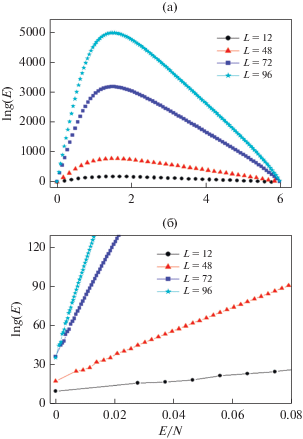
На рис. 3 представлена плотность состояний g(E) для систем с различными линейными размерами L для значения r = 1.0 (на этом и последующих графиках статистическая погрешность не превышает размеров символ, использованных для построения зависимостей). Из рисунка видно, что плотность состояний g(E) в основном состоянии для всех L стремится к отличному от нуля значению (рис. 3б), которое увеличивается с ростом L. Аналогичная картина наблюдается для всех рассмотренных значений r, причем для r = 0.0 такая зависимость наиболее ярко выражена. Такое поведение плотности состояний связано с вырождением основного состояния системы.

Рис. 3.

Плотность состояний g(E).

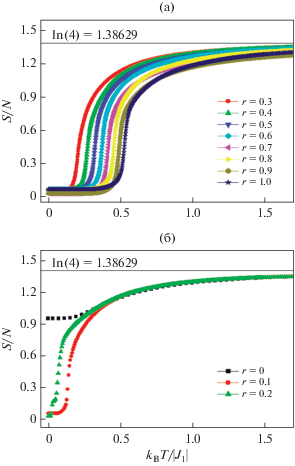
Зависимости энтропии S от температуры представлены на рис. 4. Как видно на рисунке для всего рассмотренного диапазона значений r с увеличением температуры энтропия стремится к теоретически предсказанному значению ln4. Для значения r = 0.0 в низкотемпературной области энтропия стремится к отличному от нуля значению (рис. 4б).

Рис. 4.

Температурные зависимости энтропии S/N.

В результате, это значении энтропии сильно отличается от нуля. Такое поведение энтропии свидетельствует о том, что при этом значении r основное состояние системы сильно вырождено. В диапазоне 0.1 ≤ r ≤ 1.0 энтропия стремится к близкому к нулю значению, но не к нулю. В этом диапазоне основное состояние системы имеет небольшое вырождение. Таким образом, мы видим, что учет антиферромагнитных взаимодействий следующих за ближайшими соседей приводит к уменьшению вырождения основного состояния, даже при малых значениях r.

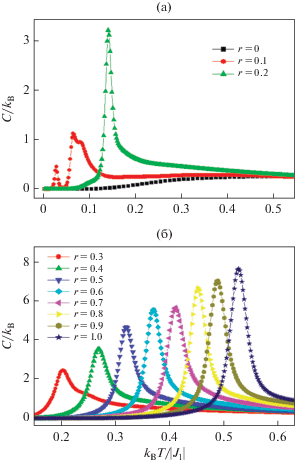
Температурные зависимости теплоемкости для разных значений r представлены на рис. 5. Как видно из рис. 5а, для значения r = 0.0 наблюдается необычное поведение, которое характеризуется отсутствием ярко выраженного пика.

Рис. 5.

Температурные зависимости теплоемкости C/kB.

Максимум теплоемкости в данном случае имеет сглаженный пик. Такая картина температурной зависимости теплоемкости обычно наблюдается для фрустрированных спиновых систем [27, 28]. Но в данной модели фрустрации отсутствуют, и такое поведение теплоемкости объясняется тем, что при r = 0.0 в данной модели не наблюдается магнитное упорядочение. Для значения r = 0.1 наблюдается расщепление теплоемкости. Такое поведение теплоемкости наблюдается в модели Изинга с фрустрациями на декорированных решетках [29, 30]. Для исследуемой нами модели расщепление теплоемкости связано с тем, что учет обменных взаимодействий следующих за ближайшими соседей приводит к появление частично упорядоченного магнитного состояния (см. рис. 2). Для значения r = 0.0 отсутствует острый пик, наблюдается сглаженный максимум, система сильно вырождена и в системе отсутствует порядок. Для всех значений r в диапазоне 0.2 ≤ r ≤ 1.0 вблизи критической точки наблюдаются отчетливые максимумы. Такое поведение объясняется частичным упорядочением системы. Рост r сопровождается с сдвигом максимумов в сторону высоких температур и увеличению значения максимумов. Увеличение абсолютных значений максимумов теплоемкости происходит за счет роста вклада обменных взаимодействий следующих за ближайшими соседей.

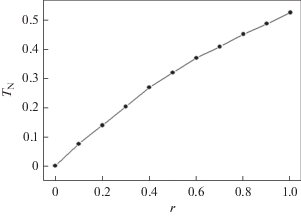
На рис. 6 приведена фазовая диаграмма зависимости критической температуры от величины взаимодействия следующих за ближайшими соседей. На диаграмме наблюдаются две фазы: частично упорядоченная и парамагнитная. Для значения r = 0.0 критическая температура равна нулю и ФП отсутствует. Это объясняется отсутствием магнитного упорядочения в данной модели при r = 0.0. Увеличение вклада влияния обменного взаимодействия следующих за ближайшими соседей в данной модели приводит к появлению ФП.

Рис. 6.

Фазовая диаграмма зависимости критической температуры от величины взаимодействия следующих за ближайшими соседей.

Для определения рода ФП в последнее время используют гистограммный анализ данных метода МК [31, 32]. Этот метод позволяет надежно определить род ФП.

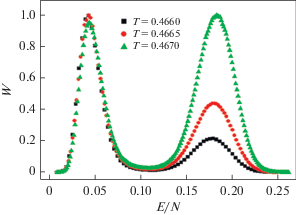
Полученные на основе гистограммного анализа данных результаты показывают, что в данной модели наблюдается ФП первого рода. Это продемонстрировано на рис. 7. На этом рисунке представлены гистограммы распределения энергии для системы с линейными размерами L = 96 для r = 1.0.

Рис. 7.

Гистограммы распределения энергии для L = 96 при различных температурах.

Графики построены при различных температурах, близких критической температуре. Из рисунка видно, что в зависимости вероятности W от энергии E для всех температур наблюдаются два максимума, которые свидетельствует о том, что в данной модели наблюдается ФП первого рода. Наличие двойного пика на гистограммах распределения энергии является достаточным условием для ФП первого рода. Отметим, что двойные пики на гистограммах распределения для исследуемой модели наблюдаются для значений r в интервале 0.1 ≤ r ≤ 1.0. Это позволяет нам утверждать о том, что в рассмотренном интервале значений r наблюдаются ФП первого рода.

ЗАКЛЮЧЕНИЕ

Исследование магнитных структур основного состояния, фазовых переходов и термодинамических свойств двумерной антиферромагнитной модели Поттса с числом состояний спина q = 4 на гексагональной решетке с учетом взаимодействий ближайших и следующих за ближайшими соседей выполнено с использованием алгоритма Ванга–Ландау метода Монте-Карло. Получены магнитные структуры основного состояния в широком интервале значений величины взаимодействия следующих за ближайшими соседей. Построена фазовая диаграмма зависимости критической температуры от величины взаимодействия следующих за ближайшими соседей. Показано, что в интервале 0.1 ≤ r ≤ 1.0 наблюдается фазовый переход первого рода. Для значения r = 0.0 наблюдается сильное вырождение основного состояния, и в системе отсутствует фазовый переход.

Исследование выполнено в рамках госзадания Минобрнауки России (тема № AAAA-A19-119051490043-5) при частичной финансовой поддержке РФФИ (проект № 19-02-00153-а).

Список литературы

  1. Diep H.T. Frustrated Spin Systems. World Scientific Publishing Co. Pte. Ltd., Singapore. 2004. P. 624.

  2. Baxter R.J. Exactly Solved Models in Statistical Mechanics. Academic, N.Y., 1982; Mir, M., 1985.

  3. Wu F.Y. Exactly Solved Models. A Journey in Statistical Mechanics. World Scientific, New Jersey, 2008.

  4. Wu F.Y. The Potts model // Rev. Mod. Phys.1982. V. 54. P. 235–268.

  5. Zhang W., Deng Y. Monte Carlo study of the triangular lattice gas with first- and second-neighbor exclusions // Phys. Rev. E. 2008. V. 78. P. 031103.

  6. Murtazaev A.K., Ramazanov M.K., Kurbanova D.R., Magomedov M.A., Murtazaev K.Sh. Phase diagrams and ground-state structures of the antiferromagnetic materials on a body-centered cubic lattice // Mater. Lett. 2019. V. 236. P. 669–671.

  7. Рамазанов М.К., Муртазаев А.К. Фазовая диаграмма антиферромагнитной модели Гейзенберга на кубической решетке // Письма в ЖЭТФ. 2019. Т. 109. Вып. 9. С. 610–614.

  8. Муртазаев А.К., Рамазанов М.К., Бадиев М.К. Фазовые переходы в модели Изинга на треугольной решетке с различными взаимодействиями межслойного обменного взаимодействия // ФНТ. 2019. Т. 45. Вып. 12. С. 1493–1497.

  9. Бадиев М.К., Муртазаев А.К., Рамазанов М.К., Магомедов М.А. Критические свойства модели Изинга в магнитном поле // ФНТ. 2020. Т. 46. Вып. 7. С. 824–828.

  10. Муртазаев А.К., Курбанова Д.Р., Рамазанов М.К. Фазовые переходы и критические свойства антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке с взаимодействиями вторых ближайших соседей // ЖЭТФ. 2019. Т. 156. Вып. 5. С. 980–988.

  11. Nauenberg M., Scalapino D.J. Singularities and Scaling Functions at the Potts-Model Multicritical Point // Phys. Rev. Lett. V. 44. P. 837–840.

  12. Cardy J.L., Nauenberg M., Scalapino D.J. Scaling theory of the Potts-model multicritical point // Phys. Rev. B. 1980. V. 22. P. 2560–2568.

  13. Ramazanov M.K., Murtazaev A.K., Magomedov M.A. Phase diagrams and ground-state structures of the Potts model on a triangular lattice // Physica A. 2019. V. 521. P. 543–550.

  14. Feldmann H., Guttmann A.J., Jensen I., Shrock R., Tsai S.-H. Study of the Potts model on the honeycomb and triangular lattices: Low-temperature series and partition function zeros // J. Phys. A. 1998. V. 31. P. 2287–2310.

  15. Kassan-Ogly F.A., Proshkin A.I. Frustrations and Ordering in Magnetic Systems of Various Dimensions // Phys. Solid State. 2018. V. 60. P. 1090–1097.

  16. Муртазаев А.К., Рамазанов М.К., Мазагаева М.К., Магомедов М.А. Фазовые переходы и термодинамические свойства модели Поттса с числом состояний спина q = 4 на гексагональной решетке // ЖЭТФ. 2019. Т. 156. Вып. 3. С. 502–506.

  17. Муртазаев А.К., Курбанова Д.Р., Рамазанов М.К. Фазовые переходы и термодинамические свойства модели Поттса с числом состояний спина q = 4 на треугольной решетке // ФТТ. 2019. Т.61. Вып. 11. С. 2195–2198.

  18. Рамазанов М.К., Муртазаев А.К., Магомедов М.А., Мазагаева М.К. Исследование фазовых переходов и термодинамических свойств модели Поттса с q = 4 на гексагональной решетке с взаимодействиями вторых ближайших соседей // ФТТ. 2020. Т. 62. Вып. 3. С. 442–446.

  19. Townsend M.G., Longworth G., Roudaut E. Triangular-spin, kagome plane in jarosites // Phys. Rev. B. 1986. V. 33. P. 4919–4926.

  20. Chiaki Y., Yutaka O. Three-dimensional antiferromagnetic q-state Potts models: application of the Wang-Landau algorithm // J. Physics A: Mathematical and General. 2001. V. 34. P. 8781–8794.

  21. Masrour R., Jabar A. Magnetic properties of mixed spin-5/2 and spin-2 Ising model on a decorated square lattice: a Monte Carlo simulation // Physica A. 2019. V. 515. P. 270–278.

  22. Муртазаев А.К., Ф.А. Кассан-Оглы, Рамазанов М.К., Муртазаев К.Ш. Исследование фазовых переходов в антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке методом Монте-Карло // ФММ. 2020. Т. 121. Вып. 4. С. 346–351.

  23. Murtazaev A.K., Kurbanova D.R., Ramazanov M.K. Phase diagram of the antiferromagnetic Heisenberg model on a bcc lattice with competing first and second neighbor interactions // Physica A. 2020. V. 545. P. 123548-1–123548-6.

  24. Masrour R., Jabar A. Magnetic properties in stacked triangular lattice: Monte Carlo approach // Physica A. 2018. V. 491. P. 926–934.

  25. Wang F., Landau D.P. Determining the density of states for classical statistical models: a random walk algorithm to produce a flat histogram // Phys. Rev. E. 2001. V. 64. P. 056101-1–056101-16.

  26. Wang F., Landau D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States // Phys. Rev. Lett. 2001. V. 86. P. 2050–2053.

  27. Kassan-Ogly F.A., Filippov B.N., Murtazaev A.K., Ramazanov M.K., Badiev M.K. Influence of field on frustrations in low-dimensional magnets // J. Mag. Mag. Mater. 2012. V. 24. P. 3418–3421.

  28. Kassan-Ogly F.A., Murtazaev A.K., Zhuravlev A.K., Ramazanov M.K., Proshkin A.I. Ising model on a square lattice with second-neighbor and third-neighbor interactions // J. Mag. Mag. Mater. 2015. V. 384. P. 247–254.

  29. Proshkin A.I., Kassan-Ogly F.A. Frustration and Phase Transitions in Ising Model on Decorated Square Lattice // Physics of Metals and Metallography. 2019. V. 120. P. 1366–1372.

  30. Kassan-Ogly F.A., Proshkin A.I. Ising Model on Planar Decorated Lattices. Frustrations and Their Influence on Phase Transitions // Physics of Metals and Metallography. 2019. V.120. P. 1359–1365.

  31. Курбанова Д.Р., Муртазаев А.К., Рамазанов М.К., Магомедов М.А., Тааев Т.А. Фрустрированная модель Поттса с числом состояний спина q = 4 на треугольной решетке // ЖЭТФ. 2020. Т. 158. Вып. 6. С. 1095–1100.

  32. Муртазаев А.К., Ризванова Т.Р., Рамазанов М.К., Магомедов М.А. Фазовые переходы и термодинамические свойства модели Поттса с числом состояний спина q = 4 на решетке Кагоме // ФТТ. 2020. Т. 62. Вып. 8. С. 1278–1282.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал