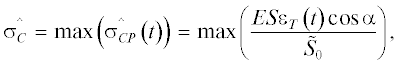Физика металлов и металловедение, 2022, T. 123, № 10, стр. 1085-1091

Исследование деформирования алюминиево-литиевого сплава пониженной плотности при ударном сжатии и локализованном сдвиге

В. А. Кузьмин^a, b, *, Ф. Ф. Галиев^a, c, В. А. Пушков^b, Е. С. Шерстобитов^a, Е. В. Кошатова^a, С. И. Герасимов^a, b, c, А. Т. Мишустин^a

^a Российский федеральный ядерный центр – Научно-исследовательский институт экспериментальной физики
607187 Саров, пр. Мира, 39, Россия

^b Саровский физико-технический институт. Филиал Национального исследовательского ядерного университета “МИФИ”
607186 Саров, ул. Духова, 6, Россия

^c Нижегородский государственный технический университет им. Р.Е. Алексеева
603950 Нижний Новгород, ул. Минина, 24, корп. 1, Россия

^* E-mail: v_a_kuzmin@mail.ru

Поступила в редакцию 06.04.2022
После доработки 06.07.2022
Принята к публикации 12.07.2022

EDN: WKUWCQ
DOI: 10.31857/S001532302210031X

Полный текст (PDF)

Аннотация

Приведены результаты исследования модели деформирования среднепрочного свариваемого коррозионностойкого алюминиево-литиевого сплава пониженной плотности при ударном нагружении, идентификация и верификация параметров модели деформирования Джонсона–Кука по результатам экспериментов. Также приведены результаты исследования деформационного критерия разрушения при сдвиговом ударном деформировании.

Ключевые слова: алюминиево-литиевый сплав 1420, ударное нагружение, скорость деформации, предел текучести, сжатие, составной стержень Гопкинсона, модель деформирования, численное моделирование, критерий разрушения

ВВЕДЕНИЕ

Методы численного моделирования, входящие в состав комплексов программ, в настоящее время являются основным рабочим инструментом при проектировании новых конструкций, оценки их стойкости к различным внешним воздействующим факторам. Данные методы – неотъемлемая часть проектирования новых и модернизации уже существующих конструкций изделий.

Необходимо отметить, что результаты, полученные в ходе расчетов, зависят непосредственно от математических моделей, их параметров, которые описывают тот или иной физический процесс. В частности, если речь идет о процессе пластического деформирования, то результаты моделирования зависят от параметров модели пластического деформирования и критериев разрушения.

Воздействия на конструкции характеризуются интенсивностью нагрузки (амплитудой и скоростью). Поэтому важно, чтобы модель деформирования по возможности учитывала интенсивность нагрузки.

Цель настоящей статьи состоит в установлении параметров модели пластического деформирования Джонсона–Кука для алюминиево-литиевого сплава 1420. Этот сплав широко применяется в авиационном и космическом машиностроении. Полученные параметры модели пластического деформирования могут быть использованы при моделировании высокоинтенсивных ударных воздействий на конструкции, выполненные из указанного сплава.

ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ МОДЕЛИ ДЕФОРМИРОВАНИЯ ДЖОНСОНА–КУКА СПЛАВА 1420

В настоящее время в практике численного моделирования для решения задач динамических ударов и анализа отклика конструкции на высокоинтенсивное воздействие применяется модель Джонсона–Кука [1–5]. Она представляет собой эмпирическую формулу, которая учитывает упрочнение, влияние скорости деформирования.

В упругой области компоненты девиатора тензора напряжений s_ij рассчитываются согласно закону Гука:

(1)

$s_{{ij}}^{{}} = 2G{{\varepsilon }_{{ij}}},$

где G – модуль сдвига; ε_ij – компоненты девиатора тензора деформации.

При пластическом деформировании поверхность текучести описывается поверхностью текучести Мизеса:

(2)

$\frac{3}{2}{{s}_{{ij}}}{{s}_{{ij}}} - \sigma _{Y}^{2} \leqslant 0,$

где σ_Y – напряжение пластического деформирования материала.

Напряжение текучести является функцией двух переменных: пластической деформации ε_p и скорости пластических деформаций ${{\dot {\varepsilon }}_{p}}.$

Таким образом, напряжение текучести в модели Джонсона–Кука определяется следующим уравнением:

(3)

${{\sigma }_{Y}} = \left( {A + B\varepsilon _{p}^{n}} \right)\left( {1 + C\ln \left( {\dot {\varepsilon }{\text{*}}} \right)} \right),$

где ε_p – пластическая деформация, $\dot {\varepsilon }{\text{*}} = {{\dot {\varepsilon }} \mathord{\left/ {\vphantom {{\dot {\varepsilon }} {{{{\dot {\varepsilon }}}_{0}}}}} \right. \kern-0em} {{{{\dot {\varepsilon }}}_{0}}}}$ – безразмерная скорость пластической деформации, ${{\dot {\varepsilon }}_{0}} = 1$ c^–1, A, B, C, n – параметры, которые определяются эмпирическим путем.

Определение параметров модели (3) выполняется на основе информации о пластических деформациях материала при разных интенсивностях деформирования.

Методика определения параметров модели (3) показана ниже.

В качестве исходных данных для определения параметров A, B, C, n используют динамические диаграммы деформирования, полученные при различных скоростях.

Так как проводится расчет при больших деформациях, кривая деформирования должна быть построена в истинных напряжениях и деформациях.

Параметры B и n характеризуют деформационное упрочнение при пластическом деформировании.

Значение параметра A модели (3) является величиной, близкой пределу текучести при статическом нагружении.

Задавшись параметром A, определяют B и n из данных о пластическом напряженно-деформированном состоянии в логарифмических координатах:

$\begin{gathered} {{\sigma }_{Y}} = A + B\varepsilon _{P}^{n}, \\ \lg \left( {{{\sigma }_{Y}} - A} \right) = \lg B + n\lg ({{\varepsilon }_{P}}). \\ \end{gathered} $^.

В этом случае массив точек c координатами (lg(σ_Yi – A)_i, lg(ε_Pi)_i) аппроксимируется линейной функцией y = kx + b методом наименьших квадратов. При этом параметры модели Джонсона–Кука определяются как k = n, B = e^lgb.

Оставшийся параметр C модели Джонсона–Кука оценивается по данным о влиянии скорости деформирования на напряжение текучести. Данный параметр определяется аппроксимацией линейной зависимостью массива точек $\left( {{{{\left( {{{\sigma _{{Yi}}^{{{\text{дин}}}}} \mathord{\left/ {\vphantom {{\sigma _{{Yi}}^{{{\text{дин}}}}} {\sigma _{Y}^{{{\text{стат}}}}}}} \right. \kern-0em} {\sigma _{Y}^{{{\text{стат}}}}}}} \right)}}_{i}};\ln ({{{\dot {\varepsilon }}}_{i}})} \right),$ причем точке с абсциссой 0 соответствует ордината 1. Массив выше указанных точек аппроксимируется линейной функцией вида y = qx + 1, где коэффициент q = С в модели Джонсона–Кука.

В общем случае для определения параметров модели решается задача параметрической оптимизации.

Параметры В и n определяются из минимума функционала:

(4)

$f\left( {B,n} \right) = \sum\limits_{i = 1}^M {{{{\left[ {\left( {{{\sigma }_{{yi}}} - A} \right) - B\varepsilon _{{pi}}^{n}} \right]}}^{2}}\xrightarrow[{B,n}]{}\min } ,$

где M – экспериментальные точки.

Для определения параметра C находится минимум функционала:

(5)

$\begin{gathered} g(C) = \\ = \sum\limits_{j = 1}^K {{{{\left[ {{{\sigma }_{{Yi}}} - \left( {A + B\varepsilon _{{pj}}^{n}} \right)\left( {1 + C\ln \varepsilon _{j}^{{ \cdot *}}} \right)} \right]}}^{2}}} \xrightarrow[C]{}\min , \\ \end{gathered} $

где K – количество скоростных режимов нагружения (скоростей деформаций).

МЕТОДИКА ЭКСПЕРИМЕНТА И МОДЕЛИРОВАНИЕ

В экспериментах использовали алюминиево-литиевый сплав 1420, имеющий химический состав согласно ОСТ 1 90048-90: Al – основа, Mg 4.5–6%, Li 1.8–2.3%, Zr 0.08–0.15%, Be 0.0002–005%, Fe 0.2%, Si 0.15%, Cu 0.05%, Ti 0.1%, Ca 0.04%, прочие примеси 0.15%. Вид полуфабриката в состоянии поставки – поковка. Средние механические свойства при статическом нагружении – предел текучести σ_0.2 = 274 МПа, σ_в = 451 МПа. Структура сплава 1420 характеризуется преобладанием равноосных зерен средним размером 66.9 ± 32.8 мкм.

На основе экспериментальных и справочных данных [6] по описанному выше способу были получены следующие параметры модели Джонсона–Кука для алюминиево-литиевого сплава 1420: A = 284 МПа, В = 427 МПа, n = 0.4, C = = 0.031.Испытания на динамическое сжатие и сдвиг образцов из сплава 1420 проводили по методу составного стержня Гопкинсона (ССГ) [7–17] с использованием пневматического нагружающего устройства для разгона ударника. На рис. 1 приведена схема проведения опытов.

Рис. 1.

Схема проведения опыта: 1 – ударник, 2 – втулки скольжения, 3 – тензодатчики (Т1–Т4), 4 – нагружающий стержень, 5 – образец, 6 – опорный стержень, 7 – упор.

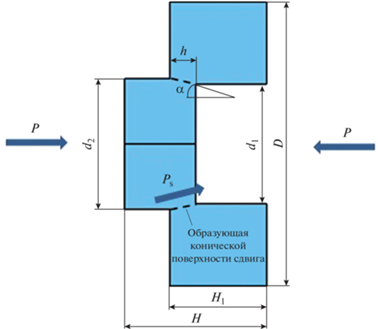
Стальной ударник 1 длиной от 300 до 500 мм разгоняется с помощью сжатого воздуха в пневматической нагружающей установке и воздействует по нагружающему стержню 4. Создаваемая при этом волна напряжения (длительностью от 120 до 200 мкс) деформирует образец 5, установленный между нагружающим 4 и опорным 6 стержнями. Стержни расположены соосно друг другу с помощью втулок скольжения 2. Импульсы деформации стержней в проходящих и отраженных волнах напряжений регистрируются с помощью наклеенных на стержни тензодатчиков 3. По зарегистрированным деформациям определяют зависимости напряжения от деформации σ(ε) и скорости деформации $\left( {\dot {\varepsilon } = {{d\varepsilon } \mathord{\left/ {\vphantom {{d\varepsilon } {dt}}} \right. \kern-0em} {dt}}} \right)$ от деформации $\dot {\varepsilon }(\varepsilon ).$ В экспериментах использовали стержни и ударник диаметром 20 мм, изготовленные из высокопрочной мартенситно-стареющей стали 005Н18К12М4Т1-ВИ (предел текучести σ_0.2 ~ ~ 2400 МПа). Длина стержней − 1000 мм, ударника − 400 мм (длительность импульса t = 160 мкс). Размеры цилиндрических образцов при испытаниях на сжатие: ∅5.5 × 2 мм. Вид образца при испытаниях на локальный сдвиг имел другую форму, его размеры приведены на рис. 2.

Рис. 2.

Сечение образца для исследования локального сдвига и его параметры: d₁ = 4.2 мм, d₂ = 4.6 мм, D = 10 мм, Н = = 5 мм, Н₁ = 3.4 мм, h = 0.9 мм, α = 12.5°.

При однородном напряженном состоянии образца формулы для напряжения, деформации и скорости деформации имеют вид [7]:

(6)

$\begin{gathered} \sigma \left( t \right) = \frac{{ES}}{{{{S}_{0}}}}{{\varepsilon }_{T}}\left( t \right), \\ \varepsilon \left( t \right) = \frac{{2C}}{{{{L}_{0}}}}\int\limits_0^t {\left[ {{{\varepsilon }_{I}}\left( t \right) - {{\varepsilon }_{T}}\left( t \right)} \right]} , \\ \dot {\varepsilon }\left( t \right) = \frac{{2C}}{{{{L}_{0}}}}\left[ {{{\varepsilon }_{I}}\left( t \right) - {{\varepsilon }_{T}}\left( t \right)} \right], \\ \end{gathered} $

где S – площадь поперечного сечения стержней, S₀– исходная площадь поперечного сечения образца, Е – модуль упругости материала мерных стержней, L₀ – начальная длина образца, С – скорость продольных волн напряжения в стрежнях, ε_I, ε_T – упругие импульсы деформации в нагружающем и прошедшем через образец импульсах напряжений соответственно. Исключая время из первых двух формул (6), строится диаграмма деформирования (σ–ε).

Проведено 7 опытов с образцами сплава 1420. Скорость ударника V_уд составила 4.2–15.3 м/с, скорость деформации $\dot {\varepsilon }$ – 1350–6000 1/с.

Определены экспериментальные значения предела текучести, соответствующие заданным скоростям ударника и скоростям деформирования. Соответствующие данные приведены в табл. 1.

Таблица 1.

Пределы текучести сплава 1420 при $\dot {\varepsilon }$ = = 1350–6000 1/с

№ оп.	V_уд, м/с	$\dot {\varepsilon }$, с^–1	σ_0.2, МПа
1	11.7	4400	352
2	15.3	6000	360
3	4.3	1350	350
4	4.2	1380	345
5	4.3	1360	356
6	4.7	1680	356
7	4.9	1720	355

Для исследования локального сдвига в качестве критерия разрушения было принято достижение значением интенсивности деформации величины, определяемой формулой:

(7)

${{\varepsilon }^{f}} = - \ln \left( {1 - \psi } \right),$

где ψ = 0.186 [6] – сужение образца после разрыва.

Согласно (7), ε^f ≈ 0.21. Такой критерий принят из соображения, что интенсивность деформации разрушения при сдвиге равна интенсивности деформации при растяжении.

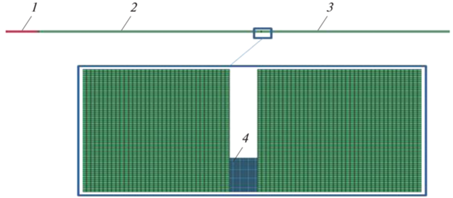
На рис. 3 показана модель задачи численного моделирования, повторяющего нагружение образцов сплава 1420 на установке ССГ при сжатии. Задача решена в двумерной осесимметричной постановке [18]. В конечно-элементной сетке использовали четырехузловые элементы. Модель содержит 400520 элементов и 407357 узлов. Характерный размер элемента модели образца составляет 0.1 мм.

Рис. 3.

Расчетная модель при моделировании сжатия: 1 – ударник, 2 – нагружающий стержень, 3 – опорный стержень, 4 – образец.

Также на рис. 4 приведена модель для моделирования сдвига.

Рис. 4.

Расчетная модель при моделировании сдвига: 1 – нагружающий стержень, 2 – опорный стержень, 3 – образец.

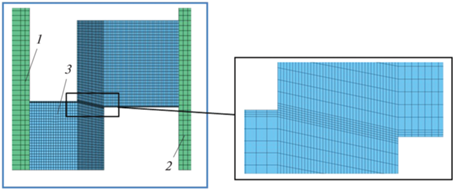
Для образцов из сплава 1420 задавалась упруго-пластическая модель Джонсона–Кука. Для ударника (сталь ХВГ), нагружающего и опорного стержней (сталь 005Н18К12М4Т1-ВИ) – упругая модель. Параметры модели материалов приведены в табл. 2.

Таблица 2.

Параметры моделей материалов

Материал	Плотность ρ, кг/м³	Модуль упругости E, МПа	Модуль сдвига G, МПа	Коэффициент Пуассона, ν	A, МПа	B, МПа	n	C
ХВГ	7850	2.1 × 10⁵	–	0.3	–	–	–	–
005Н18К12М4Т1-ВИ	7850	2.1 × 10⁵	–	0.3	–	–	–	–
1420	2470	–	2.885 × 10⁴	–	284	427	0.4	0.031

В области пластических деформаций поверхность текучести описывается поверхностью текучести Мизеса с уравнением Джонсона–Кука (3).

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ

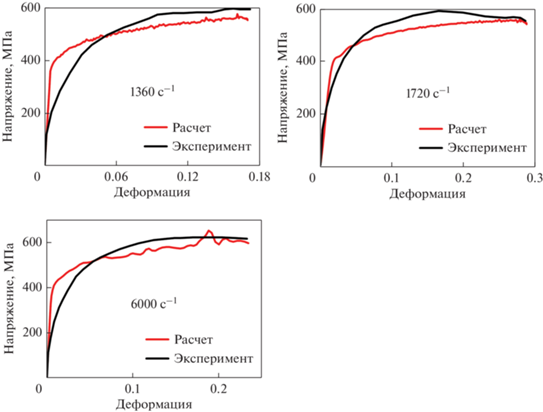
На рис. 5 приведены расчетные и экспериментальные зависимости σ(ε) при разных скоростях нагружения. Верификация показала хорошее согласование расчетных и экспериментальных диаграмм деформирования.

Рис. 5.

Расчетные и экспериментальные зависимости σ(ε) при разных скоростях нагружения.

Максимальная погрешность на участке развитого пластического деформирования не превышает 10%. Несовпадение начальных участков кривых можно объяснить влиянием вязкости материала, что отражается на более плавном переходе от участка упругого деформирования к участку пластического деформирования на зависимостях σ(ε) (см. рис. 5).

МОДЕЛИРОВАНИЕ ЛОКАЛЬНОГО СДВИГА В ОБРАЗЦАХ ИЗ СПЛАВА 1420

Проведено 7 опытов. Скорость ударника в экспериментах составила 3.9–4.3 м/с.

Амплитуды нагружающих импульсов составили σ_А = 93.0–99.5 МПа. Постопытное смещение образцов составило Δ_кон = 1.0–1.6 мм.

Для расчета был выбран опыт, в котором нагружение осуществлялось при ударе по торцу нагружающего стержня ударником длиной 400 мм со скоростью 4.3 м/с.

Среднее значение полученного из эксперимента критического напряжения сдвига σ_с, соответствующего началу локализованного сдвига, составляет 369.5 МПа.

Напряжение сдвига в образце(см. также рис. 2) рассчитывается по следующим формулам:

(8)

${{\sigma }_{C}} = {{P}_{S}}/S,\,\,\,\,{{P}_{S}} = P\cos \left( \alpha \right);$

(9)

$S = \pi \left( {\frac{{{{d}_{1}}}}{2} + \frac{{{{d}_{2}}}}{2}} \right)\sqrt {{{h}^{2}} + {{{\left( {\frac{{{{d}_{2}}}}{2} - \frac{{{{d}_{1}}}}{2}} \right)}}^{2}}} ,$

где S – рабочая площадь образца; P_S – сдвиговая компонента нагружающей силы (см. рис. 2); Р – осевая компонента нагружающей силы (см. рис. 2) (определяется из импульса деформации на нагружающем стрежне).

В результате численного расчета получено, что напряжение сдвига составляет $\sigma _{C}^{ \wedge } = 354$ МПа. Напряжение сдвига рассчитывалось по формулам:

(10)

где $E$ – модуль упругости материала опорного стержня, $S$ – площадь поперечного сечения опорного стержня, ε_T – упругий импульс деформации, прошедший через образец, α = 12.5° – угол полураствора конической поверхности сдвига, ${{\tilde {S}}_{0}} = 12.744$ мм² – площадь конической поверхности сдвига (см. рис. 2).

Относительное отличие по напряжению сдвига составляет 4.2%. Это не выше погрешности, определяемой полученными параметрами модели деформирования Джонсона–Кука.

На рис. 6 показаны формы образца после нагружения, полученные в эксперименте и численном расчете.

Рис. 6.

Форма образца после нагружения в эксперименте (а) и расчете (б).

Средние значения ширины полосы сдвига 𝓁, полученные в опытах на основе металлографического анализа, составили от 58.8 до 106.3 мкм. Авторы полагают, что такое отличие, возможно, также связано с вязкостью материала, которая увеличивает сопротивление сдвиговым напряжениям, и при более длительном процессе деформирования оказывает большее влияние на развитие полосы локализованного сдвига.

ЗАКЛЮЧЕНИЕ

В настоящей статье представлены результаты исследования параметров модели деформирования Джонсона–Кука для сплава 1420. На основе экспериментальных и справочных данных были получены следующие параметры модели Джонсона–Кука для алюминиево-литиевого сплава 1420: A = 284 МПа, В = 427 МПа, n = 0.4, C = 0.031. Идентификацию параметров модели осуществляли по экспериментальным диаграммам деформирования образцов из указанного сплава при ударном нагружении по методу составного стержня Гопкинсона.

Проведенная верификация показала хорошее согласование расчетных и экспериментальных диаграмм деформирования. Максимальная погрешность на участке развитого пластического деформирования не превышает 10%. Несовпадение начальных участков кривых можно объяснить влиянием вязко-пластических свойств материала, что отражается в наиболее плавном переходе от участка упругого деформирования к участку пластического деформирования на зависимостях σ(ε).

Также в настоящей работе приведены результаты исследования локализованного сдвига при ударном нагружении. Напряжение сдвига, полученное в эксперименте и численном расчете, отличаются не более, чем на 4.2%.

Приведенные параметры модели деформированиясплава 1420 могут быть использованы для уточнения результатов численного моделирования поведения авиационных конструкций в условиях высокоинтенсивных механических воздействийи пластического деформироания при скоростях деформирования до 6000 1/с.

Список литературы

Johnson G.R., Cook W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Proceedings of the Seventh International Symposium on Ballistic. The Hague, The Netherlands, 1983. P. 541–547.
Johnson G.R., Cook W.H. Fracture characteristics of three metals subjected to various strain rates, temperatures and pressures // Eng. Fracture Mechanics. 1985. V. 21. № 1. P. 31–48.
Кузькин В.А., Михалюк Д.С. Применение численного моделирования для идентификации параметров модели Джонсона–Кука при высокоскоростном деформировании // Вычислительная механика сплошных сред. 2010. Т. 3. № 1. С. 32–43.
Брагов А.М., Игумнов Л.А., Кайдалов В.Б., Константинов А.Ю., Лапшин Д.А., Ломунов А.К., Митенков Ф.М. Экспериментальное исследование и математическое моделирование поведения сталей марок ст.3, 20х13 и 08х18н10т в широких диапазонах скоростей деформаций и температур // ПМТФ. 2015. Т. 56. № 6. С. 51–58.
Лапшин Д.А. Расчетно-экспериментальный анализ прочности внутриобъектовых транспортных контейнеров реакторов типа БН в авариях с падением: Дис. канд. тех. наук, АО “ОКБМ Африкантов”. Нижний Новгород, 2015.
Авиационные материалы. Справочник. Том 4. Часть 1. Книга 2. Деформируемые алюминиевые сплавы / Под ред. докт. техн. наук Е.Н. Каблова. М.: ВИАМ, 2009. 170 с.
Kolsky H. An investigation of the mechanical properties of material at very high rates of loading // Proc. Phys. Soc. 1949. V. 62 B. P. 676–700.
Lindholm V.S., Yeakley L.M. High-strain rate testing: tension and compression // Experimental Mechanics. 1968. V. 8. № 1. P. 1–9.
Большаков А.П., Новиков С.А., Синицын В.А. Исследование динамических диаграмм одноосного растяжения и сжатия меди и сплава АМг6 // Проблемы прочности. 1979. № 10. С. 87–89.
Делле В.А., Носкин А.В. Влияние скорости нагружения на пластичность некоторых металлов // Инженерно-физический журн. 1959. Т. 2. № 6. С. 36–41.
Брагов А.М., Ломунов А.К. Использование метода Кольского для исследования процессов высокоскоростного деформирования материалов различной физической природы: монография. Н. Новгород: Изд-во ННГУ, 2017. 148 с.
Davies E.D.H., Hunter S.C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar // J. Mech. Phys.Sol. 1963. V. 11. P. 155–179.
Музыченко В.М., Пащенко С.И., Гуськов В.А. Применение метода составного стержня Гопкинсона при исследовании динамических свойств материалов (обзор) // Заводская лаборатория. 1986. № 1. С. 58–66.
Большаков А.П., Новиков С.А., Пылева В.П., Синицын В.А., Филиппов К.И. О получении динамических диаграмм растяжения при взрывном нагружении // ПМТФ. 1975. № 1. С. 184–186.
Большаков А.П., Коротких Ю.Г., Новиков С.А., Пуртов Ю.Б., Синицын В.А. Сравнение результатов численного эксперимента на ЭВМ и динамических испытаний сплава АМг6 методом Кольского // Проблемы прочности. 1982. № 1. С. 54–57.
Pushkov V.A., Novikov S.A., Sinitsyn V.A., Govorunov I.N. Deformation of aluminum alloys AD-1, AMg-6 andD-16 at dynamic compression and temperatures of 25–250°C // J. Phys. IV. France. 2003. V. 110. P. 135–140.
Xue Q., Gray G.T. III. Development of adiabatic shear bands in annealed 316L stainless steel: Part I. Correlation between evolving microstructure and mechanical behavior // Metal. Mater. Trans. A.2006. V. 37A. P. 2435–2446.
Дьянов Д.Ю., Корсакова Е.И., Симонов Г.П., Циберев К.В., Шувалова Е.В. Результаты верификации моделей упругопластического деформирования и разрушения, реализованных в пакете программ ЛЭГАК-ДК / Сборник докладов 9-ой научно-технической конференции. Саров, 2011.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал