Физика металлов и металловедение, 2022, T. 123, № 9, стр. 939-948

1. ВВЕДЕНИЕ

Биквадратичное обменное взаимодействие вида – $K{{({{S}_{1}} \cdot {{S}_{2}})}^{2}}$ в магнетиках с величиной спинов $S \geqslant 1$ было подробно исследовано Андерсоном [1] и Хуангом и Орбахом [2]. К настоящему времени получено достаточно много экспериментальных свидетельств существования биквадратичного обмена (см. обзор [3]), а для некоторых веществ (например, для ОЦК-железа [4]) проведены первопринципные вычисления параметра $K$ биквадратичного обмена.

Наличие биквадратичного обмена существенно влияет на характер полевого и температурного поведения магнетиков. При этом особенно интересно то, что при определенных соотношениях знаков и величин параметра $I$ билинейного обмена – $I\left( {{{S}_{1}} \cdot {{S}_{2}}} \right)$ и параметра $K$ биквадратичного обмена в магнетике может возникнуть магнитное квадрупольное упорядочение [5, 6].

Квадрупольное упорядочение характеризуется тем, что при всех температурах, включая $T = 0,$ термодинамические средние значения проекций дипольных спиновых операторов равны нулю ${{\left\langle {{{S}_{{\alpha n}}}} \right\rangle }_{{\alpha = X,Y,Z}}} = 0$ для любого узла $n$ магнитной решетки. В то же время в магнетике ниже определенной температуры возникают ненулевые термодинамические средние значения квадрупольных спиновых операторов, которые определяются как [6, 7]:

При этом следует иметь в виду, что, поскольку в неупорядоченном парамагнитном состоянии средние значения квадратов спиновых проекций $S_{{\alpha n}}^{2}$ равны между собой и удовлетворяют условию:

то переход из парамагнитного состояния в более упорядоченное характеризуется появлением либо ненулевого среднего значения квадрупольного оператора ${{q}_{0}} = {\text{\;}}\left\langle {{{Q}_{{0n}}}} \right\rangle = 3\left\langle {S_{{Zn}}^{2}} \right\rangle - S\left( {S + 1} \right) \ne 0,$ либо ${{q}_{2}} = \left\langle {{{Q}_{{2n}}}} \right\rangle = \left\langle {S_{{Xn}}^{2}} \right\rangle - \left\langle {S_{{Yn}}^{2}} \right\rangle \ne 0,$ либо ${{q}_{0}} \ne 0$ и ${{q}_{2}} \ne 0$ одновременно. Таким образом, величины ${{q}_{0}}$ и ${{q}_{2}}$ играют роль параметров квадрупольного порядка и по своему определению как разность двух величин могут быть как положительными, так и отрицательными.

Магнитная фазовая диаграмма магнетика с билинейным $I > 0$ и биквадратичным $K > 0$ параметрами обмена ближайших магнитных соседей и спинами $S = 1$ была исследована в работах Чена и Леви [5, 6]. При этом на плоскости переменных отношение параметров обмена $K{\text{/}}I$ – температура T были получены границы существования магнитоупорядоченных состояний, которые выделили ферромагнитную фазу с ненулевой относительной намагниченностью ${{\sigma }_{Z}} \equiv \left\langle {{{S}_{{Zn}}}} \right\rangle \ne 0$ и положительным квадрупольным параметром порядка ${{q}_{0}} > 0$ и квадрупольную фазу с нулевой намагниченностью ${{\left\langle {{{S}_{{\alpha n}}}} \right\rangle }_{{\alpha = X,Y,Z}}} = 0$ и отрицательным квадрупольным параметром порядка ${{q}_{0}} < 0.$ Кроме того, было рассчитано температурное поведение дипольного параметра порядка ${{\sigma }_{Z}}$ и квадрупольного ${{q}_{0}}$ соответствующих фаз как в нулевом магнитном поле $H = 0,$ так и в постоянном поле $H \ne 0.$ Однако в этой модели с биквадратичным обменом не были исследованы ни особенности изотермического намагничивания магнитоупорядоченных фаз, ни проблемы полевого поведения магнитной энтропии, что существенно для оценок возможных магнитокалорических эффектов (МКЭ) в магнетиках с биквадратичным обменом. Поэтому недавно мы провели расчеты магнитокалорических эффектов в ферромагнитной фазе магнетика с биквадратичным обменом как в случае возникновения ферромагнетизма при переходе II рода [8], так и при переходе I рода [9]. В настоящей работе рассчитан магнитокалорический эффект изотермического намагничивания в квадрупольной фазе магнетика с биквадратичным обменом и показано, что он имеет аномальный характер – увеличение магнитного поля вызывает рост магнитной энтропии.

2. СПОНТАННОЕ КВАДРУПОЛЬНОЕ УПОРЯДОЧЕНИЕ В НУЛЕВОМ МАГНИТНОМ ПОЛЕ

Гамильтониан магнетика с кубической решеткой и билинейным и биквадратичным обменом с z ближайшими соседями имеет вид:

где параметры обмена $I > 0$ и $K > 0$ положительны.

Биквадратичные произведения спинов ${{\left( {{{S}_{n}} \cdot {{S}_{{n + {{\Delta }}}}}} \right)}^{2}}$ выразим через квадрупольные операторы (1). Тогда гамильтониан (3) принимает форму [6, 7]:

При этом в преобразовании от ${{\left( {{{S}_{n}} \cdot {{S}_{{n + {{\Delta }}}}}} \right)}^{2}}$ к квадрупольным операторам дополнительно выделяется билинейное слагаемое $\left( {{{S}_{n}} \cdot {{S}_{{n + {{\Delta }}}}}} \right),$ что ведет к замене параметра $I > 0$ при билинейном обмене в (8) на эффективный параметр $J = I - \frac{1}{2}K$ [7].

Если не конкретизировать магнитную структуру упорядоченного состояния, то вводя приближение среднего поля в гамильтониане (4), получаем выражение:

Здесь ${{\sigma }_{\alpha }} \equiv {{\left\langle {{{S}_{{\alpha ,n}}}} \right\rangle }_{{\alpha = X,Y,Z}}}$ и ${{q}_{\gamma }} \equiv {{\left\langle {{{Q}_{{\gamma ,n}}}} \right\rangle }_{{\gamma = 0,2,XY,YZ,ZX}}}$ являются термодинамическими средними значениями дипольных ${{S}_{{\alpha ,n}}}$ и квадрупольных ${{Q}_{{\gamma ,n}}}$ спиновых операторов и играют роль параметров порядка. Выбор конкретного вида магнитного упорядочения определяет то, какие из параметров порядка ${{\sigma }_{\alpha }}$ и ${{q}_{\gamma }}$ в одноузельном гамильтониане ${{H}^{{{\text{MF}}}}}\left( n \right)$ следует положить равным нулю и какие будут отличны от нуля. Очевидно, что в квадрупольном состоянии все дипольные параметры порядка ${{\sigma }_{{\alpha = X,Y,Z}}} = 0$ следует положить равными нулю (намагниченность на узле отсутствует для любого направлении), но средние значения квадрупольных операторов ${{q}_{\gamma }} \ne 0.$

Предварительно попробуем установить вид квадрупольного упорядочения и его параметров порядка ${{q}_{\gamma }}\left( {T = 0} \right)$ при нулевой температуре $T = 0.$ Ограничимся случаем спина $S = 1$ и построим волновую функцию основного квадрупольного состояния $\left| {{{{{\Psi }}}_{{q0}}}\left( n \right)} \right\rangle ,$ которая, как любая собственная функция спинового гамильтониана с $S = 1$ должна быть линейной комбинацией собственных волновых функций |1❭, |0❭ и |–1❭ Z-проекции оператора спина ${{S}_{{Zn}}}{\text{:}}$ $\left| {{{{{\Psi }}}_{{qu}}}\left( n \right)} \right\rangle = a\left| 1 \right\rangle + b\left| 0 \right\rangle + c\left| { - 1} \right\rangle .$ Если учесть, что в основном квадрупольном состоянии должно отсутствовать дипольное упорядочение, т.е. потребовать:

и также учесть условие нормировки $\left\langle {{{{{{\Psi }}}_{{qu}}}\left( n \right)}} \mathrel{\left | {\vphantom {{{{{{\Psi }}}_{{qu}}}\left( n \right)} {{{{{\Psi }}}_{{qu}}}\left( n \right)}}} \right. \kern-0em} {{{{{{\Psi }}}_{{qu}}}\left( n \right)}} \right\rangle = 1,$ то из трех уравнений на коэффициенты $a,$ $b$ и $c$ можно получить три решения для этих коэффициентов и, соответственно, три варианта волновых функций квадрупольного упорядочения: причем эти волновые функции будут взаимно-ортогональными.

Выбирая $\left| {{{{{\Psi }}}_{{qu,X}}}\left( n \right)} \right\rangle $ в качестве волновой функции основного состояния для одноузельного гамильтониана ${{H}^{{{\text{MF}}}}}\left( n \right)$ (5), можно получить значения квадрупольных параметров порядка при $T = 0{\text{:}}$

Отсюда, учитывая соотношение $S_{{Xn}}^{2} + S_{{Yn}}^{2} + S_{{Zn}}^{2}$ = $ = {{\left. {S\left( {S + 1} \right)} \right|}_{{S = 1}}} = 2,$ найдем среднее значение квадратов операторов спиновых проекций в этом квадрупольном упорядочении:

Аналогично, при выборе $\left| {{{{{\Psi }}}_{{qu,Y}}}\left( n \right)} \right\rangle $ в качестве возможной волновой функции получим:

а при выборе $\left| {{{{{\Psi }}}_{{qu,Z}}}\left( n \right)} \right\rangle $ получим:

Таким образом, видно, что, если в неупорядоченной парамагнитной фазе ориентации спиновых векторов равномерно распределены по поверхности сферы в трехмерном пространстве с результатом $S_{{Xn}}^{2} = S_{{Yn}}^{2} = S_{{Zn}}^{2} = {{\left. {\frac{{S\left( {S + 1} \right)}}{3}} \right|}_{{S = 1}}} = \frac{2}{3},$ то при понижении температуры до $T = 0$ это трехмерное распределение ориентаций спинов трансформируется в равномерное распределение спиновых ориентаций по длине окружности на двумерной плоскости с результатом, например, $S_{{Zn}}^{2} = 0,$ $\left\langle {S_{{Xn}}^{2}} \right\rangle = \left\langle {S_{{Yn}}^{2}} \right\rangle = {{\left. {\frac{{S\left( {S + 1} \right)}}{2}} \right|}_{{S = 1}}} = 1.$ Следовательно, квадрупольное упорядочение при $T = 0$ выражается в том, что третье измерение пространства становится недоступным для ориентаций спиновых векторов. В кубическом магнетике осью цилиндрической симметрии такого квадрупольного порядка может быть любая из осей координат – OX, OY или OZ, что означает существование трех доменов одноосного квадрупольного упорядочения.

Добавим, что энергия основного одноосного квадрупольного состояния ${{E}_{{0,qu}}}$ (в расчете на атом) будет одинакова для любого варианта выбора оси симметрии квадрупольного порядка:

Этот результат для энергии основного состояния интересно сравнить с энергией основного ферромагнитного состояния в этой же модели обменных взаимодействий (3), (4). Основное ферромагнитное состояние с ориентацией всех спинов $S = 1$ вдоль оси OZ описывается волновой функцией $\left| {{{{{\Psi }}}_{{Z,f}}}\left( n \right)} \right\rangle = \left| 1 \right\rangle ,$ что дает ${{\sigma }_{Z}}\left( {T = 0} \right) = 1,$ ${{q}_{0}}\left( {T = 0} \right) = 1,$ а все прочие дипольные и квадрупольные параметры порядка равны 0. Поэтому энергия основного ферромагнитного состояния ${{E}_{{0,f}}}$ равна

Поэтому условие энергетической выгодности квадрупольного упорядочения при $T = 0$ ${{E}_{{0,f}}} > {{E}_{{0,qu}}}$ приводит к условию на параметры обмена $K > 2J$ (или с учетом равенства $J = I - \frac{1}{2}K$ из (4) дает требование $K > I$ для параметров обмена исходного гамильтониана (3)).

Рассмотрим для простоты случай одноосного квадрупольного упорядочения вдоль оси OZ, подразумевающий наличие параметра порядка ${{q}_{0}} \ne 0$ и равенства нулю параметра ${{q}_{2}} = 0$ (это означает равенство $\left\langle {S_{{Xn}}^{2}} \right\rangle = \left\langle {S_{{Yn}}^{2}} \right\rangle $ во всем интервале температур). Одноузельный гамильтониан ${{H}^{{{\text{MF}}}}}\left( n \right)$ (5) в приближении среднего поля для квадрупольного упорядочения примет вид:

и термодинамический потенциал (ТДП) $f$ будет равен

Самосогласованное уравнение для параметров порядка ${{q}_{0}}$ в точках экстремумов ТДП $f$ получается из условия ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {{q}_{0}}}}} \right. \kern-0em} {\partial {{q}_{0}}}} = 0$ и выглядит как

При этом уравнение (16) полезно преобразовать к альтернативной форме

Наконец, чтобы определить термодинамически устойчивые значения ${{q}_{0}},$ полученные из (16) и соответствующие локальным минимумам ТДП $f,$ от неустойчивых значений ${{q}_{0}},$ отвечающих локальным максимумам ТДП $f,$ необходимо найденные значения ${{q}_{0}}$ подставить во вторую производную ТДП по параметру порядка ${{{{\partial }^{2}}f} \mathord{\left/ {\vphantom {{{{\partial }^{2}}f} {\partial q_{0}^{2}}}} \right. \kern-0em} {\partial q_{0}^{2}}}$ и убедиться в ее положительном знаке:

Поскольку уравнения (16) или (17) для всех температур имеют также тривиальное решение ${{q}_{0}} = 0,$ соответствующее парамагнитному состоянию, то подставляя ${{q}_{0}} = 0$ в (18), находим, что парамагнитное состояние отвечает минимуму ТДП при температурах $T > {{T}_{0}},$ где

При T < T₀ парамагнитное состояние q₀ = 0 неустойчиво, так как оно соотвествует максимуму ТДП.

На рис. 1 представлены результаты расчета параметра квадрупольного порядка ${{q}_{0}}\left( t \right)$ из уравнения (16) как непрерывной функции безразмерной температуры $t = {T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}.$ Видно, что при $t > {{t}_{h}} = 1.093$ в системе существует только одно парамагнитное состояние с ${{q}_{0}}\left( t \right) = 0,$ а при $t < {{t}_{h}}$ при одной температуре всегда существует три решения для ${{q}_{0}}$ – два решения ${{q}_{0}}\left( t \right) \ne 0$ и одно тривиальное решение ${{q}_{0}}\left( t \right) = 0.$ При этом два решения ${{q}_{0}}$ отвечают двум локальным минимумам ТДП, а одно из решений ${{q}_{0}}$ – локальному максимуму ТДП, т.е. соответствуют термодинамически неустойчивому состоянию (участки значений ${{q}_{0}}\left( t \right)$ для неустойчивых состояний изображены штриховыми линиями). Важно, что локальные минимумы ТДП, местоположение которых в пространстве переменных ${{q}_{0}}$ дается найденными значениями ${{q}_{0}}\left( t \right)$ из (16), различаются по своей глубине, и что более глубокий минимум ТДП соответствует равновесному стабильному состоянию магнитной системы, тогда как состояние системы в точке менее глубокого минимума ТДП является метастабильным. Поэтому, чтобы различить эти ситуации, температурная зависимость квадрупольного параметра порядка ${{q}_{0}}\left( t \right)$ в стабильном состоянии изображена сплошной линией, а в метастабильном состоянии – штрих-пунктирной линией.

В результате видно, что парамагнитное состояние с ${{q}_{0}} = 0$ является стабильным при $t > {{t}_{{\text{C}}}}$ и метастабильным на участке ${{t}_{0}} = 1 < t < {{t}_{{\text{C}}}}.$ В точке ${{t}_{{\text{C}}}} = 1.082,$ когда локальные минимумы ТДП для парамагнитного состояния с ${{q}_{0}} = 0$ и для квадрупольного состояния с отрицательным параметром порядка ${{q}_{0}}\left( {{{t}_{{\text{C}}}}} \right) \approx - 1$ сравниваются по величине, происходит фазовый переход I рода из парамагнитного состояния в квадрупольное состояние с ${{q}_{0}}\left( t \right) < 0.$ При этом для ветви отрицательных значений ${{q}_{0}}\left( t \right) < 0$ в пределе $t \to 0$ будет ${{q}_{0}}\left( {t = 0} \right) = - 2,$ как это и следовало из обсуждения величин параметров порядка основного квадрупольного состояния (11). При температурах $0 \leqslant t < {{t}_{0}} = 1$ в роли метастабильного состояния выступает квадрупольное состояние с положительным параметром порядка ${{q}_{0}}\left( t \right) > 0,$ причем при $t \to 0$ будет ${{q}_{0}}\left( {t = 0} \right) = 1.$

На рис. 2 представлены зависимости величин безразмерного ТДП $\tilde {f} = {f \mathord{\left/ {\vphantom {f {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ как функции квадрупольного параметра порядка ${{q}_{0}}$ для трех значений безразмерной температуры $t = 1.2,$ $1.05$ и $0.9,$ которые иллюстрируют температурные изменения энергетического профиля ТДП и возникновение квадрупольного порядка. При $t = 1.2$ в парамагнитном состоянии ТДП $\tilde {f}$ имеет только один локальный минимум при ${{q}_{0}} = 0,$ а при $t = 1.05$ существует уже два локальных минимума ТДП – более глубокий при ${{q}_{0}} \approx - 1.232$ (стабильное квадрупольное состояние), и менее глубокий при ${{q}_{0}} = 0$ (метастабильное парамагнитное состояние). Наконец, при $t = 0.9$ более глубокий минимум ТДП приходится на ${{q}_{0}} = - 1.670$ (стабильное квадрупольное состояние с ${{q}_{0}} < 0$) и менее глубокий минимум на ${{q}_{0}} = 0.317$ (метастабильное квадрупольное состояние с ${{q}_{0}} > 0$).

Магнитная теплоемкость квадрупольного магнетика ${{C}_{{\text{M}}}}$ (на один атом) определяется как температурная производная внутренней энергии ${{U}_{0}}$:

Дифференцируя уравнения (16) или (17), находим:

и

Согласно результатам численного расчета, в точке фазового перехода I рода ${{t}_{{\text{C}}}} = {{{{T}_{{\text{C}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{C}}}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = $ $ = {{3{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}} \mathord{\left/ {\vphantom {{3{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}} {Kz}}} \right. \kern-0em} {Kz}} \approx 1.082$ будет ${{q}_{0}}\left( {{{t}_{{\text{C}}}} - {{0}^{ + }}} \right) \approx - 1.000,$ что дает скачок теплоемкости ${{C}_{{\text{M}}}}\left( {{{t}_{{\text{C}}}} - {{0}^{ + }}} \right) = 5.635{{k}_{{\text{B}}}}.$ Для сравнения напомним, что в обычном ферромагнетике с билинейным обменом и спином $S = 1$ скачок магнитной теплоемкости при переходе II рода в точке Кюри ${{T}_{{\text{C}}}}$ равен ${{\Delta }}{{C}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}}} \right)$ $ = {{C}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right) - {{C}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right) = 2{{k}_{{\text{B}}}}$ [10]. Таким образом, эффект скачкообразного изменения магнитной теплоемкости при переходе в квадрупольное состояние сопоставим по своей величине со скачком магнитной теплоемкости при фазовом переходе II рода в дипольное ферромагнитное состояние.

3. КВАДРУПОЛЬНЫЙ МАГНЕТИК ВО ВНЕШНЕМ МАГНИТНОМ ПОЛЕ

Рассмотрим поведение квадрупольного упорядочения, когда внешнее магнитное поле $H$ параллельно оси симметрии $OZ$ квадрупольного порядка. Так как в поле $H{\text{||}}OZ$ в спиновой системе появляется ненулевая намагниченность $m = {{\mu }_{0}}\left\langle {{{S}_{{Zn}}}\left( H \right)} \right\rangle ,$ пропорциональная среднему значению спина $\left\langle {{{S}_{{Zn}}}\left( H \right)} \right\rangle \equiv {{\sigma }_{Z}}\left( H \right),$ то одноузельный гамильтониан ${{H}^{{{\text{MF}}}}}\left( n \right)$ (5), помимо зеемановского вклада $ - {{\mu }_{0}}H{{S}_{Z}},$ необходимо дополнить вкладом от билинейного обменного взаимодействия $ - Jz{{\sigma }_{Z}}\left( H \right){{S}_{Z}}.$ Тогда в присутствии поля гамильтониан $H_{{qu,Z}}^{{{\text{MF}}}}\left( n \right)$ сменится на

Разумеется, надо иметь в виду, что в пределе $H \to 0$ будет ${{\sigma }_{Z}}\left( {H = 0} \right) = 0,$ так как в отсутствие поля магнетик находится в ненамагниченном квадрупольном состоянии.

Используя (23), получим ТДП $f\left( H \right)$ в магнитном поле:

${\text{и}}$ систему самосогласованных уравнений для параметров порядка ${{q}_{0}}$ и ${{\sigma }_{Z}}\left( H \right)$ из условия ${{\partial f\left( H \right)} \mathord{\left/ {\vphantom {{\partial f\left( H \right)} {\partial {{q}_{0}}}}} \right. \kern-0em} {\partial {{q}_{0}}}} = 0$ и ${{\partial f\left( H \right)} \mathord{\left/ {\vphantom {{\partial f\left( H \right)} {\partial {{\sigma }_{Z}}}}} \right. \kern-0em} {\partial {{\sigma }_{Z}}}} = 0$: которая может быть преобразована к альтернативной форме:

Кроме того, среди найденных из (25) или (26) значений ${{q}_{0}}$ и ${{\sigma }_{Z}}\left( H \right)$ необходимо выделить значения ${{q}_{0}}$ и ${{\sigma }_{Z}},$ отвечающие локальным минимумом ТДП $f\left( H \right).$ Для этого необходимо проверить, что найденный из (25) ${{\sigma }_{Z}}\left( H \right)$ и ${{q}_{0}}$ удовлетворяют условиям:

Наконец, магнитная энтропия ${{S}_{{\text{M}}}}\left( H \right)$ спонтанной системы в поле $H$ равна (в расчете на один атом):

и начальная магнитная восприимчивость ${{\chi }_{0}}$ имеет вид:

Для низких температур, учитывая, что при $T < 0.3{{T}_{0}}\sim 0.3{{T}_{{\text{C}}}}$ имеем ${{q}_{0}}\left( t \right) \approx - 2.000,$ получим, что восприимчивость будет экспоненциально мала:

Что же касается восприимчивости в точке перехода ${{T}_{{\text{C}}}}$ в квадрупольную фазу, то при переходе она уменьшается скачком, причем величина скачка зависит от отношения параметров эффективного билинейного обмена $J$ и биквадратичного обмена $K.$ Действительно, записывая отношение ${{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} \mathord{\left/ {\vphantom {{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)}}} \right. \kern-0em} {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)}}$ и переходя к безразмерной температуре $t = {T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = {{3{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{3{{k}_{{\text{B}}}}T} {Kz}}} \right. \kern-0em} {Kz}},$ получим:

(здесь использовано, что в критической точке ${{t}_{{\text{C}}}} \approx 1.082$ параметр порядка в нулевом поле $h = 0$ равен ${{q}_{0}}\left( {{{t}_{{\text{C}}}}} \right) \approx - 1.000$). С одной стороны, выше получено, что спонтанное квадрупольное упорядочение существует только при $J{\text{/}}K \leqslant 0.5.$ С другой стороны, наше рассмотрение ограничено областью положительных значений эффективного билинейного обмена $J{\text{/}}K \geqslant 0.$ Поэтому на интервале изменений отношений параметров обмена $0.5 \geqslant J{\text{/}}K \geqslant 0$ величина ${{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} \mathord{\left/ {\vphantom {{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)}}} \right. \kern-0em} {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)}}$ будет меняться от ${{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} \mathord{\left/ {\vphantom {{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} {{{{\left. {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)} \right|}}_{{J{\text{/}}K = 0.5}}}}}} \right. \kern-0em} {{{{\left. {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)} \right|}}_{{J{\text{/}}K = 0.5}}}}} \approx 14.195$ до ${{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} \mathord{\left/ {\vphantom {{{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} + {{0}^{ + }}} \right)} {{{{\left. {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)} \right|}}_{{J{\text{/}}K = 0}}}}}} \right. \kern-0em} {{{{\left. {{{\chi }_{0}}\left( {{{T}_{{\text{C}}}} - {{0}^{ + }}} \right)} \right|}}_{{J{\text{/}}K = 0}}}}} = 2.$

Рассмотрим теперь процесс изотермического намагничивания магнетика в квадрупольном состоянии, учитывая, что исходно, в нулевом магнитном поле, при температурах ниже точки ${{t}_{{\text{C}}}}$ фазового перехода I рода в системе существуют как устойчивое квадрупольное состояние с отрицательным параметром порядка ${{q}_{{01}}}\left( t \right) < 0,$ так и метастабильное квадрупольное состояние с положительным параметром порядка ${{q}_{{02}}}\left( t \right) > 0.$ На рис. 3 в качестве примера приведены зависимости квадрупольных параметров порядка ${{q}_{{01}}}\left( t \right) < 0,$ ${{q}_{{02}}}\left( t \right) > 0$ и связанных с ними относительных намагниченностей ${{\sigma }_{{Z1}}}\left( t \right),$ ${{\sigma }_{{Z2}}}\left( t \right)$ от безразмерного магнитного поля $h = {{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {{{k}_{{\text{B}}}}{{T}_{0}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{0}}}}$ при температуре $t = 0.95$ и отношении параметров обмена $J{\text{/}}K = 1{\text{/}}6,$ что эквивалентно отношению $I{\text{/}}K = 2{\text{/}}3$ для неперенормированных параметров обмена в (3). При этом значения параметров ${{q}_{0}}$ и ${{\sigma }_{Z}}$ в стабильном состоянии изображены сплошной линией, а в метастабильном состоянии – штрих-пунктирной. Видно, что в начале намагничивания при увеличении поля $h$ намагниченность ${{\sigma }_{{Z1}}}$ стабильного состояния с ${{q}_{{01}}}\left( t \right) < 0$ нарастает медленно, тогда как намагниченность ${{\sigma }_{{Z2}}}$ метастабильного состояния с ${{q}_{{02}}}\left( t \right) > 0$ растет гораздо быстрее. Поскольку основной вклад в понижение энергии в минимуме ТДП пропорционален $ - {{\mu }_{0}}{{\sigma }_{Z}}h$ и ${{\sigma }_{{Z2}}}\left( h \right) \gg {{\sigma }_{{Z1}}}\left( h \right),$ то это приводит к тому, что при достижении критического поля ${{h}_{{\text{C}}}} \simeq 0.313$ глубина локального минимума ТДП для состояния с ${{q}_{{02}}}\left( t \right) > 0$ становится больше, чем для состояния с отрицательным ${{q}_{{01}}}\left( t \right) < 0.$ Поэтому происходит фазовый переход I рода по полю – относительная намагниченность ${{\sigma }_{Z}}$ в критическом поле ${{h}_{{\text{C}}}}$ скачком возрастает на ${{\Delta }}{{\sigma }_{Z}} = {{\sigma }_{{Z2}}}\left( {{{h}_{C}}} \right) - {{\sigma }_{{Z1}}}\left( {{{h}_{{\text{C}}}}} \right) = 0.421 - 0.057 = 0.364,$ и состояние с ${{q}_{{02}}}\left( t \right) > 0$ становится стабильным, а состояние с ${{q}_{{01}}}\left( t \right) < 0$ – метастабильным.

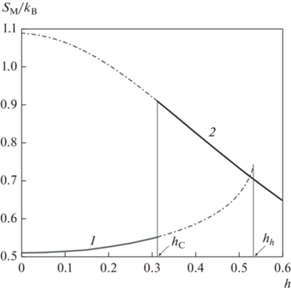
На рис. 4 представлено изменение магнитной энтропии ${{S}_{{\text{M}}}}$ при изотермическом намагничивании при тех же параметрах системы $t = 0.95$ и $J{\text{/}}K = 1{\text{/}}6$ как в стабильных состояниях (сплошные линии), так и в метастабильных состояниях (штрих-пунктирные линии). Видно, что в низких магнитных полях $h,$ когда стабильно квадрупольное состояние с ${{q}_{{01}}}\left( t \right) < 0,$ магнитная энтропия плавно растет с увеличением поля (обратный или аномальный МКЭ). В то же время, в этих же магнитных полях энтропия метастабильного квадрупольного состояния с ${{q}_{{02}}}\left( t \right) > 0$ примерно в 2 раза больше, чем в стабильном состоянии с ${{q}_{{01}}}\left( t \right) < 0,$ и при увеличении поля уменьшается подобно тому, как это происходит в обычном ферромагнетике с билинейным обменом (прямой или нормальный МКЭ). В точке фазового перехода I рода по полю ${{h}_{{\text{C}}}}$ квадрупольное состояние с отрицательным параметром порядка ${{q}_{{01}}}\left( t \right) < 0$ становится метастабильным, и при переходе системы в новое стабильное состояние с ${{q}_{{02}}}\left( t \right) > 0$ энтропия скачком возрастает на величину ${{{{\Delta }}{{S}_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\Delta }}{{S}_{{\text{M}}}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}} = {{{{S}_{{{\text{M}}2}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{M}}2}}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}} - {{{{S}_{{{\text{M1}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{{\text{M1}}}}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}} \approx 0.358$ (эффект носит аномальный характер). Однако при дальнейшем увеличении поля $h > {{h}_{{\text{C}}}}$ магнитная энтропия стабильного состояния начинает уменьшаться – МКЭ снова имеет нормальный характер.

Очевидно, что критическое магнитное поле ${{h}_{{\text{C}}}}\left( t \right)$ фазового перехода I рода между двумя состояниями с квадрупольными параметрами порядка ${{q}_{{01}}}\left( t \right) < 0$ и ${{q}_{{02}}}\left( t \right) > 0$ зависит от температуры изотермического намагничивания $t$. На рис. 5 сплошная линия изображает зависимость ${{h}_{{\text{C}}}}\left( t \right),$ причем на участке температур ${{t}_{0}} = 1 < t < {{t}_{{\text{C}}}} = 1.082,$ немного ниже точки спонтанного квадрупольного упорядочения этот переход скорее следует рассматривать как переход из квадрупольного состояния с ${{q}_{{01}}}\left( t \right) < 0$ в подмагниченное парамагнитное состояние. Видно, что при понижении температуры критическое поле ${{h}_{{\text{C}}}}\left( t \right)$ между двумя состояниями растет и при нулевой температуре намагничивания достигает значения ${{h}_{{\text{C}}}}\left( {t = 0} \right) = 0.5.$ Если вспомнить выражение (12) для энергии основного квадрупольного состояния ${{E}_{{0,qu}}}$ с параметром порядка ${{q}_{0}}\left( {t = 0} \right) = - 2$ и выражение (13) для энергии основного ферромагнитного состояния ${{E}_{{0,f}}}$ с параметрами порядка ${{\sigma }_{Z}}\left( {T = 0} \right) = 1,$ ${{q}_{0}}\left( {t = 0} \right) = 1$ и перейти к безразмерным энергиям $\tilde {E} = {E \mathord{\left/ {\vphantom {E {\left( {{{k}_{{\text{B}}}}{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {{{k}_{{\text{B}}}}{{T}_{0}}} \right)}} = {E \mathord{\left/ {\vphantom {E {\left( {{{Kz} \mathord{\left/ {\vphantom {{Kz} 3}} \right. \kern-0em} 3}} \right)}}} \right. \kern-0em} {\left( {{{Kz} \mathord{\left/ {\vphantom {{Kz} 3}} \right. \kern-0em} 3}} \right)}}$ и полям $h = {{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {\left( {{{k}_{{\text{B}}}}{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {{{k}_{{\text{B}}}}{{T}_{0}}} \right)}},$ то видно, что выполняется равенство

Таким образом, ${{h}_{{\text{C}}}}\left( {t = 0} \right)$ – это критическое магнитное поле, которое нужно приложить к системе, чтобы перестроить магнитную структуру основного состояния от квадрупольной к ферромагнитной при нулевой температуре $T = 0.$ И поэтому очевидно, что при конечных температурах состояние с ${{q}_{{02}}}\left( t \right) > 0$ в высоких полях по своей магнитной структуре следует рассматривать как ферромагнитное состояние, а не как квадрупольное, на что указывает и большая величина относительной намагниченности ${{\sigma }_{{Z2}}}\left( t \right)\sim 1$ (см. рис. 3), и характер полевых зависимостей магнитной энтропии ${{S}_{{{\text{M}}2}}}\left( h \right)$ (см. рис. 4).

Наконец укажем, что с изменением критического поля ${{h}_{{\text{C}}}}\left( t \right)$ по температуре одновременно меняется величина скачка магнитной энтропии ${{\Delta }}{{S}_{{\text{M}}}}\left( {{{h}_{{\text{C}}}}\left( t \right)} \right)$ в критическом поле, но это изменение является немонотонным (штриховая линия на рис. 5). При температурах несколько ниже точки спонтанного перехода ${{t}_{{\text{C}}}}\left( {h = 0} \right) = 1.082$ скачок энтропии сначала растет, и в рассматриваемом случае отношений $J{\text{/}}K = 1{\text{/}}6$ достигает максимума при $t \approx 0.95,$ но затем начинает резко уменьшаться, так что ${{\Delta }}{{S}_{{\text{M}}}}\left( {{{h}_{{\text{C}}}}\left( {t \to 0} \right)} \right) \to 0$ обращается в нуль при $t = 0.$ Это естественно, так как при понижении температуры резко уменьшаются энтропии обоих состояний с ${{q}_{{01}}}\left( t \right) < 0$ и ${{q}_{{02}}}\left( t \right) > 0$ и, как следствие, уменьшается их разность.

4. ЗАКЛЮЧЕНИЕ

В работе показано, что в кубическом магнетике с билинейным и биквадратичным обменами и спином $S = 1$ при достаточно большом параметре биквадратичного обмена ($K > I$) скачкообразно возникает одноосный квадрупольный порядок при понижении температуры T. Изотермическое намагничивание этого одноосного квадрупольного упорядочения вдоль оси симметрии сначала ведет к постепенному увеличению магнитной энтропии ${{S}_{{\text{M}}}},$ а затем, при достижении критического поля приводит к скачку в состояние с более высокой намагниченностью и одновременно к скачку с увеличением магнитной энтропии (обратный МКЭ).

Заметим, что в случае спина $S = 1$ параметр одноосного квадрупольного упорядочения $q(T)$ вдоль оси OZ имеет отрицательный знак в основном состоянии: ${{q}_{0}}\left( {T = 0} \right) = 3{{\left\langle {S_{Z}^{2}} \right\rangle }_{{T = 0}}} - 2 = - 2 < 0$ (ввиду того, что в этом состоянии ${{\left\langle {S_{Z}^{2}} \right\rangle }_{{T = 0}}} = 0,$ ${{\left\langle {S_{X}^{2}} \right\rangle }_{{T = 0}}} = {{\left\langle {S_{Y}^{2}} \right\rangle }_{{T = 0}}} = 1$) и что именно с отрицательным знаком параметра порядка ${{q}_{0}}\left( T \right) < 0$ связано аномальное полевое поведение магнитной энтропии. Дело в том, что, как отмечено в [7], магнитную структуру одноосного квадрупольного порядка вдоль оси $OZ$ можно представить как распределение ориентаций спиновых векторов ${{S}_{n}}$ внутри эллипсоида вращения – либо внутри сплюснутого эллипсоида с $\left\langle {S_{{Zn}}^{2}} \right\rangle < \left\langle {S_{{Xn}}^{2}} \right\rangle = \left\langle {S_{{Yn}}^{2}} \right\rangle $ и, соответственно, с отрицательным параметром порядка ${{q}_{0}}\left( T \right) = 3\left\langle {S_{{Zn}}^{2}} \right\rangle - S\left( {S + 1} \right) < 0,$ либо внутри вытянутого эллипсоида с $\left\langle {S_{{Z0}}^{2}} \right\rangle > \left\langle {S_{{Xn}}^{2}} \right\rangle = \left\langle {S_{{Yn}}^{2}} \right\rangle $ и ${{q}_{0}}\left( T \right) > 0.$ В случае спина $S = 1$ упорядочение с ${{q}_{0}}\left( T \right) < 0,$ а не с ${{q}_{0}}\left( T \right) > 0$ при $H = 0$ и при невысоких полях $H \ne 0$ дает более низкую энергию основного состояния и более низкую энергию в минимуме ТДП. При этом неравенство средних значений квадратов спиновых переменных $\left\langle {S_{{Zn}}^{2}} \right\rangle < \left\langle {S_{{Xn}}^{2}} \right\rangle = \left\langle {S_{{Yn}}^{2}} \right\rangle $ и усиление этого неравенства при понижении температуры указывают на то, что в квадрупольной структуре с ${{q}_{0}}\left( T \right) < 0$ спины ${{S}_{n}}$ стремятся выстроиться перпендикулярно оси симметрии $OZ,$ по возможности ближе к плоскости $OXY.$ Поэтому магнитное поле вдоль оси $OZ,$ перпендикулярное направлению упорядочения, усиливает беспорядок в ориентации спинов и соответственно повышает магнитную энтропию (рис. 4).

В противоположном случае квадрупольной структуры с ${{q}_{0}}\left( T \right) > 0$ спиновые векторы ${{S}_{{\text{M}}}}$ при $T = 0$ прилегают максимально близко к оси $OZ$ – либо параллельно, либо антипараллельно, так что $Z$ – проекция ${{S}_{{Zn}}}$ равна либо ${{S}_{{Zn}}} = S,$ либо ${{S}_{{Zn}}} = - S.$ Тепловые движения при конечных температурах $T \ne 0$ вызывают отклонение вектора ${{S}_{{\text{M}}}}$ от оси $OZ$ и разупорядочивают квадрупольную структуру, а магнитное поле, приложенное вдоль оси $OZ,$ напротив, усиливает упорядочение и тем самым понижает энтропию. В нашем случае $S = 1$ такое происходит в метастабильном состоянии с ${{q}_{{02}}}\left( T \right) > 0$ (рис. 4), т.е. в этом состоянии МКЭ является нормальным.