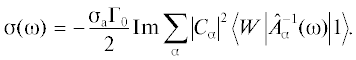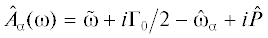Физика металлов и металловедение, 2023, T. 124, № 1, стр. 29-35

ВВЕДЕНИЕ

Системы магнитных наночастиц широко используются в современной нанотехнологии благодаря целому ряду специфических структурных, магнитных и термодинамических свойств, обнаруженных в процессе многолетних фундаментальных исследований. Мёссбауэровская спектроскопия является одним из основных методов исследования таких материалов. При этом высокая чувствительность самого метода определяется тем обстоятельством, что малый размер частиц часто оказывается решающим фактором в реализации весьма разнообразных форм спектров поглощения таких материалов [1]. Основой методических достижений в решении прикладных задач является специфический характер эволюции спектров наночастиц от хорошо разрешенной магнитной сверхтонкой структуры (секстет линий для ядер ⁵⁷Fe) при низких температурах к одиночной линии (или квадрупольному дублету линий) – при высоких. Такое поведение наблюдали еще 50 лет назад, и оно было интерпретировано в рамках теории ферромагнитных однодоменных частиц, основы которой были заложены Неелем в конце 40-х прошлого века [2]. Практически сразу для описания температурной эволюции мессбауэровских спектров была предложена простейшая двухуровневая модель релаксации однодоменной частицы с энергией аксиальной магнитной анизотропии [1]:

где K – положительная константа магнитной анизотропии, V – объем частицы, θ – угол между вектором однородной намагниченности частицы и осью анизотропии.

В дальнейшем был предложен целый ряд моделей различной степени сложности для описания разнообразных форм мессбауэровских спектров наночастиц разной магнитной природы, ферромагнитных [3–5], антиферромагнитных [6, 7] и ферримагнитных [8] в зависимости от температуры, а также магнитного поля [9]. Однако во всех этих моделях была рассмотрена простейшая форма магнитной анизотропии (1), так что вопрос о влиянии различных форм магнитной анизотропии, широко используемых в магнетизме, до сих пор фактически остался за кадром. Этот недостаток теории наиболее остро проявляется в последнее время, поскольку вектор исследований непрерывно смещается от диагностики самих магнитных частиц к изучению их функционального поведения в различных приложениях [10–12].

СПЕКТРЫ ЧАСТИЦ С АКСИАЛЬНОЙ МАГНИТНОЙ АНИЗОТРОПИЕЙ (1)

Наиболее адекватной с физической точки зрения моделью для описания магнитной динамики ансамбля ферромагнитных наночастиц с энергией анизотропии (1) является многоуровневая модель [3, 4], которая учитывает температурные возбуждения каждой частицы в виде орбит прецессии однородной намагниченности частицы M с постоянной энергией Е(θ) в эффективном магнитном поле:

где n_z – единичный вектор вдоль оси анизотропии и введено критическое поле полного перемагничивания частиц с произвольной ориентацией [13]: M₀ – намагниченность частиц. Критическое поле (3) определяет характерную частоту прецессии в локальных минимумах энергии (1): где γ – гиромагнитное отношение.

Наиболее простая ситуация реализуется в режиме медленной релаксации [4], когда скорость диффузии D вектора M существенно меньше скорости распада возбужденного состояния ядра:

где Γ₀ – ширина уровня возбужденного состояния ядра в частотных единицах. В этом случае релаксация не оказывает существенного влияния на формирование спектров сверхтонкой структуры, а сама форма спектров определяется распределением Гиббса эффективного поля (2) по равновесной заселенности стохастических состояний [4]: где T – температура, С – нормировочная константа. 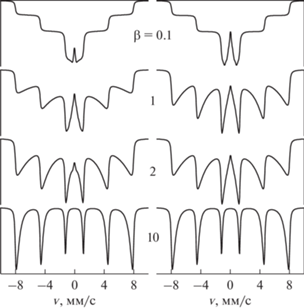В этом случае спектр поглощения гамма-кванта с энергией $E = \hbar {{\omega }}$ ансамблем хаотически ориентированных частиц сводится к усреднению по распределению эффективного сверхтонкого поля на ядре H_hf [4]: Здесь $A = {{{{{{\sigma }}}_{{\text{a}}}}\Gamma _{0}^{2}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{\text{a}}}}\Gamma _{0}^{2}} 4}} \right. \kern-0em} 4},$ σ_a – эффективная толщина поглотителя, α = (m_e, m_g) нумерует переходы с проекциями спина ядра m_e и m_g на направление H_hf, $\tilde {\omega } = \omega - {{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} \hbar }} \right. \kern-0em} \hbar },$ E₀ – энергия резонансного перехода. Интенсивности переходов на резонансных частотах ${{\omega }_{\alpha }} = ({{m}_{{\text{e}}}}{{\omega }_{{\text{e}}}} - {{m}_{{\text{g}}}}{{\omega }_{{\text{g}}}})H_{{{\text{hf}}}}^{{(0)}}$ ($H_{{{\text{hf}}}}^{{(0)}}$ – максимальная величина H_hf в пределе низких температур) определяются коэффициентами Клебша–Джордана C_α, ${{\beta }} = {{KV} \mathord{\left/ {\vphantom {{KV} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ – эффективный энергетический барьер. С помощью выражений (1), (7)–(9) можно рассчитать форму спектров поглощения с заданными параметрами.

Типичные расчетные спектры для случая (5) показаны в левой колонке рис. 1 и демонстрируют часто наблюдаемую в эксперименте трансформацию хорошо разрешенного секстета линий при низких температурах к сильно асимметричным линиям с резкими внешними фронтами и сильно размытыми к центру спектра внутренними фронтами при промежуточных температурах (или к комплексу шести перевернутых трамплинов), и наконец, к форме спектра поглощения в виде перевернутого пятиступенчатого пьедестала при высоких температурах [4]. Отметим, что в предельном случае высоких температур, $KV \ll {{k}_{{\text{B}}}}T,$ для каждого перехода в интервале частот $\tilde {\omega } \in [0,{{\omega }_{\alpha }}(1)]$ выражение для спектра поглощения сводится к простому выражению:

которое как раз и описывает нетривиальные формы спектров поглощения в виде комплекса шести трамплинов и пятиступенчатого пьедестала.

В общем случае, когда условие (5) не выполняется и релаксационными переходами между орбитами прецессии вектора M пренебрегать нельзя, наиболее простой с точки зрения реализации моделью для описания мёссбауэровских спектров является многоуровневая релаксационная модель [3, 4], основанная на квантово-механическом описании однородно намагниченной частицы с полным спином S и (2S + 1) стохастическими состояниями проекции ${{\hat {S}}_{z}}$ в рамках гамильтониана:

Фактически эта модель является квантовым аналогом общей теории релаксации однородной намагниченности статистического ансамбля однодоменных частиц в магнитном поле [14]. В этом случае спектр поглощения ансамбля хаотически ориентированных частиц описывается следующим выражением [3]:

Здесь $\left\langle W \right|$ и $\left| 1 \right\rangle $ – вектор заселенности и единичный столбец стохастических состояний; оператор определяется диагональной матрицей соответствующего сверхтонкого перехода и трехдиагональной релаксационной матрицей

Элементы этой матрицы определяются коэффициентом диффузии D:

и энергией анизотропии: которая также задает вектор заселенности стохастических состояний:

Отмечу, что в пределе (5) и больших S $ \gg $ 1 оба набора формул (1), (7)–(9) и (11)–(19) дают идентичный результат.

Типичные спектры, рассчитанные в этой модели, показаны в правой колонке рис. 1. При достаточно низких температурах, когда магнитные моменты частиц “заморожены” в локальных минимумах энергии (1), наблюдается хорошо разрешенный магнитный секстет линий. С повышением температуры существенную роль начинают играть переходы между состояниями, и в случае слабой релаксации секстет линий остается хорошо разрешенным с одинаково уширенными линиями, немного сдвинутыми к центру спектра на величину p²/2ɷ_α, где $\bar {p} = D{{e}^{{{{ - KV} \mathord{\left/ {\vphantom {{ - KV} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}}}}$ [5]. С дальнейшим повышением температуры, когда скорость релаксационных переходов становится сравнима с ларморовскими частотами прецессии спина ядра в сверхтонком поле, сверхтонкая структура спектра размывается. В пределе высоких температур происходит поочередный коллапс магнитных компонент сверхтонкой структуры для разных α в одиночную центральную линию.

АКСИАЛЬНАЯ МАГНИТНАЯ АНИЗОТРОПИЯ С ДВУМЯ КОНСТАНТАМИ

Рассмотрим ансамбль наночастиц с аксиальной магнитной анизотропией, которая описывается двумя константами K и k₂:

В этом случае эффективное магнитное поле, в котором прецессирует вектор M, принимает вид:

Из этих выражений видно, что как локальные минимумы энергии (20), так и характер прецессии вектора M в поле (21) существенным образом зависят от величины второй константы k₂. В частности, для значений

магнитный момент частицы в локальных минимумах энергии будет отклоняться в соответствии с выражением:

В частности, для k₂ = –1 двум локальным минимумам энергии (20) будет соответствовать однородная прецессия вектора M под углом θ = 45° к двум направлениям оси анизотропии. Нетрудно догадаться, что как раз в диапазоне значений (22) следует ожидать появления необычных форм мессбауэровских спектров поглощения.

Что же касается расчета спектра поглощения ансамблем хаотически ориентированных магнитных наночастиц с энергией (20), то в предельном случае медленной релаксации (5) его можно провести по формулам (7) и (8), в которых выражение (9) надо заменить на

В общем случае для расчета спектров ансамбля наночастиц можно использовать квантово-механическое описание с помощью набора формул (12)–(17) и (19), а выражение (18) заменить на

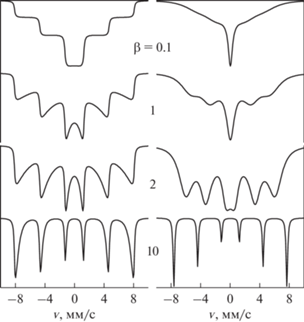
Типичные спектры, рассчитанные для двух этих случаев при k₂ = –1, показаны в левой и правой колонках рис. 2 соответственно. Для расчетов были взяты увеличенные в четыре раза значения β, поскольку энергетический барьер между локальными минимумами энергии (20) с k₂ = –1 в четыре раза меньше, чем для энергии (1). Как видно на этом рисунке, форма спектров поглощения для k₂ = –1 в предельном случае (5) (левая колонка) существенно поменялась по сравнению с формой спектров для k₂ = 0 (рис. 1, левая колонка). Во-первых, спектральные линии при низких температурах существенно уширились, магнитное сверхтонкое расщепление спектров при низких и промежуточных температурах значительно уменьшилось вследствие отклонения магнитных моментов частиц в локальных минимумах энергии в соответствии с (23). При этом максимумы линий поглощения соответствуют эффективному уменьшению величины сверхтонкого поля ${{H}_{{{\text{hf}}}}} = {{H_{{{\text{hf}}}}^{{(0)}}} \mathord{\left/ {\vphantom {{H_{{{\text{hf}}}}^{{(0)}}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ в соответствии с усреднением величины магнитного момента на ядре за счет однородной прецессии вектора M под углом θ = 45° к оси анизотропии.

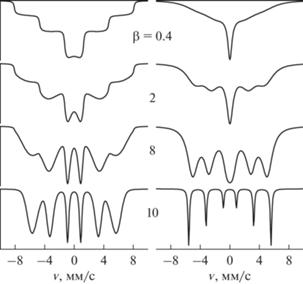
Во-вторых, с повышением температуры спектры поглощения приобретают еще одну нетривиальную форму дюн, перевернутых в экспериментальной геометрии на пропускание. В предельном случае высоких температур, $KV \ll {{k}_{{\text{B}}}}T,$ в интервале частот $\tilde {\omega } \in [0,{{\omega }_{\alpha }}(1)]$ выражение для спектра поглощения также сводится к довольно простому выражению:

Это выражение и описывает нестандартную форму спектров поглощения в виде дюн с максимумами линий поглощения, соответствующих величине

В то же время в пределе экстремально высоких температур форма спектра поглощения стремится к пятиступенчатому пьедесталу с исходным магнитным сверхтонким расщеплением, которое соответствует величине сверхтонкого поля $H_{{{\text{hf}}}}^{{(0)}},$ также в соответствии с (26).

В случае, когда условие (5) не выполняется, т.е. скорость релаксационных переходов (коэффициент диффузии D) сравнима или превышает обратное время жизни ядра в возбужденном состоянии (ширину Γ₀), наблюдается температурная эволюция формы спектров (рис. 2, правая колонка), качественно характерная для спектров для k₂ = 0 (рис. 1, правая колонка). А единственным и очень существенным различием является уменьшение магнитного сверхтонкого расщепления спектров при низких температурах вследствие отклонения магнитных моментов частиц в локальных минимумах энергии в соответствии с (23). При этом максимумы линий поглощения, которые соответствуют уменьшению величины H_hf в (27) в пределе низких температур, с повышением температуры постепенно смещаются к центру спектра за счет релаксационных процессов, стремясь к универсальной релаксационной форме с поочередным коллапсом магнитных компонент сверхтонкой структуры, которая практически не зависит от k₂.

АКСИАЛЬНАЯ МАГНИТНАЯ АНИЗОТРОПИЯ С РОМБИЧЕСКИМ ИСКАЖЕНИЕМ

Рассмотрим ансамбль наночастиц с аксиальной магнитной анизотропией с ромбическим искажением, когда главные значения тензора магнитной анизотропии вдоль соответствующих декартовых осей связаны соотношением:

а энергию частицы можно записать в следующем виде: Здесь K = K_zz – K_xx, φ – азимутальный угол, m_z и m_y – декартовы компоненты вектора m = M/M₀,

Тогда вектор M будет совершать прецессию в эффективном магнитном поле

которая определяется уравнением движения:

В нашем случае для конкретных расчетов удобно использовать уравнение для одной из компонент:

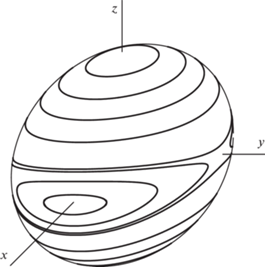
Траектории движения магнитного момента частицы с заданной энергией Е показаны на рис. 3. Отмечу, что вращения вокруг осей x и z имеют разные знаки в соответствии с (33) и (34).

Используя (29), уравнение (32) можно свести к уравнению для одной компоненты:

где ${{\omega }_{0}} = 2\gamma {{M}_{0}}\sqrt {1 - {{k}_{{yy}}}} ,$ $E{\kern 1pt} ' = {E \mathord{\left/ {\vphantom {E {KV}}} \right. \kern-0em} {KV}},$

Анализ этих выражений показывает, что существует два типа решений уравнения (35): вращение вокруг оси z в интервале $ - 1 \leqslant E{\kern 1pt} ' < - {{k}_{{yy}}}$ и вокруг оси x в интервале $ - {{k}_{{yy}}} < E{\kern 1pt} ' \leqslant 0.$ Уравнение (35) определяет временную зависимость и диапазон изменений продольной компоненты намагниченностей, которые, в свою очередь, определяют тип и характеристики траекторий движения вектора M в виде нутаций [15], т.е. самосогласованной прецессии этого вектора вокруг оси z или x с одновременными колебаниями по полярному углу в диапазоне, заданном параметрами $E{\kern 1pt} '$ и $\tilde {E}{\kern 1pt} '.$ Поскольку период высокочастотных нутаций существенно меньше характерных времен в большинстве экспериментальных методик для исследования наночастиц (в частности, в мёссбауэровской спектроскопии), нас будут интересовать средние по периоду нутаций значения компонент вектора M, заданные уравнением (35).

Следуя рутинным процедурам, подробно описанным в [7, 8, 15], и опуская промежуточные выкладки, можно получить выражения для средних значений компонент:

для заданных значений E в интервале $ - 1 < E{\kern 1pt} ' < - {{k}_{{yy}}}$ и в интервале $ - {{k}_{{yy}}} < E{\kern 1pt} ' \leqslant 0.$ Здесь $\gamma = \sqrt {\left| {{{\tilde {E}{\kern 1pt} '} \mathord{\left/ {\vphantom {{\tilde {E}{\kern 1pt} '} {E{\kern 1pt} '}}} \right. \kern-0em} {E{\kern 1pt} '}}} \right|} \leqslant 1$ и введены полные эллиптические интегралы первого рода:

Для расчета спектров поглощения в предельном случае медленной релаксации (5) воспользуемся результатами работ [7, 8]. В этом случае равновесное состояние ансамбля частиц при заданной температуре T описывается распределением Гиббса по квазистационарным состояниям (нутационным орбитам вектора M) с заданными значениями E, каждое из которых характеризуется средними значениями компонент намагниченностей ${{\bar {m}}_{z}}(E{\kern 1pt} ')$ или ${{\bar {m}}_{x}}(E{\kern 1pt} '){\text{:}}$

Тогда сечение поглощения определяется следующим выражением:

а соответствующие квазистационарным состояниям парциальные спектры поглощения $L(\omega ,x)$ определяются лоренцианами (8).

Типичные спектры поглощения ансамбля медленно релаксирующих наночастиц, рассчитанные по формулам (37)–(42), показаны на рис. 4. Отчетливо видно, что наряду с комплексом шести трамплинов при промежуточных температурах и пятиступенчатого пьедестала при высоких температурах появляются характерные провалы в центральной части спектров поглощения. Этот эффект обусловлен своеобразным “удалением” экваториальных к оси анизотропии прецессионных орбит, которым соответствуют минимальные значения средних по этим траекториям магнитных моментов, которым пропорциональны значения сверхтонкого поля. При этом, чем больше ромбическое искажение, тем больше провал в центральной части спектров поглощения.

ЗАКЛЮЧЕНИЕ

В общем случае, когда надо учитывать релаксационные переходы между орбитами прецессии вектора M, для расчета мессбауэровских спектров поглощения в случае аксиальной магнитной анизотропии с ромбическим искажением необходимо разработать и реализовать многоуровневую релаксационную модель. Решение этой задачи выходит за рамки этой статьи, но уже сейчас понятно, что такую модель надо разрабатывать в рамках квантово-механического подхода, реализованного в работе [9] для случая наночастиц в магнитном поле. В этом случае возможна ситуация с более чем двумя переходами между соседними состояниями (орбитами прецессии) в отличие от многоуровневых релаксационных моделей, представленных во втором и третьем разделах настоящей статьи.

Все представленные выше модели магнитной динамики и формализм для расчета мессбауэровских спектров наночастиц несложно обобщить на случай наличия градиента электрического поля на ядрах, когда наряду с магнитным сверхтонким взаимодействием необходимо учитывать электрическое квадрупольное сверхтонкое взаимодействие. Но уже сейчас представленные модели существенно расширяют методическую базу диагностики магнитных наноматериалов методом мессбауэровской спектроскопии, поскольку обнаруженные нетривиальные формы спектров поглощения представляют собой отличные ориентиры для проведения анализа экспериментальных спектров.

Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме FFNN-2022-0019.