Физика металлов и металловедение, 2023, T. 124, № 1, стр. 24-28

Магнитная восприимчивость сплавов ниже порога перколяции

В. И. Белоконь^a, О. И. Дьяченко^b, *, Р. В. Лапенков^a

^a Институт наукоемких технологий и передовых материалов, департамент теоретической физики и интеллектуальных технологий, Дальневосточный федеральный университет
690922 Приморский край, Владивосток, о. Русский, п. Аякс, 10, Россия

^b Институт наукоемких технологий и передовых материалов, департамент общей и экспериментальной физики, Дальневосточный федеральный университет
690922 Приморский край, Владивосток, о. Русский, п. Аякс, 10, Россия

^* E-mail: dyachenko.oi@dvfu.ru

Поступила в редакцию 19.08.2022
После доработки 18.11.2022
Принята к публикации 21.11.2022

EDN: KPUOJZ
DOI: 10.31857/S0015323022601131

Полный текст (PDF)

Аннотация

В рамках теории случайных полей взаимодействия показана возможность определения точки Кюри и парамагнитной точки Кюри, соответствующей появлению ближнего порядка. В ферромагнитных сплавах существует интервал концентраций, для которого разрушается дальний порядок, но еще сохраняется ближний. Это приводит к появлению фазы кластерного стекла, для которого характерна зависимость магнитной восприимчивости от времени и появление вязкой намагниченности. На примере сплава AuFe исследуется поведение начальной магнитной восприимчивости как функции температуры и концентрации, проводится сравнение с данными, полученными экспериментально.

Ключевые слова: магнитная восприимчивость, фаза кластерного стекла, теория случайных полей взаимодействия, температура Кюри, магнитная вязкость, сплавы

ВВЕДЕНИЕ

В последнее время активно изучаются магнетики с конкурирующим взаимодействием, такие как спиновые, структурные, сверхпроводящие стекла и т.д. Среди неупорядоченных магнетиков и сплавов большинство веществ относится к спиновым стеклам, которых на данный момент известно огромное количество – металлы, диэлектрики, полупроводники, разбавленные и концентрированные сплавы, кристаллические и аморфные вещества [1–4].

Для развития теории фазовых переходов в магнитных материалах используются различные модели. Так модель Изинга, получившая решение для одномерного случая в 1925 г., ожидала появления точного решения для двумерных решеток до 1944 г., а для объемных решеток точное решение до сих пор не найдено.

Существуют несколько моделей, описывающих спиновые стекла: модель Эдвардса–Андерсона и модель бесконечного радиуса, предложенная Шеррингтоном и Киркпатриком. Также существует эвристическая модель состояния спинового стекла, основанная на результатах численного моделирования [5, 6].

Целью данного исследования является изучение возможности использования метода случайных полей взаимодействия и модели Изинга для описания магнитной восприимчивости магнетика, находящегося в состоянии спинового стекла, на примере часто обсуждаемого сплава AuFe.

ДАЛЬНИЙ И БЛИЖНИЙ ПОРЯДОК

Как было показано в работе [7], в приближении теории случайных полей взаимодействия в рамках модели Изинга критическая концентрация обменно-взаимодействующих ионов приближенно определяется выражением:

(1)

${{p}_{c}} = \frac{2}{z},$

где $z$ – координационное число, зависящее от типа решетки. В свою очередь магнитная восприимчивость $\chi $ при температуре выше температуры Кюри Т_С вычисляется как [8]:

(2)

$\chi = \frac{{\frac{1}{{m~B}}{\text{th}}\left[ {\frac{{m~B}}{{kT}}} \right]}}{{1 - \frac{{m~{{H}_{0}}}}{{m~B}}{\text{th}}\left[ {\frac{{m~B}}{{k~T}}} \right]}}.{\text{\;}}$

В этом соотношении принято считать магнитный момент $m$ и постоянную Больцмана $k$ равными единице. Тогда температура $T,$ поле ${{H}_{0}}$ и поле $B$ измеряются в энергетических единицах и определяются как:

(3)

${{H}_{0}} = p\sum\limits_k {{{\varphi }_{k}}} ,$

(4)

${{B}^{2}} = 2p\sum\limits_k {\varphi _{k}^{2}} ,$

где $~{{\varphi }_{k}}$ – обменное поле, $p$ – концентрация обменно-взаимодействующих частиц, $T$ – абсолютная температура.

При $B \to 0$ формула (2) переходит в известное из теории молекулярного поля выражение:

(5)

$\chi = \frac{1}{{T - {{H}_{0}}}}.{\text{\;}}$

Соответственно, ${1 \mathord{\left/ {\vphantom {1 \chi }} \right. \kern-0em} \chi }$ обращается в 0 при $T = {{T}_{{\text{С}}}}$ и асимптотически при $T \to \infty $ стремится к $T - {{H}_{0}}.$ В теории молекулярного поля дальний и ближний порядок возникает одновременно. По нашему представлению, точка Кюри определяется соотношением (2), а из соотношения (5) определяется парамагнитная точка Кюри, соответствующая температуре появления ближнего порядка.

Таким образом, теория случайных полей взаимодействия позволяет различать точку Кюри и парамагнитную точку Кюри $\theta > {{T}_{{\text{C}}}},$ соответствующую появлению ближнего порядка [13].

МАГНИТНАЯ ВЯЗКОСТЬ И НАЧАЛЬНАЯ ВОСПРИИМЧИВОСТЬ

В отсутствие протекающего кластера при p < p_c дальний порядок невозможен, однако группы взаимодействующих обменно ионов (кластеры) будут сохранять магнитный момент при T < 0 и обеспечивать магнитные свойства сплава. Как следует из экспериментальных данных [14], при достаточно низких температурах магнитный момент растет пропорционально lg t, где t время действия постоянного поля H. Очевидно, что ансамбль кластеров должен обладать широким спектром времен релаксации, который обусловлен их разбросом по числу ионов и полям перемагничивания H_c. В этом случае время релаксации τ, магнитный момент кластера $m$ и его критическое поле ${{H}_{{\text{с}}}}$ будут связаны простым соотношением:

(6)

$\frac{1}{\tau } = {{f}_{0}}\exp \left[ {\frac{{ - m{{H}_{{\text{c}}}}}}{{kT}}} \right],$

где ${{f}_{0}}$ – частотный фактор, $k$ – константа Больцмана. Относительно частотного фактора в литературе существуют различные мнения, в данной работе мы связываем его с температурой Дебая, которая, например, для золота или железа имеет порядок ${{10}^{2}}$ К. Вероятность необратимого поворота магнитного момента кластера определяется “частотой попыток флуктуаций”, которая связана с упругими колебаниями ионов в кристаллической решетке. По определению частота Дебая – это максимально возможная частота фононного спектра, поэтому мы связываем частотный фактор именно с частотой Дебая. Соответственно, из выражения $\hbar {{\omega }_{{\text{D}}}} = k{{T}_{{\text{D}}}}$ оценка для ${{\omega }_{{\text{D}}}}\sim {{f}_{0}}$ имеет порядок ${{10}^{{13}}}\,\,{{{\text{с}}}^{{ - 1}}}.$

Будем предполагать, что магнитный момент кластера подобно магнитному моменту однодоменной частицы зависит от температуры следующим образом: $m~\left( T \right) = {{m}_{0}}{{\left( {1 - \frac{T}{\theta }} \right)}^{{{\beta }}}},$ где $\beta = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ [9]. Аналогично, ${{H}_{{\text{c}}}} = {{H}_{{{\text{c}},0}}}{{\left( {1 - \frac{T}{\theta }} \right)}^{{{\beta }}}}$ (${{H}_{{{\text{c}},0}}}$ – поле при $T = 0$).

Таким образом:

(7)

$\ln \left[ {{{f}_{0}}\tau } \right] = \frac{{m{{H}_{{\text{c}}}}}}{{kT}};$

(8)

$m = {{m}_{0}}{{\left( {1 - \frac{T}{\theta }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}};$

(9)

${{H}_{{\text{c}}}} = {{H}_{{{\text{c}},0}}}{{\left( {1 - \frac{T}{\theta }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}};$

(10)

$\lg \left[ {{{f}_{0}}\tau } \right] = \alpha {{m}_{0}}{{\left( {1 - \frac{T}{\theta }} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.{\text{\;}}$

Полагая распределение кластеров по $\alpha {{m}_{0}}$ равномерным (${{m}_{0}}$ – магнитный момент частицы при T = 0), получим при постоянной температуре $T~$равномерное распределение по $\lg \left[ {{{f}_{0}}\tau } \right],$ которое подтверждается опытом [12].

Если время релаксации $\tau $ меньше ${{10}^{{ - 2}}}\,\,{\text{с}}$ (характерного времени измерения магнитной восприимчивости), то восприимчивость системы частиц в случае отсутствия взаимодействия между кластерами может быть представлена следующим образом:

(11)

$\chi \sim \frac{{N\left\langle {{{m}^{2}}} \right\rangle }}{T},$

(12)

$\chi = \frac{{A{{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{T},$

где $~N$ – число кластеров, вовлеченных в процесс намагничивания: $N\sim {1 \mathord{\left/ {\vphantom {1 {B\left( T \right)}}} \right. \kern-0em} {B\left( T \right)}}\sim {1 \mathord{\left/ {\vphantom {1 {m\left( T \right)}}} \right. \kern-0em} {m\left( T \right)}},$ $\chi \sim m\sim $ $\sim {{\left( {1 - \frac{T}{\theta }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}~$ [10], $\left\langle {{{m}^{2}}} \right\rangle $ – среднее значение квадрата магнитных моментов кластеров.

Соотношение (12) справедливо при τ < $ < {{10}^{{ - 2}}}\,\,{\text{с}}~\,\,\left( {\lg \left[ {{{f}_{0}}\tau } \right] < 11} \right).$ В противном случае определенная часть магнитных моментов не будет успевать реагировать на внешнее поле, что приведет к уменьшению магнитной восприимчивости.

Рассмотрим зависимость времени релаксации от температуры для кластера с максимальным значением $\alpha {{m}_{0}}{\text{:}}$

(13)

${{x}_{1}} = \lg \left[ {{{f}_{0}}{{\tau }_{1}}} \right] = \alpha {{m}_{0}}\frac{{{{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{T}.{\text{\;}}$

При температуре $T + \Delta T{\text{:}}$

(14)

$\begin{gathered} {{x}_{2}} = \lg \left[ {{{f}_{0}}{{\tau }_{2}}} \right] = \alpha {{m}_{0}}\frac{{{{{\left( {1 - \frac{{T + \Delta T}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{T + \Delta T}} = \\ = \alpha {{m}_{0}}\left( {\frac{{{{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{T} + \frac{{\left( {T - 3\theta } \right)\Delta T}}{{3{{T}^{2}}\theta {{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right). \\ \end{gathered} $

Таким образом,

(15)

$\Delta x = \alpha {{m}_{0}}\frac{{\left( {T - 3\theta } \right)\Delta T}}{{3{{T}^{2}}\theta {{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}},$

(16)

${{x}_{2}}\left( {{{T}_{2}}} \right) - {{x}_{1}}\left( {{{T}_{1}}} \right) = \alpha {{m}_{0}}\left( {\frac{{{{{\left( {1 - \frac{{{{T}_{2}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{2}}}} - \frac{{{{{\left( {1 - \frac{{{{T}_{1}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{1}}}}} \right).$

Если при температуре ${{T}_{1}}$ максимальное время релаксации было ${{10}^{{ - 2}}}\,\,{\text{с}},$ то

(17)

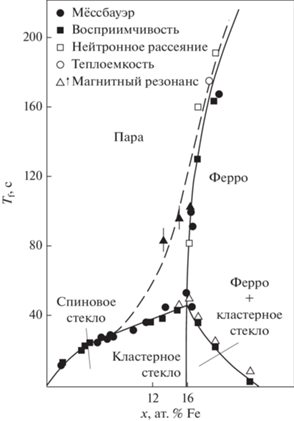
$\alpha {{m}_{0}}\frac{{{{{\left( {1 - \frac{{{{T}_{1}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{1}}}} = 11.{\text{\;}}$

Обратимся к хорошо известной зависимости точки Кюри от концентрации железа в сплаве AuFe при низких температурах (рис. 1) [11]. Очевидно, что концентрация частиц Fe $p = 0.16$ соответствует концентрационному фазовому переходу для ГЦК-решетки частиц Au $\left( {{{p}_{c}} = {2 \mathord{\left/ {\vphantom {2 z}} \right. \kern-0em} z} = 0.17} \right).$ В то же время в области $0.16 < p < 0.24$ при низких температурах обнаруживаются элементы кластерного стекла, характерные для концентрационного фазового перехода ОЦК-решетки частиц Fe $\left( {{{p}_{c}} = {2 \mathord{\left/ {\vphantom {2 z}} \right. \kern-0em} z} = 0.25} \right).$ Это обстоятельство отражает конкуренцию ОЦК- и ГЦК-решеток при уменьшении концентрации частиц Fe.

Рис. 1.

Экспериментальная магнитная фазовая диаграмма сплава AuFe [11].

Использование полученных соотношений возможно при условии известных из экспериментальных данных температур ${{T}_{1}}$ и $\theta .$ В качестве примера рассмотрим полученную экспериментально зависимость магнитной восприимчивости от температуры для сплава AuFe с различной концентрацией железа [12] (рис. 2).

Рис. 2.

Низкополевая магнитная восприимчивость $\chi \left( T \right)$ сплавов AuFe с концентрацией железа 5 и 8% [12].

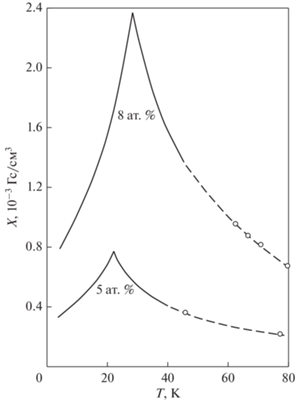
Как следует из рис. 2, при концентрации Fe $p = 0.08$ максимальная восприимчивость соответствует температуре ${{T}_{1}} = 30\,\,{\text{К}}.$ Парамагнитная точка Кюри для железа с концентрацией $0.08$ составляет приблизительно $\theta = 90\,\,{\text{К}}.$ Будем считать, что минимальным временем релаксации $\tau \approx {{10}^{{ - 13}}}\,\,{\text{с}}$ обладают изолированные ионы железа.

В этом случае, как следует из уравнений (16) и (17):

(18)

$\begin{gathered} {{x}_{2}}\left( {{{T}_{2}}} \right) - {{x}_{1}}\left( {{{T}_{1}}} \right) = \\ = \frac{{11{{T}_{1}}}}{{{{{\left( {1 - \frac{{{{T}_{1}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\left( {\frac{{{{{\left( {1 - \frac{{{{T}_{2}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{2}}}} - \frac{{{{{\left( {1 - \frac{{{{T}_{1}}}}{\theta }} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{1}}}}} \right). \\ \end{gathered} $

В качестве примера рассмотрим случай при $T < {{T}_{1}}.$ Пусть $T = {{T}_{2}} = 20\,\,{\text{К}},$ ${{T}_{1}} = 30\,\,{\text{К}},$ $\theta = 90\,\,{\text{К:}}$

(19)

${{x}_{2}}\left( {{{T}_{2}}} \right) - {{x}_{1}}\left( {{{T}_{1}}} \right) = \lg \left[ {{{f}_{0}}{{\tau }_{2}}} \right] - {\text{\;lg}}\left[ {{{f}_{0}}{{\tau }_{1}}} \right] = 7.29.$

Таким образом, в создании магнитного момента не примут участие кластеры, для которых время релаксации определяется соотношением:

(20)

$11 \leqslant \lg \left[ {{{f}_{0}}\tau } \right] \leqslant 18.29.$

Их число составляет:

(21)

$\bar {N} = N\frac{{7.29}}{{18.29}} = 0.4N.{\text{\;}}$

Соответственно магнитная восприимчивость при ${{T}_{2}} = 20\,\,{\text{К}}$ должна составлять 0.6 от максимального значения 2.4, т.е. приблизительно 1.44, что согласуется с данными, представленными на графике.

При $T > {{T}_{1}}{\text{:}}$

(22)

$\frac{{{{\chi }_{2}}\left( T \right)}}{{{{\chi }_{1}}\left( {{{T}_{1}}} \right)}} = \frac{{{{T}_{1}}}}{T}\frac{{{{{\left( {1 - \frac{T}{\theta }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{{{{\left( {1 - \frac{{{{T}_{1}}}}{\theta }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}.{\text{\;}}$

Полагая ${{T}_{1}} = 30\,\,{\text{К}}$ и ${{\chi }_{1}}\left( {{{T}_{1}}} \right) = 2.4,$ можно построить зависимость восприимчивости от температуры $\chi ~\left( T \right)$ при $T > 30~К.$

Соответственно, при $T < 30\,\,{\text{К}}$ отношение $\frac{{{{\chi }_{2}}\left( {{{T}_{2}}} \right)}}{{{{\chi }_{1}}\left( {{{T}_{1}}} \right)}}$ определяется долей кластеров, имеющих $\tau \approx {{10}^{{ - 2}}}$ с.

Таким образом, используя формулы с (16) по (20), можно построить, график зависимости $\chi (T)$ для концентрации железа 8% (рис. 3). Результаты расчета хорошо согласуются с экспериментальными данными, полученными в статье [12].

Рис. 3.

Графики зависимости магнитной восприимчивости $\chi \left( T \right)$ сплава AuFe с концентрацией железа 5 и 8%. Сплошная линия – экспериментальные данные [12], пунктирная линия – результаты расчета.

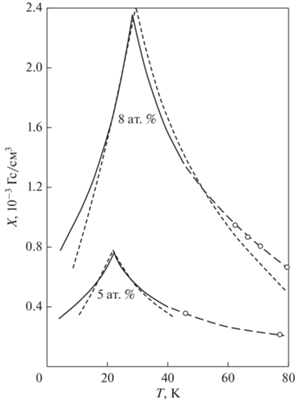
В случае сплава AuFe с концентрацией железа $p = 0.05$ температура, соответствующая максимальной восприимчивости может быть получена из следующих соображений:

(23)

$\alpha {{m}_{0}}\sim \frac{1}{{{{p}_{{\text{c}}}} - p}},\,\,\,\,{\text{при}}\,\,\,\,{{p}_{{\text{c}}}} > p,$

(24)

$\frac{{{{{\left( {\alpha {{m}_{0}}} \right)}}_{1}}}}{{{{{\left( {\alpha {{m}_{0}}} \right)}}_{2}}}} = \frac{{{{p}_{{\text{c}}}} - {{p}_{2}}}}{{{{p}_{{\text{c}}}} - {{p}_{1}}}},$

(25)

$\lg \left[ {{{f}_{0}}\tau } \right] = 11.$

Таким образом, используя формулы (13), (23)–(25), найдем температуру ${{T}_{2}}$ из соотношения:

(26)

$1 = \frac{{{{p}_{{\text{c}}}} - {{p}_{2}}}}{{{{p}_{{\text{c}}}} - {{p}_{1}}}}\frac{{{{{\left( {1 - \frac{{{{T}_{1}}}}{{{{\theta }_{1}}}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{{{T}_{1}}}}\frac{{{{T}_{2}}}}{{{{{\left( {1 - \frac{{{{T}_{2}}}}{{{{\theta }_{2}}}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}},$

где ${{T}_{1}} = 30\,\,{\text{К,}}$ ${{\theta }_{1}} = 90\,\,{\text{К}},$ ${{\theta }_{2}} = 56\,\,{\text{К}},$ ${{p}_{{\text{c}}}} = \frac{2}{{12}},$ ${{p}_{1}} = 0.08,$ ${{p}_{2}} = 0.05.$

Из формулы (26) следует, что ${{T}_{2}} = 21\,\,{\text{К}}.$ Полученный результат согласуется с экспериментальными данными (см. рис. 2).

В соответствии с формулами (8), (23)–(26), для определения магнитной восприимчивости при $p = 0.05$ воспользуемся следующим соотношением:

(27)

${{\chi }_{2}} = {{\chi }_{1}}\frac{{{{{\left( {{{p}_{{\text{c}}}} - {{p}_{1}}} \right)}}^{2}}}}{{{{{\left( {{{p}_{{\text{c}}}} - {{p}_{2}}} \right)}}^{2}}}}{{\left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right)}^{2}}\frac{{{{T}_{1}}}}{{{{T}_{2}}}}\frac{{{{{\left( {1 - \frac{{{{T}_{2}}}}{{{{\theta }_{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{{{{\left( {1 - \frac{{{{T}_{1}}}}{{{{\theta }_{1}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} = 0.72,$

где ${{\chi }_{1}} = 2.4.$

Для концентрации $p = 0.05$ график зависимости $\chi (T)$ представлен на рис. 2 пунктирной линией.

ЗАКЛЮЧЕНИЕ

Таким образом, на основании проведенных расчетов можно утверждать:

1. Поведение магнитной восприимчивости сплава AuFe в интервале концентраций от 5 до 8% удовлетворяет предположению о существенном влиянии прямого обмена на магнитное упорядочение в кластерах. На этом интервале концентраций реализуется упорядочение типа кластерного стекла с размером кластеров $\sim {\kern 1pt} \frac{1}{{{{p}_{{\text{c}}}} - p}};$

2. Как следует из формулы (1), критическая концентрация для ОЦК-решетки, характерной для железа, равна ${{p}_{{\text{c}}}} = 0.25.$ В то же время для ГЦК-решетки золота ${{p}_{{\text{c}}}} = 0.17.$ Постепенное разбавление железа золотом приводит к конкуренции ОЦК- и ГЦК-решеток, что отражается на зависимости точки Кюри от концентрации железа и приводит к появлению кластерного стекла при концентрации ниже 0.25.

Результаты исследований, представленные в статье, получены за счет средств гранта Президента Российской Федерации для государственной поддержки ведущих научных школ Российской Федерации (НШ-2559.2022.1.2).

Список литературы

Keim N.C., Paulsen J.D., Zeravcic Z., Sastry S., Nagel S.R. Memory formation in matter// Rev. Mod. Phys. 2019. V. 91. P. 035002.
Morgan I.L., Avinery R., Rahamim G., Beck R., Saleh O.A. Glassy Dynamics and Memory Effects in an Intrinsically Disordered Protein Construct // Phys. Rev. Lett. 2020. V. 125. P. 058001.
Kumar R., Sharma J., Iyer K., Sampathkumaran E. Reentrant spin-glass and transport behavior of Gd₄PtAl, a compound with three sites for Gd // J. Magn. Magn. Mater. 2019. V. 490. P. 165515.
Binder K. Spin Glasses: Experimental Facts, Theoretical Concepts, and Open Questions // Review of Modern Phys. 1986. V. 58(4). P. 801–976.
Доценко В.С. Физика спин-стекольного состояния // Успехи физ. наук. 1993. Т. 163. № 6. С. 1–37.
Коренблит И.Я., Шендер Е.Ф. Спиновые стекла и неэргодичность // Успехи физических наук. 1989. Т. 157. № 2. С. 267–310.
Белоконь В.И., Дьяченко О.И., Лапенков Р.В. Влияние диффузии на возникновение перколяционного кластера в магнетиках с прямым обменом // ФММ. 2021. Т. 122. С. 1257–1260.
Belokon V., Lapenkov R., Chibiriak E., Dyachenko O. Oguchis Magnetic susceptibility of systems with different types of interactions: The random interaction fields method // J. Magn. Magn. Mater. 2020. V. 512. P. 167 051.
Иудин Д.И. Фракталы: от простого к сложному. Н. Новгород: ННГАСУ. 2012. С. 200.
Белоконь В.И., Дьяченко О.И., Лапенков Р.В., Чибиряк Е.В. Многообразие видов магнитного упорядочения: метод случайных полей обменного взаимодействия // ФММ. 2020. Т. 121. С. 802–806.
Hagiwara M., Nagata K. Magnetism and Magnetic Interaction in a Complex Oxide Glass System Containing Deposited Clusters of Magnetite at the Superparamagnetic State // J. Phys. Soc. Japan. 1998. V. 67. P. 3590–3600.
Cannella V., Mydosh J.A. Magnetic ordering in gold-iron alloys // Phys. Rev. B-Solid State. 1972. V. 6. P. 4220.
Вонсовский С.В. Магнетизм. М.: Наука. 1971. 1032 с.
Петраковский Г.А. Спиновые стекла // Cоросовский образовательный журн. 2001. Т. 7. № 9.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал