1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 124, № 12, 2023

Физика металлов и металловедение, 2023, T. 124, № 12, стр. 1244-1252

Модель для прогнозирования размера аустенитного зерна при горячей деформации низколегированных сталей с учетом эволюции дислокационной структуры

И. И. Горбачев a, *, Е. И. Корзунова a, В. В. Попов a, Д. М. Хабибулин b, Н. В. Урцев b

a Институт физики металлов имени М.Н. Михеева УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия

b Исследовательско-технологический центр “Аусферр”
455000 Магнитогорск, ул. Ломоносова, д. 11/1, Россия

* E-mail: gorbachev@imp.uran.ru

Поступила в редакцию 19.07.2023
После доработки 28.08.2023
Принята к публикации 29.08.2023

Полный текст (PDF)

Аннотация

Предложена модель для описания поведения среднего размера аустенитного зерна и дислокационной структуры низколегированных сталей в процессе и после горячей деформации. В модели учитывается протекание процессов возврата, динамической, первичной и собирательной рекристаллизации зерен, а также индуцированное деформацией выделение карбонитридных фаз и их эволюция. Проведено сравнение результатов расчетов с имеющимися в литературе экспериментальными данными и показано их удовлетворительное согласие.

Ключевые слова: моделирование, деформация, структура, размер зерна, рекристаллизация

ВВЕДЕНИЕ

При промышленном производстве низколегированных сталей наиболее широко используемым методом горячей деформации является контролируемая прокатка. Процесс контролируемой прокатки включает две стадии. На первой – стадии черновой прокатки – деформация происходит в температурной области стабильного аустенита выше температуры рекристаллизации. На второй стадии – чистовой прокатки – деформация происходит в нижней части аустенитной области или в двухфазной (α + γ)-области в отсутствие рекристаллизации.

Основные процессы, которые определяют структуру и свойства сталей, подвергаемых горячей прокатке, – наклеп и рекристаллизация. При этом зерна деформируются, происходит искажение кристаллической решетки, увеличение плотности дислокаций. В ходе рекристаллизации образуются и растут новые, бездефектные зерна. Динамика этих процессов зависит от множества факторов, как то: исходный размер зерна, скорость и температура деформации, степень деформации, наличие сдерживающих факторов роста зерна, например, выделений вторых фаз и др. [1–5].

Моделирование фазовых и структурных превращений на различных стадиях обработки сталей и сплавов традиционно привлекает исследователей. Это обусловлено высокой практической значимостью данной области, в первую очередь, для упрощения оптимизации состава сталей и режимов их термомеханической обработки, а также создания цифровых двойников для технологических процессов [6].

Для создания моделей с максимально широкой областью применимости исследователи стараются учитывать так называемые внутренние переменные. Наиболее общие модели, использующие этот подход, учитывают такие параметры как плотность дислокаций, размер субзерен, угол разориентировки субграниц и т.п. Одна из первых подобных моделей для описания процессов, протекающих при горячей деформации и рекристаллизации, была предложена в работе [7]. Обзор имевшихся в конце 90-х гг. моделей эволюции структуры при горячей деформации выполнен в монографии [8]. На предложенные в работах [7, 8] идеи опираются и многие из более поздних работ, к примеру [2, 3, 9, 10]. Значительная часть модельных приближений и формул, которые можно встретить в указанных работах, используются и в наших недавних работах [11, 12] по моделированию горячей деформации сталей.

В подавляющем большинстве предложенных на сегодняшний день моделей для описания процессов, протекающих при горячей деформации, уделяется весьма слабое влияние строгому описанию эволюции выделений вторых фаз. Обычно используют очень упрощенные модели. В то же время это довольно важный аспект, так как выделения вторых фаз могут оказать сильное влияние на динамику процессов, сдерживая рост зерен при термической обработке. В этом смысле выглядят предпочтительными предложенные в [11, 12] модели, так как опираются на развитые в [13–16] подходы для моделирования эволюции выделений, которые учитывают сразу несколько важных для данной задачи факторов: полидисперсность ансамбля выделений, зарождение новых частиц, конечную объемную долю выделений, взаимовлияние диффузионных потоков разных элементов, возможность эволюции выделений сложного состава.

Однако в наших работах [11, 12] было использовано одно существенное упрощение – предполагалось, что весь моделируемый материал условно делится только на две части: деформированную (с повышенной плотностью дислокаций) и рекристаллизованную часть, с плотностью дислокаций, соответствующей таковой для отожженного материала (далее условно будем называть ее “равновесной”). Очевидно, что данное упрощение плохо соотносится непосредственно с процессом деформации. Кроме того, такая модель имеет ограниченную применимость для многостадийной деформации в случае, когда к следующему проходу рекристаллизационные процессы после предыдущего завершились не полностью. В настоящей работы мы попытались улучшить данную модель и преодолеть указанный недостаток.

МОДЕЛЬ

В разработанной нами модели есть две относительно независимые (но все же влияющие друг на друга) части: ответственная за описание изменения размера аустенитного зерна и дислокационной структуры и модуль для описания поведения ансамбля карбонитридных выделений.

Динамика изменения размеров зерен определяется выражением:

(1)
$\dot {D} = M\left( {{{P}_{d}} - {{P}_{z}}} \right) - \dot {X}D\ln \left( N \right)/3,$
где D – средний диаметр зерна, M – подвижность границы зерна, X – доля рекристаллизованного материала, N – число рекристаллизованных зерен, приходящихся на одно старое. ${{P}_{d}}$ и ${{P}_{z}}$ – движущая сила роста зерен и тормозящая сила со стороны частиц вторых фаз. Здесь и далее точкой сверху обозначена производная по времени.

Нетрудно заметить, что в некоторых случаях, например, при интенсивном выделении частиц вторых фаз, может оказаться, что ${{P}_{d}} < {{P}_{z}}.$ Поэтому, даже в отсутствие первичной рекристаллизации, согласно (1), размер зерна может уменьшаться, что, очевидно, некорректно. Поэтому в таких случаях первое слагаемое в (1) зануляется.

Подвижность границ зерен подчиняется аррениусовской зависимости:

(2)
$M = {{M}_{0}}{\kern 1pt} {\text{exp}}\left( { - \frac{Q}{{{{R}_{g}}T}}} \right),$
где ${{M}_{0}}$ – предэкспоненциальный множитель, Q – энергия активации, ${{R}_{g}}$ и T имеют свое обычное значение.

Выражение для описания динамики изменения среднего размера зерна (1) было взято нами в виде, подобном тому, как оно используется в ряде других работ, к примеру, [3, 7]. Первое слагаемое в (1) взято в виде, аналогичном [21]. Оно соответствует стремлению системы к росту зерна за счет уменьшения зернограничной энергии и энергии, запасенной в дислокациях. Второе слагаемое соответствует измельчению зерна при рекристаллизации.

Движущая сила роста зерен определяется выражением [17, 18]:

(3)
${{P}_{d}} = \alpha \frac{\gamma }{D} + \tau \left( {{{{{{\bar {\rho }}}}}_{{{\text{Def}}}}} - {{{{\rho }}}_{0}}} \right).$
Здесь γ – энергия границы зерна, α – безразмерная геометрическая постоянная, ${{{{\rho }}}_{0}}$ – плотность дислокаций в рекристаллизованном объеме материала, ${{\bar {\rho }}_{{{\text{Def}}}}}$ – средняя плотность дислокаций в его деформированной части, $\tau = G{{b}^{2}}{\text{/}}2$ – энергия дислокации, приходящаяся на единицу ее длины [19]:
(4)
$\tau = G{{b}^{2}}{\text{/}}2,$
где $G$ – модуль сдвига, b – модуль вектора Бюргерса.

Аналогично тому, как это сделано в наших предыдущих работах [20, 21], для cилы, сдерживающей движение границы зерна и действующей со стороны частиц второй фазы, использовано выражение, основанное на подходе, предложенном Зинером [22]. В отличие от типовых выражений зинеровского типа учитывалось распределение частиц по размерам:

(5)
${{P}_{z}} = {{\beta }}\gamma \left[ {\mathop \sum \limits_i \left( {\frac{{{{f}_{i}}}}{{{{r}_{i}}}}} \right)} \right],$
где β – безразмерная константа, ${{f}_{i}}$ и ${{r}_{i}}$ – объемная доля и размер частиц i-го размерного интервала.

В большинстве современных моделей, аналогичных представляемой в настоящей работе, к примеру, в [2, 3], в слагаемом, отвечающем за измельчение зерна при рекристаллизации, отсутствует тройка в знаменателе, в отличие от (1). Мы склонны считать это небольшой ошибкой, берущей начало из работы [7]. Более подробно см. в Приложении.

Для описания дислокационной структуры в настоящей модели вводится функция распределения по плотностям дислокаций H(ρ, t), заданная в виде гистограммы (рис. 1). При построении H(ρ, t) плотность дислокаций для каждого зерна учитывается в виде некоторого среднего значения для этого зерна. Предполагается, что есть некоторое количество зерен, в которых плотность дислокаций соответствует среднему значению плотности дислокаций определенного интервала гистограммы ${{\rho }_{i}},$ т.е. находится в пределах $\left[ {{{\rho }_{i}} - d\rho {\text{/}}2,\,\,{{\rho }_{i}} + d\rho {\text{/}}2} \right],$ (где $d\rho $ – шаг гистограммы). Таких зерен столько, что их объемная доля равна доле данного интервала гистограммы ${{H}_{i}}.$

Рис. 1.

Гистограмма для описания дислокационной структуры сплава и ее изменение на следующем временном шаге.

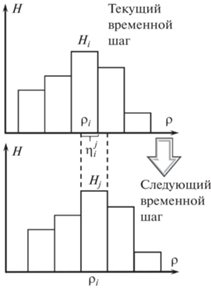
Дислокационная структура (и, соответственно, гистограмма) в процессе моделирования изменяется при протекании деформации и рекристаллизации. При деформации и возврате плотность дислокаций, соответствующая i-му интервалу, изменяется на некоторую величину $\Delta {{\rho }_{i}}$:

(6)
${{\rho }}_{i}^{'} = {{{{\rho }}}_{i}} + \Delta {{{{\rho }}}_{i}}.$
Затем гистограмма пересчитывается к исходной сетке плотностей дислокаций:
(7)
${{H}_{i}} = ~\mathop \sum \limits_j {{H}_{j}}{{\omega }}_{i}^{j},$
где ${{\omega }}_{i}^{j}$ – отношение длины пересечения i-го и j‑го интервалов ${{\eta }}_{i}^{j}$ (рис. 1) к длине исходного отрезка гистограммы. При этом i соответствует номерам интервалов на исходной гистограмме, j – номерам интервалов на новой гистограмме (после их смещения).

В предлагаемом здесь алгоритме обработка гистограммы плотностей дислокаций проходит в два этапа. На первом этапе для каждого i-го интервала гистограммы рассчитывается изменение плотности дислокаций при деформации и возврате. Для этого использовали выражение, аналогичное тому, что приводится в [3]:

(8)
${{{{\dot {\rho }}}}_{i}} = ~\frac{{\dot {\varepsilon }}}{{bl}} - {{k}_{0}}{{\dot {\varepsilon }}^{{1 - q}}}{{{{\rho }}}_{i}} - {{k}_{1}}{{{{\rho }}}_{i}}^{2}.$
Здесь $\dot {\varepsilon }$ – скорость деформации, l – длина свободного пробега дислокации (обычно принимаемая равной размеру ячейки или субзерна), ${{k}_{0}}$ – коэффициент динамического возврата [23], ${{k}_{1}}$ – коэффициент статического возврата, q – параметр материала.

Согласно [7],

(9)
${{k}_{1}} = ~2\tau {{M}_{{LA}}},$
где ${{M}_{{LA}}}$ – подвижность низкоугловых границ, которую можно оценить как [24]
(10)
${{M}_{{LA}}} = \frac{{D_{{{\text{Fe}}}}^{*}b}}{{{{k}_{{\text{B}}}}T}}~.$
Здесь $D_{{{\text{Fe}}}}^{*}$ – коэффициент самодиффузии железа, ${{k}_{{\text{B}}}}$ – постоянная Больцмана.

Для лучшего соответствия экспериментальным данным в [7] предлагается делить k1 на 2.

В большинстве аналогичных исследований учитываются вклады, отвечающие за возврат. Однако возможно, для моделирования реальных технических процессов делать это необязательно, так как аустенит относится, скорее, к материалам с низкой или средней энергией дефекта упаковки, поэтому процессы возврата в нем затруднены [19].

На втором этапе происходит учет процессов рекристаллизации. Теоретически, при горячей деформации может протекать статическая, динамическая и метадинамическая рекристаллизация.

Вплоть до настоящего времени в качестве критерия наступления динамической рекристаллизации принято опираться на выражение, полученное в [1]. В настоящем алгоритме мы тоже использовали этот критерий:

(11)
$~{{\rho }_{{{\text{cr}}}}} = \frac{{8{{\gamma }}}}{{\tau l}}.~~$

Данное выражение получено в предположении, что критический размер зародыша ${{d}_{{{\text{cr}}}}}$ равен длине свободного пробега l, в свою очередь, l – размер ячейки или субзерна может зависеть как от материала, так и от параметров процесса, например, скорости деформации [1, 3].

При протекании динамической рекристаллизации размер субзерна рассчитывали на основе выражения [3]:

(12)
$l = B{{Z}^{r}},$
где B и r – константы, Z – параметр Зинера–Холомона, который определяется как [25]
(13)
$Z = \dot {\varepsilon }{\text{exp}}\left( {\frac{{{{Q}_{Z}}}}{{{{R}_{g}}T}}} \right).$
Здесь ${{Q}_{Z}}$ – энергия активации процесса.

Для статической рекристаллизации размер рекристаллизованного зерна принимали равным критическому размеру (15). В [4] предлагается следующее выражение для оценки размера рекристаллизованного зерна:

(14)
${{D}_{{{\text{DRX}}}}} = l = {\text{С}}D_{0}^{p}{{\varepsilon }^{{{{q}_{1}}}}}{\text{exp}}\left( { - \frac{{{{Q}_{{{\text{DRX}}}}}}}{{{{R}_{g}}T}}} \right),$
где C, p, ${{q}_{1}}$ – подгоночные параметры,$~{{D}_{0}}$ – исходный размер зерна, ${{Q}_{{{\text{DRX}}}}}$ – энергия активации процесса. Однако использование этого выражения с подогнанными в [4] параметрами приводит к худшему согласию с экспериментальными данными, приведенными в [4], по сравнению с использованием (15). Кроме того, в разделе Обсуждение указана еще одна причина несколько усомниться в оптимизированных в [4] параметрах.

В качестве критерия для наступления статической рекристаллизации использован подход, описанный в [26]. Согласно [26], при отжиге растут субзерна (или ячейки), которые и являются зародышами рекристаллизации. В то же время могут идти процессы возврата, снижающие плотность дислокаций, увеличивая таким образом критический размер зародыша (15). Рекристаллизация начинается в том случае, если зародышам удается дорасти до критического размера. Этот размер определяется хорошо известным выражением, соответствующим экстремуму функции свободной энергии системы, которая складывается из зернограничной энергии и энергии, “вкачанной” в виде дислокаций. Для i-го интервала плотностей дислокаций:

(15)
$d_{{{\text{cr}}}}^{i} = \frac{{4{{\gamma }}}}{{\tau {{{{\rho }}}_{i}}}}{\text{\;}}.$

В [26] предлагается учитывать тот факт, что размеры субзерен имеют лог-нормальное распределение или распределение Рэлея. Рекристаллизация может начаться, когда максимальный размер субзерен достигает критического размера. Принимается, что для лог-нормального распределения максимальный размер в три раза больше среднего, а для распределения Рэлея – в 2.5 раза:

(16)
$3l > {{d}_{{{\text{cr}}}}}.$

Движущая сила роста субзерен подобна таковой для зерен (1), поэтому скорость роста субзерен определяется выражением [10]:

(17)
$\dot {l} = {{M}_{{LA}}}3\frac{{{{{{\gamma }}}_{{LA}}}}}{l},$
где ${{{{\gamma }}}_{{LA}}}$ – энергия малоугловых границ зерен, принимаемая равной половине энергии высокоугловых границ, γ.

В объеме материала, соответствующем i-му интервалу плотностей дислокаций, где либо ${{\rho }_{i}} > {{\rho }_{{{\text{cr}}}}},$ либо выполняется условие (16), идет рекристаллизация. Для всех таких интервалов доля ${{H}_{i}}$ уменьшается, а ${{H}_{0}}$ (доля материала с наименьшей плотностью дислокаций) – увеличивается на соответствующую величину. Для статической и метадинамической рекристаллизации:

(18)
$H_{0}^{{t + \Delta t}} = H_{0}^{t} + H_{i}^{t}\left( {1 - {{2}^{{ - \frac{{\Delta t}}{{{{t}_{{0.5}}}}}}}}} \right);$
(19)
$H_{i}^{{t + \Delta t}} = H_{i}^{t}{{2}^{{ - \frac{{\Delta t}}{{{{t}_{{0.5}}}}}}}},$
где ${{t}_{{0.5}}}$ – время, необходимое для рекристаллизации половины объема.

При этом $\dot {X}$, необходимое для расчета $\dot {D}$ (1), оценивали численно:

(20)
$\dot {X} = \frac{{H_{0}^{{t + \Delta t}} - H_{0}^{t}}}{{\Delta t}}.$

Для динамической рекристаллизации в настоящей модели было использовано следующее выражение для расчета $\dot {X}$ [7, 3]:

(21)
$\dot {X} = 6\varphi M\tau {{\bar {\rho }/}}D.$
Здесь ${{\bar {\rho }}}$ – средняя плотность дислокаций в материале, φ – доля подвижных границ зерен, которая рассчитывалась с помощью выражения [3]:

(22)
$\varphi \,\,~ = \,\,~{{\left( {0.1 + X} \right)}^{{0.5}}}\left( {1 - X} \right)\left( {\rho {\text{/}}{{\rho }_{{{\text{cr}}}}}} \right).$

Число рекристаллизованных зерен, приходящихся на одно старое, N, для статической рекристаллизации рассчитывали как

(23)
$N~ = {{\left( {{{D}_{0}}{\text{/}}\overline {{{d}_{{{\text{cr}}}}}} } \right)}^{3}},$
где $\overline {{{d}_{{{\text{cr}}}}}} $ – средний критический размер зародыша, рассчитанный на основе (15) с использованием ${{\bar {\rho }}}{\text{.}}$

Для динамической рекристаллизации:

(24)
$N\,~ = 4\varphi {{\left( {\frac{{{{D}_{0}}}}{{{{D}_{{RX}}}}}} \right)}^{2}}.$

Для расчета фактора сдерживания роста зерна со стороны выделений вторых фаз (5) необходимо иметь информацию о характеристиках ансамбля выделений – их объемные доли и размеры. За них ответственна другая часть алгоритма, которая основана на подходах, предложенных нами ранее [13, 14, 16]. Эта часть модели на основе данных об объемных долях и распределении частиц по размерам в текущий момент времени рассчитывает их на следующем временном шаге. В модели предполагается, что зарождение новых частиц происходит на дислокациях. Таким образом модуль, ответственный за дислокационную и зеренную структуру, через ${{\bar {\rho }}}$ влияет на часть модели, описывающую эволюцию выделений.

ПОРЯДОК РАСЧЕТОВ

При моделировании выполнялась пошаговая процедура, где на каждом временном шаге выполнялись следующие операции:

1. Рассчитывали объемные доли и распределение по размерам карбонитридных выделений [14].

2. Рассчитывали изменение гистограммы плотностей дислокаций. Эту процедуру выполняли в 2 этапа:

а) Сначала для каждого интервала гистограммы рассчитывали изменение плотности дислокаций при деформации и возврате (8).

б) Затем учитывали протекание рекристаллизации (18)–(19).

3. Вычисляли изменение среднего размера зерна (1).

Найденная функция распределения по плотностям дислокаций, размер зерен, объемная доля и распределение частиц по размерам служат исходными данными для расчетов на новом временном шаге и т.д.

Непосредственно в процессе деформации для каждого интервала плотностей дислокаций происходит проверка на достижение критической плотности дислокаций (11). При выполнении этого условия функция плотности дислокаций обрабатывается в соответствии с (18)–(19).

После завершения деформации $\dot {\varepsilon }$ принимается равной нулю. И далее цикл расчетов продолжается во многом аналогично тому, как и во время деформации, с той лишь разницей, что процессы, идущие непосредственно во время деформации, исключаются из рассмотрения. Размер субзерна после завершения деформации оценивается на основе (12), а затем увеличивается согласно (17). При достижении им критического размера (15) начинается статическая рекристаллизация.

ПАРАМЕТРЫ МОДЕЛИ

Термодинамические параметры и коэффициенты диффузии, необходимые для моделирования поведения карбонитридных выделений, приведены в работах [15, 16, 27].

Остальные параметры приведены в табл. 1.

Таблица 1.  

Базовые значения параметров, использованные при моделировании

Переменная Значение Источник
$B$ $26 \times {{10}^{{ - 5}}}$ [3]
$D_{{{\text{Fe}}}}^{{\text{*}}}$ $4.08 \times {{10}^{{ - 4}}}{\text{exp}}\left( { - \frac{{311{\kern 1pt} 100}}{{RT}}} \right){\text{\;}}\frac{{{{{\text{м}}}^{2}}}}{{\text{с}}}$ [28]
$G$ $81\left[ {1 - \frac{{0.91\left( {T - 300} \right)}}{{1800}}} \right]{\text{\;ГПа}}$ [29]
${{k}_{0}}$ $1971{\kern 1pt} {\text{exp}}\left( { - \frac{{60{\kern 1pt} 300}}{{RT}}} \right)$ [30]
${{M}_{0}}$ 120 м4/(Дж с) [31]
q 0.1 [30]
Q 350 кДж/моль [32]
${{Q}_{Z}}$ 320 кДж/моль [30]
$r$ –0.1 [3]
${{t}_{{0.5}}}$ $0.14{{\varepsilon }^{{0.81}}}{{\dot {\varepsilon }}^{{ - 0.87}}}{\text{exp}}\left( {\frac{{23{\kern 1pt} 000}}{{{{R}_{g}}T}}} \right)$ для метадинамической рекристаллизации [3]
$1.11 \times {{10}^{{ - 11}}}{{\varepsilon }^{{ - 2.65}}}{{\dot {\varepsilon }}^{{ - 0.33}}}{\text{exp}}\left( {\frac{{218{\kern 1pt} 000}}{{{{R}_{g}}T}}} \right)$ для статической рекристаллизации
α 4 [33]
$\beta $ 12 [34]
γ 0.5 Дж/м2 [19]
${{\rho }_{0}}$ $1.68 \times {{10}^{9}}{\text{\;exp}}\left( {\frac{{5020}}{{RT}}} \right){\text{\;}}{{{\text{м}}}^{{ - 2}}}$ [35]

ТЕСТИРОВАНИЕ МОДЕЛИ

Для оценки правильности работы предложенной модели было выполнено сравнение результатов расчетов с данными экспериментальных исследований. За основу для сравнения были взяты экспериментальные данные, полученные в [4]. Исследования были выполнены на малоуглеродистой низколегированной стали с ниобием, химический состав которой приведен в табл. 2.

Таблица 2.  

Химический состав стали, исследованной в работе [4], мас. %

C Mn Si Nb S N Mo Al
0.05 1.88 0.04 0.048 0.007 0.004 0.49 0.05

Начальный размер зерна задавали исходя из предварительной термической обработки, подробно описанной в [4]. Экспериментальные зависимости, построенные по данным, приведенным в [4], и результаты моделирования приведены на рис. 2, 3.

Рис. 2.

Изменение среднего размера аустенитного зерна в процессе деформации (по экспериментальным данным, приведенным в [4]).

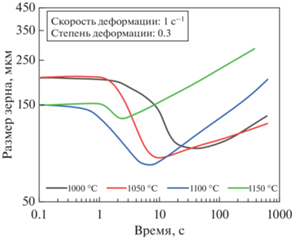
Рис. 3.

Моделирование изменения среднего размера аустенитного зерна для условий, соответствующих данным [4].

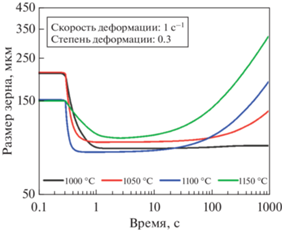
Сравнение графиков на рис. 2, 3 показывает разумное согласие результатов моделирования с экспериментом, хотя и далеко не идеальное. Видно, что в соответствии с моделью уменьшение среднего размера зерна из-за рекристаллизации происходит заметно раньше, чем в реальности. Кроме того, из экспериментальных данных следует, что рост зерна начинается практически сразу после завершения измельчения зерна, в то время как на расчетных зависимостях есть выраженный период, когда размер зерна меняется слабо. Наилучшее соответствие модели и эксперимента наблюдается для стадии нормального роста зерна.

ОБСУЖДЕНИЕ

В аналогичных работах по деформации сталей и сплавов часто практикуется подход, когда на основе серии экспериментальных результатов оптимизируется некий набор параметров модели. Обычно оказывается, что итоговая модель неплохо описывает эксперимент. Но, проведение эксперимента – достаточно трудоемкая задача, поэтому экспериментальных данных, как правило, не так уж много. Поэтому в таких исследованиях не встречается подход, который является совершенно обычным, например, для задач машинного обучения, когда весь набор данных разделяется на тренировочную и тестовую выборки, чтобы максимально объективно оценить качество обучаемой модели. К тому же оптимизация набора разнородных по природе физических параметров на относительно небольшом объеме данных может приводить к различным казусам. К примеру, в работе [4] оптимизация параметра ${{M}_{0}}$ для подвижности границы зерна привела к получению значения 1.9 × 109, что на много порядков превышает значение 120, полученное в [31] (при том, что значения энергии активации близки).

К сожалению, обозначенная проблема не имеет очевидного и простого решения. Кроме того, такое положение вещей проистекает не только и не столько из-за того, что экспериментальных данных не так много. Но и из-за недостаточно глубокой теоретической проработки некоторых важных для данной области аспектов. Так, можно услышать точку зрения, что статическая рекристаллизация может протекать только при нагреве после деформации, проведенной при более низкой температуре. А если при данной температуре и условиях деформации динамическая рекристаллизация не началась, то и статическая не пойдет. На практике при горячей деформации сталей измельчение зерна наблюдается уже при (или сразу после) деформации, как видно, к примеру, в результатах [4, 5]. Вероятно, поэтому некоторые исследователи прямо называют это именно динамической рекристаллизацией [36–38]. В то же время использование критерия (11) совместно с оптимизированными параметрами для длины свободного пробега (12) показывает, что для типовых условий горячей прокатки низколегированных сталей не достигается плотность дислокаций, необходимая для наступления динамической рекристаллизации. Таким образом, измельчение зерна, наблюдаемое согласно представленным выше расчетам, – результат протекания статической рекристаллизации. То, что статическая рекристаллизация действительно может протекать после деформации, если не было динамической, отмечается, например, в [5, 39, 40]. Отметим, что, по-видимому, к настоящему времени у исследователей не сложился вполне ясный консенсус в этой области. Так, в работе [40] в качестве критерия наступления динамической рекристаллизации приводится достижение не критической плотности дислокаций ${{\rho }_{{{\text{cr}}}}},$ а некой критической деформации, а для статической – наоборот, достижение ${{\rho }_{{{\text{cr}}}}}.$

Отметим, что в настоящей работе не использована подгонка параметров конкретно для данной модели, однако расчеты на ее основе дают вполне разумное согласие с экспериментом. Полагаем, что этого удалось достичь за счет того, что была сделана ставка на максимально возможное использование моделей и выражений, которые имеют хорошее физическое обоснование, а полуэмпирические выражения применяли только в тех случаях, когда этого было невозможно избежать.

ЗАКЛЮЧЕНИЕ

Представлен метод для прогнозирования размера зерна низколегированных сталей, подвергаемых горячей деформации. Метод основан на использовании моделей для описания динамики изменения среднего размера зерна и функции распределения по плотностям дислокаций в материале при деформации, совместно с предложенной нами ранее моделью для описания эволюции карбонитридных выделений.

Для тестирования предложенной модели проведено сравнение с имеющимися в литературе экспериментальными данными по эволюции размера зерна при деформации и последующей выдержке в температурном диапазоне стабильного аустенита. Сравнение результатов моделирования с экспериментальными данными показало их удовлетворительное согласие.

Исследования проведены за счет гранта Российского научного фонда (проект № 22-29-01106 https://rscf.ru/project/22-29-01106/, ИФМ УрО РАН).

Нет конфликта интересов.

Список литературы

  1. Roberts W., Ahlblom B. A nucleation criterion for dynamic recrystallization during hot working // Acta Metal. 1978. V. 26. № 5. P. 801–813. https://doi.org/10.1016/0001-6160(78)90030-5

  2. Madej L., Sitko M., Pietrzyk M. Perceptive comparison of mean and full field dynamic recrystallization models // Archives of Civil and Mechanical Engineering. 2016. V. 16. № 4. P. 801–813. https://doi.org/10.1016/j.acme.2016.03.010

  3. Roucoules C., Pietrzyk M., Hodgson P.D. Analysis of work hardening and recrystallization during the hot working of steel using a statistically based internal variable model // Mater. Sci. Eng.: A. 2003. V. 339. № 1–2. P. 1–9. https://doi.org/10.1016/S0921-5093(02)00120-X

  4. Sarkar S., Moreau A., Militzer M., Poole W.J. Evolution of austenite recrystallization and grain growth using laser ultrasonics // Metall and Mat Trans. A. 2008. V. 39. P. 897–907. https://doi.org/10.1007/s11661-007-9461-6

  5. Liang Sh., Levesque D., Legrand N., Zurob H.S. Use of in-situ laser-ultrasonics measurements to develop robust models combining deformation, recovery, recrystallization and grain growth // Materialia. 2020. V. 12. 100812. https://doi.org/10.1016/j.mtla.2020.100812

  6. Рудской А.И., Колбасников Н.Г. Цифровые двойники технологий термомеханической обработки стали // Металловедение и термич. обр. металлов. 2020. № 1. С. 4–11. https://doi.org/10.1007/s11041-020-00505-4

  7. Sandström R., Lagneborg R. A model for hot working occurring by recrystallization // Acta Metall. 1975. V. 23. P. 387–398. https://doi.org/10.1016/0001-6160(75)90132-7

  8. Lenart J.G., Pietyrzyk M. Cserrr L. Mathematical and physical simulation of the properties of hot rolled products. Amsterdam-Lausanne-New York-Oxford-Shannon-Singapore-Tokyo: Elsevie, 1999. 264 p. https://doi.org/10.1016/B978-0-08-042701-0.X5000-1

  9. Timoshenkov A., Warczok P., Albu M., Klarner J., Kozeschnik E., Bureau R., Sommitsch C. Modelling the dynamic recrystallization in C–Mn micro-alloyed steel during thermo-mechanical treatment using cellular automata // Comput. Mater. Sci. 2014. V. 24. P. 85–94. https://doi.org/10.1016/j.commatsci.2014.02.017

  10. Buken H., Kozeschnik E. A model for static recrystallization with simultaneous precipitation and solute drag // Metall. Mater. Trans. A. 2017. V. 48. P. 2812–2818. https://doi.org/10.1007/s11661-016-3524-5

  11. Горбачев И.И., Пасынков А.Ю., Попов В.В. Моделирование влияния горячей деформации на размер аустенитного зерна низколегированных сталей с карбонитридным упрочнением // ФММ. 2018. Т. 119. № 6. С. 582–589. https://doi.org/10.1134/S0031918X18060078

  12. Горбачев И.И., Пасынков А.Ю., Попов В.В. Моделирование эволюции карбонитридных частиц сложного состава при горячей деформации низколегированной стали // ФММ. 2018. Т. 119. № 8. С. 817–826. https://doi.org/10.1134/S0031918X18080021

  13. Popov V.V. Simulation of dissolution and coarsening of MnS precipitates in Fe-Si // Philosophical Magazine A. 2002. V. 82. № 1. P. 17–27. https://doi.org/10.1080/01418610208239993

  14. Popov V.V., Gorbachev I.I., Alyabieva J.A. Simulation of precipitates evolution in multiphase multicomponent systems with consideration of nucleation // Philosoph. Magazine. 2005. V. 85. № 22. P. 2449–2467. https://doi.org/10.1080/14786430500070750

  15. Popov V.V., Gorbachev I.I., Pasynkov A.Yu. Simulation of precipitates evolution in multiphase multicomponent systems with consideration of nucleation // Philosoph. Magazine. 2016. V. 96. № 35. P. 3632–3653. https://doi.org/10.1080/14786435.2016.1232867

  16. Горбачев И.И., Попов В.В., Пасынков А.Ю. Моделирование эволюции выделений двух карбонитридных фаз в сталях с Nb и Ti при изотермическом отжиге // ФММ. 2013. Т. 114. № 9. С. 807–817.

  17. Ding R., Guo Z.X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization // Acta Mater. 2001. V. 49. № 10. P. 3163–3175. https://doi.org/10.1016/S1359-6454(01)00233-6

  18. Hellman P., Hillert M. On the effect of second-phase particles on grain growth // Scand. J. Metall. 1975. V. 4. P. 211–219.

  19. Humphreys F.J., Hatherly M. Recrystallization and related annealing phenomena / 2nd ed. Oxford, Elsevier, 2004. 574 p. https://doi.org/10.1016/B978-0-08-044164-1.X5000-2

  20. Горбачёв И.И., Пасынков А.Ю., Попов В.В. Прогнозирование размера аустенитного зерна микролегированных сталей на основе моделирования эволюции карбонитридных выделений // ФММ. 2015. Т. 116. № 11. С. 1184–1191. https://doi.org/10.1134/S0031918X1511006X

  21. Горбачев И.И., Корзунова Е.И., Попов В.В., Хабибулин Д.М., Урцев Н.В. Моделирование роста аустенитного зерна в низколегированных сталях при аустенитизации // ФММ. 2023. Т. 124. № 3. С. 303–309. https://doi.org/10.1134/S0031918X23600100

  22. Zener C. цитиpyeтcя пo Gladman T. On the theory of the effect of precipitate particles on grain growth in metals // Proc. R. Soc. Lond. A. 1966. V. 294. P. 298–309. https://doi.org/10.1098/rspa.1966.0208

  23. Estrin Y., Mecking H. A unified phenomenological description of work hardening and creep based on one-parameter models // Acta metall. 1984. V. 32. № 1. P. 57–70. https://doi.org/10.1016/0001-6160(84)90202-5

  24. Sandström R. Subgrain growth occurring by boundary migration // Acta Metallurgica. 1977. V. 25. № 8. P. 905–911. https://doi.org/10.1016/0001-6160(77)90177-8

  25. Zener C., Hollomon J. H. Effect of strain rate upon plastic flow of steel // Journal of Applied Physics. 1944. V. 15. № 12. P. 22–32. https://doi.org/10.1063/1.1707363

  26. Zurob H.S., Bréchet Y., Dunlop J. Quantitative criterion for recrystallization nucleation in single-phase alloys: Prediction of critical strains and incubation times // Acta Mater. 2006. V. 54. № 15. P. 3983–3990. https://doi.org/10.1016/j.actamat.2006.04.028

  27. Горбачев И.И., Попов В.В., Пасынков А.Ю. Термодинамическое моделирование карбонитридообразования в сталях с Nb и Ti // ФММ. 2012. Т. 113. № 7. С. 727–735. https://doi.org/10.1134/S0031918X1207006X

  28. Diffusion in Solid Metals and Alloys // In Defect and Diffusion Forum. 1970. V. 4. P. 296–340. https://doi.org/10.4028/www.scientific.net/ddf.4.296

  29. Liu W.J., Jonas J. Characterisation of critical nucleus/matrix interface: Application to Cu–Co alloys and microalloyed austenite // Mater. Sci. Technol. 1989. V. 5. P. 8–12. https://doi.org/10.1179/mst.1989.5.1.8

  30. Pietrzyk M. Through-process modelling of microstructure evolution in hot forming of steels // J. Mater. Proces. Techn. 2002. V. 125–126. P. 53–62. https://doi.org/10.1016/S0924-0136(02)00285-6

  31. Banerjee K., Militzer M., Perez M., Wang X. Nonisothermal austenite grain growth kinetics in a microalloyed X80 linepipe steel // Metal. Mater. Trans. A. 2010. V. 41A. № 12. P. 3161–3172. https://doi.org/10.1007/s11661-010-0376-2

  32. Uhm S., Moon J., Lee Ch., Yoon J., Lee B. Prediction model for the austenite grain size in the coarse grained heat affected zone of Fe–C–Mn steels: Considering the effect of initial grain size on isothermal growth behavior // ISIJ International. 2004. V. 44. № 7. P. 1230–1237. https://doi.org/10.2355/isijinternational.44.1230

  33. Hillert M. On the theory of normal and abnormal grain growth // Acta Met. 1965. V. 13. P. 227–238. https://doi.org/10.1016/0001-6160(65)90200-2

  34. Rios P.R. Overview no. 62: A theory for grain boundary pinning by particles // Acta Metallurgica. 1987. V. 35. № 12. P. 2805–2814. https://doi.org/10.1016/0001-6160(87)90280-X

  35. Liu W.J., Jonas J. Nucleation kinetics of Ti carbonitride in microalloyed austenite // Metall. Trans. 1989. V. A 20. P. 689–697. https://doi.org/10.1007/BF02667586

  36. Serajzadeh S. A mathematical model for evolution of flow stress during hot deformation // Mater. Letters. 2005. V. 59. P. 3319–3324. https://doi.org/10.1016/j.matlet.2005.05.065

  37. Serajzadeh S. Modelling dynamic softening processes during hot working // Mater. Sci. Eng. 2005. A. 404. P. 130–137. https://doi.org/10.1016/j.msea.2005.05.040

  38. Bäcke L. Modeling the Microstructural Evolution during Hot Deformation of Microalloyed Steels // Doctoral thesis. 2009. https://www.diva-portal.org/ smash/get/diva2:216454/FULLTEXT01.pdf.

  39. Штремель М.А. Прочность сплавов. Часть II. Деформация. М.: МИСиС, 1997. 527 с.

  40. Горелик С.С., Добаткин С.В., Капуткина Л.М. Рекристаллизация металлов и сплавов. 3-е изд. М.: МИСиС, 2005. 432 с.

Дополнительные материалы

скачать ESM.docx
Приложение 1.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал