Физика плазмы, 2020, T. 46, № 1, стр. 46-56
Столкновения электростатических N-солитонов, движущихся в одном направлении и обгоняющих друг друга, в электронно-дырочной квантовой плазме
E. F. EL-Shamy a, *, M. Mahmoud b
a Department of Physics, College of Science, King Khalid University, P.O. 9004, Abha,
Kingdom of Saudi Arabia and Department of physics, Faculty of Science, Damietta University
34517 New, Damietta, Egypt
b Department of Physics, College of Science for Girls in Abha, King Khalid University
P.O. 960 Abha, Kingdom of Saudi Arabia
* E-mail: emadel_shamy@hotmail.com
Поступила в редакцию 11.01.2019
После доработки 25.04.2019
Принята к публикации 20.05.2019
Аннотация
Эффекты, сопровождающие столкновения электростатических мультисолитонов (N-солитонов), движущихся в одном направлении и догоняющих друг друга в электронно-дырочной плотной полупроводниковой плазме, исследовались с использованием редуцированной теории возмущений (РТВ) и билинейного метода Хироты (БМХ). Уравнение Кортевега-де Фриза, допускающее решение в виде N-солитонов, выводилось с использованием РТВ. Кроме этого, применялся метод БМХ, в результате чего были получены двухсолитонные и трехсолитонные решения. Анализировалось, как при столкновении догоняющих друг друга электростатических N-солитонов меняется обмен энергией между ними при изменении таких физических параметров, как плотность квантовой полупроводниковой плазмы и обменно-корреляционные члены в уравнении для электронов и дырок, которые оказывают влияние на поведение солитонов. Показано, что наличие обменно-корреляционных потенциалов приводит к уменьшению фазового сдвига N-солитона, приобретаемого в результате столкновения. Обсуждаются основные свойства N-солитонов, распространяющихся в электронно-дырочной плазме, и их возможные применения в современных наноразмерных полупроводниковых электронных устройствах.
1. ВВЕДЕНИЕ
Уникальными особенностями квантовой плазмы, отличающими ее от классической плазмы, являются очень высокая плотность частиц плазмы и ее относительно низкая температура. При исследовании квантовой полупроводниковой плазмы квантово-механическая физика используется для изучения реальных процессов, происходящих в полупроводниковых электронных устройствах. В современных наноразмерных полупроводниковых электронных устройствах тепловая длина волны де Бройля носителей заряда (электронов и дырок) сопоставима с характерными пространственными масштабами прибора. Поэтому исследование квантово-механических эффектов в квантовых полупроводниковых устройствах (например, в квантовых точках [1]) будет полезно с точки зрения изучения динамики носителей заряда. Кроме того, стремительное развитие лазерных технологий привело к созданию мощных лазеров с фемтосекундной длительностью импульсов [2, 3]. Соответственно, появилось множество новых областей исследования, таких как, например, взаимодействие мощного лазерного излучения с квантовой плазмой [4, 5]. Модель плотной полупроводниковой плазмы учитывает потенциальный барьер Бома, обменные взаимодействия и корреляции, а также давление вырожденных частиц плазмы. Таким образом, большинство упомянутых физических параметров оказывает существенное влияние на коллективное квантовое поведение электронов и дырок в полупроводниковых электронных устройствах [6–9].
В последнее время, возбуждение и неустойчивость локализованных в пространстве когерентных волн (т.е. солитонов) в квантовой полупроводниковой плазме исследовалось в ряде работ [10–17]. Например, в работе [12] были рассмотрены основные свойства уединенных волн в различных плотных полупроводниках. Было продемонстрировано, что вырожденное давление наиболее чувствительно к уменьшению амплитуды уединенных волн по сравнению с изменением других квантовых параметров. Модуляционная неустойчивость уединенных волн в плотной полупроводниковой плазме обсуждалась в более ранней работе [13]. Там было показано, что скорость затухания волны зависит от квантовых эффектов и частоты столкновений типа электрон–фонон/дырка–фонон. Позднее, в работе [16], были проведены численные расчеты с использованием типичных значений параметров нитрид-галлиевой полупроводниковой плазмы GaN, показавшие, что солитоны и периодические бегущие волны, распространяющиеся в квантовой полупроводниковой плазме, обладают отрицательными потенциалами. На самом деле, не только возбуждение и неустойчивости уединенных волн, но и встречные столкновения солитонов друг с другом рассматриваются в литературе как явления, реально происходящие в плазме. В работе [15] было численно и аналитически показано, что солитонные кольца в квантовой полупроводниковой плазме могут существовать только в виде темных солитонных плазменных колец. В работе [17] отмечалось, что амплитуда и ширина нелинейных импульсов меняются при изменении параметров потоков электронов и дырок. В недавней работе [18] было показано, что расход энергии при встречном столкновении солитонов в случае неплоской геометрии выше, чем в случае плоской.
Кроме того, многократно обсуждались столкновения N-солитонов, распространяющихся в разнообразных плазменных системах [19–25]. В одномерной системе N-солитоны могут взаимодействовать друг с другом двумя различными способами: они могут догонять друг друга или же двигаться навстречу друг другу. Столкновение движущихся в одном направлении и догоняющих друг друга солитонов (столкновение с “обгоном”) может быть исследовано, например, методом обратного преобразования рассеяния [26]. С одной стороны, встречное столкновение солитонов [27, 28], при котором угол между направлениями распространения двух солитонов равен π, может быть исследовано с помощью расширенного метода Пуанкаре–Лайтхилла–Го (РМПЛГ) [29, 30]. С другой стороны, метод РМПЛГ можно рассматривать как метод редуцированной теории возмущений (РТВ) [31]. Соответственно, метод -РМПЛГ может быть использован для исследования встречных столкновений солитонов малой конечной амплитуды. Это является комбинацией стандартной теории возмущений и метода растянутых координат Лайтхилла. Основная идея метода РМПЛГ состоит в следующем. В длинноволновом приближении применяются асимптотические разложения, как для зависимых физических величин, так и для пространственных или временных координат. В результате получается однородно адекватное асимптотическое разложение (исключающее вековые члены) и одновременно аналитические выражения для измененных траекторий N-солитонов (их фазовых сдвигов) после их взаимодействия [27]. Далее, в работах [32–34] был представлен новый метод прямого построения N-солитонных решений интегрируемых нелинейных эволюционных уравнений, таких как уравнение Кортевега-де Фриза (УКдФ). В основе метода лежит идея перехода к новой системе переменных, такой, что N-солинонные решения получаются в особенно простой форме. Поэтому, используя билинейный метод Хироты, можно аналитически получать N-солитонные решения, а затем и фазовые сдвиги, возникающие при обгоне одного N-солитона другим. Действительно, главное преимущество метода Хироты над другими методами состоит в том, что это метод алгебраический, а не аналитический. В работе [22], например, изучались столкновения акустических N-солитонов, движущихся в одном направлении в пылевой плазме, и приобретаемые при этом фазовые сдвиги. Была рассмотрена задача, в которой солитон меньшего размера, имея меньшую скорость, приближается к солитону большего размера. Происходит столкновение, при котором один солитон обгоняет другой, и после этого оба солитона сохраняют свои первоначальные формы и скорости. Фазовый сдвиг, возникающий при столкновении с “обгоном” был получен в работе [23]. С использованием билинейного метода Хироты (БМХ) [35], были получены N-солитонные решения, в которых солитоны движутся в одном направлении, и, в конечном итоге, наиболее быстро движущийся солитон обгоняет другие.
С другой стороны, для исследования распространения и встречных столкновений солитонов произвольной амплитуды обычно применяется метод квазипотенциала (потенциала Сагдеева), а также проводится соответствующее численное моделирование [36–41]. Например, численный метод PIC (particle-in-cell) моделирования используется в физике плазмы для исследования встречных столкновений солитонов [41]. Кроме того, комплект программного обеспечения F-ORTRAN был использован и протестирован на примере численного моделирования распространения стационарных солитонов и ударных волн. Тестирование показало, что соответствующие стационарные решения сохраняются и в случае решения нестационарных задач [39, 40]. В работе [41] с использованием одномерного электростатического PIC кода исследовались возможные применения РТВ. Используя условие применимости РТВ ($\varepsilon \ll 1$), была определена критическая величина ε* для параметра малости. Было показано, что при ε < ε*, аналитический результат, полученный в рамках редуцированной теории возмущений, хорошо согласуется с численным результатом PIC моделирования, тогда как при больших значениях ε > ε* появляются большие различия.
В некоторых более ранних работах [10–18] были численно и аналитически исследованы распространение, устойчивость и встречные столкновения солитонов в плотной полупроводниковой плазме. Однако, исследований столкновений с “обгоном” темных N-солитонов в плотной полупроводниковой плазме до сих пор не проводилось. Поэтому целью настоящей работы является исследование влияния плотности квантовой полупроводниковой плазмы и обменно-корреляционных потенциалов электронов и дырок на столкновения с “обгоном” N-солитонов, распространяющихся в плотной полупроводниковой плазме. Статья построена следующим образом. В разд. 2 рассмотрены модельные уравнения и выведено уравнение УКдФ. В разд. 3 для получения N-солитонных решений использован метод БМХ, а в разд. 4 приведены численные иллюстрации и проведено обсуждение результатов. В разд. 5 суммированы основные результаты и выводы.
2. МОДЕЛЬНЫЕ УРАВНЕНИЯ
Уравнения, описывающие в рамках квантово-гидродинамической (КГД) модели квантовую полупроводниковую плазму, состоящую из электронов и дырок, получены в [12–18] и выглядят следующим образом:
(1)
$\frac{{\partial {{n}_{{e,h}}}}}{{\partial t}} + \frac{{\partial \left( {{{n}_{{e,h}}}{{u}_{{e,h}}}} \right)}}{{\partial x}} = 0,$(2)
$\begin{gathered} \frac{{\partial {{u}_{{e,h}}}}}{{\partial t}} + {{u}_{{e,h}}}\frac{{\partial {{u}_{{e,h}}}}}{{\partial x}} = - {{\mu }_{{e,h}}}\frac{{\partial \phi }}{{\partial x}} + {{\gamma }_{{e,h}}}\frac{{\partial {{V}_{{xce,h}}}}}{{\partial x}} - \\ \, - {{\sigma }_{{e,h}}}n_{{e,h}}^{{ - 1/3}}\frac{{\partial {{n}_{{e,h}}}}}{{\partial x}} + 2H_{{e,h}}^{2}\frac{\partial }{{\partial x}}\left( {\frac{{{{\partial }^{2}}n_{{e,h}}^{{1/2}}{\text{/}}\partial {{x}^{2}}}}{{n_{{e,h}}^{{1/2}}}}} \right), \\ \end{gathered} $Здесь ne (nh) и ue (uh) – плотность и скорость электронов (дырок), ϕ – электростатический потенциал. В правой части уравнения для импульса (2) второй, третий и четвертый члены описывают соответственно обменно-корреляционный потенциал ${{V}_{{xce,h}}}$, вырожденное давление и потенциал Бома. В состоянии равновесия ${{n}_{{e0}}} = {{n}_{{h0}}} = {{n}_{0}}$, где ne0 (nh0) – невозмущенная плотность электронов (дырок) и n0 – суммарная плотность. В расчетах использованы следующие физические параметры для электронов (дырок):
${{\mu }_{e}} = - 1$ (${{\mu }_{h}} = \mu = m_{e}^{*}{\text{/}}m_{h}^{*}$), ${{\gamma }_{e}} = {{({{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}})}^{{ - 1}}}$ $({{\gamma }_{h}} = \mu {\text{/}}{{k}_{{\text{B}}}}{{T}_{{{\text{F}}h}}})$, ${{\sigma }_{e}} = {{(\pi {\text{/}}3)}^{{1/3}}}(\pi {{\hbar }^{2}}{\text{/}}m_{e}^{*})(n_{{e0}}^{{2/3}}{\text{/}}{{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}})$ $({{\sigma }_{h}} = {{(\pi {\text{/}}3)}^{{1/3}}}(\pi {{\hbar }^{2}}{\text{/}}m_{h}^{*})(n_{{h0}}^{{2/3}}{\text{/}}{{k}_{{\text{B}}}}{{T}_{{{\text{F}}h}}}))$, ${{H}_{e}} = \left( {\hbar {{\omega }_{{pe}}}{\text{/}}2{{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}}} \right)$ $({{H}_{h}} = (\hbar {{\omega }_{{pe}}}{\text{/}}2{{k}_{{\text{B}}}}{{T}_{{{\text{F}}h}}})\mu )$ и ${{V}_{{xce,h}}} = - 0.985({{e}^{2}}{\text{/т}})n_{{e,h}}^{{1/3}} \times $$ \times \;[1 + (0.034{\text{/}}a_{{{\text{B}}e,h}}^{*}n_{{e,h}}^{{1/3}}){\text{ln(}}1 + 18.376a_{{{\text{B}}e,h}}^{*}n_{{e,h}}^{{1/3}}{\text{)}}]$,
где $~a_{{{\text{B}}e}}^{*} = ({\text{т}}{{\hbar }^{2}}{\text{/}}m_{e}^{*}{{e}^{2}})$ $~(a_{{{\text{B}}h}}^{*} = ({\text{т}}{{\hbar }^{2}}{\text{/}}m_{h}^{*}{{e}^{2}}))$, а параметры ${{n}_{{e,h}}}$, $~{{u}_{{e,h}}}$, ϕ, x, и t нормированы, соответственно, на $~{{n}_{{e0,h0}}}$, скорость Ферми для электронов ${{V}_{{{\text{F}}e}}} = $ $ = {{({{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}}{\text{/}}m_{e}^{*})}^{{1/2}}}$, ${{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}}{\text{/}}e$, дебаевский радиус для Ферми электронов ${{\lambda }_{{{\text{DF}}e}}} = {{({{k}_{{\text{B}}}}{{T}_{{{\text{F}}e}}}{\text{/}}4\pi {{e}^{2}}{{n}_{{e0}}})}^{{1/2}}}$, и плазменную частоту электронов ${\omega }_{{{\text{pe}}}}^{{ - 1}} = {{(m_{e}^{*}{\text{/}}4\pi {{e}^{2}}{{n}_{{e0}}})}^{{1/2}}}$; ${{T}_{{{\text{Fe}}}}}$ и $m_{e}^{*}$ (${{T}_{{{\text{F}}h}}}$ и $m_{h}^{*}$) – температура Ферми и эффективная масса электрона (дырки), ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $\hbar $ – постоянная Планка, т – диэлектрическая проницаемость материала, и e – заряд электрона.
Теперь вернемся к столкновениям N-солитонов с “обгоном”. Используем хорошо известную теорию РТВ [31] для получения уравнения УКдФ. В рамках предлагаемой модели в приближении малых, но конечных амплитуд, физические величины могут быть разложены в ряд следующим образом:
(4)
$Y = {{Y}^{{\left( 0 \right)}}} + \mathop \sum \limits_{n = 1}^\infty {{\varepsilon }^{{\left( {n + 1} \right)}}}{{Y}^{{\left( n \right)}}},$(5)
$\xi = {{\varepsilon }^{{1/2}}}\left( {x - \lambda t} \right)~\quad {\text{и}}\quad \tau = {{\varepsilon }^{{3/2}}}t,$(6а)
$n_{e}^{{(1)}}(\xi ,\tau ) = \frac{{ - {{\phi }^{{\left( 1 \right)}}}\left( {\xi ,\tau } \right)}}{{\left( {{{\lambda }^{2}} - {{\alpha }_{e}} - {{\beta }_{e}} - {{\sigma }_{e}}} \right)}},$(6б)
$n_{h}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{\mu {{\phi }^{{\left( 1 \right)}}}\left( {\xi ,\tau } \right)}}{{\left( {{{\lambda }^{2}} - {{\alpha }_{h}} - {{\beta }_{h}} - {{\sigma }_{h}}} \right)}},$(6в)
$u_{e}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{ - \lambda {{\phi }^{{\left( 1 \right)}}}\left( {\xi ,\tau } \right)}}{{\left( {{{\lambda }^{2}} - {{\alpha }_{e}} - {{\beta }_{e}} - {{\sigma }_{e}}} \right)}},$(6г)
$u_{h}^{{\left( 1 \right)}}\left( {\xi ,\tau } \right) = \frac{{\mu \lambda {{\phi }^{{\left( 1 \right)}}}\left( {\xi ,\tau } \right)}}{{\left( {{{\lambda }^{2}} - {{\alpha }_{h}} - {{\beta }_{h}} - {{\sigma }_{h}}} \right)}},$Рассматривая следующие более высокие порядки по ε, мы в итоге приходим к уравнению УКдФ
(7)
$\frac{{\partial {{\phi }^{{\left( 1 \right)}}}}}{{\partial \tau }} - A{{\phi }^{{\left( 1 \right)}}}\frac{{\partial {{\phi }^{{\left( 1 \right)}}}}}{{\partial \xi }} - B\frac{{{{\partial }^{3}}{{\phi }^{{\left( 1 \right)}}}}}{{\partial {{\xi }^{3}}}} = 0,$3. СТОЛКНОВЕНИЕ N-СОЛИТОНОВ
Теперь используем метод БМХ для получения N-солитонных решений. Уравнение УКдФ (7) может быть преобразовано к стандартному виду УКдФ с помощью замены переменных $\tau \to T$, $\xi \to - {{B}^{{1/3}}}\Xi $ и ${{\phi }^{{\left( 1 \right)}}} \to 6{{B}^{{1/3}}}\Phi {\text{/}}A$
(8)
$\frac{{\partial \Phi }}{{\partial T}} + 6\Phi \frac{{\partial \Phi }}{{\partial \Xi }} + \frac{{{{\partial }^{3}}\Phi }}{{\partial {{\Xi }^{3}}}} = 0.$Исследуем явление обгона при распространении N-солитонов на примере двухсолитонных и трехсолитонных решений. Подставляя в (8) $\Phi = {{(2\log \Psi )}_{{\Xi \Xi }}}$, получаем билинейную форму уравнения (8) в виде
(9)
$\begin{gathered} \Psi {{\Psi }_{{\Xi {\rm T}}}} - {{\Psi }_{\Xi }}{{\Psi }_{{\rm T}}} + \Psi {{\Psi }_{{\Xi \Xi \Xi \Xi }}} - \\ \, - 4{{\Psi }_{\Xi }}{{\Psi }_{{\Xi \Xi \Xi }}} + 3\Psi _{{\Xi \Xi }}^{2} = 0. \\ \end{gathered} $Применяя D-оператор Хироты [32], преобразуем уравнение (9) к виду
(10)
${{D}_{\Xi }}{{D}_{{\rm T}}}\left[ {\Psi \cdot \Psi } \right] = 2\left( {\Psi {{\Psi }_{\Xi }} - {{\Psi }_{\Xi }}{{\Psi }_{{\rm T}}}} \right),$(11)
$D_{\Xi }^{4}\left[ {\Psi \cdot \Psi } \right] = 2\left( {\Psi {{\Psi }_{{\Xi \Xi \Xi \Xi }}} - 4{{\Psi }_{\Xi }}{{\Psi }_{{\Xi \Xi \Xi }}} + 3\Psi _{{\Xi \Xi }}^{2}} \right).$Подставляя (10) и (11) в (9), получаем
(12)
${{D}_{\Xi }}\left( {{{D}_{{\rm T}}} + D_{\Xi }^{3}} \right)\left[ {\Psi \cdot \Psi } \right] = 0.$Разложение функции $\Psi $ по степеням ε выглядит следующим образом: $\Psi = 1 + {{\Psi }_{1}} + {{\varepsilon }^{2}}{{\Psi }_{2}} + \ldots $, где ${{\Psi }_{1}} = {{e}^{{{{\Theta }_{1}}}}} + {{e}^{{{{\Theta }_{2}}}}},$ ${{\Psi }_{2}} = {{\gamma }_{{12}}}{{e}^{{{{\Theta }_{1}} + {{\Theta }_{2}}}}}$, ${{\Theta }_{{1,2}}} = {{k}_{{1,2}}}\Xi + $ $ + \;{{\omega }_{{1,2}}}{\rm T} + {{\alpha }_{{1,2}}}$, ${{\omega }_{{1,2}}} = - k_{{1,2}}^{3}$, ${{\gamma }_{{12}}} = {{\left( {{{k}_{1}} - {{k}_{2}}} \right)}^{2}}{\text{/}}{{\left( {{{k}_{1}} + {{k}_{2}}} \right)}^{2}}$ и ε включено в константу ${{\alpha }_{{1,2}}}$. Тогда, применяя метод Хироты, получим решение уравнения (8) в виде
(13)
$\Phi = 2\frac{{k_{1}^{2}{{e}^{{{{\Theta }_{1}}}}} + k_{2}^{2}{{e}^{{{{\Theta }_{2}}}}} + {{\gamma }_{{12}}}{{e}^{{{{\Theta }_{1}} + {{\Theta }_{2}}}}}\left( {k_{2}^{2}{{e}^{{{{\Theta }_{1}}}}} + k_{1}^{2}{{e}^{{{{\Theta }_{2}}}}}} \right) + 2{{{\left( {{{k}_{1}} - {{k}_{2}}} \right)}}^{2}}{{e}^{{{{\Theta }_{1}} + {{\Theta }_{2}}}}}}}{{{{{\left( {1 + {{e}^{{{{\Theta }_{1}}}}} + {{e}^{{{{\Theta }_{2}}}}} + {{\gamma }_{{12}}}{{e}^{{{{\Theta }_{1}} + {{\Theta }_{2}}}}}} \right)}}^{2}}}}.$Соответственно, решение уравнения (7) можно представить в виде
(14)
${{\phi }^{{\left( 1 \right)}}} = \frac{{12{{B}^{{1/3}}}}}{A}\frac{{k_{1}^{2}{{e}^{{{{\theta }_{1}}}}} + k_{2}^{2}{{e}^{{{{\theta }_{2}}}}} + {{\gamma }_{{12}}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}}}}}\left( {k_{2}^{2}{{e}^{{{{\theta }_{1}}}}} + k_{1}^{2}{{e}^{{{{\theta }_{2}}}}}} \right) + 2{{{\left( {{{k}_{1}} - {{k}_{2}}} \right)}}^{2}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}}}}}}}{{{{{\left( {1 + {{e}^{{{{\theta }_{1}}}}} + {{e}^{{{{\theta }_{2}}}}} + {{\gamma }_{{12}}}{{e}^{{{{\theta }_{1}} + {{\theta }_{2}}}}}} \right)}}^{2}}}},$При ${\tau } \gg 1$ члены ${{e}^{{ - \left( {{{\theta }_{1}} + {{\theta }_{2}}} \right)}}}$, ${{e}^{{ - \left( {2{{\theta }_{1}} + {{\theta }_{2}}} \right)}}}$, и ${{e}^{{ - \left( {{{\theta }_{1}} + 2{{\theta }_{2}}} \right)}}}$ не являются определяющими, и ими можно пренебречь. Тогда после некоторых алгебраических преобразований получаем выражение
(15)
${{\phi }^{{\left( 1 \right)}}} \approx \frac{{12{{B}^{{1/3}}}}}{A}\left( {\frac{{{{\gamma }_{{12}}}k_{1}^{2}{{e}^{{ - {{\theta }_{1}}}}}}}{{{{{({{e}^{{ - {{\theta }_{1}}}}} + {{\gamma }_{{12}}})}}^{2}}}} + \frac{{{{\gamma }_{{12}}}k_{2}^{2}{{e}^{{ - {{\theta }_{2}}}}}}}{{{{{({{e}^{{ - {{\theta }_{2}}}}} + {{\gamma }_{{12}}})}}^{2}}}}} \right).$Используя известные математические выражения ${{e}^{{ - x}}}{\text{/(}}1 + {{e}^{{ - x}}}{{{\text{)}}}^{2}}$ = ${{\operatorname{sech} }^{2}}{\text{(}}x{\text{/}}2{\text{)/}}4$ и $~{{\gamma }_{{12}}} = {{e}^{{\ln \left| {{{\gamma }_{{12}}}} \right|}}}$, получаем решение в виде суперпозиции двух солитонов
(16)
${{\phi }^{{\left( 1 \right)}}}\sim \mathop \sum \limits_{i = 1}^3 \phi _{i}^{{\left( 0 \right)}}{{\operatorname{sech} }^{2}}\left[ {\frac{{{{k}_{i}}}}{{2{{B}^{{1/3}}}}}\left( { - \xi - {{B}^{{1/3}}}k_{1}^{2}\tau + {{\delta }_{i}}} \right)} \right],$4. ПРИМЕРЫ ЧИСЛЕННЫХ ВЫЧИСЛЕНИЙ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
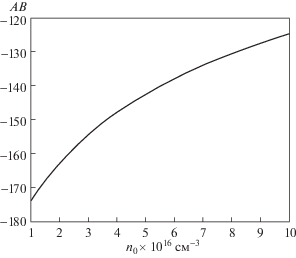
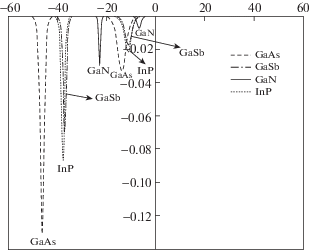
Теперь рассмотрим некоторые свойства N-солитонов, являющиеся следствием “столкновения с обгоном”, происходящего при их распространении в различных видах квантовой полупроводниковой плазмы со следующими параметрами: для GaAs плазмы (${{n}_{0}} = 4.7 \times {{10}^{{16}}}{\kern 1pt} - {\kern 1pt} {{10}^{{17}}}$ см–3, $m_{e}^{*} = 0.067{{m}_{e}}$, $m_{h}^{*} = 0.5{{m}_{e}}$ и ${\text{т}} = 12.8$); для GaSb плазмы (${{n}_{0}} = 1.6 \times $ $ \times \;{{10}^{{17}}}$ см–3, $m_{e}^{*} = 0.047{{m}_{e}}$, $m_{h}^{*} = 0.4{{m}_{e}}$ и ${\text{т}} = 15.69$); для GaN плазмы (${{n}_{0}} = {{10}^{{20}}}$ см–3, $m_{e}^{*} = 0.13{{m}_{e}}$, $m_{h}^{*} = 1.3{{m}_{e}}$ и ${\text{т}} = 11.3$), а также для InP плазмы (${{n}_{0}} = 5.7 \times {{10}^{{17}}}$ см–3, $m_{e}^{*} = 0.077{{m}_{e}}$, $m_{h}^{*} = 0.6~{{m}_{e}}$ и ${\text{т}} = 12.6$) [12, 18]. Результаты численных вычислений, показанные на рис. 1, демонстрируют, что величина AB всегда отрицательна. Здесь A и B – коэффициенты, соответственно, при нелинейном и дисперсионном членах уравнения. Следовательно, в рамках представленной модели, солитоны имеют отрицательную полярность (т.е., являются солитонами разрежения или темными солитонами). На рис. 2 можно проследить временную динамику развития событий при “столкновении с обгоном” двух темных солитонов ${{\phi }^{{\left( 1 \right)}}}$. На рисунке отрицательное (или положительное) значение времени соответствует событиям, происходящим до (или после) столкновения с обгоном. Более того, ${\tau } = 0$ является моментом времени, когда и происходит само столкновение с обгоном. Как показано на рис. 2а, при $\tau = - 10$, темный солитон (ТС) с большей амплитудой находится позади ТС с меньшей амплитудой. Затем, при $\tau {\text{ }} = - 2$ (рис. 2в), ТС с большей амплитудой начинает обгонять ТС с меньшей амплитудой. После этого, при $\tau = 0$ (рис. 2г), два темных солитона сливаются и формируют единый ТС. Далее, при $\tau = 2$ (рис. 2д), два ТС начинают разделяться, и, при $\tau = 5$ (рис. 2е) они окончательно отходят друг от друга. И, наконец, по прошествии некоторого времени, при $\tau = 10$ (рис. 2ж), мы видим, что они продолжают удаляться друг от друга. Во время столкновений с обгоном между электростатическими N-солитонами происходит обмен энергией, приводящий к изменениям фаз солитонов при их движении по своим траекториям. На рис. 3 показаны столкновения с обгоном двух темных солитонов при двух различных значениях плотности квантовой полупроводниковой плазмы n0. Очевидно, что при уменьшении плотности n0 амплитуда ТС возрастает. С физической точки зрения понятно, что при уменьшении n0 можно ожидать соответствующего уменьшения нелинейного коэффициента A; следовательно, солитон сможет переносить большую энергию и увеличить свою амплитуду. Рисунок 4 иллюстрирует поведение двух ТС при наличии или отсутствии обменно-корреляционного потенциала ${{V}_{{xce,h}}}$. В отсутствие обменно-корреляционного потенциала амплитуды обоих темных солитонов уменьшаются. Это означает, что отсутствие ${{V}_{{xce,h}}}$ может предотвратить передачу энергии при столкновении за счет уменьшения амплитуд обоих ТС. На рис. 5 можно видеть влияние n0 и ${{V}_{{xce,h}}}$ на фазовые сдвиги Δ2 , возникающие при столкновении с обгоном двух темных солитонов. Видно, что фазовый сдвиг Δ2 уменьшается при возрастании плотности плазмы n0. Кроме того, наличие обменно-корреляционного потенциала приводит к уменьшению фазового сдвига Δ2. Далее, на рис. 6 для различных значений τ показано взаимное расположение трех ТС ${{\phi }^{{\left( 1 \right)}}}$ во время столкновения с обгоном. Отметим, что показанная на рис. 6 временная эволюция взаимного расположения солитонов во время столкновения с обгоном аналогична соответствующим зависимостям, показанным на рис. 2. На рис. 7 показаны зависимости фазовых сдвигов ${{\delta }_{1}},{\text{\;}}{{\delta }_{2}},$ и $~{{\delta }_{3}}$, возникающих при столкновении трех ТС, от плотности квантовой полупроводниковой плазмы n0. Видно, что с ростом плотности n0 фазовые сдвиги уменьшаются. Теперь рассмотрим двухсолитонные и трехсолитонные решения для столкновений с обгоном, происходящих в различных видах квантовой полупроводниковой плазмы, показанные, соответственно, на рис. 8 и 9. Видно, что ТС в плазме GaAs имеет большую амплитуду, а в плазме GaN – меньшую. Для четырех видов квантовой полупроводниковой плазмы, показанных на рисунках, амплитуды темных солитонов (АТС) могут быть упорядочены следующим образом: АТСGaAs > АТСInP > АТС GaSb > АТСGaN. Это можно объяснить следующим образом: при уменьшении плотности плазмы n0 физические свойства GaAs меняются таким образом, что вызывают уменьшение нелинейного члена, и, следовательно, происходит концентрация большего количества энергии в солитоне (увеличение его амплитуды), чем в случае других видов квантовой полупроводниковой плазмы.
Рис. 2.
Взаимное расположение двух нелинейных темных солитонов в различные моменты времени τ при столкновении с обгоном, происходящем в полупроводниковой плазме GaAs: ${{k}_{1}} = 1$ и ${{k}_{2}} = 2$.
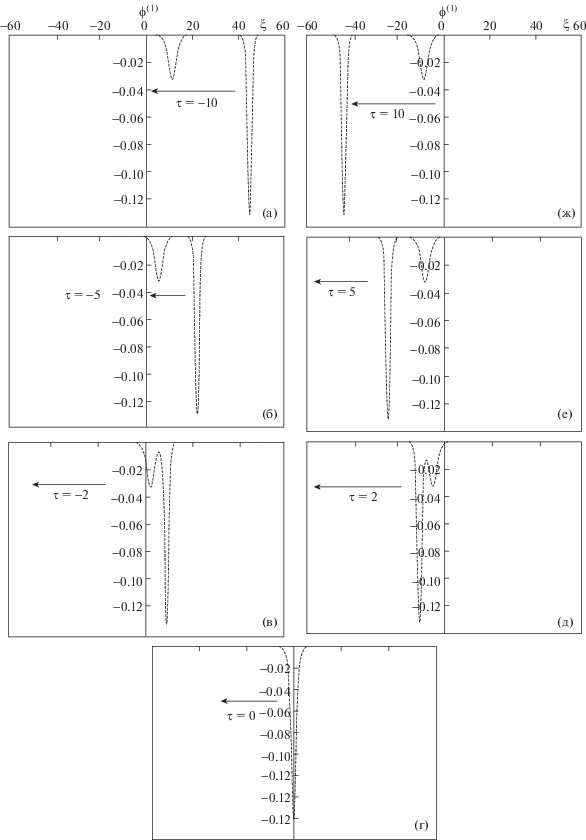
Рис. 3.
Взаимное расположение двух нелинейных темных солитонов при столкновении с обгоном при двух различных значениях плотности n0 квантовой полупроводниковой плазмы GaAs; ${{k}_{1}} = 1$ и ${{k}_{2}} = 2$.
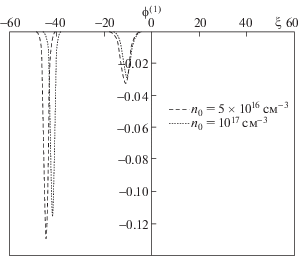
Рис. 4.
Взаимное расположение двух нелинейных темных солитонов при столкновении с обгоном в квантовой полупроводниковой плазме GaAs при наличии (точки) и в отсутствие (тире) обменно-корреляционного потенциала Vxce,h; ${{k}_{1}} = 1$ и ${{k}_{2}} = 2$.
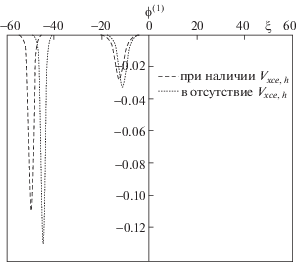
Рис. 5.
Фазовые сдвиги Δ2 , возникающие при столкновении с обгоном двух темных солитонов в полупроводниковой плазме GaAs, как функции плотности плазмы n0. Пунктирная и штриховая линии соответствуют столкновениям, происходящим в присутствии и в отсутствие обменно-корреляционного потенциала Vxce,h.
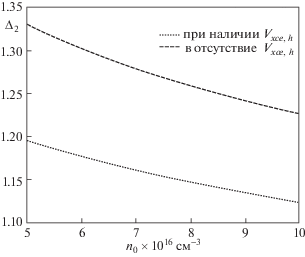
Рис. 6.
Взаимное расположение трех нелинейных темных солитонов в различные моменты времени τ при столкновении с обгоном, происходящем в полупроводниковой плазме GaAs: ${{k}_{1}} = 1$, ${{k}_{2}} = 2$ и ${{k}_{3}} = 3$.
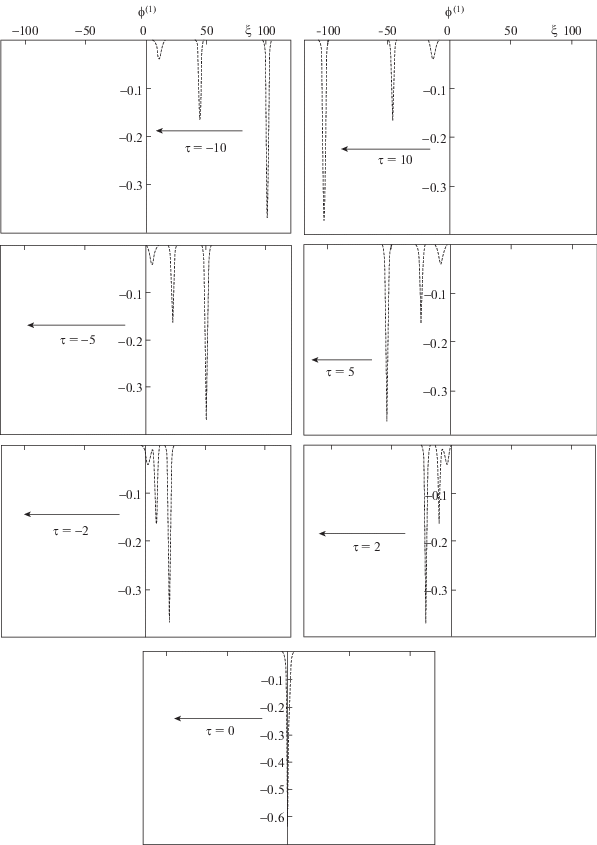
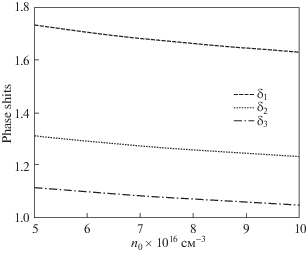
Рис. 7.
Фазовые сдвиги, возникающие при столкновении с обгоном трех темных солитонов в полупроводниковой плазме GaAs, как функции плотности плазмы n0. Штриховая, пунктирная и штрихпунктирная линии соответствуют фазовым сдвигам δ1, δ2 и δ3.
5. ЗАКЛЮЧЕНИЕ
В этой работе мы обсуждали возбуждение и столкновения с обгоном N-солитонов, распространяющихся в плотной полупроводниковой плазме. Уравнение Кортевега-де Фриза, описывающее поведение электростатических солитонов в электронно-дырочной плазме было получено с использованием редуцированной теории возмущений. Преимущества представленного подхода к описанию столкновений с обгоном N‑солитонов, распространяющихся в электронно-дырочной плотной полупроводниковой плазме, состоят в следующем: в наименьшем порядке разложения выведено уравнение УКдФ с учетом баланса нелинейных и дисперсионных эффектов. В результате учета этого баланса возникают решения в виде солитонов, которые представляют собой волны, ведущие себя как частицы. С использованием классической теории квазичастиц получены аналитические оценки времени столкновения и минимального расстояния сближения солитонов. Численный анализ представленной модели показал, что солитоны могут существовать только в виде темных солитонов. Исследована динамика поведения темных солитонов при различных параметрах (для различных видов) квантовой полупроводниковой плазмы. Полученные результаты способствуют более глубокому пониманию свойств темных солитонов, проявляющихся во время столкновений с обгоном, происходящих в различных видах квантовой полупроводниковой плазмы. Хотелось бы подчеркнуть важный факт, который состоит в том, что возникновение и распространение таких солитонов могут быть исследованы экспериментально в квантовой плазме наноразмерных устройств, в полупроводниковых квантовых ямах и в плазме, возникающей при лазерно-плазменном взаимодействии с масштабами и плазменными параметрами, близкими к соответствующим параметрам устройств, используемых в экспериментах [42].
Авторы выражают благодарность Деканату отделения научных исследований Университета имени короля Халида за финансовую поддержку этой работы в рамках программы финансирования исследовательских групп (проект № KKU–R.G.P.1/38/39). Авторы также хотели бы выразить благодарность рецензентам за полезные критические замечания и комментарии, учет которых способствовал улучшению оригинальной рукописи. Авторы также благодарят редактора и сотрудников журнала за любезную помощь в издании данной статьи.
Список литературы
Markowich P.A., Ringhofer C.A., Schmeiser C. Semiconductor Equations. Springer-Verlag, New York, 1990.
Yanovsky V., Chvykov V., Kalinchenko G., Rousseau P., Planchon T., Matsuoka T., Maksimchuk A., Nees J., Cheriaux G., Mourou G., Krushelnick K. // Opt. Express. 2008. V. 162. P. 109.
Dunne M. // Nature Phys. 2006. V. 2. P. 2.
Shukla P.K., Eliasson B. // Phys. Rev. Lett. 2007. V. 99. P. 096401.
Wang Y., Shukla P.K., Eliasson B. // Phys. Plasmas. 2013. V. 20. P. 013103.
Crouseilles N., Hervieux P.A., Manfredi G. // Phys. Rev. B. 2008. V. 78. P. 155412.
Brey L., Dempsey J., Johnson N.F., Halperin B.I. // Phys. Rev. B. 1990. V.42. P. 1240.
Shukla P.K., Eliasson B. // Phys. Rev. Lett. 2012. V. 108. P. 165007.
Ma Yu-T., Mao Sheng-H., Xue Ju-K. // Phys. Plasmas. 2011. V. 18. P. 102108.
Egorov O.A., Skryabin D.V., Lederer F. // Phys. Rev. B. 2010. V. 82. P. 165326.
Zeba I., Yahia M.E., Shukla P.K., Moslem W.M. // Phys. Lett. A. 2012. V. 376. P. 2309.
Moslem W.M., Zeba I., Shukla P.K. // Appl. Phys. Lett. 2012. V. 101. P. 032106.
Wang Y., Lü X. // Phys. Plasmas. 2014. V. 21. P. 022107.
Wang Y., Eliasson B. // Phys. Rev. B.2014. V. 89. P. 205316.
El-Shamy E.F., Gohman F.S. // Phys. Lett. A. 2014. V. 378. P. 2688.
Tolba R.E., El-Bedwehy N.A., Moslem W.M., El-Laba-ny S.K., Yahia M.E. // Phys. Plasmas. 2016. V. 23. P. 012111.
Abdelsalam U.M., Allehiany F.M., Moslem W.M. // Acta Phys. Pol. A. 2016. V. 129. P. 472.
EL-Shamy E.F., Gohman F.S., Alqahtani M.M., Al-Faify S. // Phys. Plasmas. 2018. V. 25. P. 012108.
Saha A., Chatterjee P. // Astrophys. Space Sci. 2014. V. 353. P. 169.
El-Labany S.K., El-Shamy E.F., El-Sherbeny S.K. // Astrophys. Space Sci. 2014. V. 351. P. 151.
Saha A., Pal N., Chatterjee P. // Phys. Plasmas. 2014. V. 21. P. 102101.
Mandal G., Roy K., Paul A., Saha A., Chatterjee P. // Z. Naturforsch. A. 2015. V. 70. P. 703.
Roy K., Ghorui M.K., Chatterjee P., Tribeche M. // Commun. Theor. Phys. 2016. V. 65. P. 237.
Alam M.S., Hafez M.G., Talukder M.R., Ali M.H. // Chin. Phys. B. 2017. V. 26. P. 095203.
El-Shamy E.F., El-Bedwehy N.A., Shokry M., El-Labany S.K. // Z. Naturforsch. A. 2018. V. 73. P. 893.
Su C. H., Miura R.M. // J. Fluid Mech. 1980. V. 98. P. 509.
Huang G.X., Velarde M.G. // Phys. Rev. E. 1996. V. 53. P. 2988.
El-Labany S.K., El-Shamy E.F., Abu El-Eneen M. // Astrophys. Space Sci. 2012. V. 337. P. 275.
Xue J.K. // Phys. Rev. E. 2004. V. 69. P. 016403.
El-Shamy E.F. // Phys. Plasmas. 2009. V. 16. P. 113704.
Tanituti T., Wei C. // J. Phys. Soc. Jpn. 1968. V. 24. P. 941.
Hirota R. // Phys. Rev. Lett. 1971. V. 27. P. 1192.
Hirota R. // J. Phys. Soc. Jpn. 1972. V. 33. P. 1456.
Hirota R. // J. Math. Phys. 1973. V. 14. P. 805.
Hirota R. // The Direct Method in the Soliton Theory. Cambridge University Press, Cambridge, UK 2004.
Srinivas J., Popel S.I., Shukla P.K. // J. Plasma Physics. 1996. V. 55. P. 209.
Popel S.I., Golub’ A.P., Losseva T.V. // Phys. Rev. E. 2003. V. 67. P. 056402.
Losseva T.V., Popel S.I., Golub’ A.P., Shukla P.K. // Phys. Plasmas. 2009. V. 16. P. 093704.
Losseva T.V., Popel S.I., Golub A.P. // Plasma Phys. Rep. 2012. V. 38. P. 729.
Losseva T.V., Popel S.I., Golub A.P., Izvekova Yu.N., Shukla P.K. // Phys. Plasmas. 2012. V. 19. P. 013703.
Qi X., Xu Y.X., Duan W.S., Yang L. // Phys. Plasmas. 2014. V. 21. P. 013702.
Biancalana F., Healy S.B., Fehse R., O’Reilly E.P. // Phys. Rev. A. 2006. V. 73. P. 063826.
Дополнительные материалы отсутствуют.