Физика плазмы, 2020, T. 46, № 11, стр. 985-992

О возможности низкопорогового нелинейного возбуждения косых ленгмюровских волн в плазменном филаменте СВЧ-волной обыкновенной поляризации

Е. З. Гусаков^a, А. Ю. Попов^a, *, Л. В. Симончик^b

^a Физико-технический институт им. А.Ф. Иоффе РАН
С.-Петербург, Россия

^b Институт физики им. Б.И. Степанова НАН Беларуси
Минск, Республика Беларусь

^* E-mail: a.popov@mail.ioffe.ru

Поступила в редакцию 06.04.2020
После доработки 05.05.2020
Принята к публикации 10.05.2020

DOI: 10.31857/S0367292120110037

Полный текст (PDF)

Аннотация

Изложены результаты теоретического анализа низкопороговой параметрической распадной неустойчивости пучка СВЧ-волны накачки обыкновенной поляризации электронно-циклотронного диапазона частот, приводящей к возбуждению двух косых ленгмюровских волн и развивающейся в цилиндрическом плазменном филаменте.

Ключевые слова: электронный циклотронный нагрев, CВЧ-волна, обыкновенная поляризация, косая ленгмюровская волна, плазменный филамент, параметрическая распадная неустойчивость

1. ВВЕДЕНИЕ

Электронный циклотронный резонансный нагрев (ЭЦРН) широко используется в современных тороидальных устройствах магнитного удержания высокотемпературной плазмы для дополнительного нагрева электронной компоненты и генерации токов увлечения. В частности, ЭЦРН с использованием пучков СВЧ-волн обыкновенной поляризации на частоте фундаментальной электронной циклотронной гармоники рассматривается в настоящее время как наиболее надежный метод контроля неоклассической тиринг-неустойчивости в токамаке-реакторе ITER. До недавнего времени распространение и поглощение СВЧ-волн считалось хорошо предсказуемым и адекватно описываемым в рамках линейной теории. Это представление основывалось на результатах теоретического анализа [1], проведенного в предположении монотонного профиля плотности плазмы и предсказывавшего крайне высокие пороги возбуждения нелинейных эффектов, которые могут сопровождать распространение СВЧ-волны, в частности параметрических распадных неустойчивостей (ПРН) волны накачки. Однако недавно было получено множество свидетельств, указывающих на присутствие аномальных нелинейных явлений в экспериментах по ЭЦРН плазмы. В частности, при распространении мощных пучков СВЧ-волн наблюдалось их аномальное рассеяние [2–4], а также генерация ускоренных ионов [5, 6]. Обнаруженные явления не нашли объяснения в рамках обычной теоретической модели [1], что, безусловно, делает актуальной постановку вопроса о надежности и предсказуемости этого метода дополнительного нагрева электронной компоненты плазмы. Для объяснения аномальных явлений было предложено расширение традиционной модели трехволнового взаимодействия [7, 8], которое дало возможность описать эти нелинейные явления в присутствии немонотонных профилей плотности, часто наблюдаемых в экспериментах по дополнительному СВЧ-нагреву. В результате это позволило предсказать возможность низкопорогового возбуждения ПРН СВЧ-волн и подробно описать аномальное рассеяние, наблюдаемое в экспериментах по ЭЦРН на второй гармонике резонанса с использованием волн необыкновенной поляризации в токамаке TEXTOR [7]. Выделим два ключевых элемента теории. Первый из них – возможность локализации одной [8] или обеих [7] дочерних волн из-за немонотонного профиля плотности. Второй – это возможность возбуждения абсолютной неустойчивости в присутствии пучка накачки конечной ширины. Универсальный характер предложенного механизма возбуждения нелинейных распадных неустойчивостей необыкновенной волны был продемонстрирован в модельных экспериментах, проведенных на линейной установке “Гранит” в разряде низкого давления в низкотемпературной плазме [9]. Его особенности были проанализированы аналитически в работе [10].

Как было отмечено в экспериментах по ЭЦРН плазмы с использованием СВЧ-волн обыкновенной поляризации на частоте фундаментальной ЭЦ гармоники [11, 12], распространение таких волн тоже может сопровождаться интенсивным аномальным излучением из плазмы. Последнее может быть интерпретировано как следствие развития низкопороговых параметрических распадных неустойчивостей, которые приводят к возбуждению верхнегибридных волн, локализованных в центре плазменного шнура или в окрестности локального максимума немонотонного профиля плотности [13, 14]. Отметим, что как показано в работе [15], возбуждение ПРН с низким порогом по мощности возможно и при монотонном профиле плотности в случае наличия двух точек нелинейного взаимодействия, что приводит к появлению петли обратной связи для дочерних волн: верхне-гибридной волны и ионной бернштейновской волны, – распространяющихся в противоположных направлениях.

Рассмотренные ранее сценарии параметрических распадов СВЧ-волн обыкновенной поляризации не являются единственно возможными. Представляется, что в присутствии плазменного филамента возможен также низкопороговый параметрический распад обыкновенной волны, приводящий к генерации двух локализованных вдоль направления неоднородности квазиэлектростатических колебаний, имеющих близкие частоты, которые по величине несколько меньше, чем локальная плазменная частота. На принципиальную возможность снижения порогов распадной неустойчивости в этом случае указывалось в работе [16]. Однако теоретический анализ в ней был проведен в упрощенной модели плоскослоистой плазмы в предположении бесконечной накачки. Предполагалось, что основные потери дочерних волн обусловлены столкновениями. В реальной геометрии конвективные потери из области распада вдоль направления магнитного поля из-за пространственно ограниченного распределения волн накачки доминируют над столкновительной диссипацией и определяют порог возбуждения неустойчивости.

Принципиальная возможность аномально большого поглощения мощности обыкновенной волны накачки была продемонстрирована недавно в модельном эксперименте на линейной установке “Гранит” [17], в том числе и при условиях, когда может иметь место вариант параметрического распада на две косые ленгмюровские волны. Двухплазмонный распад СВЧ-волны обыкновенной поляризации, сопровождающийся ее значительными аномальными потерями, возможен в больших термоядерных установках удержания плазмы. Для изучения его механизма, особенностей и последствий в настоящее время планируются модельные эксперименты на линейной установке и в небольших тороидальных установках удержания плазмы, что делает актуальной задачу адекватного теоретического описания этого параметрического нелинейного явления, получение оценки его инкремента и порога возбуждения с учетом реалистичной геометрии трехволнового взаимодействия.

В настоящей работе мы излагаем результаты теоретического анализа этого сценария низкопороговой параметрической распадной неустойчивости, приводящей к возбуждению двух косых ленгмюровских волн и развивающейся в цилиндрическом плазменном филаменте под действием пучка СВЧ-волны накачки обыкновенной поляризации.

2. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ ДВУМЕРНО ЛОКАЛИЗОВАННЫХ КОСЫХ ЛЕНГМЮРОВСКИХ ВОЛН

Для описания нелинейного возбуждения двух косых ленгмюровских волн, которые захвачены в плазменном филаменте, вытянутом вдоль магнитного поля, мы будем использовать две локальные системы координат: цилиндрическую $(r,\theta ,z)$ и декартову $(x,y,z)$. Эти системы координат имеют общее начало в центре плазменного образования. Координата x совпадает с направлением распространения волны, координата z направлена вдоль магнитного поля. Будем считать, что профиль плотности плазмы имеет вид

(1)

$n = \bar {n}\left( {1 - \frac{{{{r}^{2}}}}{{l_{b}^{2}}}} \right)H\left( {{{l}_{b}} - r} \right),$

где $H\left( {{{l}_{b}} - r} \right)$ – функция Хевисайда и ${{l}_{b}}$ – поперечный внешнему магнитному полю размер плазменного образования. Рассмотрим реалистичную модель трехволнового взаимодействия. Будем считать, что волна накачки обыкновенной поляризации распространяется вдоль координаты x (по r) и падает на область распада. Поле падающей волны в ВКБ приближении

(2)

$\begin{gathered} {\mathbf{E}} = {{{\mathbf{e}}}_{z}}{{E}_{z}}\left( {\mathbf{r}} \right)\exp \left( { - i{{\omega }_{0}}t} \right) + c.c = \\ \, = {{{\mathbf{e}}}_{z}}\frac{{{{E}_{0}}}}{2}\sqrt {\frac{{{{\omega }_{0}}}}{{c{{k}_{x}}\left( x \right)}}} \exp \left( {i\int\limits_{}^x {{{k}_{x}}} \left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '\; - i{{\omega }_{0}}t} \right) + c.c., \\ \end{gathered} $

где ${{E}_{0}}\left( {{{P}_{0}};y,z} \right)$ – поперечное распределение амплитуды волны в пучке, ${{P}_{0}}$ – мощность пучка,

(3)

${{k}_{x}}\left( {{{\omega }_{0}}} \right) = \frac{{{{\omega }_{0}}}}{c}\sqrt {\eta {\kern 1pt} '\left( {{{\omega }_{0}}} \right)} $

– компонента волнового вектора вдоль направления распространения пучка, $\eta {\kern 1pt} '\left( {{{\omega }_{0}}} \right)$ – действительная часть продольной компоненты тензора диэлектрической проницаемости “холодной” плазмы, явный вид которой будет приведен ниже, и c.c. – член, получающийся из первого в результате комплексного сопряжения. Предположим, что поперечные размеры пучка w существенно больше размера плазменного образования, ${{l}_{b}} \ll w$. Учтем, что волновой вектор волны накачки обычно слабо зависит от координаты. Тогда, в плазме в цилиндрической геометрии поле волны накачки (2) принимает следующий вид (т.н. представление Зоммерфельда для плоской волны [18]):

(4)

$\begin{gathered} {\mathbf{E}} = {{{\mathbf{e}}}_{z}}{{E}_{z}}\left( r \right)\exp \left( { - i{{\omega }_{0}}t} \right) + c.c = \\ \, = {{{\mathbf{e}}}_{z}}\frac{{{{E}_{0}}\left( {{{P}_{0}},0,z} \right)}}{2}\sqrt {\frac{{{{\omega }_{0}}}}{{c{{k}_{x}}}}} \sum\limits_{{{m}_{0}} = - \infty }^\infty {{{J}_{{{{m}_{0}}}}}\left( {{{k}_{x}}r} \right)} \times \\ \, \times \exp \left( {i{{m}_{0}}\theta - i{{\omega }_{0}}t} \right) + c.c. \\ \end{gathered} $

Далее мы проанализируем распад колебаний (4) на две коротковолновые косые ленгмюровские (КЛ) волны, имеющие близкие частоты в диапазоне меньше электронной плазменной, т.е. ${{\omega }_{1}},{{\omega }_{2}} = {{\omega }_{0}} - {{\omega }_{1}} < {{\omega }_{{pe}}},{{\omega }_{{ce}}}$. В слабо неоднородной плазме амплитуды дочерних продольных КЛ волн, возбуждающихся в результате параметрического распада волны накачки (4) и распространяющихся в противоположных направлениях, ${{\varphi }_{{1,2}}} \propto \exp \left( { \mp i{{\omega }_{{1,2}}}t} \right)$, описываются системой связанных уравнений

(5)

$\left\{ \begin{gathered} \left( {\varepsilon \left( {{{\omega }_{1}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{r}\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}} \right) + \eta \left( {{{\omega }_{1}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right){{\varphi }_{1}} = \hfill \\ \, = - {{{\hat {\chi }}}_{{12}}}\left[ {\frac{{{{E}_{z}}\left( {\mathbf{r}} \right)}}{H}{{\varphi }_{2}}} \right],{\text{ }} \hfill \\ \left( {\varepsilon \left( {{{\omega }_{2}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{r}\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}} \right) + \eta \left( {{{\omega }_{2}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right){{\varphi }_{2}} = \hfill \\ \, = - \hat {\chi }_{{21}}^{*}\left[ {\frac{{{{E}_{z}}\left( {\mathbf{r}} \right)}}{H}{{\varphi }_{1}}} \right]. \hfill \\ \end{gathered} \right.$

В системе уравнений (5) компоненты тензора, имеющие действительную и мнимую части, в фурье-представлении суть

$\begin{gathered} \varepsilon \left( {{{\omega }_{{1,2}}}} \right) = \varepsilon {\kern 1pt} '\left( {{{\omega }_{{1,2}}}} \right) + i\varepsilon {\kern 1pt} '{\kern 1pt} '\left( {{{\omega }_{{1,2}}}} \right) = \\ 1 - \frac{{\omega _{{pe}}^{2}}}{{\omega _{{1,2}}^{2} - \omega _{{ce}}^{2}}} \pm i\sqrt \pi \frac{{\omega _{{pe}}^{2}}}{{2\omega _{{ce}}^{2}}}\frac{{{{\omega }_{{1,2}}}}}{{\left| {{{q}_{z}}} \right|{{\upsilon }_{{te}}}}} \times \\ \end{gathered} $

(6)

$\begin{gathered} \, \times \exp \left( { - {{{\left( {\frac{{{{\omega }_{{1,2}}} - {{\omega }_{{ce}}}}}{{{{q}_{z}}{{\upsilon }_{{te}}}}}} \right)}}^{2}}} \right) \pm i\nu \frac{{\omega _{{pe}}^{2}\left( {\omega _{{1,2}}^{2} + \omega _{{ce}}^{2}} \right)}}{{{{\omega }_{{1,2}}}{{{\left( {\omega _{{1,2}}^{2} - \omega _{{ce}}^{2}} \right)}}^{2}}}}, \\ \eta \left( {{{\omega }_{{1.2}}}} \right) = \eta {\kern 1pt} '\left( {{{\omega }_{{1.2}}}} \right) + i\eta {\kern 1pt} '{\kern 1pt} '\left( {{{\omega }_{{1.2}}}} \right) = \\ \end{gathered} $

$\begin{gathered} 1 - \frac{{\omega _{{pe}}^{2}}}{{\omega _{{1,2}}^{2}}} \pm i\sqrt \pi \frac{{2\omega _{{pe}}^{2}}}{{q_{z}^{2}\upsilon _{{te}}^{2}}}\frac{{{{\omega }_{{1,2}}}}}{{\left| {{{q}_{z}}} \right|{{\upsilon }_{{te}}}}} \times \\ \, \times \exp \left( { - {{{\left( {\frac{{{{\omega }_{{1,2}}}}}{{{{q}_{z}}{{\upsilon }_{{te}}}}}} \right)}}^{2}}} \right) \pm i\nu \frac{{\omega _{{pe}}^{2}}}{{\omega _{{1,2}}^{3}}}, \\ \end{gathered} $

где $\varepsilon {\kern 1pt} '\left( {{{\omega }_{{1,2}}}} \right) > 0$, $\eta {\kern 1pt} '\left( {{{\omega }_{{1,2}}}} \right) < 0$ – действительные части компонент диэлектрического тензора. Мнимые части этих компонент тензора $\varepsilon {\kern 1pt} '{\kern 1pt} '\left( {{{\omega }_{{1,2}}}} \right)$, $\eta {\kern 1pt} '{\kern 1pt} '\left( {{{\omega }_{{1.2}}}} \right)$ описывают ЭЦ затухание, затухание Ландау и столкновительное затухание (ν – частота столкновений). Нелинейные восприимчивости в правой части уравнений (5) представляют собой дифференциальные операторы, действующие на функции в квадратной скобке. Они имеют следующий вид (см. Приложение и также [19]):

$\begin{gathered} {{{\hat {\chi }}}_{{21}}} = i\frac{{\omega _{{pe}}^{2}\left| {{{\omega }_{{ce}}}} \right|{{q}_{z}}c}}{{{{\omega }_{0}}\omega _{1}^{2}\omega _{2}^{2}{{\Delta }_{1}}{{\Delta }_{2}}}}\left( {q_{z}^{2}\left( {{{\omega }_{1}} - {{\omega }_{2}}} \right){{\Delta }_{1}}{{\Delta }_{2}}\mathop + \limits_{}^{} } \right. \\ \, + {{\omega }_{1}}\left( {\frac{{{{m}_{0}}}}{r}\left( {\frac{{{{m}_{2}}}}{r}\omega _{2}^{2}{{\Delta }_{1}} + \frac{{{{m}_{1}}}}{r}\omega _{1}^{2}{{\Delta }_{2}} - } \right.} \right. \\ \, - \left. {i\left| {{{\omega }_{{ce}}}} \right|\left( {{{\omega }_{2}}{{\Delta }_{1}}{{{\hat {q}}}_{{2r}}} + {{\omega }_{1}}{{\Delta }_{2}}{{{\hat {q}}}_{{1r}}}} \right)} \right) + \\ \end{gathered} $

(7)

$\begin{gathered} \, + {{\omega }_{2}}\left( {\left( {i\left| {{{\omega }_{{ce}}}} \right|\left( {\frac{{{{m}_{1}}}}{r}{{\Delta }_{2}} - {{\omega }_{1}}\left( {{{\omega }_{1}} - {{\omega }_{2}}} \right)\frac{{{{m}_{2}}}}{r}} \right) - } \right.} \right. \\ \left. {\mathop - \limits_{_{{_{{_{{}}}}}}} \;{{\omega }_{1}}{{\Delta }_{1}}{{{\hat {q}}}_{{1r}}} - {{\omega }_{1}}\left( {{{\omega }_{1}}{{\omega }_{2}} - {{{\left| {{{\omega }_{{ce}}}} \right|}}^{2}}} \right){{{\hat {q}}}_{{2r}}}} \right){{{\hat {q}}}_{{1r}}} + \\ \end{gathered} $

$\begin{gathered} \, + \frac{{{{m}_{1}}}}{r}\left( {\left| {{{\omega }_{{ce}}}} \right|\left( {{{\omega }_{1}}\left( {{{\omega }_{1}} - {{\omega }_{2}}} \right){{{\hat {q}}}_{{2r}}} - i{{\Delta }_{2}}{{{\hat {q}}}_{{1r}}}} \right)\mathop - \limits_{_{{_{{}}}}} } \right. \\ \, - \left. {{{\omega }_{1}}\frac{{{{m}_{2}}}}{r}\left( {{{\omega }_{1}}{{\omega }_{2}} - {{{\left| {{{\omega }_{{ce}}}} \right|}}^{2}}} \right) - \frac{{{{m}_{1}}}}{r}{{\omega }_{1}}{{\Delta }_{2}}} \right) + \\ \left. {\mathop + \limits_{}^{} \;\left. {\left. {\left. {{{\Delta }_{1}}\left( {{{\omega }_{2}}{{{\hat {q}}}_{{2r}}} + i\frac{{{{m}_{2}}}}{r}\left| {{{\omega }_{{ce}}}} \right|} \right){{{\hat {k}}}_{r}}} \right)} \right)} \right)} \right). \\ \end{gathered} $

Правила действия дифференциальных операторов первого порядка ${{\hat {k}}_{x}}$, ${{\hat {q}}_{{1r}}}$ и ${{\hat {q}}_{{2r}}}$таковы:

${{\hat {k}}_{r}}\left[ {{{E}_{z}}\left( {\mathbf{r}} \right){{\varphi }_{2}}\left( r \right)} \right] = - i{{\varphi }_{2}}\left( r \right)\partial {{E}_{z}}\left( {\mathbf{r}} \right){\text{/}}\partial r,$

$\begin{gathered} {{{\hat {q}}}_{{1r}}}\left[ {{{E}_{z}}\left( {\mathbf{r}} \right){{\varphi }_{2}}\left( r \right)} \right] = - i{{E}_{z}}\left( {\mathbf{r}} \right)\partial {{\varphi }_{2}}\left( r \right){\text{/}}\partial r - \\ \, - i{{\varphi }_{2}}\left( r \right)\partial {{E}_{z}}\left( {\mathbf{r}} \right){\text{/}}\partial r, \\ \end{gathered} $

${{\hat {q}}_{{2r}}}\left[ {{{E}_{z}}\left( {\mathbf{r}} \right){{\varphi }_{2}}\left( r \right)} \right] = - i{{E}_{z}}\left( {\mathbf{r}} \right)\partial {{\varphi }_{2}}\left( r \right){\text{/}}\partial r.$

Надо отметить, что при выводе уравнений (5) мы опустили члены, которые появляются при дифференцировании компоненты тензора ε по радиальной координате, поскольку распад колебаний (4) имеет место в окрестности локального максимума плотности, где градиентные эффекты не существенны.

При анализе системы уравнений (5) будем считать, что нелинейная связь является слабой, и используем подход теории возмущений, развитый в работе [20]. На первом шаге пренебрежем правыми частями (5) и найдем решения обыкновенных дифференциальных уравнений, которые описывают две независимые КЛ волны

$\begin{gathered} \left( {\varepsilon \left( {{{\omega }_{1}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{r}\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}} \right) + \eta \left( {{{\omega }_{1}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right){{\varphi }_{1}} = 0,{\text{ }} \\ \left( {\varepsilon \left( {{{\omega }_{2}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{r}\frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}} \right) + \eta \left( {{{\omega }_{2}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right){{\varphi }_{2}} = 0. \\ \end{gathered} $

Будем искать решение в виде

${{\varphi }_{{1,2}}}\left( {{\mathbf{r}},t} \right) = \frac{{{{\phi }_{{1,2}}}(r)}}{2}\exp \left( {i{{m}_{{1,2}}}\theta + i{{q}_{z}}z \mp i{{\omega }_{{1,2}}}t} \right) + c.c.,$

что позволяет описать две КЛ волны, распространяющиеся в противоположных направлениях по магнитному полю и по азимуту. Подставим (9) в (8) и получим уравнения для амплитуд потенциалов КЛ волн:

$\left\{ \begin{gathered} \left( {{{{\left. {\varepsilon ({{\omega }_{1}})} \right|}}_{{r = 0}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} - \frac{{m_{1}^{2}}}{{{{r}^{2}}}}} \right) - q_{z}^{2}\eta ({{\omega }_{1}},r)} \right) \times \hfill \\ \times \;{{\phi }_{1}}(r) = 0,{\text{ }} \hfill \\ \left( {{{{\left. {\varepsilon ({{\omega }_{2}})} \right|}}_{{r = 0}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} - \frac{{m_{2}^{2}}}{{{{r}^{2}}}}} \right) - q_{z}^{2}\eta ({{\omega }_{2}},r)} \right) \times \hfill \\ \times \;{{\phi }_{2}}(r) = 0, \hfill \\ \end{gathered} \right.$

где $\eta \left( {{{\omega }_{{1,2}}},r} \right) = 1 - \bar {n}{\text{/}}{{n}_{c}}\left( {{{\omega }_{{1,2}}}} \right)\left( {1 - {{r}^{2}}{\text{/}}l_{b}^{2}} \right)$ и ${{n}_{c}}\left( {{{\omega }_{{1,2}}}} \right)$ – критическая плотность на соответствующей частоте. Решения (10) могут быть выражены через обобщенные полиномы Лаггера $L_{l}^{m}$ [21]:

$\begin{gathered} {{\phi }_{{1,2}}}(r) = \\ = \frac{{{{С}_{{1,2}}}}}{{R_{{{{l}_{{1,2}}}}}^{{{{m}_{{1,2}}}}}}}\exp \left( { - \frac{{{{s}_{{1,2}}}{{{(r)}}^{2}}}}{2}} \right){{s}_{{1,2}}}{{(r)}^{{{{m}_{{1,2}}}}}}L_{{{{l}_{{1,2}}}}}^{{{{m}_{{1,2}}}}}\left( {{{s}_{{1,2}}}{{{(r)}}^{2}}} \right), \\ \end{gathered} $

где ${{С}_{{1,2}}} = {\text{const}}$, $R_{{{{l}_{{1б2}}}}}^{{{{m}_{{1,2}}}}} = \sqrt {({{l}_{{1,2}}} + {{m}_{{1,2}}})!{\text{/}}\left( {2\kappa _{{1,2}}^{2}{{l}_{{1,2}}}!} \right)} $, ${{s}_{{1,2}}}\left( r \right) = {{\kappa }_{{1,2}}}r$ – безразмерная радиальная переменная и ${{\kappa }_{{1,2}}} = {{\left( {{{{\sqrt {\left. {\bar {n}{\text{/}}\left( {{{n}_{c}}\left( {{{\omega }_{{1,2}}}} \right)\varepsilon \left( {{{\omega }_{{1,2}}}} \right)} \right)} \right|} }}_{{r = 0}}}{{q}_{z}}{\text{/}}{{l}_{b}}} \right)}^{{1/2}}} = {\text{const}}$. Собственные частоты $\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}$ ($\omega _{2}^{{{{l}_{1}},{{l}_{2}}}} = {{\omega }_{0}} - \omega _{1}^{{{{l}_{1}},{{l}_{2}}}}$) и собственные волновые числа $q_{z}^{{{{l}_{1}},{{l}_{2}}}}$ двух КЛ волн удовлетворяют системе уравнений

$\left\{ \begin{gathered} {{\left. {\frac{{\left| {\eta \left( {\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} \right|}}{{\sqrt {\varepsilon \left( {\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} }}} \right|}_{{r = 0}}}\frac{{q_{z}^{{{{l}_{1}},{{l}_{2}}}}{{l}_{b}}}}{{\sqrt {\bar {n}{\text{/}}{{n}_{c}}\left( {\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} }} = 4{{l}_{1}} + 2{{m}_{1}} + 2, \hfill \\ {{\left. {\frac{{\left| {\eta \left( {{{\omega }_{0}}\, - \,\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} \right|}}{{\sqrt {\varepsilon \left( {{{\omega }_{0}}\, - \,\omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} }}} \right|}_{{r = 0}}}{\kern 1pt} \frac{{q_{z}^{{{{l}_{1}},{{l}_{2}}}}{{l}_{b}}}}{{\sqrt {\bar {n}{\text{/}}{{n}_{c}}\left( {{{\omega }_{0}} - \omega _{1}^{{{{l}_{1}},{{l}_{2}}}}} \right)} }}\, = \,4{{l}_{2}}\, + \,2{{m}_{2}}\, + \,2, \hfill \\ \end{gathered} \right.$

где ${{m}_{1}} = {{m}_{0}} + {{m}_{2}}$.

На втором шаге процедуры теории возмущений примем во внимание эффект нелинейной связи КЛ волн в присутствии накачки (4). В этом случае их амплитуды перестают быть постоянными величинами и становятся функциями времени и координаты z, т.е. ${{C}_{{1,2}}} \to {{C}_{{1,2}}}\left( {z,t} \right)$. Для того чтобы получить уравнения, описывающие эти амплитуды, воспользуемся процедурой укорачивания. С этой целью подставим выражения (4) и (9) в (5), умножим первое из них на $\phi _{1}^{*}\exp \left( { - i{{m}_{1}}\theta - i{{q}_{z}}z} \right)$, второе – на $\phi _{2}^{*}\exp \left( { - i{{m}_{2}}\theta - i{{q}_{z}}z} \right)$ и проинтегрируем их $\frac{1}{{2\pi }}\int_0^{2\pi } {d\theta } \int_0^\infty {rdr...} $ В итоге получим

$\left\{ \begin{gathered} \frac{{\partial {{a}_{1}}}}{{\partial t}} + {{u}_{1}}\frac{{\partial {{a}_{1}}}}{{\partial z}} + {{\nu }_{{d1}}}{{a}_{1}} = {{\nu }_{{12}}}\sqrt {\frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}}} {{a}_{2}} \hfill \\ \frac{{\partial {{a}_{2}}}}{{\partial t}} - {{u}_{2}}\frac{{\partial {{a}_{2}}}}{{\partial z}} + {{\nu }_{{d2}}}{{a}_{2}} = {{\nu }_{{21}}}\sqrt {\frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}}} {{a}_{1}} \hfill \\ \end{gathered} \right..$

В уравнениях (13) использованы обозначения: ${{u}_{{1,2}}}$ – усредненные по области локализации КЛ волн их продольные по отношению к внешнему магнитному полю групповые скорости,

${{\nu }_{{d1,2}}} = \frac{{{{{\left\langle {\eta {\kern 1pt} '{\kern 1pt} '({{\omega }_{1}}) - \frac{{\eta {\kern 1pt} '({{\omega }_{1}})}}{{\varepsilon {\kern 1pt} '({{\omega }_{1}})}}\varepsilon {\kern 1pt} '{\kern 1pt} '({{\omega }_{1}})} \right\rangle }}_{{1,2}}}}}{{\sqrt {{{{\left\langle {\,\omega _{{pe}}^{2}\left( {\frac{1}{{\omega _{1}^{3}}} - \frac{{\omega _{1}^{{}}}}{{{{{\left( {\omega _{1}^{2} - \omega _{{ce}}^{2}} \right)}}^{2}}}}\frac{{\eta {\kern 1pt} '({{\omega }_{1}})}}{{\varepsilon {\kern 1pt} '({{\omega }_{1}})}}} \right)} \right\rangle }}_{1}}{{{\left\langle {\omega _{{pe}}^{2}\left( {\frac{1}{{\omega _{2}^{3}}} - \frac{{\omega _{2}^{{}}}}{{{{{\left( {\omega _{2}^{2} - \omega _{{ce}}^{2}} \right)}}^{2}}}}\frac{{\eta {\kern 1pt} '({{\omega }_{2}})}}{{\varepsilon {\kern 1pt} '({{\omega }_{2}})}}} \right)} \right\rangle }}_{2}}} }}$

– коэффициенты, описывающие затухание КЛ волн,

${{\nu }_{{12,21}}} = \frac{{\frac{1}{4}\frac{{{{E}_{0}}\left( {{{P}_{0}},0,z} \right)}}{{q_{z}^{2}H}}\int\limits_0^\infty {{{{\hat {\chi }}}_{{12,21}}}\left( r \right)\left[ {\phi _{1}^{*}\left( r \right){{\phi }_{2}}\left( r \right)\sqrt {\frac{{{{\omega }_{0}}}}{{c{{k}_{x}}}}} {{J}_{{{{m}_{0}}}}}\left( {{{k}_{x}}r} \right)} \right]rdr} }}{{\sqrt {{{{\left\langle {\omega _{{pe}}^{2}\left( {\frac{1}{{\omega _{1}^{3}}} - \frac{{\omega _{1}^{{}}}}{{{{{\left( {\omega _{1}^{2} - \omega _{{ce}}^{2}} \right)}}^{2}}}}\frac{{\eta {\kern 1pt} '({{\omega }_{1}})}}{{\varepsilon {\kern 1pt} '({{\omega }_{1}})}}} \right)} \right\rangle }}_{1}}{{{\left\langle {\omega _{{pe}}^{2}\left( {\frac{1}{{\omega _{2}^{3}}} - \frac{{\omega _{2}^{{}}}}{{{{{\left( {\omega _{2}^{2} - \omega _{{ce}}^{2}} \right)}}^{2}}}}\frac{{\eta {\kern 1pt} '({{\omega }_{2}})}}{{\varepsilon {\kern 1pt} '({{\omega }_{2}})}}} \right)} \right\rangle }}_{2}}} }}$

– коэффициенты нелинейной связи и ${{\omega }_{2}} = $ $ = {{\omega }_{0}} - {{\omega }_{1}}$. Усреднение по области локализации означает

${{\left\langle {...} \right\rangle }_{{1,2}}} = \int\limits_0^\infty {...{{{\left| {{{\phi }_{{1,2}}}} \right|}}^{2}}rdr} .$

В системе уравнений (13) также использована новая нормировка искомых функций, а именно, ${{\left| {{{a}_{{1,2}}}} \right|}^{2}}$ – это плотность энергии соответствующих плазмонов. Будем считать, что распределение волны накачки вдоль магнитного поля имеет прямоугольную форму, т.е. ${\text{|}}{{\nu }_{{12}}}{{\nu }_{{21}}}{\text{|}} = {\text{|}}{{\nu }_{0}}{{{\text{|}}}^{2}}$ при $0 < z < {{w}_{z}}$ и ${\text{|}}{{\nu }_{{12}}}{{\nu }_{{21}}}{\text{|}} = 0$ – вне этой области. Далее, будем искать экспоненциально растущие решения ${{a}_{{1,2}}}\left( {z,t} \right) \propto \exp \left( {\gamma t} \right)$, используя граничные условия ${{a}_{1}}\left( 0 \right) = 0$ и ${{a}_{2}}\left( {{{w}_{z}}} \right) = 0$. Выразим из первого уравнения амплитуду ${{a}_{2}}$

${{a}_{2}} = \sqrt {\frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}}} \left( {\frac{{\gamma + {{\nu }_{{d1}}}}}{{{{\nu }_{0}}}}{{a}_{1}} + \frac{{{{u}_{1}}}}{{{{\nu }_{0}}}}\frac{{\partial {{a}_{1}}}}{{\partial z}}} \right).$

Подставим (17) во второе уравнение

$\begin{gathered} \frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{z}^{2}}}} + \frac{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) - \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}{{{{u}_{1}}{{u}_{2}}}}\frac{\partial }{{\partial z}}{{a}_{1}} + \\ \, + \frac{{{{{\left| {{{\nu }_{0}}} \right|}}^{2}} - \left( {\gamma + {{\nu }_{{d1}}}} \right)\left( {\gamma + {{\nu }_{{d2}}}} \right)}}{{{{u}_{1}}{{u}_{2}}}}{{a}_{1}} = 0. \\ \end{gathered} $

Сделаем функциональную подстановку

${{a}_{1}} = \exp \left( { - \frac{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) - \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}{{2{{u}_{1}}{{u}_{2}}}}z} \right)f,$

которая приводит уравнение (18) к виду

$\frac{{{{\partial }^{2}}f}}{{\partial {{z}^{2}}}} + \left( {\frac{{{{{\left| {{{\nu }_{0}}} \right|}}^{2}}}}{{{{u}_{1}}{{u}_{2}}}} - \frac{{{{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) + \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}^{2}}}}{{4u_{1}^{2}u_{2}^{2}}}} \right)f = 0.$

Решение этого уравнения, удовлетворяющее граничному условию, есть

$\begin{gathered} f = \sin \left( {Qz} \right), \\ Q = \sqrt {\frac{{{{{\left| {{{\nu }_{0}}} \right|}}^{2}}}}{{{{u}_{1}}{{u}_{2}}}} - \frac{{{{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) + \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}^{2}}}}{{4u_{2}^{2}u_{1}^{2}}}} . \\ \end{gathered} $

Подставим (19) и (20) в уравнение (17) и учтем граничное условие для второй дочерней волны

$\begin{gathered} {{\left. {{{a}_{2}}} \right|}_{{z = {{w}_{z}}}}} = \sqrt {\frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}}} \times \\ \, \times \exp \left( { - \frac{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) - \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}{{2{{u}_{1}}{{u}_{2}}}}{{w}_{z}}} \right) \times \\ \end{gathered} $

$\begin{gathered} \, \times \left( {\frac{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) + \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}{{2{{u}_{2}}{{\nu }_{0}}}}\sin \left( {Q{{w}_{z}}} \right) + } \right. \\ \left. {\, + Q\frac{{{{u}_{1}}}}{{{{\nu }_{0}}}}\cos \left( {Q{{w}_{z}}} \right)} \right) = 0, \\ \end{gathered} $

что позволяет получить дисперсионное уравнение

$\cot \left( {Q{{w}_{z}}} \right) = - \frac{{\left( {{{u}_{2}}\left( {\gamma + {{\nu }_{{d1}}}} \right) + \left( {\gamma + {{\nu }_{{d2}}}} \right){{u}_{1}}} \right)}}{{2{{u}_{2}}{{u}_{1}}Q}},$

первый (наименьший) из корней которого можно приближенно представить в виде

$2\gamma \simeq - 2\frac{{{{u}_{2}}{{\nu }_{{d1}}} + {{\nu }_{{d2}}}{{u}_{1}}}}{{{{u}_{2}} + {{u}_{1}}}} + \frac{{4\sqrt {{{u}_{1}}{{u}_{2}}} }}{{{{u}_{2}} + {{u}_{1}}}}\sqrt {{{{\left| {{{\nu }_{0}}} \right|}}^{2}} - {{{\left( {\frac{{\pi \sqrt {{{u}_{1}}{{u}_{2}}} }}{{2{{w}_{z}}}}} \right)}}^{2}}} .$

Порог возбуждения параметрической неустойчивости находится из соотношения

${{\left| {{{\nu }_{0}}} \right|}^{2}}\left( {P_{0}^{{th}}} \right) = {{\left( {\frac{{\pi \sqrt {{{u}_{1}}{{u}_{2}}} }}{{2{{w}_{z}}}}} \right)}^{2}} + {{\left( {\frac{{{{u}_{2}}{{\nu }_{{d1}}} + {{\nu }_{{d2}}}{{u}_{1}}}}{{2\sqrt {{{u}_{1}}{{u}_{2}}} }}} \right)}^{2}}.$

Далее рассмотрим пример параметрического распада, сценарий которого был проанализирован в этом разделе.

3. ПРИМЕР ПАРАМЕТРИЧЕСКОГО РАСПАДА ОБЫКНОВЕННОЙ ВОЛНЫ НА ДВЕ КЛ ВОЛНЫ

Чтобы проиллюстрировать аналитические зависимости, полученные в предыдущем параграфе, мы берем параметры, которые являются типичными для модельных экспериментов в линейной плазменной установке “Гранит”. В этих экспериментах наблюдалось аномальное поглощение мощности обыкновенной волны в плазменном филаменте [17]. Плазма в аргоне создавалась с помощью высокочастотного разряда в длинной стеклянной трубке с внутренним диаметром 2l_b =22 мм, которая была ориентирована в направлении постоянного магнитного поля B₀ = = 570 Гс (подробнее см. [17]). Получаемая в разряде плазма была слабоионизованной с параметрами 〈n〉 = 2.9 × 10¹⁰ см^–3 и T_e = 1 эВ. Волна обыкновенной поляризации на частоте 2.35 ГГц распространялась вдоль прямоугольного волновода, через который под прямым углом к его оси проходит баллон с плазмой. Для этих параметров выполняется предельное соотношение ${{k}_{x}}{{l}_{b}} \ll 1$, что сильно упрощает выражение (4):

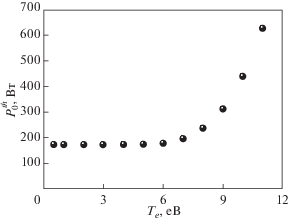
${\mathbf{E}} \simeq {{{\mathbf{e}}}_{z}}\frac{{{{E}_{0}}}}{2}{{J}_{0}}\left( {{{k}_{x}}r} \right)\exp \left( { - i{{\omega }_{0}}t} \right) + c.c.$

Мы анализируем параметрический распад волны накачки (23) на два распространяющихся в разных направлениях КЛ плазмона, частота которых близка к значению, равному половине частоты волны накачки. Частоты этих плазмонов f₁ = = 1.26 ГГц (${{m}_{1}} = 1$, ${{l}_{1}} = 0$) и f₂ = 1.09 ГГц (${{m}_{2}} = 1$, ${{l}_{2}} = 1$). Продольное волновое число этих дочерних волн равно q_z = 28.38 см^–1, а квадрат продольного показателя преломления $k_{z}^{2}{{c}^{2}}{\text{/}}\omega _{{1,2}}^{2} > 2 \times {{10}^{4}}$ с огромным запасом превосходит значения компонент тензора диэлектрической проницаемости, что позволяет обосновать использование потенциального приближения применительно к возбуждаемым в результате параметрического распада волнам. На рис. 1 показан инкремент этой неустойчивости, вычисленный по формуле (21), в зависимости от мощности волны накачки. Видно, что порог ее возбуждения равен $P_{0}^{{th}}$ = 171 Вт. Это значение близко к тем мощностям накачки, при которых наблюдалось сильное аномальное поглощение обыкновенной волны накачки в экспериментах [17]. На рис. 2 мы приводим зависимость порога неустойчивости от электронной температуры в филаменте. Для актуального для модельного эксперимента [17] диапазона электронной температуры (T_e = 0.1–5 эВ) порог этой неустойчивости определяется конвективным выносом КЛ волн вдоль по магнитному полю и остается меньше 200 Вт, однако при больших температурах он резко возрастает из-за роста затухания Ландау и электронного циклотронного затухания КЛ волн. Таким образом, двухплазмонная ПРН обыкновенной волны может иметь место в линейной экспериментальной установке при мощности генератора, доступной в эксперименте [17]. Этот результат позволяет объяснить появление аномального поглощения СВЧ-волны обыкновенной поляризации в этом эксперименте.

Рис. 1.

Инкремент распадной параметрической неустойчивости (19). Частоты дочерних КЛ-волн f₁ = = 1.26 ГГц (${{m}_{1}} = 1$, ${{l}_{1}} = 0$) и f₂ = 1.09 ГГц (${{m}_{2}} = 1$, ${{l}_{2}} = 1$). Продольное волновое число q_z = 28.38 см^–1. $P_{0}^{{th}}$ = 171 Вт.

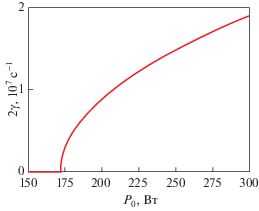
Рис. 2.

Зависимость порога неустойчивости от электронной температуры в плазменном образовании. Параметры дочерних КЛ-волн те же, что и на рис. 1.

4. ВЫВОДЫ

В настоящей статье мы проанализировали возможность низкопорогового параметрического распада волны обыкновенной поляризации на два косых ленгмюровских плазмона. Ключевым элементом теоретической модели является возможность радиальной локализации обеих дочерних волн, бегущих в азимутальном направлении. Таким образом, имеет место двумерная локализация этих колебаний в плазменном образовании, вытянутом вдоль магнитного поля. Получено выражение для инкремента неустойчивости, а также выражение, определяющее порог возбуждения неустойчивости. Показано, что это нелинейное явление может быть обнаружено в модельных экспериментах на линейной плазменной установке, что позволяет объяснить наблюдавшееся на ней аномальное поглощение СВЧ-мощности обыкновенной поляризации и делает актуальным проведение дальнейших экспериментальных исследований. Полученные аналитические зависимости предполагается использовать при дальнейшем подробном экспериментальном исследовании этого нелинейного явления для сравнения с результатами измерений.

Несмотря на драматическое различие экспериментальных параметров в линейной установке и в тороидальных установках удержания плазмы, представляется, что рассмотренный сценарий носит универсальный характер, что делает необходимым в дальнейшем исследовать этот сценарий применительно к экспериментам по ЭЦРН плазмы в токамаках и стеллараторах. При этом необходимо отказаться от предположения о малости радиуса плазменного филамента по сравнению с длиной волны накачки и учесть рефракцию волны накачки в ннм. Результаты этого анализа планируется представить в последующих публикациях.

Расчет порога и инкремента неустойчивости выполнен при поддержке гранта РФФИ-БРФФИ 18-52-00010 – F18R-040; выражения для нелинейной восприимчивости плазмы получены в рамках работ по государственному контракту ФТИ им. А.Ф. Иоффе РАН.

Список литературы

Cohen B.I., Cohen R.H., Nevins W.M., Rognlien T.D. // Rev. Mod. Phys. 1991. V. 63. P. 949.
Westerhof E., Nielsen S.K., Oosterbeek J.W., Salewski M, de Baar M.R., Bongers W.A., Bürger A., Hennen B.A., Korsholm S.B., Leipold F., Moseev D., Stejner M., Thoen D.J. and the TEXTOR Team // Phys. Rev. Lett. 2009. V. 103. 125001.
Nielsen S.K., Salewski M., Westerhof E., Bongers W., Korsholm S.B., Leipold F., Oosterbeek J.W., Moseev D., Stejner M. and the TEXTOR Team // Plasma Phys. Control. Fusion. 2013. V. 55. 115003.
Hansen S.K., Nielsen S.K., Stober J., Rasmussen J., Salewski M., Stejner M., Hoelzl M., and the ASDEX Upgrade Team // Proc. 46^th EPS Conf. Plasma Physics. 2019. ECA. V. 43C. P1.1075.
Coda S. for the TCV Team // Nucl. Fusion. 2015. V. 55. 104004.
Martínez M., Zurro B., Baciero A., Jiménez-Rey D., Tribaldos V. // Plasma Phys. Control. Fusion. 2018. V. 60. 025024.
Gusakov E.Z., Popov A.Yu. // Phys. Plasmas. 2016. V. 23. 082503.
Popov A.Yu., Gusakov E.Z. // Europhys. Lett. 2016. V. 116. P. 45002.
Altukhov A.B., Arkhipenko V.I., Gurchenko A.D., Gusa-kov E.Z., Popov A.Yu., Simonchik L.V., Usachonak M.S. // Europhys. Lett. 2019. V. 126. P. 15002.
Гусаков Е.З., Попов А.Ю., Третинников П.В. // Письма в ЖЭТФ. 2018. Т. 108. С. 83. [Gusakov E.Z., Popov A.Yu. and Tretinnikov P.V. // JETP Lett. 2018. V. 108. P. 93.]
Kubo S., Nishiura M., Tanaka K., Shimozuma T., Yoshimura Y., Igami H., Takahash H., Mutoh T., Tamura N., Tatematsu Y., Saito T., Notake T., Korsholm S.B., Meo F., Nielsen S.K., Salewski M., Stejner M. // Rev. Sci. Instrum. 2010. V. 81. 10D535.
Bruschi A., Alessi E., Bin W., D’Arcangelo O., Baioc-chi B., Belli F., Calabrò G., Casiraghi I., Cocilovo V., Figini L., Galperti C., Garavaglia S., Granucci G., Grosso G., Korsholm S.B., Lontano M., Lubyako L., Mazzotta C., Mellera V., Moro A., Nielsen S.K., Orsitto F., Ramogi-da G., Rasmussen J., Ricci D., Stejner M., Tartari U. and FTU Team // Nucl. Fusion. 2017. V. 57. 076004.
Gusakov E.Z., Popov A.Yu., Saveliev A.N., Sysoeva E.V. // Plasma Phys. Control. Fusion. 2017. V. 59. 075002.
Gusakov E.Z., Popov A.Yu. // Phys. Plasmas. 2018. V. 25. 012101.
Gusakov E.Z., Popov A.Yu., Saveliev A.N. // Plasma Phys. Control. Fusion. 2019. V. 61. P025006.
Гусаков Е.З., Федоров В.И. // Физика плазмы. 1979. V. 5. P. 469. [Gusakov E.Z., Fedorov V.I. // Sov. J. Plasma Phys. 1979. V. 5. P. 263.]
Simonchik L., Altukhov A., Arkhipenko V., Gurchenko A., Gusakov E., Popov A., Usachonak M. // Proc. 46^th EPS Conf. on Plasma Physics. 2019. ECA. V. 43C. P2.4012.
Sommerfeld A. // Partial differential equations in physics. Academic Press, 1949. V. 1.
Попов А.Ю., Третинников П.В., Гусаков Е.З., Симончик Л.В. // Физика плазмы. 2020. V. 46. P. 380. [Popov A.Yu., Tretinnikov P.V., Gusakov E.Z., Simon-chik L.V. // Plasma Phys. Rep. 2020. V. 46. P. 430.]
Гусаков Е.З., Федоров В.И. // Физика плазмы. 1979. V. 5. P. 827. [Gusakov E.Z., Fedorov V.I. // Sov. J. Plasma Phys. 1979. V. 5. P. 463.]
Abramowitz M., Stegun I.A. (Eds.) // Orthogonal Polynomials. Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing. New York: Dover. 1972. P. 775.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал