Физика плазмы, 2020, T. 46, № 7, стр. 633-644
Влияние неэкстенсивных ионов (тяжелых и легких) на ионно-звуковые солитонные волны в замагниченной пятикомпонентной кометной плазме с каппа-распределением электронов
M. Manesh a, V. Anu b, T.W. Neethu c, S. Sijo d, G. Sreekala b, C. Venugopal b, *
a Department of Physics, University of Calicut
673 635 Kerala, Malappuram, India
b School of Pure & Applied Physics, Mahatma Gandhi University, Priyadarshini Hills
686 560 Kerala, Kottayam, India
c Department of Physics, C. M. S. College
686 001 Kerala, Kottayam, India
d Department of Physics, S.B. College, Changanacherry
686 101 Kerala, Kottayam, India
* E-mail: cvgmgphys@yahoo.co.in
Поступила в редакцию 12.06.2019
После доработки 08.11.2019
Принята к публикации 20.11.2019
Аннотация
Исследованы характеристики распространения ионно-звуковых солитонов (IASW) в замагниченной кометной плазме, состоящей из ионов водорода, положительно и отрицательно заряженных ионов кислорода, горячих солнечных электронов с каппа-распределением и немного более холодных кометных электронов. С помощью вывода уравнения Захарова – Кузнецова (ZK) изучено влияние q-неэкстенсивных распределений на более легкие и на более тяжелые ионы. С помощью численного анализа уравнения ZK были тщательно изучены основные характеристики IASW, такие как амплитуда, ширина и фазовая скорость. Показано, что надтепловые электроны и неэкстенсивные ионы существенно изменяют характеристики солитонных волн. По-видимому, амплитуды солитонов хорошо коррелируют с присутствием молекул воды в кометной плазме и связанными с этим процессами фотоионизации
1. ВВЕДЕНИЕ
Уединенные волны (или солитоны) подробно изучались среди множества нелинейных явлений в плазме. Первый нелинейный анализ ионно-звуковых солитонов был сделан Сагдеевым [1]. В настоящее время ионно-звуковые солитонные волны (IASW) представляют собой основную тему современных исследований плазмы. Он начался с вывода уравнения Кортевега–де Фриза (KdV) для распространения IASW в плазме с одним типом положительного иона и электронов [2]. Распространение этого исследования на плазму, содержащую положительные и отрицательные ионы, было начато в работе [3], а на электрон-позитрон-ионную плазму в [4].
При критическом значении плотности отрицательных ионов коэффициент при нелинейном члене может быть обнулен, поэтому нужно учитывать кубическую нелинейность. Таким образом, теперь IASW описываются модифицированным уравнением Кортевега–Де Фриза (mKdV). Однако, если концентрация отрицательных ионов только близка к критическому значению, необходимо сохранять как квадратичную, так и кубическую нелинейность. В этом случае нелинейные IA волны описываются уравнением Гарднера [5]. Так как вышеупомянутые исследования были в основном одномерными (1-D), Захаров и Кузнецов расширили его до 3-D [6]; Уравнение, описывающее распространение SW в 3-D, теперь широко известно, как уравнение ZK. Эти работы положили начало новаторским исследованиям по нескольким фундаментальным аспектам солитонов, таким как их устойчивость [7], возникновение и эволюция [8–11], связь с волнами [12], другими уединенными волнами [13] и явлениями [14, 15]. Эти исследования завершились несколькими книгами о нелинейных явлениях [16–20]. Другие исследователи IASW сосредоточились на влиянии примесей [21], супер-IA солитонах [22] и различных аспектах ионно-звуковых пылевых солитонов [23–25]. В плазме, описываемой немаксвелловскими распределениями, Саху и Ройчоудхури [26] исследовали влияние надтепловых электронов и эффектов, вызванных цилиндрической геометрией, на солитонные IA-волны путем вывода уравнения ZK. Они наблюдали уменьшение доли надтепловых электронов, увеличение амплитуды солитонных электростатических потенциальных структур. Уравнение ZK также описывает поведение слабо нелинейных IA-волн в плазме с холодными ионами и горячими изотермическими электронами при наличии однородного магнитного поля [27, 28]. Трехмерное обобщенное уравнение Захарова–Кузнецова (EZK) было получено Эль-Лабани и др. [29] для нелинейных ленгмюровских волн с небольшими, но конечными амплитудами, и исследовано как аналитически, так и численно.
Вазваз [30] изучил уравнение Гарднера, также называемое “комбинированным уравнением KdV–mKdV”, и предложил новый гиперболический анзац для получения солитонных решений. Го и др. [31] исследовали нелинейное распространение IA-волн в одномерной незамагниченной плазме положительных и отрицательных ионов и нетепловых электронов с распределением Цаллиса, через которое проходит пучок отрицательных ионов. Полученное уравнение Гарднера подробно обсуждалось, чтобы выявить влияние параметров плазмы на IASW сжатия и разрежения.
Недавно IA-солитоны были изучены Рехманом и Мишрой [32] в бесстолкновительной плазме, состоящей из теплых адиабатических ионов, изотермических позитронов и двухтемпературного распределения электронов. Для системы были выведены уравнения Кортевега–Де Вриза (KdV), модифицированные уравнения KdV (-mKdV) и Гарднера. Солитонное решение уравнения Гарднера показало, что существует критическое значение отношения температур холодных и горячих электронов β = Tc/Th, ниже которого существуют только солитоны разряжения, а выше – только KdV солитоны сжатия.
В плазме разных космических сред наблюдаются значительные отклонения от хорошо известного распределения Максвелла из-за наличия частиц высокой энергии в хвосте распределения. Используя данные о солнечном ветре, Васюлунас впервые предсказал немаксвелловское распределение, характеризуемое спектральным индексом каппа (κ); более низкие значения каппа соответствуют более высокому вкладу надтепловых частиц [33].
Неэкстенсивная статистическая механика, которая привлекает широкое внимание в течение последних трех десятилетий, показывает отклонение от энтропийных измерений Больцмана–Гиббса–Шеннона (B–G–S). Неэкстенсивная энтропия, которая является обобщением B–G–S энтропии, была впервые предложена К. Цаллисом [34]. Он обобщил стандартную аддитивную природу энтропии на нелинейный неэкстенсивный случай, введя параметр q: стандартной обобщенной статистике B–G–S или максвелловскому распределению соответствует q = 1. Каппа-распределение максимизирует энтропию неэкстенсивной статистической механики при ограничениях канонического ансамбля. Эта энтропийная формулировка была исследована несколькими авторами в 1970-х г. [35–37], но ее окончательный вид и использование в статистической механике принадлежали Цаллису [34]. В плазменных средах, где существенны дальнодействующие взаимодействия, такие как авроральная зона, магнитосфера, кольца планет и солнечный ветер, максвелловское описание может быть неадекватным, поэтому такие системы целесообразно моделировать распределениями типа Цаллиса (q-неэкстенсивного) или каппа-распределением.
Как упоминалось выше, каппа-распределения определяются с помощью спектрального индекса κ, который определяет наклон хвоста высокой энергии в спектре скоростей частиц плазмы; чем меньше значение κ, тем больше число высокоэнергетичных частиц. Кроме того, при $\kappa \to \infty $, каппа-распределение сводится к распределению Максвелла [38]. С другой стороны, распределение Цаллиса, которое характеризуется параметром неэкстенсивности q (q является мерой отклонения данного распределения от распределения Максвелла – Больцмана), ведет себя очень по-разному в двух диапазонах –1 < q < 1 и q > 1. В первом диапазоне распределение отлично от нуля во всем интервале скоростей, от –∞ до +∞, и отражает избыток надтепловых частиц в немаксвелловском хвосте; при q > 1 распределение Цаллиса сводится к распределению Максвелла. Наконец, эти два индекса связаны: $\kappa = - {{(1 - q)}^{{ - 1}}}$ [39].
Ионно-звуковые (IA) солитоны изучались в плазме, где электроны и ионы описывались q-неэкстенсивными распределениями. Оказалось, когда электроны описывались распределением Цаллиса, меньшее значение q соответствовало большей ширине солитона [40]. Было обнаружено существование IA-солитонов сжатия и разряжения в двухкомпонентной плазме, где электроны описывались q-неэкстенсивным распределением [41].
Недавно было показано, что в четырехкомпонентной пылевой плазме, содержащей неэкстенсивные электроны и двухтемпературные ионы, существуют солитоны как положительной, так и отрицательной полярности [42]. Аналогично, IASW также изучались в четырехкомпонентной плазме положительно заряженных легких ионов, отрицательных тяжелых ионов, и неэкстенсивных электронов и позитронов. Оказалось, что IA‑солитоны Гарднера отличаются от KdV и m-KdV солитонов [43]. В других исследованиях IASW рассмотрено влияние двухтемпературных неэкстенсивных электронов [44–47], или горячих электронов, описываемых распределением Кернса–Цаллиса [48], горячих электронов и позитронов, описываемых неэкстенсивными распределениями [49–51], и пылевой плазмы с неэкстенсивными электронами [52]. Другие аспекты изучения IASW, по крайней мере, с одной компонентой, описываемой неэкстенсивным распределением, включают неплоскую геометрию [51, 53, 54], модуляционную неустойчивость [55]; столкновения двух IASW [56] и двойные слои [57].
Подробно описанная кометная плазма содержит возникающие в ней более тяжелые ионы, плотность которых зависит от расстояния до ядра, ионы водорода и электроны с разными температурами. Однако Чейзи и др. [58] однозначно идентифицировали отрицательно заряженные ионы кислорода в коме кометы Галлея; позволяя моделировать эту плазму как плазму с ионными парами (O+, O–), с другими более легкими и более тяжелыми ионами, составляющими другие ионные компоненты. Различные исследования также показали, что кометная среда имеет более одной компоненты электронов [59]. Интересно отметить, что недавно две компоненты электронов, наблюдаемые в комете 67P/Чурюмова–Герасименко, были смоделированы с помощью каппа-распределений [60].
Таким образом, кометная плазма моделируется пятикомпонентной плазмой, состоящей из отрицательно и положительно заряженных ионов кислорода, каппа-распределенных электронов солнечного (более горячего) и кометного (более холодного) происхождения, а также ионов водорода. В первом приближении, более тяжелые пары ионов (O– и O+) рассматриваются как неэкстенсивные. Отметим, что устойчивость ионно-звуковых волн изучалась в плазме парных фуллеренов, моделируемой q-неэкстенсивными распределениями [61]. Это исследование было попыткой объяснить ионно-звуковые волны, наблюдаемые в парной фуллерен-ионной плазме, наблюдаемой в лаборатории [62]. Во втором приближении, динамика более легких ионов (H+) определяется с использованием неэкстенсивного распределения, в то время как более тяжелые ионы описываются гидродинамическими уравнениями. Чтобы изучить трехмерную динамику солитонных IA-волн, методом редуктивного возмущения выводится уравнение ZK. Оказалось, что надтепловая часть электронов и неэкстенсивность ионов значительно изменяют различные характеристики солитонной волны, такие как амплитуда, ширина и фазовая скорость.
Работа организована следующим образом: Раздел 1 содержит введение. В разд. 2 сформулирована теоретическая модель и основные уравнения. Раздел 3 посвящен выводу уравнения Захарова–Кузнецова, а его решение получено в разд. 4. Результаты и их обсуждение описаны в разд. 5, а заключительный раздел 6 содержит выводы.
2. ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ И ОСНОВНЫЕ УРАВНЕНИЯ
По причинам, изложенным выше, изучается IASW в намагниченной пятикомпонентной кометной плазме, состоящей из отрицательно и положительно заряженных ионов кислорода (соответственно представленных индексами “1” и “2”), каппа-распределенных горячих электронов солнечного происхождения, более холодных электронов кометного происхождения, и ионов водорода. Внешнее статическое магнитное поле направлено вдоль оси z. В равновесии для нейтральности заряда требуется
2.1. Случай I: неэкстенсивные пары ионов
Динамика ионов водорода теперь описывается следующими трехмерными нормированными гидродинамическими уравнениями:
(1)
$\frac{{\partial {{N}_{{\text{H}}}}}}{{\partial T}} + \nabla \cdot ({{N}_{{\text{H}}}}{{{\mathbf{V}}}_{{\text{H}}}}) = 0,$(2)
$\frac{{\partial {{{\mathbf{V}}}_{{\text{H}}}}}}{{\partial T}} + ({{{\mathbf{V}}}_{{\text{H}}}} \cdot \nabla ){{{\mathbf{V}}}_{{\text{H}}}} = - \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\nabla \varphi + {{\Omega }_{{\text{H}}}}({{{\mathbf{V}}}_{{\text{H}}}} \times {\mathbf{z}}).$Уравнения (1) и (2) нормированы так: $\varphi = e\phi {\text{/}}{{k}_{B}}{{T}_{1}}$, ${{V}_{j}} = {{v}_{j}}{\text{/}}{{c}_{s}}$, $T = t{{\omega }_{{p1}}}$, где ${{c}_{s}} = $ ${{\left( {{{Z}_{1}}{{k}_{B}}{{T}_{1}}{\text{/}}{{m}_{1}}} \right)}^{{1/2}}}$ и ${{\omega }_{{p1}}} = $ $ = {{(4\pi Z_{1}^{2}{{e}^{2}}{{n}_{{10}}}{\text{/}}{{m}_{1}})}^{{1/2}}}$. Переменные x, y и z нормированы с помощью ${{\lambda }_{{D1}}} = {{({{Z}_{1}}{{k}_{B}}{{T}_{1}}{\text{/}}(4\pi Z_{1}^{2}{{e}^{2}}{{n}_{{10}}}))}^{{1/2}}}$, и ${{N}_{{\text{H}}}} = {{n}_{{\text{H}}}}{\text{/}}{{n}_{{{\text{H0}}}}}$. Циклотронная частота ионов водорода ${{Z}_{{\text{H}}}}e{{B}_{0}}{\text{/}}{{m}_{{\text{H}}}}c)$ нормирована на плазменную частоту ${{\omega }_{{p1}}}$ отрицательных ионов кислорода.
Нормированные плотности надтепловых электронов (холодных кометных и более горячих солнечных) и неэкстенсивных ионов кислорода соответственно определяются выражениями
(3)
${{n}_{{ce}}} = {{\left( {1 - \frac{\phi }{{{{\sigma }_{{ce}}}\left( {{{\kappa }_{{ce}}} - 3{\text{/}}2} \right)}}} \right)}^{{ - ({{\kappa }_{{ce}}} - 1/2)}}},$(4)
${{n}_{{se}}} = {{\left( {1 - \frac{\phi }{{{{\sigma }_{{se}}}\left( {{{\kappa }_{{se}}} - 3{\text{/}}2} \right)}}} \right)}^{{ - ({{\kappa }_{{se}}} - 1/2)}}},$Нормированное уравнение Пуассона после подстановки (3) в (6) имеет вид:
(7)
$\begin{gathered} \, - {{N}_{H}}\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{2}}} \right) + \\ \, + {{\mu }_{{ce}}}{{\left( {1 - \frac{\phi }{{{{\sigma }_{{ce}}}\left( {{{\kappa }_{{ce}}} - 3{\text{/}}2} \right)}}} \right)}^{{ - ({{\kappa }_{{ce}}} - 1/2)}}} \\ \end{gathered} $В уравнении (7), ${{\mu }_{{ce}}} = {{n}_{{ce0}}}{\text{/}}({{Z}_{1}}{{n}_{{10}}})$, ${{\mu }_{{se}}} = {{n}_{{se0}}}{\text{/}}({{Z}_{1}}{{n}_{{10}}})$, ${{\mu }_{{\text{H}}}} = {{n}_{{{\text{H}}0}}}{\text{/}}({{Z}_{1}}{{n}_{{10}}})$, ${{\mu }_{2}} = {{n}_{{20}}}{\text{/}}({{Z}_{1}}{{n}_{{10}}})$, ${{\sigma }_{{ce}}} = {{T}_{{ce}}}{\text{/}}{{T}_{1}}$, ${{\sigma }_{{se}}} = $ $ = {{T}_{{se}}}{\text{/}}{{T}_{1}}$, и $\sigma = {{T}_{1}}{\text{/}}{{T}_{2}}$
Компоненты X, Y, и Z уравнения (2) имеют вид:
(8)
$\begin{gathered} \frac{{\partial {{V}_{{{\text{H}}X}}}}}{{\partial T}} + \left( {{{V}_{{{\text{H}}X}}}\frac{\partial }{{\partial X}} + {{V}_{{{\text{H}}Y}}}\frac{\partial }{{\partial Y}} + {{V}_{{{\text{H}}Z}}}\frac{\partial }{{\partial Z}}} \right){{V}_{{{\text{H}}X}}} = \\ \, = - \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial \phi }}{{\partial X}} + {{\Omega }_{{\text{H}}}}{{V}_{{{\text{H}}Y}}}, \\ \end{gathered} $(9)
$\begin{gathered} \frac{{\partial {{V}_{{{\text{H}}Y}}}}}{{\partial T}} + \left( {{{V}_{{{\text{H}}X}}}\frac{\partial }{{\partial X}} + {{V}_{{{\text{H}}Y}}}\frac{\partial }{{\partial Y}} + {{V}_{{{\text{H}}Z}}}\frac{\partial }{{\partial Z}}} \right){{V}_{{{\text{H}}Y}}} = \\ \, = - \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial \phi }}{{\partial Y}} - {{\Omega }_{{\text{H}}}}{{V}_{{{\text{H}}X}}}, \\ \end{gathered} $(10)
$\begin{gathered} \frac{{\partial {{V}_{{{\text{H}}Z}}}}}{{\partial T}} + \left( {{{V}_{{{\text{H}}X}}}\frac{\partial }{{\partial X}} + {{V}_{{{\text{H}}Y}}}\frac{\partial }{{\partial Y}} + {{V}_{{{\text{H}}Z}}}\frac{\partial }{{\partial Z}}} \right){{V}_{{{\text{H}}Z}}} = \\ \, = - \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial \phi }}{{\partial Z}}. \\ \end{gathered} $Уравнение Пуассона (7) может быть развернуто так
(11)
$\begin{gathered} \frac{{{{\partial }^{2}}\phi }}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{Y}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{Z}^{2}}}} = {{\mu }_{{\text{H}}}} - \\ \, - {{N}_{{\text{H}}}}\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{2}}} \right) + {{\alpha }_{1}}\phi + {{\alpha }_{2}}{{\phi }^{2}} + {{\alpha }_{3}}{{\phi }^{3}}, \\ \end{gathered} $2.2. Случай II: неэкстенсивные легкие ионы
Динамика парных ионов теперь описывается следующими нормированными гидродинамическими уравнениями:
(14)
$\frac{{\partial {{{\mathbf{V}}}_{1}}}}{{\partial T}} + ({{{\mathbf{V}}}_{1}} \cdot \nabla ){{{\mathbf{V}}}_{1}} = \nabla \phi - {{\Omega }_{1}}\left( {{{V}_{{1y}}}{\mathbf{i}} - {{V}_{{1x}}}{\mathbf{j}}} \right),$(15)
$\frac{{\partial {{{\mathbf{V}}}_{2}}}}{{\partial T}} + ({{{\mathbf{V}}}_{2}} \cdot \nabla ){{{\mathbf{V}}}_{2}} = - \frac{{{{Z}_{2}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{2}}}}\nabla \phi + {{\Omega }_{2}}\left( {{{V}_{{2y}}}{\mathbf{i}} - {{V}_{{2x}}}{\mathbf{j}}} \right).$Здесь N1 и N2 – соответственно нормированные плотности ионов O– и O+, а V1 и V2 представляют соответствующие нормированные скорости.
Нормированные плотности надтепловых электронов такие же, как в (3) и (4), в то время как для неэкстенсивных ионов водорода
(16)
${{N}_{{\text{H}}}} = {{\left( {1 - {{\sigma }_{{\text{H}}}}(q - 1)\phi } \right)}^{{\frac{{3q - 1}}{{2(q - 1)}}}}},$Нормированное уравнение Пуассона после подстановки (3), (4) и (16) теперь выглядит так:
(17)
$\begin{gathered} {{\nabla }^{2}}\phi = {{N}_{1}} - {{N}_{2}}\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{{\text{H}}}}} \right) - \\ \, - \left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{2}}} \right){{\left( {1 - {{\sigma }_{{\text{H}}}}(q - 1)\phi } \right)}^{{\frac{{3q - 1}}{{2(q - 1)}}}}} + \\ \, + {{\mu }_{{ce}}}{{\left( {1 - \frac{\phi }{{{{\sigma }_{{ce}}}\left( {{{\kappa }_{{ce}}} - 3{\text{/}}2} \right)}}} \right)}^{{ - ({{\kappa }_{{ce}}} - 1/2)}}} + \\ \, + {{\mu }_{{se}}}{{\left( {1 - \frac{\phi }{{{{\sigma }_{{se}}}\left( {{{\kappa }_{{se}}} - 3{\text{/}}2} \right)}}} \right)}^{{ - ({{\kappa }_{{se}}} - 1/2)}}}. \\ \end{gathered} $Это уравнение можно развернуть как
(18)
$\begin{gathered} \frac{{{{\partial }^{2}}\phi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{z}^{2}}}} = {{N}_{1}} - {{N}_{2}}\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{{\text{H}}}}} \right) + \\ \, + {{\mu }_{2}} - 1 + {{\rho }_{1}}\phi + {{\rho }_{2}}{{\phi }^{2}} + {{\rho }_{3}}{{\phi }^{3}} \\ \end{gathered} $3. ВЫВОД УРАВНЕНИЯ ЗАХАРОВА–КУЗНЕЦОВА
Для исследования солитонных волн с малой амплитудой в рассматриваемой плазме используется метод редуктивного возмущения. Для этого используются преобразования [63]
Чтобы применить технику редуктивного возмущения, различные параметры можно разложить как
(19)
${{N}_{{\text{H}}}} = 1 + \varepsilon N_{{\text{H}}}^{{(1)}} + {{\varepsilon }^{2}}N_{{\text{H}}}^{{(2)}} + \ldots ,$(20)
${{V}_{{{\text{H}}X}}} = {{\varepsilon }^{{3/2}}}V_{{{\text{H}}X}}^{{(1)}} + {{\varepsilon }^{2}}V_{{{\text{H}}X}}^{{(2)}} + \ldots ,$(21)
${{V}_{{{\text{H}}Y}}} = {{\varepsilon }^{{3/2}}}V_{{{\text{H}}Y}}^{{(1)}} + {{\varepsilon }^{2}}V_{{{\text{H}}Y}}^{{(2)}} + \ldots ,$(22)
${{V}_{{{\text{H}}Z}}} = \varepsilon V_{{{\text{H}}Z}}^{{(1)}} + {{\varepsilon }^{2}}V_{{{\text{H}}Z}}^{{(2)}} + \ldots ,$3.1. Уравнение ZK для случая I
Подставляя (19)–(23) в (8)–(11), мы приравниваем коэффициенты при различных степенях ε. Из коэффициентов порядка ${{\varepsilon }^{{3/2}}}$ получаются члены первого порядка:
(24)
$N_{{\text{H}}}^{1} = \frac{{V_{{{\text{H}}Z}}^{1}}}{\lambda },\quad V_{{{\text{H}}Z}}^{1} = \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{1}{\lambda }{{\phi }^{1}},$(25)
$V_{{{\text{H}}Y}}^{1} = \frac{1}{{{{\Omega }_{{\text{H}}}}}}\frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial {{\phi }^{1}}}}{{\partial \xi }},\quad V_{{{\text{H}}X}}^{1} = - \frac{1}{{{{\Omega }_{{\text{H}}}}}}\frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial {{\phi }^{1}}}}{{\partial \eta }}.$Линейное дисперсионное соотношение, дающее фазовую скорость волны, имеет вид
(26)
${{\lambda }_{1}} = \sqrt {\frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{2}}} \right)}}{{{{\alpha }_{1}}}}} .$Приравнивание коэффициентов порядка ${{\varepsilon }^{2}}$ в (8) и (9) дает
(27)
$V_{{{\text{H}}X}}^{2} = \frac{{{{\lambda }_{1}}}}{{\Omega _{{\text{H}}}^{2}}}\frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial \chi \partial \xi }},$(28)
$V_{{{\text{H}}Y}}^{2} = \frac{{{{\lambda }_{1}}}}{{\Omega _{{\text{H}}}^{2}}}\frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial \eta \partial \chi }}.$Приравнивая коэффициенты порядка ${{\varepsilon }^{{5/2}}}$ в (1) и (10), получаем
(29)
$\begin{gathered} \frac{{\partial N_{{\text{H}}}^{1}}}{{\partial \tau }} - {{\lambda }_{1}}\frac{{\partial N_{{\text{H}}}^{2}}}{{\partial \chi }} + \frac{{\partial V_{{{\text{H}}X}}^{2}}}{{\partial \xi }} + \frac{{\partial V_{{{\text{H}}Y}}^{2}}}{{\partial \eta }} + \\ \, + \frac{\partial }{{\partial \chi }}(V_{{{\text{H}}Z}}^{2} + N_{{\text{H}}}^{1}V_{{{\text{H}}Z}}^{1}) = 0, \\ \end{gathered} $(30)
$\frac{{\partial V_{{{\text{H}}Z}}^{1}}}{{\partial \tau }} - {{\lambda }_{1}}\frac{{\partial V_{{{\text{H}}Z}}^{2}}}{{\partial \chi }} + V_{{{\text{H}}Z}}^{1}\frac{{\partial V_{{{\text{H}}Z}}^{1}}}{{\partial \chi }} + \frac{{{{Z}_{{\text{H}}}}}}{{{{Z}_{1}}}}\frac{{{{m}_{1}}}}{{{{m}_{{\text{H}}}}}}\frac{{\partial {{\phi }^{2}}}}{{\partial \chi }} = 0.$И наконец, приравнивание коэффициентов при ε2 из уравнения Пуассона (11) дает
(31)
$\begin{gathered} \frac{{{{\partial }^{2}}\phi }}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{\eta }^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{\chi }^{2}}}} = \\ \, = - N_{{\text{H}}}^{2}\left( {1 + {{\mu }_{{ce}}} + {{\mu }_{{se}}} - {{\mu }_{2}}} \right) + {{\alpha }_{1}}{{\phi }^{2}} + {{\alpha }_{2}}{{({{\phi }^{1}})}^{2}}. \\ \end{gathered} $Подставляя значения из (24)–(28) в (29)–(31) и пренебрегая членами второго порядка, получаем уравнение ZK
(32)
$\begin{gathered} \frac{{\partial {{\phi }^{1}}}}{{\partial \tau }} + {{A}_{1}}{{\phi }^{1}}\frac{{\partial {{\phi }^{1}}}}{{\partial \chi }} + {{B}_{1}}\frac{{{{\partial }^{3}}{{\phi }^{1}}}}{{\partial {{\chi }^{3}}}} + \\ \, + {{C}_{1}}\frac{\partial }{{\partial \chi }}\left( {\frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial {{\eta }^{2}}}}} \right) = 0. \\ \end{gathered} $Выражения для коэффициентов в (32) имеют вид
и3.2. Уравнение ZK для случая II
Следуя той же математической процедуре, как в случае I, и упрощая, получаем уравнение ZK для случая II в виде
(33)
$\frac{{\partial {{\phi }^{1}}}}{{\partial \tau }} + {{A}_{2}}{{\phi }^{1}}\frac{{\partial {{\phi }^{1}}}}{{\partial \chi }} + {{B}_{2}}\frac{{{{\partial }^{3}}{{\phi }^{1}}}}{{\partial {{\chi }^{3}}}} + {{C}_{2}}\frac{\partial }{{\partial \chi }}\left( {\frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{\phi }^{1}}}}{{\partial {{\eta }^{2}}}}} \right) = 0.$Теперь фазовая скорость
Коэффициенты в (33) имеют вид
4. РЕШЕНИЕ УРАВНЕНИЯ ЗАХАРОВА–КУЗНЕЦОВА
Решение уравнения ZK находится как в [63, 64]
где $\zeta = {{l}_{x}}X + {{l}_{y}}Y + {{l}_{z}}Z - {{U}_{0}}\tau $, в случае I, амплитуда солитона ${{\psi }_{m}} = 3{{U}_{0}}{\text{/}}({{A}_{1}}{{l}_{x}})$, а в случае II, она ${{\psi }_{m}} = 3{{U}_{0}}{\text{/}}({{A}_{2}}{{l}_{x}})$. Ширина солитона $\omega $ для случая I, $\omega = 2\sqrt {({{B}_{1}}l_{x}^{3} + {{C}_{1}}{{l}_{x}}(l_{y}^{2} + l_{z}^{2})){\text{/}}{{U}_{0}}} $; а для случая II, $\omega = 2\sqrt {({{B}_{2}}l_{x}^{3} + {{C}_{2}}{{l}_{x}}(l_{y}^{2} + l_{z}^{2})){\text{/}}{{U}_{0}}} $. Здесь U0 – постоянная скорость, нормированная с помощью Cs, а ${{l}_{x}}$, ${{l}_{y}}$, и ${{l}_{z}}$ соответствуют направляющим косинусам вдоль осей X, Y и Z.5. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
Полученное уравнение ZK применимо к любой плазме. Однако данная работа посвящена плазме кометы Галлея. Для этого случая наблюдались следующие значения параметров: ${{n}_{{\text{H}}}} = 4.95$ см–3 для плотности и ${{T}_{{\text{H}}}} = 8 \times {{10}^{4}}$ K для температуры ионов водорода. Температура солнечных (или горячих) электронов была ${{T}_{{se}}} = 2 \times {{10}^{5}}$ K [65], температура второй компоненты фотоэлектронов составляла ${{T}_{{ce}}} = 2 \times {{10}^{4}}$ K. Отрицательно заряженные ионы кислорода с энергией ~1 эВ и плотностями ≤1 см–3 были зарегистрированы Чейзи и др. [58]. Поэтому мы приняли плотность положительных ионов кислорода ${{n}_{{20}}} = 0.5$ см–3 и отрицательных ионов кислорода ${{n}_{{10}}} = 0.05$ см–3 при фоновом магнитном поле 8 × 105 Гс [58, 65].
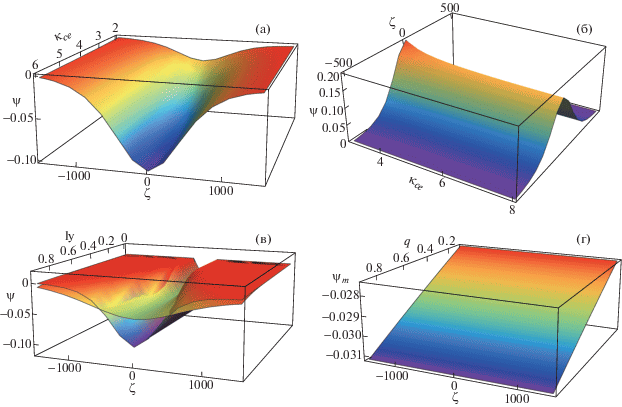
На рисунке 1а показана зависимость профиля IASW от спектрального индекса кометных электронов ${{\kappa }_{{ce}}}$. Для рисунка использованы следующие параметры: ${{\kappa }_{{se}}} = 2$, ${{n}_{{10}}} = 0.05$ см–3, ${{n}_{{20}}} = 0.5$ см–3, ${{n}_{{20}}} = 4.95$ см–3, ${{T}_{{ce}}} = 2 \times {{10}^{4}}$ K, ${{T}_{{se}}} = 2 \times {{10}^{5}}$ K, ${{T}_{1}} = {{T}_{2}} = 1.16 \times {{10}^{4}}$ K, ${{Z}_{1}} = 1$, ${{Z}_{2}} = 2$ и $q = 0.2$. Видно, что амплитуда солитонной волны увеличивается с увеличением значения каппа кометных (более холодных) электронов ${{\kappa }_{{ce}}}.$ На рис. 1б снова показана зависимость профилей солитонов от спектрального индекса кометы ${{\kappa }_{{ce}}}$, когда более легкие ионы водорода проявляют неэкстенсивное поведение. В этом случае изменение профиля демонстрирует поведение, прямо противоположное показанному на рис. 1а; амплитуда солитонной волны несколько уменьшается с увеличением спектрального индекса ${{\kappa }_{{ce}}}.$ Важно отметить, что природа солитона преобразуется из разреженной в сжимающую, когда мы меняем неэкстенсивность более тяжелых ионов кислородной пары на неэкстенсивность более легких ионов водорода. На рис. 1в представлено изменение профиля солитона в зависимости от направляющего косинуса. На рисунке внутренняя кривая соответствует ${{l}_{x}}$ = 0.25, а внешняя кривая – ${{l}_{x}}$ = 0.5. Видно, что с увеличением значения ${{l}_{x}}$ амплитуда солитонной волны также увеличивается. Из рисунка также следует, что подобные изменения существуют и для ${{l}_{y}}$. Рисунок 1г представляет собой график, где показано изменение амплитуды солитонной IA-волны с неэкстенсивным параметром q при ${{\kappa }_{{se}}} = {{\kappa }_{{ce}}} = 2$. Все остальные параметры такие же, как и в предыдущих случаях. Видно, что увеличение значения q для неэкстенсивных парных ионов увеличивает амплитуду солитонной IA-волны.
Рис. 1.
Изменение профиля солитона как функция ${{\kappa }_{{ce}}}$ для неэкстенсивных парных ионов (O+ и O–) (случай I) (a); для неэкстенсивных ионов H+ (случай II) (б). Изменение профиля солитона как функция направляющих косинусов для неэкстенсивных парных ионов (O+ и O–) (случай I) (в). Изменение амплитуды солитона как функция q для неэкстенсивных парных ионов (O+ и O–) (г).
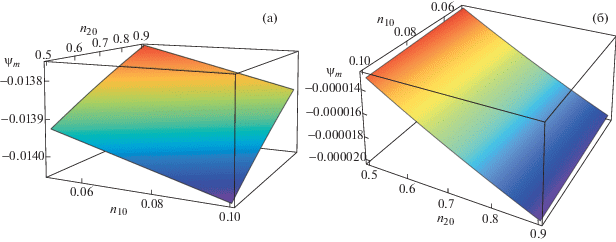
На рис. 2 показано изменение амплитуды ${{\psi }_{m}}$ у солитонной IA-волны с плотностями отрицательно и положительно заряженных ионов кислорода (соответственно ${{n}_{{10}}}$ и ${{n}_{{20}}}$) при ${{\kappa }_{{ce}}} = 2$ и q = 0.2. Все остальные параметры такие же, как на рис. 1. На рис. 2а представлен случай неэкстенсивных парных ионов, а на рис. 2б – случай неэкстенсивных более легких ионов. Показано, что для неэкстенсивных парных ионов (рис. 2а) увеличение плотности положительных ионов кислорода уменьшает величину амплитуды солитонной IA-волны. Однако амплитуда увеличивается с увеличением плотности отрицательно заряженных ионов кислорода. В случае неинтенсивных более легких ионов водорода (рис. 2б) амплитуда солитонной волны возрастает с ростом плотности, как положительных, так и отрицательных ионов кислорода.
Рис. 2.
Зависимость амплитуды ${{\psi }_{m}}$ от ${{n}_{{10}}}$ и ${{n}_{{20}}}$ для неэкстенсивных парных ионов (a); для неэкстенсивных легких ионов (б).
На рис. 3 изображено изменение фазовой скорости солитонной IA-волны в зависимости от спектрального индекса ${{\kappa }_{{ce}}}$ и параметра неэкстенсивности q для парных ионов. Выбранные параметры такие же, как на рис. 1а. Из рисунка видно, что фазовая скорость λ1 резко возрастает с увеличением доли надтепловых парных ионов. Если вместо парных ионов считать неэкстенсивными легкие ионы водорода (рис. 3б), то получается то же изменение, что и на рис. 3, т. е. замена неэкстенсивности от ионов кислорода к ионам водорода не оказывает существенного влияния на фазовую скорость.
Рис. 3.
Зависимость фазовой скорости λ1 от q и ${{\kappa }_{{ce}}}$ для неэкстенсивных парных ионов (a); для неэкстенсивных легких ионов (б).
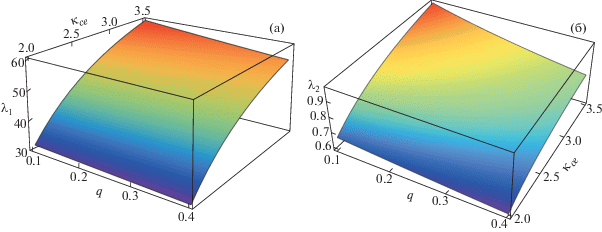
На рис. 4 снова показано изменение фазовой скорости солитонной IA-волны в зависимости от плотности более тяжелых ионов O+ и O– при ${{\kappa }_{{ce}}}$ = 2 и q = 0.3. Все остальные параметры такие же, как на рис. 1. Видно, что в случае неэкстенсивных парных ионов фазовая скорость уменьшается с увеличением плотности положительно заряженных ионов кислорода, и в то же время она увеличивается с увеличением плотности отрицательно заряженных ионов кислорода. Но когда мы возьмем неэкстенсивные более легкие ионы (рис. 4б), фазовая скорость увеличивается с плотностью как отрицательно, так и положительно заряженных ионов кислорода. Кроме того, изменение фазовой скорости является более значительным для измнения плотности положительно заряженных ионов кислорода.
Рис. 4.
Зависимость фазовой скорости λ1 от ${{n}_{{10}}}$ и ${{n}_{{20}}}$ для неэкстенсивных парных ионов (a); фазовой скорости λ2 от ${{n}_{{10}}}$ и ${{n}_{{20}}}$ для неэкстенсивных легких ионов (б).
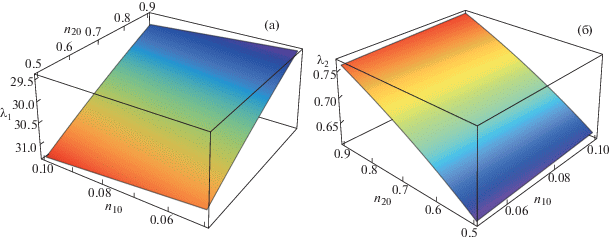
Изменение ширины солитона ($\omega $) в зависимости от ${{\kappa }_{{ce}}}$ и q изображено на рис. 5; используемые параметры такие же, как на рис. 1. В случае как неэкстенсивных парных ионов, так и неэкстенсивных более легких ионов (соответственно, рис. 5а и 5б) ширина уменьшается с увеличением параметра q. Но это изменение круче для неэкстенсивных более легких ионов водорода (рис. 5б). Также видно, что ширина резко увеличивается с ${{\kappa }_{{ce}}}$ для обоих случаев.
Рис. 5.
Зависимость ширины ω от q и ${{\kappa }_{{ce}}}$ для неэкстенсивных парных ионов (a); для неэкстенсивных легких ионов (б).
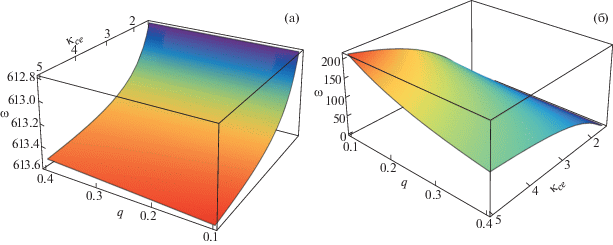
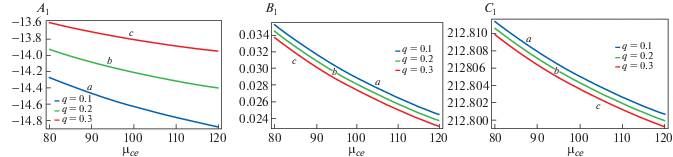
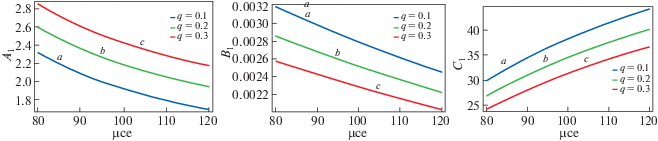
Изменение коэффициента нелинейности A1, дисперсионных коэффициентов B1 и C1 изображено далее. Таким образом, рис. 6 представляет собой график зависимости коэффициентов в (32) от ${{\mu }_{{ce}}}$ как функции параметра неэкстенсивности q парных ионов; остальные параметры такие же, как на рис. 1а. Кривая (а) построена для q = 0.1, кривая (б) для q = 0.2 и кривая (в) для q = 0.3. Видно, что коэффициент нелинейности A1 увеличивается с увеличением неэкстенсивности q парных ионов, а дисперсионные члены B1 и C1 уменьшаются с увеличением q.
На рис. 7 приведена зависимость коэффициентов в (33) от функции параметра неэкстенсивности q ионов водорода. Важно отметить, что вариации всех коэффициентов аналогичны изменениям на рис. 6 (за исключением C2). Несмотря на то, что значения коэффициентов меняются, характер их зависимости от q остается тем же самым, когда мы обмениваемся неэкстенсивной природой с более тяжелыми и более легкими ионами.
Недавно Сабеткар и Дорранян [63] исследовали роль надтепловой компоненты и неэкстенсивности на наклонно распространяющихся звуковых пылевых структурах в замагниченной плазме, состоящей из двух компонент ионов, описываемых неэкстенсивными функциями распределения, электронов, описываемых каппа-распределением, и отрицательно заряженных пылевых частиц. Они обнаружили, что амплитуда солитона увеличивалась с увеличением параметра неэкстенсивности q. Наш вывод из рис. 1г согласуется с этим наблюдением.
Другое наблюдение Сабеткара и Дорраняна состояло в том, что фазовая скорость солитонной волны увеличивалась с увеличением значения каппа электронов и уменьшалась с увеличением относительной плотности электронов. Результаты рис. 3a и 4a также согласуются с этим результатом Сабеткара и Дорраняна [63].
Аббаси и Пажо [66] исследовали влияние захваченных электронов на IA-солитоны в плазме с надтепловыми электронами и ионами. Они обнаружили, что ширина солитонов увеличивалась с увеличением спектральных показателей электронов. Наши выводы из рис. 5 согласуются с этим результатом.
Положительно заряженные ионы кислорода (О+) и связанные с ними фотоэлектроны образуются при диссоциации молекул воды [65]. Кроме того, диссоциация этих молекул фотонами с энергией в диапазоне 36–100 эВ приводит к образованию как отрицательных ионов кислорода (O–), так и ионов водорода (H–) [67, 68]. Рисунок 2а показывает, что амплитуда уединенных IA-волн уменьшается с увеличением плотности положительных ионов кислорода (${{n}_{{20}}}$). Она также увеличивается с увеличением плотности отрицательных ионов кислорода. Таким образом, наши результаты показывают, что амплитуды солитонных волн, по-видимому, хорошо коррелируют с присутствием молекул воды в кометной плазме и соответствующими процессами фотоионизации.
IA-волны являются популярным диагностическим инструментом и дают информацию об электронных температурах, массах ионов, относительных концентрациях сортов ионов и даже о скоростях дрейфа в неоднородной плазме [69]. Волна наблюдалась у комет Галлея [70], Джакобини–Циннера [71] и 67P/Чурюмова–Герасименко [72, 73], и хорошо изучена в кометных средах [74, 75]. Естественные усиления IA-волн, экспериментально наблюдаемые в ионосфере, были объяснены в терминах солитонных волн сжатия, распространяющихся с ионно-звуковыми скоростями [76]. Перезарядочное охлаждение кометной плазмы, наблюдаемое миссией Вега, было объяснено в терминах солитонной волны разряжения и слабой ударной волны [77]. Кроме того, конденсация, обнаруженная с помощью наземных наблюдений за хвостом кометы Галлея, интерпретировалась с помощью солитонных волн [78]. Наконец, систематический анализ фотографических изображений хвоста кометы Галлея выявил наличие ряда у солитонных волн и узлов, или областей с более высокой плотностью вещества [79].
4. ЗАКЛЮЧЕНИЕ
В статье рассмотрены ионно-звуковые солитонные волны в замагниченной пятикомпонентной кометной плазме с положительно и отрицательно заряженными ионами кислорода, более легкими ионами водорода и каппа-описанием горячих и холодных электронов, путем вывода уравнение ZK. Было широко изучено влияние q‑неэкстенсивных распределений двух более тяжелых ионов и одного более легкого иона. При замене неэкстенсивности парных ионов на неэкстенсивность более легких ионов природа солитона трансформируется из разреженной в сжатую. Надтепловая компонента электронов и неэкстенсивность ионов существенно изменяют амплитуду, ширину и фазовую скорость солитонной волны. Также изучалась зависимость нелинейных и дисперсионных коэффициентов от параметра неэкстенсивности q. Показано, что амплитуда солитонных волн, по-видимому, хорошо коррелирует с присутствием молекул воды в кометной плазме и со связанными процессами фотоионизации.
Список литературы
SagdeevR.Z., Leontovich M.A. Reviews of Plasma Physics. 1966. V. 4. P. 23.
Washimi H., Taniuti T. Phys. Rev. Lett. 1966. V. 17. P. 996.
Das G.C., Tagare S.G. Plasma Phys. Control. Fusion. 1975. V. 17. P. 1025.
Popel S.I., Vladimirov S.V., Shukla P.K. Phys. Plasmas. 1995. V. 2. P. 716.
Watanabe S. J. Phys. Soc. Japan. 1984. V. 53. P. 950.
Zakharov V.E., Kuznetsov E.A. Sov. Phys. JETP. 1974. V. 39. P. 285.
Kadomstev B.B., Petiashvili V.I. Sov. Phys. Doklady. 1970. V. 15. P. 539.
Druma V.S. JETP Lett. 1973. V. 19. P. 219.
Petiashvili V.I. J. Plasma Phys. 1976. V. 2. P. 257.
KarpmanV.I., Belashov V.Yu. Phys. Lett. A. 1991. V. 154. P. 131.
Vladimirov S.V., Yu M.Y. Phys. Rev. E. 1993. V. 48. P. 2136.
Boldyrev S.A., Vladirimov S.V., Tystovich V.N. Sov. J. Plasma Phys. 1992. V. 18. P. 727.
Belashov V., Belashova E.S. J. Atmos. Sol. Terr. Phys. 2015. V. 136. P. 150.
Pokhotelov O.A., Stenflo L., Shukla P.K. Plasma Phys. Reports. 1996. V. 22. P. 852.
Dubinov A.E., Kolotkov D.Y. Rev. Mod. Plasma Phys. 2018. V. 2. P. 2.
Sagdeev R.Z., Galeev A.A. Nonlinear Plasma Theory, Ed. by T.M. O’Neil and D.L. Book. W. A. Benjamin, New York, 1969.
Karpman V.I. Nonlinear Waves in Dispersive Media. Pergamon, Oxford, 1975.
Novikov S., Manakov S.V., Pitaevskii L.P., Zakharov V.E. Theory of Solitons: The Inverse Scattering Method. Consultants Bureau, New York, 1984.
Petiashvili V., Pokhotelov O. Solitary Waves in Plasmas and in the Atmosphere. Gordon and Breach, Philadelphia, 1992.
Belashov V.Yu., Vladimirov S.V. Solitary Waves in Complex Media: Theory. Simulation and Applications. Springer, Berlin, 2005.
Popel S.I., Yu M.Y. Cont. Plasma Phys. 1995. V. 35. P. 103.
Dubinov A.E., Kolotkov D.Yu. Plasma Phys. Reports. 2012. V. 38. P. 909.
Popel S.I., Golub A.P., Losseva T.V., Ivlev A.V., Khrapak S.A., Morfill G. Phys. Rev. E. 2003. V. 67. P. 056402.
Losseva T.V., Popel S.I., Golub A.P., Shukla P.K. Phys. Plasmas. 2009. V. 16. P. 093704.
Losseva T.V., Popel S.I., Golub A.P., Izvekova Yu.N., Shukla P.K. Phys. Plasmas. 2012. V. 19. P. 013703.
Sahu B., Roychoudhury R. EPL. 2012. V. 100. P. 15001.
Khater A.H., Callebaut D.K., Malfliet W., Seadawy A.R. Phys. Scr. 2001. V. 64. P. 533.
Khater A.H., Callebaut D.K., Seadawy A.R. Phys. Scr. 2003. V. 67. P. 340.
El-Labany S.K., Moslem W.M., El-Awady E.I., Shukla P.K. Phys. Lett. A. 2010. V. 375. P. 159.
Wazwaz A.M. Commun. Nonlinear Sci. Numer. Simul. 2007. V. 12. P. 1395.
Guo S., Liquan M., Zhang Z. Phys. Plasmas. 2015. V. 22. P. 052306.
Rehman M.A., Mishra M.K. Phys. Plasmas. 2016. V. 23. P. 012302.
Vasyliunas V.M. J. Geophys. Res. 1968. V. 73. P. 2839.
Tsallis C. J. Stat. Phys. 1988. V. 52. P. 479.
Daroczy Z. Information & Control. 1970. V. 16. P. 36.
Sharma B.D., Taneja I.J. Metrika. 1975. V. 22. P. 205.
Dial G. Information Sciences. 1982. V. 27. P. l.
Summers D., Thorne R.M. Phys. Fluids B. 1991. V. 3. P. 1835.
Leubner M.P. Astrophys. Space Sci. 2002. V. 282. P. 573.
Dubinova I.D., Dubinov A.E. Tech. Phys. Lett. 2006. V. 32. P. 575.
Tribeche M., Djebarni L., Amour R. Phys. Plasmas. 2010. V. 17. P. 042114.
Sabetkar A., Dorranian D. J. Plasma Phys. 2014. V. 80. P. 565.
Jannat N., Ferdousi M., Mamun A.A. Plasma Phys. Rep. 2016. V. 42. P. 678.
Shalini, Saini N.S., Misra A.P. Phys. Plasmas. 2015. V. 22. P. 092124.
Sreekala G., Manesh M., Neethu T.W., Anu V., Sijo S., Venugopal C. Plasma Phys. Rep. 2018. V. 44. P. 102.
Chahal B.S., Singh M., Shalini, Saini N.S. Physica A: Stat. Mech. Appl. 2018. V. 491. P. 935.
Hatami M.M., Tribeche M. Physica A: Stat. Mech. Appl. 2018. V. 491. P. 55.
Bala P., Gill T.S., Bains A.S., Kaur H. Ind. J. Phys. 2017. V. 91. P. 1625.
Ghosh B., Banerjee S. Turkish J. Phys. 2016. V. 40. P. 1.
Chowdhury N.A., Mannan A., Hasan M.M., Ma-mun A.A. arXiv: 1706.05634v1. 2017.
Kaur S., Bala P. IOSR-JAP. 2017. V. 9. P. 51.
Saha A., Chatterjee P. Braz. J. Phys. 2015. V. 45. P. 419.
Ashraf S., Mandal G., Mamun A.A. Phys. Sci. Intl. J. 2015. V. 6. P. 236.
El-Depsy A., Selim M.M. Eur. Phys. J. Plus. 2016. V. 131. P. 431.
Bouzit O., Tribeche M., Bains A.S. Phys. Plasmas. 2015. V. 22. P. 4506.
El-Shamy E.F., Tribeche M., El-Taibany W.F. Cent. Eur. J. Phys. 2014. V. 12. P. 805.
Ghebache S., Tribeche M. Physica A: Stat. Mech. Appl. 2016. V. 447. P. 180.
Chaizy P., Reme H., Sauvaud J.A., d’Uston C., Lin R.P., Larson D.E., Mitchell D.L., Zwickl R.D., Baker D.N., Bame S.J., Feldman W.C., Fuselier S.A., Huebner W.F., McComas D.J., Young D.T., Nature. 1991. V. 349. P. 393.
Zwickl R.D., Baker D.N., Bame S.J., Feldman W.C., Fuselier S.A., Huebner W.F., McComas D. J., Young D.T. Geophys. Res. Lett. 1986. V. 13. P. 401.
Broiles T.W., Livadiotis G., Burch J.L., Chae K., Clark G., Cravens T.E., Davidson R., Erikkson A., Frahm R.A., Fuselier S.A., Goldstein J., Goldstein R., Henri P., Madanian H., Mandt K., Mokashi P., Pollock C., Rahmati A., Samara M., and Schwartz S.J. J. Geophys. Res. 2016. V. 121. P. 7407.
Saberian E., Esfandyari-Kalejahi A. arXiv 1311.0193v1. 2013.
Oohara W., Date D., and Hatekeyama R. Phys. Rev. Lett. 2005. V. 95. P. 175003.
Sabetkar A., Dorranian D. Phys. Scr. 2015. V. 90. P. 035603.
Liu Z., Dan W., He G. Phys. Plasmas. 2008. V. 15. P. 083702.
Brinca A.L., Tsurutani B.T. Astron. Astrophys. 1987. V. 187. P. 311.
Abbasi H., Pajouh H.H. Phys. Plasmas. 2007. V. 14. P. 012307.
Hunniford C.A., Scully S.W.J., Dunn K.F., Latimer C.J. J. Phys. B. 2007. V. 40. P. 1225.
Cordiner M.A., Charnley S.B. Meteoritics & Planet. Sci. 2014. V. 49. P. 21.
Hershkowitz N., Ghim Y.-C. Plasma Sci. Tech. 2009. V. 18. P. 014018.
Oya H., Marioka A., Miyake W., Smith E.J., Tsurutani B.T. Nature. 1986. V. 321. P. 307.
Scarf F.L., Corotini F.V., Kennel C.F., Gurnett D.A., Ip W.H., Smith E.J. Science. 1986. V. 232. P. 377.
Gunell H., Nilsson H., Hamrin M., Eriksson A., Odel-stad E., Maggiolo R., Henri P., Vallieres X., Attwegg K., Tzou C.-Y., Rubin M., Glassmeier K.-H., Wieser G.S., Wedlund C.S., Keyser J.D., Dooghe F., Cessateur G., Gibbons A. A&A. 2017. V. 600. P. A3.
Rehman S., Shah A., Haque H. The Astron. J. Lett. 2019. V. 880. P. L13.
Gopinathan S., Sebastian S., Abraham N.P., Devi S.E., Chandu V., Gangadharan R. Open Access Library Journal. 2014. V. 1. P. 1.
Abraham N.P., Sebastian S., Sreekala G., Devi S.E., Renuka G., Venugopal C. Astrophys. Space Sci. 2014. V. 349. P. 49.
Ekeberg J., Wannberg G., Eliasson L., Stasiewicz K. Ann. Geophys. 2010. V. 28. P. 1899.
Oberc P., Parzyldo W., Koperski P., Klimov S. Adv. SpaceRes. 1989. V. 9. P. 347.
Koshevaya S.V., Tecpoyotl-T M., Gutierrez-D E.A., Burlak G.N., Kotsarenko A.N. RevMexAA (Serie de Conferencias). 2000. V. 9. P. 112.
Voelzke M.R., Izaguirre L.S. Planet. & Sp. Sci. 2012. V. 65. P. 104.
Дополнительные материалы отсутствуют.