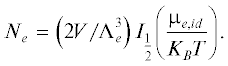1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 46, № 7, 2020

Физика плазмы, 2020, T. 46, № 7, стр. 645-657

К расчету электропроводности горячей плотной неидеальной плазмы

Mofreh R. Zaghloul *

Department of Physics, College of Sciences, United Arab Emirates University
P.O.B. 15551 Al-Ain, UAE

* E-mail: Mofreh R Zaghloul@yahoo.uae

Поступила в редакцию 14.06.2019
После доработки 21.10.2019
Принята к публикации 19.12.2019

Полный текст (PDF)

Аннотация

Вновь рассматриваются факторы, влияющие на расчет электропроводности в системах с горячей плотной неидеальной плазмой. Помимо верхней границы ионизации и кулоновского логарифма, тщательно исследованы и оценены существенные особенности, относящиеся к обрезанию внутренней статистической суммы, сильной кулоновской связи и возбужденным электронным состояниям. Особый интерес вызвало изучение часто возникающей проблемы получения пересекающихся изотерм электропроводности при высоких плотностях. Разработана улучшенная модель для прогноза электропроводности горячей плотной материи, которая используется для расчета электропроводности частично ионизованной и частично вырожденного вещества при высокой плотности энергии. По сравнению с результатами конкурирующих моделей из литературы, прогнозы по настоящей модели показали лучшее физическое поведение, позволившее избежать проблемы получения пересекающихся изотерм при высоких плотностях.

Ключевые слова: неидеальная плазма, электропроводность

1. ВВЕДЕНИЕ

Необходимость точного прогнозирования электропроводности неидеальной плазмы в широкой области фазового пространства плотность – температура (ρ–T) представляет первостепенный интерес для понимания и оптимизации многих технологических приложений, включая эксперименты с высокой плотностью энергии и импульсные мощные установки, предназначенные для получения термоядерной плазмы с инерциальным удержанием [1–7]. Моделирование электропроводности плотных неидеальных плазменных систем требует информации о равновесных заселенностях компонент плазмы и о соответствующих сечениях столкновений [8–11]. Моделирование равновесия, расчет внутренней статистической суммы и оценки сечений рассеяния заряженных частиц в плотной неидеальной плазменной среде были серьезно изучены в серии недавних публикаций [12–18]. В работах [12–16] в рамках химической картины пересматривается проблема установления статистическо-термодинамически согласованных конечных статистических сумм в связанном состоянии для неидеальных многокомпонентных плазменных систем. Исследования указали на слабые стороны и серьезные несоответствия, скрытые в моделях, широко используемых в литературе. Для устранения неоднозначностей и обеспечения статистическо-термодинамической согласованности в терминах решения обратной задачи вводится обобщенная непротиворечивая формулировка. В [17] в решение уравнения состояния и ионизационного равновесия внесены дальнейшие улучшения, позволяющие применить химическую модель и метод минимизации свободной энергии к режиму сильной связи. С другой стороны, в [18] в рамках теории обрезания для объяснения экранирования заряда в плазменной среде в качестве прицельного параметра обрезания широко использовалось расстояние, не зависящее от скорости, и формула рассеяния Резерфорда, что является неточным и воплощает явное несоответствие. Вместо этого вводится новый физически обоснованный выбор расстояния обрезания, используемый при получении замкнутой формы выражения для кулоновского логарифма, который показал лучшее согласие с экспериментально восстановленными данными и лучшее физическое поведение по сравнению с предыдущими выражениями для обрезания, используемыми в литературе в течение нескольких десятилетий. Возможно, здесь уместно сослаться на соответствующую работу А.В. Филиппова и др. о различных методах определения кулоновского логарифма в неидеальной и вырожденной плазме [19].

В настоящей работе мы исследуем и оцениваем факторы, влияющие на расчет электропроводности плотных неидеальных плазменных систем, и вводим новые поправки и улучшения в простую модель для расчета электропроводности при высокой плотности энергии.

2 . ТЕОРИЯ

2.1. Уравнение состояния и плотности заселенности

Расчет уравнения состояния и плотности заселенности различных компонент плазмы (нейтральных атомов и многозарядных ионов при различных состояниях возбуждения в дополнение к голым ядрам и свободным электронам) может быть выполнен в химической модели или в “химической картине”, где структурированные частицы рассматриваются как элементарные члены термодинамического ансамбля вместе с голыми ядрами и свободными электронами. В химической модели строится аддитивная функция свободной энергии Гельмгольца, где взаимодействия и связи между различными компонентами учитываются в терминах конфигурационного члена и схемы для плавного обрезания внутренней статистической суммы. Для простоты мы ограничимся случаем плазмы, генерируемой из полностью диссоциированных молекул, где сумма разделяемых компонент свободной энергии может быть записана так:

(1)
$F = {{F}_{e}} + \mathop \sum \limits_{s = 0,1,2, \ldots \ldots .,Z} {{F}_{{s,~~ideal}}} + {{F}_{{conf}}} + {{F}_{{zero{\text{ - }}of{\text{ - }}energy}}}$
Fe – свободная энергия для свободных электронов, Fs.ideal – идеальная свободная энергия для тяжелых частиц с кратностью вырождения s, Fconf – конфигурационная составляющая свободной энергии, и слагаемое Fzero-of-energy учитывает тот факт, что все энергии должны быть отнесены к одному и тому же эталонному значению.

Для частично вырожденного электронного газа можно использовать свободную энергию идеального Ферми-газа равновесных электронов, где

(2)
$\begin{gathered} {{F}_{e}} = - {{P}_{e}}V + {{N}_{e}}{{\mu }_{{e,id}}} = \\ = \;~ - \left( {\frac{{2{{K}_{B}}TV}}{{{\Lambda }_{e}^{3}}}} \right){{I}_{{\frac{3}{2}}}}\left( {\frac{{{{\mu }_{{e,id}}}}}{{{{K}_{B}}T}}} \right) + {{N}_{e}}{{\mu }_{{e,id}}}, \\ \end{gathered} $

В этой формуле T – абсолютная равновесная температура, V – объем системы, KB – постоянная Больцмана, Λe – средняя тепловая длина волны электронов, Pe – электронное давление, μe.id – химический потенциал идеального электронного Ферми-газа, а Iν – полный интеграл Ферми–Дирака, определяемый как

(3)
${{I}_{\nu }}\left( \vartheta \right) = \frac{1}{{{\Gamma }\left( {\nu + 1} \right)}}\mathop \smallint \limits_0^\infty \frac{{{{y}^{\nu }}}}{{\exp \left( {y - \vartheta } \right) + 1}}~dy.$

Химический потенциал электронов μe.id связан с числом свободных электронов в системе

(4)

Даже при очень высокой плотности тяжелые частицы остаются классическими из-за их больших масс, и их идеальная классическая свободная энергия определяется классическим выражением

(5)
$\begin{gathered} {{F}_{{id,clc}}} = - {{K}_{B}}T\mathop \sum \limits_{s = 0,1,..,Z} {{N}_{s}} \times \\ \times \;\left( {ln\left[ {{{{\left( {\frac{{2\pi {{m}_{s}}{{K}_{B}}T}}{{{{h}^{2}}}}} \right)}}^{{3/2}}}\frac{{V{{Q}_{{int,s}}}}}{{{{N}_{s}}}}} \right] + 1} \right), \\ \end{gathered} $
где ms – масса частицы с кратностью вырождения s, h – постоянная Планка, а Qint,s – внутренняя статистическая сумма частицы с кратностью вырождения s. Следуя анализу [16], внутренние статистические суммы структурированных частиц можно оценить с помощью выражения
(6)
$\begin{gathered} {{Q}_{{int}}}\left( {T,V,\left\{ N \right\}} \right) = \left[ {1 - {{w}_{0}}\left( {T,V,\left\{ N \right\}} \right)} \right] \\ + \;\mathop \sum \limits_{i = 0}^\infty {{g}_{i}}{{w}_{i}}\left( {T,V,\left\{ N \right\}} \right){{e}^{{ - {{\varepsilon }_{i}}/{{K}_{B}}T}}}, \\ \end{gathered} $
где gi – статистический вес i-го уровня, энергия которого относительно основного уровня равна εi. Вероятности заселенности wi(T, V, {N}) должны быть получены из микрополей плазмы. Предполагается, что они должны непрерывно и монотонно уменьшаться с плотностью, что приводит к физически разумному непрерывному переходу между связанными и свободными состояниями с естественным и плавным обрезанием внутренней статистической суммы электронов. Первый член в правой части уравнения (6) является необходимой поправкой (по сравнению с обычной формулировкой из литературы), чтобы сохранить хотя бы одно состояние основного уровня при экстремально высоких плотностях. При таких экстремальных условиях все выражения для вероятностей заселенности, известные в литературе, приводят к исчезновению w0(T, V, {N}), что в корне разрушает структуру статистической задачи.

Член свободной энергии конфигурации Fconf учитывает различные конфигурационные эффекты, такие как кулоновские взаимодействия между заряженными частицами FCoul, интенсивное короткодействующее отталкивание твердого ядра Fhs, поправки Ван-дер-Ваальса FvdW и исключенный объемный член Fbn:

(7)
${{F}_{{conf}}} = {{F}_{{Coul}}} + {{F}_{{hs}}} + {{F}_{{vdW}}} + {{F}_{{bn}}}.$

Различные модели и выражения для FCoul, Fhs, FvdW и Fbn можно найти в работе [20]. Модель учитывает все доступные возбужденные состояния (собраны Национальным институтом стандартов и технологий (NIST) [21]). Вычислительная схема, используемая для минимизации функции свободной энергии и определения детальной плотности заселенности для всех компонент плазмы, объяснена в [17, 22].

2.2 Сечения рассеяния и кулоновский логарифм

Тот факт, что существуют два точных выражения для электропроводности на предельных границах слабой и полной ионизации, привел к тому, что в промежуточной области использовались различные интерполяционные формулы. Простейший подход к оценке электропроводности в режиме частичной ионизации основан на линейном правиле смешивания аддитивных частот столкновений для электронно-ионных и электронно-нейтральных взаимодействий. В этой простой модели предполагается, что полное удельное сопротивление σ–1, плазмы является суммой удельных сопротивлений, связанных с нейтральными и заряженными частицами [8, 11, 23–27]:

(8)
${{\sigma }^{{ - 1}}} = \sigma _{{e - n}}^{{ - 1}} + \sigma _{{e - i}}^{{ - 1}},$
где σe – n и σe – i – соответственно электропроводности в предельных случаях слабой и полной ионизации. Электрон-нейтральную проводимость можно рассчитать, используя среднее электрон-нейтральное (e – n) сечение переноса импульса, ${{\bar {Q}}_{{e - n}}}$, оцененное в борновском приближении с использованием экранированного поляризационного потенциала по формуле Дежарле [28]. Следует отметить, что формула Дежарле [28] предсказывает среднее сечение e – n, зависящее от температуры и плотности.

Электрон-ионная проводимость, с другой стороны, может быть задана выражением Спитцера–Харма [29] для полностью ионизованной плазмы с учетом электронных столкновений

(9)
${{\sigma }_{{e - i}}} = \frac{1}{{38.0}}\frac{{{{T}^{{1.5}}}}}{{{{Z}_{{av}}}}}\frac{{{{\gamma }_{E}}\left( {{{Z}_{{av}}}} \right)}}{{\ln {\Lambda }}},$
где Zav – среднее ионизационное состояние плазмы, ln Λ – кулоновский логарифм, а коэффициент γE(Zav) учитывает рассеяние электронов на электронах и может быть выражен как в [30]. Большинство трудностей и неточностей, возникающих при оценке σe – i для неидеальной плазмы, связаны с оценкой кулоновского логарифма ln Λ.

В сильно неидеальном режиме использование классической парной теории обрезания с учетом экранирования заряда и неидеальных эффектов возможно и надежно. Однако использование расстояния, независимого от скорости, в качестве прицельного параметра обрезания, вместе с формулой рассеяния Резерфорда для учета экранирования заряда в плазменной среде недавно было подвергнуто тщательному анализу. Было обнаружено, что оно отражает явную несогласованность и неточность [18]. Был введен новый физически обоснованный выбор расстояния обрезания, использованный для получения замкнутой формы выражения для эффективного сечения переноса импульса или кулоновского логарифма, где

(10)
$\ln {\Lambda } \to \exp \left( {\frac{{3{\text{/}}2}}{{{{{\Lambda }}_{s}}}}} \right){{E}_{1}}\left( {\frac{{3{\text{/}}2}}{{{{{\Lambda }}_{s}}}}} \right),$
где E1 – интегральная показательная функция и ${{\Lambda }_{s}} = {{r}_{s}}{\text{/}}{{\bar {b}}_{0}}$, где ${{\bar {b}}_{0}}$ – прицельный параметр для рассеяния 900 частиц со средней тепловой энергией (3/2 KBT), а rs представляет расстояние обрезания, rcut, или прицельный параметр обрезания для кулоновской силы конечного дальнодействия, определяемой как

(11)
$\begin{gathered} F(\vec {r}) = - \frac{{z{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}}}\hat {r},\quad r \leqslant {{r}_{{cut}}} = 0, \\ r > {{r}_{{cut}}}. \\ \end{gathered} $

Также получено простое приближение для кулоновского логарифма в (10), не содержащее специальных функций, которое может быть удовлетворительно использовано с максимальной ошибкой менее 5%:

(12)
$\ln {\Lambda } \approx \frac{{1.0 + \ln \left( {1.0 + 0.1377~{{{\Lambda }}_{s}}} \right)}}{{1.0 + 1.5{\text{/}}{{{\Lambda }}_{s}}}}.$

Вышеприведенное выражение просто сводится к ln Λs при Λs → ∞. Сравнение с экспериментальными данными при уменьшенной кулоновской проводимости показало лучшее согласие и лучшее физическое поведение полученных выражений по сравнению с предыдущими выражениями обрезания из литературы, включая наши предыдущие выражения [31].

Плотности заселенности для всех компонент плазмы, включающие возбужденные и высокие состояния ионизации, могут быть определены и использованы вместе с новой формулой для кулоновского логарифма (10) при расчете электропроводности в режиме сильной связи.

3. ОЦЕНКА ФАКТОРОВ, ВЛИЯЮЩИХ НА ПРОВОДИМОСТЬ: РАСЧЕТЫ

3.1. Вероятности заселенности и электронные статистические суммы

В литературе внутренняя статистическая сумма электронов, использующая весовые коэффициенты граничного состояния, обычно формулируется в виде

(13)
${{Q}_{{int}}}\left( {T,V,\left\{ N \right\}} \right) = \mathop \sum \limits_{i = 0}^\infty {{g}_{i}}{{w}_{i}}\left( {T,V,\left\{ N \right\}} \right){{e}^{{ - {{\varepsilon }_{i}}/{{K}_{B}}T}}}.$

Весовой коэффициент wi(T, V, {N}) является соответствующей вероятностью заселенности i-го энергетического уровня, зависящей от состояния [32, 33]. Весовой коэффициент wi должен упасть почти до нуля, поскольку энергия связи уровня ниже невозмущенного континуума стремится к нулю, чтобы обеспечить естественное обрезание внутренней статистической суммы. В схеме ступенчатого обрезания, обычно используемой для установления конечных статистических сумм связанных состояний [26, 27, 34, 35], вероятность заселенности просто представляется ступенчатой функцией, весовой коэффициент wi(T, V, {N}) равен

(14)
$\begin{array}{*{20}{c}} {{{w}_{i}} = 1}&{{\text{for}}\quad ~{{\varepsilon }_{i}} < I - {\Delta }I\left( {T,V,\left\{ N \right\}} \right)} \\ {{{w}_{i}} = 0}&{{\text{for}}\quad ~{{\varepsilon }_{i}} \geqslant I - {\Delta }I\left( {T,V,\left\{ N \right\}} \right)} \end{array},$
где ΔI(T, V, {N}) относится к члену, традиционно известному как снижение энергии ионизации, в первую очередь зависящему от свободной энергии конфигурации.

С другой стороны, различные непрерывные формы, которые монотонно уменьшаются по мере увеличения силы соответствующих взаимодействий, были предложены и использованы в литературе (см., например, [32, 33, 36–38]), чтобы обеспечить физически приемлемые непрерывные переходы между связанными и свободными состояниями. Следует отметить, что использование так называемой статистической суммы Планка–Ларкина (PLPF), обычно встречающейся в рамках “физической картины” внутри “химической модели”, хотя и противоречиво, но во всех отношениях эквивалентно использованию вероятности заселенности, зависящей от температуры как

(15)
${{w}_{{i,PLPF}}}\left( T \right) = \left( {1 - {{e}^{{\left( {{{\varepsilon }_{i}} - I} \right)/{{K}_{B}}T}}}\left[ {1 - \frac{{\left( {{{\varepsilon }_{i}} - I} \right)}}{{{{K}_{B}}T}}} \right]} \right).$

Из выражения (15) видно, что как вероятность заселенности Планка–Ларкина, так и PLPF стремятся к нулю, когда температура возрастает до высоких значений, независимо от плотности или от силы взаимодействий, что, несомненно, является значительной проблемой.

Оценка влияния внутренней статистической суммы на расчет электропроводности происходит главным образом через учет ионизационного равновесия и среднего состояния ионизации. Обоснование использования выражения (6), в котором мы сохраняем, по крайней мере, одно состояние основного уровня вместо выражения (13) при использовании непрерывной вероятности заселенности, хорошо понято и теоретически оправдано. С другой стороны, использование вероятности заселенности PL, зависящей от температуры, которая ошибочно обращается в нуль при очень высоких температурах, независимо от силы взаимодействия, недостаточно оправдано и очень спорно. Соответственно, при этой оценке мы рассматриваем эффект непрерывной зависимости заселенности, зависящей от состояния, и сравниваем его со схемой ступенчатого обрезания, одновременно используя форму (6) для оценки функций разбиения. Поскольку существует множество предлагаемых форм непрерывных вероятностей заселенности, наше внимание здесь будет уделено качественному и физическому поведению результатов, а не числовым значениям.

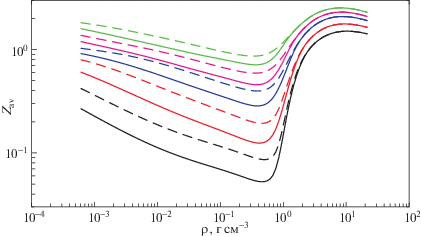
На рисунках 1a и 1б показано влияние непрерывных (пунктирные линии) и ступенчато обрезанных вероятностей заселенности (сплошные линии) при обрезании электронных статистических сумм, использованных в расчетах средних состояний ионизации алюминия и лития. Хотя схема ступенчатого обрезания совместима с принятой моделью для свободной энергии конфигурации, она имеет немаловажный недостаток, заключающийся в создании резких переходов из связанных в свободные состояния, приводящих к кусочно-непрерывным функциям плотности для электронной статистической суммы и, следовательно, для среднего состояния ионизации. Это определяет острые края, появляющиеся в изотермах проводимости [26, 27]. Следует отметить, что такие края более остры в случае лития (низкий Z) по сравнению с алюминием (более высокий Z). Это явно связано с более высокими энергиями ионизации Li+ и Li++ по сравнению с Al+ и Al++. Для диапазона температур, показанного на рис. 1а и рис. 1б, в основном в континуум будут удаляться электроны из M-оболочки алюминия.

Рис. 1.

Влияние непрерывных (пунктирные линии) и ступенчато обрезанных вероятностей заселенности (сплошные линии) для электронных статистических сумм при вычислении среднего состояния ионизации для алюминия (a) и лития (б).

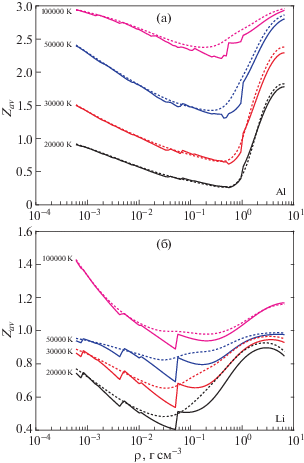
Стоит отметить, что использование схемы ступенчатой отсечки для обрезания статистических сумм ухудшает ситуацию и даже приводит к катастрофическим последствиям при расчете термодинамических свойств, зависящих от производных внутренней статистической суммы электронов.

3.2. Исключение возбужденных состояний

Также полезно и поучительно исследовать и количественно оценить эффект предположения об исключении электронных возбужденных состояний (обрезания на основном уровне), впервые предложенного Зельдовичем и Райзером [39] и впоследствии использованного многими авторами в упрощенных вычислениях, при расчетах ионизационного равновесия. На рис. 2 представлено среднее состояние ионизации Al-плазмы, рассчитанное как функция плотности для пяти различных изотерм (10 000, 14 000, 20 000, 25 000 и 31 600 K). Пунктирные кривые построены без учета состояний возбуждения, когда электронные статистические суммы были аппроксимированы статистическими весами основных состояний g0, а сплошные кривые включали все возбужденные состояния, доступные в обширной базе данных NIST. Главной особенностью, которую можно увидеть из рисунка, является то, что результаты, включающие возбужденные состояния, показывают значительно более низкие степени ионизации в большей части области расчетов. Чтобы понять поведение результатов вычислений на рис. 2, надо учесть, что влияние включения возбужденных состояний при вычислениях Zav зависит как от значений электронных статистических сумм, так и от заселенности связанных возбужденных состояний. При очень высоких плотностях высокие ионизационные состояния существуют из-за ионизации давлением, в результате чего заселенность связанных/возбужденных состояний в этой области мала. Соответственно, исключение возбужденных состояний в этой области фазового ρ−T-пространства не оказывает заметного влияния на вычисления Zav. С другой стороны, для промежуточных и умеренно высоких плотностей, ионизация компенсируется рекомбинацией, атомы и ионы сильнее возбуждаются до того, как они ионизируются, что приводит к плотной заселенности связанных/воз-бужденных состояний. При этих обстоятельствах исключение возбужденных состояний в этой области фазового ρ–T-пространства окажет значительное влияние на вычисления, что видно на рис. 2. Подобное поведение наблюдалось и для литиевой плазмы, что подтверждает полученные данные и выводы.

Рис. 2.

Влияние исключения возбужденных состояний на среднее состояние ионизации алюминия для пяти изотерм (сверху вниз, 10000, 14000, 20000, 25000 и 31600 K). Пунктирные кривые получены без учета возбужденных состояний, а сплошные кривые – с возбужденными состояниями.

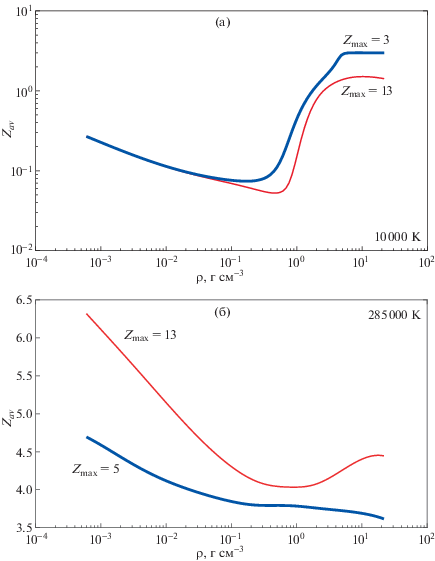
3.3. Верхняя граница ионизации (проблема конечного элемента выборки)

Другой возможный источник ошибки при расчете ионизационного равновесия возникает, когда максимальное состояние ионизации оказывается меньше атомного номера рассматриваемого химического элемента. Это приближение было принято в некоторых исследованиях, описанных в литературе, особенно для элементов с высоким Z, что привело к так называемой проблеме конечного элемента выборки. Чтобы исследовать и количественно оценить результирующую ошибку для случая Al-плазмы, было рассчитано ионизационное равновесие для алюминия при T = 10 000 K и 285000 K. Сначала использовалось атомное число алюминия 13, а затем было установлено максимальное состояние ионизации +3 при 10 000 K, принятое в работе [9], и +5 при 285000 K, принятое в работе [10]. На рис. 3а сделано сравнение для случая T = 10 000 К. Как видно из рисунка, даже для такой относительно низкой температуры результирующая ошибка является значительной, а среднее состояние ионизации переоценено. Однако на рис. 3б приведено сравнение для случая T = 285 000 К. При такой высокой температуре ожидается, что состояния ионизации выше +5 будут доминирующими в широком диапазоне плотностей. Рисунок показывает, что, как и ожидалось, значительная ошибка возникает при низких и высоких плотностях. При умеренной плотности ошибки все еще существенны, и их нельзя игнорировать.

Рис. 3.

Влияние границы высокой ионизации на расчет Zav для алюминия (проблема конечного элемента выборки): а) – 10000 K; б) – 285000 K.

3.4. Кулоновская связь

Точного решения многочастичной проблемы кулоновских взаимодействующих систем не существует, и возможны только приближенные неидеальные модели, или модели связи. Многие модели, созданные и предложенные для описания поведения неидеальной плазмы, собраны в серии обзоров (см., например, [20, 40–43]). Поскольку ни одна из таких моделей неидеальности не может считаться строго точной, надежность моделей будет определяться на основе физического поведения конечных результатов. В этом смысле, количественное сравнение с экспериментальными измерениями, если оно возможно, будет играть дополнительную роль.

Здесь проводится сравнение двух широко используемых моделей. Одна – модель Дебая–Хюккеля, основанная на теории Дебая–Хюккеля для классических заряженных сфер. В рамках этой модели поправка к свободной энергии, учитывающая влияние конечных ионных радиусов на термодинамические свойства, выражается как

(16)
$\begin{gathered} {{F}_{{Coul}}} = - ~\frac{{{{K}_{B}}TV}}{{12~\pi \lambda _{D}^{3}}}\frac{3}{{{{{\left( {a{\text{/}}{{\lambda }_{D}}} \right)}}^{3}}}} \times \\ \times \;\left[ {\ln \left( {1 + \frac{a}{{{{\lambda }_{D}}}}} \right) - \frac{a}{{{{\lambda }_{D}}}} + \frac{1}{2}{{{\left( {\frac{a}{{{{\lambda }_{D}}}}} \right)}}^{2}}} \right], \\ \end{gathered} $
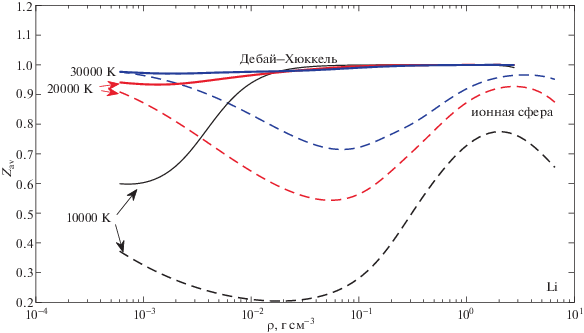
где ${{\lambda }_{D}} = {\text{ }}{{\left( {{{\varepsilon }_{0}}{{K}_{B}}T{\text{/}}{{e}^{2}}\left( {{{n}_{e}} + \sum\nolimits_s {{{n}_{s}}{{s}^{2}}} } \right)} \right)}^{{1/2}}}$ – дебаевский радиус, a – конечный ионный диаметр. В широко распространенной форме этой модели, известной как лямбда-приближение [40, 44], классический ионный диаметр заменяется квантовой длиной, зависящей от температуры: a(T) = = ΛB/8, где ΛB – средняя тепловая длина волны де Бройля для электронов. Другая модель – модель ионной сферы, в которой ионы с зарядом Z расположены в центрах единичных сферических ячеек плотно упакованной решетки. Каждая ячейка содержит Z свободных электронов и, следовательно, электрически нейтральна [38]. Соответствующая избыточная свободная энергия для системы может быть записана как
(17)
${{F}_{{Coul}}} = - \frac{9}{{10}}\frac{{{{e}^{2}}}}{{4\pi {{\varepsilon }_{{0~}}}{{R}_{0}}}}\mathop \sum \limits_s {{N}_{s}}~{{s}^{2}},$
где R0 – радиус ионной сферы.

На рис. 4 показано среднее состояние ионизации для лития, рассчитанное с использованием модели Дебая–Хюккеля (сплошные линии) и модели ионной сферы (пунктир) для 10 000 K, 20 000 K и 30000 K. Как видно из рисунка, расчеты по модели Дебая–Хюккеля дают пересекающиеся изотермы, помимо того, что они возможны только для более узкого диапазона плотностей, чем результаты модели ионной сферы, которая дает физически правдоподобные непересекающиеся изотермы. Для температур, показанных на рисунке, ясно, что среднее состояние ионизации, предсказываемое моделью Дебая–Хюккеля, всегда выше, чем предсказанное моделью ионной сферы. Это означает, что модель Дебая–Хюккеля недоучитывает снижение потенциала ионизации. Можно сделать вывод, что модель ионной сферы дает лучшее приближение для кулоновской неидеальности в сильно связанных системах.

Рис. 4.

Среднее состояние ионизации для лития, рассчитанное с использованием лямбда-приближения Дебая–Хюккеля (сплошные линии) и модели ионной сферы (пунктирные линии) при трех разных температурах.

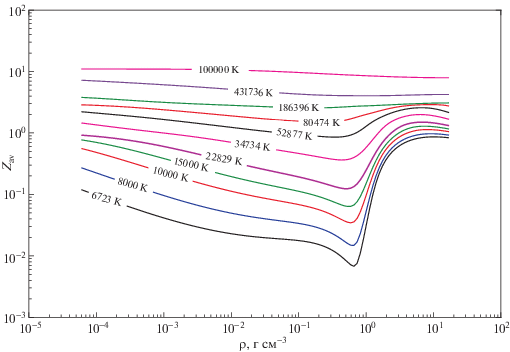
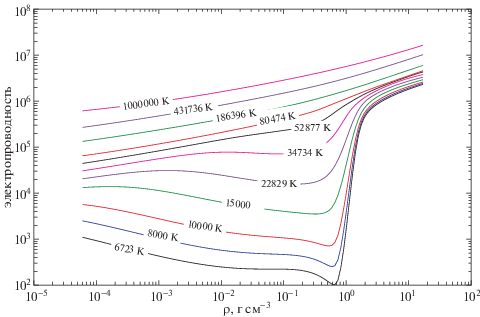
На рис. 5 показаны изотермы среднего ионизационного состояния алюминиевой плазмы, рассчитанные с использованием модели ячеек Зейтца–Вигнера или ионной сферы, с учетом возбужденных состояний, и с учетом ионизационных состояний вплоть до атомного номера алюминия. Показанные изотермы приведены снизу вверх для температур до 6723 K (критическая температура, согласно [17]), затем изотермы от 7000 до 12000 K с шагом 1000 K, за которыми следуют изотермы от 15000 до 106 K, равномерно распределенные по логарифмической шкале с шагом Δlog10 (T) = 0.0912. Модель дает непересекающиеся изотермы среднего состояния ионизации даже для очень близких температур.

Рис. 5.

Изотермы среднего ионизационного состояния, Zav, для алюминия.

3.5. Кулоновский логарифм

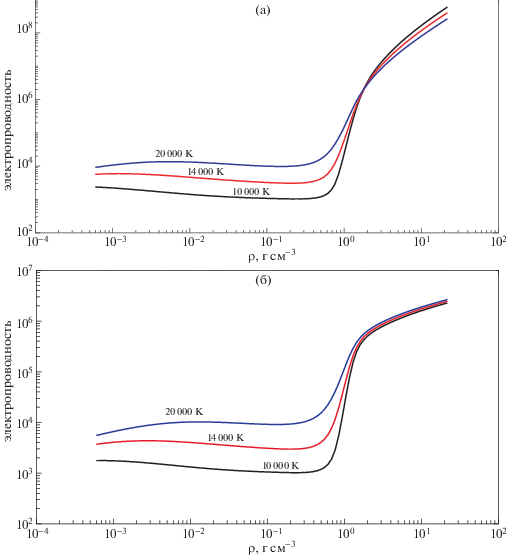
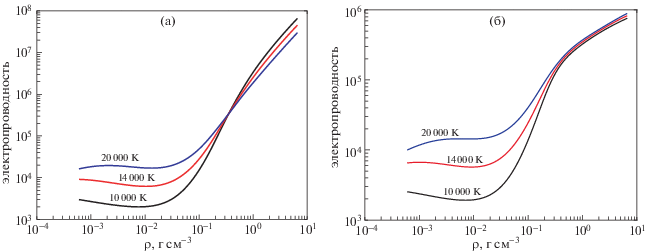
В расчетах электропроводности алюминиевой и литиевой плазмы учитывались плотности заселенностей, рассчитанные выше, с максимальным состоянием ионизации, равным атомному номеру рассматриваемого элемента, и включающие все возбужденные состояния, имеющиеся в базе данных NIST. Также рассматривались два различных выражения для кулоновского логарифма, следующие из теории обрезания: a) точное выражение, где в качестве прицельного параметра обрезания использовано расстояние, не зависящее от скорости, и формула рассеяния Резерфорда [31]; и б) обрезание с постоянным расстоянием ближайшего сближения, которое эквивалентно расстояниям, зависимым от скорости, в качестве прицельных параметров при обрезании [18]. Пример таких расчетов для алюминия показан на рис. 6а и 6б. Как видно из рис. 6а, обычно используемый прицельный параметр обрезания, независимый от скорости, дает физически некорректные пересекающиеся изотермы проводимости, так как ранее было показано [18], что он является непоследовательным и неточным. С другой стороны, использование обрезания с постоянным расстоянием ближайшего сближения, или же эквивалентного обрезания с прицельными параметрами, зависящими от скорости, устраняет эту проблему и создает непересекающиеся изотермы даже для очень близкого и точного набора изотерм, показанного на рис. 6б. Те же результаты, полученные для лития, показаны на рис. 7. Таким образом, в данной модели для расчета электропроводности плотных неидеальных плазменных систем сделан физически обоснованный выбор прицельного параметра обрезания, зависящего от скорости.

Рис. 6.

Пример изотермы электропроводности алюминия с использованием (а) расстояния, не зависящего от скорости, как прицельного параметра обрезания, и (б) обрезания с постоянным расстоянием ближайшего сближения, или эквивалентными прицельными параметрами обрезания, зависящими от скорости.

Рис. 7.

Пример изотермы электропроводности лития с использованием (а) расстояния, не зависящего от скорости, как прицельного параметра при обрезании и (б) обрезания с постоянным расстоянием ближайшего сближения, или эквивалентных прицельных параметров обрезания, зависящих от скорости.

4. МОДЕЛЬ ЭЛЕКТРОПРОВОДНОСТИ И РЕЗУЛЬТАТЫ

4.1. Модель

Основываясь на вышеупомянутой оценке и результатах, представленная модель для расчета электропроводности сильно связанных плазменных систем будет включать в себя вычисление плотностей заселенностей путем минимизации функции свободной энергии (1) с идеальными компонентами, введенными в (2) и (5). Внутренние статистические суммы электронов оцениваются с использованием выражения (6) с непрерывными вероятностями заселенности типа, заданного Зальцманом в [38]. Избыточная кулоновская свободная энергия из модели ячеек ионной сферы (17) используется для коррекции неидеальности, а выражения для других конфигурационных членов (Fhs, FvdW, Fbn) взяты из [17, 20]. Электрон-нейтральная проводимость определяется по формуле Дежарле [28], а электрон-ионная проводимость определяется по выражению (9) с использованием новой формулы для кулоновского логарифма (10) с учетом рассеяния электронов на электронах через фактор γE(Zav), который можно выразить как в [30].

В качестве примеров, модель была использована для расчета электропроводности в сильно связанных системах алюминиевой и литиевой плазмы. Полученные результаты обсуждаются ниже.

4.2. Результаты

В литературе описаны многочисленные экспериментальные измерения электропроводности сильно связанных плазменных систем, генерируемых взрывающимися металлическими проволочками [45–49] или ударно сжатым водородом и благородными газами [50, 51]. Разумная подборка доступных измерений электропроводности сильно связанной алюминиевой плазмы использована для сравнения с модельными предсказаниями.

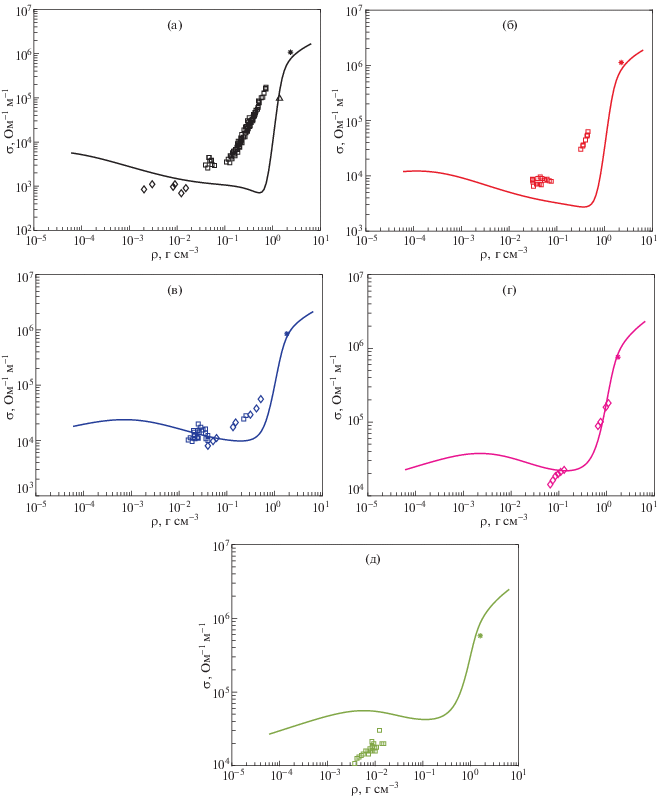
На рис. 8a–д проведено сравнение изотерм расчетной электропроводности алюминиевой плазмы с экспериментальными измерениями Де Сильва и Касторуса [45], Криша и Кунзе [46], Бенаге и др. [47, 48] и Мостовича и Чан [49]. Как видно из рисунка, получено хорошее согласие между предсказаниями данной модели и экспериментальными измерениями; однако отсутствие данных о сопутствующих экспериментальных неопределенностях (ошибках) позволяет сделать лишь качественные, а не количественные выводы. Общая зависимость изотерм электропроводности от плотности аналогична результатам Редмера [9] и Кима [11]. Характерной особенностью является локальный минимум и последующее увеличение электропроводности, которое проявляется при низких температурах и высокой плотности в результате увеличения роли рекомбинации и образования связанных состояний с более высокими плотностями, а с другой стороны – усиление ионизации из-за высокой плотности или ионизация давлением.

Рис. 8.

Сравнение изотерм рассчитанной электропроводности Al с экспериментальными измерениями. а) – 10000 К, б) – 14000 К, в) – 20000 К, г) – 25000 К, д) – 30000 К. Сплошные кривые – расчеты по настоящей модели, квадраты – измерения [45], ромбы – измерения [46], звездочки – измерения [47, 48], треугольники – измерения [49].

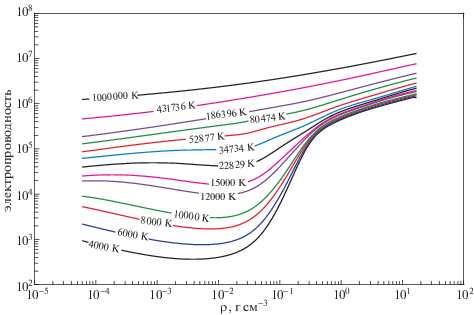
На рис. 9 приведены изотермы электропроводности алюминия $\sigma {{(\rho )}_{T}}$ при тех же температурах, что на рис. 5. Изотермы с очень высокими температурами соответствуют полной термической ионизации. Как и ожидалось, на этих изотермах с ростом плотности электропроводность увеличивается. Поведение изотерм при низких T в основном было объяснено выше. Однако наиболее важным достижением является получение непересекающихся изотерм при очень высокой плотности; т.е. ожидаемое правильное физическое поведение, отсутствующее в большинстве исследований, описанных в литературе. Подобное поведение получено для изотерм проводимости лития, представленных на рис. 10, что подтверждает вышеуказанные характеристики данной модели электропроводности.

Рис. 9.

Электропроводность Al-плазмы в широком диапазоне температур и плотностей.

Рис. 10.

Электропроводность Li плазмы.

5. ВЫВОДЫ

Часто встречающаяся проблема возникновения пересекающихся изотерм в теоретических предсказаниях электропроводности сильно связанных плазменных систем изучается путем исследования ряда факторов влияния. Исследования и оценки существенных особенностей, относящихся к обрезанию внутренней статистической суммы, кулоновской сильной связи, электронным возбужденным состояниям, а также к высокой границе ионизации и к кулоновскому логарифму, позволили создать улучшенную простую модель для предсказания электропроводности горячего плотного вещества. Модель используется для расчета электропроводности частично ионизованного и частично вырожденного алюминия и лития, где прогнозы по настоящей модели показали правильное физическое поведение и образование непересекающихся изотерм при высоких плотностях.

Автор хотел бы отметить ценные предложения, полученные от анонимных рецензентов. Автор также хотел бы поблагодарить проф. А.В. Де Сильва за предоставление экспериментальных данных. Работа поддержана проектом UAEU-UPAR, контракт G00002907.

Список литературы

  1. Hollandsworth C.E., Powell J.D., Keele M.J., Hum-mer C.R. // J. Appl. Phys. 1998. V. 84 (9). P. 4992.

  2. Powell J.D., Thornhill L.D. // IEEE Trans. Magn. 2001. V. 37 (1). P. 183.

  3. Sanford T.W.L., Mock R.C., Spielman R.B., Peterson D.L., Mosher D., Roderick N.F. // Phys. Plasmas. 1998. V. 5 (10). P. 3755.

  4. Slutz S.A., Herrmann M.C., Vesey R.A., Sefkow A.B., Sinars D.B., Rovang D.C., Peterson K.J., Cuneo M.E. // Phys. Plasmas. 2010. V. 17. 056303.

  5. Gomez M.R., Slutz S.A., Sefkow A.B., Sinars D.B., Hahn K.D., Hansen S.B., Harding E.C., Knapp P.F., Schmit P.F., Jennings C.A., Awe T.J., Geissel M., Ro-vang D.C., Chandler G.A., Cooper G.W., Cuneo M.E., Harvey-Thompson A.J., Herrmann M.C., Hess M.H., Johns O., Lamppa D.C., Martin M.R., McBride R.D., Peterson K.J., Porter J.L., Robertson G.K., Rochau G.A., Ruiz C.L., Savage M.E., Smith I.C., Stygar W.A., Ve-sey R.A. // Phys. Rev. Lett. 2014. V. 113. 155003.

  6. Stygar W.A., Awe T.J., Bailey J.E., Bennett N.L., Breden E.W., Campbell E.M., Clark R.E., Cooper R.A., Cuneo M.E., Ennis J.B., Fehl D.L., Genoni T.C., Gomez M.R., Greiser G.W. et al. // Phys. Rev. Special Topics – Accelerators and Beams. 2015. V. 18. 110401.

  7. Fortov V.E. Extreme States of Matter-High Energy Density Physics. Springer International Publishing, Switzerland, 2016.

  8. Mitchener M., Kruger C.H. Jr. Partially Ionized Gases. New York: Wiley, 1973.

  9. Redmer R. // Phys. Rev. E. 1999. V. 59. P. 1073.

  10. Kuhlbrodt S., Redmer R. // J. Phys. A: Math. Gen. 2003. V. 36. P. 6027.

  11. Kim D.-K., Kim I. // Phys. Rev. E. 2003. V. 68. 056410.

  12. Zaghloul M.R. // Phys. Plasmas. 2010. V. 17. 062701-10.

  13. Zaghloul M.R. // Phys. Plasmas. 2010. V. 17. 124706-3.

  14. Zaghloul M.R.// Phys. Plasmas. 2010. V.17. 122903-13. https://doi.org/10.1063/1.3528269

  15. Zaghloul M.R. // Eur. Phys. J. 2011. H 36. P. 401. See also Erratum // Eur. Phys. J. 2013. H 38. P. 279.

  16. Zaghloul M.R. // Phys. Letters A. 2013. V. 377 (15). P. 1119.

  17. Zaghloul M.R. // High Energy Density Physics. 2018. V. 26. P. 8.

  18. Zaghloul M.R. // IEEE Trans. Plasma Sci. 2018. V. 46. P. 390.

  19. Филиппов А.В., Старостин А.Н., Грязнов В.К. // ЖЭТФ. 2018. Т. 153. С. 514. [A.V. Filippov, A.N. Starostin, V.K. Gryaznov // JETP. V. 126 (3). P. 430 (2018)].

  20. Ebeling W., Forster A., Fortov V.E., Gryaznov V.K., Polishchuk A.Y. Thermophysical Properties of Hot Dense Plasmas. Stuttgart, Leizig, 1991.

  21. Martin W.C., Fuhr J.R., Kelleher D.E., Musgrove A., Podobedova L., Reader J., Saloman E.B., Sansonet-ti C.J., Wiese W.L., Mohr P.J., Olsen K. NIST Atomic Spectra Data-base, Version 2.0. National Institute of Standards and Technology, Gaithersburg, MD, 2002.

  22. Zaghloul M.R. // Phys. Plasmas. 2015. V. 22. 062701.

  23. Günther K., Radtke R. Electric Properties of Weakly Nonideal Plasmas. Base, Boston, Stuttgart, lBirkhäuser, 1984.

  24. Zollweg R.J., Liebrmann R.W. // J. Appl. Phys. 1987. V. 62. P. 3621.

  25. Adams J.R., Shilkin N.S., Fortov V.E., Gryaznov V.K., Mintsev V.B., Redmer R., Reinholz H., Röpke G. // Phys. Plasmas. 2007. V. 14. 062303.

  26. Zaghloul M.R. // Phys. Plasmas. 2008. V. 15 (4). 042705-1.

  27. Fu Z.-J., Quan W., Zhang W., Li Z., Zheng J., Gu Y., Chen Q. // Phys. Plasmas. 2017. V. 24. 013303.

  28. Desjarlais M.P. // Contrib. Plasma Phys. 2001. V. 41. P. 267.

  29. Spitzer L., Härm R.// Phys. Rev. 1953. V. 89. P. 977.

  30. Bespalov I.M., Polishchuk A.Ya.// Sov. Tech. Phys. Lett. 1989. V. 15 (1). P. 39.

  31. Zaghloul M.R., Bourham M.A., Doster J.M., Powell J.D. // Phys. Lett. A. 1999. V. 262. P. 86.

  32. Hummer D.G., Mihalas D. // Astrophys. J. 1988. V. 331. P. 794.

  33. Potekhin A.Y. // Phys. Plasmas.1996. V. 3 (11). P. 4156.

  34. Griem H.R. // Phys. Rev. 1962. V. 128. P. 997.

  35. Fu Z.J., Chen Q.F., Chen X.R. //Contrib. Plasma Phys. 2012. V. 52 (4). P. 251.

  36. Fermi E. // Z. Phys. 1924. V. 26. P. 54.

  37. Zimmerman G.B., More R.M. // J. Quanti. Spectrosc. Rad. Trans. 1980. V. 23. P. 517.

  38. Salzmann D. Atomic Physics in Hot Plasmas. Oxford University Press, 1998.

  39. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, Физматлит, 1966. [Ya.B. Zel’dovich and Yu.P. Raizer. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena. Academic Press, New York (1966)]

  40. Ebeling W., Kraeft W.D., Kremp D. Theory of Bound States and Ionization Equilibrium in Plasmas and Solids. Berlin: Akademie-Verlag, 1976.

  41. Фортов В.Е., Храпак А.Г., Якубов И.Т. Физика неидеальной плазмы. М.: Физматлит, 2004. [V. E. Fortov, I.T. Yakubov. Physics of Nonideal Plasma, Hemisphere, New York, 1990]

  42. Transport and Optical Properties of Nonideal Plasma. Eds: I. T. Iakubov, G.A. Kobzev, M.M. Popovich. Springer, 1995.

  43. Ebeling W., Fortov V.E., Filinov V. Quantum Statistics of Dense Gases and Nonideal Plasmas. Springer, 2017.

  44. Beule D., Ebeling W., Forster A. // Physica A. 1997. V. 241. P. 719.

  45. De Silva A.W., Katsourous J.D. // Phys. Rev. E. 1998. V. 57 (5). P. 5945.

  46. Krisch I., Kunze H.-J. // Phys. Rev. E. 1998. V. 58. P. 6557.

  47. Benage J.F., Shanahan W.R., Murillo M.S. // Phys. Rev. Lett. 1999. V. 83. P. 2953.

  48. Benage J.F. Jr. // Phys. Plasmas. 2000. V. 7 (5). P. 2040.

  49. Mostovych A.N., Chan Y. // Phys. Rev. Lett. 1997. V. 79. No. 25. P. 5094.

  50. Fortov V.E., Ternovo V.Ya., S.V. Kvitov, V.B. Mintsev, D.N. Nikolaev, A.A. Pyalling, A.S. Filimonov // JETP Lett. 1999. V. 69. P. 926 .

  51. Mintsev V.B., Fortov V.E. // J. Phys. A: Math. Gen. 2006. V. 39. P. 4319.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал