Физика плазмы, 2020, T. 46, № 7, стр. 658-666

О дрейфовом движении заряженных частиц в неоднородных магнитном и сильном электрическом полях

Н. А. Марусов^a, b, c, Е. А. Сорокина^a, c, *, В. И. Ильгисонис^d

^a НИЦ “Курчатовский институт”
Москва, Россия

^b Московский физико-технический институт
Долгопрудный, Россия

^c Российский университет дружбы народов
Москва, Россия

^d Государственная корпорация по атомной энергии “Росатом”
Москва, Россия

^* E-mail: sorokina.ekaterina@gmail.com

Поступила в редакцию 19.12.2019
После доработки 13.02.2020
Принята к публикации 20.02.2020

DOI: 10.31857/S0367292120070069

Полный текст (PDF)

Аннотация

Исследованы особенности дрейфового движения нерелятивистской заряженной частицы в медленно меняющихся магнитном и сильном электрическом полях, для которых неприменимо предположение о малости скорости электрического дрейфа по отношению к полной скорости частицы. Вариационные принципы дрейфового движения распространены на случай сильного электрического поля. Получен обобщeнный лагранжиан Литтлджона и с его помощью продемонстрирован переход к расширенной системе дрейфовых уравнений, содержащей дополнительные скорости дрейфов. Показана возможность ускорения частицы за счет дрейфового движения вдоль сильного электрического поля.

Ключевые слова: движение заряженных частиц, дрейфовая теория, электрический дрейф, скрещенные электрическое и магнитное поля

1. ВВЕДЕНИЕ

Дрейфовая теория – классический метод исследования движения заряженных частиц в адиабатических электрическом и магнитном полях. Как и любая другая модель, описывающая поведение консервативной механической системы, дрейфовая теория может быть математически формализована в рамках механики Лагранжа [1]. Впервые возможность использования уравнений Лагранжа для поиска интегралов движения дрейфовых уравнений, связанных с пространственной симметрией поля при постоянных во времени электрическом E и магнитном B полях, была показана Морозовым и Соловьевым в работе [2]. Полученная авторами функция Лагранжа $L{\text{*}}$ не имеет строгой физической интерпретации и формально вводится как лагранжиан частицы нулевой массы, движущейся в эффективном магнитном поле ${\mathbf{B}}{\text{*}} = \nabla \times {\mathbf{A}}{\text{*}}$:

(1)

$L{\text{*}} = {\mathbf{A}}{\text{*}} \cdot {\mathbf{\dot {R}}};\quad {\mathbf{A}}{\text{*}} = {\mathbf{A}} + \frac{{{{{v}}_{{||}}}}}{\Omega }{\mathbf{B}}.$

Здесь ${\mathbf{\dot {R}}}$ – производная по времени от радиус-вектора ведущего центра; $\Omega = ZeB{\text{/}}mc$ – циклотронная частота, m и Ze – масса и заряд частицы, c – скорость света; ${{v}_{\parallel }}$ – компонента скорости частицы вдоль магнитного поля ${\mathbf{B}} = \nabla \times {\mathbf{A}}$. Отметим, что при выводе (1) априори используются условия сохранения энергии и магнитного момента, которые напрямую не следуют из самих уравнений Лагранжа. Позднее Литтлджоном [3] была построена гамильтонова теория движения ведущего центра (см. ссылки в обзоре [4]). Лагранжиан Литтлджона выводится путем усреднения функции Лагранжа заряженной частицы по циклотронному периоду, а следующие из вариационного принципа дрейфовые уравнения обладают точными законами сохранения фазового объема и энергии (для постоянных во времени полей), что обобщает и развивает полученные ранее результаты Морозова и Соловьева.

Движение заряженной частицы в медленно меняющихся электрическом и магнитном полях удобно представить в виде суперпозиции продольного и поперечного (по отношению к направлению магнитного поля) движений. Традиционный подход классической дрейфовой теории состоит в разделении движения заряженной частицы в плоскости, перпендикулярной магнитному полю, на быстрое вращение по ларморовской окружности и медленное смещение ее ведущего центра, называемое дрейфом. Возникновение дрейфа связывается с действием на заряженную частицу какой-либо силы, отличной от силы Лоренца, а также с пространственно-временными неоднородностями электрического и магнитного полей. Вышеуказанное разделение на “быстрое” и “медленное” движения заведомо правомерно, когда изменения полей на ларморовской длине и циклотронном периоде относительно невелики. При этом понятие “дрейф” принято относить ко временным интервалам движения, превышающим период обращения частицы по ларморовской окружности.

Хорошо известно, что в вырожденном случае движения заряженной частицы в однородном магнитном поле под действием постоянной силы разделение движения на ларморовское вращение и смещение ведущего центра является точным. В силу этого существует принципиальная возможность расширения стандартной дрейфовой теории на случай сильных электрических полей, для которых скорость электрического дрейфа ${{{\mathbf{V}}}_{E}} = c[{\mathbf{E}} \times {\mathbf{B}}]{\text{/}}{{B}^{2}}$ сопоставима с полной скоростью частицы $v$. В то же время в случае нерелятивистского движения отношение электрического поля к магнитному полю считается малым, $E{\text{/}}B \sim v{\text{/}}c \ll 1$. Такая ситуация реализуется, например, в установках по ускорению плазмы в скрещенных полях, принцип работы которых основан на естественном разделении масштабов между ларморовскими радиусами заряженных компонент плазмы в относительно слабом магнитном поле: разряды Пеннинга, магнетронные разряды, стационарные плазменные двигатели А.И. Морозова (СПД), ионные источники с замкнутым дрейфом электронов и др. [5]. Расширение дрейфовой теории на случай сильного электрического поля приводит к появлению новых членов в дрейфовом уравнении движения [6, 7], представляющих собой комбинации электрического поля с неоднородностями электрического и магнитного полей [8].

Настоящая работа имеет методический характер и призвана привлечь внимание читателей к особенностям дрейфового движения заряженных частиц в скрещенных полях с сильной электрической компонентой, что необходимо, в частности, для корректной интерпретации результатов кинетического моделирования холловских разрядов – направления, активно развиваемого в настоящее время – см., например, [9, 10]. Система дрейфовых уравнений в сильном электрическом поле, полученная в [6], выведена в терминах механики Лагранжа. На примере модельных конфигураций электрического и магнитного полей продемонстрирован ряд ключевых эффектов, описание которых выходит за рамки классической дрейфовой теории.

Работа построена следующим образом. В разделе 2 в рамках подхода, развитого в [3], представлен вывод функции Лагранжа для ведущего центра частицы, движущейся в сильном электрическом поле. При помощи уравнений Эйлера–Лагранжа продемонстрирован переход к известной системе дрейфовых уравнений, учитывающей поправки к движению ведущего центра частицы в сильном электрическом поле. В разделе 3 представлены результаты численного расчета траекторий движения заряженной частицы в некоторых модельных конфигурациях скрещенных полей, демонстрирующих эффекты, связанные с дрейфом частиц в сильном электрическом поле. Основные результаты работы суммированы в Заключении.

2. ДРЕЙФОВАЯ ТЕОРИЯ В СЛУЧАЕ СИЛЬНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ В ТЕРМИНАХ МЕХАНИКИ ЛАГРАНЖА

Выведем уравнения дрейфовой теории, расширенной на случай сильного электрического поля, используя лагранжев формализм. Зададим функцию Лагранжа заряженной частицы в виде функции независимых переменных координат q, скоростей ${\mathbf{\dot {q}}}$ и времени t:

(2)

$L({\mathbf{q}},{\mathbf{\dot {q}}},t) = {\mathbf{p}} \cdot {\mathbf{\dot {q}}} - H({\mathbf{q}},{\mathbf{p}},t).$

Здесь точкой обозначено дифференцирование по времени; функция $H({\mathbf{q}},{\mathbf{p}},t)$ – гамильтониан заряженной частицы в электрическом и магнитном полях, заданный выражением

(3)

$H({\mathbf{q}},{\mathbf{p}},t) = \frac{1}{{2m}}\mathop {\left[ {{\mathbf{p}} - \frac{{Ze}}{c}{\mathbf{A}}({\mathbf{q}},t)} \right]}\nolimits^2 + Ze\Phi ({\mathbf{q}},t),$

где A – векторный потенциал магнитного поля: ${\mathbf{B}} = \nabla \times {\mathbf{A}}$; Φ – электростатический потенциал, определяющий напряженность электрического поля в соответствии с выражением ${\mathbf{E}}\;\; = $ $ = - \nabla \Phi - (1{\text{/}}c)\partial {\mathbf{A}}{\text{/}}\partial t$.

Полагая ${\mathbf{r}} = {\mathbf{q}}$ и ${\mathbf{v}} = (1{\text{/}}m)({\mathbf{p}} - (Ze{\text{/}}c){\mathbf{A}})$, запишем лагранжиан в переменных $({\mathbf{r}},{\mathbf{v}})$:

(4)

$L = \left[ {\frac{{Ze}}{c}{\mathbf{A}}({\mathbf{r}},t) + m{\mathbf{v}}} \right] \cdot {\mathbf{\dot {r}}} - \left[ {Ze\Phi ({\mathbf{r}},t) + \frac{m}{2}{\text{|}}{\mathbf{v}}{{{\text{|}}}^{2}}} \right].$

Далее переменные v и ${\mathbf{\dot {r}}}$ будут рассматриваться как независимые.

Для перехода к описанию дрейфового движения представим радиус-вектор частицы r в виде суперпозиции радиус-вектора ведущего центра R и ларморовского радиуса ${{\rho }_{L}}$:

(5)

${\mathbf{r}} = {\mathbf{R}} + {{\rho }_{L}},$

где

(6)

${{\rho }_{L}} = \frac{{[{\mathbf{u}} \times \Omega ]}}{{{{\Omega }^{2}}}}.$

Здесь введена ${\mathbf{u}} = {{{\mathbf{v}}}_{ \bot }} - {{{\mathbf{V}}}_{E}}$ – скорость циклотронного вращения частицы в системе отчета, движущейся со скоростью электрического дрейфа; ${{{\mathbf{v}}}_{ \bot }}$ – компонента скорости частицы поперек магнитного поля $\Omega = - Ze{\mathbf{B}}{\text{/}}mc$.

Введем тройку единичных ортогональных векторов

(7)

${\mathbf{b}} = [{{{\mathbf{e}}}_{1}} \times {{{\mathbf{e}}}_{2}}],\quad {{{\mathbf{e}}}_{1}} = [{{{\mathbf{e}}}_{2}} \times {\mathbf{b}}],\quad {{{\mathbf{e}}}_{2}} = [{\mathbf{b}} \times {{{\mathbf{e}}}_{1}}],$

где ${\mathbf{b}} = {\mathbf{B}}{\text{/}}B$ – единичный вектор, направленный вдоль магнитного поля. Векторы ${{{\mathbf{e}}}_{1}}$ и ${{{\mathbf{e}}}_{2}}$ легко определить, задав один из них в виде ${{{\mathbf{e}}}_{1}} = {\mathbf{u}}{\text{/}}u$; тогда второй вектор, в силу соотношения (6), будет равен ${{{\mathbf{e}}}_{2}} = (\Omega {\text{/}}u){{\rho }_{L}}$. Заданные таким образом орты ${{{\mathbf{e}}}_{1}}$ и ${{{\mathbf{e}}}_{2}}$ вращаются вокруг вектора b с частотой Ω, поэтому они также могут быть выражены через фазу ларморовского вращения θ в виде

${{{\mathbf{e}}}_{1}} = {{{\mathbf{e}}}_{i}}{\text{cos}}\theta + {{{\mathbf{e}}}_{j}}{\text{sin}}\theta ,\quad {{{\mathbf{e}}}_{2}} = - {{{\mathbf{e}}}_{i}}{\text{sin}}\theta + {{{\mathbf{e}}}_{j}}{\text{cos}}\theta ,$

где ${{{\mathbf{e}}}_{{i,j}}}$ – единичные ортогональные векторы в плоскости ларморовского вращения частицы $[{{{\mathbf{e}}}_{i}} \times {{{\mathbf{e}}}_{j}}] = {\mathbf{b}}$.

При помощи соотношений (5)–(7) вектор скорости и радиус-вектор частицы записываются в виде

(8)

${\mathbf{v}} = {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}} + u{{{\mathbf{e}}}_{1}},\quad {\mathbf{r}} = {\mathbf{R}} + \frac{u}{\Omega }{{{\mathbf{e}}}_{2}}.$

Подстановка (8) в лагранжиан (4) дает

(9)

$\begin{gathered} L = m\left\{ {\frac{\Omega }{B}{\mathbf{A}}({\mathbf{r}},t) + {{v}_{\parallel }}{\mathbf{b}}({\mathbf{r}},t) + {{{\mathbf{V}}}_{E}}({\mathbf{r}},t) + u{{{\mathbf{e}}}_{1}}} \right\} \times \\ \, \times \left( {{\mathbf{\dot {R}}} + \left( {\mathop {\frac{u}{\Omega }{{{\mathbf{e}}}_{2}}}\limits^\centerdot } \right)} \right) - \\ \, - \left\{ {Ze\Phi ({\mathbf{r}},t) + \frac{m}{2}{\text{|}}{{v}_{\parallel }}{\mathbf{b}}({\mathbf{r}},t) + {{{\mathbf{V}}}_{E}}({\mathbf{r}},t) + u{{{\mathbf{e}}}_{1}}{{{\text{|}}}^{2}}} \right\}. \\ \end{gathered} $

Далее используем стандартное для дрейфовой теории представление о порядке величин: $({{\rho }_{L}} \cdot \nabla ){\mathbf{C}} \sim \varepsilon {\mathbf{C}}$, $\varepsilon \ll 1$, где C – произвольный медленно меняющийся вектор. Усредним выражение (9) по циклотронному периоду, определяя при этом все величины в точке нахождения ведущего центра с точностью до второго порядка малости по ε:

${\mathbf{C}}({\mathbf{r}}) = {\mathbf{C}}({\mathbf{R}}) + {{\rho }_{{Li}}}\frac{{\partial {\mathbf{C}}({\mathbf{R}})}}{{\partial {{R}_{i}}}} + \frac{1}{2}{{\rho }_{{Li}}}{{\rho }_{{Lj}}}\frac{{{{\partial }^{2}}{\mathbf{C}}({\mathbf{R}})}}{{\partial {{R}_{i}}\partial {{R}_{j}}}} + O({{\varepsilon }^{3}}).$

Это в итоге дает

$\begin{gathered} L = m\left\{ {\frac{\Omega }{B}{\mathbf{A}} + {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}}} \right\} \cdot {\mathbf{\dot {R}}} + \\ \, + \left( {\mathop {\frac{{mu}}{\Omega }}\limits^\centerdot } \right)\left\{ {\frac{u}{{2B}}\left( {\nabla \cdot {\mathbf{A}} - {\mathbf{b}} \cdot ({\mathbf{b}} \cdot \nabla ){\mathbf{A}}} \right) + \frac{{{{v}_{\parallel }}u}}{{2\Omega }}\nabla \cdot {\mathbf{b}} + } \right. \\ \end{gathered} $

(10)

$\begin{gathered} \, + \left. {\frac{u}{{2\Omega }}\left( {\nabla \cdot {{{\mathbf{V}}}_{E}} - {\mathbf{b}} \cdot ({\mathbf{b}} \cdot \nabla ){{{\mathbf{V}}}_{E}}} \right)} \right\} - \\ \, - \left( {\frac{{m{{u}^{2}}}}{{2\Omega }}} \right)\left\{ {1 - \frac{{{{v}_{\parallel }}}}{\Omega }{\mathbf{b}} \cdot \nabla \times {\mathbf{b}} - \frac{1}{\Omega }{\mathbf{b}} \cdot \nabla \times {{{\mathbf{V}}}_{E}}} \right\}\dot {\theta } - \\ \end{gathered} $

$\begin{gathered} - \;Ze\left( {\Phi + \frac{{{{u}^{2}}}}{{4{{\Omega }^{2}}}}{{\nabla }^{2}}\Phi } \right) + \frac{m}{2}\left( {v_{\parallel }^{2} + V_{E}^{2} + {{u}^{2}}\mathop \times \limits_{_{{_{{_{{_{{}}}}}}}}} } \right. \\ \, \times \left. {\left\{ {1 - \frac{{{{v}_{\parallel }}}}{{2\Omega }}{\mathbf{b}} \cdot \nabla \times {\mathbf{b}} - \frac{1}{{2\Omega }}{\mathbf{b}} \cdot \nabla \times {{{\mathbf{V}}}_{E}}} \right\}} \right). \\ \end{gathered} $

В (10) все сглаженные величины как функции координат определены в точке нахождения ведущего центра R.

Выражение (10) содержит член с $\nabla \cdot {\mathbf{A}} - $ $ - {\mathbf{b}} \cdot ({\mathbf{b}} \cdot \nabla ){\mathbf{A}}$, при занулении которого за счет соответствующей калибровки векторного потенциала A, как это делается в классической электродинамике¹ ¹, слагаемое c $d(mu{\text{/}}\Omega ){\text{/}}dt$ становится второго порядка малости. Тогда, с точностью до нулевого порядка, функция Лагранжа (10) может быть записана в искомой форме

(11)

$L = \frac{{Ze}}{c}{\mathbf{A}}{\text{*}} \cdot {{{\mathbf{\dot {R}}}}_{d}} - \frac{{{{m}^{2}}c}}{{2Ze}}\mu \dot {\theta } - h.$

Здесь

(12)

${\mathbf{A}}{\text{*}} = {\mathbf{A}} + \frac{{mc}}{{Ze}}({{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}})$

– модифицированный векторный потенциал, $\mu = {{u}^{2}}{\text{/}}B$ – магнитный момент и h – сглаженная функция Гамильтона заряженной частицы, определяемая выражением

$h = Ze\Phi + \frac{m}{2}\left( {v_{\parallel }^{2} + V_{E}^{2} + \mu B} \right),$

что в удерживаемом порядке совпадает с функцией (3). Функция Лагранжа (11) с точностью до отброшенных членов высших порядков малости обобщает известный лагранжиан Литтлджона [3, 4] на случай сильного поперечного электрического поля ${{{\mathbf{E}}}_{ \bot }} = O(1)$.

Первое слагаемое в (11) по форме² ² совпадает с лагранжианом Морозова–Соловьева (1) с поправкой к модифицированному векторному потенциалу, связанной с ${{{\mathbf{V}}}_{E}}$. Как показано в [2], в случае ${\mathbf{b}} \cdot \nabla \times {\mathbf{b}} = 0$ уравнение движения ведущего центра можно представить в виде³ ³

(13)

$[{\mathbf{\dot {R}}} \times {\mathbf{B}}{\text{*}}] = 0,$

что формально совпадает с уравнением движения частицы пренебрежимо малой массы в некотором фиктивном магнитном поле ${\mathbf{B}}{\text{*}} = \nabla \times {\mathbf{A}}{\text{*}}$. Из уравнения (13) следует, что траектория ведущего центра пролегает вдоль силовых линий ${\mathbf{B}}{\text{*}}$, т. е.

(14)

${\mathbf{\dot {R}}} = \frac{{{{v}_{\parallel }}}}{B}{\mathbf{B}}{\text{*}}.$

Обобщение (14) на случай ${\mathbf{b}} \cdot \nabla \times {\mathbf{b}} \ne 0$ и ${\mathbf{b}} \cdot \nabla \times $ $ \times \;{{{\mathbf{V}}}_{E}} \ne 0$ может быть проделано путем замены в знаменателе B на $B_{\parallel }^{*} = {\mathbf{b}} \cdot {\mathbf{B}}{\text{*}}$. В рамках классической дрейфовой теории строгий вывод уравнения (14), обобщенного на случай ${\mathbf{b}} \cdot \nabla \times {\mathbf{b}} \ne 0$, был проделан Бузером в работе [11].

Используя уравнения Лагранжа

(15)

$\frac{d}{{dt}}\frac{{\partial L}}{{\partial \mathop {\dot {q}}\nolimits_i }} - \frac{{\partial L}}{{\partial {{q}_{i}}}} = 0,$

получим расширенную систему дрейфовых уравнений в сильном электрическом поле. Подставляя в (15) в качестве обобщенных координат ${{q}_{i}} = {{v}_{\parallel }},\mu ,\theta $ и лагранжиан (11) как функцию шести независимых переменных $L = L({\mathbf{R}},{{v}_{\parallel }},\mu ,\theta )$, найдем

(16)

${\mathbf{b}} \cdot {\mathbf{\dot {R}}} = {{v}_{\parallel }},\quad \dot {\theta } = - \Omega ,\quad \dot {\mu } = 0.$

Из первого уравнения (при ${{q}_{1}} = {{v}_{\parallel }}$) следует, что произведение ${\mathbf{b}} \cdot {\mathbf{\dot {R}}}$ равняется проекции скорости частицы ${{v}_{\parallel }}$ на направление магнитного поля в точке нахождения ведущего центра; второе уравнение (при ${{q}_{2}} = \mu $) показывает, что производная по времени от фазы ларморовского вращения θ с точностью до членов нулевого порядка совпадает с циклотронной частотой: $\dot {\theta } = - \Omega + O(\varepsilon )$; и, наконец, третье уравнение (при ${{q}_{3}} = \theta $) дает сохранение магнитного момента μ.

Далее, для ${{q}_{i}} = {{R}_{i}}$, с точностью до первого порядка получим

(17)

$Ze{\mathbf{E}}{\text{*}} + \frac{{Ze}}{c}[{\mathbf{\dot {R}}} \times {\mathbf{B}}{\text{*}}] = \frac{m}{2}(\nabla V_{E}^{2} + \mu \nabla B),$

где

(18)

${\mathbf{E}}{\text{*}} = - \nabla \Phi - \frac{1}{c}\frac{{\partial {\mathbf{A}}{\text{*}}}}{{\partial t}} = {\mathbf{E}} - \frac{m}{{Ze}}\frac{\partial }{{\partial t}}({{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}}).$

Умножая (17) векторно на b с учетом ${\mathbf{b}} \cdot {\mathbf{\dot {R}}} = {{v}_{\parallel }}$, получим уравнение для ${\mathbf{\dot {R}}}$ в виде

(19)

$\begin{gathered} {\mathbf{\dot {R}}} = \frac{1}{{B_{\parallel }^{*}}}\left( {{{v}_{\parallel }}{\mathbf{B}}{\text{*}} + c[{\mathbf{E}}{\text{*}} \times {\mathbf{b}}]\mathop + \limits_{_{{_{{}}}}} } \right. \\ \, + \left. {\frac{{mc}}{{2Ze}}[{\mathbf{b}} \times (\nabla V_{E}^{2} + \mu \nabla B)]} \right). \\ \end{gathered} $

Здесь также $B_{\parallel }^{*} = {\mathbf{b}} \cdot {\mathbf{B}}{\text{*}}$. Выражение для ${\mathbf{\dot {R}}}$ записывается в более привычном виде суммы дрейфовых слагаемых [8] путем разложения $1{\text{/}}B_{\parallel }^{*}$ в (19) по ε с точностью до членов первого порядка малости:

${\mathbf{\dot {R}}} = {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}} + \frac{{{{u}^{2}}}}{{2\Omega }}\frac{{[{\mathbf{b}} \times \nabla B]}}{B} + \frac{{v_{\parallel }^{2}}}{\Omega }[{\mathbf{b}} \times ({\mathbf{b}} \cdot \nabla ){\mathbf{b}}] + $

(20)

$\begin{gathered} \, + \frac{c}{{B\Omega }}\mathop {\left( {\frac{{\partial {{{\mathbf{E}}}_{ \bot }}}}{{\partial t}} + {{v}_{\parallel }}\left( {{\mathbf{b}} \cdot \nabla } \right){{{\mathbf{E}}}_{ \bot }} + \left( {{{{\mathbf{V}}}_{E}} \cdot \nabla } \right){{{\mathbf{E}}}_{ \bot }}} \right)}\nolimits_ \bot + \\ \, + \frac{{{{v}_{\parallel }}}}{\Omega }\left( {[{\mathbf{b}} \times ({{{\mathbf{V}}}_{E}} \cdot \nabla ){\mathbf{b}}] - \frac{{c{{{\mathbf{E}}}_{ \bot }}}}{{{{B}^{2}}}}{\mathbf{b}} \cdot \nabla B + \left[ {{\mathbf{b}} \times \frac{{\partial {\mathbf{b}}}}{{\partial t}}} \right]} \right) - \\ \end{gathered} $

$\, - \frac{{c{{{\mathbf{E}}}_{ \bot }}}}{{\Omega {{B}^{2}}}}\left( {{{{\mathbf{V}}}_{E}} \cdot \nabla B + \frac{{\partial B}}{{\partial t}}} \right).$

Первая строчка уравнения (20) хорошо известна из классической дрейфовой теории [6, 12]. Остальные слагаемые пропорциональны $\varepsilon {{V}_{E}}{\text{/}}v$ и $\varepsilon {{({{V}_{E}}{\text{/}}v)}^{2}}$ и отсутствуют в стандартной дрейфовой теории ввиду предположения ${{V}_{E}} \ll v$. В работе [6] указанные слагаемые были получены в компактной форме: $[{\mathbf{b}} \times \left( {\partial {\mathbf{v}}{\text{/}}\partial t + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}}} \right)]{\text{/}}\Omega $, где ${\mathbf{v}} = $ $ = {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}}$ – формально эквивалентной поперечной к B компоненте гидродинамического уравнения движения холодной плазмы. При этом поправки к массовой скорости V, связанные с движением такой плазмы в сильном электрическом поле, могут быть получены и из гидродинамических уравнений путем разложения конвективного члена $\left( {{\mathbf{V}} \cdot \nabla } \right){\mathbf{V}}$ по степеням $1{\text{/}}\Omega $. Вторая строчка уравнения (20) описывает дрейфы, связанные с изменением электрического поля: первый член – известный поляризационный дрейф в нестационарном поле ${\mathbf{E}}(t)$, и два дополнительных слагаемых, связанных с неоднородностью ${\mathbf{E}}({\mathbf{r}})$ вдоль направлений магнитного поля и электрического дрейфа. Третья и четвертая строчки содержат дрейфы, вызванные неоднородностью и нестационарностью магнитного поля. Заметим, что уравнение движения ведущего центра с эффектами сильного электрического поля использовалось при построении квазигидродинамических моделей, описывающих динамику сильно разреженной плазмы в магнитном поле [13, 14]. Случай движения частицы в слабом электрическом, но сильно неоднородном магнитном поле рассмотрен в [15].

Чтобы замкнуть систему уравнений ведущего центра, остается получить уравнение на ${{v}_{\parallel }}$. Для этого умножим выражение (17) скалярно на ${\mathbf{B}}{\text{*}}$. С учетом (18) это дает

$\frac{{d{{v}_{\parallel }}}}{{dt}} = \frac{{{\mathbf{B}}{\text{*}}}}{{B_{\parallel }^{*}}}\left\{ {\frac{{Ze}}{m}{\mathbf{E}} - \left( {{{v}_{\parallel }}\frac{{\partial {\mathbf{b}}}}{{\partial t}} + \frac{{\partial {{{\mathbf{V}}}_{E}}}}{{\partial t}}} \right)} \right. - \left. {\frac{1}{2}(\nabla V_{E}^{2} + \mu \nabla B)} \right\},$

что по аналогии с (19) можно привести к стандартному виду

(21)

$\frac{{d{{v}_{\parallel }}}}{{dt}} = \frac{{Ze}}{m}{\mathbf{b}} \cdot {\mathbf{E}} + \frac{{\mu B}}{2}\nabla \cdot {\mathbf{b}} + {{{\mathbf{V}}}_{E}} \cdot \frac{{d{\mathbf{b}}}}{{dt}}.$

Уравнения (16), (20), (21), формируют искомую систему дрейфовых уравнений в сильном электрическом поле.

Используя уравнение (21), нетрудно получить выражение, описывающее приращения кинетической энергии $K = m(v_{\parallel }^{2} + \mu B + V_{E}^{2}){\text{/}}2$, которое, как и в [6], имеет вид

(22)

$\frac{{dK}}{{dt}} = Ze({\mathbf{\dot {R}}} \cdot {\mathbf{E}}) + \frac{{m\mu B}}{2}\frac{{\partial B}}{{\partial t}}.$

В статических полях $\partial (E,B){\text{/}}\partial t = 0$ из уравнения (22) вытекает закон сохранения энергии

$K + Ze\Phi = {\text{const}}.$

3. ПРИМЕРЫ ДРЕЙФОВОГО ДВИЖЕНИЯ В СИЛЬНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Влияние сильного электрического поля на характер дрейфового движения заряженных частиц исследовалось численно. Поочередно рассматривались конфигурация с однородным магнитным полем ${\mathbf{B}} = {\text{const}}$ и неоднородным электрическим ${\mathbf{E}} = {\mathbf{E}}({\mathbf{r}})$ полем и конфигурация с неоднородным магнитным ${\mathbf{B}} = {\mathbf{B}}({\mathbf{r}})$ и однородным электрическим ${\mathbf{E}} = {\text{const}}$ полем. Направление полей было выбрано строго поперечным (${\mathbf{E}} \bot {\mathbf{B}}$). Для каждой конфигурации были рассчитаны точные траектории движения положительно заряженной ($Z > 0$) частицы ${\mathbf{r}}$ и ее ведущего центра. Последняя определялась путем вычитания из радиус-вектора частицы текущего значения вектора ларморовского вращения, ${\mathbf{r}} - {{\rho }_{L}}$. Полученные траектории сравнивались с результатами численного расчета траекторий дрейфового цента ${{{\mathbf{R}}}_{{cl}}}$ (уравнение (20) без учета дрейфов в сильном электрическом поле) и R (полное уравнение (20)). Компоненты скорости частицы, фигурирующие в уравнении (20), рассчитывались из точных уравнений движения.

В качестве естественной нормировки пространственных и временных масштабов задачи использовались ларморовский радиус (${\mathbf{\tilde {r}}} = {\mathbf{r}}{\text{/}}{{\rho }_{{L0}}}$ = = ${\mathbf{r}}Ze{{B}_{0}}{\text{/}}({{v}_{0}}mc)$) и циклотронный период ($\tilde {t} = $ $ = t2\pi {{\Omega }_{0}} = $ $t2\pi Ze{{B}_{0}}{\text{/}}(mc)$), значения которых рассчитывались в начальный момент времени $t = 0$. Величина электрического поля задавалась при помощи безразмерного параметра $\varkappa $ = $c{{E}_{0}}{\text{/}}{{v}_{0}}{{B}_{0}}$ (${{E}_{0}}$ – значение электрического поля в точке нахождения частицы в начальный момент времени), естественным образом возникающего при выбранной нормировке. В строго поперечных полях параметр $\varkappa $ равен отношению ${{V}_{{E0}}}{\text{/}}{{v}_{0}}$. Ниже символ “тильда” у безразмерных величин опущен.

3.1. Конфигурация с неоднородным электрическим полем

В неоднородном электрическом и однородном магнитном полях уравнение (20) редуцируется к виду

${\mathbf{\dot {R}}} = {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}} + \frac{c}{{B\Omega }}\mathop {\left( {{{v}_{\parallel }}\left( {{\mathbf{b}} \cdot \nabla } \right){{{\mathbf{E}}}_{ \bot }} + \left( {{{{\mathbf{V}}}_{E}} \cdot \nabla } \right){{{\mathbf{E}}}_{ \bot }}} \right)}\nolimits_ \bot ,$

и содержит два дополнительных члена, связанные с сильным электрическим полем ${\mathbf{E}}({\mathbf{r}})$.

Рассмотрим конфигурацию типа квадрупольной линзы с потенциалом $\Phi = - ({{E}_{0}}{\text{/}}{{r}_{0}})xy$ (здесь ${{r}_{0}} = \sqrt {x_{0}^{2} + y_{0}^{2}} $ – исходное положение частицы), помещенную в однородное магнитное поле ${\mathbf{B}} = {{B}_{0}}{{{\mathbf{e}}}_{z}}$ (${{B}_{0}} = {\text{const}}$), см. рис. 1а. Пример траекторий движения заряженной частицы и ее ведущего центра в рассматриваемой системе представлен на рис. 1б. Без учета дополнительных дрейфов в электрическом поле классическая траектория дрейфового центра ${{{\mathbf{R}}}_{{cl}}}$ пролегает вдоль эквипотенциальей $\Phi = {\text{const}}$ и со временем асимптотически приближается к оси x. Под действием дополнительного дрейфа $ \sim {\kern 1pt} \left( {{{{\mathbf{V}}}_{E}} \cdot \nabla } \right){{{\mathbf{E}}}_{ \bot }}$ (ассоциируемого с действием центробежной силы ${{{\mathbf{F}}}_{c}} = - m({{{\mathbf{V}}}_{E}} \cdot \nabla ){{{\mathbf{V}}}_{E}}$), одна из компонент которого направлена вдоль электрического поля E, ведущий центр частицы R пересекает ось x. Другая компонента дополнительного дрейфа сонаправлена с электрическим дрейфом ${{{\mathbf{V}}}_{E}}$, поэтому за равный промежуток времени ведущий центр R частицы смещается на большее расстояние вдоль оси x, чем ${{{\mathbf{R}}}_{{cl}}}$. Проведенный расчет демонстрирует хорошее согласие траектории движения ведущего центра R с точными траекториями движения заряженной частицы, см. 1б.

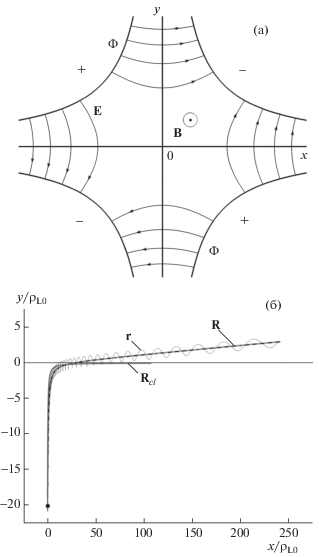
Рис. 1.

Конфигурация квадрупольной электростатической линзы с осевым магнитным полем (а); траектории движения в рассматриваемой конфигурации (б): ${\mathbf{r}}$ – траектория частицы; R и ${{{\mathbf{R}}}_{{cl}}}$ – траектории движения ведущего центра, рассчитанные с учетом дополнительных дрейфов в электрическом поле и без них соответственно; штриховая линия – точная траектория движения ведущего центра; черный кружок – стартовая позиция частицы ($x = 0,$ $y = - 20{{\rho }_{{L0}}}$). Здесь ${{{v}}_{\parallel }} = 0$, ${{{v}}_{ \bot }} = {{{v}}_{0}}$: ${{{v}}_{x}} = {{{v}}_{y}} = {{{v}}_{0}}{\text{/}}\sqrt 2 $, $\varkappa = 0.5$.

Интересный эффект, проявляющийся в рассмотренной конфигурации, связан с увеличением энергии частицы за счет дрейфа в скрещенных полях вдоль электрического поля E. В соответствии с выражением (22), приращение кинетической энергии при ${\mathbf{B}} = {\text{const}}$ и ${{v}_{\parallel }} = 0$ описывается уравнением

$\frac{{dK}}{{dt}} = \frac{{m{{c}^{2}}}}{{{{B}^{2}}}}{{{\mathbf{E}}}_{ \bot }} \cdot ({{{\mathbf{V}}}_{E}} \cdot \nabla ){{{\mathbf{E}}}_{ \bot }}.$

Указанный эффект не может быть описан в рамках классического дрейфового приближения, так как $Ze\left( {{{{\mathbf{E}}}_{ \bot }} \cdot {{{{\mathbf{\dot {R}}}}}_{{cl}}}} \right)$ = $Ze\left( {{\mathbf{E}} \cdot {{{\mathbf{V}}}_{E}}} \right) \equiv 0$. На рис. 2 изображено изменение энергии частицы во времени на траектории рис. 1б. Легко видеть, что даже при незначительном смещении траектории ведущего центра R вдоль электрического поля (порядка нескольких ларморовских радиусов), кинетическая энергия частицы увеличивается на порядок.

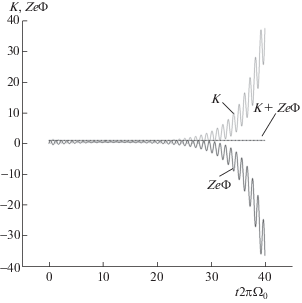
Рис. 2.

Зависимости кинетической K и потенциальной ZeΦ энергий частицы, нормированных на начальное значение энергии, от времени t. Время расчета совпадает со временем расчета траектории на рис. 1б.

3.2. Конфигурация с неоднородным магнитным полем

Рассмотрим движение заряженной частицы в конфигурации магнитного поля прямого тока ${\mathbf{B}} = {{{\mathbf{e}}}_{\varphi }}{{B}_{0}}{{r}_{0}}{\text{/}}r$, помещенного в однородное электрическое поле ${\mathbf{E}} = - {{E}_{0}}{{{\mathbf{e}}}_{z}}$ (${{E}_{0}} = {\text{const}}$), см. рис. 3а. Используется цилиндрическая система координат $\{ r,\varphi ,z\} $. В указанной геометрии уравнение (20) сводится к виду

$\begin{gathered} {\mathbf{\dot {R}}} = {{v}_{\parallel }}{\mathbf{b}} + {{{\mathbf{V}}}_{E}} + \frac{{u_{ \bot }^{2}{\text{/}}2 + v_{\parallel }^{2}}}{\Omega }\frac{{[{\mathbf{b}} \times \nabla B]}}{B} - \\ \, - \frac{{{{c}^{2}}}}{{\Omega {{B}^{3}}}}{{{\mathbf{E}}}_{ \bot }}({{{\mathbf{E}}}_{ \bot }} \cdot [{\mathbf{b}} \times \nabla B]), \\ \end{gathered} $

из которого следует, что движение ведущего центра заряженной частицы поперек магнитного поля складывается из электрического, тороидального (сумма градиентного и центробежного дрейфов), и дополнительного дрейфа в сильном электрическом поле, возникающего в случае ${{{\mathbf{V}}}_{E}} \cdot \nabla B \ne 0$. Так как дополнительный “электрический” дрейф имеет квадратичную зависимость от вектора электрического поля, его направление всегда противоположно тороидальному дрейфу. Очевидно, что при условии ${{u}^{2}} + 2v_{\parallel }^{2} = 2V_{E}^{2}{\text{/}}B$ возможна полная компенсация тороидального дрейфа. При ${{v}_{\parallel }} = 0$ из условия сохранения магнитного момента легко найти критическую точку ${{r}_{{crit}}}$, в которой ${{\dot {R}}_{z}} = 0$

${{r}_{{crit}}} = {{r}_{0}}\mathop {\left( {\frac{{\mu {{B}_{0}}}}{{2V_{{E0}}^{2}}}} \right)}\nolimits^{1/3} .$

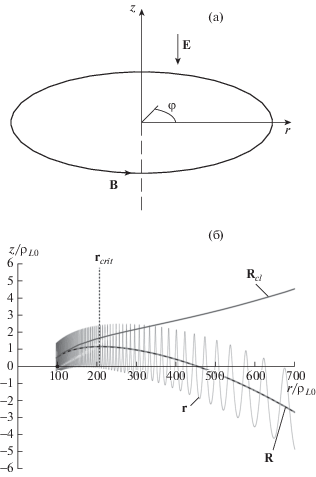
Рис. 3.

Конфигурация магнитного поля прямого тока и аксиального электрического поля (а); траектории движения в плоскости $r$–$z$ (б): r – траектория частицы; R и ${{{\mathbf{R}}}_{{cl}}}$ – траектории движения ведущего центра, рассчитанные с учетом дополнительных дрейфов в электрическим поле и без них соответственно; штриховая линия – точная траектория движения ведущего центра; черный кружок – стартовая позиция частицы ($r = 100{{\rho }_{{L0}}}$, $z = 0$). Здесь ${{{v}}_{\parallel }} = 0$, ${{{v}}_{ \bot }} = {{{v}}_{0}}$: ${{{v}}_{r}} = {{{v}}_{z}} = {{{v}}_{0}}{\text{/}}\sqrt 2 $, $\varkappa = 0.2$.

Пример траектории заряженной частицы и ее ведущего центра при ${{v}_{\parallel }} = 0$ и $\varkappa = 0.2$ представлен на рис. 3б. Без учета дополнительного дрейфа ведущий центр частицы, описываемый вектором ${{{\mathbf{R}}}_{{cl}}}$, смещается вдоль осей r и z под действием электрического и тороидального дрейфов, соответственно. В действительности, после прохождения критической точки $r = {{r}_{{crit}}}$ частица начинает дрейфовать против тороидального дрейфа в направлении электрического поля, что подтверждается результатами численного расчета – см. кривые R и r на рис. 3б. В свою очередь смещение ведущего центра вдоль электрического поля приводит к изменению кинетической энергии частицы по закону

$\frac{{dK}}{{dt}} = m\left[ {\frac{{{{u}^{2}}}}{2} + v_{\parallel }^{2} - V_{E}^{2}} \right]({{{\mathbf{V}}}_{E}} \cdot \nabla B).$

Результаты расчета временной эволюции кинетической энергии при разных значениях величины электрического поля ${{E}_{0}}$ (параметра $\varkappa $) представлены на рис. 4а. Видно, что в слабом электрическом поле ($\varkappa = 0.05$ и $\varkappa = 0.1$) на заданном интервале времени частица теряет энергию, двигаясь против поля. При $\varkappa = 0.2$ частица также замедляется на интервале $r \in [{{r}_{0}},{{r}_{{crit}}})$, но после прохождения критической точки $r = {{r}_{{crit}}}$, в которой $dK{\text{/}}dt = 0$, напротив начинает ускоряться, см. рис. 3б. Траектории движения ведущего центра, рассчитанные при разных значениях параметра $\varkappa $, представлены на рис. 3б.

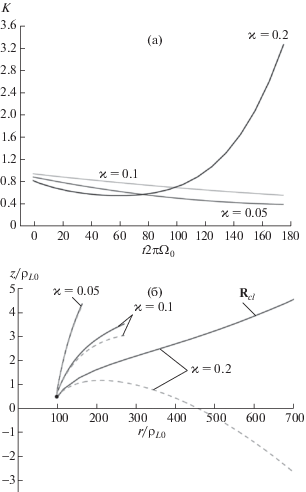
Рис. 4.

Зависимости сглаженной кинетической энергии частицы K от времени t, соответствующие траекториям ведущего центра на рис. 4б (а); траектории движения ведущего центра заряженной частицы в плоскости $r$–$z$ в магнитном поле прямого тока и аксиальном электрическом поле: сплошные линии – траектории движения классического дрейфового центра, рассчитанные без учета дополнительных дрейфов в электрическим поле; штриховые линии – точные траектории движения ведущего центра; черный кружок – стартовая позиция частицы (r = $ = 100{{\rho }_{{L0}}},$ $z = 0$). Здесь ${{{v}}_{\parallel }} = 0$, ${{{v}}_{ \bot }} = {{{v}}_{0}}$: ${{{v}}_{r}} = {{{v}}_{z}} = {{{v}}_{0}}{\text{/}}\sqrt 2 $, $\varkappa = 0.05$, $\varkappa = 0.1$, $\varkappa = 0.2$.

На основе эффекта “дрейфового ускорения” (изменения кинетической энергии частицы при дрейфе в направлении электрического поля) в конфигурации, аналогичной рассмотренной выше, в работе [16] была предложена схема рекуперации тепловой энергии плазмы в энергию электрического поля. Результаты [16] опирались на модель классической дрейфовой теории, в рамках которой приращение кинетической энергии предопределено направлением полей, т.е. $dK{\text{/}}dt < 0$ при ${{{\mathbf{V}}}_{E}} \cdot \nabla B < 0$ и наоборот. Учет дополнительных дрейфов ограничивает радиальный размер пространственной области, в которой частицы теряют свою энергию, величиной ${{r}_{{crit}}}$, которая в случае достаточно сильного электрического поля, ${\text{|}}{{V}_{E}}{\text{|}} \sim 0.1{\text{|}}{{{v}}_{0}}{\text{|}}$, по порядку величины составляет $ \sim {\kern 1pt} {{10}^{2}}{{\rho }_{L}}$.

4. ЗАКЛЮЧЕНИЕ

Выполнен анализ дополнительных (по сравнению с классической дрейфовой теорией) слагаемых в уравнении дрейфового движения ведущего центра (20). Показано, что дрейфовое движение нерелятивистской заряженной частицы в скрещенных медленно меняющихся электрическом и магнитном полях с сильной электрической компонентой отличается от предсказаний классической дрейфовой теории и имеет специфические составляющие, вклад которых в итоговое движение может быть весьма значителен. Дополнительные дрейфы вызваны неоднородностью поля в направлении B и ${{{\mathbf{V}}}_{E}}$ и их учет важен, если скорость ${\mathbf{E}} \times {\mathbf{B}}$-дрейфа сопоставима с полной скоростью частицы. Получен обобщенный лагранжиан Литтлджона (10) и с его помощью продемонстрирован переход к системе уравнений расширенной дрейфовой теории (16), (20) и (21).

Численно исследованы особенности дрейфового движения частицы в некоторых модельных конфигурациях скрещенных полей. Показано, что динамика ведущего центра в сильном электрическом поле существенно отличается от обычного ${\mathbf{E}} \times {\mathbf{B}}$-дрейфа. Особенностью движения в сильном электрическом поле является наличие компоненты дрейфовой скорости вдоль электрического поля ${{{\mathbf{E}}}_{ \bot }}$. Такое смещение, в свою очередь, приводит к изменению кинетической энергии частицы, так как ${\mathbf{\dot {R}}} \cdot {{{\mathbf{E}}}_{ \bot }} \ne 0$. В постоянном магнитном поле такое “дрейфовое” ускорение очевидно не описывается классической дрейфовой теорией, в которой ${{{\mathbf{V}}}_{E}} \cdot {\mathbf{E}} \equiv 0$. Важно отметить, что, поскольку дополнительные дрейфы обусловлены неоднородностью электрического и магнитного полей, они зависят от заряда и массы заряженных частиц, и, таким образом, способны вносить вклад в генерацию тока в плазме, как и известный поляризационный ток.

Работа частично поддержана Министерством науки и высшего образования РФ (соглашение № 3.2223.2017/4.6) (раздел 3) и Программой РУДН “5-100” (раздел 2).

Список литературы

Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 1. Механика. М.: Наука, 1988.
Морозов А.И., Соловьев Л.С. // ДАН СССР. 1959. Т. 128. С 506.
Littlejohn R.G. // J. Plasma Phys. 1983. V. 29. P. 111. https://doi.org/10.1017/S002237780000060X
Cary J.R., Brizard A.J. // Rev. Mod. Phys. 2009. V. 81. P. 693. https://doi.org/10.1103/RevModPhys.81.693
Морозов А.И. Плазменные ускорители / Под ред. Л.А. Арцимовича, С.Д. Гришина, Г.Л. Гродзовского, Л.В. Лескова, А.И. Морозова, А.А. Поротникова, А.М. Дороднова, В.Г. Падалки, М.И. Пергамента. М.: Машиностроение, 1973. С. 5.
Морозов А.И., Соловьев Л.С. Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. Вып. 2. С. 177.
Нортроп Т., Адиабатическая теория заряженных частиц / Под ред. Н. Н. Семашко. М.: Атомиздат, 1967.
Ильгисонис В.И. Классические задачи физики горячей плазмы. М.: Издательский дом МЭИ, 2015.
Charoy T., Boeuf J.P., Bourdon A., Carlsson J.A., Chabert P., Cuenot B., Eremin D., Garrigues L., Hara K., Kaganovich I.D., Powis A.T., Smolyakov A., Sydoren-ko D., Tavant A., Vermorel O., Villafana W. // Plasma Sources Sci. Technol. 2019. V. 28. P. 105010. https://doi.org/10.1088/1361-6595/ab46c5
Boeuf J.P., Garrigues L. // Phys. Plasmas. 2018. V. 25. P. 061204. https://doi.org/10.1063/1.5017033
Boozer A.H. // Phys. Fluids. 1980. V. 23. P. 904. https://doi.org/10.1063/1.863080
Сивухин Д.В. Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. Вып. 1. С. 7.
Рудаков Л.И., Сагдеев Р.З. Физика плазмы и проблема управляемых термоядерных реакций / Под ред. М.А. Леонтовича. М.: Издательство Академии Наук СССР, 1958. Т. 3. С. 268.
Волков Т.Ф. Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1964. Вып. 4. С. 3.
Ходжаев К.Ш., Чирков А.Г., Шаталов С.Д. // ПМТФ. 1981. 4. С. 3.
Тимофеев А.В. // Физика плазмы. 1978. Т. 4. В. 4. С. 826.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал