1. На главную
  2. Электронные версии
  3. Физика плазмы
  4. T. 48, № 1, 2022

Физика плазмы, 2022, T. 48, № 1, стр. 54-70

Сравнительное моделирование динамики волны ионизации в Ne и Ar в рамках уравнений сплошной среды

К. К. Трусов *

Физический институт им. П.Н. Лебедева РАН
Москва, Россия

* E-mail: trusovkk@lebedev.ru

Поступила в редакцию 06.08.2020
После доработки 09.06.2021
Принята к публикации 11.06.2021

Полный текст (PDF)

Аннотация

Проведено численное одномерное моделирование динамики волны ионизации отрицательной полярности в Ne и Ar под действием приложенного электростатического поля в приближении локальной энергии модели сплошной среды, применительно к развитию стримеров в газах. Для этого модельные уравнения представлены в безразмерной форме, построены аппроксимации аналитическими функциями коэффициента ударной ионизации газов, подвижности и диффузии электронов на основе данных экспериментов и теоретических расчетов в широком диапазоне величин приведенной напряженности поля до 10–4–5 × 104 Тд. Получены численные решения уравнений для плотности электронов позади фронта, скорости его движения и толщины в диапазоне напряженности поля 50–4 × 103 Тд. Оценены величины двух безразмерных параметров, представляющих собой отношение скоростей релаксации электронов в газе к скорости наведенных внешним полем изменений. Необходимым условием, ограничивающим применение рассматриваемой модели к оценкам динамики волны ионизации газа, выступает требование, чтобы оба параметра значительно превышали единицу. Величины параметров уменьшаются с ростом приведенной напряженности поля и, в частности, равны 10 при величине последней ≈1180 Тд.

Ключевые слова: волна ионизации газа, приближение локального равновесия, численное моделирование

1. ВВЕДЕНИЕ

Для численных оценок динамики фронта волны ионизации (ФВИ) в газах, применительно к развитию стримеров под действием приложенного электростатического поля, многими авторами на протяжении последних десятилетий развивалась и применялась так называемая “fluid model” или модель сплошной среды (см. [1–5] и ссылки в них). Модель основана на диффузионно-дрейфовых уравнениях баланса электронов и ионов, электростатическом уравнении Пуассона для поля и феноменологическом представлении транспортных и ионизационных характеристик частиц газа. Ее дифференциальные уравнения в частных производных представляют собой уравнения сплошной среды, в которых все переменные величины и коэффициенты являются функциями локального электрического поля (приближение локального поля). Такой подход к описанию динамики частиц ограничивает диапазон применения модели тем, что, во-первых, наведенные извне пространственно-временные изменения поля и плотности частиц плазмы должны протекать медленнее, чем процессы релаксации частиц в среде, и, во-вторых, входящие в уравнения коэффициенты и переменные должны быть макроскопическими характеристиками, т.е. усредненными по массиву частиц, удовлетворять условию локального равновесия и быть функциями локального поля. В этом случае решения модельных уравнений показывают динамику развития и скорости движения ФВИ, плотности свободных электронов за фронтом, а также профиль самого фронта.

Детальный аналитический и численный анализ одномерных (1D) уравнений модели был предложен в [3, 4] применительно к азоту. Упрощение задачи до 1D анализа применительно к стримеру обосновано тем, что толщина ФВИ в головке стримера во много раз меньше ее диаметра. Это дает возможность в первом приближении считать фронт состоящим из небольших квазиплоских участков и в каждом отдельном участке моделировать его динамику 1D уравнениями плоского фронта. С тех пор модель широко применялась также для оценок динамики ФВИ в воздухе. Однако применение ее к другим газам, в том числе инертным, представляет значительный интерес, но остается весьма ограниченным и касается, как правило, лишь отдельных параметров ФВИ в них.

Позднее модель [3, 4] была усовершенствована путем учета зависимости подвижности μe и тензора диффузии De электронов от приведенной напряженности электрического поля и получила название “classic fluid model” [6, 7], т.е. классическая модель сплошной среды. В свою очередь, эта модель также подверглась дальнейшему пересмотру и развитию, что привело к созданию моделей сплошной среды более высокого порядка [6–12], учитывающих динамику средней энергии электронов в волне (приближение локальной энергии), гибридных моделей [9–11, 13] и моделей, основанных на применении методов динамики частиц, Монте-Карло и решении кинетического уравнения Больцмана [9, 10, 12–14]. Для расчета ионизационных и транспортных характеристик электронов в газах также применяются методы динамики частиц [15–17], Монте-Карло [18–21] и решение уравнения Больцмана [11, 12, 22–24]. Но каждый более прогрессивный подход к описанию ФВИ сопровождается усложнением модели физических процессов и, как неизбежное следствие, приводит к значительному росту объема, сложности и трудоемкости компьютерных вычислений. В настоящее время указанные выше методы рассматриваются как наиболее многообещающие способы моделирования ФВИ с учетом стохастических и нелокальных эффектов. В то же время, модель сплошной среды второго порядка, учитывающая динамику плотности электронов и их средней энергии (приближение локальной энергии), остается привлекательной благодаря своей обоснованности при умеренной трудоемкости компьютерных расчетов. И, как видно из сравнительных оценок основных параметров ФВИ следуя разным моделям [7, 10, 12], эта модель показывает результаты значительно более близкие к моделям динамики частиц, чем классическая модель сплошной среды. В основном она применяется в диапазоне низких и средних величин ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} < 500$ Тд, где E и n0 обозначают вектор напряженности электрического поля и плотность частиц газа соответственно. Здесь и далее величины $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ выражены в таунсендах, 1 Тд = 10–21 В · м2, если не оговорено особо. Внимание к указанному диапазону во многом объясняется тем, что в лабораторных условиях стримеры наблюдаются и исследуются именно в этом диапазоне напряженности, однако значительный прогресс в технике генерации высоковольтных импульсов напряжения с фронтом наносекундной и субнаносекундной длительности стимулирует интерес к более высоким напряженностям поля. Наиболее частым практическим объектом моделирования служат азот и воздух.

По отношению к инертным газам, модели сплошной среды первого и второго порядка (в приближениях локального поля и энергии), наряду с другими моделями, были применены в [12] для численных оценок 1D ФВИ отрицательной полярности в Ne в диапазоне $125 < {{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} < $ < 460 Тд. Позднее 1D модель первого порядка при фиксированных величинах μe и De использовалась для численной оценки характеристик ФВИ противоположных полярностей в Ne в диапазоне ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} < 2.75 \times {{10}^{3}}$ Тд [25]. В частности, вследствие значительного отличия транспортных и ионизационного коэффициентов Ne от аналогичных у азота, толщина ФВИ в Ne заметно отличалась от аналогичных в азоте. Такой результат стимулировал оценку величины отношения $K = \Delta {{l}_{{{\text{ФВИ}}}}}{\text{/}}\lambda $ для фронтов обеих полярностей, где ΔlФВИ – толщина ФВИ и λ – средняя длина свободного пробега электрона. По сути, K показывает, насколько медленны наведенные возмущения по сравнению с одной из масштабных характеристик самого газа. Чем больше K превышает единицу, тем лучше уравнения сплошной среды подходят для обсуждаемой задачи. Оценка K для Ne в [25] показала, что его величина применительно к положительному фронту уменьшается до 3 при ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} \approx 2.44 \times {{10}^{3}}$ Тд, а в случае отрицательного фронта K превышает 10 во всем диапазоне численного моделирования. Но необходимо подчеркнуть, что K – не единственный параметр, ограничивающий диапазон применимости модели сплошной среды. Так, условие медленности наведенных изменений в среде по сравнению со скоростью релаксации энергии электронов также вносит серьезные ограничения и заслуживает внимания.

Эксперименты со скользящим разрядом в трех инертных газах [26] показали значительное различие между газами в его характеристиках, как временных, так и пространственных, что подчеркивает значимость индивидуальных параметров газов и целесообразность сравнительной оценки развития разряда в предпробойный период.

Исходя из вышесказанного, представляется целесообразным выполнить численное моделирование параметров волны ионизации в Ne, Ar, Xe и N2 (в качестве газа сравнения), следуя модели сплошной среды второго порядка, в приближении локальной энергии в наиболее широком диапазоне вариации $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$. Сравнительный расчет по единой методике и алгоритму вычислений интересен по нескольким причинам. Во-первых, численное моделирование такого типа уже проводилось для Ne в [12] и N2 в [11, 12] и сравнение результатов будет целесообразно с точки зрения проверки методики расчетов. Во-вторых, индивидуальные зависимости ионизационных и транспортных характеристик электронов от $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ в указанных газах значительно различаются. В-третьих, перечисленные газы объединяет их однокомпонентный состав и отсутствие эффекта прилипания электронов, но различает моноатомная структура инертных газов и молекулярная азота. В-четвертых, сравнительные результаты моделирования для Ne, Ar и Xe интересны для интерпретации наблюдаемых в экспериментах различий в структуре плазмы разряда в них [26]. В-пятых, результаты численных оценок динамики ФВИ даже в рамках одной модели могут значительно зависеть от примененной методики и алгоритма вычислений, что видно, например, из результатов [27] на примере N2. Кроме того, результаты оценок также зависят от методов определения транспортных и ионизационных характеристик электронов (см. [11, 22–24] и ссылки в них). В-шестых, желательно провести моделирование в наиболее широком диапазоне величин $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, допустимом для применяемой модели.

Таким образом, поставленная задача предполагает следующие этапы решения.

а) Аппроксимация аналитическими функциями зависимости коэффициента ударной ионизации атомов α, подвижности μe и коэффициента диффузии De электронов от величины $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ в наиболее широком диапазоне ее вариации, на основе известных экспериментальных и теоретических данных.

б) Моделирование параметров ФВИ в инертных газах по единой методике и алгоритму вычислений.

в) Сравнительный анализ полученных результатов.

Конечно, наибольшей точности результатов можно ожидать при применении в расчетах наиболее современных моделей, основанных на методах динамики частиц или решении уравнения Больцмана. Однако чрезвычайная трудоемкость и сложность таких вычислений вынуждают выбирать вариант моделирования, компромиссный между сложностью и точностью. Поскольку сформулированная выше задача ориентирована больше на сравнительный анализ газов, чем на абсолютную точность результатов для каждого из них, в качестве компромисса выбрана модель сплошной среды в приближении локальной энергии.

Следуя поставленной задаче в рамках выбранной модели, в настоящей работе проведена оценка характеристик 1D ФВИ отрицательной полярности в Ne и Ar в зависимости от напряженности приложенного поля (средней энергии электронов). Также, исходя из полученных данных о толщине и скорости движения ФВИ, средней энергии электронов предложена оценка двух параметров, характеризующих отношение скорости процессов во фронте к скорости релаксации электронов.

2. СИСТЕМА УРАВНЕНИЙ МОДЕЛИРОВАНИЯ И АНАЛИТИЧЕСКИЕ АППРОКСИМАЦИИ

2.1. Дифференциальные уравнения диффузионно-дрейфовой модели сплошной среды

Система дифференциальных уравнений, описывающих динамику ФВИ в рамках различных моделей, зависит от того, сколько и какие моменты функции распределения учитываются при анализе кинетического уравнения Больцмана [6, 7, 11, 12, 24]. Для численных оценок нами выбрана компромиссная модель сплошной среды второго порядка в приближении локальной энергии, с применением в ней ионизационных и транспортных характеристик электронов, базирующихся на экспериментальных данных и рассчитанных методами динамики частиц. Модель рассматривает баланс плотности заряженных частиц и средней энергии электронов в газе. Ее основные положения, допущения и система диффузионно-дрейфовых уравнений сформулированы и обсуждались, например, в [6, 7, 11, 12, 24] (см. также ссылки в них). Важнейшими допущениями представляются: (i) искомые функции в уравнениях – напряженность поля, плотность частиц, энергия электронов, скорость – являются макроскопическими, т.е. усредненными; (ii) коэффициенты α, μe и De являются макроскопическими функциями локального поля/средней энергии электронов; (iii) наведенные внешним полем изменения в среде протекают медленнее характерных времен релаксации частиц. Соответственно, принятые допущения налагают ограничения на область применения модели в целом. Так, например, к сильно разреженным газам, в которых столкновения частиц редки и определение макроскопических характеристик затруднено, применение модели проблематично. Кроме того, к газовым системам, размеры которых сравнимы или меньше характерных длин релаксации частиц, приложение модели также необоснованно. На практике модель применяется главным образом в диапазоне малых и умеренных величин ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} < 500$ Тд для оценок развития стримеров в газах при давлении порядка атмосферного. В настоящей работе рассматриваются ее решения в диапазоне до ≈4 × 103 Тд с учетом следующих соображений.

а) Модель предполагает медленность возмущений, наведенных в среде внешним воздействием, по сравнению со скоростью релаксации электронов, как во времени, так и в пространстве. Для оценки условия медленности возмущений необходимы сведения о толщине ФВИ, скорости его движения и энергии электронов, которые определяются только в результате моделирования. Если искомые данные для азота можно найти в опубликованных работах, то аналогичных данных для инертных газов недостаточно.

б) Коэффициенты α, μe и De электронов должны удовлетворять условию локального равновесия, и диапазон их обоснованного применения принципиально важен. Физические основания их использования подтверждены моделированием динамики поведения облака электронов в диапазонах $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ 1.4–5.6 × 103 Тд (Ne) [20], 56–5.66 × × 103 Тд (Ar) [21], 14–3 × 103 Тд (N2) [19], 100–3.5 × × 103 Тд (N2) [28], а также при более высоких величинах напряженности вплоть до появления релятивистских электронов (He, Ne, Ar, Kr, Xe, N2) (см. [15–17, 29, 30] и ссылки в них). Таким образом, коэффициенты α, μe и De сохраняют физический смысл в широком диапазоне напряженности поля, по крайней мере, до 4 × 103 Тд, в котором проводилось наше моделирование динамики ФВИ.

в) 1D модели более высокого порядка, гибридные и на основе методов динамики частиц, при применении к неону и азоту показывают отличие плотности электронов, создаваемой волной, и скорости ее движения в пределах 10–15% от аналогичных величин, оцениваемых, следуя обсуждаемой модели, в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ до 103 Тд [6, 9–12, 31]. Внимательный анализ профиля ФВИ в этих же работах показывает, что толщина ФВИ в разных моделях почти одинакова даже в том случае, когда в передней части фронта зарождаются высокоэнергетичные электроны [8, 9, 31]. Хотя количество таких электронов растет при увеличении $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, оно, тем не менее, составляет лишь малую часть от общего числа свободных электронов во фронте и позади него, что следует из теоретических оценок (см. [32, 33] и ссылки в них) и экспериментов, ориентированных на достижение максимальной плотности таких электронов [34]. Таким образом, высокоэнергетичные электроны можно рассматривать в качестве источника начальных электронов впереди ФВИ, а для описания основной массы электронов во фронте, так называемых “bulk electrons”, применять модель сплошной среды [35].

г) Никакие дополнительные источники свободных электронов в газе впереди ФВИ, как, например, его фотоионизация или ионизация воздействием космических лучей, естественной радиоактивности и т.д. в настоящей работе не рассматриваются по следующим причинам. Физический механизм фотоионизации газа был предложен и обсуждается на протяжении десятков лет применительно к воздуху и смесям N2–O2 с различным соотношением компонентов [36–40]. В сравнительных исследованиях с альтернативными источниками фотоионизации отводится преобладающая роль, хотя возникают и сомнения относительно ее эффективности при высокой напряженности поля [41]. Плотность электронов ${{n}_{e}} \approx {{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{4}}$ см–3 от альтернативных источников расценивается как недостаточная для развития ФВИ [40, 42]. Но к чистым однокомпонентным газам, например, инертным или азоту, механизм фотоионизации трудно применим и для них вопрос о свободных электронах впереди ФВИ остается открытым.

Для моделирования динамики ФВИ воспользуемся системой уравнений, представленной в [12] в виде

$\begin{gathered} {{\partial }_{t}}{{n}_{e}} + {{\nabla }_{{\mathbf{r}}}} \cdot {{{\mathbf{j}}}_{e}} = {\text{source,}} \\ {{\partial }_{t}}{{n}_{ + }} = {\text{source,}} \\ \end{gathered} $
(1)
$\begin{gathered} {{\partial }_{t}}(\varepsilon {{n}_{e}}) = - \frac{5}{3}{{\nabla }_{{\mathbf{r}}}}(\varepsilon {{{\mathbf{j}}}_{e}}) + e{\mathbf{E}}{{{\mathbf{j}}}_{e}} - {{n}_{e}}\sum\limits_{\text{c}} {{{k}_{{\text{c}}}}{{\varepsilon }_{{\text{c}}}}} , \\ {{\nabla }_{{\mathbf{r}}}} \cdot {\mathbf{E}} = \frac{e}{{{{\varepsilon }_{0}}}}\left( {{{n}_{ + }} - {{n}_{e}}} \right), \\ {{{\mathbf{j}}}_{e}} = - {{n}_{e}}{{\mu }_{e}}{\mathbf{E}} - {{{\mathbf{D}}}_{e}}{{\nabla }_{{\mathbf{r}}}}{{n}_{e}}, \\ \end{gathered} $
$\begin{gathered} {\text{source}} = {{n}_{e}}{{\mu }_{e}}{{\alpha }_{0}}f, \\ \varepsilon = F\left( {\left| {\mathbf{E}} \right|} \right), \\ \end{gathered} $
где E обозначает напряженность электрического поля; r и t – пространственная координата и время; ne(r,t) и n+(r,t) – плотности электронов и ионов; ε0 –диэлектрическая постоянная; ε – средняя энергия электронов; f – функция ионизации газа, определяемая коэффициентом ударной ионизации газа α как $f = \left| {\mathbf{E}} \right|\alpha (\varepsilon ){\text{/}}{{\alpha }_{0}}$; α0 – параметр, характеризующий зависимость α от ε; e – абсолютная величина заряда электрона. Слагаемое $ - {{n}_{e}}\sum\nolimits_{\text{c}} {{{k}_{{\text{c}}}}{{\varepsilon }_{{\text{c}}}}} $ в третьем уравнении (1) представляет собой скорость потерь энергии свободными электронами при столкновениях, выраженную произведением плотности электронов на скорость потери энергии одним электроном $\sum\nolimits_{\text{c}} {{{k}_{{\text{c}}}}{{\varepsilon }_{{\text{c}}}}} $, просуммированную по всем типам столкновений электрона с атомами, упругим и неупругим. Здесь kc – частота столкновений типа “с” и εc – энергия, теряемая электроном при одном столкновении данного типа. Последнее уравнение в (1) устанавливает взаимосвязь между средней энергией электронов и напряженностью поля $\left| {\mathbf{E}} \right|$, которая рассчитывается для каждого газа индивидуально, например, методом динамики частиц [15–17] или решением уравнения Больцмана [11, 12].

Газ находится под действием внешнего однородного электростатического поля напряженностью E+. Коэффициенты α, μe, De электронов, а также f, выражены в (1) как функции локальной энергии электронов ε и индивидуальны для каждого газа.

В частном случае одномерной задачи система уравнений (1) упрощается и по аналогии с [4] может быть преобразована в безразмерное представление

${{\partial }_{\tau }}\sigma = {{\partial }_{x}}\left( {M\sigma Y + M{{D}_{{{\text{II}}}}}{{\partial }_{x}}\sigma } \right) + M\sigma {{f}_{{{\text{бр}}}}}\left( {\left| Y \right|} \right),$
(2)
$\begin{gathered} {{\partial }_{\tau }}Y = - M\left( {\sigma Y + {{D}_{{{\text{II}}}}}{{\partial }_{x}}\sigma } \right), \\ {{\partial }_{\tau }}(\sigma \varepsilon {\kern 1pt} *) = \frac{5}{3}{{\partial }_{x}}(M\sigma Y\varepsilon {\kern 1pt} *\; + M{{D}_{{{\text{II}}}}}\varepsilon {\kern 1pt} *{{\partial }_{x}}\sigma ) + \\ \, + YM(\sigma Y + {{D}_{{{\text{II}}}}}{{\partial }_{x}}\sigma ) - \sigma \sum\limits_{\text{c}} {k_{{\text{c}}}^{*}} \varepsilon _{{\text{c}}}^{*}, \\ \end{gathered} $
$\varepsilon {\kern 1pt} * = \Phi \left( Y \right).$

Здесь x, τ обозначают безразмерные координату и время; σ, Y и ε* – безразмерные плотность электронов, скалярная напряженность поля вдоль оси x и средняя энергия электронов соответственно; DII – безразмерный коэффициент продольной диффузии электронов; fбр – безразмерная функция ионизации; M – безразмерная подвижность электронов, определяемая соотношением

(3)
${\rm M} = \frac{{{{\mu }_{e}}\left( {\left| Y \right|} \right)}}{{{{\mu }_{e}}\left( {\left| Y \right| = 1} \right)}} = \frac{{{{\mu }_{e}}\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}{{{{\mu }_{e}}\left( {{{E}_{0}}{\text{/}}{{n}_{0}}} \right)}},$
как подвижность, нормированная к своей величине при |E| = E0. При преобразовании (1) в (2) использованы введенные ранее в [4] соотношения связи размерных и безразмерных единиц
(4)
$\begin{gathered} x = \left| {\mathbf{r}} \right|{{\alpha }_{0}},\quad \tau = \frac{t}{{{{t}_{{\text{0}}}}}},\quad {\mathbf{Y}} = \frac{{\mathbf{E}}}{{{{E}_{{\text{0}}}}}},\quad {{D}_{{{\text{II}}}}} = \\ \, = \frac{{{{D}_{e}}{{\alpha }_{{\text{0}}}}}}{{{{\mu }_{e}}{{E}_{{\text{0}}}}}},\quad \sigma = \frac{{{{n}_{e}}e}}{{{{\varepsilon }_{0}}{{\alpha }_{0}}{{E}_{0}}}}, \\ \end{gathered} $
но, в отличие от [4], параметр t0 получил новое определение ${{t}_{0}} = 1{\text{/}}{{\alpha }_{0}}{{E}_{0}}{{\mu }_{e}}(\left| {\mathbf{E}} \right| = {{E}_{0}})$ и введено дополнительное соотношение связи ε* = εα0/eE0, где E0 – параметр зависимости α от напряженности поля (смотри раздел 2.2), а параметр $e{{E}_{0}}{\text{/}}{{\alpha }_{0}}$ имеет размерность энергии и является характеристикой конкретного газа.

Важной особенностью системы уравнений (2) является ее полная безразмерность как по координатам и учитываемым в ней коэффициентам, так и по искомым функциям. Ниже в разделах 2.2–2.5 будет показано, что в условиях локального равновесия все входящие в уравнения (2) коэффициенты можно аппроксимировать функциями только безразмерной приведенной напряженности поля $Y = {{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}}$ или, с учетом последнего уравнения в (2), средней энергии ε*. В таком случае, 1D решения (1) для плотности электронов позади ФВИ, его толщины и скорости движения должны зависеть только от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$(или средней энергии электронов ε). Но такое утверждение допустимо только в рамках рассматриваемой модели, которая ограничена допущениями и приближениями при выводе ее уравнений.

Для инициирования развития ФВИ в произвольной точке x0 необходимо задать небольшое начальное количество локально расположенных электронов, например, в виде [4]

(5)
$\sigma \left( {x,\tau = 0} \right) = \left( {0.1 - 0.0001} \right){\text{exp}}\left[ { - {{{\left( {x - {{x}_{0}}} \right)}}^{2}}} \right].$

Поскольку поиск решений (2) проводился в широком диапазоне вариации напряженности Y, предэкспоненциальный множитель в (5) варьировался в процессе вычислений с целью оптимизации и проверки устойчивости решений относительно начального условия. В итоге, в расчетах применялось такое количество начальных электронов, которое не оказывало никакого влияния на динамику ФВИ.

Таким образом, для моделирования динамики ФВИ в рамках одномерных уравнений (2) необходимы сведения о зависимости безразмерных коэффициентов M, DII, fбр, $k_{{\text{c}}}^{*}$, $\varepsilon _{{\text{c}}}^{*}$ и функции Φ от напряженности поля (средней энергии электронов) для конкретного газа. Решение этой части задачи в отношении первых трех коэффициентов рассматривается ниже путем численных оценок и аппроксимаций аналитическими функциями в широком диапазоне их зависимости от напряженности поля/энергии электронов, построенных путем объединения массивов известных экспериментальных и теоретических данных. Аналитическое представление наиболее удобно для интеграции в расчетную схему. Коэффициенты $k_{{\text{c}}}^{*}$, $\varepsilon _{{\text{c}}}^{*}$ рассчитаны, по аналогии с [11, 12], исходя из имеющихся данных о сечениях столкновений электронов с атомами, включая ионизацию, и соответствующих этим столкновениям величин потери энергии электроном [16, 17]. Функции Φ приняты в том виде, в каком они были ранее рассчитаны для рассматриваемых газов методом динамики частиц и решением уравнения Больцмана [11, 12, 16, 17, 30].

В отношении предлагаемых ниже оценок и аппроксимаций коэффициентов M, DII и fбр следует заметить следующее. На практике применяются различные методы экспериментального измерения и теоретического расчета транспортных характеристик электронов в газах. Так, в [43] систематизированы результаты измерений с указанием конкретных методов их получения, среди которых измерения в стационарном и импульсном поле, в скрещенных полях, по времени пролета частиц и др. Методы расчета также разнообразны в зависимости от поставленной задачи. Например, в [22, 23] на примере Ar показаны сравнительные результаты расчета μe, De и α путем решения уравнения Больцмана и методом Монте-Карло для стационарного и импульсного таунсендовского развития электронной лавины, а также по времени пролета электронами заданного промежутка. Показано хорошее совпадение результатов при относительно низких величинах $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} \leqslant 250$ Тд и их заметное расхождение (до 30%) с ростом $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ до умеренных 566 Тд, когда на результат расчета влияет рождение новых электронов благодаря растущей ионизации атомов. Исходя из вышесказанного, ниже в своих оценках транспортных коэффициентов мы опирались на данные экспериментов в диапазоне низких/умеренных величин $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ и расчетные данные при более высоких величинах методами динамики частиц и решением уравнения Больцмана. Именно динамические методы расчета наиболее подходят для рассматриваемой нестационарной задачи.

2.2. Аппроксимация коэффициента ударной ионизации

Аппроксимации коэффициента ионизации атомов Ne и Ar построены на основе экспериментальных измерений [43, 44] и теоретических расчетов [16, 17, 29, 30] методом динамики частиц, по сути близким к методу Монте-Карло.

Немонотонный характер зависимости α от $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ отмечался еще в [45]. Нисходящая ветвь зависимости при высоких $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ объясняется уменьшением сечений электронных столкновений всех типов с ростом напряженности. Для He и Ne уменьшение $\alpha (\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}})$ при высоких напряженностях, а также насыщение аналогичной зависимости у Ar были впервые численно рассчитаны методом Монте-Карло в [20] и [21] в диапазонах 10–5.6 × 103 и 56–5.66 × 103 Тд соответственно. Эти же расчеты показали, что искомые величины соответствуют условию локального равновесия в этих газах во всем диапазоне вычислений. В [15–17, 29, 30] немонотонные зависимости были рассчитаны методом динамики частиц и аналогичные выводы распространены на еще более широкий диапазон $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$. Очень важный результат авторов гласил, что при соответствующей табуляции макроскопические коэффициенты ударной ионизации, подвижности и диффузии электронов сохраняют физический смысл и соответствуют условию локального равновесия вплоть до величин $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, при которых образуются релятивистские электроны. Такое заключение дает основания для применения результатов [16, 17, 20, 21, 29, 30] в (1) и (2) при расчетах в рамках рассматриваемой модели сплошной среды.

Ранее, коэффициент α в Ne было предложено аппроксимировать функциями

(6а)
$\frac{\alpha }{p} = A{\text{exp}}\left[ { - \sqrt {B\frac{p}{{\left| {\mathbf{E}} \right|}}} } \right],\quad [46,47],$
(6б)
$\frac{\alpha }{p} = A{{\left( {\frac{{\left| {\mathbf{E}} \right|}}{p}} \right)}^{{s - b{\text{ln}}\left( {\left| {\mathbf{E}} \right|/p} \right)}}},\quad [48],$
(6в)
$\frac{\alpha }{{{{n}_{0}}}} = A{\text{exp}}\left[ { - \sqrt[3]{{B\frac{{{{n}_{0}}}}{{\left| {\mathbf{E}} \right|}}}}} \right],\quad [49],$
где p – давление газа; A, B, s, b – константы. Из этих функций только (6б) уменьшается при высоких напряженностях, а (6в) наиболее точно аппроксимирует экспериментальные данные в диапазоне 5.5–1.13 × 103 Тд [25]. Для расширенного диапазона 5.5–1.5 × 104 Тд функция (6а) в [16, 29] была трансформирована в
(7)
$\frac{\alpha }{p} = A{\text{exp}}\left[ { - \sqrt {B\frac{p}{{\left| {\mathbf{E}} \right|}}} - C\frac{{\left| {\mathbf{E}} \right|}}{p}} \right],$
где C – константа. Эта функция хорошо соответствует результатам расчета этой же работы при высоких значениях $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, но в диапазоне ≤30 Тд она, как и (6а), занижает коэффициент ионизации вплоть до 9 раз при ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = 5.5$ Тд относительно экспериментальных величин [43]. По аналогии с (7) мы изменили функцию (6в) на
(8)
$\frac{\alpha }{{{{n}_{0}}}} = A{\text{exp}}\left[ { - \sqrt[3]{{B\frac{{{{n}_{0}}}}{{\left| {\mathbf{E}} \right|}}}} - С\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right],$
которая наиболее близко аппроксимирует экспериментальные и расчетные данные Ne в расширенном диапазоне ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}} = 5.5{\kern 1pt} - {\kern 1pt} 1.5 \times {{10}^{4}}$ Тд. Именно эта функция при значениях констант A = = 10.3 × 10–16 см2, B = 7.87 × 103 Тд и C = 3.3 × × 10‒4 1/Тд для комнатной температуры применялась в численных расчетах ниже. Константы A и B связаны с ранее введенными параметрами α0 и E0 соотношениями A = α0/n0 и B = E0/n0.

Приведенный коэффициент ударной ионизации Ar [17, 30, 43, 44] хорошо аппроксимируется функцией (7), которая после замены p на n0 приобретает вид

(9)
$\frac{\alpha }{{{{n}_{0}}}} = A{\text{exp}}\left[ { - \sqrt {B\frac{{{{n}_{0}}}}{{\left| {\mathbf{E}} \right|}}} - C\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right]$
и применялась далее в расчетах динамики ФВИ в Ar при величинах констант A = 10.4 × 10–16 см2, B = 2.14 × 103 Тд и C = 8 × 10–5 1/Тд для комнатной температуры. Аппроксимации (8) и (9) иллюстрируются на рис. 1.

Рис. 1.

Аппроксимации (8) и (9) зависимости приведенного коэффициента ударной ионизации газов от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}$ при комнатной температуре. Сплошная кривая – Ne, штриховая – Ar.

2.3. Аппроксимация безразмерной подвижности электронов

2.3.1. Ne. Результаты экспериментальных измерений скорости дрейфа электронов |Vдр| в Ne в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} = {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{3}}$ Тд приведены в [20, 43, 44], а теоретических расчетов величин μen0 путем решения уравнения Больцмана – в [12]. Для более высоких значений $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ известны только теоретические расчеты |Vдр| методом динамики частиц [16, 29, 30]. Совокупность этих данных, используя соотношение |Vдр| = μe|E| и определение (3), позволяет оценить величины M в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} = {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} 2 \times {{10}^{4}}$ Тд и построить аппроксимацию

$M\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right) = $
(10)
$\begin{gathered} \, = \left\{ {2.2\frac{{{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{ - 0.62}}} + 0.33 + 2 \times {{{10}}^{{ - 7}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{1.5}}}}}{{1 + 25{\text{exp}}\left[ { - 57{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{0.36}}}} \right]}}} \right. + \\ \, + 0.53{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}^{{0.01}}}\left. {{\text{exp}}\left[ { - \frac{{{{{\left| {20 - \left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right|}}^{{1.5}}}}}{{9000}}} \right]} \right\} \times \\ \end{gathered} $
$\, \times \left[ {1 - \exp \left( { - 400{{{\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right)}}^{{0.5}}}} \right)} \right].$

Соответствие этой аппроксимации имеющимся данным литературы показано на рис. 2. Увеличение подвижности M в области высоких $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, вытекающее из расчетов [16, 29, 30], объясняется уменьшением сечений столкновений электрона всех типов с атомами в области >103 Тд. В диапазоне умеренных величин $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$, где расчетные и экспериментальные данные перекрываются, отмечается их удовлетворительное соответствие друг другу.

Рис. 2.

Зависимость безразмерной подвижности электронов M в Ne от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}$ при комнатной температуре. Сплошная линия – аппроксимация (10); пунктирная – расчет по теоретическим данным о |Vдр| [16, 29, 30]; штрихпунктирная – расчет по теоретическим данным о μen0 [12]; кружки – расчет по экспериментальным данным о |Vдр| [20, 43, 44].

2.3.2. Ar. Для этого газа аппроксимация M построена на объединении экспериментальных [21, 43] и теоретических [17, 30] данных о |Vдр|, полученных методом динамики частиц. Оба массива данных дополняют друг друга, удовлетворительно согласуются в области перекрытия и приводят к аппроксимации M функцией

(11)
$\begin{gathered} M\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right) = \\ \, = 6.1\frac{{{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{ - 0.8}}} + 0.15 + 4.3 \times {{{10}}^{{ - 7}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{1.27}}}}}{{1 + 0.18{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{ - 0.55}}}{\text{exp}}\left( { - 900\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}} + \\ \, + 0.87{{\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right)}^{{0.01}}}{\text{exp}}\left[ { - \frac{{{{{\left| {5 - \left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right|}}^{{1.05}}}}}{{500}}} \right], \\ \end{gathered} $
соответствие которой данным литературы показано на рис. 3. Аналогично Ne, увеличение M в области >103 Тд у Ar объясняется также уменьшением сечений.

Рис. 3.

Зависимость безразмерной подвижности электронов M в Ar от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}$ при комнатной температуре. Сплошная линия – аппроксимация (11); штриховая – расчет по теоретическим данным о |Vдр| [17, 30]; кружки – расчет по экспериментальным данным о |Vдр| [21, 43].

Суммируя приведенные выше данные о α/n0 и M двух газов, можно отметить, что авторы [16, 17, 20, 21, 29, 30, 48] показали:

– во-первых, значительное уменьшение коэффициента ударной ионизации и одновременное увеличение подвижности электронов в области высоких величин $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$. Такая тенденция не выявляется непосредственно из результатов экспериментов, но не противоречит им и вытекает из теоретических расчетов методами Монте-Карло и динамики частиц, т.е. с учетом стохастических эффектов;

– во-вторых, то, что эти макроскопические коэффициенты сохраняют физический смысл и соответствуют условию локального равновесия в области напряженностей, значительно превышающих 103 Тд;

– в-третьих, допустимость применения макроскопических коэффициентов α и μe в уравнениях модели сплошной среды (1) и (2) как функций локального электрического поля (средней энергии электронов).

2.4. Аппроксимация безразмерного коэффициента диффузии электронов

2.4.1. Ne. Зависимость продольной компоненты безразмерного тензора диффузии электронов ${{D}_{{{\text{II}}}}}\left( {{{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}} \right)$ была вычислена в [25] на основании теоретического расчета Den0 и μen0 в [12] путем решения уравнения Больцмана в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} = {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{3}}$ Тд. А результаты экспериментальных измерений по методу времени пролета электронов (time-of-flight) взяты из [20]. Для рассматриваемой одномерной задачи важно то, что в [12, 20, 25] приведены результаты именно для продольной компоненты тензора диффузии. Монотонный рост DII в области 103–104 Тд поддерживается монотонным увеличением средней энергии электронов в этой же области, рассчитанным в [16, 29, 30] методом динамики частиц. Хотя средняя энергия электронов ассоциируется с поперечной компонентой тензора диффузии следуя соотношению Нернста–Эйнштейна–Таунсенда, трудно ожидать, чтобы две компоненты тензора изменялись в противоположных направлениях с увеличением $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}$ в этом диапазоне. Как будет видно далее, у Ar монотонный рост DII поддерживается экспериментальными данными. Принимая во внимание, что рассчитанная в [12] зависимость μen0 показала очень хорошее соответствие экспериментам (рис. 2), мы далее опираемся на результат расчета Den0 этой же работы. Полученная таким путем аппроксимация DII в Ne функцией

(12)
${{D}_{{{\text{II}}}}}\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right) = \frac{{1 + 2.4 \times {{{10}}^{{ - 3}}}(\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}) + 4 \times {{{10}}^{{ - 6}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{2}} - 4.4 \times {{{10}}^{{ - 10}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{3}} + 6.8 \times {{{10}}^{{ - 14}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{4}}}}{{19.9 + 4420\,{\text{exp}}\left( { - 4.6{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{0.35}}}} \right)}}$
и ее соответствие данным экспериментов [20] показаны на рис. 4.

Рис. 4.

Зависимость продольной компоненты безразмерного тензора диффузии электронов DII от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}$ в Ne при комнатной температуре. Сплошная линия – аппроксимация (12); пунктирная линия – расчет по данным [12]: кружки – расчет по экспериментальным данным [20]. Константы A и B из (8) для Ne применены в расчетах.

2.4.2. Ar. Наиболее детальные измерения продольной компоненты тензора De/μe в Ar в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} = 2 \times {{10}^{{ - 4}}}{\kern 1pt} - {\kern 1pt} 6 \times {{10}^{3}}$ Тд и их сравнение с результатами других работ представлены в [43, 50]. Измерения в [50] при высоких напряженностях выполнены в статическом поле в сочетании с высокочастотным. Данные указанных двух источников легли в основу аппроксимации DII(|E|/n0) для Ar функцией

(13)
$\begin{gathered} {{D}_{{{\text{II}}}}}\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right) = 2.4 \times {{10}^{{ - 4}}} + 15\frac{{1 + 4 \times {{{10}}^{{ - 3}}}(\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}) - 4.9 \times {{{10}}^{{ - 7}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{2}} + 2.8 \times {{{10}}^{{ - 11}}}{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{3}}}}{{1 + 10{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{ - 0.13}}}{\text{exp}}\left[ { - 1.3{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{0.5}}}} \right]}} \times \\ \, \times \left\{ {896{{{\left( {\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right)}}^{2}}{\text{exp}}\left[ { - 4.5{{{\left| {1 - 286\frac{{\left| {\mathbf{E}} \right|}}{{{{n}_{0}}}}} \right|}}^{{1.7}}}} \right] + \frac{{{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{1.2}}}}}{{1 + 175{{{\left( {\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}}} \right)}}^{{1.2}}}}}} \right\}, \\ \end{gathered} $
которая показана на рис. 5.

Рис. 5.

Зависимость продольной компоненты безразмерного тензора диффузии электронов DII от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{{\text{0}}}}}}} \right. \kern-0em} {{{n}_{{\text{0}}}}}}$ в Ar при комнатной температуре. Сплошная линия – аппроксимация (13); кружки – расчет по экспериментальным данным [50]; крестики – расчет по экспериментальным данным [43]. Константы A и B из (9) для Ar применены в расчетах.

2.5. Оценка суммарной частоты столкновений электрона с атомами $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}} $ и скорости потери энергии электроном $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{с}}}^{*}} $

2.5.1. Ne. Оценка частоты неупругих столкновений каждого типа “с” электрона с атомами проводилась по формуле [51]

(14)
${{k}_{{\text{c}}}} = {{n}_{0}}{{\left( {\frac{2}{{{{m}_{e}}}}} \right)}^{{1/2}}}\int\limits_0^\infty {\Psi (\varepsilon )} {{\sigma }_{{\text{c}}}}(\varepsilon )\varepsilon d\varepsilon ,$
где me – масса электрона; σc(ε) – сечение столкновения типа “c”; $\Psi (\varepsilon )$ – функция распределения электронов по энергии. В качестве справочных использовались систематизированные в [16] данные литературы по структуре уровней атома Ne, энергиям и сечениям возбуждения его 4 наиболее значимых уровней, а также ионизации. Для сравнения, в [12] учитывались 7 уровней атома Ne, из которых три наиболее слабых привносят лишь незначительный вклад в суммарную частоту столкновений.

Величина энергии, теряемой электроном при ионизации атома, оценивалась исходя из результатов измерений энергетического спектра электронов, рожденных при ионизации [52], по методике [9], согласно которым энергия рожденного электрона ε2 оценивается как

(15)
${{\varepsilon }_{2}} = B\tan \left[ {p\arctan \frac{{{{\varepsilon }_{1}} - I}}{{2B}}} \right],$
где ε1 – энергия налетающего электрона; p – случайное число, равномерно распределенное в интервале 0–1; I = 21.6 эВ – потенциал ионизации атома Ne; B = 13 эВ [52]. В таком случае, средняя величина энергии, теряемой ионизующим атом электроном, равна ${{\varepsilon }_{{{\text{ион}}}}} = {{\varepsilon }_{2}} + I$ с последующим усреднением по параметру p. Потеря энергии электрона εc при его неупругом возбуждающем столкновении типа “c” с атомом принималась равной энергии возбуждения данного атомного уровня.

Вклад упругих столкновений в суммарные $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}} $ и $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{с}}}^{*}} $ оценивался не расчетом, как в (14), а по аналогии с [11, 12, 24, 53, 54] (см. также ссылки в этих работах), опираясь на частоты передачи импульса ${{\nu }_{{\text{m}}}} = {e \mathord{\left/ {\vphantom {e {{{m}_{e}}{{\mu }_{e}}}}} \right. \kern-0em} {{{m}_{e}}{{\mu }_{e}}}}$ и энергии ${{\nu }_{e}} = $ $ = {{2{{\nu }_{{\text{m}}}}{{m}_{e}}} \mathord{\left/ {\vphantom {{2{{\nu }_{{\text{m}}}}{{m}_{e}}} {{{m}_{{{\text{Ne}}}}}}}} \right. \kern-0em} {{{m}_{{{\text{Ne}}}}}}}$ электроном в приближении me ≪ ≪ mNe, где mNe – масса атома Ne. Последнее приближение оправдано тем, что ${{2{{m}_{e}}} \mathord{\left/ {\vphantom {{2{{m}_{e}}} {{{m}_{{{\text{Ne}}}}} \approx 5.4 \times {{{10}}^{{ - 5}}}}}} \right. \kern-0em} {{{m}_{{{\text{Ne}}}}} \approx 5.4 \times {{{10}}^{{ - 5}}}}}$. Поскольку сечение упругих столкновений электрона с атомом Ne в диапазоне $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} \leqslant {{10}^{4}}$ Тд превышает сечения неупругих столкновений, то вклад упругих столкновений в суммарную частоту значителен. По сути, νm характеризует “эффективную” частоту столкновений электронов с атомом с учетом их анизотропии, которая, как показано на примере азота в [55], приводит к значительному различию между сечениями столкновений и передачи импульса. Вклад упругих столкновений в суммарную потерю энергии электроном незначителен, так как при столкновении такого типа коэффициент передачи энергии электрона атому мал и пропорционален ${{2{{m}_{e}}} \mathord{\left/ {\vphantom {{2{{m}_{e}}} {{{m}_{{Ne}}} \approx }}} \right. \kern-0em} {{{m}_{{Ne}}} \approx }}$ 5.4 × 10–5 [47], что проявляется в разнице между νm и νe. Скорость потери энергии электроном при упругих столкновениях оценивалась как ${{\nu }_{e}}\left( {\varepsilon - 3k{{T}_{0}}{\text{/}}2} \right)$, где k и T0 – постоянная Больцмана и температура газа соответственно [11, 12, 53, 54]. Результаты оценки безразмерных $\nu _{{\text{m}}}^{*}$ и суммарной частоты неупругих столкновений $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}} $, включая ударную ионизацию, а также скорости потери энергии электроном при упругих и неупругих столкновениях с атомом Ne показаны на рис. 6, 7. Для сравнения, на рис. 6 приведены аналогичные данные расчета [12], переведенные в безразмерное представление, и можно отметить удовлетворительное соответствие данных друг другу. Из рис. 7 хорошо видно, что скорость потери энергии электроном определяется преимущественно неупругими столкновениями всех типов, а упругие играют лишь незначительную роль.

Рис. 6.

Зависимость безразмерных суммарной частоты неупругих столкновений $\sum\nolimits_{\text{с}} {k_{{\text{c}}}^{*}} $ и частоты передачи импульса $\nu _{{\text{m}}}^{*}$ электронов от их средней энергии ε в Ne при комнатной температуре. Сплошная и штриховая линии – $\sum\nolimits_{\text{с}} {k_{{\text{c}}}^{*}} $ по данным настоящей работы и [12]. Штрихпунктирная и пунктирная линии – $\nu _{{\text{m}}}^{*}$ по данным настоящей работы и [12].

Рис. 7.

Зависимость безразмерной скорости потери энергии электроном $\nu _{e}^{*}\left( {\varepsilon {\kern 1pt} * - 3k{{T}_{0}}{{\alpha }_{0}}{\text{/}}2e{{E}_{0}}} \right)$ при его упругих и $\sum\nolimits_{\text{с}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{c}}}^{*}} $ при неупругих столкновениях с атомом Ne от средней энергии электронов ε при комнатной температуре. Сплошная линия – неупругие столкновения, штриховая – упругие.

2.5.2. Ar. Оценка суммарной частоты столкновений и скорости потери энергии электроном для этого газа выполнены аналогично Ne на основе систематизированных в [17] данных литературы по структуре уровней атома Ar, энергиям и сечениям возбуждения 5 наиболее значимых групп уровней, а также ионизации. Величина потери энергии электроном при ионизации также оценивалась следуя (15) при B = 10 эВ, однако авторы [52] констатировали более низкую точность своей оценки параметра B для Ar по сравнению с Ne. Результаты оценки частоты столкновений и скорости передачи энергии в Ar приведены на рис. 8, 9.

Рис. 8.

Зависимость безразмерных суммарной частоты неупругих столкновений $\sum\nolimits_{\text{с}} {k_{{\text{c}}}^{*}} $ (сплошная линия) и частоты передачи импульса $\nu _{{\text{m}}}^{*}$ (штриховая линия) электронов от их средней энергии ε в Ar при комнатной температуре.

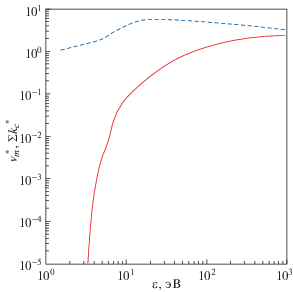
Рис. 9.

Зависимость безразмерной скорости потери энергии электроном $\nu _{e}^{*}\left( {\varepsilon {\kern 1pt} * - 3k{{T}_{0}}{{\alpha }_{0}}{\text{/}}2e{{E}_{0}}} \right)$ при его упругих и $\sum\nolimits_{\text{с}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{c}}}^{*}} $ при неупругих столкновениях с атомом Ar от средней энергии электронов ε при комнатной температуре. Сплошная линия – неупругие столкновения, штриховая – упругие.

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

3.1. Результаты моделирования динамики ФВИ

Уравнения (2) решались каждый раз при фиксированной величине напряженности внешнего электростатического поля ${{Y}^{ + }} = {{\left| {{{{\mathbf{E}}}^{ + }}} \right|} \mathord{\left/ {\vphantom {{\left| {{{{\mathbf{E}}}^{ + }}} \right|} {{{E}_{{\text{0}}}}}}} \right. \kern-0em} {{{E}_{{\text{0}}}}}}$, которая затем варьировалась в широком диапазоне. Диапазон вариации Y+ простирался от $Y_{{{\text{пор}}}}^{ + } = {{{{E}_{{{\text{пор}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{пор}}}}}} {{{E}_{{\text{0}}}}}}} \right. \kern-0em} {{{E}_{{\text{0}}}}}}$, ниже которой ФВИ не развивался вообще, до величины, соответствующей ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = 4 \times {{10}^{3}}$ Тд, хотя диапазон аппроксимаций коэффициентов значительно шире. Ограничение диапазона сверху обусловлено тем, что при некоторых, оцененных ниже, величинах Y+ нарушается одно из основных требований применяемой модели, а именно медленности наведенных изменений в среде по сравнению со скоростью релаксации среды.

Как уже отмечалось в разделе 2.1, получаемые решения для плотности электронов за ФВИ варьировались в пределах нескольких порядков при изменении Y+. Поэтому начальная плотность электронов (5) также варьировалась путем изменения предэкспоненциального множителя. Начальная точка x0 инициирования ФВИ располагалась в середине пространственного домена вычислений, вдали от его границ. Необходимо заметить, что начальная плотность (5) задавалась лишь как точечный источник небольшого количества стартовых электронов в точке x0. При достаточно малом количестве таких электронов они не влияют на динамику развития и движения ФВИ вдали от x0. Путем вариации в расчетах предэкспоненциального множителя в (5) оценивалось максимальное количество стартовых электронов, меньше которого они никак не влияли на искомые решения для ФВИ.

В расчетах применялся сравнительно широкий пространственно-временной домен моделирования. Размер пространственной части домена обычно составлял x = 6 × 103 при шаге сетки до Δx = 0.01–0.02. Размер временной части домена достигал τ = 105 при шаге сетки до Δτ = 0.05. Наибольший временной домен применялся при величинах Y+, близких к порогу возбуждения ФВИ, когда время развития ФВИ максимально. Наименьший шаг пространственной сетки использовался вблизи максимальных величин Y  +, когда глубина ФВИ близка к минимальной.

Общая картина развития и формирования ФВИ в условиях локального равновесия известна по многочисленным работам: с момента τ = 0 начинается рост плотности облака электронов в точке x0, по мере ее роста напряженность поля постепенно экранируется нарастающим пространственным зарядом и начинает формироваться ФВИ. Этот начальный период представляет собой переходной процесс, в течение которого меняются все пространственные и временные характеристики плотности электронов, напряженности поля, средней энергии электронов. Интенсивность и скорость изменений зависят от величины приложенного поля и характеристик газа. В результате формируется устойчивый ФВИ со стабильным пространственным профилем, движущийся с постоянной скоростью, и его параметры фиксируются и обсуждаются. Полученные решения для плотности электронов за установившимся ФВИ и скорости его движения в обоих газах приведены на рис. 10, 11 для наглядности в обычном, размерном представлении как ${{n}_{e}}{\text{/}}n_{0}^{2}$ и ${{V}_{{{\text{ФВИ}}}}}$ соответственно. Для сравнения, на рис. 11 треугольниками показаны результаты расчета скорости волны в Ne [12] при атмосферном давлении и можно отметить хорошее совпадение результатов. Также, на этом рисунке линиями показаны результаты аналитической оценки скорости отрицательного фронта следуя соотношению

(16)
${{v}_{{{\text{ФВИ}}}}} = \left| {{{Y}^{ + }}} \right| + 2\sqrt {{{D}_{{{\text{II}}}}}{{f}_{{{\text{бр}}}}}\left( {\left| {{{Y}^{ + }}} \right|} \right)} ,$
полученному в [4] в приближении локального поля модели сплошной среды при фиксированных коэффициентах диффузии и подвижности электронов, не зависящих от напряженности поля/их средней энергии. Для преобразования результата оценки (16) в обычное, размерное представление на рис. 11 применялись соотношения связи (3), (4). На рис. 10, 11 приведены также результаты оценки плотности электронов и скорости движения ФВИ в рамках классической модели сплошной среды. На рис. 12, 13 показаны примеры пространственного распределения σ и Y в установившемся фронте волны (вдоль оси движения фронта x) для Ne и Ar, полученные в рамках приближения локальной энергии и классической модели сплошной среды. На обоих рисунках фронт движется справа налево. Каждый из представленных параметров нормирован по амплитуде к 1 для удобства сопоставления.

Рис. 10.

Зависимость плотности электронов ${{n}_{e}}{\text{/}}n_{0}^{2}$ позади ФВИ отрицательной полярности от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ в Ne и Ar при комнатной температуре. Квадраты – Ne, приближение локальной энергии; наклонные крестики – Ne, классическая модель; кружки – Ar, приближение локальной энергии; прямые крестики – Ar, классическая модель.

Рис. 11.

Зависимость скорости ${{V}_{{{\text{ФВИ}}}}}$ ФВИ отрицательной полярности от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ в Ne и Ar при комнатной температуре. Квадраты – Ne, приближение локальной энергии; треугольники – по данным расчета для Ne в [12], приближение локальной энергии; наклонные крестики – Ne, классическая модель; кружки – Ar, приближение локальной энергии; прямые крестики – Ar, классическая модель; сплошная и штриховая линии – оценка следуя (16) для Ne и Ar соответственно.

Рис. 12.

Распределение безразмерных плотности электронов σ и напряженности поля Y во фронте волны вдоль оси x в момент времени τ = 14000 в Ne. Сплошная и штрихпунктирная линии – σ в приближении локальной энергии и классической модели соответственно; штриховая и пунктирная линии – Y в приближении локальной энергии и классической модели соответственно. ФВИ движется справа налево. Кривые нормированы по амплитуде к 1, ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ = = 950 Тд.

Рис. 13.

Распределение безразмерных плотности электронов σ и напряженности поля Y во фронте волны вдоль оси x в момент времени τ = 2500 в Ar. Сплошная и штрихпунктирная линии – σ в приближении локальной энергии и классической модели, соответственно; штриховая и пунктирная линии – Y в приближении локальной энергии и классической модели, соответственно. ФВИ движется справа налево. Кривые нормированы по амплитуде к 1, ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ = = 900 Тд.

В решениях (2) фиксировались также толщина ФВИ $\Delta {{x}_{{{\text{ФВИ}}}}}$, определяемая по уровню 0.1–0.9 от максимальной напряженности поля перед фронтом, и разница между максимальной энергией электронов $\varepsilon _{{{\text{макс}}}}^{*}$ в передней части фронта и энергией $\varepsilon _{{{\text{мин}}}}^{*}$ позади него, до которой энергия электрона релаксирует в результате прохождения фронта. По этим параметрам оценивалось соблюдение двух необходимых условий правомерности применения модели сплошной среды. Во-первых, одним из допущений при выводе уравнений сплошной среды из уравнения Больцмана является требование медленности наведенных внешним полем возмущений по сравнению со временем релаксации 1/νm [11, 12, 24, 53, 54]. В [56] при рассмотрении модели сплошной среды четвертого порядка, учитывающей в уравнениях плотность и поток электронов, а также плотность и поток их энергии, было показано, что такая модель допускает упрощение до модели второго порядка, опирающейся только на плотность и энергию электронов, без заметной потери точности, если соблюдается то же условие медленности. Поскольку показателем частоты изменения поля во фронте может служить величина ${{v}_{{{\text{ФВИ}}}}}{\text{/}}\Delta {{x}_{{{\text{ФВИ}}}}}$, обратная его длительности, где ${{v}_{{{\text{ФВИ}}}}}$ – безразмерная скорость движения фронта, то отмеченное выше условие принимает вид

(17)
$Q = v_{{\text{m}}}^{*}{{\Delta }}{{x}_{{{\text{ФВИ}}}}}{\text{/}}{{v}_{{{\text{ФВИ}}}}} \gg 1.$

Во-вторых, если максимальная энергия электрона во фронте волны равна $\varepsilon _{{{\text{макс}}}}^{*}$, а средняя энергия, отдаваемая им при одном столкновении, составляет $\left\langle {\varepsilon {\kern 1pt} *} \right\rangle $, то для релаксации к энергии $\varepsilon _{{{\text{мин}}}}^{*}$ такой электрон в течение промежутка времени, равного длительности фронта, должен испытать не менее ${\text{(}}\varepsilon _{{{\text{макс}}}}^{*} - \varepsilon _{{{\text{мин}}}}^{*}{\text{)/}}\left\langle {\varepsilon {\kern 1pt} *} \right\rangle $ столкновений c атомами. На самом деле последнее отношение энергий внутри фронта не постоянно, а уменьшается с максимального почти до нуля, и его усредненное значение по толщине фронта примерно в два раза меньше. Среднюю по всем типам неупругих столкновений энергию, отдаваемую электроном, можно оценить как $\left\langle {\varepsilon {\kern 1pt} *} \right\rangle = \sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{c}}}^{*}} {\text{/}}\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}} $, и тогда искомое требование принимает вид

(18)
$S = 2\frac{{\Delta {{x}_{{{\text{ФВИ}}}}}}}{{{{v}_{{{\text{ФВИ}}}}}}}\frac{{\sum\limits_{\text{c}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{c}}}^{*}} }}{{\varepsilon _{{{\text{макс}}}}^{*} - \varepsilon _{{{\text{мин}}}}^{*}}} \gg 1.$

С увеличением приложенного внешнего поля оба параметра Q и S уменьшаются и накладывают ограничение сверху на область применения рассматриваемой модели. Результаты оценки этих параметров для двух газов приведены на рис. 14, 15 в зависимости от приложенного поля ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$. Видно, что из двух условий (17) и (18), именно условие (18) наиболее сильно ограничивает сверху диапазон применения модели. Хотя зависимости Q и S от напряженности поля заметно отличаются в двух газах, удивительно то, что условная граница S = 10 в обоих газах соответствует ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \approx 1180$ Тд.

Рис. 14.

Зависимость параметров Q и S от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ в Ne. Квадраты – Q, кружки – S.

Рис. 15.

Зависимость параметров Q и S от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ в Ar. Квадраты – Q, кружки – S.

3.2. Обсуждение результатов

Безразмерное представление уравнений модели сплошной среды в приближении локального поля, при фиксированных величинах подвижности и коэффициента диффузии электронов, было предложено в [4]. Его можно расширить и применить к модели в приближении локальной энергии, определив дополнительно два параметра – безразмерную подвижность электронов M в соответствии с (3) и энергию eE0/α0. Величина последней постоянна для конкретного газа и оценивается как 76.3 и 20.5 эВ для Ne и Ar при комнатной температуре соответственно. Как показывают аппроксимации входящих в уравнения коэффициентов (разделы 2.2–2.5), они все в условиях локального равновесия могут быть представлены функциями только Y или ε*. Следовательно, решения уравнений для искомых параметров ФВИ должны иметь ту же функциональную зависимость. Однако безразмерный подход не расширяет диапазон применения модели безгранично, например, путем вариации плотности частиц газа при постоянной напряженности поля, или наоборот. Его применение ограничено допущениями, принятыми при формулировке модели (1) из уравнения Больцмана ([6, 7, 11, 12, 24, 53, 54] и ссылки в них), наиболее важные из которых отмечены в разделе 2.1 и отражены, в частности, в безразмерных параметрах Q и S (рис. 14, 15). Безразмерное представление, с одной стороны, предлагает удобную шкалу для сопоставления результатов различных работ и, с другой стороны, позволяет применять результаты моделирования к газоразрядным системам различного масштаба, не выходя, однако, за рамки допущений и предположений самой модели.

Сочетание экспериментальных и теоретических данных, рассчитанных методами Монте-Карло, динамики частиц и решением уравнения Больцмана, о транспортных и ионизационных коэффициентах исследуемых газов показало их взаимодополняемость и близкое соответствие друг другу. Важно то, что оба массива данных удовлетворяют условию локального равновесия, зависят от локальных величин поля/средней энергии электрона и их применение в уравнениях сплошной среды (1), (2) оправдано. Коэффициенты α/n0, M и DII изменяются на несколько порядков величин в пределах диапазона моделирования ФВИ. Объединение данных позволило предложить аналитические аппроксимации этих коэффициентов в широком диапазоне вплоть до $\left| {\mathbf{E}} \right|{\text{/}}{{n}_{0}} = {{10}^{{ - 4}}}{\kern 1pt} - {\kern 1pt} 5 \times {{10}^{4}}$ Тд. Выбор несколько громоздких функций (10)–(13) обусловлен желанием поточнее представить каждую кривую во всем диапазоне одной функцией, однако даже в таком виде они, если и замедляют вычислительный процесс, то незначительно. На рис. 2–5 заметны локальные отклонения аппроксимаций от референсных величин в сравнительно узких интервалах ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$. Но в задаче настоящей работы такие отклонения не оказывают значимого влияния на результат моделирования ФВИ, поскольку в пределах толщины фронта напряженность поля изменяется от максимальной до нуля, т.е. весь спектр величин напряженности поля и, соответственно, транспортных и ионизационных коэффициентов участвует в развитии и движении ФВИ. Это показали отдельные тестовые вычисления при локально варьируемых коэффициентах. Более важным видится общий характер зависимости коэффициентов от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ – форма и изгиб кривых, диапазон величин коэффициентов.

Характер зависимости α/n0, M и DII от ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ качественно различен. Так, коэффициент ударной ионизации и подвижность электронов изменяются немонотонно с ростом ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ в области выше 103 Тд (рис. 1–3), что объясняется уменьшением сечений столкновений электронов с атомами в сильном поле. Напротив, коэффициент диффузии DII монотонно растет с увеличением ${{\left| {\mathbf{E}} \right|} \mathord{\left/ {\vphantom {{\left| {\mathbf{E}} \right|} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$, что коррелирует с монотонным увеличением средней энергии электронов в Ne, Ar и других инертных газах [12, 16, 17, 29, 30].

Формальные численные решения уравнений (2) на рис. 10–13 показывают монотонную зависимость параметров волны от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ приложенного поля во всем диапазоне моделирования, хотя два из трех коэффициентов немонотонны. Монотонный рост скорости ФВИ можно качественно объяснить, опираясь на (16): несмотря на немонотонность α/n0 и M, скорость дрейфа электронов и произведение DIIfбр остаются монотонно растущими функциями ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$. В каждом из двух газов наклон зависимости VФВИ от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ (рис. 11), удовлетворительно коррелирован с оценочным следуя (16), но количественно величины скорости различаются в зависимости от используемой модели. При этом результат численного моделирования VФВИ в Ne в рамках приближения локальной энергии настоящей работы и [12] хорошо соответствуют друг другу (рис. 11). Различие VФВИ между газами, достигающее 4.5–10 раз в пределах диапазона моделирования, объясняется совокупной разницей индивидуальных коэффициентов α/n0, M и DII газов.

В отношении плотности электронов позади ФВИ следует отметить, что, в отличие от скорости фронта и, как видно из рис. 10, она в каждом газе практически одинакова в приближениях локального поля и энергии модели сплошной среды. Ее значения в разных газах тоже достаточно близки друг к другу при том, что атомы Ne и Ar значительно различаются по размеру, массе, структуре атомных уровней и сечениям/энергиям их возбуждения. Существенные различия между газами видны также в транспортных свойствах электронов (рис. 1–5). Как следствие различий, частота столкновений и скорость потери энергии электроном в Ar почти в 6.5–7 раз выше, чем в Ne (рис. 6–9). Тем не менее, плотность электронов позади ФВИ в обоих газах близка при слабом поле и разница между ними плавно возрастает всего до 2 раз при ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \approx 1200$ Тд (рис. 10). Отмеченная особенность решений для плотности электронов есть результат сочетания параметров каждого из двух газов, в котором коэффициент ионизации, по-видимому, играет наиболее важную роль. Так, в [4] для приближения локального поля в частном случае фиксированной подвижности электронов и De = 0 была предложена аналитическая оценка плотности электронов позади ФВИ в виде

${{n}_{e}} = \frac{{{{\varepsilon }_{0}}}}{e}\int\limits_0^{\left| {{{{\mathbf{E}}}^{ + }}} \right|} {\alpha (E)dE,} $
в которой плотность электронов зависит только от интеграла коэффициента ионизации по всему спектру от 0 до |E+|. Здесь ε0 и e – диэлектрическая постоянная и абсолютная величина заряда электрона соответственно. Хотя данную оценку нельзя применить непосредственно к рассматриваемому приближению локальной энергии, на качественном уровне роль коэффициента ионизации она показывает.

Толщина ФВИ (рис. 12, 13), с одной стороны, в каждом газе слабо зависит от применяемой модели вычислений (локального поля или энергии), а, с другой стороны, в несколько раз различается между газами. В пункте в) раздела 2.1 уже отмечалось со ссылками на опубликованные работы, что близкие друг другу профили и толщина ФВИ в азоте регистрируются не только в моделях сплошной среды, но также и в моделях более высокого порядка: гибридных и динамики частиц, даже при зарождении высокоэнергетичных электронов внутри и вблизи ФВИ. Таким образом, толщина ФВИ мало чувствительна к используемой модели вычислений. Но при близких величинах толщины ФВИ в разных моделях, профиль фронта в них все же не идентичен, что заметно в результатах упомянутых работ и на рис. 12, 13. Различие толщины ФВИ между газами не поддается точной аналитической оценке, но качественно может быть обосновано следующим образом: в [9] отмечалось, что в передней области ФВИ, где $\left| {\mathbf{E}} \right| \approx \left| {{{{\mathbf{E}}}^{ + }}} \right|$, плотность электронов зависит от пространственной координаты z примерно как ${{n}_{e}} \propto \exp (z{\text{/}}l)$, где в приближении фиксированных величин транспортных коэффициентов

$l = \sqrt {\frac{{{{D}_{e}}(\left| {{{{\mathbf{E}}}^{ + }}} \right|)}}{{{{\mu }_{e}}(\left| {{{{\mathbf{E}}}^{ + }}} \right|)\left| {{{{\mathbf{E}}}^{ + }}} \right|\alpha (\left| {{{{\mathbf{E}}}^{ + }}} \right|)}}} ,$
а из рис. 1–5 можно оценить, что при ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \approx $ ≈ 900–950 Тд величина l в Ar в примерно в 2.3 раза меньше, чем в Ne, т.е. инкремент экспоненциального роста ne в Ar значительно больше. Но, поскольку максимальная плотность электронов позади ФВИ в обоих газах различается менее чем в 2.1 раза, в Ar следует ожидать меньшую толщину ФВИ, что качественно согласуется с результатами моделирования ФВИ на рис. 12, 13.

В разделе 3.1 предложены два безразмерных параметра, Q и S, выражающие отношения “эффективной” частоты столкновений электронов с атомами и частоты релаксации энергии электронов в столкновениях к частоте наведенных возмущений (обратной длительности ФВИ) в газе. Условие Q, S ≫ 1, т.е. быстрая релаксация электронов по двум параметрам, является необходимым условием локальности процессов при выводе уравнений сплошной среды из кинетического уравнения Больцмана и от кратности превышения единицы этими параметрами зависит степень корректности модели. Результат численной оценки Q и S для двух газов в зависимости от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ на рис. 14, 15 показывает в первом приближении те области, в которых рассматриваемое приближение заведомо неприменимо. Так, формальные решения (2), по крайней мере в области ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \geqslant 1500$ Тд, нельзя считать физически обоснованными, поскольку здесь уже S < 5. На рис. 14, 15 видно также, что параметр S резко снижается и в области ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \leqslant 100$ Тд (примерно соответствует ε < 8–10 эВ), где $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}} $ и $\sum\nolimits_{\text{c}} {k_{{\text{c}}}^{*}\varepsilon _{{\text{c}}}^{*}} $ крайне малы (рис. 6–9). Таким образом, диапазон применения модели ограничен параметрами Q и S как сверху, так и снизу. Более точно количественную оценку пограничных величин Q и S может предложить моделирование с учетом нелокальных эффектов. Если же границу определить условием Q, S = 10, то сверху для обоих газов она близка к ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \approx $ ≈ 1180 Тд (рис. 14, 15).

Здесь уместно упомянуть еще один безразмерный параметр $K = \Delta {{l}_{{{\text{ФВИ}}}}}{\text{/}}\lambda $, количественно оцененный для Ne в [25] и отмеченный во Введении. Наряду с Q и S, параметр K накладывает свое ограничение на диапазон применения модели. Но ограничение диапазона ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ по этому параметру оказалось менее строгим, чем по Q и S, и его можно не принимать во внимание.

Резюмируя, можно сказать следующее. Во-первых, модель сплошной среды в приближении локальной энергии для оценки динамики ФВИ принята нами как компромиссный, между точностью получаемых результатов и сложностью расчетов, подход к сравнительному анализу разных газов. Безразмерное представление ее уравнений (2) и решений предлагает удобную основу для сопоставления результатов разных работ с разными газами в единой шкале. Несомненно, что привлечение более развитых моделей к расчетам повысит точность результатов, если потребуется. Во-вторых, ионизационные и транспортные коэффициенты электронов в Ar и Ne удовлетворяют условию локального равновесия, сохраняют физический смысл во всем диапазоне моделирования динамики ФВИ и поэтому их применение в модельных уравнениях (1) и (2) оправдано. В-третьих, сравнение решения (2) для ФВИ в Ne с полученными ранее в [12] по доступным для этого параметрам приводят к выводу, что принятая методика и алгоритм численного моделирования ФВИ, предложенные для этого аппроксимации и оценки необходимых коэффициентов показывают удовлетворительный результат моделирования. В-четвертых, на основе полученных решений для Ar и Ne оценены величины и зависимость от ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}}$ двух предложенных безразмерных параметров Q и S, характеризующих отношение скорости релаксации электронов к скорости наведенных внешним полем изменений. Требование Q, S ≫ 1 является необходимым условием, ограничивающим область применения модели сплошной среды в приближении локальной энергии для моделирования динамики ФВИ стримера. В частности, применительно к Ar и Ne, Q, S > > 10 при ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \leqslant 1180$ Тд.

4. ЗАКЛЮЧЕНИЕ

Применительно к развитию стримера в газах, проведена численная оценка характеристик ФВИ отрицательной полярности в Ne и Ar на основе 1D диффузионно-дрейфовых уравнений сплошной среды в приближении локальной энергии. Для этого система уравнений представлена в безразмерном виде, построены аппроксимации коэффициентов ударной ионизации газов, безразмерных подвижности и продольной компоненты тензора диффузии электронов аналитическими функциями в диапазоне вплоть до ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} = {{10}^{{ - 4}}} - 5 \times {{10}^{4}}$ Тд, основанные на известных экспериментальных и теоретических данных. Численным решением уравнений получены оценки плотности электронов позади фронта ионизации, скорости движения и толщины фронта в диапазоне ${\text{|}}{{{\mathbf{E}}}^{ + }}{\text{|/}}{{n}_{0}} \leqslant 4 \times {{10}^{3}}$ Тд. Оценкой двух безразмерных параметров, характеризующих необходимое условие медленности наведенных возмущений в газе по сравнению со скоростью релаксации электронов, показаны ограничения на диапазон применения уравнений сплошной среды в моделировании, обусловленные этими параметрами.

Список литературы

  1. Schunk R.W. // Rev. Geophys. 1977. V. 15. P. 429.

  2. Dhali S.K., Williams P.F. // J. Appl. Phys. 1987. V. 62. P. 4696.

  3. Vitello P.A., Penetrante B.M., Bardsley J.N. // Phys. Rev. E. 1994. V. 49. P. 5574.

  4. Ebert U., van Saarloos W., Caroli C. // Phys. Rev. E. 1997. V. 55. P. 1530.

  5. Kanzari Z., Yousfi M., Hamani A. // J. Appl. Phys. 1998. V. 84. P. 4161.

  6. Li C., Ebert U., Hundsdorfer W. // J. Comput. Phys. 2010. V. 229. P. 200.

  7. Li C., Teunissen J., Nool M., Hundsdorfer W., Ebert U. // Plasma. Sources. Sci. Technol. 2012. V. 21. P. 055019.

  8. Ebert U., Montijn C., Briels T.M.P., Hundsdorfer W., Meulenbrock B., Rocco A., Veldhuisen E.M. // Plasma. Sources. Sci. Technol. 2006. V. 15. P. S118.

  9. Li C., Brok W.J.M., Ebert U., Mullen J.J.A.M. // J. A-ppl. Phys. 2007. V. 101. P. 123305.

  10. Li C., Ebert U., Brok W.J.M., Hundsdorfer W. // J. Phys. D: Appl. Phys. 2008. V. 41. P. 032005.

  11. Dujko S., Markosyan A.H., White R.D., Ebert U. // J. Phys. D: Appl. Phys. 2013. V. 46. P. 475202.

  12. Markosyan A.H., Teunissen J., Dujko S., Ebert U. // Plasma. Sources. Sci. Technol. 2015. V. 24. P. 065002.

  13. Chanrion O., Bonaventura Z., Cinar D., Bourdon A., Neubert T. // Environ. Res. Lett. 2014. V. 9. P. 055003.

  14. Chanrion O., Neubert T. // J. Comput. Phys. 2008. V. 227. P. 7222.

  15. Ткачев А.Н., Яковленко С.И. // Письма ЖЭТФ. 2003. Т. 77. № 5. С. 264.

  16. Ткачев А.Н., Феденев А.А., Яковленко С.И. // КСФ. 2004. № 5. С. 8.

  17. Ткачев А.Н., Феденев А.А., Яковленко С.И. // ЖТФ. 2007. Т. 77. № 6. С. 22.

  18. Saelee H.T., Lucas J. // J. Phys. D: Appl. Phys. 1977. V. 10. P. 343.

  19. Kucucarpaci H.N., Lucas J. // J. Phys. D: Appl. Phys. 1979. V. 12. P. 2123.

  20. Kucucarpaci H.N., Saelee H.T., Lucas J. // J. Phys. D: Appl. Phys. 1981. V. 14. P. 9.

  21. Kucucarpaci H.N., Lucas J. // J. Phys. D: Appl. Phys. 1981. V. 14. P. 2001.

  22. Sakai Y., Tagashira H., Sakamoto S. // J. Phys. D: Appl. Phys. 1977. V. 10. P. 1035.

  23. Tagashira H., Sakai Y., Sakamoto S. // J. Phys. D: Appl. Phys. 1977. V. 10. P. 1051.

  24. Hagelaar G.J.M., Pitchford I.C. // Plasma. Sources. Sci. Technol. 2005. V. 14. P. 722.

  25. Trusov K.K. // Plasma. Sources. Sci. Technol. 2018. V. 27. P. 095009.

  26. Трусов К.К. // Физика плазмы. 2017. Т. 43. № 8. С. 703.

  27. Bagheri B., Teunissen J., Ebert U., Becker M.M., Chen S., Ducasse O., Eichwald O., Loffhagen D., Luque A., Mihailova D., Plewa J.M., Dijk J., Yousfi M. // Plasma. Sources. Sci. Technol. 2018. V. 27. P. 095002.

  28. Hoder T., Loffhagen D., Vorac J., Becker M.M., Brandenburg R. // Plasma. Sources. Sci. Technol. 2016. V. 25. P. 025017.

  29. Tkachev A.N., Yakovlenko S.I. // Central. Europ. J. Phys. 2004. V. 2. P. 579.

  30. Ткачев А.Н., Яковленко С.И. // Труды ИОФ РАН. 2007. Т. 63. С. 64.

  31. Li C., Ebert U., Hundsdorfer W. // J. Phys. D: Appl. Phys. 2009. V. 42. P. 202003.

  32. Тарасенко В.Ф., Яковленко С.И. // Труды ИОФ РАН. 2007. Т. 63. С. 7.

  33. Ткачев А.Н., Яковленко С.И. // Труды ИОФ РАН. 2007. Т. 63. С. 102

  34. Tarasenko V.F. // Plasma. Sources. Sci. Technol. 2020. V. 29. P. 034001.

  35. Naidis G.V., Tarasenko V.F., Babaeva N.Y., Lomaev M.I. // Plasma. Sources. Sci. Technol. 2018. V. 27. P. 013001.

  36. Loeb L.B. Electrical coronas. Their basis physical mechanism. Berkeley, CA: University of California Press, 1965.

  37. Железняк М.Б., Мнацаканян А.К., Сизых С.В. // Теплофизика высоких температур. 1982. Т. 20. С. 423.

  38. Kulikovsky A.A. // J. Phys. D: Appl. Phys. 2000. V. 33. P. L5.

  39. Nijdam S., Wetering F.M.J.H., Blanc R., Veldhuizen E.M., Ebert U. // J. Phys. D: Appl. Phys. 2010. V. 43. P. 145204.

  40. Wormeester G., Pancheshnyi S., Luque A., Nijdam S., Ebert U. // J. Phys. D: Appl. Phys. 2010. V. 43. P. 505201.

  41. Brisset A., Gazeli K., Magne L., Pasquiers S., Jeanney P., Marode E., Tardiveau P. // Plasma. Sources. Sci. Technol. 2019. V. 28. P. 055016.

  42. Nijdam S., Wormeester G., Veldhuizen E.M., Ebert U. // J. Phys. D: Appl. Phys. 2011. V. 44. P. 455201.

  43. Dutton J. // J. Phys. Chem. Ref. Data. 1975. V. 4. P. 577.

  44. Григорьев И.С., Мейлихов Е.З. Физические величины. Справочник. М.: Энергоатомиздат, 1991.

  45. Meek J.M., Craggs J.D. Electrical breakdown of gases. Oxford: Clarendon Press, 1953.

  46. Ward A.L. // J. Appl. Phys. 1962. V. 33. P. 2789.

  47. Райзер Ю.П. Физика газового разряда. М.: Наука, 1992.

  48. Королев Ю.Д., Месяц Г.А. Физика импульсного пробоя газов. М.: Наука, 1991.

  49. Трусов К.К. // Физика плазмы. 2008. Т. 34. С. 374.

  50. Лисовский В.А. // Письма ЖТФ. 1998. Т. 24. С. 49.

  51. Aleksandrov N.L., Kochetov I.V. // J. Phys. D: Appl. Phys. 1996. V. 29. P. 1476.

  52. Opal C.B., Peterson W.K., Beaty E.C. // J. Chem. Phys. 1971. V. 55. P. 4100.

  53. Robson R.E., White R.D., Petrovic Z.Lj. // Rev. Mod. Phys. 2005. V. 77. P. 1303.

  54. White R.D., Robson R.E., Dujko S., Nicolotopoulos P., Li B. // J. Phys. D: Appl. Phys. 2009. V. 42. P. 194001.

  55. Phelps A.V., Pitchford // Phys. Rev. A. 1985. V. 31. P. 2932.

  56. Becker M.M., Loffhagen D. // Adv. Pure Math. 2013. V. 3. P. 343.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал