Физика плазмы, 2022, T. 48, № 5, стр. 410-429
Профиль уединенной ионно-звуковой волны в плазме с отрицательными ионами
Ю. В. Медведев *
Объединенный институт высоких температур РАН
Москва, Россия
* E-mail: medve@mail.ru
Поступила в редакцию 19.12.2021
После доработки 01.02.2022
Принята к публикации 05.02.2022
- EDN: GZMECX
- DOI: 10.31857/S0367292122200045
Аннотация
Представлен метод для численного расчета профиля уединенной ионно-звуковой волны в плазме с отрицательными ионами и, как частный случай, в электрон-ионной плазме. Предложены новые формулы для аналитического описания профиля уединенной волны сжатия и профиля уединенной волны разрежения при малых амплитудах. Проведено сравнение профилей уединенных волн, рассчитанных по предложенным здесь и по известным формулам, как между собой, так и с соответствующими профилями, полученными с помощью решения полной системы уравнений, описывающей плазму. В большинстве случаев наименьшее отклонение от решения полной системы уравнений имеет профиль, рассчитанный по предлагаемым формулам.
1. ВВЕДЕНИЕ
Распространение уединенных ионно-звуковых волн в бесстолкновительной плазме исследуется достаточно давно. Большинство исследований было проведено для волн сравнительно малых амплитуд, которые, в соответствии с установившейся терминологией [1], принято называть ионно-звуковыми солитонами. Для краткости ниже в названиях этих волн мы будем опускать слова “ионно-звуковая”/“ионно-звуковой”. Это не приведет к какой-либо неопределенности, поскольку другие типы волн здесь не рассматриваются.
Наиболее подробно изучены генерация и распространение солитонов в двухкомпонентной электронно-ионной плазме (ЭИП). Исследования проводились как теоретически [1–24], так и экспериментально [25–30]. Значительное число работ посвящено изучению солитонов, распространяющихся в трехкомпонентной плазме с отрицательными ионами (ПОИ), состоящей из электронов, положительных ионов и отрицательных ионов. Теоретические аспекты обсуждаются в работах [31–38], экспериментальные исследования представлены в работах [39–51]. ПОИ в естественных условиях наблюдается в D-слое и в нижней части E-слоя ионосферы. В лабораторных условиях плазма, содержащяя отрицательные ионы водорода ${{{\text{H}}}^{ - }}$ и дейтерия ${{{\text{D}}}^{ - }}$, может использоваться для создания высокоэнергетичных пучков нейтральных частиц для термоядерных исследований [52]. ПОИ применяют для обработки материалов. В частности, в [51, 53] сообщалось об использовании ПОИ для производства материалов, основанных на фуллеренах. ПОИ может использоваться в устройствах для накачки газовых лазеров [54]. ПОИ представляет значительный интерес как физический объект с необычными волновыми свойствами. В бесстолкновительной ПОИ можно наблюдать солитоны и бесстолкновительные ударные волны, причем не только сжатия, но и разрежения. Цитируемые выше работы как раз посвящены исследованию нелинейных явлений в ПОИ. Заметим, что даже если реальная плазма состоит из нескольких сортов ионов, во многих случаях доминирующими являются только один сорт положительных ионов и только один сорт отрицательных ионов. В таких случаях использование модели трехкомпонентной плазмы может быть вполне приемлемым [40–44, 48–50].
В настоящее время основное внимание исследователей продолжает привлекать процесс взаимодействия между уединенными волнами. Встречные и обгонные столкновения уединенных волн изучаются достаточно давно [1, 6, 9, 25, 26, 40–42, 46]. В современных исследованиях уединенных волн и их взаимодействия между собой используются новые подходы [19, 24, 37], исследуются случаи с немаксвелловским распределением электронов [16, 20] или рассматриваются столкновения уединенных волн больших амплитуд [19, 22, 55–58].
Практически любая задача об уединенных волнах в плазме начинается с решения уравнений, определяющих форму волны, или с формирования волны, имеющей определенную заранее заданную форму, найденную из тех или иных предположений. Форма является одним из главных элементов, характеризующих уединенную волну. Как правило, она однозначно определяется амплитудой волны при заданных параметрах плазмы. Форма волны, а также скорость ее распространения, при заданной амплитуде могут быть определены из решения полной системы уравнений, описывающих движение плазмы, дополненных соответствующими начальными и граничными условиями. Поэтому при создании уединенной волны необходимо, чтобы ее характеристики: амплитуда, скорость распространения и форма, все вместе, соответствовали такому решению. Только в таком случае волна в дальнейшем распространяется устойчиво без каких-либо изменений. Попытка образовать уединенную волну, создавая структуру, которая не соответствует решению полной системы уравнений, приведет к распаду структуры. В процессе эволюции из нее может выделиться уединенная волна. При этом амплитуда, скорость распространения и форма первоначальной структуры изменятся таким образом, чтобы в конечном итоге они, все вместе, соответствовали бы некоторому решению полной системы уравнений. Строго говоря, единого решения, единой формулы, которая могла бы описывать форму всех уединенных волн в плазме, нет.
Полная система уравнений, описывающих плазму, достаточно сложна, и для ее решения приходится прибегать к численным методам и описывать профиль уединенной волны численным решением. Вместе с тем, если амплитуда волны достаточно мала, то исходная система уравнений может быть упрощена. В ряде случаев решение упрощенной системы уравнений может быть представлено в аналитическом виде, описывающем некоторый определенный класс солитонов. При этом форма солитона, в частности, его ширина, определенная тем или иным образом, оказывается однозначно зависимой от амплитуды.
Наиболее распространенным является прием, при котором полную систему уравнений упрощают таким образом, чтобы получить уравнение Кортевега–де Вриза (КдВ) [4, 8, 10–13, 16, 19–21, 31–37]. Это уравнение может быть решено аналитически. Аналитические решения уравнения КдВ удобны для изучения различных задач о солитонах. В частности, при численных исследованиях эволюции солитона или взаимодействия между солитонами их начальный профиль устанавливают по аналитической формуле, более всего соответствующей рассматриваемой задаче [17, 19–22]. Строго говоря, при таком подходе исследуются свойства и поведение солитонов КдВ и принимается, что полученные результаты могут приближенно описывать и солитоны в плазме.
Однако в ряде случаев при формировании уединенных волн используются аналитические формулы даже тогда, когда условие малости амплитуды не соблюдается [22]. Иногда при создании начальной структуры просто создают начальное возмущение плотности частиц, например, гауссовское [18, 23, 51]. Очевидно, что в таких случаях создается структура, которая не является уединенной волной, и она не всегда может эволюционировать с течением времени так, что возникнет уединенная волна. Эволюция произвольных начальных возмущений разного рода подробно исследовалась [5, 9, 27, 59]. Как правило, если уединенная волна и образуется, то этот процесс может занять достаточно большое время. В частности, потребуется время, чтобы формирующаяся сверхзвуковая уединенная волна оторвалась от возникающего за ней осцилляторного следа. Кроме того, не только форма, но также амплитуда и скорость распространения образовавшейся волны заметно изменятся по сравнению с первоначально заданными амплитудой и скоростью [22]. Очевидно, что такая ситуация затрудняет исследование. Например, при численном изучении столкновений уединенных волн как расчетная область, так и время расчета должны быть существенно увеличены для того, чтобы исследовалось столкновение образовавшихся с течением времени уединенных волн, а не столкновение произвольно заданных структур.
Самый прямой способ избежать подобных проблем состоит в том, чтобы находить профиль уединенной волны из решения полной системы уравнений, описывающих плазму, а не использовать решение упрощенных уравнений или произвольно заданную форму. Нахождение такого решения в ряде случаев может быть сведено к численному решению уравнения Пуассона (см., например, [60]). В настоящей статье предлагается метод получения численного решения для нахождения профиля уединенной волны в трехкомпонентной ПОИ и, как частный случай, в двухкомпонентной ЭИП. На самом деле, этот метод может быть достаточно просто обобщен и на случай плазмы более сложного состава.
Отметим, что предлагаемый метод многократно использовался автором при изучении столкновений уединенных волн [55–58] и при изучении прохождения уединенной волны через границу между ЭИП и ПОИ [61]. Исследования выполнялись с помощью метода частиц в ячейке для уединенных волн больших амплитуд, в том числе, амплитуд, близких к критическим амплитудам. Начальное состояние уединенной волны задавалось в соответствии с получеными численными решениями с помощью соответствующего подбора координат и скоростей частиц. В дальнейшем созданная таким образом уединенная волна распространялась по невозмущенной плазме без каких либо изменений ее амплитуды, скорости распространения и формы вплоть до столкновения с другой уединенной волной или с каким либо препятствием.
Во многих случаях при выводе аналитических формул для профиля уединенной волны используют редуктивный метод возмущений, с помощью которого из исходной системы уравнений получают уравнение КдВ для члена первого порядка в разложении по малому параметру и ограничиваются нахождением его решения. Вместе с тем, для нахождения решения при малых амплитудах нет необходимости непременно получать уравнение КдВ. В частности, можно воспользоваться обычным подходом, при котором исходные уравнения разлагаются по малым величинам, и в конечном итоге решается упрощенное уравнение Пуассона. В этой работе показано, что при таком подходе в случае ПОИ можно получить упрощенное уравнение Пуассона, в котором учтены члены до четвертого порядка малости включительно. Решение такого уравнения можно представить в удобном аналитическом виде. Чтобы оценить, насколько полученные новые формулы для профилей уединенной волны сжатия (УВС) и уединенной волны разрежения (УВР) лучше или хуже известных формул, мы сравниваем рассчитанные по разным формулам профили уединенных волн не очень большой амплитуды как между собой, так и с профилями уединенных волн, рассчитанными с помощью численного решения полной системы уравнений. Проведенное сравнение показывает, что профили, рассчитанные по полученным здесь формулам, отклоняются от решений полной системы уравнений меньше, чем профили, рассчитанные по известным формулам.
В данной работе представлен метод для численного расчета профиля уединенной волны в ПОИ и в ЭИП, а также предложены новые формулы для аналитического описания профиля уединенной волны при малых амплитудах в таких плазмах.
2. ОСНОВНЫЕ УРАВНЕНИЯ И МЕТОД ИХ РЕШЕНИЯ
В данной статье изучается распространение уединенной волны в бесстолкновительной трехкомпонентной ПОИ, электроны которой распределены по закону Больцмана. Как и в цитируемых выше работах, задача рассматривается в одномерном приближении. В таких задачах имеется физически выделенное направление, направление сверхзвукового распространения волны. В таких условиях можно ожидать, что влияние неодномерности будет мало, и это подтверждает многолетний опыт исследований уединенных волн в плазме. Было показано, что основные свойства, особенности и закономерности распространения и взаимодействия уединенных волн, наблюдаемые в экспериментах, очень хорошо согласуются с теоретическими положениями, полученными в одномерном приближении. С теорией сравнивались результаты экспериментов в ЭИП [25, 26, 28] и в ПОИ [40–44, 46–48, 51]. Сравнения с теорией проводились как для УВС, так и для УВР, при разных соотношениях плотностей отрицательных и положительных ионов, при разных соотношениях ионных масс и на разных устройствах с разными характерными продольным и поперечным размерами исследуемой области. Согласие теории и эксперимента служит косвенным подтверждением актуальности таких теоретических исследований.
Движения бесстолкновительной плазмы описываются системой уравнений Власова. Во многих случаях, когда температуры ионов не очень велики, для описания процессов в плазме можно использовать более простой подход, основанный на системе уравнений для моментов функций распределения. Соответствующая замкнутая система уравнений в приближении трех моментов [62] может быть выведена в предположении, что тепловыми потоками ионов можно пренебречь. В безразмерном виде такая система уравнений записывается следующим образом:
(1)
$\begin{gathered} \frac{{\partial {{n}_{j}}}}{{\partial t}} + {{V}_{j}}\frac{{\partial {{n}_{j}}}}{{\partial x}} + {{n}_{j}}\frac{{\partial {{V}_{j}}}}{{\partial x}} = 0, \\ \frac{{\partial {{V}_{j}}}}{{\partial t}} + {{V}_{j}}\frac{{\partial {{V}_{j}}}}{{\partial x}} + \frac{1}{{{{m}_{j}}{{n}_{j}}}}\frac{\partial }{{\partial x}}({{n}_{j}}{{T}_{j}}) + \mu \frac{{\partial \varphi }}{{\partial x}} = 0, \\ \end{gathered} $При обезразмеривании использовались следующие величины
(2)
$\begin{gathered} {{m}_{i}},\quad {{n}_{{i0}}},\quad {{Z}_{i}}{{T}_{{e0}}},\quad {{({{m}_{i}}{\text{/}}4\pi {{Z}_{i}}{{e}^{2}}{{n}_{{i0}}})}^{{1/2}}}, \\ {{({{T}_{{e0}}}{\text{/}}4\pi {{e}^{2}}{{n}_{{i0}}})}^{{1/2}}},\quad {{({{Z}_{i}}{{T}_{{e0}}}{\text{/}}{{m}_{i}})}^{{1/2}}},\quad {{T}_{{e0}}}{\text{/}}e, \\ \end{gathered} $Условие квазинейтральности в невозмущенной области запишется в виде
Мы будем рассматривать волну, распространяющуюся стационарно. В системе отсчета волны все величины зависят от одной переменной $z = x - Dt$, где D – скорость распространения волны. Поэтому при замене переменных дифференциальные уравнения (1) становятся обыкновенными дифференциальными уравнениями, из которых первые четыре уравнения можно свести к алгебраическим уравнениям
(5)
$\begin{gathered} \, = \frac{1}{2}{{\left( {D - {{V}_{{i0}}}} \right)}^{2}} + {{\varphi }_{0}} + \frac{3}{2}{{T}_{{i0}}}, \\ {{n}_{j}}\left( {D - {{V}_{j}}} \right) = {{n}_{{j0}}}\left( {D - {{V}_{{j0}}}} \right), \\ \end{gathered} $Здесь и ниже в формулах для удобства чтения мы сохранили равную единице величину ${{n}_{{i0}}}$. В уравнениях (5) слева стоят величины в произвольной точке z, а справа стоят величины в точке ${{z}_{0}}$, находящейся в невозмущенной области с невозмущенными значениями потенциала ${{\varphi }_{0}}$, плотностей ${{n}_{{i0}}}$ и ${{n}_{{j0}}}$ и потоковых скоростей ионов ${{V}_{{i0}}}$ и ${{V}_{{j0}}}$. Для простоты положим ${{V}_{{i0}}} = {{V}_{{j0}}} = 0$ и, как мы условились выше, ${{\varphi }_{0}} = 0$. Тогда из (5) при заданном D можно найти значения величин в произвольной точке $z$:
(6)
$\begin{gathered} {{V}_{i}} = D - D{{\left[ {\frac{{2{{\theta }_{i}}}}{{1 + {{\theta }_{i}} - \psi - \sqrt {{{{(1 + {{\theta }_{i}} - \psi )}}^{2}} - 4{{\theta }_{i}}} }}} \right]}^{{1/2}}}, \\ {{n}_{j}} = {{n}_{{j0}}}{{\left( {2{{\theta }_{j}}} \right)}^{{ - 1/2}}} \times \\ \, \times {{\left[ {1 + {{\theta }_{j}} - \mu \psi - \sqrt {{{{(1 + {{\theta }_{j}} - \mu \psi )}}^{2}} - 4{{\theta }_{j}}} } \right]}^{{1/2}}}, \\ \end{gathered} $Здесь мы перенормировали потенциал φ, вводя величину ψ, использование которой упрощает формулы.
В предельном случае плазмы с холодными ионами ${{\theta }_{i}} \to 0$ и ${{\theta }_{j}} \to 0$ получаем следующие зависимости:
(7)
$\begin{gathered} {{n}_{i}} = {{n}_{{i0}}}{{\left( {1 - \psi } \right)}^{{ - 1/2}}},\quad {{V}_{i}} = D(1 - \sqrt {1 - \psi )} , \\ {{n}_{j}} = {{n}_{{j0}}}{{(1 - \mu \psi )}^{{ - 1/2}}},\quad {{V}_{j}} = D(1 - \sqrt {1 - \mu \psi } ). \\ \end{gathered} $В (6) и (7) ионные плотности представлены в виде функций от ψ. Обозначим эти функции для краткости через ${{n}_{i}}(\psi )$ и ${{n}_{j}}(\psi )$ и подставим их в уравнение Пуассона. Получим уравнение для функции $\psi (z)$
(8)
$\frac{{{{d}^{2}}\psi }}{{d{{z}^{2}}}} = \frac{1}{\kappa }\left[ {{{n}_{{e0}}}\exp (\kappa \psi ) - {{Z}_{i}}{{n}_{i}}(\psi ) - {{Z}_{j}}{{n}_{j}}(\psi )} \right].$Домножим это уравнение на $d\psi {\text{/}}dz$ и проинтегрируем его по z от точки ${{z}_{0}}$ в невозмущенной области до текущего значения z, имея в виду, что в точке ${{z}_{0}}$ как значение величины $\psi $, так и ее первая производная из-за однородности невозмущенной области равны нулю:
(9)
$\psi {{{\text{|}}}_{{z = {{z}_{0}}}}} = 0,\quad {{\left. {\frac{{d\psi }}{{dz}}} \right|}_{{z = {{z}_{0}}}}} = 0.$В результате получим
где(11)
$\begin{gathered} \mathcal{K}(\psi ) = \frac{{{{Z}_{i}}{{n}_{{i0}}}}}{{{{\kappa }^{2}}}} \times \\ \, \times \left\{ {(1 + \rho )\left[ {\exp (\kappa \psi ) - 1} \right] - \kappa [{{\mathcal{N}}_{i}}(\psi ) + {{\mathcal{N}}_{j}}(\psi )]} \right\}, \\ \end{gathered} $(12)
$\begin{gathered} {{\mathcal{N}}_{j}}(\psi ) = \rho \int\limits_0^\psi \frac{{{{n}_{j}}(\xi )}}{{{{n}_{{j0}}}}}d\xi = \\ \, = 2\frac{\rho }{\mu }\left[ {1 + \frac{1}{3}{{\theta }_{j}} - \frac{1}{{3\sqrt {2{{\theta }_{j}}} }}\Upsilon ({{\theta }_{j}},\mu \psi )} \right]. \\ \end{gathered} $Здесь мы ввели величину $\rho = {{Z}_{j}}{{n}_{{j0}}}{\text{/}}{{Z}_{i}}{{n}_{{i0}}}$ и функцию
В случае холодных ионов ${{\theta }_{i}} = 0$ и ${{\theta }_{j}} = 0$ выражения для ${{\mathcal{N}}_{i}}(\psi )$ и ${{\mathcal{N}}_{j}}(\psi )$ упрощаются:
(13)
$\begin{gathered} {{\mathcal{N}}_{i}}(\psi ) = 2\left( {1 - \sqrt {1 - \psi } } \right), \\ {{\mathcal{N}}_{j}}(\psi ) = 2{\kern 1pt} \frac{\rho }{\mu }\left( {1 - \sqrt {1 - \mu \psi } } \right). \\ \end{gathered} $Таким образом, задача сводится к решению уравнения Пуассона при условии (9). Решение описывает уединенную волну, поскольку на фазовой плоскости $(\psi ,\;d\psi {\text{/}}dz)$ при этом условии оно соответствует сепаратрисе, которая отделяет финитное движение от инфинитного.
Разделяя переменные в (10), проведем интегрирование по z от точки экстремума в профиле волны ${{z}_{m}} = {{x}_{m}} - Dt$ до произвольного $z = x - Dt$. Величина ${{z}_{m}}$ может быть принята равной нулю, если считать, что мы определяем профиль волны в начальный момент времени $t = 0$ и при этом амплитуда находится в точке ${{x}_{m}} = 0$. Величина ψ при интегрировании меняется от экстремального значения ${{\psi }_{m}}$ до соответствующего значения $\psi (z)$. В результате получим решение, которое представляет собой неявную зависимость ψ от координаты z
(14)
$ \pm \sqrt 2 z = \int\limits_{{{\psi }_{m}}}^\psi \frac{{d\xi }}{{{{{[\mathcal{K}(\xi )]}}^{{1/2}}}}}.$Для расчета профиля уединенной волны задание только амплитуды волны ${{\psi }_{m}}$ (или ${{\varphi }_{m}}$) недостаточно. Необходимо еще задать соответствующее значение ее скорости распространения D. Из уравнения (10) легко видеть, что связь между этими двумя величинами устанавливает уравнение
В общем случае произвольных ионных температур подробная запись уравнения (15) довольно громоздка. В случае плазмы с холодными ионами ${{\theta }_{i}} = {{\theta }_{j}} = 0$, который мы и будем далее рассматривать, это уравнение приобретает вид
(16)
$\begin{gathered} (1 + \rho )\left[ {\exp (\kappa {{\psi }_{m}}) - 1} \right] - \\ \, - 2\kappa \left[ {1 - \sqrt {1 - {{\psi }_{m}}} + \frac{\rho }{\mu }\left( {1 - \sqrt {1 - \mu {{\psi }_{m}}} } \right)} \right] = 0. \\ \end{gathered} $Численное решение (16) дает зависимость κ = $ = \kappa ({{\psi }_{m}})$ (или $D = D({{\psi }_{m}})$), зная которую можно определить амплитуды потоковых скоростей ионов по формулам (7), а также найти решение (14).
Формула (14) может быть использована для вычисления профиля уединенной волны в ПОИ, причем как для УВС, так и для УВР. Она представляет собой обобщение аналогичной формулы для профиля уединенной волны в ЭИП [63, 64] на случай ПОИ. Поэтому для расчетов по формуле (14) можно применить метод вычисления несобственного интеграла, предложенный в [63, 64]. Особенность в интеграле (14) имеется на нижнем пределе интегрирования в соответствии с (15). Численное интегрирование выражений, подобных (14), как правило, не представляет труда. В [63, 64] было предложено выделить особенность в малой области и вычислить интеграл по этой области аналитически с любой требуемой точностью, а по оставшейся области, не содержащей особенности, провести интегрирование стандартным методом. Для рассматриваемого интеграла (14) можно получить соотношение
(17)
$\begin{gathered} \int\limits_{{{\psi }_{m}}}^\psi \frac{{d\xi }}{{{{{[\mathcal{K}(\xi )]}}^{{1/2}}}}} = \int\limits_{{{\psi }_{m}} + \Delta \psi }^\psi \frac{{d\xi }}{{{{{[\mathcal{K}(\xi )]}}^{{1/2}}}}} + 2{{\left[ {\frac{{\Delta \psi }}{{\mathcal{K}{\kern 1pt} '({{\psi }_{m}})}}} \right]}^{{1/2}}} - \\ \, - \frac{1}{6}\mathcal{K}{\kern 1pt} '{\kern 1pt} '({{\psi }_{m}}){{\left[ {\frac{{\Delta \psi }}{{\mathcal{K}{\kern 1pt} '({{\psi }_{m}})}}} \right]}^{{3/2}}}, \\ \end{gathered} $После того, как рассчитан профиль $\psi (z)$, профили ионных плотностей и скоростей можно легко найти по формулам (6) в общем случае или по формулам (7) в случае плазмы с холодными ионами.
Описанный метод мы будем использовать для численного расчета профиля уединенной волны, и именно с таким профилем мы будем сравнивать профили уединенных волн, рассчитанные по рассматриваемым ниже аналитическим формулам.
3. АМПЛИТУДНЫЙ ДИАПАЗОН УЕДИНЕННЫХ ВОЛН В ПОИ
Как известно, уединенные волны в ЭИП могут существовать только в ограниченном диапазоне амплитуд [3]. Рассмотрим вопрос о диапазоне возможных амплитуд в ПОИ. Очевидно, уединенная волна в плазме с холодными ионами может существовать, если существует решение уравнения (16), определяющего связь между амплитудой ${{\psi }_{m}}$ и величиной $\kappa = \kappa ({{\psi }_{m}})$ (или между амплитудой потенциала ${{\varphi }_{m}}$ и скоростью распространения $D = D({{\varphi }_{m}})$).
Уравнение (16) содержит квадратные корни из выражений, в которые входит амплитуда волны ${{\psi }_{m}}$. Подкоренные выражения не должны принимать отрицательные значения. Поэтому амплитуда УВС $\psi _{m}^{ + } > 0$ не должна превосходить значение $\psi _{{cr}}^{ + } = 1$, которое принято называть критическим [3], а амплитуда УВР $\psi _{m}^{ - } < 0$ не должна опускаться ниже критического значения $\psi _{{cr}}^{ - } = 1{\text{/}}\mu < 0$. Зная параметры плазмы ρ и μ и решая уравнение (16) при заданных критических амплитудах $\psi _{{cr}}^{ + }$ и $\psi _{{cr}}^{ - }$, можно определить соответствующие критические значения величины $\kappa $: $\kappa _{{cr}}^{ + }$ и $\kappa _{{cr}}^{ - }$, критические амплитуды потенциала $\varphi _{{cr}}^{ + }$ и $\varphi _{{cr}}^{ - }$, а также критические значения остальных величин.
С другой стороны, скорость распространения уединенной волны D не может быть ниже скорости звука, которая в ПОИ с холодными ионами имеет вид
В предельном случае $D \to {{c}_{0}}$ амплитуда потенциала ${{\varphi }_{m}} = \kappa {{\psi }_{m}}$ принимает минимально (максимально) возможное для УВС (УВР) значение $\varphi _{s}^{ + }$ ($\varphi _{s}^{ - }$), которое не всегда оказывается равным нулю. Это значение можно найти из решения того же уравнения (16) при заданном $\kappa = (1{\text{/}}2)c_{0}^{2}$. Таким образом, амплитуда потенциала должна находиться в пределах между значением $\varphi _{s}^{ + }$ и критическим значением $\varphi _{{cr}}^{ + }$ для УВС или значением $\varphi _{s}^{ - }$ и критическим значением $\varphi _{{cr}}^{ - }$ для УВР.
Представление о том, как выглядит область допустимых амплитуд потенциала в широком диапазоне значений ${{n}_{{j0}}}$, дает рис. 1, где эти области построены для двух случаев, часто встречающихся в экспериментах: в первом случае плазма содержит, кроме электронов, ионы ${\text{A}}{{{\text{r}}}^{ + }}$ и ${{{\text{F}}}^{ - }}$ (${{m}_{j}} = 0.476$, $\mu = - 2.102$), во втором случае ионные компоненты состоят из ${\text{A}}{{{\text{r}}}^{ + }}$ и ${\text{SF}}_{6}^{ - }$ (${{m}_{j}} = 3.657$, $\mu = - 0.273$). Отметим, что подобные рисунки областей существования уединенных волн в ПОИ впервые были представлены в работах [43, 44], где также содержатся соответствующие экспериментальные подтверждения. Из рисунка видно, что при плотностях отрицательных ионов, меньших некоторого определенного значения ${{n}_{{j0}}} = n_{{j0}}^{*}$, область допустимых амплитуд УВС простирается от нуля до критического значения $\varphi _{{cr}}^{ + }$, а УВР либо вообще не существуют при малых ${{n}_{{j0}}}$, либо диапазон их допустимых амплитуд начинается не с нуля, а с некоторого не равного нулю значения. Иными словами, УВР как угодно малой амплитуды не существуют при ${{n}_{{j0}}} < n_{{j0}}^{*}$. Однако при ${{n}_{{j0}}} > n_{{j0}}^{*}$ ситуация меняется на противоположную. Теперь УВР имеют диапазон допустимых амплитуд, простирающийся от нуля до критического значения. А УВС не могут иметь как угодно малую амплитуду. Они либо имеют диапазон амплитуд, начинающейся не с нуля, а с некоторого не равного нулю значения, либо вообще не существуют при больших ${{n}_{{j0}}}$. Плотность ${{n}_{{j0}}} = n_{{j0}}^{*}$ является границей между двумя областями значений ${{n}_{{j0}}}$, при которых в одной области существуют УВС, а в другой – УВР, причем речь идет о волнах, амплитуды которых могут быть как угодно малыми11. На самой границе ${{n}_{{j0}}} = n_{{j0}}^{*}$ оба диапазона допустимых амплитуд УВС и УВР простираются от нуля до соответствующего критического значения, и существует непрерывный переход от положительных амплитуд к отрицательным. Эти особенности существования УВС и УВР малых амплитуд в разных областях значений ${{n}_{{j0}}}$ должны учитываться при аналитических исследованиях профиля уединенной волны.
Рис. 1.
Области допустимых амплитуд уединенных волн на плоскости $({{n}_{{j0}}},{{\varphi }_{m}})$: $CW$ – область УВС, $RW$ – область УВР. $\varphi _{{cr}}^{ + }$ представлено толстыми сплошными кривыми, $\varphi _{{cr}}^{ - }$ – толстыми штриховыми кривыми. $\varphi _{s}^{ + }$ показано штриховыми кривыми, $\varphi _{s}^{ - }$ – пунктирными кривыми. Стрелками указаны точки соединения областей УВС и УВР при ${{n}_{{j0}}} = n_{{j0}}^{*}$: ${{m}_{j}} = 0.476$ (a), ${{m}_{j}} = 3.657$ (б).

4. УЕДИНЕННЫЕ ВОЛНЫ МАЛЫХ АМПЛИТУД
4.1. Формулы профилей уединенных волн
Для последующего сравнения с нашими результатами здесь уместно кратко напомнить хорошо известные аналитические решения для описания профиля уединенных волн при малых амплитудах и записать эти решения в наших единицах.
По-видимому, впервые аналитическое выражение для профиля уединенной волны было представлено в работах [2, 3] для случая ЭИП с холодными ионами. Это выражение было выведено для уединенных волн малых амплитуд с помощью разложения до членов третьего порядка включительно, и была получена формула для профиля потенциала $\phi = \phi (x - Dt)$
(19)
$\begin{gathered} \phi = \frac{{3{{D}^{4}}}}{{3 - {{D}^{4}}}}\left( {1 - \frac{1}{{{{D}^{2}}}}} \right)\;{{ \times }} \\ {{ \times }}\;{\text{sec}}{{{\text{h}}}^{2}}\left[ {\frac{1}{2}{{{\left( {1 - \frac{1}{{{{D}^{2}}}}} \right)}}^{{1/2}}}(x - Dt)} \right]. \\ \end{gathered} $Здесь и ниже мы выделяем случай ЭИП с помощью замены обозначения потенциала φ на ϕ.
Что касается уединенных волн в ПОИ, а также в других плазмах сложного состава, то для нахождения их профилей, как правило, используется редуктивный метод возмущений. В этом методе плотности и потоковые скорости частиц, а также потенциал разлагаются по степеням малого параметра ϵ, а исходные уравнения преобразуются к новым переменным. Эти переменные выбираются таким образом, чтобы исходная система уравнений после приравнивания коэффициентов при одинаковых степенях $\epsilon $ преобразовалась в систему уравнений, в которой уравнение для возмущения потенциала первого порядка оказывается уравнением КдВ. В частности, для трехкомпонентной плазмы с отрицательными ионами было предложено использовать переменные
где C – некоторая скорость. После преобразований было получено, что $C$ должно равняться скорости звука ${{c}_{0}}$, определяемой по (18), и найдено уравнение для возмущения потенциала первого порядка ${{\varphi }_{1}}$ [31](20)
$\frac{{\partial {{\varphi }_{1}}}}{{\partial \tau }} + A{{\varphi }_{1}}\frac{{\partial {{\varphi }_{1}}}}{{\partial \xi }} + B\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{\xi }^{3}}}} = 0.$Постоянные коэффициенты A и B в наших единицах имеют вид
(21)
$A = - \frac{{{{c}_{0}}}}{2} + \frac{{3({{Z}_{i}}{{n}_{{i0}}} + {{\mu }^{2}}{{Z}_{j}}{{n}_{{j0}}})}}{{2{{n}_{{e0}}}c_{0}^{3}}},\quad B = \frac{{{{c}_{0}}}}{{2{{n}_{{e0}}}}},$Находя стационарное решение уравнения (20) и обозначая амплитуду потенциала уединенной волны через $\varphi _{m}^{{(n)}}$, можно получить выражение для профиля потенциала уединенной волны ${{\varphi }^{{(n)}}}$ в ПОИ и выражение, определяющее связь между амплитудой и скоростью распространения уединенной волны. После преобразования к исходным переменным эти выражения имеют вид
(22a)
${{\varphi }^{{(n)}}} = \varphi _{m}^{{(n)}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{{\left( {\frac{{A\varphi _{m}^{{(n)}}}}{{12B}}} \right)}}^{{1/2}}}(x - Dt)} \right],$Формулы (22) упрощаются в частном случае ЭИП. Подставим в (22) соответствующие значения величин в ЭИП: ${{n}_{{e0}}} = 1,$ ${{c}_{0}} = 1,$ $A = 1,$ $B = 1{\text{/}}2$. В результате получим
(23a)
$\phi = {{\phi }_{m}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{{\left( {\frac{{{{\phi }_{m}}}}{6}} \right)}}^{{1/2}}}(x - Dt])} \right],$Коэффициент $A$ в уравнении (20) может принимать как положительные, так и отрицательные значения, а также может быть равным нулю. Из (22a) видно, что при $A > 0$ амплитуда потенциала $\varphi _{m}^{{(n)}}$ должна быть положительной, а при $A < 0$ – отрицательной. Если же коэффициент $A$ равен нулю, то в уравнении (20) исчезает нелинейный член, и поэтому не может быть баланса между нелинейностью и дисперсией, а это означает, что решение уравнения не может иметь вид уединенной волны. На самом деле уединенная волна может существовать и в этом случае, но она описывается другим уравнением. В частности, было предложено рассмотреть член следующего порядка, чтобы учесть нелинейность для данного конкретного случая. Используя редуктивный метод возмущений с несколько иной заменой переменных $\xi = \epsilon (x - Ct),$ $\tau = {{\epsilon }^{3}}t$ в исходных уравнениях и используя условие $A = 0$, можно получить модифицированное уравнение КдВ для возмущения потенциала первого порядка (см., например, [33, 47, 49])
(24)
$\frac{{\partial {{\varphi }_{1}}}}{{\partial \tau }} + {{A}_{m}}\varphi _{1}^{2}\frac{{\partial {{\varphi }_{1}}}}{{\partial \xi }} + {{B}_{m}}\frac{{{{\partial }^{3}}{{\varphi }_{1}}}}{{\partial {{\xi }^{3}}}} = 0,$(25)
${{A}_{m}} = - \frac{{{{c}_{0}}}}{4} + \frac{{15({{Z}_{i}}{{n}_{{i0}}} + {{\mu }^{3}}{{Z}_{j}}{{n}_{{j0}}})}}{{4{{n}_{{e0}}}c_{0}^{5}}},\quad {{B}_{m}} = \frac{{{{c}_{0}}}}{{2{{n}_{{e0}}}}}.$Найдя стационарное решение этого уравнения и вводя амплитуду уединенной волны $\varphi _{m}^{{(m)}}$, можно записать формулу для профиля потенциала уединенной волны ${{\varphi }^{{(m)}}}$
(26a)
${{\varphi }^{{(m)}}} = \pm \varphi _{m}^{{(m)}}{\text{sech}}\left[ {{{{\left( {\frac{{{{A}_{m}}{{{(\varphi _{m}^{{(m)}})}}^{2}}}}{{6{{B}_{m}}}}} \right)}}^{{1/2}}}(x - Dt)} \right],$Записанные здесь в наших единицах известные формулы для профиля потенциала уединенной волны будем использовать ниже для сравнения с предлагаемыми новыми формулами.
4.2. Профили уединенных волн малой амплитуды
4.2.1. Разложение $\mathcal{K}(\psi {\mathbf{)}}$ по степеням ψ. Задача о нахождении профиля уединенной волны, по сути дела, сводится к задаче о решении нелинейного уравнения Пуассона (10)–(11). Запишем это уравнение для случая уединенных волн малых амплитуд, распространяющихся в плазме с холодными ионами. Для этого разложим выражение $\mathcal{K}(\psi )$, определяемое по формулам (11) и (13), по степеням ψ и сохраним члены до 4-го порядка малости включительно. Получим
(27)
$\mathcal{K}(\psi ) = \frac{{{{Z}_{i}}{{n}_{{i0}}}}}{{2\kappa }}{{\psi }^{2}}\left( {{{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}}} \right),$Видно, что все коэффициенты ${{a}_{i}}$ определяются скоростью распространения волны D, а также характеризующими ионный состав величинами μ и ρ. От значения последних зависит скорость звука ${{c}_{0}}$ и значения введенных здесь скоростей ${{c}_{1}}$ и ${{c}_{2}}$:
(29)
${{c}_{1}} = {{\left[ {\frac{{3(1 + \rho {{\mu }^{2}})}}{{1 + \rho }}} \right]}^{{1/4}}},\quad {{c}_{2}} = {{\left[ {\frac{{15(1 + \rho {{\mu }^{3}})}}{{1 + \rho }}} \right]}^{{1/6}}}.$Эти скорости, как и скорость звука ${{c}_{0}}$, являются характеристиками ионного состава плазмы. Анализируя их зависимости от невозмущенной плотности отрицательных ионов ${{n}_{{j0}}}$, можно определить возможные знаки коэффициентов ${{a}_{i}}$ и, тем самым, возможные типы уединенных волн. Такие зависимости для рассматриваемых здесь плазм представлены на рис. 2.
Рис. 2.
Зависимости скоростей ${{c}_{0}}$, ${{c}_{1}}$ и ${{c}_{2}}$ от невозмущенной плотности отрицательных ионов ${{n}_{{j0}}}$: ${{m}_{j}} = 0.476$ (a), ${{m}_{j}} = 3.657$ (б).

Прежде всего, заметим, что, поскольку скорость распространения уединенной волны $D > {{c}_{0}}$, коэффициент ${{a}_{0}} > 0$ всегда. Область существования уединенных волн на рис. 2 находится выше кривой ${{c}_{0}}({{n}_{{j0}}})$. При этом скорость D уединенных волн малых амплитуд не должна быть намного больше скорости звука ${{c}_{0}}$. В таком случае, как видно из рисунка, скорость $D < {{c}_{2}}$, и, следовательно, коэффициент ${{a}_{2}} < 0$. Исключение составляют редко реализуемые случаи, когда невозмущенная плотность отрицательных ионов имеет довольно большое значение в диапазоне $0.67 < {{n}_{{j0}}} < 0.79$ при ${{m}_{j}} = 3.657,$ $\mu = - 0.273$, и тогда ${{a}_{2}} > 0$.
Что касается коэффициента ${{a}_{1}}$, то его знак зависит от того, какая из скоростей, $D$ или ${{c}_{1}}$, больше. Из (28) можно видеть, что при ${{c}_{1}} > D > {{c}_{0}}$ коэффициент ${{a}_{1}} < 0$. При $D > {{c}_{1}}$, в том числе и после точки пересечения кривых ${{c}_{0}}({{n}_{{j0}}})$ и ${{c}_{1}}({{n}_{{j0}}})$ на рис. 2, т.е. при $D > {{c}_{0}} > {{c}_{1}}$ коэффициент ${{a}_{1}} > 0$. И, наконец, при $D = {{c}_{1}}$, т.е. на кривой ${{c}_{1}}({{n}_{{j0}}})$, коэффициент ${{a}_{1}} = 0$.
При дальнейшем рассмотрении мы будем считать, что коэффициенты ${{a}_{0}} > 0$ и ${{a}_{2}} < 0$ всегда. Какую роль играет знак коэффициента ${{a}_{1}}$, можно понять при рассмотрении возможных амплитуд уединенной волны. В общем случае произвольных амплитуд последние должны удовлетворять уравнению (15). В рассматриваемом здесь случае малых амплитуд это уравнение можно записать в виде
Корни этого уравнения обозначим через $\psi _{m}^{ + }$ и $\psi _{m}^{ - }$:
(31)
$\psi _{m}^{ + } = - \frac{{\Delta + {{a}_{1}}}}{{2{{a}_{2}}}} > 0,\quad \psi _{m}^{ - } = \frac{{\Delta - {{a}_{1}}}}{{2{{a}_{2}}}} < 0,$Мы рассматриваем малые амплитуды, и в выражениях для $\psi _{m}^{ + }$ и $\psi _{m}^{ - }$ знак коэффициента ${{a}_{1}}$ должен быть таким, чтобы допускалась возможность как угодно малого значения для амплитуды. Очевидно, что $\psi _{m}^{ + }$ может быть как угодно мало только при ${{a}_{1}} < 0$, а $\psi _{m}^{ - }$ – только при ${{a}_{1}} > 0$. Таким образом, знак коэффициента ${{a}_{1}}$ определяет тип уединенной волны как угодно малой амплитуды. В случае ${{a}_{1}} < 0$ уединенная волна является УВС, а в случае ${{a}_{1}} > 0$ – УВР. Условие ${{a}_{1}} = 0$ определяет границу между областями существования УВС и УВР. Это условие может быть выполнено только для одной пары уединенных волн, УВС и УВР, с точно заданной скоростью распространения $D = {{c}_{1}}({{n}_{{j0}}})$, которая определяются плотностью отрицательных ионов в невозмущенной области ${{n}_{{j0}}}$ (величину μ считаем заданной). Сама граница ${{a}_{1}} = 0$ находится на кривой ${{c}_{1}}({{n}_{{j0}}})$ в широком диапазоне значений ${{n}_{{j0}}}$ от нуля до точки пересечения кривых ${{c}_{1}}({{n}_{{j0}}})$ и ${{c}_{0}}({{n}_{{j0}}})$ (выделенная точка на рис. 2). После этой точки пересечения для уединенных волн со скоростью распространения D, слегка превышающей скорость звука ${{c}_{0}}({{n}_{{j0}}})$, коэффициент ${{a}_{1}} > 0$, т.е. волны малых амплитуд должны быть волнами разрежения. Отсюда видно, что пересечение кривых ${{c}_{1}}({{n}_{{j0}}})$ и ${{c}_{0}}({{n}_{{j0}}})$ должно происходить при плотности, которая отделяет области существования УВС и УВР как угодно малых амплитуд. Ранее при обсуждении численных решений уравнения (16) на рис. 1 такая плотность была обозначена через $n_{{j0}}^{*}$. Теперь мы можем легко определить ее значение из уравнения ${{c}_{1}}(n_{{j0}}^{*}) = {{c}_{0}}(n_{{j0}}^{*})$:
(32)
$\begin{gathered} n_{{j0}}^{*} = \frac{{{{Z}_{i}}}}{{4{{Z}_{j}}{{\mu }^{2}}}} \times \\ \, \times \left\{ {2\mu - 3(1 + {{\mu }^{2}}) + \sqrt {{{{[3(1 + {{\mu }^{2}}) - 2\mu ]}}^{2}} - 16{{\mu }^{2}}} } \right\}. \\ \end{gathered} $Для рассматриваемых здесь случаев ${{m}_{j}} = 0.476,$ $\mu = - 2.102$ и ${{m}_{j}} = 3.657,$ $\mu = - 0.273$ при ${{Z}_{i}} = 1$ и ${{Z}_{j}} = - 1$ согласно (32) значения $n_{{j0}}^{*}$ равны 0.10225 и 0.54197 соответственно. Сравнение этих значений с теми значениями, которые были получены при численном расчете по формуле (16) (рис. 1), показывает их полное совпадение.
Как мы уже упоминали при обсуждении уравнения КдВ (20), знак коэффициента A совпадает со знаком амплитуды уединенной волны и, следовательно, значение $A = 0$ является еще одним условием, которое определяет границу между УВС и УВР. Очевидно, что это условие должно выполняться при ${{n}_{{j0}}} = n_{{j0}}^{*}$. Чтобы убедиться в этом, достаточно преобразовать выражение (21) для A к виду:
из которого при $A = 0$ следует полученное выше соотношение ${{c}_{1}} = {{c}_{0}}$, выполняющееся при ${{n}_{{j0}}} = n_{{j0}}^{*}$. Заметим, что формула (32) была получена ранее как раз из условия $A = 0$ (см., например, [47, 49]).4.2.2. Решение уравнения Пуассона. Рассмотрим уравнение Пуассона для случая уединенных волн малых амплитуд. Подставим разложение (27) величины $\mathcal{K}(\psi )$ в уравнение Пуассона (10):
(34)
${{\left( {\frac{{d\psi }}{{dz}}} \right)}^{2}} = \frac{{{{Z}_{i}}{{n}_{{i0}}}}}{\kappa }{\kern 1pt} {{\psi }^{2}}\left( {{{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}}} \right).$Разделяя переменные, запишем это уравнение в интегральном виде
(35)
$ \pm \sqrt {\frac{{{{Z}_{i}}{{n}_{{i0}}}}}{\kappa }} \int\limits_{{{z}_{m}}}^z dz = \int\limits_{{{\psi }_{m}}}^\psi \frac{{d\psi }}{{\psi \sqrt {{{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}}} }}.$Здесь, как и при выводе формулы (14), положим для простоты, что ${{z}_{m}} = 0$. Как было установлено, ${{a}_{0}} > 0$. Находя для этого случая интеграл в правой части (35), получим
(36)
$\begin{gathered} \mp \frac{1}{D}\sqrt {2{{Z}_{i}}{{n}_{{i0}}}{{a}_{0}}} z = \\ \, = \ln \left| {\frac{{2{{a}_{0}} + {{a}_{1}}\psi + 2\sqrt {{{a}_{0}}({{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}})} }}{\psi }} \right|_{{{{\psi }_{m}}}}^{\psi }. \\ \end{gathered} $Нетрудно установить, что числитель дроби, стоящей под знаком модуля в (36), всегда положительный, а сама дробь на нижнем пределе принимает значение $ \pm \Delta $, где знак плюс соответствует УВС, а знак минус – УВР. Из (36) можно видеть, что текущее значение величины ψ на верхнем пределе должно быть таким, чтобы ${{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}} \geqslant 0$. Решение этого неравенства при положительных ψ представляет собой диапазон значений ψ в УВС с амплитудой $\psi _{m}^{ + }$: $0 \leqslant \psi \leqslant \psi _{m}^{ + }$. Решение неравенства при отрицательных ψ дает диапазон значений ψ в УВР с амплитудой $\psi _{m}^{ - }$: $\psi _{m}^{ - } \leqslant \psi \leqslant 0$. С учетом этих замечаний перепишем уравнение (36) следующим образом:
(37)
$Y = \ln \frac{{2{{a}_{0}} + {{a}_{1}}\psi + 2\sqrt {{{a}_{0}}({{a}_{0}} + {{a}_{1}}\psi + {{a}_{2}}{{\psi }^{2}})} }}{{ \pm \Delta \psi }},$(38)
$\begin{gathered} Y = \mp \frac{1}{D}\sqrt {2{{Z}_{i}}{{n}_{{i0}}}{{a}_{0}}} z = \\ = \; \mp {{\left[ {{{n}_{{e0}}}\left( {1 - \frac{{c_{0}^{2}}}{{{{D}^{2}}}}} \right)} \right]}^{{1/2}}}(x - Dt). \\ \end{gathered} $Здесь мы для краткости записали уравнение одновременно для двух случаев. В первом случае в знаменателе дроби под знаком логарифма выбираем знак плюс, и тогда вся дробь при $\psi > 0$ будет положительной, что позволяет опустить знак модуля. Такое уравнение будет описывать распределение $\psi > 0$ в УВС. Во втором случае выбираем знак минус, и тогда вся дробь будет положительной при $\psi < 0$, т.е. уравнение будет описывать УВР.
Из уравнения (37) нетрудно найти обратную функцию $\psi (z)$ и получить выражения для профилей волн, которые обозначим через ${{\psi }^{ + }}$ для УВС и через ${{\psi }^{ - }}$ для УВР. Умножая эти профили на κ, получим профили потенциала φ, которые обозначим аналогичным образом через ${{\varphi }^{ + }}$ и ${{\varphi }^{ - }}$ для УВС и УВР соответственно. Профили имеют вид
(39)
${{\psi }^{ + }} = \frac{{2{{a}_{0}}}}{{\Delta {\text{ch}}(Y) - {{a}_{1}}}},\quad {{\varphi }^{ + }} = \frac{{6{{D}^{2}}({{D}^{2}} - c_{0}^{2})}}{{R{\text{ch}}(Y) - ({{D}^{4}} - c_{1}^{4})}},$(40)
$\begin{gathered} {{\psi }^{ - }} = - \frac{{2{{a}_{0}}}}{{\Delta {\text{ch}}(Y) + {{a}_{1}}}}, \\ {{\varphi }^{ - }} = - \frac{{6{{D}^{2}}({{D}^{2}} - c_{0}^{2})}}{{R{\text{ch}}(Y) + ({{D}^{4}} - c_{1}^{4})}}, \\ \end{gathered} $Из этих выражений для профилей уединенных волн следует, что амплитуды УВС и УВР должны быть соответственно равны
(41)
$\psi _{m}^{ + } = \frac{{2{{a}_{0}}}}{{\Delta - {{a}_{1}}}},\quad \varphi _{m}^{ + } = \frac{{6{{D}^{2}}({{D}^{2}} - c_{0}^{2})}}{{R - ({{D}^{4}} - c_{1}^{4})}},$(42)
$\psi _{m}^{ - } = - \frac{{2{{a}_{0}}}}{{\Delta + {{a}_{1}}}},\quad \varphi _{m}^{ - } = - \frac{{6{{D}^{2}}({{D}^{2}} - c_{0}^{2})}}{{R + ({{D}^{4}} - c_{1}^{4})}},$Рассмотрим более подробно случай ${{a}_{1}} = 0$, который определяет границу между областями существования УВС и УВР. Как мы уже упоминали, эта граница находится на кривой ${{c}_{1}}({{n}_{{j0}}})$, и здесь возможно существование только одной УВС и одной УВР, которые обе распространяются с точно заданной скоростью $D = {{c}_{1}}$, определяемой плотностью ${{n}_{{j0}}}$. Амплитуды этой пары волн можно найти из уравнения (30) при ${{a}_{1}} = 0$:
(43)
${{\left. {\psi _{m}^{ \pm }} \right|}_{{{{a}_{1}} = 0}}} = {{\left. { \pm \sqrt { - \frac{{{{a}_{0}}}}{{{{a}_{2}}}}} } \right|}_{{D = {{c}_{1}}}}} = \pm 4\sqrt {3\frac{{c_{1}^{2} - c_{0}^{2}}}{{c_{2}^{6} - c_{1}^{6}}}} .$При каждом ${{n}_{{j0}}} < n_{{j0}}^{*}$ все УВС будут иметь положительную амплитуду, меньшую, чем ${{\left. {\psi _{m}^{ + }} \right|}_{{{{a}_{1}} = 0}}}$, а все УВР будут иметь отрицательную амплитуду, меньшую (большую по абсолютной величине), чем ${{\left. {\psi _{m}^{ - }} \right|}_{{{{a}_{1}} = 0}}}$. Представление о том, как изменяется амплитуда потенциала $\varphi _{m}^{ \pm }{{|}_{{{{a}_{1}} = 0}}} = \kappa \psi _{m}^{ \pm }{{|}_{{{{a}_{1}} = 0}}}$ в зависимости от ${{n}_{{j0}}}$ вблизи $n_{{j0}}^{*}$ дает рис. 3. Видно, что при незначительном отклонении плотности от $n_{{j0}}^{*}$ происходит очень быстрый рост амплитуды потенциала на границе ${{c}_{1}}({{n}_{{j0}}})$. Каждому значению ${{n}_{{j0}}}$ соответствует своя пара уединенных волн со своей скоростью распространения $D = {{c}_{1}}({{n}_{{j0}}})$ и своей амплитудой. Диапазон возможных амплитуд оказывается довольно большим при очень малом изменении плотности ${{n}_{{j0}}}$. В грубом приближении можно сопоставить всем парам уединенных волн, и соответственно, всем их амплитудам, одну и ту же плотность ${{n}_{{j0}}} = n_{{j0}}^{*}$. Поступая таким образом, мы отказываемся от границы между УВС и УВР в виде кривой ${{c}_{1}}({{n}_{{j0}}})$, и устанавливаем границу как точно заданное значение плотности ${{n}_{{j0}}} = n_{{j0}}^{*}$. На этой границе возможно распространение уединенных волн малых амплитуд с произвольной скоростью распространения $D \ne {{c}_{1}}$. При этом амплитуда уединенной волны будет определяться той же формулой (43), но в ней надо заменить ${{c}_{1}}$ на D. Диапазон возможных амплитуд можно оценить, например, из рис. 3.
Рис. 3.
Зависимости амплитуды потенциала ${{\left. {\psi _{m}^{ \pm }} \right|}_{{{{a}_{1}} = 0}}}$ от ${{n}_{{j0}}}$ на границе ${{c}_{1}}({{n}_{{j0}}})$ (сплошные кривые); $\varphi _{s}^{ + }$ показано штриховыми кривыми, $\varphi _{s}^{ - }$ – пунктирными кривыми: ${{m}_{j}} = 0.476$ (a), ${{m}_{j}} = 3.657$ (б).

В этом приближении будем полагать, что хотя $D \ne {{c}_{1}}$, но при этом величиной ${{a}_{1}}$ и величиной ${{D}^{4}} - c_{1}^{4}$ в (39) и (40) можно пренебречь. Тогда выражения для профилей УВС и УВР, которые могут существовать при ${{n}_{{j0}}} = n_{{j0}}^{*}$, примут вид
(44a)
$\begin{gathered} {{\left. {{{\psi }^{ \pm }}} \right|}_{{{{a}_{1}} \sim 0}}} = {{\left. { \pm \sqrt { - \frac{{{{a}_{0}}}}{{{{a}_{2}}}}} } \right|}_{{D \sim {{c}_{1}}}}}{\text{sech}}(Y) = \\ \, = \pm 4\sqrt {3\frac{{{{D}^{2}} - c_{0}^{2}}}{{c_{2}^{6} - {{D}^{6}}}}} \,{\text{sech}}\left( {\frac{1}{D}\sqrt {2{{Z}_{i}}{{n}_{{i0}}}{{a}_{0}}} z} \right), \\ \end{gathered} $(44b)
$\begin{gathered} {{\left. {{{\varphi }^{ \pm }}} \right|}_{{{{a}_{1}} \sim 0}}} = \\ = {{\left. { \pm \varphi _{m}^{ \pm }} \right|}_{{{{a}_{1}} \sim 0}}}{\text{sech}}\left\{ {{{{\left[ {{{n}_{{e0}}}\left( {1 - \frac{{c_{0}^{2}}}{{{{D}^{2}}}}} \right)} \right]}}^{{1/2}}}(x - Dt)} \right\}, \\ \end{gathered} $(44c)
${{\left. {\varphi _{m}^{ \pm }} \right|}_{{{{a}_{1}} \sim 0}}} = {{\left[ {12\left( {1 - \frac{{c_{0}^{2}}}{{{{D}^{2}}}}} \right){{{\left( {\frac{{c_{2}^{6}}}{{{{D}^{6}}}} - 1} \right)}}^{{ - 1}}}} \right]}^{{1/2}}}.$Очевидно, что если в эти формулы подставить $D = {{c}_{1}}$, то мы получим профиль одной УВС и одной УВР на границе ${{c}_{1}}({{n}_{{j0}}})$ при соответствующей плотности ${{n}_{{j0}}} \leqslant n_{{j0}}^{*}$.
Интересно сравнить эти формулы с известным решением (26) для профиля потенциала при ${{n}_{{j0}}} = n_{{j0}}^{*}$. Для этого сначала преобразуем выражение (25) для ${{A}_{m}}$:
Подставляя ${{A}_{m}}$ и ${{B}_{m}}$ в формулы (26), получим
(46a)
${{\varphi }^{{(m)}}} = \pm \varphi _{m}^{{(m)}}{\text{sech}}\left\{ {{{{\left[ {2{{n}_{{e0}}}\left( {\frac{D}{{{{c}_{0}}}} - 1} \right)} \right]}}^{{1/2}}}(x - Dt)} \right\},$(46b)
$\begin{gathered} D = {{c}_{0}}\left[ {1 + \frac{{{{{(\varphi _{m}^{{(m)}})}}^{2}}}}{{24}}\left( {\frac{{c_{2}^{6}}}{{c_{0}^{6}}} - 1} \right)} \right], \\ \varphi _{m}^{{(m)}} = {{\left[ {24\left( {\frac{D}{{{{c}_{0}}}} - 1} \right){{{\left( {\frac{{c_{2}^{6}}}{{c_{0}^{6}}} - 1} \right)}}^{{ - 1}}}} \right]}^{{1/2}}}. \\ \end{gathered} $Учтем, что при малых амплитудах $D \gtrsim {{c}_{0}}$ стоящая в (44) величина $(1 - c_{0}^{2}{\text{/}}{{D}^{2}}) \approx 2(1 - {{c}_{0}}{\text{/}}D)$. Можно видеть, что основное различие между формулами состоит в том, что малой величиной в (44) является величина $(1 - {{c}_{0}}{\text{/}}D)$, а в формуле (46) – величина $(D{\text{/}}{{c}_{0}} - 1)$. Обе величины одного порядка. Можно ожидать, что профили потенциала, рассчитанные по обеим формулам, будут почти одинаковыми.
4.2.3. Профили уединенных волн с точностью до членов третьего порядка малости. Определенный интерес может представлять и более грубое приближение, при котором в разложении $\mathcal{K}(\psi )$ сохраняются члены до третьего порядка малости включительно, а члены четвертого порядка не учитываются. Такое приближение существенно отличается от предыдущего, где амплитуда ${{\psi }_{m}}$ принимает два разных значения, одно – для УВС, другое – для УВР. В этом же приближении амплитуда определяется уравнением (30), где слева опущен последний член, и существует лишь один корень ${{\bar {\psi }}_{m}}$:
(47)
${{a}_{0}} + {{a}_{1}}{{\bar {\psi }}_{m}} = 0,\quad \quad {{\bar {\psi }}_{m}} = - \frac{{{{a}_{0}}}}{{{{a}_{1}}}}.$Здесь и ниже для этого приближения мы переобозначили величину ψ и потенциал φ, добавив сверху черту, чтобы отличать их от соответствующих величин в ранее рассмотренном приближении более высокого порядка. Тогда амплитуда потенциала ${{\bar {\varphi }}_{m}} = \kappa {{\bar {\psi }}_{m}}$ запишется в виде
(48)
${{\bar {\varphi }}_{m}} = - 3{{D}^{2}}\frac{{{{D}^{2}} - c_{0}^{2}}}{{{{D}^{4}} - c_{1}^{4}}}.$Используя формулу (47) для амплитуды на нижнем пределе в (36) при ${{a}_{2}} = 0$, можно получить выражение для профиля величины $\bar {\psi }$, а затем записать выражение для профиля потенциала $\bar {\varphi }$:
(49a)
$\begin{gathered} \bar {\psi } = - \frac{{{{a}_{0}}}}{{{{a}_{1}}}}{\text{sec}}{{{\text{h}}}^{2}}\left( {\frac{1}{2}Y} \right) = \\ \, = 6\frac{{{{D}^{2}} - c_{0}^{2}}}{{c_{1}^{4} - {{D}^{4}}}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {\frac{1}{{2D}}\sqrt {2{{Z}_{i}}{{n}_{{i0}}}{{a}_{0}}} (x - Dt)} \right], \\ \end{gathered} $(49b)
$\bar {\varphi } = {{\bar {\varphi }}_{m}}{\text{sec}}{{{\text{h}}}^{2}}\left\{ {\frac{1}{2}{{{\left[ {{{n}_{{e0}}}\left( {1 - \frac{{c_{0}^{2}}}{{{{D}^{2}}}}} \right)} \right]}}^{{1/2}}}(x - Dt)} \right\},$(49c)
${{\bar {\varphi }}_{m}} = 3{{D}^{2}}\frac{{{{D}^{2}} - c_{0}^{2}}}{{c_{1}^{4} - {{D}^{4}}}} = 3\left( {1 - \frac{{c_{0}^{2}}}{{{{D}^{2}}}}} \right){{\left( {\frac{{c_{1}^{4}}}{{{{D}^{4}}}} - 1} \right)}^{{ - 1}}}.$В (49) профиль УВС и профиль УВР описываются одной и той же формулой. Является ли уединенная волна волной сжатия или волной разрежения определяется знаком коэффициента ${{a}_{1}}$ (${{a}_{0}} > 0$ всегда). Здесь также, как и в случае решения с точностью до членов четвертого порядка малости, если ${{a}_{1}} < 0$ $({{D}^{4}} < c_{1}^{4})$, то имеет место УВС ${{\bar {\psi }}_{m}} = - {{a}_{0}}{\text{/}}{{a}_{1}} > 0$, а если ${{a}_{1}} > 0$ $({{D}^{4}} > c_{1}^{4})$, то мы имеем УВР ${{\bar {\psi }}_{m}} < 0$. Условие ${{a}_{1}} = 0$ $({{D}^{4}} = c_{1}^{4})$ при заданном $\mu $ определяет то значение плотности отрицательных ионов, которое разграничивает области существования УВС и УВР как угодно малых амплитуд.
Проведем сравнение этих формул с известными формулами (22), полученными с помощью редуктивного метода возмущений. Преобразуем сначала уравнения (22). Используя выражение (33) для коэффициента $A$, получим
(50a)
${{\varphi }^{{(n)}}} = \varphi _{m}^{{(n)}}{\text{sec}}{{{\text{h}}}^{2}}\left\{ {\frac{1}{2}{{{\left[ {2{{n}_{{e0}}}\left( {\frac{D}{{{{c}_{0}}}} - 1} \right)} \right]}}^{{1/2}}}(x - Dt)} \right\},$(50b)
$\begin{gathered} D = {{c}_{0}}\left[ {1 + \frac{{\varphi _{m}^{{(n)}}}}{6}\left( {\frac{{c_{1}^{4}}}{{c_{0}^{4}}} - 1} \right)} \right], \\ \varphi _{m}^{{(n)}} = 6\left( {\frac{D}{{{{c}_{0}}}} - 1} \right){{\left( {\frac{{c_{1}^{4}}}{{c_{0}^{4}}} - 1} \right)}^{{ - 1}}}. \\ \end{gathered} $Если в этих формулах положить $D \gtrsim {{c}_{0}}$, то нетрудно видеть, что они отличаются от формул (49) тем, что здесь малой величиной является $(D{\text{/}}{{c}_{0}} - 1)$ в отличие от $(1 - {{c}_{0}}{\text{/}}D)$ в (49). Обе величины одного порядка, т.е. решение, полученное с помощью редуктивного метода возмущений, имеет точность до членов третьего порядка малости.
Рассмотрим профиль потенциала (49b) в случае электрон-ионной плазмы $\rho = 0$, имея в виду, что при этом ${{c}_{0}} = 1,$ ${{n}_{{e0}}} = 1,$ $c_{1}^{4} = 3$. Распределение потенциала в такой плазме ϕ можно записать в подробном виде
(51a)
$\phi = {{\left. {\bar {\varphi }} \right|}_{{\rho = 0}}} = {{\phi }_{m}}{\text{sec}}{{{\text{h}}}^{2}}\left[ {\frac{1}{2}{{{\left( {1 - \frac{1}{{{{D}^{2}}}}} \right)}}^{{1/2}}}(x - Dt)} \right],$При очень малых амплитудах скорость волны $D \to 1$. Для этого случая из уравнений (51) можно получить выражение для профиля потенциала ϕ и выражение для связи между амплитудой потенциала волны ${{\phi }_{m}}$ и скоростью ее распространения D:
(52a)
$\phi \approx 3(D - 1)\,{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{{\left( {\frac{{D - 1}}{2}} \right)}}^{{1/2}}}(x - Dt)} \right],$Если перейти в систему отсчета, движущуюся со скоростью звука, то скорость волны будет составлять треть от ее амплитуды, что характерно для солитонов, описываемых уравнением КдВ. Более того, в таком виде выражение для потенциала действительно удовлетворяет уравнению КдВ
Легко видеть, что полученные в этом приближении формулы (51) и (52) для профиля уединенной волны в ЭИП полностью совпадают с известными формулами (19) и (23) соответственно.
4.3. Расчеты профилей уединенных волн
В этом разделе мы представляем результаты расчетов профилей уединенных волн, полученных с помощью предлагаемых здесь формул, и сравниваем их с расчетами, выполненными по известным формулам, а также с решениями (14)–(17) исходной системы уравнений (1) (раздел 2).
Чтобы каждый раз не повторять, каким образом получена та или иная формула для профиля уединенной волны, введем их краткие наименования. Так формулы (22), (23) и (26), полученные с помощью редуктивного метода возмущений будем называть формулами в КдВ-приближении и формулами в мКдВ-приближении, соответственно. Формулы (39)–(42), полученные с точностью до членов 4-го порядка малости включительно, назовем формулами 4-го порядка, а формулы (48), (49) и (51), (52), выведенные с точностью до членов 3-го порядка малости включительно, назовем формулами 3-го порядка.
Прежде всего, отметим, что диапазон допустимых амплитуд для каждой из рассматриваемых здесь формул в существенной степени определяется заисимостью между амплитудой уединенной волны ${{\varphi }_{m}}$ и скоростью ее распространения $D$, представленной в этой формуле. Чем больше отклонение зависимости $D = D({{\varphi }_{m}})$ от зависимости, даваемой решением уравнения (16), полученного при решении исходной системы уравнений, тем меньше диапазон допустимых амплитуд и тем больше отклонение рассчитанного по формуле профиля от решения исходной системы уравнений. Чтобы иметь представление о таких отклонениях, мы приводим на рис. 4 и 5 зависимости $D = D({{\varphi }_{m}})$, как полученные в результате численного решения уравнения (16), так и вычисленные по рассматриваемым аналитическим формулам. Представлены расчеты при разных плотностях ${{n}_{{j0}}}$ для двух вариантов ионного состава.
Рис. 4.
Зависимость $D = D({{\varphi }_{m}})$ в случае ${{m}_{j}} = 0.476$ при разных значениях невозмущенной плотности отрицательных ионов ${{n}_{{j0}}}$: $a$ – 0, $b$ – 0.04, $c$ – 0.10225 (a), $c$ – 0.10225, $d$ – 0.2, $e$ – 0.3, $f$ – 0.4 (б). Толстые сплошные кривые – расчет по (16), сплошные кривые и кружки – расчет по формулам 4-го порядка (41), (42), штриховые кривые – расчет по формуле 3-го порядка (48). В случае ЭИП (кривые $a$) штриховая кривая – расчет по (51b), короткие штрихи – расчет по (52b). Тонкими горизонтальными линиями показаны области значений амплитуд, при которых уединенные волны не существуют, а вертикальными пунктирными линиями – значение ${{\varphi }_{m}} = 0$.

Рис. 5.
Зависимость $D = D({{\varphi }_{m}})$ в случае ${{m}_{j}} = 3.657$ при разных значениях невозмущенной плотности отрицательных ионов ${{n}_{{j0}}}$: $a$ – 0.3, $b$ – 0.4, $c$ – 0.5, $d$ – 0.54197 (a), $d$ – 0.54197, $e$ – 0.6, $f$ – 0.65, $g$ – 0.7 (б). Толстые сплошные кривые – расчет по (16), сплошные кривые и кружки – расчет по формулам 4-го порядка (41), (42), штриховые кривые – расчет по формуле 3-го порядка (48). Тонкими горизонтальными линиями показаны области значений амплитуд, при которых уединенные волны не существуют, а вертикальными пунктирными линиями – значение ${{\varphi }_{m}} = 0$.

Одной из особенностей этих зависимостей является наличие областей значений амплитуд ${{\varphi }_{m}}$, где уединенные волны существовать не могут. Диапазон таких амплитуд при любом значении плотности ${{n}_{{j0}}}$ легко видеть, если на рис. 1 провести вертикальную линию ${{n}_{{j0}}} = {\text{const}}$. На рис. 4 и 5 на зависимости $D = D({{\varphi }_{m}})$, рассчитанной по (16), область значений ${{\varphi }_{m}}$, где уединенная волна не существует, обозначена тонкой горизонтальной линией. Существование подобной области значений ${{\varphi }_{m}}$, хотя и не всегда точно такой же, следует также из рассматриваемых здесь аналитических зависимостей.
На рис. 4а и 5а показаны зависимости $D = D({{\varphi }_{m}})$ для УВС при невозмущенных плотностях отрицательных ионов, меньших чем $n_{{j0}}^{*}$, в том числе и в случае ЭИП ${{n}_{{j0}}} = 0$, которому соответствуют кривые a на рис. 4а. В этом случае зависимость $D = D({{\varphi }_{m}})$, посчитанная по форму-ле (52b), совпадает с аналогичной зависимостью, следующей из (16), в более широком диапазоне ${{\varphi }_{m}}$, чем это имеет место для зависимости (51b). На рис. 4б и 5б такие же зависимости представлены для УВР при невозмущенных плотностях отрицательных ионов, больших чем $n_{{j0}}^{*}$. Кроме того на рисунках представлен случай ${{n}_{{j0}}} = n_{{j0}}^{*}$ (кривые $c$ на рис. 4 при ${{m}_{j}} = 0.476$ и кривые d на рис. 5 при ${{m}_{j}} = 3.657$). При такой плотности существуют как УВС, так и УВР как угодно малых амплитуд. Область допустимых амплитуд УВС непрерывно переходит в область допустимых амплитуд УВР. Естественно, в таком случае формула (48), выведенная с точностью до членов третьего порядка включительно, не применима (${{a}_{1}} = 0$), и никаких расчетов по ней на рисунках не представлено. Из рисунков хорошо видно, что расчеты по формулам (41), (42), которые получены с точностью до членов четвертого порядка включительно, совпадают с зависимостями, рассчитанными по (16), в гораздо большем диапазоне амплитуд, чем расчеты по формуле (48), в которой учитываются только члены до третьего порядка включительно. Исключением из этого является случай ЭИП, где зависимость (52b) при больших амплитудах (${{\varphi }_{m}} \geqslant 0.3$) отклоняется от зависимости, рассчитанной по (16), несколько меньше, чем зависимость (51b).
Если амплитуда уединенной волны достаточно мала, то расчет ее профиля можно выполнить по любой из рассматриваемых здесь формул, и результат будет примерно одним и тем же. Полученные таким образом профили будут достаточно близки к решению (14)–(17) исходной системы уравнений (1). Однако, если амплитуда волны не очень мала, то профили будут отличаться друг от друга. Отличия будут хорошо заметны, например, при амплитуде ${{\varphi }_{m}} = 0.2$, которую мы и выбираем для расчетов, иллюстрирующих отклонение профилей, рассчитанных по той или иной формуле, от профиля, получаемого при решении (14)–(17) исходной системы уравнений. Как мы увидим, эти отклонения, на первый взгляд, не очень велики22. Однако, если профиль потенциала $\varphi (z)$ задан неправильно, то с ошибкой будут заданы также и профили ионных скоростей ${{V}_{i}}(z)$ и ${{V}_{j}}(z)$. Хотя при этом ошибки в задании ионных скоростей в каждой отдельной точке $z$ небольшие, но их наличие приводит к весьма заметной ошибке в задании энергии волны, которая заключена, в основном, в кинетической энергии всех ионов, вовлеченных волной в движение. Несоответствие энергии волны ее амплитуде приведет к изменению и амплитуды, и скорости распространения, и формы волны. Это очень наглядно и убедительно проиллюстрировано в работе [22].
Насколько хорошо рассматриваемые формулы описывают профиль уединенной волны в ЭИП, иллюстрирует рис. 6 (здесь и на ряде последующих рисунков для лучшего разрешения мы показываем только половину профиля солитона). Видно, что расчет по формуле 4-го порядка (39) чуть более близок к решению (14)–(17) исходной системы уравнений, чем это дает расчет по формуле в КдВ-приближении (23a) и идентичной ей формуле 3-го порядка (52a), а расчет по формуле того же порядка (51a) сильно отличается от решении (14)–(17). Здесь, казалось бы, более грубая формула (52a) дает более точный результат, чем исходная формула (51a). Это обусловлено тем, что зависимость $D = D({{\varphi }_{m}})$ по (52b) оказывается более близкой к решению (16), чем та же зависимость по (51b) (рис. 4). Подобные соотношения между разными решениями имеют место и при бóльших амплитудах.
Рис. 6.
Профиль уединенной волны в ЭИП при амплитуде ${{\phi }_{m}} = 0.2$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, сплошная кривая и кружки – расчет по формуле 4-го порядка (39), штриховая кривая – расчет по формуле 3‑го порядка (51a). Формула 3-го порядка (52a) и формула в КдВ-приближении (23a), полностью совпадающие, представлены окружностями.

В случае ПОИ для описания профиля уединенной волны используют формулу (22), выведенную с помощью редуктивного метода возмущений. Рассмотрим сначала, как эта формула представляет зависимость $D = D({{\varphi }_{m}})$ в сравнении с формулами 4-го порядка (41), (42) и с формулой 3-го порядка (48), а также с расчетом, полученным при решении уравнения (16). Такое сравнение для случая ${{n}_{{j0}}} = 0.3$ показано на рис. 7. При этой плотности отрицательных ионов уединенные волны как угодно малых амплитуд могут существовать в ПОИ с ${{m}_{j}} = 0.476$ только в случае волн разрежения (${{n}_{{j0}}} > n_{{j0}}^{*} = 0.10225$), а в ПОИ с ${{m}_{j}} = 3.657$ – только в случае волн сжатия (${{n}_{{j0}}} < n_{{j0}}^{*} = 0.54197$). Из рис. 7 видно, что наименьшее отклонение от решения уравнения (16) дает расчет по формулами 4-го порядка (41), (42) как для УВС, так и для УВР. Несколько большее отклонение наблюдается при расчете $D = D({{\varphi }_{m}})$ по формуле в КдВ-приближении (22b) для УВС. Значительно большее отклонение имеет место при расчете по той же формуле в случае УВР. Даже расчет по формуле 3-го порядка (48) для УВР отклоняется от решения уравнения (16) меньше. Отметим, что подобная картина наблюдается и при других значениях плотности ${{n}_{{j0}}}$. Очевидно, что чем больше отклонение зависимости $D = D({{\varphi }_{m}})$ от аналогичной зависимости, рассчитанной по (16), тем хуже данная формула будет описывать профиль уединенной волны.
Рис. 7.
Зависимость $D = D({{\varphi }_{m}})$ при ${{n}_{{j0}}} = 0.3$: ${{m}_{j}} = 0.476$ (a), ${{m}_{j}} = 3.657$ (б). Толстые сплошные кривые – расчет по (16), сплошные кривые и кружки – расчет по формулам 4-го порядка (41), (42), штриховые кривые – расчет по формуле 3-го порядка (48). Расчет по формуле в КдВ-приближении (22b) показан окружностями.
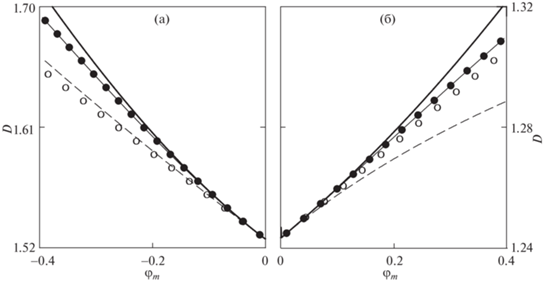
Сравнение профилей, рассчитанных по разным формулам, представлено на рис. 8 для УВС с амплитудой $\varphi _{m}^{ + } = 0.2$ и на рис. 9 для УВР с амплитудой $\varphi _{m}^{ - } = - 0.2$. Профиль потенциала в КдВ-приближении (22a) в случае УВС отклоняется от решения (14)–(17) исходной системы уравнений заметно больше, чем профиль, рассчитанный по формуле 4-го порядка (39), но несколько меньше, чем профиль, определенный по формуле 3-го порядка (49b). В случае УВР профиль потенциала в КдВ-приближении (22a) также заметно больше отклоняется от решения (14)–(17) исходной системы уравнений, чем профиль, рассчитанный по формуле 4-го порядка (40), и практически полностью совпадает с профилем (49b). Как видно, в обоих случаях наилучшее приближение к решению (14)–(17) исходной системы уравнений дают предлагаемые здесь формулы, полученные с точностью до четвертого порядка малости включительно.
Рис. 8.
Профиль УВС в ПОИ с ${{m}_{j}} = 3.657$ при ${{n}_{{j0}}} = 0.3$, $\varphi _{m}^{ + } = 0.2$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, сплошная кривая и кружки – расчет по формуле 4-го порядка (39), штриховая кривая – расчет по формуле 3-го порядка (49b). Расчет по формуле в КдВ-приближении (22a) показан окружностями.

Рис. 9.
Профиль УВР в ПОИ с ${{m}_{j}} = 0.476$ при ${{n}_{{j0}}} = 0.3$, $\varphi _{m}^{ - } = - 0.2$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, сплошная кривая и кружки – расчет по формуле 4-го порядка (40), штриховая кривая – расчет по формуле 3-го порядка (49b). Расчет по формуле в КдВ-приближении (22a) показан окружностями.

Рисунки 10 и 11 иллюстрируют случай, когда уединенную волну малой амплитуды обычно принято интерпретировать как мКдВ-солитон при невозмущенной плотности отрицательных ионов ${{n}_{{j0}}} = n_{{j0}}^{*}$. При этом профиль солитона предлагается описывать с помощью стационарного решения (22b) модифицированного уравнения КдВ (24). Из рис. 10 видно, что профиль УВС с амплитудой $\varphi _{m}^{ + } = 0.2$, рассчитанный по формуле 4-го порядка (39), практически полностью совпадает с решением (14)–(17) исходной системы уравнений, а решение в мКдВ-приближении (26a) дает несколько более узкий профиль. Расчет по формуле профиля уединенной волны на границе ${{a}_{1}} = 0$ (44b) также более близок к решению (14)–(17), чем расчет по формуле (26a). Чтобы небольшие различия были видны, расчет по (44b) показан на вкладке в увеличенном масштабе.
Рис. 10.
Профиль УВС в ПОИ с ${{m}_{j}} = 0.476$ при ${{n}_{{j0}}} = 0.10224951$, $\varphi _{m}^{ + } = 0.2$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, кружки – расчет по формуле 4-го порядка (39), окружности – расчет по формуле в мКдВ-приближении (26a). Штриховая кривая на вставке – расчет по формуле профиля на границе ${{a}_{1}} = 0$ (44b).

Рис. 11.
Профиль УВР в ПОИ с ${{m}_{j}} = 0.476$ при ${{n}_{{j0}}} = 0.10224951$, $\varphi _{m}^{ - } = - 0.2$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, кружки – расчет по формуле 4-го порядка (40), окружности – расчет по формуле в мКдВ-приближении (26a), штриховая кривая – расчет по формуле профиля на границе ${{a}_{1}} = 0$ (44b).

В случае УВР с амплитудой $\varphi _{m}^{ - } = - 0.2$ (рис. 11) расчеты по формуле 4-го порядка (40) и решение (26a) мКдВ-уравнения практически совпадают, причем оба заметно отклоняются от решения (14)–(17) исходной системы уравнений. Чуть большее отклонение дает расчет по формуле профиля на границе ${{a}_{1}} = 0$ (44b). Профиль солитона, описываемый этими решениями, оказывается более широким, чем это следует из решения (14)–(17). Обратим внимание на то, что согласно формулам (26a) и (44b) профили УВС и УВР симметричны относительно нулевого потенциала, и это имеет место при плотности ${{n}_{{j0}}} = n_{{j0}}^{*}$, которая определяется условием ${{c}_{1}} = {{c}_{0}}$ (или $A = 0$). С другой стороны, из формул 4-го порядка (39) и (40) видно, что для симметрии профилей УВС и УВР необходимо, чтобы выполнялось другое условие $D = {{c}_{1}}$. Поэтому симметрия этих решений при рассматриваемой плотности ${{n}_{{j0}}} = n_{{j0}}^{*}$ может быть только при $D \sim {{c}_{0}}$, т.е. при очень малых амплитудах. Если же $D$ заметно отличается от ${{c}_{0}}$, как это имеет место в рассматриваемом случае, профили УВС и УВР симметричными не будут. Хорошей иллюстрацией сказанного может служить рис. 12, где представлены зависимости $D = D({{\varphi }_{m}})$ для рассматриваемых здесь формул. Видно, что зависимость $D = D({{\varphi }_{m}})$, рассчитанная по (16), как и аналогичная зависимость, следующая из формул 4-го порядка (41), (42), не симметричны. Уже поэтому расчеты по формулам в мКдВ-приближении могут давать большую погрешность при не очень малой амплитуде. Сравнивая этот рисунок с рис. 10 и 11, можно заметить, что чем меньше отклоняется рассчитанная для рассматриваемой формулы зависимость $D = D({{\varphi }_{m}})$ от рассчитанной по (16) зависимости, тем меньше отклоняется соответствующий профиль от решения (14)–(17) исходной системы уравнений.
Рис. 12.
Зависимость $D = D({{\varphi }_{m}})$ в случае ${{m}_{j}} = 0.476$ при ${{n}_{{j0}}} = 0.10224951$. Толстые сплошные кривые – расчет по (16), кружки – расчет по формулам 4-го порядка (41), (42), окружности – расчет по формуле в мКдВ-приближении (26b), штриховые кривые – расчет по формуле профиля на границе ${{a}_{1}} = 0$ (44c).

К такому же выводу приведет нас рассмотрение несколько необычного случая, суть которого состоит в следующем. Из рис. 4б, где представлены, в основном, зависимости $D = D({{\varphi }_{m}})$ в УВР, в случаях ${{n}_{{j0}}} = 0.2$ и ${{n}_{{j0}}} = 0.3$ можно видеть небольшой диапазон положительных амплитуд, в котором зависимость $D = D({{\varphi }_{m}})$ по формуле 4-го порядка (41) для УВС хорошо совпадает с решением уравнения (16). И это имеет место при больших амплитудах. Поэтому можно предположить, что и профили УВС, рассчитанные для таких амплитуд по формуле 4-го порядка (39), будут близки к решению (14)–(17) исходной системы уравнений. Чтобы убедиться в этом, мы построили такие профили потенциала в случае большой амплитуды $\varphi _{m}^{ + } = 0.5$ (рис. 13). Видно, что профиль УВС, построенный по формуле (39) при такой большой амплитуде, практически полностью совпадает с решением (14)–(17) исходной системы уравнений. Обратим внимание на то, что в этом случае ${{n}_{{j0}}} > n_{{j0}}^{*}$ и, следовательно, УВС как угодно малых амплитуд существовать не могут. Минимальная амплитуда УВС при ${{n}_{{j0}}} = 0.2$ равна $\varphi _{s}^{ + } = 0.4425$ (рис. 1). Таким образом, с помощью формулы 4-го порядка удается довольно хорошо описать профиль УВС большой амплитуды, но при этом сама амплитуда лишь ненамного превышает минимально допустимую амплитуду. Очевидно, что аналогичный расчет профиля УВС нельзя произвести по формуле в КдВ-приближении (22a), поскольку эта формула при ${{m}_{j}} = 0.476$ и ${{n}_{{j0}}} = 0.2$ описывает только УВР.
Рис. 13.
Профиль УВС большой амплитуды при ${{m}_{j}} = 0.476$, ${{n}_{{j0}}} = 0.2$, $\varphi _{m}^{ + } = 0.5$. Толстая сплошная кривая – решение (14)–(17) исходной системы уравнений, кружки – расчет по (39).

Представленные рисунки демонстрируют применимость формул (39)–(42) при любых плотностях ${{n}_{{j0}}}$. При этом следует иметь в виду, что при ${{n}_{{j0}}} < n_{{j0}}^{*}$ имеет место УВС и профиль рассчитывается по (39), а при ${{n}_{{j0}}} > n_{{j0}}^{*}$ имеет место УВР и профиль рассчитывается по (40). При ${{n}_{{j0}}} = n_{{j0}}^{*}$ расчет ведется по (39) для УВС и по (40) для УВР, так как в этом случае профиль УВР нельзя получить из профиля УВС с помощью изменения знака, как это имеет место для солитона модифицированного уравнения КдВ.
5. ЗАКЛЮЧЕНИЕ
В данной работе рассмотрен вопрос об определении профиля уединенной волны в плазме с отрицательными ионами, в том числе, как частный случай, в электрон-ионной плазме.
Представлен метод численного расчета профиля уединенной волны. Уединенная волна, профиль которой рассчитан по этому методу, распространяется по плазме без изменения амплитуды, скорости распространения и формы. Метод позволяет рассчитывать профиль уединенной волны любой амплитуды, включая амплитуды, близкие к критической.
Предложены формулы для аналитического описания профиля УВС и профиля УВР при малых амплитудах в плазме с отрицательными ионами и в электрон-ионной плазме. Формулы выведены с точностью до членов четвертого порядка малости включительно. Формулы применимы при любом отношении плотности отрицательных ионов к плотности положительных ионов, в том числе, и при таком отношении, когда для описания профиля обычно используется решение модифицированного уравнения Кортевега–де Вриза.
Проведено сравнение профилей уединенной волны, рассчитанных по предлагаемым здесь формулам и по известным формулам, как между собой, так и с соответствующими профилями, полученными с помощью численного решения исходной системы уравнений, описывающих плазму. В большинстве случаев наименьшее отклонение от решения исходной системы уравнений имеет профиль, рассчитанный по предлагаемым формулам.
Список литературы
Zabusky N.J., Kruskal M.D. // Phys. Rev. Lett. 1965. V. 15. P. 240.
Веденов A.A., Велихов E.П., Сагдеев P.3. // Ядерный синтез. 1961. Т. 1. С. 82.
Сагдеев Р.З. // Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Атомиздат, 1964. Вып. 4. С. 20.
Washimi H., Taniuti T. // Phys. Rev. Lett. 1966. V. 17. P. 996.
Березин Ю.А., Карпман В.И. // ЖЭТФ. 1966. Т. 51. С. 1557.
Biskamp D., Parkinson D. // Phys. Fluids. 1970. V. 13. P. 2295.
Schamel H. // Plasma Phys. 1972. V. 14. P. 905.
Tappert F. // Phys. Fluids. 1972. V. 15. P. 2446.
Sakanaka P.H. // Phys. Fluids. 1972. V. 15. P. 304.
Tagare S.G. // Plasma Phys. 1973. V. 15. P. 1247.
Satya Y.S., Goswami B.N. // Phys. Lett. 1977. V. 61A. P. 388.
Malik H.K., Singh S., Dahiya R.P. // Phys. Plasmas. 1994. V. 1. P. 1137.
Tagare S.G. // Phys. Plasmas. 2000. V. 7. P. 883.
McKenzie J.F. // Phys. Plasmas. 2002. V. 9. P. 800.
Дубинова И.Д., Дубинов А.Е. // Письма в ЖТФ. 2006. Т. 32. Вып. 13. С. 43.
Ghosh U.N., Chatterjee P., Roychoudhury R. // Phys. Plasmas. 2012. V. 19. P. 012113.
Kakad A., Omura Y., Kakad B. // Phys. Plasmas. 2013. V. 20. P. 062103. https://doi.org/10.1063/1.4810794
Kakad B., Kakad A., Omura Y. // J. Geophys. Res. Space Physics. 2014. V. 119. P. 5589. https://doi.org/10.1002/2014JA019798
Qi X., Xu Y.-X., Duan W.-S., Zhang L.-Y., Yang L. // Phys. Plasmas. 2014. V. 21. P. 082118. https://doi.org/10.1063/1.4894218
El-Tantawy S.A., Wazwaz A.M., Schlickeiser R. // Plasma Phys. Control. Fusion. 2015. V. 57. P. 125012.
Qi X., Xu Y.-X., Zhao X.-Y., Zhang L.-Y., Duan W.-S., Yang L. // IEEE Trans. Plasma Sci. 2015. V. 43. P. 3815. https://doi.org/10.1109/TPS.2015.2477102
Sharma S., Sengupta S., Sen A. // Phys. Plasmas. 2015. V. 22. P. 022115.
Jenab S.M.H., Spanier F. // Phys. Plasmas. 2016. V. 23. P. 102306.
Jenab S.M.H., Spanier F. // Phys. Plasmas. 2017. V. 24. P. 032305.
Ikezi H., Taylor R.J., Baker D.R. // Phys. Rev. Lett. 1970. V. 25. P. 11.
Ikezi H. // Phys. Fluids. 1973. V. 16. P. 1668.
Okutsu E., Nakamura Y. // Plasma Phys. 1979. V. 21. P. 1053.
Pierre T., Bonhomme G., Cussenot J.R., Leclert G. // Phys. Lett. 1983. V. 95A. P. 159.
Lonngren K.E. // Plasma Phys. 1983. V. 25. P. 943.
Yi S., Bai E.-W., Lonngren K.E. // Phys. Plasmas. 1997. V. 4. P. 2436.
Das G.C., Tagare S.G. // Plasma Phys. 1975. V. 17. P. 1025.
Das G.C. // Plasma Phys. 1977. V. 19. P. 363.
Watanabe S. // J. Phys. Soc. Jpn. 1984. V. 53. P. 952.
Tagare S.G., Reddy R.V. // Plasma Phys. Control. Fusion. 1987. V. 29. P. 671.
Malik H.K., Dahiya R.P. // Phys. Plasmas. 1994. V. 1. P. 2872.
Mishra M.K., Chhabra R.S. // Phys. Plasmas. 1996. V. 3. P. 4446.
Verheest F., Hellberg M.A., Hereman W.A. // Phys. Plasmas. 2012. V. 19. P. 092302.
Дубинов А.Е., Колотков Д.Ю. // Химия высоких энергий. 2012. Т. 46. С. 427.
Ludwig G.O., Ferreira J.L., Nakamura Y. // Phys. Rev. Lett. 1984. V. 52. P. 275.
Nakamura Y., Tsukabayashi I. // Phys. Rev. Lett. 1984. V. 52. P. 2356.
Nakamura Y., Ferreira J.L., Ludwig G.O. // J. Plasma Phys. 1985. V. 33. P. 237.
Nakamura Y., Tsukabayashi I. // J. Plasma Phys. 1985. V. 34. P. 401.
Nakamura Y., Tsukabayashi I., Ludwig G.O., Ferrei-ra J.L. // Phys. Lett. 1985. V. 113A. P. 155.
Nakamura Y. // J. Plasma Phys. 1987. V. 38. P. 461.
Cooney J.L., Gavin M.T., Lonngren K.E. // Phys. Fluids B. 1991. V. 3. P. 2758.
Cooney J.L., Gavin M.T., Williams J.E., Aossey D.W., Lonngren K.E. // Phys. Fluids B. 1991. V. 3. P. 3277.
Cooney J.L., Aossey D.W., Williams J.E., Lonngren K.E. // Phys. Rev. E. 1993. V. 47. P. 564.
Cooney J.L., Aossey D.W., Williams J.E., Gavin M.T., Kim H.S., Hsu Y.-C., Scheller A., Lonngren K.E. // Plasma Sources Sci. Technol. 1993. V. 2. P. 73.
Yi S., Cooney J.L., Kim H.-S., Amin A., El-Zein Y., Lonngren K.E. // Phys. Plasmas. 1996. V. 3. P. 529.
Yi S., Lonngren K.E. // Phys. Plasmas. 1997. V. 4. P. 2893.
Oohara W., Hatakeyama R., Ishiguro S. // Plasma Phys. Control. Fusion. 2002. V. 44. P. 1299.
Bacal M., Hamilton G.W. // Phys. Rev. Lett. 1979. V. 42. P. 1538.
Hirata T., Hatakeyama R., Mieno T., Iizuka S., Sato N. // Plasma Sources Sci. Technol. 1996. V. 5. P. 288.
Byszewski W.W. // J. Appl. Phys. 1989. V. 66. P. 103.
Medvedev Yu.V. // J. Phys. Commun. 2018. V. 2. 045001.
Медведев Ю.В. // Физика плазмы. 2018. Т. 44. С. 475.
Медведев Ю.В. // Физика плазмы. 2019. Т. 45. С. 250.
Medvedev Yu. // Eur. Phys. J. D. 2019. V. 73. P. 157. https://doi.org/10.1140/epjd/e2019-100067-4
Medvedev Yu.V. // Plasma Phys. Control. Fusion. 2014. V. 56. P. 025005.
Johnston C.R., Epstein M. // Phys.Plasmas. 2000. V. 7. P. 906.
Medvedev Yu. // Eur. Phys. J. D. 2021. V. 75. P. 6. https://doi.org/10.1140/epjd/s10053-020-00007-1
Gurevich A.V., Pitaevsky L.P. // Prog. Aerospace Sci. 1975. V. 16. P. 227.
Медведев Ю.В. // Физика плазмы. 2009. Т. 35. С. 70.
Медведев Ю.В. Нелинейные явления при распадах разрывов в разреженной плазме. М.: Физматлит, 2012.
Дополнительные материалы отсутствуют.


