Физика Земли, 2020, № 1, стр. 109-117
Зависимость погрешности определения параметров землетрясений от набора записей поверхностных волн
А. С. Фомочкина 1, 2, *, Б. Г. Букчин 2
1 Российский государственный университет нефти и газа (национальный исследовательский университет)
им. И.М. Губкина
г. Москва, Россия
2 Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия
* E-mail: nastja_f@bk.ru
Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019
Аннотация
Для определения фокального механизма и глубины очага землетрясения часто используют записи излученных поверхностных волн, которые могут быть зашумлены. Поэтому они предварительно отбираются и фильтруются с помощью программы спектрально-временного анализа в определенной полосе периодов. В работе предлагается исследование зависимости погрешности определения параметров события (глубины и фокального механизма) от используемого набора записей. Для этого применяется статистический метод “cкладного ножа” (“jackknife”). Результаты представлены для четырех событий: сильнейшего афтершока в Тохоку 11.03.2011 г., землетрясения в Непале 25.04.2015 г. и двух землетрясений на Аляске 23.01 и 30.11.2018 г. Анализ, проведенный по данным событиям, показал, что влияние набора записей зависит от фокального механизма и глубины землетрясения, количества записей и детализации параметрической сетки, использованной при построении модели очага.
ВВЕДЕНИЕ
В предлагаемой работе мы рассматриваем определение фокального механизма и глубины очага землетрясения по записям поверхностных волн, а именно были использованы фундаментальные моды Лява и Рэлея, зарегистрированные станциями сетей IRIS, GEOSCOPE и GEOFON. Волновые формы и данные об эпицентре и времени события взяты с сайта USGS11. Часто станции группируются по азимуту относительно эпицентра. Для анализа поверхностных волн имеет смысл это распределение предварительно сглаживать. Кластеризацию станций мы проводим с помощью программы FmtVes, разработанной в Институте теории прогноза землетрясений и математической геофизики РАН22. Для рассмотрения каждой записи мы используем спектрально-временное представление сигнала [Ландер и др., 1973] и подвергаем ее фильтрации в определенной полосе периодов с помощью программы СВАН, также разработанной в ИТПЗ РАН2, после чего запись может быть забракована как неудовлетворительная, и тогда выбирается другая станция из группы. Может случиться так, что записи сильно зашумлены предшествующими или последующими событиями (например, форшоками или афтершоками) и количество отобранных записей не так велико. При этом записи на отдельных станциях могут сильно изменять результат. В связи с этим встал вопрос о влиянии набора записей на качество получаемого решения. Для анализа этого влияния предлагается использовать статистический метод “складного ножа”.
ОПРЕДЕЛЕНИЕ ФОКАЛЬНОГО МЕХАНИЗМА ЗЕМЛЕТРЯСЕНИЯ, ЕГО ГЛУБИНЫ И СЕЙСМИЧЕСКОГО МОМЕНТА ПО ДЛИННОПЕРИОДНЫМ АМПЛИТУДНЫМ СПЕКТРАМ ПОВЕРХНОСТНЫХ ВОЛН
Скорости поверхностных волн в реальной Земле не известны с достаточной точностью. Поэтому, как правило, мы используем для определения параметров источника лишь амплитудные спектры поверхностных волн.
Описывая источник в приближении тензора момента, мы рассматриваем мгновенную точечную сдвиговую дислокацию (двойной диполь) на глубине h. Такой источник задается пятью параметрами: его глубиной, фокальным механизмом, определяемым тремя углами (простирания ψ, падения δ и подвижки λ) и сейсмическим моментом М0. Четыре первых параметра мы определяем прямым перебором их возможных значений на сетке в параметрическом пространстве, а пятый параметр М0 – минимизируя отличия (невязку ε) наблюденных амплитудных спектров от их теоретических значений для каждой текущей комбинации значений остальных параметров. Значения параметров, минимизирующие невязку, мы рассматриваем как оценки этих параметров. Для оценки степени разрешения каждого из этих четырех параметров мы строим четыре частные функции невязки: εh(h), εψ(ψ ), εδ(δ) и ελ(λ). Детальное описание метода и примеры применения можно найти в работах [Букчин и др., 1992; Lasserre et al., 2001; Букчин и др., 2015].
Как известно, фокальный механизм не может быть однозначно определен из амплитудных спектров поверхностных волн. Для каждого двойного диполя существует три эквивалентных ему двойных диполя, излучающих поверхностные волны с тем же амплитудным спектром. Эти четыре эквивалентных решения представляют две пары механизмов, повернутых относительно друг друга вокруг вертикальной оси на 180° и в каждой паре отличающихся друг от друга противоположным направлением подвижки. Поэтому частные функции невязки амплитудных спектров для углов простирания и подвижки являются периодическими с периодом 180°. Для выбора одного из четырех эквивалентных фокальных механизмов мы сравниваем синтетические фазовые спектры поверхностных волн на очень длинных периодах (обычно не короче 100 с), рассчитанные для каждого из этих четырех решений, с наблюденными фазовыми спектрами. В качестве оптимального фокального механизма выбирается тот, для которого эти спектры наиболее близки. Аналогично для этой цели могут быть использованы знаки первых вступлений Р-волн. В этом случае для выбора оптимального механизма мы сравниваем знаки первых вступлений, рассчитанные для каждого из этих четырех решений, с наблюденными полярностями.
ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ПАРАМЕТРОВ ОЧАГА ОТ ИСПОЛЬЗУЕМОГО НАБОРА ЗАПИСЕЙ ПОВЕРХНОСТНЫХ ВОЛН МЕТОДОМ “СКЛАДНОГО НОЖА”
Для исследования погрешности, связанной с неустойчивостью решения к изменению используемого набора записей поверхностных волн, мы применяем один из методов генерации повторной выборки (ресэмплинга), а именно метод “складного ножа”. Данный метод был разработан Морисом Кенуи в 1949 г. [Quenouille, 1949] и доработан Джоном Тьюки в 1958 г. [Tukey, 1958].
Метод используется для оценки погрешности в статистическом выводе (обобщение информации, полученной из выборки, для получения представления о свойствах генеральной совокупности).
Оценка погрешности ${{\sigma }_{{jack}}}$ вычисляется по следующей формуле [Tichelaar et al., 1989]:
На начальном этапе применения метода мы считаем, что все варианты ресэмплинга имеют одинаковые веса, то есть wi = 1/n. В качестве данных для оценки параметра используем записи поверхностных волн. В ресэмлинге исключаем по одной записи, т.е. j = 1, k = n – 1. Каждый из оцениваемых параметров мы рассматриваем отдельно, поэтому p = 1. Тогда формула приобретает вид:
С помощью данного метода было проведено исследование оценки зависимости решения от используемого набора записей для четырех сильных событий: сильнейшего афтершока в Тохоку 11.03.2011 г., землетрясения в Непале 25.04.2015 г. и двух землетрясений на Аляске 23.01 и 30.11.2018 г. Данные землетрясения имеют магнитуду выше 7.0 и при этом характеризуются различными фокальными механизмами и глубиной. Для определения их параметров были использованы различные наборы записей поверхностных волн.
СИЛЬНЕЙШИЙ АФТЕРШОК ЯПОНСКОГО ЗЕМЛЕТРЯСЕНИЯ В ТОХОКУ 11.03.2011, Mw = 8.4
Сильнейший афтершок землетрясения в Тохоку произошел через полчаса после основного толчка. В результате его записи оказались сильно зашумленными излучением предшествующего главного события. С помощью программы спектрально-временного анализа СВАН мы отфильтровали в полосе периодов от 100 до 200 с и использовали для определения параметров изучаемого события фундаментальные моды Лява и Рэлея, зарегистрированные 13 станциями сетей IRIS, GEOSCOPE и GEOFON. Расположение этих станций приведено на рис. 1а. Шаг сетки для углов фокального механизма был выбран равным 1°. В табл. 1 представлены фокальные механизмы и фазовые невязки для четырех эквивалентных решений, полученных из анализа амплитудных спектров поверхностных волн. Как видно из табл. 1, оптимальным является решение 1. Частная функция невязки для глубины источника и наилучшее из четырех эквивалентных решений приведены на рис. 1б и 1в. Полученные значения углов простирания, падения и подвижки: 33, 89 и 91° соответственно. Полученное значение сейсмического момента равно 0.46 × 1022 Н м. Это значение соответствует значению моментной магнитуды Mw = = 8.4. Наша оценка глубины наилучшего точечного источника равна 10 км.
Рис. 1.
Карта станций регистрации поверхностных волн, использованных для определения параметров точечного мгновенного источника. Темные треугольники соответствуют волнам Рэлея, светлые треугольники – волнам Лява (а). Частная функция невязки для глубины источника (б). Оптимальное решение в приближении двойного диполя (в).
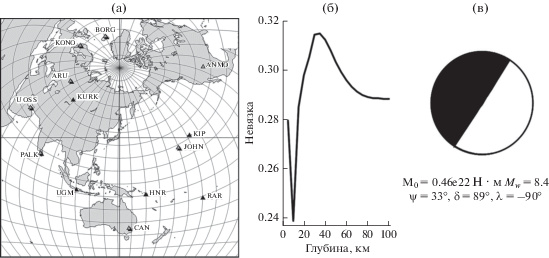
Таблица 1.
Фокальные механизмы и фазовые невязки для четырех эквивалентных решений, полученных из анализа амплитудных спектров поверхностных волн
| Номер решения | Угол падения, град | Угол простирания, град | Угол подвижки, град | Нормированная фазовая невязка |
|---|---|---|---|---|
| 1 | 89 | 33 | 91 | 0.345 |
| 2 | 89 | 213 | 91 | 0.483 |
| 3 | 89 | 213 | –89 | 0.621 |
| 4 | 89 | 33 | –89 | 0.717 |
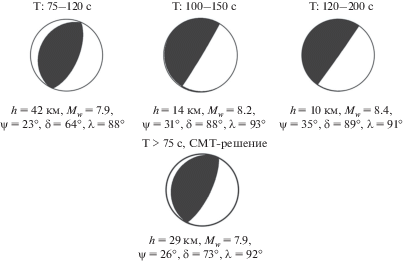
Решение, полученное нами, не совпадает с решением из Глобального СМТ каталога33. Это связано с выбранным диапазоном периодов. Дело в том, что при перемещении этого диапазона из области периодов, недостаточно длинных для использования приближения точечного мгновенного источника, в область более длинных периодов оценки параметров очага существенно изменяются. Когда же периоды становятся достаточно длинными и указанное приближение – адекватным, оценки параметров перестают изменяться с дальнейшим ростом периодов. Поэтому нами был выбран диапазон периодов от 100 до 200 с. Если же использовать диапазон более коротких периодов (от 75 до 120 с), то решение совпадает с решением из Глобального СМТ-каталога, как видно из рис. 2.
Для исследования оценки погрешности для афтершока в Тохоку методом “складного ножа” применялась следующая детализация параметрической сетки: угол падения с шагом 0.1° от 86° до 90°, угол простирания с шагом 0.5° от 14° до 58°, угол подвижки с шагом 0.2° от 86° до 97° и глубина с шагом 0.5 км от 5 до 20 км, количество используемых записей n = 20. Результаты приведены в табл. 2.
Таблица 2.
Оценка погрешности методом “складного ножа” для афтершока в Тохоку
| Параметры | Угол падения, град | Угол простирания, град | Угол подвижки, град | Глубина, км |
|---|---|---|---|---|
| Среднее значение | 89.09 | 34.45 | 90.75 | 10.35 |
| Оценка погрешности | 0.46 | 6.78 | 1.03 | 5.56 |
Полученные значения оценки погрешности являются вполне допустимыми. Можно утверждать, что используемый набор записей и выбранная детальность параметрической сетки являются достаточными для определения параметров очага. Иначе решение может быть получено с большой ошибкой. Так мелкофокусное землетрясение, одна из нодальных плоскостей которого является субгоризонтальной, требует высокой детальности параметрической сетки. Это связано с тем, что небольшие изменения угла падения существенно меняют диаграмму поверхностно-волнового излучения и оценку моментной магнитуды события [Букчин, 2006; Bukchin et al., 2010].
ЗЕМЛЕТРЯСЕНИЕ В НЕПАЛЕ 25.04.2015, Mw = 7.9
Для оценки сейсмического момента, фокального механизма и глубины наилучшего двойного диполя для землетрясения в Непале мы использовали амплитудные спектры основных мод Лява и Рэлея в спектральной полосе от 200 до 250 с. С помощью программ спектрально-временного анализа и плавающей фильтрации были отобраны 15 записей волн Лява и 16 записей волн Рэлея, зарегистрированных станциями мировых сетей IRIS и GEOSCOPE. Расположение этих станций приведено на рис. 3а. Обозначения – те же, что и на рис. 1а. В табл. 3 представлены фокальные механизмы и фазовые невязки для четырех эквивалентных решений, полученных из анализа амплитудных спектров поверхностных волн. Как видно из таблицы, оптимальным является решение 1. Частная функция невязки для глубины источника и наилучшее из четырех эквивалентных решений приведены на рис. 3б и 3в. Для фокального механизма были получены следующие значения углов: 102° для угла простирания, 84° для угла падения и 90° для угла подвижки. Фокальный механизм представлен на рис. 3б. Для глубины наилучшего точечного источника было получено значение 12 км, а для сейсмического момента значение 0.8 × 1021 Н м, которое соответствует значению магнитуды Mw = 7.9. Данное решение существенно не отличается от решения из Глобального СМТ-каталога3.
Рис. 3.
Карта расположения станций (а). Частная функция невязки для глубины источника (б). Оптимальное решение в приближении двойного диполя (в). Обозначения – те же, что и на рис. 1.
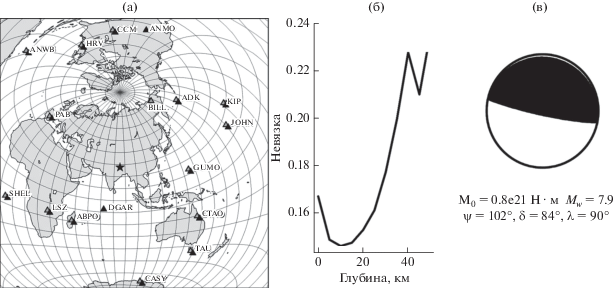
Таблица 3.
Фокальные механизмы и фазовые невязки для четырех эквивалентных решений, полученных из анализа амплитудных спектров поверхностных волн
| Номер решения | Угол падения, град | Угол простирания, град | Угол подвижки, град | Нормированная фазовая невязка |
|---|---|---|---|---|
| 1 | 84 | 102 | 90 | 0.253 |
| 2 | 84 | 282 | 90 | 0.325 |
| 3 | 84 | 282 | –90 | 0.612 |
| 4 | 84 | 102 | –90 | 0.718 |
Для исследования оценки погрешности методом “складного ножа” применялась следующая детализация параметрической сетки: угол падения с шагом 2° от 60° до 90°, угол простирания с шагом 2° от 80° до 140°, угол подвижки с шагом 2° от 60° до 120° и глубина с шагом 2 км от 0 до 40 км, количество записей n = 31. Результаты приведены в табл. 4.
Таблица 4.
Оценка погрешности методом “складного ножа” для землетрясения в Непале
| Параметры | Угол падения, град | Угол простирания, град | Угол подвижки, град | Глубина, км |
|---|---|---|---|---|
| Среднее значение | 85.23 | 106.71 | 92.77 | 5.42 |
| Оценка погрешности | 6.02 | 6.55 | 6.02 | 4.98 |
В данном случае большинство погрешностей больше, чем в случае с землетрясением в Тохоку. Это связано с тем, что шаг по углам гораздо больше и при этом землетрясение также неглубокое и одна из нодальных плоскостей субгоризонтальна. Но в то же время и записей рассматривается больше, поэтому погрешности принимают допустимые значения.
АЛЯСКИНСКОЕ ЗЕМЛЕТРЯСЕНИЕ 23.01.2018, Mw = 7.9
Для оценки параметров землетрясения в приближении двойного диполя мы использовали амплитудные спектры основных мод Лява и Рэлея в спектральной полосе от 150 до 250 с. С помощью программ спектрально-временного анализа и плавающей фильтрации на 21 станции мировых сетей IRIS и GEOSCOPE были отобраны как записи волн Лява, так и записи волн Рэлея. Лишь на двух станциях (GUMO и АTD) записи волн Рэлея не были отобраны. Карта расположения станций приведена на рис. 4а. Обозначения – те же, что и на рис. 1а.
Рис. 4.
Карта расположения станций (а). Частная функции невязки для глубины источника (б). Оптимальное решение в приближении двойного диполя (в). Обозначения те же, что и на рис. 1.
Оптимальным из четырех эквивалентных решений, полученных из анализа амплитудных спектров поверхностных волн, считаем то, что наилучшим образом согласуется с зарегистрированными знаками первых вступлений. Функция невязки для глубины источника (оценка глубины равна 20 км) и его фокальный механизм (сдвиг с незначительным взбросом) приведены на рис. 4б и 4в. Полученная величина сейсмического момента 0.82 × 1021 Н м соответствует магнитуде Mw = 7.9. Данное решение существенно не отличается от решения из Глобального СМТ-каталога3.
Для исследования оценки погрешности методом “складного ножа” применялась следующая детализация параметрической сетки: угол падения с шагом 2° от 60° до 90°, угол простирания с шагом 2° от 60° до 120°, угол подвижки с шагом 2° от 0° до 60° и глубина с шагом 2 км от 0 до 50 км, количество записей n = 40. Результаты приведены в табл. 5.
Таблица 5.
Оценка погрешности методом “складного ножа” для землетрясения в Аляске 23.01.2018 г.
| Параметры | Угол падения, град | Угол простирания, град | Угол подвижки, град | Глубина, км |
|---|---|---|---|---|
| Среднее значение | 75.35 | 260 | 22 | 20.45 |
| Оценка погрешности | 5.85 | 0 | 0 | 6.47 |
Как мы видим, в данном случае несколько погрешностей принимают нулевые значения. Это означает, что удаление любой из записей не приводит к изменению данных параметров. Шаг параметрической сетки такой же, как и в предыдущем рассматриваемом событии. Наличие нулевых погрешностей мы связываем с большим количеством записей и с тем, что ни одна из нодальных плоскостей не является субгоризонтальной.
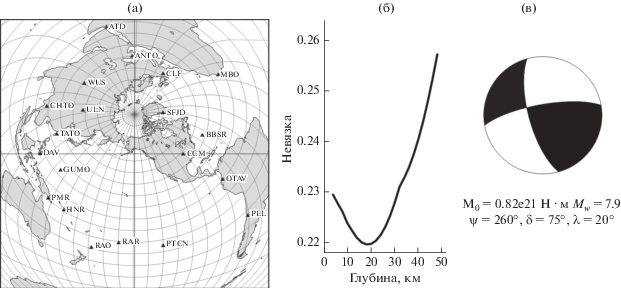
АЛЯСКИНСКОЕ ЗЕМЛЕТРЯСЕНИЕ 30.11.2018, Mw = 7.1
Для оценки фокального механизма и глубины источника мы использовали спектры 18 основных моды Лява и 19 мод Рэлея в полосе периодов от 70 до 250 с. Карта распределения использованных станций сейсмических сетей IRIS и GEOSCOPE приведена на рис. 5а. Функция невязки для глубины источника (оценка глубины равна 65 км) и его фокальный механизм приведены на рис. 5б и 5в. Полученная величина сейсмического момента 0.54 × 1020 Н м соответствует магнитуде Mw = 7.1. Для выбора наилучшего из эквивалентных решений использовали знаки первых вступлений Р-волн. Полученное решение существенно не отличается от решения из Глобального СМТ-каталога3.
Рис. 5.
Карта расположения станций (а). Частная функция невязки для глубины источника (б). Оптимальное решение в приближении двойного диполя (в). Обозначения – те же, что и на рис. 1.
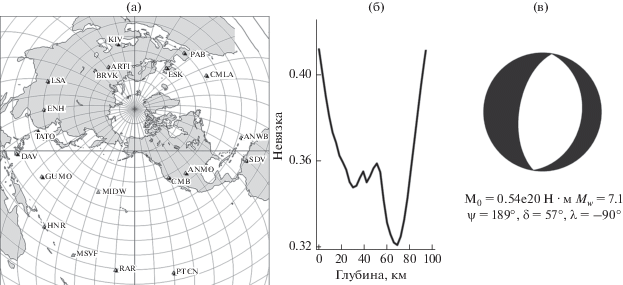
Для исследования оценки погрешности методом “складного ножа” применялась следующая детализация параметрической сетки: угол падения с шагом 3° от 45° до 90°, угол простирания с шагом 3° от 0° до 90°, угол подвижки с шагом 3° от 0° до 120° и глубина с шагом 3 км от 20 до 80 км, количество записей n = 37. Результаты приведены в табл. 6.
Таблица 6.
Оценка погрешности методом “складного ножа” с шагом 3° для землетрясения в Аляске 30.11.2018 г.
| Параметры | Угол падения, град | Угол простирания, град | Угол подвижки, град | Глубина, км |
|---|---|---|---|---|
| Среднее значение | 57.00 | 188.59 | –89.76 | 65.49 |
| Оценка погрешности | 0.00 | 6.15 | 4.91 | 6.63 |
Также для анализа влияния шага параметрической сетки и набора записей для данного события приведем таблицу с шагом по углам в 2°. Результаты приведены в табл. 7.
Таблица 7.
Оценка погрешности методом “складного ножа” с шагом 2° для землетрясения в Аляске 30.11.2018 г.
| Параметры | Угол падения, град | Угол простирания, град | Угол подвижки, град | Глубина, км |
|---|---|---|---|---|
| Среднее значение | 57.16 | 186 | –88 | 65.49 |
| Оценка погрешности | 3.28 | 0.00 | 0.00 | 0.00 |
Для данного события рассматривается почти такое же количество записей как и для предыдущего рассмотренного события на Аляске. Приведенные таблицы соответствуют различным шагам параметрической сетки. Как мы видим, уменьшение шага приводит к тому, что единственный параметр, погрешность которого ненулевая – это угол падения. Все остальные параметры никак не меняются при удалении любой из записей. Это связано с тем, что используемый набор записей довольно представительный и при этом само землетрясение глубже, чем предыдущие.
ВЫВОДЫ
Определение фокального механизма и глубины очага землетрясения по спектрам поверхностных волн заставляет нас задуматься о влиянии используемого набора записей на качество полученного решения. Исследование, предложенное в данной работе, показало, что в зависимости от параметров очага землетрясения, количества записей и шага параметрической сетки это влияние может быть различным. Так, мы видим на примере Аляскинских землетрясений, что в случае, когда у нас достаточно много записей (40 и 37) и ни одна из нодальных плоскостей источника не является субгоризонтальной, удаление любой записи никак не влияет на некоторые параметры (оценка погрешности равна 0). При этом уменьшение шага параметрической сетки приводит к уменьшению количества изменяемых параметров, как это видно на втором рассмотренном Аляскинском землетрясении, где при шаге параметрической сетки в 2°, удаление записи отражается только на угле падения. Для землетрясения в Непале подобный шаг продолжает влиять на оценку погрешностей. Это связано с меньшим количеством записей и параметрами самого землетрясения. В то же время, рассматривая афтершок в Тохоку, мы видим, что даже шаг параметрической сетки меньше 1° не влечет за собой нулевых оценок. Это объясняется тем, что используется только 20 записей, одна из нодальных плоскостей источника является субгоризонтальной, а его глубина значительно меньше длины волны. В этом случае небольшие изменения угла падения существенно меняют диаграмму поверхностно-волнового излучения и оценку моментной магнитуды события. В перспективе предполагается дальнейшее детальное изучение зависимостей точности определения параметров землетрясений от используемого набора данных.
Список литературы
Букчин Б.Г., Левшин А.Л., Ратникова Л.И., Дост Б., Нолет Г. Оценка пространственно-временных характеристик очага Спитакского землетрясения по широкополосным записям поверхностных волн. Проблемы прогноза землетрясений и интерпретация сейсмических данных // Вычислительная сейсмология. Вып. 25. М.: Наука. 1992. С. 238–250.
Букчин Б.Г. Особенности излучения поверхностных волн мелкофокусным источником // Физика Земли. № 8. 2006. С. 88–93.
Букчин Б.Г., Фомочкина А.С., Панца Ж.Ф. Определение параметров очагов землетрясений с высоким разрешением. Современные методы обработки и интерпретации сейсмологических данных. Материалы Десятой Международной сейсмологической школы. Обнинск: ГС РАН. 2015. С. 49–53.
Ландер А.В., Левшин А.Л., Писаренко В.Ф., Погребинский Г.А. О спектрально-временном анализе колебаний. Вычислительные и статические методы интерпретации сейсмических данных // Вычислительная сейсмология. Вып. 6. М.: Наука. 1973. С. 236–249.
Bukchin B., Clévédé E., Mostinskiy A. Uncertainty of moment tensor determination from surface wave analysis in case of shallow earthquake // J. Seismology. 2010. V. 14. № 3. P. 601–614.
Lasserre C., Bukchin B., Bernard P., Tapponnier P., Gaudemer Y., Mostinsky A., Rong Dailu Source parameters and tectonic origin of the June 1st, 1996 Tianzhu (Mw = 5.2) and July 21st, 1995 Yongden (Mw = 5.6) earthquakes, near Haiyuan fault (Gansu, China) // Geophysical J. International. 2001. V. 144. P. 206–220.
Quenouille M.H. Approximate Tests of Correlation in Time-Series // J. Royal Statistical Society, Series B. 1949. V. 11. P. 68–84.
Tichelaar B.W., Ruff L.J. How Good Are Our Best Models? Jackknifing, Bootstrapping, and Earthquake Depth // Eos. 1989. V. 70. № 20. P. 593–606.
Tukey J.W. “Bias and Confidence in Not-quite Large Samples (Preliminary Report)”. Annals of Mathematical Statistics. 1958. V. 29(2). P. 614.
Дополнительные материалы отсутствуют.