1. На главную
  2. Электронные версии
  3. Физика Земли
  4. № 1, 2020

Физика Земли, 2020, № 1, стр. 118-132

О кинематической генерации магнитных мод блоховского типа

В. А. Желиговский 1, *, Р. А. Чертовских 2, **

1 Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия

2 Исследовательский центр систем и технологий (SYSTEC), Университет Порту
Порту, Португалия

* E-mail: vlad@mitp.ru
** E-mail: roman@fe.up.pt

Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019

Полный текст (PDF)

Аннотация

Рассмотрена кинематическая генерация течением электропроводной жидкости, периодическим в пространстве, магнитных мод вида произведения трехмерного поля, имеющего такую же периодичность, на гармонику Фурье с произвольным постоянным волновым вектором ${\mathbf{q}}.$ Приведены примеры расчета магнитных мод с максимальным по ${\mathbf{q}}$ инкрементом роста для поля скорости общего положения, в котором присутствует магнитный $\alpha $-эффект, и для центрально-симметричного поля скорости, в котором $\alpha $-эффект отсутствует, но есть отрицательная магнитная вихревая диффузия. Показано, что магнитные моды с максимальным по ${\mathbf{q}}$ инкрементом роста характеризуются слабым разделением пространственных масштабов, поэтому ни один из указанных эффектов не может считаться основным механизмом их генерации.

Ключевые слова: кинематическое магнитное динамо, генерация магнитного поля, теорема Блоха, магнитный α-эффект, отрицательная магнитная вихревая диффузия.

1. ВВЕДЕНИЕ

Направление исследований по теории магнитного динамо в ИТПЗ (тогда еще Отделе вычислительной геофизики ИФЗ АН СССР) было заложено во второй половине 1980-х гг. в работах М.М. Вишика. В статьях [Вишик, 1986; 1987] он рассмотрел задачу о длинномасштабном кинематическом динамо для стационарного потока электропроводной жидкости, в которой считается, что характерные пространственные масштабы магнитных мод значительно превышают пространственный период течения. Отношение этих масштабов $\varepsilon $ – малый параметр задачи, и решение – длинномасштабная магнитная мода, т.е. собственная функция оператора магнитной индукции и отвечающее ей собственное значение – были разложены в степенные ряды по этому параметру. Используя теорию возмущения линейных эллиптических операторов [Като, 1972], он доказал, что при определенных условиях построенные ряды сходятся. В работе [Вишик, 1987] был математически строго рассмотрен пример течения, в котором присутствует магнитный $\alpha $-эффект (названный в этой статье $\gamma $-эффектом), предсказанный в работе [Steenbeck et al., 1966] (см. также [Краузе, Рэдлер, 1984]) на физическом уровне строгости. (Разложения [Вишик, 1987] эквивалентны разложениям [Roberts, 1970], если магнитная мода имеет вид короткомасштабного поля, амплитудно-модулированного длинномасштабной гармоникой Фурье; они были построены независимо от работы [Roberts, 1970], тогда нам неизвестной.) В дальнейшем, М.М. Вишик [1988] построил разложение в степенной ряд по $\sqrt \eta $ функции Грина оператора магнитной индукции и использовал его для доказательства невозможности быстрого динамо при отсутствии у течения траекторий с положительными показателями Ляпунова (где $\eta $ – коэффициент магнитной молекулярной диффузии). Этот результат был впоследствии уточнен в работе [Klapper, Young, 1995], где выведены оценки для инкремента роста магнитного поля в терминах топологической энтропии потока.

Одновременно проводились численные [Соловьев, 1985а; б; 1987а; б] и численно-аналитические [Рузмайкин и др., 1989] исследования генерации магнитного поля осесимметрическим течением Куэтта–Пуазейля. Это винтовое течение несжимаемой жидкости между двумя соосными цилиндрами, вращающимися с разными угловыми скоростями, описываемое решением бессилового уравнения Навье–Стокса с ненулевым градиентом давления. В цилиндрической системе координат скорость этого течения имеет три компоненты, зависящие определенным образом от расстояния $r$ до общей оси цилиндров, но не от высоты $z$ вдоль оси цилиндра и азимута $\phi ,$ поэтому магнитные моды имеют вид $H(r)exp({\text{i}}(n\phi + \alpha z)),$ где $n$ и $\alpha $ – соответственно целочисленный и действительный параметры задачи. Было численно показано для различных краевых условий, что такое течение способно возбуждать магнитное поле, которое концентрируется вокруг цилиндра определенного радиуса. ВКБ-методом было построено разложение профиля магнитной моды как функции радиуса по степеням $R_{m}^{{ - 1/4}}$ (где ${{R}_{m}}$ – магнитное число Рейнольдса) и выведено уравнение для определения радиуса концентрации магнитного поля.

Совместное использование аналитических и вычислительных методов оказалось плодотворным также и для исследования кинематической генерации длинномасштабного магнитного поля стационарными пространственно-периодическими короткомасштабными течениями в пределе существенного разделения масштабов (см. [Желиговский, 2010] и расширенный перевод этой монографии на английский язык [Zheligovsky, 2011]). В этом случае наличие или отсутствие генерации определяется свойствами предельного дифференциального оператора в медленных пространственных переменных ${\mathbf{X}} = \varepsilon {\mathbf{x}}$, для которого старшие члены разложения магнитной моды, усредненной по быстрым переменным, и ее собственного значения являются собственной функцией и собственным значением соответственно.

В общем случае (в частности при отсутствии симметрий у потока), в течении наблюдается магнитный $\alpha $-эффект. В этом случае предельный оператор – т.н. оператор $\alpha $-эффекта – дифференциальный оператор первого порядка по медленным переменным (диффузионное слагаемое в нем отсутствует). Его спектр симметричен относительно мнимой оси [Вишик, 1987], что гарантирует возбуждение длинномасштабных магнитных мод с инкрементами роста порядка $\varepsilon .$ Однако в классе течений, имеющих зеркальную антисимметрию относительно некоторой плоскости, спектр оператора $\alpha $-эффекта чисто мнимый, т.е. $\alpha $-эффект способен только поддерживать гармонические колебания магнитных мод на временных масштабах порядка $1{\text{/}}\varepsilon $ [Andrievsky et al., 2019a]. В этом случае генерация также гарантирована, но она обеспечена действием другого механизма – отрицательной магнитной вихревой диффузии, описываемой т.н. оператором вихревой диффузии – дифференциальным оператором второго порядка по медленным переменным.

Явление магнитной вихревой (турбулентной) диффузии естественно изучать на примере течений, имеющих центр симметрии, поскольку $\alpha $-эффект у них отсутствует. В отличие от $\alpha $-эффекта, наличие магнитной вихревой диффузии не гарантирует работу длинномасштабного магнитного динамо. Генерация происходит, если вихревая диффузия отрицательна, т.е. если усредненное взаимодействие флуктуирующих компонент поля скорости и магнитного поля способно нейтрализовать молекулярную диффузию; при этом инкремент роста магнитного поля порядка ${{\varepsilon }^{2}}.$ Впервые это явление было обнаружено численно в трехмерных течениях [Roberts, 1972], зависящих от двух пространственных переменных, и в модифицированном течении Тейлора–Грина [Lanotte et al., 1999], зависящем от всех трех переменных.

Тензоры магнитного $\alpha $-эффекта и магнитной вихревой диффузии были выведены в работах [Вишик, 1987; Lanotte et al., 1999] в терминах решений вспомогательных задач, описывающих флуктуирующую часть первых членов разложения длинномасштабных магнитных мод. Эти тензоры можно также выразить через решения вспомогательных задач для оператора, сопряженного к оператору магнитной индукции [Zheligovsky, 2011; Andrievsky et al., 2015] с использованием эквивалентности сопряженного оператора оператору магнитной индукции для обратного потока. Данные представления удобны как для проведения расчетов (число вспомогательных задач, которые необходимо решить для вычисления тензора магнитной вихревой диффузии, вдвое меньше, чем при использовании исходного выражения [Lanotte et al., 1999]), так и для анализа длинномасштабной генерации (например, с их помощью в работах [Andrievsky et al., 2015; Rasskazov et al., 2018] установлено, как связаны между собой тензоры для некоторого потока ${\mathbf{v}}$ и противоположного ему $ - {\mathbf{v}}$). Отметим, что решения вспомогательных задач и для оператора магнитной индукции, и для сопряженного к нему легко разложить в степенной ряд по малому магнитному числу Рейнольдса ${{R}_{m}},$ а тогда при умеренных ${{R}_{m}}\, \lesssim \,100$ тензоры $\alpha $-эффекта и вихревой диффузии можно вычислять, используя Паде-аппроксимации достаточно большого порядка сумм таких степенных рядов для элементов этих тензоров [Gama et al., 2019]. Для магнитных мод, генерируемых $\alpha $-эффектом или вихревой диффузией, и имеющих вид короткомасштабного поля (т.е. поля, имеющего те же пространственные периоды, что и поле скорости), амплитудно-модулированного длинномасштабной гармоникой Фурье, аналитически найдены инкременты роста (см. [Rasskazov et al., 2018]); в случае $\alpha $-эффекта полученные выражения эквивалентны независимо найденным ранее в работе [Roberts, 1970]).

В рамках теории динномасштабного динамо показана несущественность для генерации наличия спиральности у генерирующего течения. Спиральность некоторого соленоидального поля ${\mathbf{f}}$ есть пространственное среднее скалярного произведения ${\mathbf{f}} \cdot \Phi ,$ где $\Phi $ – векторный потенциал поля ${\mathbf{f}} = {\text{rot}}{\kern 1pt} \Phi ;$ она является важной топологической характеристикой ${\mathbf{f}},$ а именно степени заузленности интегральных (силовых) линий этого поля [Moffatt, Ricca, 1992]. Эвристически, генерируют магнитные поля течения достаточно сложной структуры, поэтому естественны предположения о связи способности потока быть динамо со спиральностью поля скорости течения ${\mathbf{v}}$ [Краузе, Рэдлер, 1984; Rädler, Brandenburg, 2008; Moffatt, 2014] (в т.ч. поскольку в идеальной магнитогидродинамике магнитное поле имеет свойство вмороженности [Моффат, 1980]) или с т.н. кинетической спиральностью, т.е. спиральностью завихренности ${\text{rot}}{\kern 1pt} {\kern 1pt} {\mathbf{v}}$ (см., например, [Moffatt, 2016]; наличие такой зависимости представляло бы интерес, поскольку при естественных краевых условиях интеграл этой спиральности по всему объему идеальной жидкости, а также по специально выбранным подобъемам внутри нее – гидродинамические инварианты [Moreau, 1961; Moffatt, 1969]). Эта связь была продемонстрирована в некоторых частных случаях: при некоторых дополнительных предположениях вычисленный в электродинамике средних полей коэффициент $\alpha $-эффекта изотропной турбулентности пропорционален средней кинетической спиральности в пределе большой проводимости (см., например, [Rädler, 2007]); это же соотношение было выведено в работе [Moffatt, 1974] в лагранжевых координатах для вращательно-симметричной турбулентности идеальной магнитогидродинамики. В пределе малых локальных магнитных чисел Рейнольдса коэффициент турбулентного $\alpha $-эффекта выражается через спектр спиральности [Moffatt, 1970; Moffatt, Proctor, 1982], непосредственно связанный со спиральностью завихренности.

Эти результаты объясняют повышенное внимание исследователей к проявлениям спиральности в МГД-системах (так, на момент написания данной статьи Google дает 12200 результатов по запросу “kinetic helicity”). Такое внимание мало оправдано. Первые контрпримеры к тезису о важности кинетической спиральности для способности течения быть гидромагнитным динамо были построены десятилетия назад: в работе [Gilbert et al., 1988] опровергнута необходимость для генерации наличия у течения ненулевого спектра спиральности, а в работе [Zheligovsky, Galloway, 1998] показано, что гексагональное течение Кристоферсона [Christopherson, 1940] способно кинематически генерировать короткомасштабное магнитное поле, хотя плотность спиральности завихренности этого течения равна нулю в каждой точке пространства:

(1)
${\mathbf{v}} \cdot {\text{rot}}\,{\mathbf{v}} = 0.$

“Для работы длинномасштабного нелинейного динамо не требуется много спиральности” [Graham et al., 2012]. В статье [Rasskazov et al., 2018] описано 6 семейств стационарных трехмерных потоков с поточечно нулевой спиральностью завихренности (1), и численно показано на многих примерах, что течения пяти из этих семейств могут кинематически генерировать при достаточно малой молекулярной диффузии и короткомасштабные магнитные поля, и длинномасштабные посредством обоих механизмов – как с помощью $\alpha $-эффекта, так и отрицательной вихревой диффузии. Рассматривая в качестве течений поля ${\text{rot}}{\kern 1pt} {\kern 1pt} {\mathbf{w}}$ для полей ${\mathbf{w}},$ найденных в работе [Rasskazov et al., 2018], было также численно показано [Andrievsky et al., 2019b], что и течения с поточечно нулевой спиральностью поля скорости способны генерировать и короткомасштабные, и длинномасштабные магнитные поля. Поскольку течения четырех семейств из пяти, для которых проводились вычисления, имеют нулевой спектр спиральности, полученные результаты показывают, что спиральности полей вида ${{( - \Delta )}^{\beta }}{\mathbf{v}}$ или ${{( - \Delta )}^{\beta }}{\text{rot}}\,{\mathbf{v}}$ (где $\Delta $ – оператор Лапласа, а $\beta $ – произвольное действительное число) не характеризуют способность течения ${\mathbf{v}}({\mathbf{x}})$ несжимаемой жидкости функционировать в качестве динамо. Напротив, доказано [Andrievsky et al., 2015], что элементы вычисленного асимптотическими методами в пределе сильного разделения масштабов симметризованного тензора $\alpha $-эффекта пропорциональны спиральностям $\int_{{{\mathbb{T}}^{3}}} {{{\mathbf{s}}}_{n}} \cdot {\text{rot}}\,{{{\mathbf{s}}}_{k}}{\text{d}}{\mathbf{x}}$ токов ${\text{rot}}\,{{{\mathbf{s}}}_{k}},$ связанных с нейтральными магнитными модами ${{{\mathbf{s}}}_{k}};$ здесь ${{\mathbb{T}}^{3}}$ – параллелепипед периодичности короткомасштабного течения и мод ${{{\mathbf{s}}}_{n}}.$

Теория длинномасштабной МГД устойчивости также применима для исследования слабонелинейных возмущений МГД и конвективных гидромагнитных режимов. В работе [Chertovskih et al., 2010] были рассмотрены ветви режимов, возникающие при тепловой конвекции электропроводной жидкости в бесконечном горизонтальном слое, параметризованные скоростью его вращения относительно вертикальной оси. Численное изучение слабонелинейных длинномасштабных возмущений этого потока показало [Chertovskih, Zheligovsky, 2015], что либо с течением времени они затухают, либо демонстрируют сингулярное поведение: наблюдается их рост и коллапс за конечное время.

Однако указанные результаты, как было сказано, получены в предположении значительного разделения масштабов, при котором отношение масштабов $\varepsilon $ инфинитезимально мало, и вывод о наличии динамо или о поведении слабонелинейного возмущения определяется первым членом разложения инкремента роста магнитного поля или возмущения по этому параметру. С точки зрения физических приложений представляет большой интерес вопрос о том, как эти результаты меняются в случае, когда отношение масштабов конечно, и, в частности, при каком $\varepsilon $ инкремент роста максимален. Асимптотических решений для ответа на этот вопрос недостаточно: инкременты роста магнитного поля пропорциональны $\varepsilon $ и ${{\varepsilon }^{2}}$ для случая магнитного $\alpha $-эффекта и вихревой диффузии, соответственно, что побуждает рассматривать как можно большие $\varepsilon ,$ но для больших $\varepsilon $ асимптотические решения непригодны. Настоящая статья посвящена рассмотрению данного вопроса в приложении к кинематическим динамо.

Математическая постановка задачи приведена в следующем разделе. В разделе 3 выведено точное расчетное выражение для градиента инкремента роста магнитного поля как функции волнового вектора ${\mathbf{q}}$ плоской волны, осуществляющей амплитудную модуляцию магнитной моды, и найдены некоторые ${\mathbf{q}},$ при которых выполнено условие локального максимума: этот градиент равен 0. В разделе 4 приведены результаты расчетов максимального по ${\mathbf{q}}$ инкремента роста таких магнитных мод для двух модельных течений. В последнем разделе мы интерпретируем их как указывающие на отсутствие необходимости магнитного $\alpha $‑эффекта и вихревой диффузии, основанных на разделении пространственных масштабов, для генерации магнитного поля планет земного типа.

2. ПОСТАНОВКА ЗАДАЧИ

В задаче кинематического динамо предполагается, что магнитное поле настолько слабо, что сила Лоренца не оказывает воздействия на течение электропроводной жидкости [Моффат, 1980]. Если скорость течения v(x) стационарна, то она эквивалентна задаче на собственные значения:

(2)
$\mathfrak{L}{\mathbf{B}} = \lambda {\mathbf{B}}$
для оператора магнитной индукции

$\mathfrak{L}:{\mathbf{B}} \mapsto \eta \Delta {\mathbf{B}} + {\text{rot}}({\mathbf{v}} \times {\mathbf{B}}).$

Магнитная мода ${\mathbf{B}}$ – это собственная функция оператора $\mathfrak{L},$ а действительная часть собственного значения $\lambda $ – ее инкремент роста. В дальнейшем считаем, что скорость имеет период $2\pi $ по каждой декартовой переменной ${{x}_{i}},$ и что жидкость несжимаема, т.е. поле скорости (как и магнитная мода) соленоидально.

При изучении возбуждения длинномасштабного поля предполагают [Желиговский, 2010; Zheligovsky, 2011], что магнитная мода зависит не только от быстрой пространственной переменой ${\mathbf{x}}$, но и от медленной ${\mathbf{X}} = \varepsilon {\mathbf{x}}.$ Моду и собственное значение раскладывают в степенной ряд по малому отношению масштабов $\varepsilon {\text{:}}$

${\mathbf{B}} = \sum\limits_{n = 0}^\infty {{{{\mathbf{B}}}_{n}}({\mathbf{X}},{\mathbf{x}}){\kern 1pt} {\kern 1pt} {{\varepsilon }^{n}}} ,\,\,\,\,\lambda = \sum\limits_{n = 0}^\infty {{{\lambda }_{n}}{{\varepsilon }^{n}}} .$

Подстановкой этих рядов в (2) получают иерархию уравнений, последовательно решая которые, можно вычислить все члены разложений. Это линейные неоднородные эллиптические уравнения в частных производных по быстрым переменным. Условия их разрешимости принимают вид уравнений в частных производных по медленным переменным. Первое из них – задача на собственные значения, определяющая среднее главного члена разложения магнитного поля и главный член разложения собственного значения. Для течений общего вида она оказывается задачей на собственные значения для оператора $\alpha $-эффекта, а, например, если v(x) имеет центр симметрии, то тензор $\alpha $-эффекта равен нулю, и возникает задача на собственные значения для оператора вихревой диффузии. В обоих случаях она допускает решения, в которых собственная функция – гармоника Фурье по медленным переменным; тогда все члены разложения моды оказываются пропорциональны этой гармонике, т.е. мода представляет собой короткомасштабное поле, амплитудно-модулированное длинномасштабной гармоникой. Однако эту задачу на собственные значения можно поставить в конечной области медленных переменных, на границе которой заданы физически значимые краевые условия для среднего поля, отличные от условия пространственной периодичности; тогда длинномасштабная модуляция магнитных мод имеет другую, более сложную структуру.

Нас интересует решение задачи о динамо, в котором дополнительный пространственный масштаб магнитной моды, независимый от пространственных периодов течения, не обязательно бесконечно длинный. Как и при использовании подхода теории устойчивости к длинномасштабным возмущениям, возможно численное решение задачи в быстрых переменных в кубе периодичности течения ${{\mathbb{T}}^{3}} = {{[0,2\pi ]}^{3}},$ но для решения полной задачи во всем пространстве компьютерные ресурсы недостаточны. Поэтому, в отличие от случая бесконечного малого отношения масштабов, содержательное рассмотрение возможно только для магнитных мод ${\mathbf{B}}$, модулированных гармоникой Фурье:

(3)
${\mathbf{B}} = {{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}({\mathbf{x}}),$
где короткомасштабный вектор ${\mathbf{b}}$ имеет те же периоды, что и поле скорости. В этом случае в уравнении (2) экспонента $exp({\text{i}}{\mathbf{q}} \cdot {\mathbf{x}})$ сокращается, и оно редуцируется в задачу на собственные значения в кубе периодичности ${{\mathbb{T}}^{3}}$ для ${\mathbf{b}}$, как и требовалось. Функции вида (3) возникают в физике твердого тела: по теореме Блоха [Bloch, 1929] решение уравнения Шредингера с пространственно-периодическим потенциалом, описывающее состояние электронов с энергией, принадлежащей разрешенной зоне, имеет вид произведения функции такой же периодичности на плоскую волну. Анзац (3) часто применяется в теории динамо, например, так вводилась длинномасштабность моды при изучении $\alpha $-эффекта в работе [Roberts, 1970], а также зависимость магнитного поля от координат, от которых не зависит поле скорости, в работах [Roberts, 1972; Соловьев, 1985а; б; 1987а; б; Рузмайкин и др., 1989]. В подобном исследовании [Zheligovsky et al., 2001] вычисления проведены для волновых векторов ${\mathbf{q}}$ с компонентами только 0 и 1/2 (что было вызвано недостаточной мощностью доступного для выполнения той работы компьютера).

Для моды (3) получаем из (2) задачу на собственные значения:

(4)
$\mathfrak{M}{\mathbf{b}} = \lambda ({\mathbf{q}}){\mathbf{b}},$
для оператора

(5.1)
$\mathfrak{M}:{\mathbf{b}} \mapsto {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}\mathfrak{L}({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}) = $
(5.2)
$ = \mathfrak{L}{\mathbf{b}} + 2{\text{i}}\eta ({\mathbf{q}} \cdot \nabla ){\mathbf{b}} - \eta {{\left| {\mathbf{q}} \right|}^{2}}{\mathbf{b}} + {\text{i}}{\mathbf{q}} \times ({\mathbf{v}} \times {\mathbf{b}}).$

Необходимо найти волновой вектор ${\mathbf{q}},$ для которого (при данном $\eta $) инкремент роста моды (3) $\gamma ({\mathbf{q}}) = {\text{Re}}\lambda ({\mathbf{q}})$ максимален. Достаточно рассмотреть ${\mathbf{q}}$ в кубе $\left| {{{q}_{k}}} \right| \leqslant 1{\text{/}}2,$ поскольку:

${{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}} = {{{\text{e}}}^{{{\text{i}}({\mathbf{q}} - {\mathbf{n}}) \cdot {\mathbf{x}}}}}{{{\text{e}}}^{{{\text{i}}{\mathbf{n}} \cdot {\mathbf{x}}}}}{\mathbf{b}},$
и если вектор ${\mathbf{n}}$ имеет целочисленные компоненты, то поле ${{{\text{e}}}^{{{\text{i}}{\mathbf{n}} \cdot {\mathbf{x}}}}}{\mathbf{b}}$ имеет те же периоды, что и поле скорости ${\mathbf{v}}({\mathbf{x}}).$ Более того, согласно уравнению, комплексно-сопряженному к (4), инкременты роста у полей (3) с противоположными волновыми векторами одинаковы, поэтому достаточно найти максимум в параллелепипеде:

(6)
$\begin{gathered} \mathbb{Q} = {\text{\{ }}{\mathbf{q}}|0 \leqslant {{q}_{1}} \leqslant 1{\text{/}}2, - 1{\text{/}}2 \leqslant {{q}_{2}} \leqslant 1{\text{/}}2, \\ - 1{\text{/}}2 \leqslant {{q}_{3}} \leqslant 1{\text{/}}2{\text{\} }}. \\ \end{gathered} $

3. ЧИСЛЕННЫЙ ПОДХОД

Задачу на поиск максимума решали с помощью метода градиентного спуска [Press et al., 1997]. Производные инкремента $\gamma $ по компонентам вектора ${\mathbf{q}}$ можно вычислять, используя биортогональность собственных функций линейного оператора и сопряженного к нему. Дифференцирование (4) по ${{q}_{n}}$ дает

(7)
$\begin{gathered} (\mathfrak{M} - \lambda )\frac{{\partial {\mathbf{b}}}}{{\partial {{q}_{n}}}} + 2{\text{i}}\eta \frac{{\partial {\mathbf{b}}}}{{\partial {{x}_{n}}}} - 2\eta {{q}_{n}}{\mathbf{b}} + \\ + \,\,{\text{i}}{{{\mathbf{e}}}_{n}} \times ({\mathbf{v}} \times {\mathbf{b}}) = \frac{{\partial \lambda }}{{\partial {{q}_{n}}}}{\mathbf{b}}, \\ \end{gathered} $
где ${{{\mathbf{e}}}_{n}}$ – орт декартовой системы координат. Определим скалярное произведение $( \cdot , \cdot )$ в пространстве Лебега равенством:
$({{{\mathbf{b}}}_{1}},{{{\mathbf{b}}}_{2}}) = \int\limits_{{{\mathbb{T}}^{3}}} {{{{\mathbf{b}}}_{1}} \cdot \overline {{{{\mathbf{b}}}_{2}}} \,{\text{d}}{\mathbf{x}}} ,$
где черта означает комплексное сопряжение. Оператор $\mathfrak{M}{\text{*,}}$ сопряженный к $\mathfrak{M},$ находим из определяющего тождества $(\mathfrak{M}{{{\mathbf{b}}}_{1}},{{{\mathbf{b}}}_{2}})$ = $({{{\mathbf{b}}}_{1}},\mathfrak{M}{\text{*}}{{{\mathbf{b}}}_{2}}){\text{:}}$
(8.1)
$\mathfrak{M}{\text{*}}:{\mathbf{b}} \mapsto {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{{\mathfrak{L}}^{ * }}({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}) = $
(8.2)
$ = \mathfrak{L}{\text{*}}({\mathbf{b}}) + 2{\text{i}}\eta ({\mathbf{q}} \cdot \nabla ){\mathbf{b}} - \eta {{\left| {\mathbf{q}} \right|}^{2}}{\mathbf{b}} - {\text{i}}{\mathbf{v}} \times ({\mathbf{q}} \times {\mathbf{b}}),$
где
(9)
$\mathfrak{L}{\text{*}}:{\mathbf{b}} \mapsto \eta \Delta {\mathbf{b}} - {\mathbf{v}} \times {\text{rot}}\,{\mathbf{b}}$
– оператор, сопряженный к $\mathfrak{L}.$ Когда $\mathfrak{M}$ имеет собственное значение $\lambda ,$ сопряженный оператор имеет собственное значение $\overline \lambda .$ Соответствующую собственную функцию $\mathfrak{M}{\text{*}}$ обозначим ${\mathbf{b}}{\text{*}}$ и нормируем ее соотношением:

(10)
$({\mathbf{b}},{\mathbf{b}}*) = 1.$

Скалярное умножение (7) на ${\mathbf{b}}{\text{*}}$ дает:

$2{\text{i}}\eta \left( {\frac{{\partial {\mathbf{b}}}}{{\partial {{x}_{n}}}},{\mathbf{b}}{\text{*}}} \right) - 2\eta {{q}_{n}} + {\text{i}}({\mathbf{v}} \times {\mathbf{b}},{\mathbf{b}}{\text{*}} \times {{{\mathbf{e}}}_{n}}) = \frac{{\partial \lambda }}{{\partial {{q}_{n}}}}.$

Градиент инкремента роста моды находим, как действительную часть этого равенства:

(11)
$\frac{{\partial \gamma }}{{\partial {{q}_{n}}}} = - 2\eta {\text{Im}}\left( {\frac{{\partial {\mathbf{b}}}}{{\partial {{x}_{n}}}},{\mathbf{b}}{\text{*}}} \right) - 2\eta {{q}_{n}} - {\text{Im}}({\mathbf{v}} \times {\mathbf{b}},{\mathbf{b}}{\text{*}} \times {{{\mathbf{e}}}_{n}}).$

Собственные функции ${\mathbf{b}}$ и ${\mathbf{b}}{\text{*,}}$ отвечающие доминирующим собственным значениям с максимальной (для данных ${\mathbf{q}}$ и $\eta $) действительной частью, вычисляли стандартным псевдоспектральным методом программой, описанной в [Zheligovsky, 1993]. Расчет результата действия оператора $\mathfrak{M}$ на данное поле ${\mathbf{b}}$ выполняли программой вычисления $\mathfrak{L}{\mathbf{b}},$ где согласно (5.1) целочисленные волновые числа ${{n}_{k}}$ при вычислении ротора и оператора Лапласа были заменены на ${{n}_{k}} + {{q}_{k}},$ без программирования дополнительных слагаемых $\mathfrak{M},$ явно выписанных в (5.2). Аналогично, условие соленоидальности моды (3) в терминах коэффициентов Фурье собственной функции

${\mathbf{b}} = \sum\limits_{\mathbf{n}} {{{{{\mathbf{\hat {b}}}}}_{{\mathbf{n}}}}{{{\text{e}}}^{{{\text{i}}{\mathbf{n}} \cdot {\mathbf{x}}}}}} $
принимает вид условия ортогональности ${{{\mathbf{\hat {b}}}}_{{\mathbf{n}}}}\, \cdot \,({\mathbf{n}}\, + \,{\mathbf{q}})$ = 0 для всех волновых векторов ${\mathbf{n}}.$

Для вычисления собственных функций ${\mathbf{b}}{\text{*}}$ оператора $\mathfrak{M}{\text{*}}$ применяли ту же программу с обращением поля скорости ${\mathbf{v}} \to - {\mathbf{v}}.$ Из (8.1) и равенства

(12)
$\mathfrak{M}{\text{*}}{\mathbf{b}}{\text{*}} = \overline \lambda {\mathbf{b}}{\text{*}}$
следует
(13)
${{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{{\mathfrak{L}}^{ - }}({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{F}}) = \overline \lambda {\mathbf{F}},$
где ${{\mathfrak{L}}^{ - }}$ – оператор магнитной индукции для обратного поля скорости (как и для случая оператора $\mathfrak{M},$ из-за наличия в (13) экспонент ${{{\text{e}}}^{{ \pm {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}$ вычисления проводятся в ${{\mathbb{T}}^{3}}$ со сдвигом волновых чисел ${{n}_{k}} \to {{n}_{k}} + {{q}_{k}}$) и

${\mathbf{F}} = {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\text{rot}}({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}{\text{*}}).$

Уравнение (12) эквивалентно

${{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}(\eta \Delta - \overline \lambda )({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}{\text{*}}) = {\mathbf{v}} \times {\mathbf{F}},$
где $\overline \lambda $ и правая часть становятся известны после решения задачи (13), а оператор слева легко обращается в пространстве коэффициентов Фурье.

В принципе, для решения задачи оптимизации можно решать систему трех уравнений

(14)
${{\partial \gamma } \mathord{\left/ {\vphantom {{\partial \gamma } {\partial {{q}_{n}}}}} \right. \kern-0em} {\partial {{q}_{n}}}} = 0.$
Заметим, однако, что выражения (11) для производных верны для собственных значений, остающихся при изменении ${{q}_{n}}$ на одной ветви, тогда как максимальные инкременты роста на разных интервалах ${{q}_{n}}$ могут отвечать разным ветвям, а в точках их сопряжения сохраняется непрерывность инкремента по ${{q}_{n}},$ но не его дифференцируемость. Дифференцируемость может также пропадать в концах ветвей, где происходят бифуркации. Такая негладкость – существенная помеха при решении системы нелинейных уравнений. Кроме того, при поиске глобального максимума необходимо найти все решения, что в случае нелинейной системы проблематично [Press et al., 1997].

Укажем некоторые решения системы (14). Условия локального максимума (14), очевидно, выполнены при ${\mathbf{q}} = 0,$ если собственное значение оператора магнитной индукции $\mathfrak{L}$ действительно, т.к. в этом случае собственные функции ${\mathbf{b}}$ и ${\mathbf{b}}{\text{*}}$ действительнозначны; при этом ограничений на кратность этого собственного значения нет. Пусть теперь все компоненты ${\mathbf{q}} \ne 0$ равны $ \pm 1{\text{/}}2$ или 0, а собственное значение $\lambda $ в задаче (4) действительно и однократно (такие решения (4) мы встречали в расчетах). Тогда, если ${\mathbf{b}}$ – решение задачи (4), то комплексное сопряжение этого равенства с учетом (5.1) показывает, что ${{{\text{e}}}^{{ - 2{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}\overline {\mathbf{b}} $ – тоже ее решение, имеющее период $2\pi $ по каждой переменной и отвечающее тому же $\lambda .$ В силу одномерности этого собственного подпространства, поля ${{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}({{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}\overline {\mathbf{b}} \pm {{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}),$ по крайней мере одно из которых не равно 0, – также из этого же подпространства. Следовательно, в качестве решения задачи (4) можно выбрать ${\mathbf{b}} = {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{f}}({\mathbf{x}}),$ где ${\mathbf{f}}$ – действительнозначное поле. Аналогично, из (8.1) и (12) находим, что собственная функция оператора $\mathfrak{M}{\text{*}},$ отвечающая этому же $\lambda ,$ имеет вид ${\mathbf{b}}{\text{*}} = {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{f}}{\text{*}}({\mathbf{x}}),$ где ${\mathbf{f}}{\text{*}}$ действительнозначно. Подставляя эти выражения в (11), находим, что два первых слагаемых справа взаимно сокращаются (и каждое из них равно 0, когда ${{q}_{n}} = 0$), а третье равно 0, т.е. равенства (14) выполнены. Отметим, однако, что для полей общего вида, обладающих магнитным $\alpha $-эффектом, среди решений такого вида системы уравнений (14) мы не встречали локальных максимумов инкремента роста.

В следующем разделе также рассмотрено возбуждение магнитного поля центрально-симметричным течением (т.е. ${\mathbf{v}}({\mathbf{x}}) = - {\mathbf{v}}( - {\mathbf{x}})$). Если в этом случае $\lambda $ – собственное значение оператора $\mathfrak{M},$ отвечающее собственной функции ${\mathbf{b}}({\mathbf{x}}),$ то поле $\overline {{\mathbf{b}}( - {\mathbf{x}})} ,$ как легко проверить, – тоже собственное, и отвечает собственному значению $\overline \lambda .$ Кроме того, в этом случае векторы ${\mathbf{q}},$ все компоненты которых равны $ \pm 1{\text{/}}2$ или 0, оказываются решениями системы (14) даже, если собственное значение $\lambda $ в задаче (4) комплексное. Для доказательства заметим, что в силу (5.1) и (4) уравнение для собственного значения $\overline \lambda ,$ как отмечено выше, можно представить в виде:

$\mathfrak{L}({{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}({{{\text{e}}}^{{2{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}\overline {{\mathbf{b}}( - {\mathbf{x}})} )) = \overline \lambda {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}({{{\text{e}}}^{{2{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}\overline {{\mathbf{b}}( - {\mathbf{x}})} ).$
Равенство, комплексно-сопряженное к этому, показывает, что ${{{\text{e}}}^{{ - 2{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}( - {\mathbf{x}})$ – собственная функция оператора $\mathfrak{M},$ отвечающая собственному значению $\lambda .$ Однако по предположению о виде волнового вектора ${\mathbf{q}}$ это поле $2\pi $-периодично по каждой декартовой координате, а, значит, поля ${{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}({{{\text{e}}}^{{{\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}({\mathbf{x}}) \pm {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{b}}( - {\mathbf{x}}))$ – также собственные, отвечающие $\lambda .$ Соответственно, ${\mathbf{b}} = {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{f}}({\mathbf{x}}),$ где ${\mathbf{f}}$ – центрально-симметричное или центрально-антисимметричное векторное поле. По предположению о простоте собственного значения $\lambda $ реализуется только одна из этих возможностей. Аналогично легко показать, что собственная функция оператора $\mathfrak{M}{\text{*}},$ отвечающая $\overline \lambda ,$ имеет вид ${\mathbf{b}}{\text{*}} = {{{\text{e}}}^{{ - {\text{i}}{\mathbf{q}} \cdot {\mathbf{x}}}}}{\mathbf{f}}{\text{*}}({\mathbf{x}}),$ где ${\mathbf{f}}{\text{*}}$ тоже центрально-симметричное или центрально-антисимметричное поле. При этом ${\mathbf{f}}$ и ${\mathbf{f}}{\text{*}}$ имеют один и тот же тип симметрии, т.к. в противном случае $({\mathbf{b}},{\mathbf{b}}{\text{*}}) = 0,$ что исключает выполнение равенства (10), а возможность такой нормировки гарантируется общей теорией несамосопряженных операторов. Подстановкой этих выражений для ${\mathbf{b}}$ и ${\mathbf{b}}{\text{*}}$ в (11) убеждаемся, что, как и ранее, два первых слагаемых справа взаимно сокращаются (и каждое из них равно 0, когда ${{q}_{n}} = 0$), а третье равно 0, в силу чего равенства (14) выполнены. Среди решений системы (14) такого вида нам встречались и локальные, и глобальные максимумы инкремента (см. раздел 2). Указанное обстоятельство повышает интерес к работе [Zheligovsky et al., 2001], где анализировали генерацию магнитных мод вида (3) только для волновых векторов рассмотренного в данном абзаце вида.

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

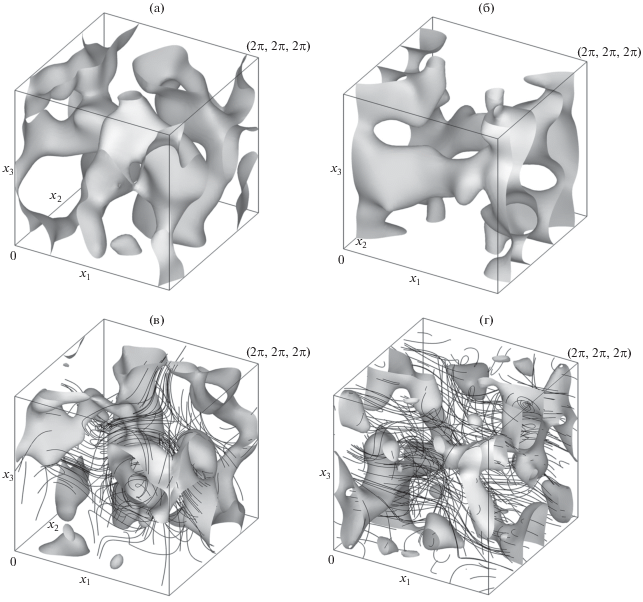
Поведение инкремента роста магнитного поля (3) изучали на примере двух модельных трехмерных течений с нулевым средним, синтезированных как конечные ряды Фурье, состоящие из гармоник, волновые числа которых не превосходят 7, с псевдослучайными коэффициентами, изначально равномерно распределенными на интервале $[0,1].$ Коэффициент гармоники с волновым вектором ${\mathbf{n}}$ умножен на ${{4}^{{ - |{\mathbf{n}}|}}}$ и спроецирован на плоскость, ортогональную ${\mathbf{n}},$ чтобы течение было соленоидально. Течения нормализованы так, что среднеквадратичная скорость равна 1, поэтому магнитное число Рейнольдса можно оценить как $1{\text{/}}\eta .$ Все коэффициенты Фурье второго течения мнимы, вследствие чего оно центрально-симметрично относительно начала координат (т.е. ${\mathbf{v}}({\mathbf{x}}) = - {\mathbf{v}}( - {\mathbf{x}})$). Таким образом, в первом течении (но не во втором) имеет место магнитный $\alpha $-эффект, а во втором – магнитная вихревая диффузия. Энергетический спектр так построенных полей скорости монотонно спадает на 12 порядков с 1-го по 13-й сферический слой единичной толщины в пространстве волновых векторов. Соответственно, модельные течения гладкие и периодичны по декартовым переменным, но имеют достаточно сложную пространственную структуру (см. рис. 1). (Как иллюстрация структуры течений, на рис. 1в, 1г показан некоторый набор траекторий частиц жидкости, продолжающихся до пересечения с гранями куба периодичности.)

Рис. 1.

Изоповерхности плотности кинетической энергии ${{{{{\left| {\mathbf{v}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {\mathbf{v}} \right|}}^{2}}} 2}} \right. \kern-0em} 2}$ (а), (б) и завихренности $\left| {{\text{rot}}{\mathbf{v}}} \right|$ (в), (г) первого (а), (в) и второго (б), (г) модельных течений, для которых проведены расчеты, на уровнях 50% (для первого течения) и 60% (для второго течения) от соответствующих максимумов. На рис. (в), (г) также показаны отрезки некоторых траекторий частиц жидкости. Изображен один куб периодичности течений.

Задачу поиска максимального в $\mathbb{Q}$ инкремента ${{\gamma }_{{max}}} = ma{{x}_{{\mathbf{q}}}}\gamma ({\mathbf{q}})$ решали численно для относительно больших молекулярных диффузий $\eta \geqslant 0.03,$ что не требует большого пространственного разрешения. При $\eta \geqslant 0.1$ для представления решения использовано ${{32}^{3}}$ гармоники Фурье, что обеспечивает падение энергетического спектра вычисленных собственных функций ${\mathbf{b}}$ и ${\mathbf{b}}{\text{*}}$ не менее 8 порядков; при $0.03 \leqslant \eta < 0.1$ использовано ${{48}^{3}}$ гармоник, падение энергетического спектра составляет не менее 6 порядков.

4.1. Течение с α-эффектом

На рис. 2б, 2в показаны инкременты роста $\gamma $ доминирующих магнитных мод (3) для волновых векторов ${\mathbf{q}}$ из области $\mathbb{Q}$ (6), вычисленные для первого рассмотренного модельного течения при $\eta = 0.1.$ Рис. 2а демонстрирует наличие магнитного $\alpha $-эффекта; на нем показаны инкременты роста ${{\gamma }_{{\alpha }}}$ (в медленном времени масштаба порядка $1{\text{/}}\varepsilon $) длинномасштабных магнитных мод, генерируемых $\alpha $-эффектом. График имеет вертикальную асимптоту при $\eta \approx 0.034;$ при этой величине молекулярной диффузии начинается генерация короткомасштабного магнитного поля. Такая сингулярность была обнаружена в работе [Andrievsky et al., 2019a]; для поля скорости общего положения соответствующие асимптотические разложения длинномасштабной магнитной моды и ее инкремента роста рассмотрены в работе [Andrievsky et al., 2019b].

Рис. 2.

Максимальный инкремент роста длинномасштабного магнитного поля ${{{\gamma }}_{{\alpha }}}{\text{,}}$ генерируемого $\alpha $-эффектом, в первом модельном течении, как функция молекулярной магнитной диффузии $\eta $ (а). Точки: вычисленные величины ${{\gamma }_{{\alpha }}}.$ Тонкая прямая – вертикальная асимптота ${{\gamma }_{{\alpha }}}$ в точке начала генерации короткомасштабного магнитного поля. Инкремент роста $\gamma $ доминирующих магнитных мод (3) для ${{q}_{1}} = 0,$ ${{q}_{3}} = 0.4$ (сплошная линия) и ${{q}_{1}} = 0.05,$ ${{q}_{3}} = 0.15$ (пунктирная линия) как функции ${{q}_{2}}$ при $\eta = 0.1$ (б). Изоповерхности инкремента $\gamma $ в области $\mathbb{Q}$ (.7) волновых векторов ${\mathbf{q}}$ для первого модельного течения при $\eta = 0.1$ на уровнях 25%, 50%, 75% и 90% от максимального в $\mathbb{Q}$-инкремента (в).

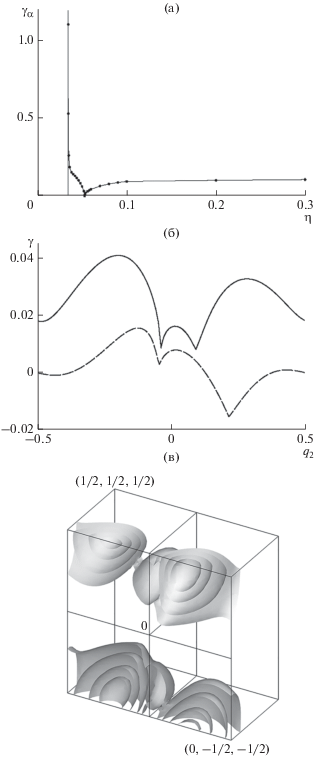
На рис. 2б инкременты роста при $\eta = 0.1$ показаны как функции компоненты ${{q}_{2}}$ волнового вектора при ${{q}_{1}} = 0,$ ${{q}_{3}} = 0.4$ и ${{q}_{1}} = 0.05,$ ${{q}_{3}} = 0.15;$ из этих графиков видно, что доминирующими при таких параметрах оказываются две ветви мод, и в точках перехода от одной ветви к другой доминирующий инкремент теряет дифференцируемость, как обсуждено в разделе 3. (Эти графики также иллюстрируют периодичность инкрементов роста доминирующих мод с периодом 1 по каждой компоненте волновых векторов ${\mathbf{q}}$.)

На рис. 2в приведены изоповерхности инкремента роста $\gamma $ доминирующих магнитных мод (3) при $\eta = 0.1.$ Ось ${{q}_{1}}$ направлена перпендикулярно плоскости рисунка в сторону от читателя, ось ${{q}_{3}}$ вертикальна. Самые дальние от читателя изоповерхности отвечают минимальному из изображенных уровню 25% от максимума инкремента в параллелепипеде $\mathbb{Q},$ и далее уровни растут при приближении к фронтальной плоскости ${{q}_{1}} = 0.$ Максимальный в $\mathbb{Q}$ инкремент роста, равный 0.041, достигается при ${\mathbf{q}} \approx (0.002,0.209, - 0.430)$ (что соответствует $\varepsilon = \left| {{\kern 1pt} {\mathbf{q}}{\kern 1pt} } \right| \approx 0.478$). Для рассматриваемого течения в кубе ${{[ - 1{\text{/}}2,1{\text{/}}2]}^{3}}$ периодичности по ${\mathbf{q}}$ локальных максимумов инкрементов два, они отвечают противоположным ${\mathbf{q}},$ и оба максимума глобальные. Поскольку они оба расположены вблизи плоскости ${{q}_{1}} = 0,$ на рис. 2в возникают четыре локальных максимума при рассечении надвое этой плоскостью систем изоповерхностей вокруг двух указанных глобальных максимумов в кубе ${{[ - 1{\text{/}}2,1{\text{/}}2]}^{3}}$ и их копий при параллельном переносе на период вдоль вертикальной оси ${{q}_{3}}$. У вертикальной срединной плоскости ${{q}_{2}} = 0$ упорядоченность изоповерхностей на рис. 2в нарушена, что вызвано потерей дифференцируемости максимальных инкрементов при смене ветвей собственных значений (которую иллюстрирует рис. 2б: на каждой из двух указанных прямых в $\mathbb{Q}$ максимальный инкремент достигается на двух различных ветвях) и относительной грубостью сетки $21 \times 41 \times 41$ точек в $\mathbb{Q},$ где были вычислены инкременты для построения рис. 2в.

На рис. 3а представлены результаты вычисления максимальных (по волновым векторам ${\mathbf{q}}$) инкрементов ${{\gamma }_{{max}}}$ роста магнитных мод формы (3). Для рассматриваемого модельного течения эти инкременты демонстрируют монотонный рост при уменьшении молекулярной диффузии $\eta ,$ что согласуется с физическими представлениями о ее влиянии. Отметим, что поведение инкрементов никак не коррелирует с эффективностью $\alpha $-эффекта (которую естественно соотносить с максимальным инкрементом роста генерируемого $\alpha $-эффектом длинномасштабного магнитного поля в медленном времени, см. рис. 2а): “точечное” прекращение генерации $\alpha $-эффектом (происходящее, когда среднее собственное значение симметризованного тензора $\alpha $-эффекта обращается в 0 [Roberts, 1970; Rasskazov et al., 2018]) при $\eta \approx 0.053$ никак не сказывается на монотонном росте максимального инкремента роста моды (3) при уменьшении $\eta ;$ равным образом, график рис. 3а не отражает никаких драматических явлений в окрестности точки $\eta \approx 0.034$ начала генерации короткомасштабных магнитных полей, в которой инкремент мод, генерируемых $\alpha $-эффектом, сингулярен и обращается в $ + \infty .$

Рис. 3.

Максимальный в $\mathbb{Q}$-инкремент ${{\gamma }_{{max}}}$ роста магнитной моды (3) для первого модельного течения (а) и волновой вектор ${\mathbf{q}},$ при котором достигается максимальный инкремент; (б) как функции молекулярной магнитной диффузии $\eta .$ Точки: вычисленные величины ${{\gamma }_{{max}}}$ (а). Сплошная линия: $\left| {\mathbf{q}} \right|,$ штриховые: ${{q}_{k}},$ длина штриха увеличивается с индексом $k$ (б).

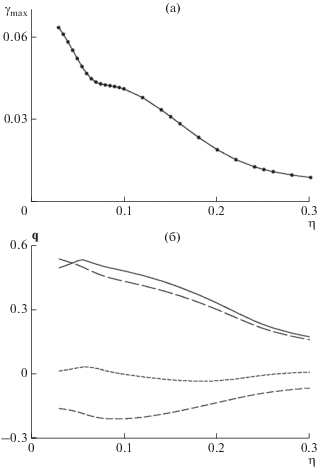
Рисунок 3б показывает, при каких волновых векторах достигается максимум инкрементов роста моды (3). Если ${{q}_{1}}$ и ${{q}_{2}}$ заключены в пределах $ - 0.2 < {{q}_{k}} < 0.1,$ то ${{q}_{3}}$ несколько превышает 1/2 при η ≲ 0.055, и соответствующие волновые векторы ${\mathbf{q}}$ формально не попадают в выделенную область $\mathbb{Q}.$ Тем не менее, мы не корректировали представленные на графике величины ${{q}_{3}} > 1{\text{/}}2$ (вычитая 1 из них), чтобы проиллюстрировать гладкость зависимости каждой компоненты ${\mathbf{q}}$ от молекулярной диффузии. Такая коррекция, однако, выполнена при расчете $\varepsilon = \left| {\mathbf{q}} \right|$ (при переходе ${{q}_{3}}$ через пороговую величину $\eta \approx 0.055$ в этом графике не возникает разрыв, но появляется излом). Полученная зависимость представляется физически естественной: с увеличением диффузии, т.е. с ростом $\eta ,$ течение возбуждает поля с пространственными структурами, имеющими все бóльшие пространственные масштабы и тем самым все менее поддающиеся разрушению молекулярной диффузией; слабое разделение масштабов, отвечающее значительным $\varepsilon = \left| {\mathbf{q}} \right|,$ у генерируемых мод возможно только при относительно малой молекулярной диффузии.

4.2. Течение с вихревой диффузией

Инкременты роста $\gamma $ доминирующих магнитных мод (3), рассчитанные при $\eta = 0.1$ для волновых векторов из $\mathbb{Q}$ (6) для второго, центрально-симметричного модельного течения, приведены на рис. 4б, 4в. Рисунок 4а иллюстрирует присутствие отрицательной магнитной вихревой диффузии. Обозначим ${{\gamma }_{{{\text{eddy}}}}}({\mathbf{q}})$ инкремент роста (в медленном времени масштаба порядка ${{\varepsilon }^{{ - 2}}}$) длинномасштабных магнитных мод вида (3), генерируемых вихревой диффузией. Минимум ${{\eta }_{{min}}} = mi{{n}_{{\mathbf{q}}}}( - {{\gamma }_{{{\text{eddy}}}}})$ называется минимальной вихревой диффузией; генерация происходит, если ${{\eta }_{{min}}} < 0,$ т.е. вихревая диффузия отрицательна. На графике ${{\eta }_{{min}}}$ (рис. 4а) видна вертикальная асимптота при $\eta \approx 0.028$ в точке начала генерации короткомасштабного магнитного поля. Впервые аномально большая отрицательная вихревая диффузия, связанная с ее сингулярностью в точке начала генерации короткомасштабного поля, была обнаружена и объяснена в работе [Zheligovsky et al., 2001].

Рис. 4.

Минимальная магнитная вихревая диффузия ${{\eta }_{{min}}}$ во втором модельном течении как функция молекулярной диффузии $\eta $ (а). Точки: вычисленные величины ${{\eta }_{{min}}}$. Тонкая прямая – вертикальная асимптота ${{\eta }_{{min}}}$ в точке начала генерации короткомасштабного магнитного поля. Инкремент роста $\gamma $ доминирующих магнитных мод (3) для ${{q}_{1}} = 0.2,$ ${{q}_{2}} = - 0.45$ (сплошная линия) и ${{q}_{1}} = 0.2,$ ${{q}_{2}} = - 0.475$ (пунктирная линия) как функции ${{q}_{3}}$ при $\eta = 0.1$ (б). Изоповерхности инкремента в области $\mathbb{Q}$ (.7) волновых векторов ${\mathbf{q}}$ для второго модельного течения при $\eta = 0.1$ на уровнях 25%, 50%, 75% и 90% от максимального в $\mathbb{Q}$ инкремента роста (в).

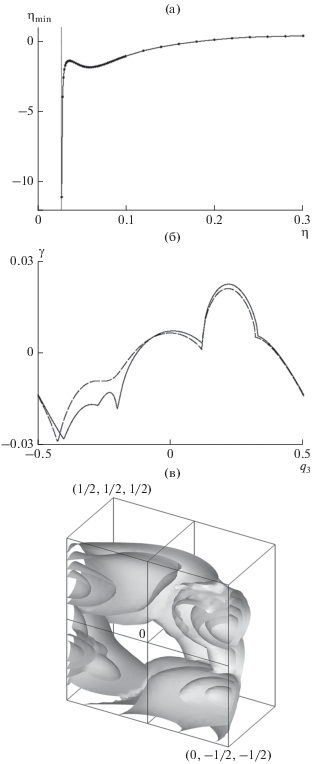
Зависимости инкремента $\gamma $ от компоненты ${{q}_{3}}$ волнового вектора для ${{q}_{1}} = 0.2,$ ${{q}_{2}} = - 0.45$ и ${{q}_{1}} = 0.2,$ ${{q}_{2}} = - 0.475$ при $\eta = 0.1$ (рис. 4б) демонстрируют, что доминирующими при этих параметрах оказываются соответственно пять и две ветви магнитных мод (3). Как и на рис. 2б, видно, что в точках смены ветвей доминирующие инкременты не дифференцируемы (см. раздел 3), и что инкременты имеют период 1 по ${{q}_{3}}$ (как и по обеим другим компонентам ${\mathbf{q}}$).

Изоповерхности инкремента роста доминирующих магнитных мод (3) (рис. 4в) построены по величинам инкремента, рассчитанным при $\eta = 0.1$ на сетке $21 \times 41 \times 41$ точек в $\mathbb{Q}.$ Оси направлены как на рис. 2в. Изоповерхности при удалении от фронтальной плоскости ${{q}_{1}} = 0$ отвечают убывающим уровням инкремента роста. Максимальный в $\mathbb{Q}$-инкремент равен 0.038, что по порядку величины совпадает с максимумом при $\eta = 0.1$ для первого модельного течения. В кубе периодичности волновых векторов ${{[ - 1{\text{/}}2,1{\text{/}}2]}^{3}}$ два глобальных и два локальных максимума. Они расположены вблизи фронтальной плоскости ${{q}_{1}} = 0,$ при ${\mathbf{q}} \approx \pm (0.039, - 0.471,0.200)$ (глобальные) и ${\mathbf{q}} = (0, \pm 1{\text{/}}2,0)$ (локальные максимумы), что отвечает отношениям масштабов $\varepsilon = \left| {\mathbf{q}} \right| \approx 0.513$ и 1/2 соответственно. Четыре локальных максимума в $\mathbb{Q}$ на рис. 4в возникают при разрезании этой плоскостью систем изоповерхностей вокруг четырех указанных максимумов. Как и на рис. 2в, у вертикальной срединной плоскости ${{q}_{2}} = 0$ нарушена упорядоченность изоповерхностей; это вызвано потерей дифференцируемости максимальных инкрементов при смене ветвей доминирующих собственных значений (см. рис. 4б), и относительной грубостью сетки, где заданы данные для построения изоповерхностей. Изоповерхность на минимальном из показанных на рис. 4в уровне 25% от максимального в $\mathbb{Q}$-инкремента роста имеет вид “гофрированной” поверхности, что также есть следствие грубости использованной сетки.

Рис. 5а показывает график максимальных (по волновым векторам ${\mathbf{q}}$) инкрементов ${{\gamma }_{{max}}}$ роста мод (3). Как и для первого модельного течения (рис. 3а), в целом эти инкременты при уменьшении молекулярной диффузии $\eta $ растут, что физически осмысленно. Однако в отличие от случая первого течения, максимальные инкременты теперь принадлежат трем независимым ветвям. На ветви, отвечающей наибольшим из рассмотренных $\eta $, максимальный инкремент, равный 0, достигается при ${\mathbf{q}} = 0$ (пунктирная линия на рис. 5а). Эта ветвь состоит из нейтральных мод (3), т.е. соответствующее собственное значение равно 0. Их существование следует из того [Арнольд и др., 1982; Zheligovsky, 2011], что все векторы–константы принадлежат ядру оператора $\mathfrak{L}{\text{*}}$ (9), сопряженного оператору магнитной индукции (поэтому линейно-независимых короткомасштабных нейтральных магнитных мод не менее трех, и если их три, то у ограничения $\mathfrak{L}$ на собственное подпространство, отвечающее нулевому собственному значению, нет жордановых клеток размера 2 или более). Как обсуждено в разделе 3, условия локального максимума (14) в данном случае тривиально выполнены при любом $\eta $. Однако эта ветвь изображена не на всей ширине рисунка, а только в том интервале $\eta $, где нулевые инкременты роста являются локальными (для ${\mathbf{q}}$ в малой окрестности нуля) максимумами инкрементов. (Строго говоря, это проверено для $\eta $, изображенных жирными точками на графиках рис. 5а, и только в этих отдельных точках; если в интервале $\eta \gtrsim 0.183$ эта величина, очевидно, является глобальным максимумом, то для меньших $\eta $ это утверждение нетривиально.) Следующая при уменьшении $\eta $ (средняя) ветвь максимальных инкрементов (штриховая линия) отвечает волновому вектору ${\mathbf{q}} = (0,1{\text{/}}2,0).$ В разделе 3 доказано, что это ${\mathbf{q}}$ также является решением системы (14). Инкременты этой ветви являются глобальными максимумами при $0.137 \lesssim \eta \lesssim 0.183.$ Наконец, при самых малых $\eta $, изображенных на рис. 5а, ветвь максимальных инкрементов опять сменяется. Волновые векторы, на которых достигаются максимумы на этой ветви (сплошная линия), изображены на рис. 5б.

Рис. 5.

То же, что на рис. 3, для второго модельного течения. На графиках (б) приведены длина (после переноса в $\mathbb{Q}$) и компоненты вектора ${\mathbf{q}}$ для левой ветви (сплошная линия) на графике (а).

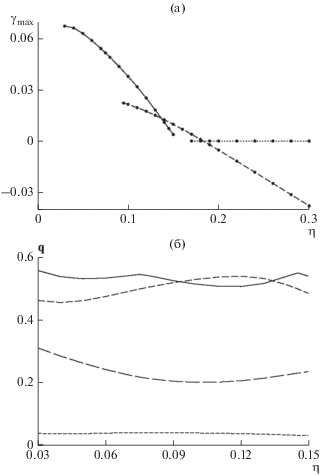
Как и в случае первого модельного течения, поведение максимальных в $\mathbb{Q}$-инкрементов роста магнитных мод (3) не коррелирует с действием механизма длинномасштабной генерации: три ветви инкрементов на рис. 5а ничем не напоминают график максимального инкремента роста длинномасштабного магнитного поля, генерируемого отрицательной вихревой диффузией, на рис. 4а. Например, на рис. 5а никак не отображается сингулярность вихревой диффузии в точке начала генерации короткомасштабного магнитного поля $\eta \approx 0.028.$

Как и компонента ${{q}_{3}}$ для первого модельного течения (см. рис. 3б), ${{q}_{2}}$ несколько превышает 1/2 при $0.076 \lesssim \eta \lesssim 0.144;$ векторы ${\mathbf{q}}$ с такими компонентами не попадают в область $\mathbb{Q}$ (6). При построении графиков индивидуальных компонент ${{q}_{k}}$ эти векторы не были перенесены в $\mathbb{Q},$ чтобы показать гладкость зависимости ${\mathbf{q}},$ на которых достигаются максимумы, от молекулярной диффузии. Расчет $\varepsilon = \left| {\mathbf{q}} \right|$ выполнен для эквивалентных ${\mathbf{q}}$ в $\mathbb{Q}$ (отсюда изломы в точках перехода ${{q}_{2}}$ через порог 1/2 при $\eta \approx 0.076$ и 0.0144). Таким образом, при η ≲ 0.183, когда максимальные инкременты достигаются на двух ветвях, изображенных сплошной и штриховой линиями, $\left| {\mathbf{q}} \right| \geqslant 1{\text{/}}2,$ что отвечает слабому разделению масштабов; при бóльших $\eta $ динамо не работает, максимальный инкремент роста, равный нулю, имеют короткомасштабные магнитные моды при ${\mathbf{q}} = 0.$ Существенное разделение масштабов, при котором у доминирующих мод $\varepsilon = \left| {\mathbf{q}} \right|$ мало, и их генерация происходит именно вследствие действия механизма отрицательной вихревой диффузии, не обнаружено.

5. ЗАКЛЮЧИТЕЛЬНЫЕ КОММЕНТАРИИ

Исследовано возбуждение магнитных мод вида (3) пространственно-периодическими течениями несжимаемой жидкости. Магнитный $\alpha $-эффект, а для центрально-симметричных течений вихревая диффузия оказываются частными случаями рассмотренного механизма, реализующимися при ${\mathbf{q}} \to 0.$ В сценарии Л.Д. Ландау развития турбулентности предполагалось постепенное усложнение течения с появлением в последовательности бифуркаций временны́х периодичностей, несоизмеримых с уже присутствующими в течении. Исследованный в данной работе динамо-механизм аналогичен этому сценарию (хотя в нем предполагается появление дополнительных пространственных частот). При учете нелинейности МГД процессов он способен самовоспроизводиться: когда возбуждаются новые несоизмеримые со старыми основные частоты в магнитном поле, под действием силы Лоренца они переносятся и в течение жидкости, после чего в МГД возмущении нового режима могут вновь возникнуть дополнительные основные частоты.

Волновой вектор ${\mathbf{q}}$ магнитной моды (3) произволен, но, поскольку максимальные инкременты мод имеют период 1 по каждой компоненте ${{q}_{k}},$ и поскольку равным, но противоположным по знаку ${\mathbf{q}}$ отвечают одинаковые максимальные инкременты, мы сосредоточились на их расчете в параллелепипеде волновых векторов $\mathbb{Q}$ (6). Для этого было синтезировано два модельных течения вида тригонометрических полиномов с псевдослучайными коэффициентами и быстро затухающим энергетическим спектром. В одном из них возникает магнитный $\alpha $-эффект, другой центрально-симметричен, и поэтому $\alpha $-эффект в нем отсутствует, но имеет место отрицательная магнитная вихревая диффузия.

Оба указанных эффекта могут возбуждать длинномасштабное поле, когда отношение масштабов достаточно мало. Однако описанные в данной статье расчеты для двух модельных течений показали, что максимальный инкремент роста имеют магнитные моды, у которых длина волнового вектора ${\mathbf{q}}$ не слишком мала (порядка половины при рассмотренных величинах коэффициента молекулярной магнитной диффузии), что соответствует незначительному разделению масштабов, и растет с ростом магнитного числа Рейнольдса. Поэтому неочевидно, что генерацию магнитного поля в данном случае надо относить на счет действия именно $\alpha $-эффекта или магнитной вихревой диффузии. Чтобы магнитный $\alpha $-эффект был значителен, кроме достаточного разделения масштабов необходимо наличие достаточно развитой структуры у короткомасштабного течения. Такие условия характерны для процессов на пространственных масштабах, отвечающих инерционному интервалу спектра турбулентности, для которых локальное магнитное число Рейнольдса ${{R}_{m}}$ уже мало. Они возникают, когда ${{R}_{m}}$ меньше гидродинамического числа Рейнольдса, что характерно для планетарных динамо.

Указанный результат позволяет предполагать, что в природных гидромагнитных динамо присутствует непрерывная шкала масштабов, слабо разделенных между собой, и турбулентное течение данного пространственного масштаба генерирует магнитное поле несколько (но не значительно) большего масштаба. Возможно, эта картина верна только при относительно малых ${{R}_{m}},$ для которых нами проведен численный эксперимент. Она усложняется нелинейным взаимодействием между полями разных масштабов, составляющих эту шкалу. Если же данная картина генерации магнитных полей верна и при больших ${{R}_{m}},$ то мы приходим к выводу, что явление генерации сложнее, чем это следует из представлений о главенствующей роли магнитного $\alpha $-эффекта. Тогда, в частности, теряет фатальность для процессов генерации астрофизических магнитных полей катастрофическое подавление $\alpha $-эффекта (т.н. $\alpha $-quenching) при больших ${{R}_{m}}.$

В современных численных моделях геодинамо, как правило, использованы вычислительно приемлемые коэффициенты молекулярных диффузий, на порядки величины бóльшие известных к настоящему времени оценок их величины во внешнем ядре Земли, однако некоторые результаты такого моделирования тем не менее реалистичны. Предложенное объяснение [Старченко, 2017; Starchenko, 2019] этого неожиданного успеха состоит в том, что геодинамо характеризуется величинами т.н. турбулентной (вихревой, в нашей терминологии) диффузии, схожими с использованными в численных моделях. Косвенно это подтверждают полученные нами результаты, объясняющие формирование повышенной эффективной диффузии следующим образом. Из рис. 5а следует (если он отражает ситуацию общего положения), что (как и в случае $\alpha $-эффекта) для центрально-симметричных течений на пространственных масштабах, для которых локальное магнитное число Рейнольдса порядка 1 и меньше, магнитным модам (3) присуще значительное разделение масштабов. Соответственно, определена вихревая диффузия, и она усиливает молекулярную (см. рис. 4а), действуя при этом на поля существенно бóльших пространственных масштабов, чем периоды поля скорости. Это останавливает обратный каскад магнитной энергии (при условии когерентного действия элементарных ячеек короткомасштабного турбулентного течения). Аналогичный механизм, связанный с вихревой вязкостью, по-видимому, способен останавливать и обратный каскад кинетической энергии течения, однако этот вопрос требует отдельного изучения.

Полученный вывод об отсутствии необходимости эффектов, базирующихся на разделении масштабов, для генерации магнитных полей планет земного типа основан на проведенных расчетах для только двух течений, моделирующих мелкомасштабную турбулентную составляющую течения расплава в ядре планеты. Мы, однако, полагаем, что этот вывод слабо зависим от деталей структуры таких компонент течений и потому универсален. Хотя алгоритм построения использованных нами модельных течений предполагает их репрезентативность, в дальнейшем необходимо провести более детальное исследование рассмотренного круга вопросов. В частности, естественно проверить этот вывод для течений, отвечающих разным законам затухания энергетического спектра (например, колмогоровскому закону).

Отметим, что тензоры вихревой диффузии, построенные асимптотическими методами, как правило, анизотропны, что в приведенном выше объяснении не принимается во внимание, но это несоответствие, вероятно, можно объяснить стохастичностью турбулентных течений. В связи с этим уместно следующее замечание. Чаще всего для вычислительных экспериментов в теории МГД устойчивости к длинномасштабным возмущениям и кинематического динамо используют стационарные пространственно-периодические короткомасштабные течения. Однако эти эксперименты призваны моделировать процессы в турбулентных течениях, а периодические стационарные течения, очевидно, не лучшим образом отвечают этому предназначению. И предложенный в настоящей статье подход, и подход теории устойчивости к длинномасштабным возмущениям, описанный в работах [Желиговский, 2010; Zheligovsky, 2011], легко (по крайней мере, в принципе) переносятся на случай пространственно-квазипериодических (имеющих две или более несоизмеримые частоты по данному направлению), а также периодических или квазипериодических по времени течений. Использование в расчетах таких течений, очевидно, позволит лучше имитировать короткомасштабную турбулентность.

Примененный здесь подход не может быть непосредственно перенесен на длинномасштабные слабонелинейные возмущения МГД систем, такие как исследованные в работе [Chertovskih, Zheligovsky, 2015] возмущения конвективного динамо. Однако, поскольку, как нами установлено, инкременты роста магнитных возмущений при достаточно больших магнитных числах Рейнольдса достигают максимума при умеренных отношениях масштабов, изучение поведения слабонелинейных возмущений даже при относительно больших отношениях периодов возмущаемого состояния и возмущения – например, в диапазоне 1 : 2÷1 : 4 – представляет большой интерес и может быть выполнено численно.

Список литературы

  1. Арнольд В.И., Зельдович Я.Б., Рузмайкин А.А., Соколов Д.Д. Стационарное магнитное поле в периодическом потоке // Докл. АН СССР. 1982. Т. 266. С. 1357–1351.

  2. Вишик М.М. Периодическое динамо. Математические методы в сейсмологии и геодинамике / Под ред. Кейлис-Борока В.И., Левшина А.Л. // Вычислительная сейсмология. Вып. 19. М.: Наука. 1986. С. 186–215.

  3. Вишик М.М. Периодическое динамо. II. Численное моделирование и анализ геофизических процессов / Под ред. Кейлис-Борока В.И., Левшина А.Л. Вычислительная сейсмология. Вып. 20. М.: Наука. 1987. С. 12–22.

  4. Вишик М.М. О возбуждении магнитного поля трехмерным стационарным потоком проводящей жидкости при больших магнитных числах Рейнольдса // Изв. АН СССР. Сер. Физика Земли. 1988. 3. С. 3–12.

  5. Желиговский В.А. Математическая теория устойчивости магнитогидродинамических режимов к длинномасштабным возмущениям. М.: Красанд. УРСС. 2010. 352 с.

  6. Като Т. Теория возмущений линейных операторов. М.: Мир. 1972. 740 с. (Пер. с англ.: Kato T. Perturbation theory for linear operators. Berlin: Springer. 1995. 2nd ed. 619 p.)

  7. Краузе Ф., Рэдлер К.-Х. Магнитная гидродинамика средних полей и теория динамо. М.: Мир. 1984. 320 с. (Пер. с англ.: Krause F., Rädler K.-H. Mean-field magnetohydrodynamics and dynamo theory. Berlin: Academic-Verlag. 1980. 271 p.)

  8. Моффат Г.К. Возбуждение магнитного поля в проводящей среде. М.: Мир. 1980. 342 с. (Пер. с англ.: Moffatt H.K. Magnetic field generation in electrically conducting fluids. Cambridge Univ. Press. 1978. 320 p.)

  9. Рузмайкин А.А., Соколов Д.Д., Соловьев А.А., Шукуров А.М. Течение Куэтта–Пуазейля как винтовое динамо // Магнитная гидродинамика. 1989. 1. С. 9–14.

  10. Соловьев А.А. Возбуждение магнитного поля осесимметричным движением проводящей жидкости // Изв. АН СССР. Сер. Физика Земли. 1985а. 4. С. 101–103.

  11. Соловьев А.А. Описание области значений параметров спирального течения Куэтта–Пуазейля проводящей жидкости, при которых возможно возбуждение магнитного поля // Изв. АН СССР. Сер. Физика Земли. 1985б. 12. С. 40–47.

  12. Соловьев А.А. Возбуждение магнитного поля движением проводящей жидкости при больших значениях магнитного числа Рейнольдса // Изв. АН СССР. Сер. Физика Земли. 1987а. 5. С. 77–80.

  13. Соловьев А.А. Возбуждение магнитного поля спиральным течением проводящей жидкости. М.: ИФЗ АН СССР. 1987б. 132 с.

  14. Старченко С.В. Энергетические параметры геодинамо совместимые с аналитическими, численными, палеомагнитными моделями и наблюдениями // Физика Земли. 2017. 6. С. 110–124.

  15. Andrievsky A., Brandenburg A., Noullez A., Zheligovsky V. Negative magnetic eddy diffusivities from test-field method and multiscale stability theory // Astrophysical J. 2015. V. 811. 135. 24 p. [arxiv.org/abs/1501.04465].

  16. Andrievsky A., Chertovskih R., Zheligovsky V. Negative magnetic eddy diffusivity due to oscillogenic $\alpha $-effect // Physica D. 2019a. V. 399. P. 58–72. [arxiv.org/abs/1711.02390].

  17. Andrievsky A., Chertovskih R., Zheligovsky V. Pointwise vanishing velocity helicity of a flow does not preclude magnetic field generation // Phys. Rev. E. 2019b. V. 99. 033204. 9 p. [arxiv.org/abs/1811.00859].

  18. Bloch F. Über die Quantenmechanik der Elektronen in Kristallgittern. Zeitschrift für Physik A // Hadrons and Nuclei. 1929. V. 52. P. 555–600.

  19. Chertovskih R., Gama S.M.A., Podvigina O., Zheligovsky V. Dependence of magnetic field generation by thermal convection on the rotation rate: a case study // Physica D. 2010. V. 239. P. 1188–1209. [arxiv.org/abs/0908.1891].

  20. Chertovskih R., Zheligovsky V. Large-scale weakly nonlinear perturbations of convective magnetic dynamos in a rotating layer // Physica D. 2015. V. 313. P. 99–116. [arxiv.org/ abs/1504.06856].

  21. Christopherson D.G. A note on the vibration of membranes // Quart. J. Math. 1940. V. 11. P. 63–65.

  22. Gama S.M.A., Chertovskih R., Zheligovsky V. Computation of kinematic and magnetic $\alpha $-effect and eddy diffusivity tensors by Padé approximation // Fluids. 2019. V. 4. 110. 25 p.

  23. Gilbert A.D., Frisch U., Pouquet A. Helicity is unnecessary for alpha effect dynamos, but it helps // Geophys. Astrophys. Fluid Dynamics. 1988. V. 42. P. 151–161.

  24. Graham J.P., Blackman E.G., Mininni P.D., Pouquet A. Not much helicity is needed to drive large-scale dynamos // Phys. Rev. E. 2012. V. 85. 066406. 5 p.

  25. Klapper I., Young L.S. Rigorous bounds on the fast dynamo growth rate involving topological entropy // Communications Math. Phys. 1995. V. 173. P. 623–646.

  26. Lanotte A., Noullez A., Vergassola M., Wirth A. Large-scale dynamo by negative magnetic eddy diffusivities // Geophys. Astrophys. Fluid Dyn. 1999. V. 91. P. 131–146.

  27. Moffatt H.K. The degree of knottedness of tangled vortex lines // J. Fluid Mech. 1969. V. 35. P. 117–129.

  28. Moffatt H.K. Turbulent dynamo action at low magnetic Reynolds number // J. Fluid Mech. 1970. V. 41. P. 435–452.

  29. Moffatt H.K. The mean electromotive force generated by turbulence in the limit of perfect conductivity // J. Fluid Mech. 1974. V. 65. P. 1–10.

  30. Moffatt H.K. Helicity and singular structures in fluid dynamics // Proc. Nat. Ac. Sci. USA. 2014. V. 111(10). P. 3663–3670.

  31. Moffatt H.K. Helicity and celestial magnetism // Proc. R. Soc. A. 2016. V. 472. 20160183. 17 p.

  32. Moffatt H.K., Ricca R.L. Helicity and the Călugăreanu invariant // Proc. R. Soc. Lond. A. 1992. V. 439. P. 411–429.

  33. Moffatt H.K., Proctor M.R.E. The role of the helicity spectrum function in turbulent dynamo theory // Geophys. Astrophys. Fluid Dynamics. 1982. V. 21. P. 265–283.

  34. Moreau J.-J. Constantes d’un îlot tourbillonnaire en fluide parfait barotrope // C. R. hebd. séanc. Acad. Sci. Paris. 1961. V. 252. P. 2810–2813.

  35. Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. Numerical recipes in Fortran. The art of scientific computing. Cambridge Univ. Press. 1997. 2nd ed. 1002 p.

  36. Rädler K.-H. Mean-field dynamo theory: early ideas and today’s problems / Magnetohydrodynamics. Historical evolution and trends. Fluid mechanics and its applications. V. 80 / Eds. Molokov S., Moreau R., Moffatt K. Springer. 2007. P. 55–72.

  37. Rädler K.-H., Brandenburg A. $\alpha $-effect dynamos with zero kinetic helicity // Phys. Rev. E. 2008. V. 77. 026405. 6 p.

  38. Rasskazov A., Chertovskih R., Zheligovsky V. Magnetic field generation by pointwise zero-helicity three-dimensional steady flow of incompressible electrically conducting fluid // Phys. Rev. E. 2018. V. 97. 043201. 24 p. [arxiv.org/ abs/1708.08770].

  39. Roberts G.O. Spatially periodic dynamos // Phil. Trans. Roy. Soc. Lond. 1970. V. A266. P. 535–558.

  40. Roberts G.O. Dynamo action of fluid motions with two-dimensional periodicity // Phil. Trans. Roy. Soc. Lond. V. A271. 1972. P. 411–454.

  41. Starchenko S.V. Simple planetary convection and magnetism estimations via scaling and observations / Problems of Geocosmos-2018: Proc. XII International Conference and School / Eds. Yanovskaya T.B., Kosterov A., Bobrov N.Yu., Divin A.V., Saraev A.K., Zolotova N.V. Springer. 2019. P. 179–189.

  42. Steenbeck M., Krause F., Rädler K.-H. Berechnung der mittleren Lorentz-Feldstärke $\overline {{\mathbf{v}} \times {\mathbf{b}}} $ für ein elektrisch leitendes Medium in turbulenter, durch Coriolis–Kräfte beeinfluißter Bewegung // Z. Naturforsch. 1966. V. 21a. P. 369–376. (Engl. transl.: A calculation of the mean electromotive force in an electrically conducting fluid in turbulent motion, under the influence of Coriolis forces / Roberts P.H., Stix M. The turbulent dynamo: A translation of a series of papers by F. Krause, K.-H. Rädler, and M. Steenbeck. Tech. Note NCAR-TN/IA-60. Boulder, Colorado. 1971. P. 29–47. http://nldr.library.ucar.edu/repository/assets/technotes/ TECH-NOTE-000-000-000-045.pdf .)

  43. Zheligovsky V.A. Numerical solution of the kinematic dynamo problem for Beltrami flows in a sphere // J. Scientific Computing. 1993. V. 8. P. 41–68.

  44. Zheligovsky V.A. Large-scale perturbations of magnetohydrodynamic regimes: linear and weakly nonlinear stability theory. Lecture Notes in Physics. V. 829. Heidelberg: Springer-Verlag. 2011. 330 p.

  45. Zheligovsky V.A., Galloway D.J. Dynamo action in Christopherson hexagonal flow // Geophys. Astrophys. Fluid Dynamics. 1998. V. 88. P. 277–293.

  46. Zheligovsky V.A., Podvigina O.M., Frisch U. Dynamo effect in parity-invariant flow with large and moderate separation of scales // Geophys. Astrophys. Fluid Dynamics. 2001. V. 95. P. 227–268. [arxiv.org/abs/nlin/0012005].

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал