1. На главную
  2. Электронные версии
  3. Физика Земли
  4. № 1, 2020

Физика Земли, 2020, № 1, стр. 96-108

Общий закон подобия для землетрясений в приложении к оценке сейсмической опасности и ассоциированных рисков

А. К. Некрасова 1, *, В. Г. Кособоков 1, **, И. А. Парвез 2, ***, Х. Тао 3, ****

1 Институт теории прогноза землетрясений и математической геофизики, РАН
г. Москва, Россия

2 Центр математического и компьютерного моделирования
г. Бангалор, Индия

3 Харбинский политехнический университет
г. Харбин, Китайская Народная Республика

* E-mail: nastia@mitp.ru
** E-mail: volodya@mitp.ru
*** E-mail: parvez@csir4pi.in
**** E-mail: taoxiaxin@aliyun.com

Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019

Полный текст (PDF)

Аннотация

Распределение числа сейсмических событий по магнитуде – закон Гутенберга–Рихтера играет наиважнейшую роль в оценке сейсмической опасности территории. Предложенное в 1988 г. обобщение этого основного закона сейсмологии, позволяет учитывать специфику распределения эпицентров сейсмических событий при изменении масштаба рассмотрения, что крайне важно для адекватного пересчета повторяемости в область меньшего размера на территории рассмотрения (например, в мегаполисе). В 2002 г. Пер Бак предложил двойственную формулировку Общего закона подобия для землетрясений (ОЗПЗ), использующую вместо числа землетрясений в определенный период времени величину обратную частоте их возникновения – время между сейсмическими событиями. В том же году в Институте теории прогноза и математической геофизики РАН был разработан модифицированный алгоритм робастной оценки параметров ОЗПЗ (Scaling Coefficients Estimation, SCE) для построения карт сейсмической опасности территорий, подверженных сейсмическим воздействиям. Настоящий краткий обзор посвящен использованию ОЗПЗ в приложении к проблеме оценки сейсмической опасности и ассоциированных рисков.

Ключевые слова: сейсмическая опасность, Общий закон подобия для землетрясений, население, максимальное пиковое ускорение, сейсмический риск.

ВВЕДЕНИЕ

Оценка сейсмической опасности требует адекватного представления о распределении землетрясений разной силы. В настоящее время поисковый запрос “unified scaling law for earthquakes” в интернет системе Google в доли секунды выдает миллионы ссылок на работы, непосредственно связанные с исследованиями сейсмичности и использующими в той или иной форме Общий закон подобия для землетрясений (ОЗПЗ), обобщающий одно из соотношений Гутенберга–Рихтера [Gutenberg, Richter, 1944; 1956]. Закон повторяемости Гутенберга–Рихтера, как правило, формулируется в виде соотношения, которое устанавливает связь между среднегодовым числом землетрясений N(M) и магнитудой M в некотором пространственно-временном объеме:

(1)
${\text{l}}{{{\text{g}}}_{{10}}}N\left( M \right) = a + b\left( {5--M} \right),\,\,\,\,{{M}_{--}} \leqslant M \leqslant {{M}^{--}},$
где коэффициент a характеризует средний уровень сейсмической активности во всем пространственно-временном объеме рассматриваемой территории, а b – соотношение числа землетрясений в соседних диапазонах магнитуд. Существующие карты, оценивающие сейсмическую опасность, приемлемо соответствуют картированию показателя сейсмической активности a. Однако следует заметить, что эти карты, как правило, переоценивают опасность в асейсмичных зонах из-за (1) произвольного выбора вероятностного пространства (обычно, пуассоновского по времени и определяемого гауссовским разбиением единицы по пространству) и (2) недооценки влияния классического масштабирования, которое игнорирует сложную (фрактальную) структуру мест возможного возникновения эпицентров землетрясений. Возможно, более точная модификация закона подобия для землетрясений была предложена в 1988 г. [Kosobokov, Mazhkenov, 1988; Кейлис-Борок и др., 1989] и позволяет учитывать изменение масштабов территории рассмотрения и распределения эпицентров сейсмических событий по площади:

(2)
${\text{l}}{{{\text{g}}}_{{10}}}N\left( {M,L} \right) = A + B\left( {5--M} \right) + C{\text{l}}{{{\text{g}}}_{{10}}}L.$

Формулировка Общего закона подобия для землетрясений (ОЗПЗ), использующая вместо числа землетрясений в определенный период времени двойственную величину – время между сейсмическими событиями, была предложена в 2002 г. [Bak et al., 2002; Christensen et al., 2002], что мотивировало разработку модифицированного алгоритма робастной оценки параметров ОЗПЗ (Scaling Coefficients Estimation, SCE) и их глобального картирования [Nekrasova, Kossobokov, 2002; Кособоков, Некрасова, 2004]. Карты коэффициентов ОЗПЗ, полученные в Институте теории прогноза землетрясений и математической геофизики РАН по данным Глобальной базы данных о гипоцентрах землетрясений за 1964–2002 гг. [GHDB..., 2015] вошли в Отчет Российской Академии наук об основных научных достижениях за 2002 г. [Отчет …, 2003].

ОЗПЗ позволяет дать оценку ожидаемой максимальной магнитуды землетрясений в местах их возникновения, что определяет возможность расчетов и картирования ожидаемых параметров сотрясений (например, пиковое ускорение грунта PGA или макросейсмическая интенсивность I0) на территории исследуемого региона. После тщательного тестирования свидетельствами сейсмических проявлений (например, зарегистрированные в прошлом значения PGA или I0) такая карта может быть использована на практике для оценивания конкретных рисков последствий землетрясений для населения, городов и инфраструктур (например, на основании данных переписи населения, инвентаризации зданий и иных сооружений инфраструктуры).

За прошедшие годы карты сейсмической опасности на основе ОЗПЗ в терминах повторяемости сейсмических событий максимальной ожидаемой магнитуды построены для нескольких регионов мира, различающихся как по размерам территории, так и по уровню сейсмической активности [Parvez et al., 2018; Kossobokov, Nekrasova, 2018a; 2018b; Parvez et al., 2014; 2017; Nekrasova et al., 2011; 2015; 2016; Некрасова, Кособоков, 2005; 2006; 2009; 2016; Некрасова и др., 2015; Кособоков, Некрасова, 2004; Nekrasova, Kossobokov, 2003]. В частности, на территории Российской Федерации карты на основе расчетов коэффициентов ОЗПЗ построены для Прибайкалья, Алтая, Саян, Большого Кавказа и полуострова Крым. Карты сейсмической опасности построены также для полуострова Индостан, штата Гуджарат (Индия), провинции Ланьчжоу (Китай) и автономной области Фриули-Венеция-Джулия (Италия).

Пилотные расчеты модельных сейсмических рисков для населения предложены для перечисленных выше территорий, а также для отдельных крупнейших городов в их пределах. Показано, что игнорирование фрактального характера пространственного распределения землетрясений может привести к значительной недооценке сейсмической опасности и ассоциированных рисков и, как следствие, к незапланированным значительным потерям и ущербу в случае их возникновения.

ПРИМЕНЕНИЕ ОЗПЗ ПРИ ИЗУЧЕНИИ СЕЙСМИЧЕСКОГО РЕЖИМА В ПРОСТРАНСТВЕННОМ И ВРЕМЕННОМ МАСШТАБАХ

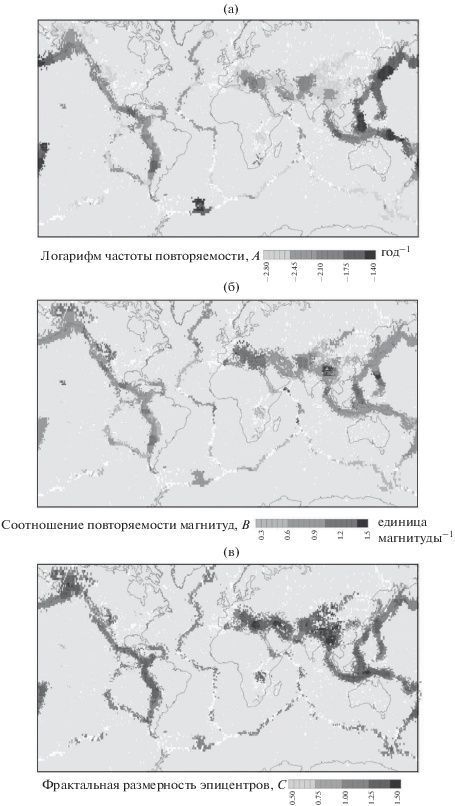
Детальное описание модифицированной версии алгоритма SCE для определения параметров ОЗПЗ представлено в работе [Nekrasova et al., 2015]. Отметим, что свободные параметры алгоритма, накладывают определенные ограничения на возможность его применения и используемые исходные данные. В частности, для корректного применения алгоритма SCE необходим каталог сейсмических событий за продолжительный период (от десятка лет и более) при наличии однородной по техническим параметрам сети, регистрации. Очевидно, что результаты расчетов зависят от исходных данных, а именно от полноты регистрации сейсмических событий, от изменений порога регистрации в процессе технических изменений и совершенствования параметров сети сейсмографов, от точности определения координат эпицентра и, в меньшей степени, глубины сейсмических событий. Используемый каталог во многом определяет предварительный выбор оптимального набора свободных параметров алгоритма. Анализ данных каталога является обязательным предварительным этапом применения SCE-алгоритма. Так, например, при упомянутом выше глобальном картировании параметров ОЗПЗ были использованы данные о всех сейсмических событиях с магнитудой 4.0 и выше из каталога Геологической службы США за 1964–2002 гг. [Global Hypocentres Data Base]. При этом коэффициенты ОЗПЗ, представленные на рис. 1, оценивались в масштабе элементов глобальной плитовой тектоники размером от 50 до 1000 км с использованием 5 ступеней пространственной иерархии ячеек линейного размера от ½ до 8 градусов земного меридиана. Согласно работам [Nekrasova, Kossobokov, 2002; Кособоков, Некрасова, 2004], логарифмическая оценка сейсмической активности (коэффициент A) изменяется в основном в пределах от –2.5 до –1.2 (рис. 2а), что соответствует повторяемости землетрясений с магнитудой 5.0 от менее одного в 300 лет до трех в пятьдесят лет. Значения наклона графика повторяемости (коэффициент B) сосредоточены в основном между 0.6 и 1.1 (рис. 2б), а фрактальная размерность множества сосредоточения эпицентров (коэффициент C) изменяется от менее 1.0 до 1.4 и выше (рис. 2в). Полученные оценки ошибок коэффициентов ОЗПЗ демонстрируют (рис. 2г) практически по всему миру высокую степень согласия с данными мировых наблюдений в широком диапазоне магнитуд и размеров области исследования.

Рис. 1.

Глобальное распределение коэффициентов Общего закона подобия для землетрясений.

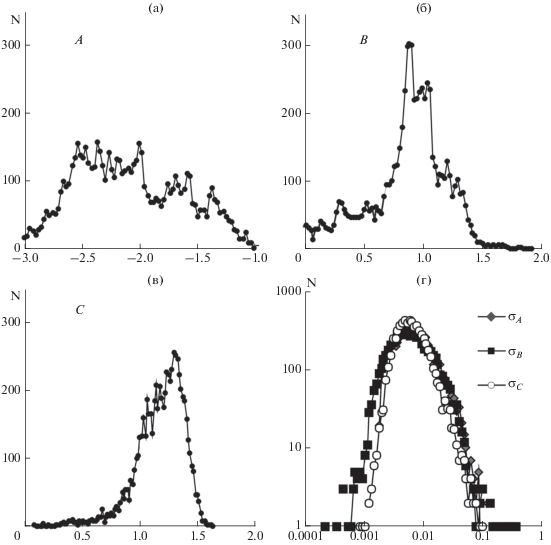
Рис. 2.

Гистограммы глобального распределения параметров ОЗПЗ: (а) – A; (б) – B; (в) – C; (г) – σA, σB, σC (график в би-логарифмическом масштабе).

Оценки параметров ОЗПЗ на базе продолжительного интервала времени могут быть использованы при построении карт сейсмической опасности рассматриваемой территории и будут рассмотрены ниже. Изменение значений параметров ОЗПЗ в среднесрочном масштабе времени характеризует динамику сейсмичности изучаемого региона. В частности, было обнаружено [Bak et al., 2002; Kossobokov, Nekrasova, 2017; 2019], что контрольный параметр ОЗПЗ, а именно, величина η = N–1 × × 10B(5– M) × LC находится в долгосрочной перспективе, на одном из довольно устойчивых уровней своего значения и время от времени, в среднесрочной перспективе, переключается с одного на другой уровень в результате критического перехода, связанного, в том числе, с возникновением сильного землетрясения.

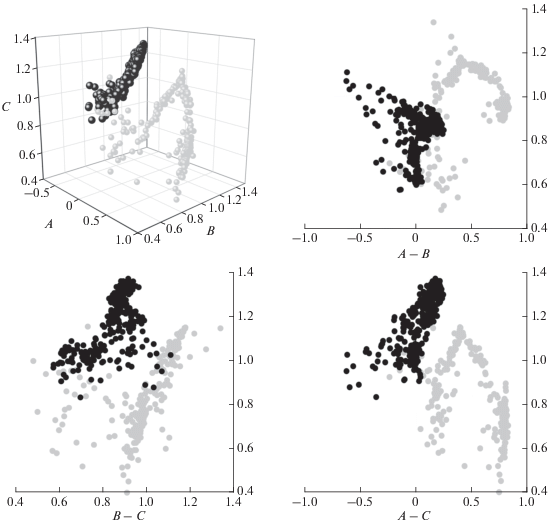
В качестве примера приведем локальные оценки параметров ОЗПЗ для итальянской автономной области Фриули–Венеция–Джулия [Nekrasova et al., 2018]. Были использованы данные регионального каталога землетрясений Национального института океанологии и экспериментальной геофизики (Италия) (OGS), за период с 1996 по март 2018 гг. Коэффициенты ОЗПЗ оценены по данным о событиях с магнитудой 2.0 и выше для пространственных ячеек линейного размера 1/16 градуса земного меридиана (порядка 6.9 км) и 5-ти ступеней пространственной иерархии. При этом детальность и точность регистрации локального каталога позволили оценить значения коэффициентов ОЗПЗ для последовательных шестилетних временных интервалов со сдвигом в 1 год. На рис. 3 представлены значения коэффициентов A, B и С для двух шестилетних интервалов времени (в начальном, 1996–2001 гг., для которого надежные оценки получены в 214 ячейках, и конечном, 2012–2017 гг., для которого надежные оценки получены в 311 ячейках), а также их проекции на координатные плоскости. Следует отметить, что в оценках начального шестилетнего периода землетрясение, произошедшее 12.04.1998 г. (сильнейшее в регионе за исследуемый период), и его многочисленные афтершоки безусловно повысили значения коэффициентов A и B и одновременно понизили значения коэффициента C в ячейках из области высокой концентрации эпицентров. При отсутствии сильных событий в период с 2012 по 2017 гг. значения коэффициентов ОЗПЗ более концентрированы в пределах A около 0, B от 0.6 до 1.0 и C выше 1. Сложное взаимное расположение в 3D-значений коэффициентов ОЗПЗ указывает на нетривиальность корреляционных связей между параметрами и значительное разнообразие характеристик сейсмического потока в пределах рассматриваемого региона, а также очевидно свидетельствует в пользу существенной изменчивости в динамике последовательности землетрясений во времени.

Рис. 3.

Значения коэффициентов ОЗПЗ в автономной области Фриули–Венеция–Джулия для начального (2001 г., серые символы) и конечного (2017 г., черные символы) шестилетних интервалов времени.

Согласно [Nekrasova et al., 2018] критический переход, ассоциированный с землетрясением 12.04.1998 г., характеризуется изменением контрольного параметра ОЗПЗ в полтора раза от уровня среднего значения η менее 0.2 в 1997 г. до более 0.3 в 2002–2004 гг.

ПОСТРОЕНИЕ КАРТ СЕЙСМИЧЕСКОЙ ОПАСНОСТИ НА ОСНОВЕ ОЗПЗ

Региональные оценки коэффициентов A, B и C могут быть использованы для определения и картирования на основе ОЗПЗ максимальной магнитуды ожидаемой в заданный временной интервал. Действительно, согласно (2), число событий заданной магнитуды Мj, ожидаемых в течение T лет NT(Mj) = T × N(Mj, L0), где L0 – линейный размер ячейки, для которой определены картированные коэффициенты ОЗПЗ. При этом максимальные значения Mj, для которых NT(Mj) ≥ p (для 0 ≤ p ≤ 1), могут рассматриваться в качестве магнитуд наиболее сильных землетрясений, ожидаемых в каждой из ячеек карты с вероятностью p за время T [Parvez et al., 2014].

Очевидно, что надежность карт сейсмической опасности (в частности, построенных на основе ОЗПЗ) повышается при привлечении результатов распознавания мест возможного возникновения сильных событий [Кособоков, Соловьев, 2018], а также надежных свидетельств об исторических и палеоземлетрясениях. Построение карт сейсмической опасности на территории Российской Федерации, основанное на результатах применения методов ОЗПЗ и распознавания образов в сочетании с данными исторического каталога сейсмических событий, использовалось для Крыма и Большого Кавказа, Прибайкалья, Алтая и Саян [Nekrasova et al., 2015; Kossobokov, Nekrasova, 2018a; 2018b].

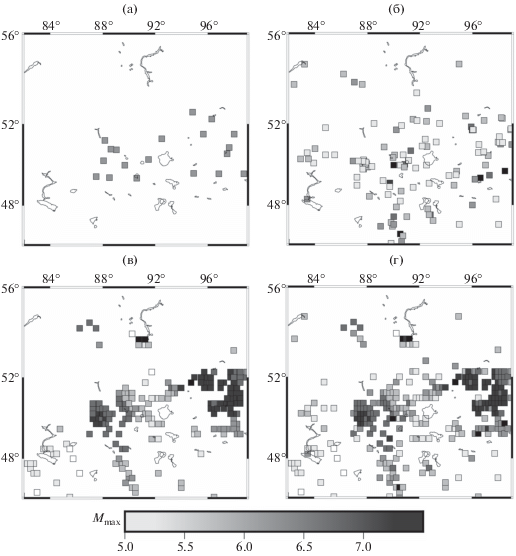
В качестве примера рассмотрим подробнее недавно опубликованные результаты для территории Алтая и Саян, где дополнительно были использованы карты морфоструктурного районирования (MSZ) и распознавания мест возможного возникновения сильных землетрясений с магнитудой M ≥ 6.0 [Горшков и др.. 2018]. Из 63 пересечений MSZ региона на рис. 4а приведены 19, распознанных как высокосейсмичные для территории Алтая и Саян, в том числе места, где согласно историческим данным такие события не зарегистрированы. На рис. 4б представлены использованные данные об исторических землетрясениях для рассматриваемой территории с 1734 г. [Kondorskaya et al., 1982]. Карта максимальной магнитуды Mmax для территории Алтая и Саян (рис. 4в), ожидаемой с вероятностью возникновения 10% в период 50 лет, получена на основе (1) оценки коэффициентов ОЗПЗ в каждой из 207 пространственных ячеек линейного размера 1/4° с двумя и более сейсмическими событиями из используемого регионального каталога за 1997–2015 гг., составленного по ежегодникам “Землетрясения Северной Евразии” в 1997–2009 гг. [Starovoit, 2015] и “Землетрясения России” в 2003–2015 гг. [Malovichko, 2017]; (2) пространственной иерархии четырехкратного удвоения, а также (3) выбора значений параметров p и T, который соответствует широко распространенному критерию при оценке сейсмической опасности в терминах характеристик сотрясаемости. Финальная карта сейсмической опасности в терминах максимальной магнитуды Mmax для территории Алтая и Саян, представленная на рис. 4г, является комбинацией карт 4а, 4б и 4в с выбором максимальной оценки в случае пересечения значений в одном узле.

Рис. 4.

Карты сейсмической опасности для территории региона Алтай–Саяны в терминах наиболее вероятной максимальной магнитуды Mmax в ячейках 1/4 × 1/4° регулярной сетки: (а) – высокоопасные узлы MSZ, признанные подверженными землетрясениям магнитудой 6.0 или более; (б) – максимум наблюденной магнитуды в 1734–2017 гг. из каталога [Кондорская и др., 1982 г.] и Глобального каталога землетрясений USGS ANSS (https://earthquake.usgs.gov/ earthquakes/search/ от 18.09.2017 г.); (в) – максимальная ожидаемая величина Mmax, рассчитанная на основе ОЗПЗ и параметров p = 10% и T = 50 лет; (г) – комбинированная карта Mmax.

Для построения основанных на ОЗПЗ карт сейсмической опасности территории в терминах сотрясаемости необходимо преобразовать карту значений Mmax, что возможно с использованием неодетерминистского моделирования многообразия сценариев возможных наиболее сильных землетрясений [Panza et al., 2001]. Для упрощения расчетов можно воспользоваться одной из эмпирических формул затухания параметров сотрясения. Так, например, для пикового ускорения на скальном основании (PGA, peak ground acceleration) для каждой ячейки-источника с ожидаемым землетрясением магнитуды Mmax рассчитаем ускорение, вызванное им в точке – приемнике по формуле, мотивированной неодетерминистским моделированием землетрясений [Parvez et al., 2001]:

(3)
$Acc({{M}_{{{\text{max}}}}},D) = {\text{const}}\,\, \times g \times {{D}^{{--1.5}}} \times {\text{exp}}({{M}_{{{\text{max}}}}}--5),$
где: D – расстояние между источником и приемником на сетке 1/4 × 1/4°, const = 6.0; g = 9.81 м/с2 – постоянная силы тяжести, а exp (x) – экспонента (натуральная) величины x. Значение PGA в точке определяется как максимум значений ускорения, рассчитанных в этой точке по всем ячейкам-источникам рассматриваемой территории.

СРАВНЕНИЕ ОЦЕНОК СЕЙСМИЧЕСКОЙ ОПАСНОСТИ НА ОСНОВЕ ОЗПЗ, НЕОДЕТЕРМИНИСТСКИХ И ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ

Результаты Глобальной программы оценки сейсмической опасности (GSHAP, 1992–1999 гг.) [Shedlock et al., 2000; Giardini et al., 2003] и продолжающийся в настоящее время проект Global earthquake model (GEM), направленный на уточнение оценок сейсмической опасности и сейсмического риска для отдельных регионов мира на основе вероятностных подходов, дают возможность сравнить, региональные карты сейсмической опасности, полученные на основе ОЗПЗ, а также провести ретроспективную оценку надежности результатов сравниваемых методов.

Для каждой региональной карты сейсмической опасности, построенной на основе ОЗПЗ в терминах PGA, проведено ее сравнение с результатами проекта GSHAP (архивированные данные в формате ASCII GSHPUB.dat доступны на сайте http://static.seismo.ethz.ch/gshap/gshpub.zip и содержат значения на карте Общего сейсмического районирования Российской Федерации ОСР-97-A).

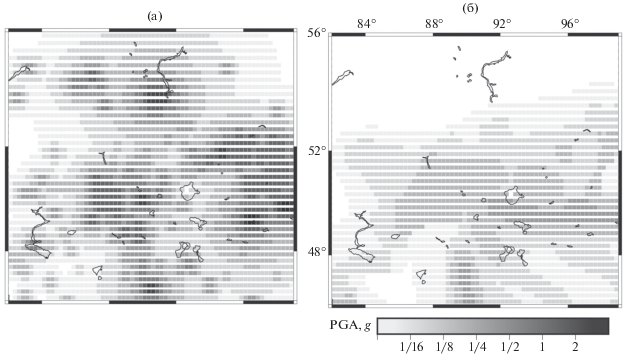
В качестве примера на рис. 5 приведены карты возможной сотрясаемости для территории Алтая и Саян в терминах PGA, полученные на основе ОЗПЗ и в рамках проекта GSHAP. Расчеты PGA на основе ОЗПЗ приведены для максимальных ожидаемых магнитуд, полученных для территории Алтая и Саян и описанных в предыдущем параграфе. Заметим, что карта сейсмической опасности на основе ОЗПЗ (PGAОЗПЗ) более детальна и контрастна, чем карта проекта GSHAP (PGAGSHAP) для этой территории. Также отмечено [Кособоков, Некрасова, 2011; Nekrasova et al., 2015; Kossobokov, Nekrasova, 2018a; 2018b], что значения PGAGSHAP довольно часто противоречат реальным параметрам сильных землетрясений, в то время как примеры использования методологии ОЗПЗ с такими данными более согласованы. Так, например, значения PGA в 131 эпицентре землетрясений с магнитудой 5.0 или более в регионе Алтай и Саяны, в период с 1761 по 2017 гг., в 52 случаях превышают в 2 и более раз значения PGA на карте проекта GSHAP. При этом отношение значения PGA в эпицентре к значению PGAGSHAP больше 4 в 26 случаях и больше 8 в 13 случаях. Примечательно, что PGAGSHAP в эпицентрах всех семи землетрясений с магнитудой 7.0 и выше в 2 и более раз меньше определений наблюденной сотрясаемости, причем недооценка превышает 4 для 6 и 8 для 5 сильнейших землетрясений региона.

Рис. 5.

Карты максимального пикового ускорения от землетрясения магнитуды Mmax для территории региона Алтай–Саяны: (a) – по расчетам методики ОЗПЗ, (б) – согласно финальным картам GSHAP.

Оценка сейсмической опасности на основе ОЗПЗ в регионах проводилась не только для территории в целом, но и для отдельных крупных городов. В табл. 1 приведены результаты оценки сейсмической опасности для 11 городов с населением более 100 000 жителей (данные Федеральной службы государственной статистики РФ за 2016 г.), подверженных воздействию землетрясений в Алтае-Саянском регионе. В табл. 1 два максимальных значения численности населения, площади города S, PGAGSHAP и PGAОЗПЗ выделены жирным шрифтом, что позволяет наглядно оценить сложные комбинации возможностей. Например, наиболее населенный город региона Новосибирск имеет минимальное значение сейсмической опасности на карте GSHAP, в то время как по оценкам на основе ОЗПЗ он на четвертом месте; города Кызыл имеет минимальную площадь из представленных городов и занимает 1-е место как наиболее сейсмически опасный по PGAGSHAP, а по PGAОЗПЗ делит 1-е и 2-е место с городом Абакан. Следует отметить, что отношение оценок PGAОЗПЗ/PGAGSHAP раскрывает недопустимую недооценку сейсмической опасности по программе GSHAP в восьми из 11 крупных городов региона (в 4 или более раз, жирный курсив в последней колонке табл. 1).

Таблица 1.  

Оценка ожидаемого максимального пикового ускорения PGA для основных городов территории Алтая и Саян

Город Население S, км2 PGA, g Отношение PGAОЗПЗ/PGAGSHAP
GSHAP ОЗПЗ
Абакан 165 214 112.4 0.06 >1 >16
Ачинск 109 155 103.0 0.02 0.15 7.80
Барнаул 612 401 321.0 0.04 0.07 1.55
Бийск 210 115 291.7 0.10 0.09 0.88
Кемерово 532 981 282.3 0.02 0.16 7.85
Красноярск 1 083 865 348.0 0.02 0.14 6.04
Кызыл 109 918 97.4 0.20 >1 >5
Новокузнецк 547 904 424.3 0.05 0.61 11.89
Новосибирск 1 602 915 505.6 0.02 0.29 11.71
Оскемен* 321 251 540.0 0.06 0.24 4.27
Томск 524 669 297.2 0.02 0.07 3.32

Примечание. * Оскемен (Казахстан) ранее назывался Усть-Каменогорск.

Для территории Индийской провинции Гуджарат, где за последние 150 лет произошли два разрушительных землетрясения (16.06.1819 г., Mw ~ 7.8, и 26.01.2001 г. Mw ~ 7.7), возможно сравнение нескольких оценок сейсмической опасности, полученных разными методами [Parvez et al., 2017]. На рис. 6 представлены карты сейсмической опасности в терминах максимально возможного ускорения на скальном основании, полученные с использованием ОЗПЗ, на основе неодетерминистских расчетов DGA (design ground acceleration [Panza et al., 2001]) и на основе вероятностного подхода GSHAP. Расчет максимально возможного ускорения проводился для стандартной вероятности превышения 10% в период 50 лет (карта на основе ОЗПЗ рис. 6а, карта DGA10% рис. 6в и карта GSHAP рис. 6д соответственно), а также для неодетерминистской оценки DGA без ограничения на период повторяемости и DGA 2%, учитывающей повторяемость 2475 лет (рис. 6б, 6г соответственно). На рис. 6е приведено распределение оценок сейсмической опасности в терминах PGA для всех пяти карт.

Рис. 6.

Карты максимально ожидаемого пикового ускорения от землетрясения для территории штата Гуджарат (Индия). Примечание: (a) – по расчетам методики ОЗПЗ; (б) – по стандартным расчетам неодетерминистской оценки сотрясаемости; (в) – по расчетам неодетерминистской оценки сотрясаемости для 475 лет; (г) – по расчетам неодетерминистской оценки сотрясаемости для 2475 лет; (д) – согласно финальным картам GSHAP; (е) – распределение оценок максимально ожидаемого ускорения для карт (а)–(д).

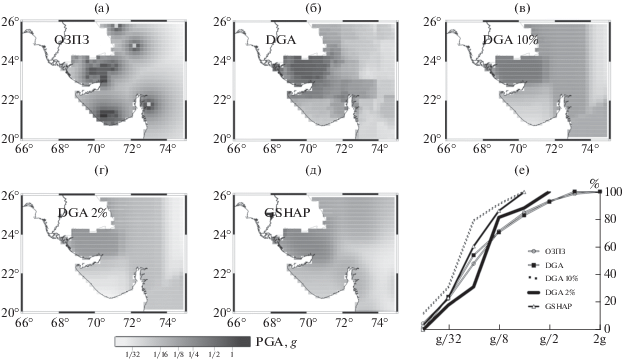
Отметим, что для территории штата Гуджарат оценки ниболее вероятной значительной сотрясаемости грунта порядка g/8 и более по стандартному методу DGA и на основе ОЗПЗ согласуются между собой, имея расхождения в пространственном распределении сильных сотрясений. Оценки сотрясаемости на основе трех других подходов недооценивают сейсмическую опасность для территории штата в 2–4 раза, а в случае сотрясаемости, сопоставимой с зафиксированной при землетрясении 2001 г., недооценка определения по GSHAP и DGA10% достигает фактора 8.

ОЦЕНКА СЕЙСМИЧЕСКОГО РИСКА НА ОСНОВЕ ОЗПЗ

Применение метода ОЗПЗ может быть использовано и при оценке сейсмического риска. Напомним, что математически любой вид риска является результатом свертки опасности с объектом риска, подверженным опасности, и с уязвимостью этого объекта:

(4)
$R(s) = H(s) \otimes O(s) \otimes V(O(s)),$
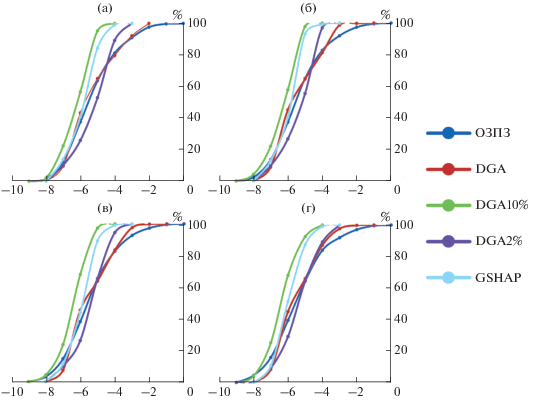
где: s определяет положение в пространстве и может быть точкой, линией или некоторой областью на/или под поверхностью Земли; Н(s) – опасность явления; O(s) описывает объекты, подверженные риску в месте s; V(O(s)) описывает уязвимости этих объектов риска. (При этом H(s), O(s) и V(O(s)) могут зависеть от времени.)

В качестве иллюстрации общего проблемно ориентированного подхода, а также многообразия факторов, влияющих на оценку риска, приведем пример оценок сейсмического риска с использованием демографических данных о населении. Воспользуемся представленными ранее оценками сейсмической опасности для штата Гуджарат (Индия). В предлагаемом примере в качестве свертки использовано умножение, хотя возможна и более сложная функциональная зависимость. На рис. 7 представлены распределения оценок модельных рисков: (а) – при равной уязвимости каждого отдельного человека, Ri(s) = = H(s) ⋅ $\int_s P ,$ где $\int_s P $ – интеграл от плотности населения в ячейке s, т.е. число лиц, находящихся на площади ячейки s; (б) – при персональной уязвимости, линейно возрастающей с плотностью населения в данном месте, Rii(s) = H(s) ⋅ $\int_s {P \cdot P} $; (в) и (г) – соответствуют двум нелинейным предположениям об уязвимости, зависящим от плотности населения, Riii(s) = H(s) ⋅ $\int_s {P \cdot {{P}^{2}}} $ и Riv (s) = H(s) ⋅ $\int_s {P \cdot {{P}^{3}}} $ соответственно. Значения каждого из четырех модельных рисков приведены в единицах, нормированных по отношению к его максимальному значению на карте. Как и следовало ожидать, распределение рисков следуют тенденциям сейсмической опасности, поэтому подход ОЗПЗ дает наиболее консервативные оценки, в то время как оценки проекта GSHAP и DGA10% кажутся слишком оптимистичными, если не приводить в качестве аргументации дополнительные субъективные предположения. Одновременно становится очевидным то, что в областях наиболее высокой концентрации населения при увеличении зависимости уязвимости от его плотности происходит сокращение территории повышенного риска. Этот пример является довольно естественной и яркой демонстрацией того, как фактор уязвимости может изменить само представление о риске.

Рис. 7.

Распределение оценок сейсмического риска R(s) для населения провинции Гуджарат (Индия) для пяти моделей оценки сейсмической опасности H(s). Примечание: (а) Ri(s) = H(s) ⋅ $\int_s P ;$ (б) Rii(s) = H(s) ⋅ $\int_s {P \cdot P;} $ (в) Riii(s) = H(s) ⋅ $\int_s {P \cdot {{P}^{2}}} ;$ (г) Riv(s) = H(s) $ \cdot \,\int_s {P \cdot {{P}^{3}}} .$

ЗАКЛЮЧЕНИЕ

Оценки сейсмической опасности и ассоциированных рисков в настоящее время довольно неопределенны. В отсутствие данных за многие тысячи лет вероятностные оценки повторяемости землетрясений остаются научно несостоятельными. Наш весьма краткий обзор одного из новых подходов к проблеме, основанный на ОЗПЗ, раскрывает возможность гораздо более высоких рисков, чем на существующих широко распространенных картах вероятностной оценки сейсмической опасности. В подходе учитывается естественное фрактальное распределение мест землетрясений вместе с тектоническими данными и аргументами распознавания образов. Исследования этого направления, ведущиеся в настоящее время в Институте теории прогноза землетрясений и математической геофизики РАН, вносят скромный вклад в срочный пересмотр карт вероятностных оценок сейсмической опасности путем улучшения базовых методологий. Очевидно, что эти работы пока не учитывают реальные экономические и социальные факторы оценки рисков, как и роль влияния топографии и грунтов, а также размера и параметров очага для крупных и/или сложных сейсмических событий. Эти важные соображения должны быть учтены при внедрении в будущих практических оценках и картировании сейсмической опасности и рисков.

Список литературы

  1. Горшков А.И., Соловьёв А.А., Жарких Ю.И. Распознавание мест возможного возникновения сильных землетрясений в регионе Алтай–Саяны–Прибайкалье // Докл. РАН. 2018. Вып. № 3. Т. 479.

  2. Кейлис-Борок В.И., Кособоков В.Г., Мажкенов С.А. О подобии в пространственном распределении сейсмичности. Теория и алгоритмы интерпретации геофизических данных // Вычислительная сейсмология. Вып. 22. М.: Наука. 1989. Т. 28. С. 40.

  3. Кособоков В.Г., Соловьёв А.А. Распознавание образов в задачах оценки сейсмической опасности // Чебышевский сборник. 2018. Т. 19. Вып. 4. С. 53–88.

  4. Кособоков В.Г., Некрасова А.К. Карты Глобальной программы оценки сейсмической опасности (GSHAP) ошибочны // Вопросы инженерной сейсмологии. 2011. Т. 38. № 1. С. 65–76.

  5. Кособоков В.Г., Некрасова А.К. Общий закон подобия для землетрясений: глобальная карта параметров. Анализ геодинамических и сейсмических процессов // Вычислительная сейсмология. Вып. 35. М.: ГЕОС. 2004. С. 160–175.

  6. Некрасова А.К., Кособоков В.Г. Общий закон подобия для землетрясений: Крым и Северный Кавказ // Докл. РАН. 2016. Т. 470. № 4. С. 468–470.

  7. Некрасова А.К., Кособоков В.Г., Парвез И.А. Оценка сейсмической опасности и сейсмического риска на основе Общего закона подобия для землетрясений: Гималаи и прилегающие регионы // Физика Земли. 2015. № 2. С. 116–125.

  8. Некрасова А.К., Кособоков В.Г. Общий закон подобия для землетрясений: мегаполисы и городские агломерации. Некоторые проблемы геодинамики // Вычисл. сейсмология. Вып. 39. М.: КРАСАНД. 2009. С. 265–300.

  9. Некрасова А.К., Кособоков В.Г. Общий закон подобия для землетрясений. Прибайкалье // Докл. РАН. 2006. Т. 407. № 5. С. 679–681.

  10. Некрасова А.К., Кособоков В.Г. Временные вариации параметров Общего закона подобия для землетрясений на востоке острова Хонсю (Япония) // Докл. РАН. 2005. Т. 405. № 4. С. 529–532.

  11. Отчет о деятельности Российской Академии наук в 2002 году. Основные результаты в области естественных, технических, гуманитарных и общественных наук. Науки о Земле. Академик-секретарь Отделения академик О.А. Богатиков. Геолого-геофизические науки. Сейсмология. М. 2003.

  12. Садовский М.А., Болховитинов Л.Г., Писаренко В.Ф. О свойстве дискретности горных пород // Изв. АН СССР. Сер. Физика Земли. 1982. № 12. С. 3–18.

  13. Садовский М.А., Голубева Т.В., Писаренко В.Ф., Шнирман М.Г. Характерные размеры горной породы и иерархические свойства сейсмичности // Изв. АН СССР. Сер. Физика Земли. 1984. Т. 20. С. 87–96.

  14. Bak P., Christensen K., Danon L., Scanlon T. Unified Scaling Law for Earthquakes // Phys Rev Lett. 2002. V. 88. P. 178 501–178 504.

  15. Christensen K., Danon L., Scanlon T., Bak P. Unified scaling law for earthquakes. Proc Natl Acad Sci. 2002. V. 99. Suppl 1. P. 2509–2513.

  16. GHDB Global Hypocenters Data Base CD-ROM // NEIC/USGS, Denver, CO, 1989 and its updates through December 2015.

  17. Giardini D., Grünthal K., Shedlock P. Zhang The GSHAP Global Seismic Hazard Map // Ann Geofis. 1999. V. 42(6). P. 1225–1228.

  18. Giardini D., Grünthal G., Shedlock K.M., Zhang P. The GSHAP Global Seismic Hazard Map / Lee W., Kanamori H., Jennings P. and Kisslinger C. (eds.). International Handbook of Earthquake & Engineering Seismology. 2003. International Geophysics Series 81 B. Academic Press, Amsterdam. P. 1233–1239.

  19. Gutenberg B., Richter C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944. V. 34. P. 185–188.

  20. Gutenberg B., Richter C.F. Seismicity of the Earth, 2nd ed., Princeton University Press, Princeton, N.J. 1954. 310 p.

  21. Kondorskaya N.V., Shebalin N.V., Khrometskaya Ya.A., Gvishiani A.D. New catalog of strong earthquakes in the U.S.S.R. from ancient times through 1977. World Data Center A for Solid Earth Geophysics. 1982. Report SE-31. 609 p.

  22. Kosobokov V.G., Mazhkenov S.A. Times of increased probability of large earthquakes in the Eastern Tien Shan diagnosed by the M8 algorithm D.K. Chowdhury (ed.). Computational Seismology and Geodynamics. 1994. Am. Geophys. Un. 1, Washington, D.C.: The Union. P. 16–19.

  23. Kossobokov V., Nekrasova A. Global Seismic Hazard Assessment Program Maps Are Misleading // Eos Trans AGU 91(52). 2010. Fall Meet Suppl, Abstract U13A-0020.

  24. Kossobokov V., Nekrasova A. Global seismic hazard assessment program maps are erroneous // Seismic Instruments 2012. V. 48(2). P. 162–170.

  25. Kossobokov V.G., Mazhkenov S.A. Spatial characteristics of similarity for earthquake sequences: Fractality of seismicity. Lecture Notes of the Workshop on Global Geophysical Informatics with Applications to Research in Earthquake Prediction and Reduction of Seismic Risk (15 Nov. 16 Dec., 1988). ICTP. Trieste. 1988. 15 p.

  26. Kossobokov V.G., Nekrasova A. Earthquake Hazard and Risk Assessment based on Unified Scaling Law for Earthquakes: Greater Caucasus and Crimea // J. Seismology. 2018a. V. 22. P. 1157–1169. https://doi.org/10.1007/s10950-018-9759-4

  27. Kossobokov V.G., Nekrasova A. Earthquake Hazard and Risk Assessment based on Unified Scaling Law for Earthquakes: Altai–Sayan Region // Natural Hazards. 2018b. V. 93(3). P. 1435–1449. https://doi.org/10.1007/s11069-018-3359-z

  28. Kossobokov V.G., Nekrasova A. Aftershock sequences of the recent major earthquakes in New Zealand // Pure and Applied Geophysics. 2019. V. 176. P. 1–23. https://doi.org/10.1007/s00024-018-2071-y

  29. Kossobokov V.G., Nekrasova A. Characterizing Aftershock Sequences of the Recent Strong Earthquakes in Central Italy // Pure Appl. Geophys. 2017. V. 174. P. 3713–3723. https://doi.org/10.1007/s00024-017-1624-9

  30. Magrin A., Parvez I.A., Vaccari F., Peresan A., Rastogi B.K., Cozzini S., Bisignano D., Romanelli F., Ashish P., Choudhury K.S., Roy R.R., Mir G.F. Panza, Neo-deterministic definition of seismic and tsunami hazard scenarios for the territory of Gujarat (India) / S. D’Amico (ed.). Earthquakes and Their Impact on Society. Springer Natural Hazards. 2016. P. 193–212.

  31. Malovichko A.A. (ed.). The earthquakes of Russia in 2015. GS RAS, Obninsk. 2017. P. 212 (inc. CD-ROM).

  32. Nekrasova A., Kossobokov V.G., Tao X., Tao Z., Wang L. Spatial pattern of seismicity in Central China recognized by USLE // World Earthquake Engineering. 2016. V. 32(2). P. 170–175 (in Chinese).

  33. Nekrasova A.K., Kossobokov V.G., Peresan A. Seismic Dynamics in Northeastern Italy. 1995–2018. Abstract S12B-02, AGU. 2018. Washington DC, 10-14 Dec. https://agu.confex.com/agu/fm18/meetingapp.cgi/Paper/433069

  34. Nekrasova A., Kossobokov V., Parvez I.A., Tao X. Seismic hazard and risk assessment based on the unified scaling law for earthquakes // Acta Geod Geophys. 2015. V. 50(1). P. 21–37. https://doi.org/10.1007/s40328-014-0082-4

  35. Nekrasova A., Kossobokov V. Generalized Gutenberg-Richter recurrence law: Global map of parameters // Geophysical Research Abstracts. № 5. 2003. Abstracts of the Contributions of the EGS-AGU-EGU Joint Assembly, Nice, France, 06-11 April, (CD-ROM): EAE03-A-03801.

  36. Nekrasova A., Kossobokov V. Generalizing the Gutenberg-Richter scaling law. EOS Trans. 2002. AGU. V. 83(47). Fall Meet. Suppl., Abstract NG62B-0958.

  37. Nekrasova A.V., Kossobokov A., Aoudia A., Perezan G.F., Panza A. Multiscale Application of the Unified Scaling Law for Earthquakes in the Central Mediterranean area and Alpine region // Pure Appl. Geophys. 2011. V. 168. P. 297–327. Springer Basel AG. https://doi.org/10.1007/s00024-010-0163-4

  38. OGS, Istituto Nazionale di Oceanografia e Geofisica Sperimentale, Centre of Seismological Research, consists of network bulletins, 1977–1999 (published on CDROM), and bulletins, 2000–2018. (both available on web-site http://www.crs.inogs.it/

  39. Panza G.F., Romanelli F., Vaccari F. Seismic wave propagation in laterally heterogeneous anelastic media: theory and applications to seismic zonation // Adv Geophys. 2001. V. 43. P. 1–95.

  40. Parvez Imtiyaz A., Nekrasova A., Kossobokov V. Seismic hazard and risk assessment based on Unified Scaling Law for Earthquakes: thirteen principal urban agglomerations of India // Nat Hazards. 2018. https://doi.org/10.1007/s11069-018-3261-8

  41. Parvez I.A., Gusev A., Panza G.F., Petukhin A. Preliminary determination of the interdependence among strong motion amplitude, earthquake magnitude and hypocentral distance for the Himalayan region // Geophys J. Int. 2001. V. 144. P. 577–596.

  42. Parvez I.A., Nekrasova A., Kossobokov V. Estimation of seismic hazard and risks for the Himalayas and surrounding regions based on Unified Scaling Law for Earthquakes // Natural Hazards. 2014. V. 71(1). P. 549–562.

  43. Parvez I.A., Vaccari F., Panza G.F. A deterministic seismic hazard map of India and adjacent areas // Geophys. J. Int. 2003. V. 155. P. 489–508.

  44. Pravez I., Nekrasova A.K., Kossobokov V.G. Earthquake Hazard and Risk Assessment Based on Unified Scaling Law for Earthquakes: State of Gujarat, India // Pure Appl. Geophys. 2017. V. 174. P. 1441–1452. Springer International Publishing.

  45. Soloviev A.A., Gvishiani A.D., Gorshkov A.I., Dobrovolsky M.N., Novikova O.V. Recognition of Earthquake Prone Areas: Methodology and Analysis of the Results // Izvestiya, Physics of the Solid Earth. 2014. V. 50(2). P. 151–168.

  46. Starovoit O.E. (ed.). The earthquakes of Northern Eurasia, 2009. FSIS GS RAS, Obninsk. 2015. P. 394. (inc. CD-ROM).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал