Физика Земли, 2020, № 1, стр. 86-95

1. ВВЕДЕНИЕ

А. Гусев [Gusev, 2013; 2014; 2018] привлек внимание к проблеме моделирования сейсмического источника, для которого упругое смещение в дальней зоне обладает двумя свойствами: (а) высокочастотный (ВЧ) спектр спадает, как ${{\omega }^{{ - 2}}},$ и при этом, (б) асимптотика не зависит от направления на приемник. Первое свойство традиционно называют омега-квадрат-поведением, а второе потерей направленности излучения. Квадратичное затухание спектра общепринято в инженерной практике, хотя не исключается конечность частотного диапазона такого поведения [Гусев и др., 2017]. Аналогично обстоит дело и с универсальностью свойства (б). В работах [Kurzon et al., 2014; Wen et al., 2014] имеются контрпримеры, относящиеся к частотному диапазону: $\omega > {{\omega }_{0}},$ где ${{\omega }_{0}}$ есть угловая частота Брюна [Brune, 1970]. Любые исключения подчеркивают сложность задачи А. Гусева и требуют понимания условий, при которых реализуются указанные свойства (а), (б).

Для решения проблемы А. Гусев предложил две, близкие по сути, кинематические модели очага с элементами стохастического поведения [Gusev, 2014; 2018]. Они позволили воспроизвести ключевые свойства ВЧ излучения: существование двух угловых частот, плоский участок спектра ускорения после второй угловой частоты (что эквивалентно свойству (а)), и слабый (в модели 2014 г.) эффект направленности излучения. В этих моделях важную роль играет фрактальная природа фронта разрыва. Чтобы воспроизвести указанные особенности, фронт по терминологии А. Гусева должен быть “кружевным”, т.е. очень изрезанным и многосвязным. Поскольку анализ и настройка моделей осуществлялись численно, ответ на вопрос о природе свойств (а), (б) остался открытым. В частности, неясно, насколько сложной должна быть кружевная структура фронта разрыва в условиях (а), (б).

Ниже мы собираемся показать, что для реализации свойства (а) достаточно иметь слегка негладкий фронт разрыва, а для реализации свойства (б) достаточна гладкость распределений шумовой компоненты фронта. Отсюда можно заключить, что фрактальные модели удачно дополняют классические гладкие модели очага [Aki, Richards, 1980]. Причина в том, что в классических моделях свойство (а) неустойчиво, а свойство (б), как правило, отсутствует. Однако добавление слегка негладкой шумовой компоненты фронта позволяет устранить эту неустойчивость и дополнительно реализовать свойство (б). Это наблюдение содержится в технически сложной работе автора [Molchan, 2015]. Представленный ниже анализ обладает большей общностью и простотой.

2. ОБЩИЕ ЗАМЕЧАНИЯ

Известно [Aki, Richards, 1980], что поле смещений в дальней зоне допускает представление:

Здесь: ${{G}_{{rec}}}$ – положение приемника; $\Sigma $ – плоскость разрыва с координатами $({{g}_{1}},{{g}_{2}}) = {\mathbf{g}};$ $f$ – функция источника, т.е. локальная скорость подвижки $\Delta \dot {u}({\mathbf{g}},t);$ ${\mathbf{\gamma }}_{\Sigma }^{{}}$ – ортогональная проекция направления гипоцентр – приемник: ${\mathbf{\gamma }}$ – на плоскость $\Sigma ;$ $\left\langle { \cdot , \cdot } \right\rangle $ – скалярное произведение; $с$ – скорость распространения волн; ${{t}_{0}}c$ – расстояние от гипоцентра до приемника; $d{\mathbf{g}} = d{{g}_{1}}d{{g}_{2}}$ – элемент площади.

Для простоты сигнал в представлении (1) рассматривается в скалярном виде.

Применяя преобразование Фурье, получим из (1) двойственное спектральное представление:

Здесь $\hat {f}({\mathbf{k}},\omega )$ пространственно-временное преобразование Фурье функции $f{\mathbf{(x}}): = f{\mathbf{(g}},t),$ продолженной нулем за пределы своего ограниченного носителя ${{\Omega }_{f}}.$

Задача омега-квадрат-поведение спектра звучит так: описать физически естественный класс функций очага $f{\mathbf{(x}}),$ для которых $\hat {f}({\mathbf{p}}\omega ),$ ${\mathbf{р}} = ({{ - {{{\mathbf{\gamma }}}_{\Sigma }}} \mathord{\left/ {\vphantom {{ - {{{\mathbf{\gamma }}}_{\Sigma }}} c}} \right. \kern-0em} c},1)$ имеет устойчивую ${{\omega }^{{ - 2}}}$ асимптотику, т.е. наблюдаемую на достаточно массивном множестве направлений ${\mathbf{\gamma }}.$

В силу линейности преобразования Фурье проще изучать локальные фрагменты $f{\mathbf{(x}}),$ а именно $f{\mathbf{(x}}\left| {{{{\mathbf{x}}}_{{0i}}}} \right|) = f({\mathbf{x}})\varphi ({\mathbf{x}}\left| {{{{\mathbf{x}}}_{{0i}}})} \right..$ Здесь $\varphi ({\mathbf{x}}\left| {{{{\mathbf{x}}}_{{0i}}}} \right.)$ – вспомогательные, бесконечно гладкие, с ограниченным носителем (финитные) функции: они равны 0 вне малой окрестности точки ${{{\mathbf{x}}}_{{0i}}},$ ${{О}_{{{{x}_{{0i}}}}}},$ равны 1 в меньшей окрестности 0.5${{О}_{{{{x}_{{0i}}}}}}$ и в сумме дают единицу: $\sum {\varphi ({\mathbf{x}}\left| {{{{\mathbf{x}}}_{{0i}}})} \right.} = 1.$ Описанные фрагменты не искажают функцию $f{\mathbf{(x}})$ вблизи выбранных точек ${{{\mathbf{x}}}_{{0i}}}$ и гладко обнуляют ее вне малых окрестностей. Высокочастотную асимптотику фрагмента:

будем трактовать как вклад окрестности точки ${{{\mathbf{x}}}_{0}}$ в асимптотику $\hat {u}(\omega ).$ Фрагментация функции очага позволяет описывать асимптотику спектра в терминах возможных локальных особенностей функции $f{\mathbf{(x}}).$ При этом не требуется конкретизация модели $f{\mathbf{(x}})$ в целом. Кроме того, рассматриваемые ниже особенности $f{\mathbf{(x}})$ имеют точечный характер и поэтому их спектральный вклад (3) не будет зависеть от выбора вспомогательных функций.

Ниже рассмотрены два типа локальных особенностей функции очага: кусочно-гладкие и фрактальные.

3. ГЛАДКИЕ ФУНКЦИИ ОЧАГА

В этом разделе функция очага $f{\mathbf{(x}}),$ ${\mathbf{x}} = $ ${\mathbf{(g}},t)$ предполагается гладкой внутри ограниченного носителя ${{\Omega }_{f}} \in {{R}^{3}}.$ Для любой внутренней точки ${{{\mathbf{x}}}_{0}} = ({{{\mathbf{g}}}_{0}},{{t}_{0}})$ из ${{\Omega }_{f}},$ фрагмент $f({\mathbf{x}}\left| {{{{\mathbf{x}}}_{0}})} \right.$ в этом случае можно считать финитной (т.е. с ограниченным носителем) гладкой функцией. Поэтому его ВЧ вклад в асимптотику (2) пренебрежимо мал, точнее $\left| {\hat {f}({\mathbf{p}}\omega \left| {{{{\mathbf{x}}}_{{\mathbf{0}}}})} \right.} \right| < C{{\omega }^{{ - n}}},$ если конечен порядок гладкости, $n,$ функции $f{\mathbf{(x}}).$ Это хорошо известный факт из теории преобразования Фурье [Федорюк, 1987].

Следовательно, в гладком случае ВЧ асимптотика $\hat {u}(\omega )$ определяется свойствами функции очага вблизи границы носителя ${{\Omega }_{f}}$ и свойствами самой границы $\partial {{\Omega }_{f}}.$

Назовем границу $\partial {{\Omega }_{f}}$ фронтальной поверхностью очага. В окрестности точки ${{{\mathbf{x}}}_{0}} \in \partial {{\Omega }_{f}}$ будем описывать ее в явном виде $t = {{t}_{r}}({\mathbf{g}}),$ предполагая функцию ${{t}_{r}}({\mathbf{g}})$ гладкой или кусочно-гладкой. Индекс $r$ связан с английским термином “rupture”. Наблюдаемый аналог ${{t}_{r}}({\mathbf{g}})$ (“arrival function”):

определяет время пробега сигнала от точки разрушения ${\mathbf{g}}$ до удаленного приемника. Изолинии ${{t}_{а}}({\mathbf{g}})$ назовем изохронами.

В литературе поведение функции очага вблизи фронта разрыва до конца не формализовано. Допускается, что на стадии фазы залечивания трещины функция очага ограничена [Madariaga et al., 1998; Nielsen, Madariaga, 2003]. В активной фазе разрушения, классические модели (см. [Костров, 1964; Madariaga, 1977; 1983]) демонстрируют сингулярность типа “обратного квадратного корня”, ${1 \mathord{\left/ {\vphantom {1 {\sqrt \cdot }}} \right. \kern-0em} {\sqrt \cdot }}.$ Строгое обоснование этой сингулярности в рамках теории упругости дано в работе [Herrero et al., 2006]. Объединяя оба случая, будем рассматривать функцию источника в окрестности ${{{\mathbf{x}}}_{0}}$ следующего вида:

где ${{a}_{ + }} = \max (a,0).$ Физически интересны значения $\beta = 1$ и $\beta = 1{\text{/}}2.$ В первом случае получаем ограниченность $f,$ а во втором сингулярность типа обратного квадратного корня.

Следующие два утверждения являются следствиями леммы Эрдейи и метода стационарной фазы (см приложение А1).

Уверждение 1. Пусть ${{{\mathbf{x}}}_{0}} = ({{{\mathbf{g}}}_{0}},{{t}_{0}})$ точка границы $\partial {{\Omega }_{f}},$ в окрестности которой функция$f{\mathbf{(x}})$ допускает представление (5) с гладкими функциями ${{t}_{r}}({\mathbf{g}})$ и $V({\mathbf{g}},t) \ne 0.$

Пусть в окрестности ${{{\mathbf{g}}}_{0}}$ на границе существует ровно одна и притом невырожденная стационарная точка ${{{\mathbf{g}}}_{s}}$ функции ${{t}_{a}}({\mathbf{g}}),$ т.е. $\nabla {{t}_{a}}({{{\mathbf{g}}}_{s}}) = 0$ и полная кривизна поверхности ${{t}_{a}}({\mathbf{g}})$ в этой точке ненулевая: ${{K}_{s}} \ne 0.$ Тогда ВЧ вклад ${{{\mathbf{x}}}_{0}}$ в спектр источника имеет порядок $O({{\omega }^{{ - ({\beta } + 1)}}}),$ а амплитуда вклада зависит от направленности излучения через стационарную точку. Более точно:

Искомое квадратичное затухание спектра реализуется при $\beta = 1,$ т.е. в случае ограниченности $f{\mathbf{(x}})$ в окрестности ${{{\mathbf{g}}}_{0}}.$

При отсутствии стационарных точек спектральный вклад фрагмента имеет порядок $o({{\omega }^{{ - 2}}})$ при любом $\beta > 0.$

Детали обоснования (6) вынесены в Приложение А2.

Сверхзвуковой (super shear) эффект. Существование регулярной стационарной точки ${{{\mathbf{g}}}_{s}}$ у функции ${{t}_{a}}({\mathbf{g}})$ означает, что

Пусть ${\mathbf{v}}({\mathbf{g}}) = ({{{v}}^{1}}({\mathbf{g}}),{{{v}}^{2}}({\mathbf{g}}))$ вектор скорости фронта в точке ${\mathbf{g}}.$ Продифференцируем соотношение $t = {{t}_{r}}({\mathbf{g}}\left| {{{{\mathbf{x}}}_{0}}} \right.)$ по t, учтем (7) и неравенство $\left| {{{{\mathbf{\gamma }}}_{\Sigma }}} \right| \leqslant 1.$ В результате получим необходимое условие существования стационарной точки: где ${{{v}}_{r}}({{{\mathbf{g}}}_{s}})$ – полное значение скорости.

Полученное неравенство означает, что в стационарной точке разрыв должен опережать волну по скорости: ${{{v}}_{r}}({{{\mathbf{g}}}_{s}}) \geqslant c.$ Такое явление возможно, хотя для землетрясений наблюдается редко [Madariaga et al., 2000]. В последнее время оно стало объектом интенсивного изучения теоретически, численно и экспериментально (см., например, [Rosakis et al., 1999; Dunham, Archuleta, 2004; Yang, Gao, 2004; Bizzari et al., 2010; Marty et al., 2019]).

В классической модели в работе [Костров, 1964] функция очага имеет вид f(g, t) = $ = {{Ad} \mathord{\left/ {\vphantom {{Ad} {dt({v}_{r}^{2}{{t}^{2}} - {{{\left| {\mathbf{g}} \right|}}^{2}})_{ + }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {dt({v}_{r}^{2}{{t}^{2}} - {{{\left| {\mathbf{g}} \right|}}^{2}})_{ + }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}$ и, значит, фронтальная поверхность образует конус: ${{({{{v}}_{r}}t)}^{2}} = {{\left| {\mathbf{g}} \right|}^{2}}.$ Кривизна конической поверхности равна нулю. Поэтому, согласно (6), ВЧ вклад всех стационарных точек конической фронтальной поверхности в ${{\omega }^{{ - 2}}}$ – асимптотику равен нулю.

Смягчим требование о существовании стационарной точки на фронтальной поверхности ${{t}_{r}}({\mathbf{g}}),$ заменив стационарность условной стационарностью.

Пусть ${{t}_{r}}({\mathbf{g}})$ теряет гладкость на линии $l:{{g}_{2}} = \psi ({{g}_{1}}).$ Будем считать, что ${{t}_{r}}({\mathbf{g}})$ представлена двумя гладкими поверхностями $t_{r}^{ \pm }({\mathbf{g}})$ с общим гладким краем, расположенным над гладкой кривой $l.$ Рассмотрим сужение ${{t}_{a}}({\mathbf{g}})$ на линию $l:S({{g}_{1}}) = {{t}_{a}}({{g}_{1}},\psi ({{g}_{1}})).$ Точку ${{{\mathbf{\tilde {g}}}}_{s}} = ({{\tilde {g}}_{{1s}}},\psi ({{\tilde {g}}_{{1s}}}))$ назовем условной стационарной точкой на ${{t}_{r}}({\mathbf{g}}),$ если $S{\kern 1pt} '({{\tilde {g}}_{{1s}}}) = 0.$ Условная стационарная точка считается регулярной, если:

Утверждение 2. Пусть ${{{\mathbf{x}}}_{0}} = ({{{\mathbf{g}}}_{0}},{{t}_{0}})$ точка границы $\partial {{\Omega }_{f}},$ в окрестности которой функция$f{\mathbf{(x}})$ допускает представление (5) с гладкой функцией $V({\mathbf{g}},t) \ne 0$ и кусочно-гладким фронтом ${{t}_{r}}({\mathbf{g}}),$ указанным выше. Пусть существует условная регулярная стационарная точка ${{{\mathbf{\tilde {g}}}}_{s}} = ({{\tilde {g}}_{{1s}}},\psi ({{\tilde {g}}_{{1s}}}))$ и при этом единственная в окрестности ${{{\mathbf{x}}}_{0}} = ({{{\mathbf{g}}}_{0}},{{t}_{0}}).$ Тогда спектральный вклад фрагмента$f({\mathbf{x}}\left| {{{{\mathbf{x}}}_{0}})} \right.$ имеет порядок $O\left( {{{\omega }^{{ - ({\beta } + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})}}}} \right),$ а амплитуда спектра зависит от направленности излучения через стационарную точку. Более точно:

где:

В условиях $\nabla t_{r}^{ \pm }({\mathbf{g}}\left| {{{{\mathbf{x}}}_{0}}} \right.) \ne {{{{{\mathbf{\gamma }}}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{{\mathbf{\gamma }}}_{\Sigma }}} c}} \right. \kern-0em} c},$ величину $\Delta $ всегда можно считать конечной и ненулевой.

Детали обоснования (10) вынесены в Приложение А3.

Замечания. В рассмотренном случае:

– ${{\omega }^{{ - 2}}}$ поведение спектра реализуется при физически естественном значении параметра $\beta = 1{\text{/}}2;$

– допустимые направления, на которых может быть зафиксирована асимптотика (10), либо отсутствуют, либо образуют конечный сегмент в плоскости очага.

Действительно, условная стационарная точка ${{{\mathbf{\tilde {g}}}}_{s}}$ является точкой экстремума функции ${{t}_{а}}({\mathbf{g}})$ при условии, что она рассматривается на линии $l:L({\mathbf{g}}) = 0.$ Применяя метод Лагранжа к условному экстремуму, заключаем, что точка ${{{\mathbf{\tilde {g}}}}_{s}}$ вместе с неизвестной константой $\lambda $ определяются соотношением:

Остается заметить, что если уравнение (12) разрешимо для вектора ${{\hat {\gamma }}_{\Sigma }}$, тогда оно разрешимо и для любого вектора:

с новой константой ${{\lambda }^{{\varepsilon }}} = \lambda - \varepsilon .$

4. ФУНКЦИЯ ИСТОЧНИКА ФРАКТАЛЬНОГО ТИПА

Существует другое, формально идентичное (1), интегральное представление смещения в дальней зоне, где исходная функция $f$ интерпретируется как локальный сброс напряжения в момент преодоления барьера (асперити) [Kostrov, Das, 1988; Boatwright, 1988; Gusev, 1989]. В этом случае физические ограничения на $f$ расплывчаты. В работе [Mikumo, Miyatake, 1979] численно исследовалась проблема случайного сброса напряжений на разломе. Процесс разрушения оказался довольно хаотичным, без четко различимого фронта разрыва. Это обстоятельство стимулировало стохастический или фрактальный подход к кинематическим моделям очага.

В работе [Gusev, 2014] численно исследовалась следующая модель:

где: $\phi (t) \geqslant 0$ гладкая функция на полуоси $t > 0,$ $\phi (0) \ne 0 \cup \infty $ и $\phi (t) = 0$ вне $[0,{{t}_{0}}];$ $V({\mathbf{g}})$ есть локальный сброс напряжений в ${\mathbf{g}},$ не зависящий от времени; ${{t}_{r}}({\mathbf{g}})$ момент разрыва и соответственно сброса напряжений в ${\mathbf{g}};$ $V({\mathbf{g}})$ и ${{t}_{r}}({\mathbf{g}})$ непрерывны. Фронтальная поверхность разрыва почти плоская и односторонне направлена: Здесь: ${{{\mathbf{\gamma }}}_{r}},$ $\left| {{{{\mathbf{\gamma }}}_{{\mathbf{r}}}}} \right| = 1$ – доминирующее направление распространения разрыва; $\nu $ – его средняя скорость, а $\delta {{t}_{r}}({\mathbf{g}})$ – малое возмущение.

В этой модели носитель $f$ определяется соотношением:

Функция $f$ гладкая по $t$ для внутренних точек ${{\Omega }_{f}}.$ Поэтому основной вклад в асимптотику $\hat {u}(\omega )$ вносят точки фронтальной поверхности $\partial {{\Omega }_{f}}.$ Более того, он исходит от точек передней границы: $t = {{t}_{r}}({\mathbf{g}}),$ где $f$ как функция во всем пространстве, терпит разрыв.

В модели работы [Gusev, 2014] функции ${{t}_{r}}({\mathbf{g}})$ и $V({\mathbf{g}})$ фрактальны, т.е. имеют порядок гладкости меньше 1. Для описания таких объектов больше подходит язык случайных функций. В этом случае требуемая функция погружается в ансамбль реализаций с подходящими свойствами (в данном случае, с фиксированным свойством дробной гладкости).

Будем говорить, что случайная функция $\xi ({\mathbf{g}})$ имеет гладкость порядка $0 < {{H}_{\xi }} < 1,$ если

где: E – символ математического ожидания; $C({\mathbf{g}}) > 0$ гладкая функция; степенной показатель ${{H}_{\xi }}$ известен как параметр Херста (Hurst).

При рассмотрении ансамбля реализаций, индивидуальный спектр $\hat {u}(\omega )$ траектории случайного процесса приходится заменять среднеквадратичным (root-mean-square):

В условиях (14, 15)

Отсюда, предполагая статистическую независимость случайных компонент $\delta {{t}_{r}}({\mathbf{g}})$ и $V({\mathbf{g}}),$ получим основное спектральное соотношение для дважды стохастической модели (14):

Здесь: ${{m}_{V}}({{{\mathbf{g}}}_{1}},{{{\mathbf{g}}}_{2}}) = EV({{{\mathbf{g}}}_{1}})V({{{\mathbf{g}}}_{2}})$ является корреляционной функцией поля $V({\mathbf{g}}),$ а ${{\chi }_{r}}$ – характеристическая функция приращений $\delta {{t}_{r}}({\mathbf{g}}){\text{:}}$

Соотношение (20) позволяет качественно понять, когда спектр очага слабо зависит от направления ${\mathbf{D}}.$

Пусть распределение $\xi = \delta {{t}_{r}}({{{\mathbf{g}}}_{1}})$ – $\delta {{t}_{r}}({{{\mathbf{g}}}_{2}})$ имеет гладкую финитную плотность. Тогда его характеристическая функция ${{\chi }_{r}}(\omega \left| {{{{\mathbf{g}}}_{1}}} \right.,{{{\mathbf{g}}}_{2}})$ быстро убывает по частоте при ${{{\mathbf{g}}}_{1}} \ne {{{\mathbf{g}}}_{2}}.$ Поэтому ВЧ асимптотику (20) определяет малая окрестность диагонали ${{{\mathbf{g}}}_{1}}$ = ${{{\mathbf{g}}}_{2}},$ где подынтегральная функция $\exp \left( {i\omega \left\langle {{\mathbf{D}},{{{\mathbf{g}}}_{1}} - {{{\mathbf{g}}}_{2}}} \right\rangle } \right)$ слабо зависит от направленности излучения. Эта идея может быть реализована для широкого класса распределений $\xi .$ Ниже, только для простоты изложения, мы будем считать это распределение гауссовским.

Утверждение 3.Пусть выполнены следующие условия:

a) случайные компоненты модели (14, 15), $V({\mathbf{g}}),$ $\delta {{t}_{r}}({\mathbf{g}})$ статистически независимы;

б) поле сброса напряжений $V({\mathbf{g}})$ таково, что ${{m}_{V}}({{{\mathbf{g}}}_{1}},{{{\mathbf{g}}}_{2}}) > 0,$ ${{m}_{V}}({\mathbf{g}},{\mathbf{g}}) < C$ и $E{{(V({{{\mathbf{g}}}_{1}}) - V({{{\mathbf{g}}}_{2}}))}^{2}}$ ≤ $ \leqslant C{{\left| {{{{\mathbf{g}}}_{1}} - {{{\mathbf{g}}}_{2}}} \right|}^{{2h}}},$ $h > 0;$

в) приращения поля $\delta {{t}_{r}}({\mathbf{g}})$ распределены по Гауссу со средним 0 и дисперсией

где $\sigma ({{{\mathbf{g}}}_{1}},{{{\mathbf{g}}}_{2}})$ – гладкая функция, отграниченная от нуля и бесконечности;

г) $\phi (t) = {{t}_{ + }}^{{{\beta } - 1}}\varphi (t),$ где $0 < \beta \leqslant 1,$ а $\varphi (t) \geqslant 0$ – гладкая финитная функция и $\varphi (0) > 0.$

Тогда:

т.е. ВЧ асимптотика спектра очага степенная и не зависит от направленности излучения.

Замечания:

– согласно (23), ВЧ спектр учитывает корреляции случайных компонент модели только на диагонали. Это означает, что ВЧ асимптотику спектра формирует некогерентное излучение точек очага. Необходимость этого свойства подчеркивалось в работах А. Гусева;

– модель Гусева соответствует параметру $\beta = 1.$ В этом случае слегка шероховатая фронтальная поверхность, т.е. поверхность с параметром Херста $H$ близким к 1, устойчиво порождает близкое к омега-квадрат-поведение спектра. Ситуация резко меняется в предельном случае $H = 1,$ когда фронтальная поверхность может быть гладкой. Как показано выше (Утверждение 1), в этом случае квадратичное убывание спектра обеспечивают регулярные стационарные (и фактически неустойчивые) точки фронтальной поверхности. Используя слабую шероховатость с $H \approx 1,$ мы, грубо говоря, стабилизируем поле стационарных точек и, как результат, получаем устойчивое для всех направлений почти омега-квадрат-поведение спектра. Дополнительные условия позволяют также устранить свойство направленности излучения;

– все сказанное относится и к другому физически интересному случаю, когда параметр $\beta = 1{\text{/}}2.$ Для него омега-квадрат-поведение спектра реализуется с менее гладкой фронтальной поверхностью, а именно, с параметром Херста $H = 2{\text{/}}3.$

5. ОБСУЖДЕНИЕ: ИЗОХРОНЫ И АСИМПТОТИКА

Поясним неформально, из чего складывается ВЧ асимптотика спектра очага. В наших примерах функция очага вблизи фронтальной границы имеет особенность вида $(t - {{t}_{r}}({\mathbf{g}}))_{ + }^{{^{{{\beta } - 1}}}}$ с $\beta = 1$ или $\beta = 1{\text{/}}2.$ Поэтому Фурье-преобразование по времени дает ВЧ вклад порядка ${{\omega }^{{ - {\beta }}}}$ (Лемма Эрдейи, А1). Дополнительный вклад исходит от Фурье-преобразования по пространству. Здесь важна аналитическая структура функции ${{t}_{a}}({\mathbf{g}}) = {{t}_{0}} - \left\langle {{\mathbf{g,}}{{{{{\mathbf{\gamma }}}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{{\mathbf{\gamma }}}_{\Sigma }}} c}} \right. \kern-0em} c}} \right\rangle + {{t}_{r}}({\mathbf{g}}),$ т.е. времени прихода сигнала из точки разрыва к удаленному приемнику в направлении ${{{\mathbf{\gamma }}}_{\Sigma }}.$ Эта функция играет роль фазы в интеграле Фурье вида

Роль финитной гладкой функции $\varphi $ в асимптотике интеграла несущественна и сводится к тому, чтобы пренебрегать границей области интегрирования. Помня об этом, рассмотрим (24) с $\varphi $ = 1 в малой окрестности ${{G}_{0}}$ точки ${{{\mathbf{g}}}_{0}}.$

Пусть $A(t)$ мера точек из ${{G}_{0}},$ где ${{t}_{a}}({\mathbf{g}}) < t.$ Тогда интеграл (24) преобразуется к виду $I({{1}_{{{{G}_{0}}}}})$ = =$\int_{{{t}_{ - }}}^{{{t}_{ + }}} {{{e}^{{i{\omega }t}}}} dA(t).$ Плотность меры, $\dot {A}(t),$ можно интерпретировать как интенсивность изолиний (изохрон) функции ${{t}_{a}}({\mathbf{g}})$ на множестве ${{G}_{0}}.$ Подобный объект не нов для сейсмологов (см. [Spudich, Frazer, 1984]). Его важность связана с тем, что аналитические свойства плотности $\dot {A}(t)$ тесно связаны с ВЧ асимптотикой $I({{1}_{{{{G}_{0}}}}}).$

В качестве примера рассмотрим сначала Утверждение 1. Здесь ${{t}_{a}}({\mathbf{g}})$ имеет в ${{G}_{0}}$ единственную невырожденную стационарную точку ${{{\mathbf{g}}}_{s}}.$ Поэтому в подходящей системе координат можно считать, что ${{{\mathbf{g}}}_{s}} = 0,$ ${{t}_{a}}({\mathbf{g}}) = - \left( {g_{1}^{2} \pm g_{2}^{2}} \right).$ Рассмотрим более простой эллиптический случай, отвечающий знаку (+). В этом случае (см. рис. 1а) изохроны подобны эллипсам, которые стягиваются к стационарной точке. Тогда ${{A}_{ + }}(t) \approx C - \pi {{( - t)}_{ + }}$ в малой окрестности $t = 0.$ В результате $\dot {A}(t)$ имеет разрыв в момент $t = 0,$ что определяет вклад интеграла $I({{1}_{{{{G}_{0}}}}})$ в ВЧ асимптотику порядка ${{\omega }^{{ - 1}}}.$ Соответственно суммарный вклад стационарной точки имеет порядок ${{\omega }^{{ - {\beta }}}}{{\omega }^{{ - 1}}}.$

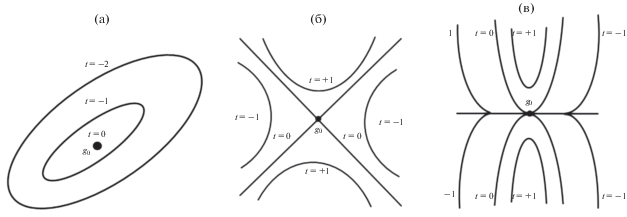
В гиперболическом случае ${{t}_{a}}({\mathbf{g}}) = - \left( {g_{1}^{2} - g_{2}^{2}} \right)$ изохроны представлены на рис. 1б, а величина $\dot {A}(t) \approx c\ln \left| t \right|,$ $\left| t \right| \ll 1.$ Преобразование Фурье $\ln \left| t \right|,$ как обобщенной функции, есть $ - 0.5\pi {{\left| \omega \right|}^{{ - 1}}},$ $\omega \ne 0$ [Брычков, Прудников, 1977], что позволяет сохранить прежнее заключение о спектре.

В Утверждении 2 пространство делится на две части линией $l.$ В каждой из них, при подходящем выборе системы координат, можно считать, что линия раздела совпадает с осью ${{g}_{1}}$, критическая точка ${{{\mathbf{\tilde {g}}}}_{s}} = 0,$ ${{t}_{a}}({\mathbf{g}}) = g_{1}^{2} + {{g}_{2}},$ ${{g}_{2}} \leqslant 0$ и ${{t}_{a}}({{g}_{1}},{{g}_{2}})$ = = $ - {{t}_{a}}({{g}_{1}}, - {{g}_{2}})$ для ${{g}_{2}} \geqslant 0.$ В этом примере (см. рис. 1в) изохроны сначала пересекают линию $l.$ Их следы на линии окружают и стягиваются к ${{{\mathbf{\tilde {g}}}}_{s}};$ в критический момент t = 0 изохроны касаются линии $l,$ а затем удаляются от нее. В результате при малых t простой счет дает, $A(t) \approx C - k( - t)_{ + }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}.$ По Лемме Эрдейи (А1) преобразование Фурье $\dot {A}(t)$ дает вклад в ВЧ асимптотику порядка ${{\omega }^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}.$ Суммарный вклад стационарной точки имеет порядок ${{\omega }^{{ - {\beta }}}}{{\omega }^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}.$

В Утверждении 3 поле ${{t}_{a}}({\mathbf{g}})$ имеет дробную гладкость порядка $H < 1$ в каждой точке пространства и предполагается случайным. В стохастическом анализе плотность изохрон имеет специальное название: “occupation density”. При сделанных нами предположениях плотность $\dot {A}(t)$ определена для почти всех реализаций ансамбля [Xiao, 2013]. При этом гладкость $\dot {A}(t)$ неограниченно растет с уменьшением гладкости исходного поля ${{t}_{a}}({\mathbf{g}})$ [Geman, Horowitz, 1978]. Поэтому роль степени негладкости фронтальной поверхности в ВЧ асимптотике спектра очага должна падать, когда изрезанность фронта растет. Это отражено в финальной ВЧ асимптотике ${{\omega }^{{ - {\beta } - 1{\text{/}}H}}},$ найденной в Утверждении 3.

Эвристическое объяснение указанной асимптотики требует обоснования следующих шагов: 1) ВЧ асимптотика интеграла $I({{1}_{{{{G}_{0}}}}})$ = $\int_{{{t}_{ - }}}^{{{t}_{ + }}} {{{e}^{{i{\omega }t}}}} dA(t)$ зависит в основном от концевых точек ${{t}_{ \pm }};$ 2) если невозмущенный линейный фронт распространяется вдоль оси ${{g}_{1}},$ тогда $dA(t) \approx Cd{{g}_{1}}$ вблизи ${{t}_{ + }} = \max t;$ 3) случайное возмущение фронтальной поверхности, согласно (17), дает связь $dt \approx K{{(d{{g}_{1}})}^{H}}.$ Отсюда, $dA(t) \approx C{{(dt)}^{{1{\text{/}}H}}},$ т.е. при $t$, близких к ${{t}_{ + }},$ имеем $\dot {A}(t) \approx C({{t}_{ + }} - t)_{ + }^{{ - 1 + 1{\text{/}}H}}.$ Лемма Эрдейи дает искомый порядок асимптотики ${{\omega }^{{ - 1{\text{/}}H}}}$ для интеграла $I({{1}_{{{{G}_{0}}}}}).$

6. ВЫВОДЫ

Мы рассмотрели гладкие и фрактальные локальные особенности функции очага. Особенности первого типа позволяют при определенных условиях воспроизвести омега-квадрат-поведение спектра в дальней зоне. Источником такого поведения может быть нестандартное условие, при котором скорость фронта разрушения превышает скорость S-волны. В гладких моделях асимптотика спектра зависит от направленности излучения; при этом локальный источник степенной асимптотики проявляется, в лучшем случае, в приемниках, образующих отрезок одномерной дуги.

Введение фрактальности в модель функции очага оказывает стабилизирующее влияние на решение рассмотренной задачи. Более точно, фрактальность позволяет устойчивым образом воспроизвести в дальней зоне и квадратичное затухание спектра, и потерю направленности излучения. Омега-квадрат-поведение можно реализовать (условно говоря) и в активной фазе разрушения, и на стадии залечивания. Однако требования к гладкости фронтальной поверхности не одинаковы: $H = 2{\text{/}}3$ (активная фаза) против $H \approx 1$ (фаза залечивания), что физически вполне естественно. Но в обоих случаях высокая степень негладкости ($H < 1{\text{/}}2$) фронтальной поверхности не совместима с омега-квадрат-поведением спектра. Что касается свойства потери направленности излучения, здесь важно сочетать негладкость ($H < 1$) фронтальной поверхности с гладкостью распределений, описывающих приращения шумовой компоненты этой поверхности. Эти заключения вполне конструктивны для целей моделирования функции очага.