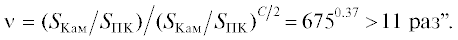Физика Земли, 2020, № 1, стр. 77-85

1. ВВЕДЕНИЕ

Долговременная интенсивность сейсмических событий является базовой характеристикой сейсмичности в задачах сейсморайонирования и сейсмического риска. В ее основе лежит закон повторяемости Гутенберга–Рихтера:

Здесь $\lambda (\Delta ,M)$ интенсивность или среднее число событий в единицу времени, имеющих магнитуду $ \geqslant {\kern 1pt} M$ в области $\Delta .$

Не существует единой методологии картирования параметров $(a,b)$ с учетом диапазона магнитуд $\Delta M = ({{M}_{ - }},{{M}_{ + }}).$ Однако в общих чертах, традиционный подход опирается на сейсмотектоническое зонирование территории, выбор подходящих зон с постоянными значениями каждого из указанных параметров и их последующее статистическое оценивание (см., например, [Молчан, Подаецкая, 1973; Молчан и др., 1996]). В силу дефицита статистики разрушительных землетрясений дискуссионными могут быть как сами элементы зонирования, так и выбор магнитудных диапазонов.

В этой связи интересна серия публикаций [Кособоков, Некрасова, 2004; Некрасова, Кособоков , 2006; 2009; Nekrasova et al., 2011; Nekrasova et al., 2015; Кособоков, Соловьев, 2018], где обращается внимание на важность учета “фрактальной природы землетрясений”. Рассматривая проблему сейсмического риска для мегаполисов мира, авторы заключают, что недооценка фрактальности в распределении сейсмичности заметно снижает риски. “Общий уровень занижения повторяемости слишком велик, чтобы не учитываться при расчетах сейсмического риска и потерь, так необходимых для принятия мер по предупреждению бедствия и его последствий” [Некрасова, Кособоков, 2006].

Альтернативный подход авторы видят в “Общем законе подобия для землетрясений” (ОЗПЗ), который предсказывает интенсивность событий магнитуды $ \geqslant {\kern 1pt} M$ в области ${{\Delta }_{L}}$ размера $L,$ ${{\Delta }_{L}} \subset {{\Delta }_{{{{L}_{0}}}}},$ согласно формуле:

Здесь: ${{\Delta }_{{{{L}_{0}}}}}$ – область, в центре которой расположена целевая область ${{\Delta }_{L}};$ $A$ – ожидаемое число событий $ \geqslant {\kern 1pt} {{M}_{0}}$ в год в ${{\Delta }_{{{{L}_{0}}}}};$ $C$ – фрактальная размерность эпицентров событий $ \geqslant {\kern 1pt} M$ в ${{\Delta }_{{{{L}_{0}}}}}.$

В сейсмологической литературе соотношение (2) впервые появилось в работе [Кейлис-Борок и др., 1989] как пример подобия сейсмичности.

Ниже, в разделе 2, мы описываем метод ОЗПЗ и его применение к задачам сейсмического риска. Чтобы снять противоречия, в разделе 3 соотношение (2) трактуется как нормировка в законах сейсмичности Бака. Далее, в разделе 4, на базе точных понятий фрактальности и мультифрактальности обсуждается оптимальный выбор параметра $C.$ Чтобы упростить чтение, разделы 3 и 4 снабжены итоговыми заключениями.

2. МОДЕЛИ СЕЙСМИЧНОСТИ: ТРАДИЦИОННЫЕ И ОЗПЗ

Для сравнения напомним одну из моделей сейсмичности, основанную на традиционном законе повторяемости [Молчан и др., 1996; Molchan et al., 1997]. В этой модели закон (1) представлен кусочно-линейным соотношением по пространству и магнитуде. При фиксированном диапазоне магнитуд $\Delta M,$ параметр активности $а$ более детален по пространству, чем параметр $b.$ Иначе говоря, область с постоянным значением $b$ ($b$-зона) разбита на подобласти с постоянными значениями $a.$ Линейный размер $b$-зоны существенно больше максимального размера очага из диапазона магнитуд $\Delta M.$ Чем больше сила землетрясений, тем больше размеры $b$-зоны. Это обусловлено необходимостью исключить возможные артефакты в виде “характеристических” событий [Wesnousky, 1994] и тем самым расширить область применимости модели (1).

В результате возникает многомасштабное представление закона (1) с параметрами ${{(a,b,\Delta M)}_{i}}$ для подходящих пространственных зон. Поясним его на примере. Для описания потенциально разрушительных землетрясений ($M > 3.8$) Италии в работах [Молчан и др., 1996; Molchan et al., 1997] были использованы два магнитудных уровня: ${{\Delta }_{1}}M = 3.5 - 5$ и ${{\Delta }_{2}}M = 5 - 7.$ Параметр $a$ первого уровня постоянен на элементах сейсмотектонической регионализации ($a$-зоны), с типичными размерами: 40-130 км в длину и 20-30 км в ширину. Измельчению этих участков препятствовала статистика землетрясений. Зоны с постоянным значением $b$ составлены из $a$-зон так, чтобы $b$-зоны были согласованы по размерам с магнитудными диапазонами${{\Delta }_{i}}M$ и при этом объединяли сейсмически связанные элементы исходной регионализации, т.е. были едины с точки зрения тектоники в соответствующем масштабе. Таких $b$-зон 1-го уровня оказалось 10, а зон второго уровня 3. Детализация $а$-параметра в $b$-зонах второго уровня связана с нетривиальной проблемой пространственной локализации сильных землетрясений. Из-за скудности статистики решение этого вопроса неединственно и может зависеть от конкретных приложений при получении верхних/нижних оценок риска.

Для сравнения с ОЗПЗ важны следующие элементы описанной модели: 1) неформальный подход к пространственному картированию параметров закона повторяемости и 2) дифференцированный по магнитуде и пространству учет условий, сохраняющих подобие в повторяемости событий. Препятствия подобию подробно анализировались в работе [Ben-Zion, 2008].

В приведенном примере главный вклад в число параметров модели вносят элементы исходной сейсмотектонической регионализации, а с учетом статистики землетрясений, а-зоны первого уровня (${{\Delta }_{1}}M = 3.5 - 5$).

3. ОЗПЗ КАК НОРМИРОВКА

Потеря свойства аддитивности в модели (2) означает, что мера сейсмической интенсивности устроена сложнее. Чтобы скорректировать модель, обратимся к истории вопроса.

Термин “Общий закон подобия для землетрясений” впервые появился в работе Бака [Bak et al., 2002] как Unified Scaling Law for Earthquake (USLE), однако с другой смысловой нагрузкой соотношения (2). Чтобы уточнить исходное понятие, рассмотрим сейсмическую зону G и покроем ее регулярной сеткой с шагом $L.$ Пусть $\xi (L \times L)$ некоторая статистика сейсмических событий $ \geqslant {\kern 1pt} M$ в ячейке $L \times L$ за время $\Delta T.$ Следуя и обобщая Бака, будем говорить, что сейсмичность обладает свойством USLE, если после подходящей нормировки статистики: ${{a}_{L}}\xi (L \times L),$ где ${{a}_{L}} = f(L,M,\Delta T),$ ее распределение, усредненное по всем ячейкам $L \times L,$ не зависит от $L,M,\Delta T.$ Усредненное распределение можно интерпретировать как распределение нормированной статистики в случайно выбранной ячейке пространства. Возможен и более сильный вариант USLE, когда распределение нормированной статистики одно и то же для всех сейсмоактивных ячеек. Тогда термин Unified следует заменить согласно [Сorral, 2003] на Universal.

В качестве примера USLE-статистики в работах [Bak et al., 2002; Сorral, 2003; 2004] рассмотрен интервал времени ${{\tau }_{L}}$ между двумя последовательными событиями в ячейке $L \times L.$ Эта статистика интересна тем, что ее естественная нормировка должна быть пропорциональной интенсивности $\lambda ({{\Delta }_{L}},M)$ событий манитуды $ \geqslant {\kern 1pt} M$ в ${{\Delta }_{L}} = L \times L,$ поскольку в условиях стационарности режима среднее значение $E\lambda ({{\Delta }_{L}},M){{\tau }_{L}} = 1$ не зависит от параметров. Учитывая закон повторяемости Гуттенберга–Рихтера по магнитуде и фрактальность распределения по пространству (подробнее см. ниже), в работе [Bak et al., 2002] предложен нормировочный коэффициент для ${{\tau }_{L}}$ в виде:

где ${{d}_{f}}$ (как и С) интерпретируется как фрактальная размерность эпицентров.

Формально правые части (6) и (2) совпадают параметрически, но отличаются по содержанию и целям использования: (6) это нормировка сейсмичности, а (2) ее оценка. Кроме того, исходя из предложенных авторами методов оценивания, фрактальные параметры ${{d}_{f}}$ и $С$ оказались разными по типу размерности (см. ниже).

Согласно работам [Bak et al., 2002; Corral, 2003; 2004] нормированное распределение статистики ${{\tau }_{L}}$ неплохо согласуется с Гамма-распределением, имеющим плотность $p(x) = с{{x}^{{{\gamma } - 1}}}{{e}^{{ - x}}}.$ Это наблюдение относится к полным каталогам, включающим афтершоки. Теоретический анализ показал [Molchan, 2005], что ${{\tau }_{L}}$ как USLE–статистика реализуется лишь для однородного пуассоновского потока событий, что противоречит реальной сейсмичности и оценке параметра $\gamma ,$ значимо отличной от 1.

“Универсальность распределения” нормированной величины ${{\tau }_{L}}$ кажущаяся и обязана подходящей визуализации распределений ${{a}_{L}}{{\tau }_{L}},$ а именно в log-log шкале [Molchan, Kronrod, 2007]. В такой системе координат хорошо подтверждается согласие хвостов распределений ${{a}_{L}}{{\tau }_{L}},$ но скрыто расхождение распределений в области умеренных значений указанных статистик. Поведение распределений ${{a}_{L}}{{\tau }_{L}}$ в области малых значений имеет степенной характер и обязано закону Омори, а в области больших значений оно экспоненциальное и обязано пуассоновости основных событий. Таким образом, USLE-закон для статистики ${{\tau }_{L}}$ синтезирует факты, хорошо известные сейсмологам.

Оставаясь в рамках идеологии П. Бака, более естественно искать такую оптимальную нормировку статистики $\xi (L \times L),$ при которой распределение ${{a}_{L}}\xi (L \times L)$ в случайной ячейке $L \times L$ предельно слабо зависит от параметров $\Delta T,L,M$ и при этом остается невырожденным.

Термин “предельно слабо” означает выбор такой нормировки, при которой распределения ансамблей $\{ {{a}_{L}}\xi (L \times L)\} $ с разными $L$ наиболее близки друг к другу в подходящей метрике. Учитывая недостатки представления распределений в работах [Bak et al., 2002; Corral, 2003; 2004], расхождение распределений оценивалось авторами [Molchan, Kronrod, 2005] в метрике Леви [Феллер, 1967]. В этой метрике измеряется наибольший зазор между графиками двух распределений в направлении вектора (–1.1). Метрика Леви наиболее чувствительна к отклонениям распределений в области центральных значений случайных величин.

Термин невырожденности предельного распределения означает, что нормированная статистика при $L \ll 1$ не вырождается в ноль или бесконечность. Особая роль малых масштабов $L$ связана с тем, что только при $L \to 0$ относительно корректно можно говорить о фрактальности.

Проблема оптимальной нормализации была рассмотрена в работах [Molchan, Kronrod, 2005; 2007] для двух статистик ${{\tau }_{L}}$ и ${{n}_{L}},$ где ${{n}_{L}}$ – число событий $ \geqslant {\kern 1pt} M$ в случайно выбранной ячейке $L \times L$ за время $\Delta T.$ При невозможности разделить типичные и нетипичные ячейки, анализ долговременной статистики ${{n}_{L}}$ в случайной ячейке $L \times L,$ является естественной альтернативой соотношению (2). Чисто теоретический пример сейсмичности, в которой статистика ${{n}_{L}}$ обладает в точности свойством USLE, предложен в работе [Писаренко, Голубева, 1996].

Поскольку $E{{n}_{L}} = \lambda ({{\Delta }_{L}},M)\Delta T,$ нормировка статистики ${{n}_{L}}$ опять связана с интенсивностью событий в $L \times L{\text{:}}$

Соотношения (6), (7) определяют только структуру нормировок, но не означают совпадения параметров, относящихся к обеим статистикам ${{\tau }_{L}},{{n}_{L}}.$

Оптимальное значение ${{d}_{f}}$ может зависеть и от выбора статистики и от того, как мы определим случайность или, что то же, вес ячейки $L \times L$ при осреднении распределений.

Будем выбирать ячейку $L \times L$ с вероятностью

где ${{\Lambda }_{p}}$определяется условием $\sum {{{w}_{p}}(L \times L)} = 1.$ Вариант $p = 0$ предполагает равновероятными все сейсмогенные ячейки. Этот вариант использовался в работе [Bak et al., 2002]. Вариант $p = 1$ выглядит наиболее естественно, поскольку вес ячейки пропорционален наблюденному числу в ней событий. Большие $p > 1$ позволяют локализовать с разной степенью разрешения места высокой сейсмической активности.

Для однородной по пространству мультифрактальной меры сейсмичности (точные определения см. ниже) авторы работы [Molchan, Kronrod, 2005] конструктивно описали неоднозначность выбора оптимального параметра ${{d}_{f}}$ и подтвердили выводы на примере сейсмичности разлома Сан-Андреас. В частности, оптимальная нормировка статистики ${{n}_{L}}$ для событий $M > {\text{2}}$ достигается с ${{d}_{f}} \approx 1.8$ в случае весового параметра $p = 0,$ и с ${{d}_{f}} \approx 1.2$ в случае $p = 1.$ Указанные эмпирические оценки ${{d}_{f}}$ заметно разные и обе относятся к диапазону масштабов $L = 10 - 100$ км. Авторы работы [Некрасова, Кособоков, 2009], используя $С \approx 1.2,$ оценили эффект применения метода ОЗПЗ к г. Лос-Анджелес величиной (5): $\nu = 6.2.$ При оценке Бака $С \approx 1.8,$ эффект снижается почти вчетверо: $\nu \approx 1.6,$ что подтверждает важность правильного выбора фрактального параметра.

3.1. Вывод

Модель сейсмической интенсивности (2) не обладает свойством аддитивности и поэтому нуждается в коррекции. Рассматривая ОЗПЗ как нормировку статистики ${{n}_{L}}$ в случайной ячейке, можно заметно ослабить (но не устранить) зависимость ее распределения от масштаба. В результате коррекция соотношения (2) приобретает стохастический вид:

где о коэффициентах $\{ \xi ({{\Delta }_{L}})\} $ известно только то, что распределение каждого $L$-ансамбля корректирующих множителей $\{ \xi ({{\Delta }_{L}})\} $ слабо зависит от масштаба. Здесь ячейки ${{\Delta }_{L}}$ образуют сетку с шагом $L,$ а ${{L}_{0}}$ масштаб области с однородными (см. ниже) фрактальными свойствами меры сейсмичности. Скорректированная модель (9) вместо точечных оценок интенсивности позволяет строить в лучшем случае доверительные интервалы для $\lambda ({{\Delta }_{L}},M),$ что снижает ее практическую ценность.

Модель (9) проверялась на событиях (М > 2) разлома Сан-Андреас [Molchan, Kronrod, 2005] и, конечно, нуждается в обосновании в каждом конкретном случае региона и диапазона магнитуд. Нетривиальные примеры распределений $\{ \xi ({{\Delta }_{L}})\} $ представлены в работе [Molchan, Kronrod, 2005].

Выбор параметра $С$ не однозначен и требует специального анализа, представленного ниже.

4. МУЛЬТИФРАКТАЛЬНОСЬ И ПАРАМЕТР С

Чтобы понять природу параметров С, ${{d}_{f}}$ в соотношениях (2), (6), необходимы точные определения фрактальности и мультифрактальности. Эти понятия неизбежно связаны с бесконечно малыми пространственными масштабами, недостижимыми при анализе сейсмичности. Однако другого пути нет, если нужно понять те подводные камни, которые скрыты при формальном использовании этих понятий на макроуровне.

Интенсивность событий магнитуды $ \geqslant {\kern 1pt} M$ в ячейках $\Delta ,$ $\lambda (\Delta ,M),$ определяет при фиксированном значении $M$ меру $\mu (\Delta )$ на подмножествах сейсмоактивной зоны. Как чисто математический объект меру $\mu (\Delta )$ называют мультифракталом, если, грубо говоря, ее носитель можно разложить в сумму подмножеств ${{S}_{\alpha }}$, таких что в подходящей системе окрестностей ${{\Delta }_{L}},$ своей для каждой точки $g \in {{S}_{{\alpha }}},$ мера демонстрирует сингулярность типа $\alpha {\text{:}}$

(Запись $x\sim y$ означает, что $x{\text{/}}y \approx 1$ при $L \ll 1$).

Заметим, что гладкая мера на плоскости имеет, как правило, параметр $\alpha = 2.$

Набор пар $(\alpha ,f(\alpha )),$ где$f(\alpha )$ дробная размерность множества ${{S}_{{\alpha }}},$ определяет мультифрактальный спектр меры. В теоретических работах дробная размерность ассоциируется с размерностью Хаусдорфа, а в физических приложениях (менее строгих) с боксовой размерностью. По определению спектр монофрактала (или просто фрактала) состоит из одной пары, а спектр однородного мультифрактала один и тот же для разных частей носителя меры.

Спектр однородного мультифрактала содержит точку, у которой сингулярность совпадает с размерностью, ${{\alpha }_{0}} = f({{\alpha }_{0}}).$ Такая размерность называется информационной ${{D}_{1}}$, поскольку все точки с указанной сингулярностью образуют множество полной меры: $\mu ({{S}_{{{{{\alpha }}_{{\text{0}}}}}}}) = \mu ( \cup {{S}_{{\alpha }}}).$ Иначе говоря, соотношение (10) имеет место с $\alpha = {{D}_{1}}$ в подходящей малой окрестности любой точки пространства, типичной для меры $\mu ( \cdot ).$ На макромасштабном уровне понятие типичности уже обсуждалось в разделе 2. На микроуровне антиподы типичным точкам мультифрактальной меры многолики и представлены объединением подмножеств ${{S}_{\alpha }}$ точек с однородной сингулярностью $\alpha \ne {{D}_{1}}.$ Как и на макроуровне, множества ${{S}_{{\alpha }}}$ не известны. Любая сингулярность (10) может быть выявлена, как правило, статистическими методами, но без привязки к конкретной точке пространства.

Конструктивным признаком мультифрактальности меры является приближенно линейное соотношение:

при малых размерах шага решетки и разных фиксированных $p.$ Для простоты записи здесь мера нормирована, т.е. имеет полную единичную массу, и потому $\tau (1) = 0.$ Суммирование в (11) ведется по ячейкам ненулевой $\mu $-меры, что на языке сейсмичности соответствует сейсмоактивным ячейкам.

Известно, что в условиях выпуклости кривой $\left[ { - \tau (p)} \right],$ величины $\tau (p)$ полностью определяют мультифрактальный спектр меры. В частности, множество сингулярностей типа (10) в регулярной ситуации совпадает с множеством значений ${{d\tau (p)} \mathord{\left/ {\vphantom {{d\tau (p)} {dp}}} \right. \kern-0em} {dp}}: = \dot {\tau }(p).$ Приведем точные соотношения для базовых (в приложениях) размерностей: боксовая размерность носителя меры ${{D}_{0}} = - \tau (0),$ информационная размерность ${{D}_{1}} = \dot {\tau }(1),$ корреляционная размерность ${{D}_{2}} = \tau (2)$ [Hentschel, Procaccia, 1983; Feder, 1988].

И размерности, и сингулярности меры формально объясняют степенную параметризацию в (2), (6). С одной стороны (10) эквивалентно грубому соотношению $\mu ({{\Delta }_{L}}) \propto {{L}^{\alpha }}$ для малых масштабов вблизи точек из ${{S}_{{\alpha }}}.$ (Символ $x \propto y$ означает, что $x{\text{/}}y$ медленно меняется при $L \to 0$). Любое множество ${{S}_{{\alpha }}}$ однородной мультифрактальной меры всюду плотно на ее носителе. Поэтому любая сингулярность меры является претендентом на фрактальный параметр в (2), (6). Среди них определенное преимущество имеет сингулярность $\alpha = {{D}_{1}},$ поскольку является типичной для меры.

Рассмотрим размерность $f(\alpha ).$ Число элементов покрытия произвольного фрактального множества $S$ растет степенным образом: $N(L) \propto {{L}^{{ - {{d}_{S}}}}},$ где ${{d}_{S}}$ есть боксовая размерность $S$. Возьмем в качестве $S$ носитель меры. Тогда в среднем для элементов его покрытия $\mu ({{\Delta }_{L}}) \propto N{{(L)}^{{ - 1}}} \propto {{L}^{{{{D}_{0}}}}}.$ Поэтому на роль параметра ${{d}_{f}}$ в (2), (6) может претендовать размерность ${{D}_{0}},$ что и было реализовано в работе [Bak et al., 2002]. Аналогично, полагая $S = {{S}_{{\alpha }}},$ мы получим $\mu ({{\Delta }_{L}}) \propto {{L}^{{{{d}_{f}}}}}$ с ${{d}_{f}} = f(\alpha ).$ Обе интерпретации степенного поведения меры согласованы, если $\alpha = f(\alpha ) = {{D}_{1}},$ т.е. когда $S$ есть множество типичных точек меры.

Описанные возможности для фрактального параметра в (2), (6) не решают задачу его оптимального выбора, когда речь идет о случайной ячейке ${{\Delta }_{L}}.$ Согласно работе [Molchan, Kronrod, 2005], если случайность ячейки описывается распределением (8) с параметром $p \geqslant 0,$ тогда:

Поскольку $\tau (1) = 0,$ $d_{{\text{f}}}^{{{\text{opt}}}}$ совпадает с боксовой размерностью, $d_{{\text{f}}}^{{{\text{opt}}}}(0) = {{D}_{0}},$ при p = 0, и с корреляционной размерностью, $d_{{\text{f}}}^{{{\text{opt}}}}(1) = {{D}_{2}},$ при p = 1. Указанные выше эмпирические оценки $d_{{\text{f}}}^{{{\text{opt}}}}$ для разлома Сан-Андреас подтвердили это теоретическое заключение на масштабах 10–100км.

Выбор случайной ячейки с частотой, пропорциональной числу в ней событий, представляется естественным. Он тесно связан с информационной размерностью. Поэтому теоретическое предсказание $d_{{\text{f}}}^{{{\text{opt}}}}(1) = {{D}_{2}}$ вместо ${{D}_{1}}$ на первый взгляд неожиданно. На самом деле соотношение (12) есть результат сбалансированного учета типичных и нетипичных точек в мультифрактальной мере в зависимости от процедуры случайного выбора и поэтому представляет собой своеобразное осреднение размерностей.

В работах [Кособоков, Некрасова, 2004] методика оценивания параметра $С$ ориентирована на получение корреляционной размерности ${{D}_{2}}.$ Выбор ${{D}_{2}} \ne 2$ означает признание нетипичных ячеек, хотя само соотношение (2) такую возможность исключает.

4.2. Вывод

В отдельных и пока немногих районах мира меру сейсмической интенсивности слабых событий можно считать мультифрактальной. Для мультифрактальной сейсмичности соотношение (12) определяет оптимальный фрактальный параметр $С$ в (2). Он обслуживает меру сейсмической интенсивности в случайной ячейке масштаба $L \ll {{L}_{0}},$ где ${{L}_{0}}$ – масштаб мультифрактальной однородности, а случайность описывается вероятностями (8). Параметр $С$ совпадает с корреляционной размерностью, если выбор ячейки пропорционален сейсмической активности в этой ячейке.

Соотношения (2), (6) априори предполагают независимость фрактальной размерности от магнитуды, что само по себе неочевидно при сравнении сильных и слабых событий. Кажется правдоподобным, что в таких регионах как Калифорния или Италия сильные события тяготеют к разломам, а слабые рассеяны по пространству. А это должно повышать размерность слабых.

При соблюдении условия (14) надежный анализ фрактальности для крупных событий представляется сомнительным.

5. ЗАКЛЮЧЕНИЕ

Мы проанализировали метод картирования долговременной интенсивности землетрясений под названием “Обобщенный закон подобия для землетрясений” (ОЗПЗ). В его основе лежит содержательная и до сих пор неиспользованная в приложениях гипотеза о фрактальности меры сейсмической интенсивности. На пути практического применения метода имеются серьезные препятствия: 1) фрактальность/мультифрактальность меры сейсмической интенсивности надежно подтверждена лишь в небольшом числе регионов мира и только для слабых землетрясений. Экстраполяция фрактальных свойств слабой сейсмичности на сильную, что важно при бедности статистики разрушительных землетрясений, нуждается в серьезном обосновании; 2) модель меры интенсивности ОЗПЗ не обладает необходимым свойством аддитивности, что ведет к противоречиям и необоснованному заключению: “Следствием фрактальной природы землетрясений и, в частности, их распределения в пространстве является обычное занижение традиционных оценок сейсмической опасности” [Некрасова, Кособоков, 2006]. Поэтому вопрос об использовании фрактальных свойств сейсмичности для задач сейсмического риска остается открытым; 3) не следует преувеличивать роль фрактальности в задачах риска, где главную роль играют сильные события, а обоснование даже их пространственного носителя затруднено. Дело в том, что разрушительный эффект события магнитуды M проявляется в некоторой пространственной зоне ${{G}_{{J(M)}}}$ (например, J-и балльная изосейста). Поэтому риск для точечного объекта ${{g}_{0}}$ определяется интегрально, т.е. суммарной интенсивностью событий М в зоне ${{G}_{{J(M)}}}$ с центром ${{g}_{0}},$ [Кейлис-Борок и др., 1984]. В этом случае достаточно иметь сглаженную, а значит, нефрактальную меру сейсмичности плюс контрольные интегралы сейсмической интенсивности в подходящих областях.

Примеры корректного использования ОЗПЗ связаны с методологией П. Бака, когда соотношение (2) используется как подходящая нормировка сейсмичности на разных масштабах (см. раздел 3). В этом случае действительно возникают нетривиальные, слабо зависимые от масштаба, законы распределения. Но они характеризуют не сейсмичность конкретных ячеек заданного размера, а сейсмичность случайно выбранной из них ячейки. Идея рандомизации пространственной ячейки, несомненно, интересна с точки зрения получения законов подобия в сейсмичности.