Физика Земли, 2020, № 1, стр. 62-76

Стабильная модификация закона повторяемости землетрясений и перспективы ее применения в сейсморайонировании

В. Ф. Писаренко¹, М. В. Родкин^{1, 2, *}, Т. А. Рукавишникова¹

¹ Институт теории прогноза землетрясений и математической геофизики РАН
г. Москва, Россия

² Институт морской геологии и геофизики ДВО РАН
г. Южно-Сахалинск, Россия

^* E-mail: rodkin@mitp.ru

Поступила в редакцию 25.04.2019
После доработки 17.06.2019
Принята к публикации 24.06.2019

DOI: 10.31857/S000233372001010X

Полный текст (PDF)

Аннотация

Предложена новая составная модель распределения магнитуд землетрясений, статистически удовлетворительно описывающая их распределение как в диапазоне слабых и умеренных землетрясений (закон Гутенберга–Рихтера), так и в области сильнейших событий (обобщенный закон Парето, являющийся одним из предельных законов теории экстремальных значений). На примере Японии и Курил (по данным GCMT-каталога) показано, что модель достаточно хорошо описывает сейсмичность в кругах, содержащих не менее 80 основных событий в диапазоне уверенной регистрации m ≥ 5.3. Требование по числу событий задает статистическое ограничение на разрешающую способность предлагаемой модели. Для указанных регионов это ограничение допускает надежную оценку параметров сейсмичности для областей радиусом 300 км по сетке 2 × 2°. Использование указанной модели в разработанной нами ранее статистической методике оценки сейсмического риска [Писаренко, Родкин, 2007; Pisarenko, Rodkin, 2010; 2013] дает теоретическую базу для развития этой методики как в плане большей робастности результатов оценки сейсмичности, так и лучшего пространственного разрешения, приближающегося к масштабу карт общего сейсмического районирования.

Ключевые слова: новый закон повторяемости землетрясений, предельные распределения теории вероятностей, сейсмическое районирование.

ВВЕДЕНИЕ

Закон повторяемости землетрясений Гутенберга–Рихтера является общепризнанным, универсальным законом сейсмологии. Его можно сформулировать следующим образом. Если в некотором, достаточно большом, сейсмоактивном регионе достаточно долго наблюдать землетрясения, то распределение их числа N по магнитудам m будет иметь следующий вид:

(1)

$\lg (N) = a + b(m - {{m}_{0}}),$

где: N – число землетрясений с магнитудами меньше m; m₀ – нижний порог регистрации землетрясений; a, b – параметры закона (они могут иметь различные значения в различных сейсмических регионах). Разъяснению физического смысла закона Гутенберга–Рихтера, статистической оценке его параметров и различным его модификациям посвящено огромное количество работ [Gutenberg, Richter, 1942; 1949; 1956; Kagan, 1994; 1999; Utsu, 1999; Wu, 2000; Golitsyn, 2001; Chechowski, 2003]. Сейсмологи настолько уверовали в справедливость и универсальность закона Гутенберга–Рихтера, что, например, нижнюю границу представительности любого каталога определяют обычно не с помощью каких-то, относящихся к этому вопросу данных, а просто с помощью нахождения нижнего порога, “за которым перестает выполняться закон Гутенберга–Рихтера” (нарушается линейность соотношения (1)).

Однако почти сразу же после начала триумфального применения закона Гутенберга–Рихтера в сейсмологической практике стала выявляться его “Ахиллесова пята” – неопределенность его поведения в диапазоне очень больших магнитуд. А этот диапазон как раз представляет наибольший интерес в важнейшей практической проблеме – оценке сейсмического риска. Закон Гутенберга–Рихтера стали записывать не в виде (1) для числа землетрясений, а для нормированного числа землетрясений, характеризуемого статистической функцией распределения магнитуд F(m). Функция F(m) показывает, какова вероятность того, что очередное (случайное) землетрясение в данном регионе будет иметь магнитуду меньше m. Для закона Гутенберга–Рихтера (1) функция F(m) имеет вид:

(2)

$F\left( m \right) = 1 - \exp \left[ { - b\left( {m - {{m}_{0}}} \right)} \right];\,\,\,\,m \geqslant {{m}_{0}}.$

Отметим сразу одну важную черту закона (2). Если считать, что соотношение (2) справедливо на бесконечном полуинтервале m ≥ m₀, то среднее значение энергии землетрясения (энергия Е приблизительно пропорциональна exp(3.45m)) M(E) окажется бесконечным, т.к. наблюдаемые значения параметра b всегда намного меньше 3.45 (в формулах выше для простоты использованы натуральные, а не десятичные логарифмы, переход к привычным значениям наклона графика повторяемости осуществляется пересчетом b/2.3). Здесь М – символ математического ожидания. Этот факт всегда вселял опасения при использовании неограниченного закона Гутенберга–Рихтера. Заметим, что экспоненциальному закону для магнитуд (2) соответствует степенной закон Парето для распределения энергий Е:

(3)

$f\left( E \right) = 1 - {{\left( {{{E}_{0}}/E} \right)}^{\beta }},\,\,\,\,E \geqslant {{E}_{0}},$

где: β = b/3.45; E₀ – энергия, соответствующая нижнему порогу магнитуд m₀. Плотность закона (3) имеет вид:

(4)

$f(E) = \beta {{({{E}_{0}})}^{\beta }}/{{E}^{{\beta + {\text{ }}1}}},\,\,\,\,E \geqslant {{E}_{0}}.$

Наиболее простой и чаще всего применяемой (в основном, из-за своей простоты) моделью, модифицирующей закон Гутенберга–Рихтера в области больших магнитуд и обеспечивающей конечность величин средней сейсмической энергии, стала модель усеченного закона Гутенберга–Рихтера (truncated Gutenberg–Richter law):

(5)

$F(m) = C\{ 1 - \exp [ - b(m - {{m}_{0}})]\} ,\,\,\,\,{{m}_{0}} \leqslant m \leqslant {{M}_{{{\text{max}}}}},$

где С – нормирующая константа С = {1 – exp[–b × × (M_max– m₀)]}^–1. Имеется огромное количество работ, посвященных исследованию различных аспектов этой модели [Молчан, 1973; Писаренко, 1989; 1991; 1995; Kijko, Sellevol, 1989; 1992; Dargahi-Noubary, 1983; 2000; Wesnousky, 1994; Грачев и др., 1996; Pisarenko et al., 1996; Писаренко, Лысенко, 1997; Ward 1997; Cosentino et al., 1997; Kijko, Graham, 1998; Kagan, 1999; 2002a; 2002b; Utsu, 1999; Kijko, 2004]. Параметр M_max, называемый максимальной возможной региональной магнитудой, прочно вошел в сейсмологическую практику, несмотря на его вполне очевидные недостатки и выявившуюся на практике большую неустойчивость его статистических оценок. Модель (5) слишком грубо и не вполне адекватно характеризует поведение распределения магнитуд в области больших значений (на хвосте распределения). Ввиду явной неудовлетворительности модели (5), были предприняты различные попытки модифицировать распределение Гутенберга–Рихтера (2).

В работах [Kagan, 1994; 1997а; Kagan, Schoenberg, 2001] к степенной плотности закона Парето (4) добавлялся экспоненциальный сомножитель exp(–γx), обеспечивающий конечность средней энергии. Эта модель не получила, однако, широкого распространения из-за искусственно выбранного экспоненциального убывания плотности энергии, которое, к тому же, искажало линейное поведение закона Гутенберга–Рихтера в области достаточно часто наблюдаемых магнитуд, обусловленное самоподобием сейсмического процесса в широком диапазоне масштабов.

В работах [Молчан и др., 1996; Molchan et al., 1997] на примере Италии предлагалась двухмасштабная модель сейсмичности. Весь исследуемый регион разделяется на зоны двух масштабов: зоны мелкого масштаба (длина 40–130 км: магнитуды 3.5 < М < 5.0) и зоны крупного масштаба (длина 175–400 км: магнитуды М > 6.0). Диапазон магнитуд 5 < M < 6 полагается промежуточным. Каждая из зон мелкого масштаба входит в какую-то зону крупного масштаба. В результате для одной и той же территории Италии получаются две разные пары параметров, характеризующих сейсмичность. Первый параметр a характеризует среднюю сейсмическую активность, а второй параметр b задает наклон графика повторяемости Гутенберга–Рихтера. Таким образом, для территории Италии получаются две пары оценок сейсмичности (a₁, b₁) и (a₂, b₂). Первая пара получена по событиям с магнитудами 3.5 < М < 5.0 и по зонам мелкого масштаба. Вторая пара получена по событиям с магнитудами М > 6.0 и по зонам крупного масштаба. Важно отметить, что в этом подходе для сильных землетрясений подразумевается, что функция распределения магнитуд (нормированная средняя сейсмическая интенсивность) имеет вид экспоненты, что соответствует неограниченному закону Гутенберга–Рихтера. Как замечают авторы статьи [Молчан, 1996], вопрос о параметризации сейсмической интенсивности в интервале самых больших значений магнитуд остается открытым. Для нас далее существенно, что в работах этого цикла показано, что модель с одинаковым наклоном графика повторяемости во всем диапазоне магнитуд не выполняется.

В работах [Писаренко, Родкин, 2007; 2009; Pisarenko, Rodkin, 2010; Pisarenko et al., 2008; 2014] изучались модели распределений самых больших магнитуд (модели хвоста распределения). Для решения этой проблемы был предложен подход, основанный на теории экстремальных значений. Использование максимальных значений m_max(τ), наблюдаемых в некотором регионе за определенный промежуток времени τ, позволило применить мощный математический аппарат предельных теорем теории экстремальных значений и эффективно решать многие статистические вопросы, связанные с этой проблемой. Заметим сразу, что m_max(τ) в отличие от параметра M_max является случайной величиной. При этом она определена вполне корректно, а ее распределение можно эффективно моделировать, используя два предельных распределения теории экстремальных значений: Обобщенное Распределение Экстремумов (Generalised Extreme Value distribution – GEV) и Обобщенное Распределение Парето (Generalised Pareto Distribution – GPD). Эти методы были весьма успешно применены для решения задач оценки сейсмического риска ([Писаренко, Родкин, 2007; Pisarenko, Rodkin, 2010]) и для других геофизических задач [Pisarenko et al., 2014]. Так, например, за год до реализации мегаземлетрясения Тохоку (2011) была показана достаточно высокая вероятность возникновения в Японии землетрясений с магнитудой М9+, ранее полагавшихся в Японии невозможными [Pisarenko, Rodkin, 2010].

При этом, однако, обнаружилось, что для надежной оценки параметров искомых предельных распределений необходимо использовать данные о большом (десятки событий) числе землетрясений с экстремально большими магнитудами, отвечающими хвосту распределения. Надежные оценки параметров получались для мирового каталога или для достаточно обширных сейсмических регионов типа Японии [Pisarenko, Rodkin, 2010]. А для задачи оценки сейсмического риска желательно иметь существенно более детальные пространственные характеристики сейсмичности. В настоящей работе мы предлагаем метод статистической оценки параметров сейсмического риска, который может быть применен не только к большим сейсмическим регионам, но и к их отдельным частям, т.е. метод с большей разрешающей способностью по пространству. Это открывает возможность использования этого метода в задачах сейсмического районирования.

СОСТАВНАЯ МОДЕЛЬ ЗАКОНА ПОВТОРЯЕМОСТИ ЗЕМЛЕТРЯСЕНИЙ

Поскольку экспоненциальный закон Гутенберга–Рихтера хорошо работает в диапазоне малых и умеренных магнитуд, а на хвосте распределения можно использовать предельный закон распределения максимальных значений GPD, возникает естественная идея использовать для функции распределения магнитуд F(m) составную модель:

(6)

$F(m) = \left\{ \begin{gathered} {{C}_{1}}\{ 1 - \exp [ - b(m - {{m}_{0}})]\} ,\,\,\,\,{{m}_{0}} \leqslant m \leqslant h, \hfill \\ {{C}_{1}}\{ 1 - \exp [ - b(h - {{m}_{0}})]\} {\text{ + }} \hfill \\ + \,\,{{C}_{2}}\{ 1 - {{[1 + (\xi /s)(m - h)]}^{{ - 1/}}}^{\xi }\} , \hfill \\ h \leqslant m \leqslant {{M}_{{{\text{max}}}}} = h - s/\xi ,\,\,\,\,\xi < {\text{ }}0. \hfill \\ \end{gathered} \right.$

Вторая ветвь представляет собой закон GPD с отрицательным параметром формы ξ < 0. Подобная модель использовалась нами ранее (см. [Pisarenko et al., 2008]) с положительным ξ > 0 (неограниченный закон распределения сейсмических моментов) для генерирования искусственных каталогов при оценивании разброса оценок. В данной работе мы используем отрицательные ξ < 0 (отвечающие конечному распределению магнитуд). В подавляющем большинстве случаев с достаточным числом сильных событий, применяя нашу методику, мы в качестве оптимального получали отрицательное значение параметра формы ξ, указывающее на конечность соответствующего распределения [Pisarenko, Rodkin, 2010; 2013].

Естественно потребовать, чтобы обе ветви модели гладко сопрягались при m = h, то есть, чтобы были равны не только значения плотности распределения, но и правая и левая производные плотности. Эта модель предлагается для описания распределения магнитуд в некотором конечном (неизвестном) диапазоне. Приведем подробное описание модели.

Модель (6) содержит 5 неизвестных параметров. Порог h разделяет 2 ветви модели, законы Гутенберга–Рихтера и GPD; b, m₀, s, ξ – параметры; C₁, C₂ – константы (они зависят от указанных параметров), которые должны обеспечить нормировку функции распределения F(m) и ее непрерывность:

(7)

$\begin{gathered} {{C}_{1}} = 1/\{ 1{\text{ }} + bs\exp [ - b(h - {{m}_{0}})] - \exp [ - b(h - {{m}_{0}})]\} , \\ {{C}_{2}} = 1 - {{C}_{1}}\{ 1 - {\text{exp}}[ - b(h - {{m}_{0}})]\} . \\ \end{gathered} $

Если обозначить:

${{С}_{3}} = {{С}_{1}}[1 - {\text{exp}}[ - b(h - {{m}_{0}})],$

то наша модель запишется в виде:

(8)

$F\left( m \right) = \left\{ \begin{gathered} {{C}_{1}}\{ 1{\text{ }}--{\text{exp}}[--b(m--{{m}_{0}})]\} ,\,\,\,\,{{m}_{0}} \leqslant m \leqslant h, \hfill \\ {{С}_{3}} + {{C}_{2}}\left\{ {1 - {{{\left[ {1 + \left( {\xi /s} \right)\left( {m - h} \right)} \right]}}^{{ - 1/\xi }}}} \right\}, \hfill \\ h \leqslant m \leqslant {{M}_{{{\text{max}}}}} = h - s/\xi ,\,\,\,\,\xi < 0. \hfill \\ \end{gathered} \right.$

Определение нижней границы представительности каталога m₀ обычно не вызывает затруднений. По существу, в этой составной модели остаются 4 неизвестных параметра h, b, s, ξ, которые необходимо оценить по имеющимся данным. Как показали многочисленные проверки на региональных каталогах, такая статистическая задача не всегда является устойчивой и робастной. Особенно большие проблемы статистической устойчивости появляются при оценивании параметров h, ξ для небольших локальных каталогов объемом не более 80–150 событий. Возникает потребность уменьшить количество неизвестных параметров, подлежащих оценке. Для этой цели используется условие непрерывности не только плотности распределения в точке сочленения ветвей, но и непрерывности ее первой производной. Это представляется естественным, поскольку плотность вероятности магнитуд должна описывать некий плавный физический механизм перехода от самоподобного процесса генерирования малых и средних толчков к процессу генерирования крупнейших событий, связанных с большими блоками и конечной толщиной земной коры. Из непрерывности производной плотности f(m) в точке m = h следует соотношение:

(9)

$s = (1 + \xi )/b.$

Итак, мы предлагаем составную модель (8) с ограничениями, обусловленными требованием непрерывности плотности распределения магнитуд f(m) и ее производной в точке сочленения ветвей m = h. В окончательном виде модель имеет вид:

(10)

$F(m) = \left\{ \begin{gathered} {{C}_{1}}\{ 1 - \exp [ - b(m - {{m}_{0}})]\} ,\,\,\,\,{{m}_{0}} \leqslant m \leqslant h, \hfill \\ {{С}_{3}} + {{C}_{2}}\{ 1 - {{[1 + {{(m - h)}^{ - }}\xi b/(1 + \xi )]}^{{ - 1/}}}^{\xi }\} , \hfill \\ h \leqslant m \leqslant {{M}_{{{\text{max}}}}} = h - (1 + \xi )/(b\xi ), \hfill \\ - 1 < \xi < 0; \hfill \\ \end{gathered} \right.$

$\begin{gathered} {{C}_{1}} = 1/(1 + \xi \exp [ - b(h - {{m}_{0}})]), \\ {{C}_{2}} = (1 + \xi )\exp [ - b(h - {{m}_{0}})]/(1 + \\ + \,\,\xi \exp [ - b(h - {{m}_{0}})]), \\ {{C}_{3}} = \{ 1 - \exp [ - b(h - {{m}_{0}})]\} /(1 + \xi \exp [ - b(h - {{m}_{0}})]). \\ \end{gathered} $

Модель содержит уже только 3 неизвестных параметра: h, b, ξ; значение m₀ предполагается известным. Ниже мы описываем результаты применения модели (10) для субрегионального описания сейсмичности Японии и региона Курил.

ПРИМЕНЕНИЕ СОСТАВНОЙ МОДЕЛИ К РЕГИОНУ ЯПОНИИ

Рассмотрим каталог GСМТ для региона Японии 1976–2016 гг. (4.29 ≤ m ≤ 9.08; h ≤ 70 км; 1734 события). Требование выполнимости закона Гутенберга–Рихтера указывает, что в качестве нижней границы можно выбрать m = 5.3, при этом остается 804 события. Для выделения афтершоков применяем оконный метод с окном Байеси–Пасуцки–Заляпина–Циона ([Baiesi, Paczuski, 2004; Zalyapin, Ben-Zion, 2013]), использующий обобщенное расстояние между двумя толчками. Следуя методике [Zalyapin, 2013], определим обобщенное расстояние D_k(i) от k-ого события каталога до последующего i-ого события следующим образом:

(11)

${{D}_{k}}(i) = \left\{ {\begin{array}{*{20}{c}} {\left( {{{t}_{i}}--{{t}_{k}}} \right)r{{{\text{ }}}^{f}} \times {\text{1}}{{{\text{0}}}^{{--b{{m}_{k}}}}},}&{\left( {{{t}_{i}}--{\text{ }}{{t}_{k}}} \right) > 0,} \\ {\infty ;}&{({{t}_{i}}--{\text{ }}{{t}_{k}}) \leqslant 0,} \end{array}} \right.$

где: r – эпицентральное расстояние в км между толчками; f – фрактальная размерность распределения эпицентров [Zalyapin, Ben-Zion, 2013]. Мы использовали значение f = 1.18, обеспечившее в проведенных нами ранее расчетах наибольшую эффективность – выделения афтершоков. Процедура исключения афтершоков следующая. Сначала берется наибольшее событие (t_k, m_k) в каталоге и с помощью окна (11) отбираются из последующих событий только те, у которых расстояние D_k(i) меньше выбранного порога Н. Эти события объявляются афтершоками главного толчка (t_k, m_k). Эти афтершоки и главное событие удаляются из каталога, и из оставшихся снова берется наибольшее событие. Выделение афтершоков производится до исчерпания всего каталога. Мы использовали порог различения афтершоков H = 10^–5, показавший наилучшую эффективность в предварительных расчетах. Использованное окно, основанное на расстоянии (11), отличается от обычно используемых окон [Zhuang et al., 2011] тем, что связывает расстояние между событиями по пространству и по времени с помощью соотношения (11), в то время как классические окна налагают ограничения на пространство и время раздельно. Это приводит к повышению эффективности выделения афтершоков при сохранении присущей методу окон простоте такой процедуры.

После применения этого окна остается 396 главных толчков (49.3%).

Оценки параметров модели ищутся стандартным методом максимального правдоподобия как значения параметров, максимизирующих функцию правдоподобия L(h, b, ξ,):

(12)

$L(h,b,\xi )~ = \prod\limits_{k = 1}^{k = n} f (\left. {{{m}_{k}}} \right|h,b,\xi ),$

где (m₁, …, m_n) – магнитуды выборки основных событий каталога.

Для всего региона Японии мы получили: ξ = = –1.226 × 10^–10; b = 1.998, напомним, что для перехода к привычным значениям b надо произвести пересчет b/ln(10), что дает 0.868:

(13)

$h = 5.64.$

Качество подгонки составной модели к каталогу мы оценили с помощью расстояния Колмогорова KD:

(14)

$KD = {{n}^{{1/2}}}{\text{max}}\left| {F(m/\xi ,b,h) - {{F}_{n}}(m)} \right|,$

где: F(m/ξ, b, h) – функция распределения составной модели (10) для основных событий; (ξ, b, h) – оценки параметров, полученные методом максимального правдоподобия; F_n(m) – выборочная функция распределения. Для региона Японии мы получили KD = 0.495. Для того, чтобы оценить значимость этого расстояния, мы использовали метод имитации процедуры оценивания (см. [Stephen, 1974]). Такая процедура, вместо стандартного использования таблиц распределения Колмогорова, необходима потому, что эти таблицы рассчитаны для случая, когда теоретическая функция распределения F(m) известна заранее и нет никаких подгоняемых параметров. Мы сгенерировали с помощью случайных чисел 5000 каталогов, каждый из которых содержал, как и каталог Японии, 396 событий с распределением магнитуд (10) и при значениях параметров (13). По 5000 каталогам мы получили, что вероятность превышения наблюденного значения KD = 0.495 при нашей процедуре оценивания равна 0.91. Эту вероятность в приводимых ниже таблицах мы будем обозначать pvKD. Чем больше расстояние Колмогорова (хуже соответствие теоретической и эмпирической функций распределения), тем меньше эта вероятность. Обычно качество подгонки считают приемлемым, если pvKD > 0.10. Таким образом, как видно из седьмого столбца табл. 1, для региона Японии составная трехпараметрическая модель со значениями параметров (13) обеспечивает весьма хорошее согласие.

Таблица 1.

Параметры сейсмичности ячеек для района Японии

Широта, долгота центра круга	Число главных толчков M_max	lg(–ξ); в скобках (–ξ)	b	h	KD	pvKD	Q_0.5(50)	Q_0.9(50)
Вся Япония	396 (191; 204) 9.08	–9.911 ± 0.011 (–1.226 × 10^–10)	1.998 ± 0.105	5.64 ± 0.26	0.495	0.91	8.60 ± 0.16	9.55 ± 0.22
34 138	86 (20; 66) 7.37	–0.813 ± 0.314 (–0.154)	1.559 ± 0.327	5.46 ± 0.29	0.596	0.57	7.30 ± 0.26	7.73 ± 0.43
34 140	141 (20; 121) 7.37	–0.854 ± 0.273 (–0.140)	1.748 ± 0.282	5.39 ± 0.36	0.535	0.73	7.25 ± 0.23	7.63 ± 0.37
34 142	132 (21; 111) 7.00	–0.580 ± 0.086 (–0.263)	1.354 ± 0.309	5.41 ± 0.33	0.51	0.79	6.97 ± 0.14	7.16 ± 0.21
36 138	120 (20; 100) 6.67	–0.484 ± 0.105 (–0.328)	1.275 ± 0.299	5.43 ± 0.30	0.71	0.28	6.74 ± 0.11	7.19 ± 0.14
36 140	195 (175; 20) 7.00	–0.419 ± 0.082 (–0.381)	1.904 ± 0.219	6.36 ± 0.24	0.64	0.54	6.35 ± 0.10	7.10 ± 0.12
36 142	187 (162; 34) 9.08	–8.941 ± 0.023 (–1.145 × 10^–9)	2.089 ± 0.144	6.32 ± 0.22	0.47	0.94	8.10 ± 0.20	9.00 ± 0.25
38 140	175 (152; 23) 9.08	–8.873 ± 0.028 (–1.340 × 10^–9)	1.954 ± 0.155	6.34 ± 0.23	0.63	0.68	8.26 ± 0.23	9.22 ± 0.31
38 142	205 (183; 22) 9.08	–9.620 ± 0.019 (–2.398 × 10^–10)	2.042 ± 0.144	6.49 ± 0.26	0.67	0.54	8.21 ± 0.20	9.15 ± 0.27
38 144	149 (126; 23) 9.08	–8.777 ± 0.027 (–1.670 × 10^–9)	1.799 ± 0.148	6.41 ± 0.25	1.01	0.0069	8.43 ± 0.25	9.47 ± 0.34
40 142	169 (101; 68) 9.08	–8.927 ± 0.025 (–1.182 × 10^–9)	1.762 ± 0.139	6.43 ± 0.25	0.66	0.59	8.56 ± 0.25	9.63 ± 0.33
40 144	155 (116; 39) 9.08	–9.461 ± 0.017 (–3.463 × 10^–10)	1.802 ± 0.144	6.03 ± 0.17	0.51	0.89	8.44 ± 0.25	9.49 ± 0.33
42 142	120 (100; 20) 8.26	–10.758 ± 0.035 (–1.747 × 10^–11)	2.016 ± 0.185	6.19 ± 0.20	0.77	0.34	7.98 ± 0.23	8.92 ± 0.33
42 144	125 (105; 20) 8.26	–8.420 ± 0.037 (–3.800 × 10^–9)	2.130 ± 0.195	6.14 ± 0.19	0.59	0.72	7.85 ± 0.23	8.74 ± 0.31

Виртуальные 5000 каталогов были обсчитаны аналогично исходному каталогу главных событий, и наряду с оценками параметров ξ, b, h мы получили также оценки квантилей Qq(τ). Квантиль Qq(τ) – это обратная функция по отношению к функции распределения максимальной магнитуды на заданном отрезке времени τ, которая равна:

(15)

$\begin{gathered} \Psi (m) = \\ = {{\left[ {{\text{exp}}( - \lambda \tau (1 - F(m)) - {\text{exp}}( - \lambda \tau )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{exp}}( - \lambda \tau (1 - F(m)) - {\text{exp}}( - \lambda \tau )} \right]} {\left[ {1 - \exp ( - \lambda \tau )} \right]}}} \right. \kern-0em} {\left[ {1 - \exp ( - \lambda \tau )} \right]}}, \\ \end{gathered} $

где λ – интенсивность Пуассоновского потока главных толчков (см. [Pisarenko, Rodkin, 2010]). Для оценок (11–13) и τ = 50 лет мы рассчитали квантили уровня 0.50 и 0.90: Q_0.50(50) = 8.60 ± 0.16 и Q_0.90(50) = 9.55 ± 0.22. Эти квантили мы используем и ниже. Квантиль Q_0.50(50) характеризует величину типичного события за срок эксплуатации сооружений массовой застройки (примерно 50 лет); квантиль Q_0.90(50) отвечает стандарту вероятности величины воздействия для карты ОСР-2016-А (превышение с вероятностью 10% за 50 лет).

Оценка разброса производилась по 5000 виртуальным каталогам. Квантиль Q_q(τ) можно рассматривать как верхнюю доверительную границу для случайной величины m_max(τ) с уровнем доверия q, поскольку по определению квантиля эта величина не будет превзойдена указанным максимумом с вероятностью q. Отметим, что для совокупности виртуальных каталогов наблюдается четко выраженная корреляция величин параметра формы ξ со значениями квантилей Q_q(τ); уменьшению значений параметра формы ξ по абсолютной величине отвечает рост значений квантилей Q_q(τ).

Ниже мы проанализируем связь квантилей Q_q(τ) со значениями параметров формы ξ для субрегинов Японии и Курил.

Применим теперь описанную выше методику к оценке параметров по сетке 2 × 2° для региона Японии. Вокруг каждой точки этой сетки мы будем брать круг радиуса R и рассматривать землетрясения из этого круга. Для целей сейсмического районирования желательно иметь как можно более детальное описание сейсмичности, т.е. выбирать радиус R как можно меньшим. С другой стороны, для более или менее надежной оценки параметров модели статистика требует достаточно большого числа наблюдений. Это требование заставляет увеличивать радиус R. Нужен компромисс, который не всегда можно формализовать и решить однозначно. В результате многочисленных экспериментов мы пришли к следующей процедуре выбора R. В круге радиуса R используемая оценка параметра h должна быть такова, чтобы на каждую из ветвей приходилось не менее 40 независимых событий с магнитудами m ≥ 5.3. Таким образом, в круге радиуса R должно быть не менее 80 наблюдений. В противном случае оценки максимального правдоподобия для параметров (ξ, b, h) становятся крайне неустойчивыми. В результате многочисленных экспериментов мы пришли к единому компромиссному значению для региона Японии R = 300 км. Для этого радиуса мы и провели оценивание параметров нашей модели и квантилей Q_0.5(50) и Q_0.9(50). Результаты оценивания приведены в табл. 1.

Во втором столбце под общим числом толчков n в данном круге указано, как оно распределяется между левой Гутенберга–Рихтера и правой (GPD) ветвями составной модели, ниже указана максимальная магнитуда в данном круге. В 7-ом столбце таблицы приведена вероятность превышения наблюденного в данном круге расстояния Колмогорова. Для 12 точек эта вероятность превышает 0.28 и только для одной точки № 9 эта вероятность меньше 0.1. Напомним, что для истинной модели эта вероятность имеет равномерное на отрезке [0; 1] распределение, поэтому в среднем она может заходить за порог 0.1 в одной десятой всех случаев. Поэтому одна из 13 точек вполне может чисто случайно оказаться меньше значения 0.1 даже для истинной модели. Отсюда мы можем заключить, что составная модель достаточно хорошо описывает имеющийся каталог землетрясений Японии 1976–2016 гг. по сетке 2 × 2° с радиусом круга 300 км.

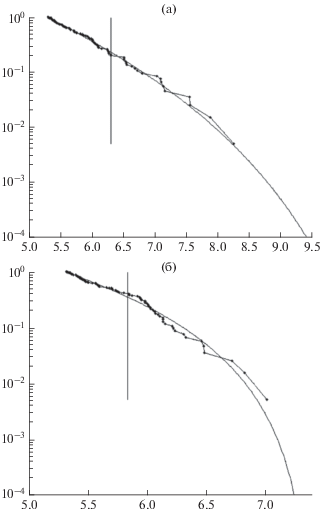
На рис. 1а–1в показаны примеры подгонки нашей модели к 3 субрегионам Японии. На рис. 1а, 1б качество подгонки высокое, расстояния Колмогорова в этих примерах равны соответственно 0.60 и 0.51. На рис. 1в подгонка наихудшая, расстояние Колмогорова равно 1.01.

Рис. 1.

Примеры аппроксимации составной моделью для субрегионов Японии: (a) – ячейка с центром (34°, 138°), 86 событий, KD = 0.57; (б) – ячейка с центром (34°, 142°), 132 события, KD = 0.51; (в) – ячейка с центром (38°, 144°), 149 событий, KD = 1.01. Круги радиусом 300 км. Вертикальная линия разделяет две ветви модели.

(16)

$\begin{gathered} f\left( m \right) = C{{\left( {{{M}_{{{\text{max}}}}} - m} \right)}^{{ - 1/\xi - 1}}}, \\ C - {\text{константа, зависящая}}\,{\text{от}}\,\left( {{{m}_{0}},\xi ,b,h} \right), \\ \end{gathered} $

(17)

$\begin{gathered} {{Q}_{q}}\left( \tau \right) = h - s/\xi \left[ {1 - {{{\left( {1 - \tilde {q}} \right)}}^{{ - \xi }}}} \right],{\text{ }} \\ \tilde {q} = \left[ {1 + \left( {1/\lambda \tau } \right)\ln \left( q \right)} \right] - {{C}_{1}}{{C}_{3}})/{{C}_{2}}, \\ \end{gathered} $

C₁, C₃, C₂ – константы, из соотношений (10); q > > C₁C₃. Здесь предполагается, что интенсивность потока независимых событий λ (среднее число событий с магнитудами ≥m₀ в единицу времени) такова, что exp(λτ) $ \gg $ 1. Если ξ положить равным нулю (неограниченный закон Гутенберга–Рихтера, для которого M_max = ∝), то выражение для квантиля (17) упрощается:

(18)

${{Q}_{q}}(\tau ) = {{m}_{0}} + (1/b)\ln (\lambda \tau )--(1/b)\ln [\ln (1/q)].$

Его можно использовать как приближение при малых по абсолютной величине значениях оценок ξ: |ξ| < 10^–3. Отличие оценки квантилей по формуле (18) от оценок максимального правдоподобия при |ξ| < 10^–3 не превышает 0.01, что заметно ниже обычной погрешности величины Q_q(τ).

Поскольку использованный нами каталог GCMT 1976–2016 гг. (40 лет) довольно короток по сравнению с возможными вековыми вариациями сейсмического режима, и к тому же в регионе Японии за этот период произошло мегаземлетрясение Тохоку (11.03.2011 гг.), мы решили провести “исторический эксперимент”, который покажет, насколько устойчива предлагаемая нами схема оценивания параметров к таким редким, экстремальным событиям. Мы применили нашу схему к интервалу каталога (1976–10.03.2011 гг.), не включающего мегасобытие, и сравнили результаты с результатами, полученными по полному каталогу 1976–2016 гг. Конечно, такой эксперимент очень “невыгоден” для нашей модели: события масштаба Тохоку случаются на земном шаре очень редко, а тем более в каком-либо конкретном регионе. С одной стороны, статистическая схема, не должна быть “обрушена” никаким одиночным событием, даже такого типа, как Тохоку. С другой стороны, никакая схема не должна исключать некоторое влияние мегасобытия на результаты, исключать заранее мегасобытие (как это делают иногда в статистике, исключая “выбросы”) было бы неверно с физической точки зрения. Ведь мегасобытие произошло, и оценка его масштаба не являлась ошибкой. Мы все же решили провести подобный “исторический” эксперимент, заранее предупредив о том, что он искусственно ставит схему расчета в тяжелое положение, которое в реальности, при анализе сейсмичности некоего региона, имеет очень малую вероятность реализации. Результаты сравнения приведены в табл. 2.

Таблица 2.

Сравнения результатов расчетов за два интервала времени

Широта, долгота	ξ 1976–2016	ξ 1976–2011	b 1976–2016	b 1976–2011	Q_0.5(50) 1976–2016	Q_0.5(50) 1976–2011	Q_0.9(50) 1976–2016	Q_0.9(50) 1976–2011
Вся Япония	–1.23 × 10^–10	–0.077	2.00	1.96	8.60	8.29	9.55	8.92
34 138	–0.154	–0.165	1.56	1.49	7.30	7.34	7.73	7.76
34 140	–0.140	–0.154	1.75	1.64	7.25	7.29	7.63	7.66
34 142	–0.263	–0.302	1.35	1.19	6.97	6.97	7.17	7.14
36 138	–0.328	–0.352	1.28	1.17	6.74	6.75	6.88	6.87
36 140	–0.381	–0.391	1.91	1.83	6.98	6.99	7.10	7.11
36 142	–1.15 × 10^–9	–0.133	2.09	1.99	8.10	7.60	9.00	8.05
38 140	–1.34 × 10^–9	–0.093	1.95	1.90	8.26	7.87	9.22	8.46
38 142	–2.40 × 10^–10	–0.074	2.04	2.01	8.21	7.87	9.13	8.49
38 144	–1.67 × 10^–9	–0.084	1.80	1.78	8.43	8.00	9.47	8.66
40 142	–1.18 × 10^–9	–0.107	1.76	1.82	8.56	8.47	9.63	9.51
40 144	–3.46 × 10^–10	–0.148	1.80	1.87	8.44	8.34	9.49	9.34
42 142	–1.75 × 10^–11	–3.40 × 10^–9	2.02	2.02	7.98	7.98	8.92	8.91
42 144	–3.80 × 10^–9	–6.97 × 10^–10	2.13	2.14	7.85	7.84	8.74	8.72

Из оценок параметров, показанных в табл. 2, можно сделать следующие выводы.

В целом предложенная схема оценок показала приемлемую робастность при сравнении результатов, полученных по каталогам с учетом (весь каталог) и без учета (расчет за интервал времени 1976–2011 гг.) до и после мегаземлетрясения Тохоку. Будем характеризовать близость двух наборов оценок Х = (x₁,…,x_n) и Y = (y₁,…,y_n) средней относительной разностью:

$\rho = \frac{1}{n}\mathop \sum \limits_{k = 1}^n \left| {\frac{{{{x}_{k}} - {{y}_{k}}}}{{0.5\left( {{{x}_{k}} + {{y}_{k}}} \right)}}} \right|,$

при этом Х – это оценки по интервалу 1976–2016 гг.; Y – оценки по интервалу 1976–2011 гг.

Из табл. 2 (13 кругов радиусом 300 км) получаем следующие характеристики:

Параметр b: ρ = 0.080 (8%). Максимальная абсолютная разница 0.16.

Квантиль Q_0.5(50): ρ = 0.042 (4.2%). Максимальная абсолютная разница 0.50.

Квантиль Q_0.9(50): ρ = 0.031 (3.1%). Максимальная абсолютная разница 0.95.

Параметр формы для 8 точек принимает очень малые значения (порядка 10^–8–10^–10), поэтому брать относительные значения для этих точек некорректно. Для оставшихся 5 точек средняя относительная разница параметра формы ξ имеет значение 0.080 (8%). Мы видим, что даже появление такого гигантского события, как Тохоку, не “обрушило” нашу схему оценивания и относительные разности величин оценок составляют 3–8%. Как и ожидалось, наиболее изменчивым оказался параметр формы. Квантили значительно изменились в 4 кругах в непосредственной близости от эпицентра Тохоку, а в 9 остальных кругах они изменились весьма слабо.

ПРИМЕНЕНИЕ СОСТАВНОЙ МОДЕЛИ К РЕГИОНУ КУРИЛ

В качестве второго пробного региона для применения нашей модели мы взяли соседний регион Курил за те же годы 1976–2016 гг., m ≥ 5.3. С помощью той же процедуры использования окна Заляпина–Байеси с порогом H = 10^–5 и показателем степени эпицентрального расстояния df = = 1.18 было выделено 307 главных толчков (55.02%); отметим, что процент основных событий оказался несколько выше, чем для района Японии (где он составил 49%).

Для региона Курил мы так же, как и для Японии, взяли значение радиуса круга R = 300 км. Для этого радиуса мы провели оценивание параметров нашей модели и квантилей Q_0.5(50), Q_0.9(50). Результаты оценивания приведены в табл. 3.

Таблица 3.

Параметры сейсмичности ячеек для района Курил

Широта, долгота центра ячейки	Число толчков M_max	lg(–ξ) в скобках (–ξ)	b	h	KD	pvKD	Q_0.5(50)	Q_0.9(50)
Все Курилы	307 (184; 123) 8.30	–1.403 ± 0.366 (–0.0395)	1.832 ± 0.152	5.84 ± 0.62	0.83	0.16	8.35 ± 0.30	9.12 ± 0.27
44 148	100 (79; 21) 8.25	–0.8814 ± 0.306 (–0.1314)	1.364 ± 0.205	6.31 ± 0.43	0.54	0.72	8.18 ± 0.38	8.84 ± 0.60
44 150	116 (96; 20) 8.25	–0.8184 ± 0.294 (–0.1519)	1.417 ± 0.210	6.54 ± 0.43	0.60	0.58	8.15 ± 0.33	8.73 ± 0.55
46 152	118 (98; 20) 8.30	–9.852 ± 0.034 (1.407 × 10^–10)	1.814 ± 0.167	6.26 ± 0.21	0.46	0.95	8.26 ± 0.36	9.30 ± 0.36
46 154	99 (68; 31) 8.30	–9.657 ± 0.030 (2.204 × 10^–10)	2.125 ± 0.222	5.83 ± 0.18	0.83	0.24	7.75 ± 0.24	8.63 ± 0.34
48 154	118 (20; 98) 8.30	–1.877 ± 0.459 (–0.0133)	2.198 ± 0.264	5.40 ± 0.34	0.64	0.49	7.36 ± 0.29	8.41 ± 0.48
48 156	108 (20; 88) 8.30	–1.623 ± 0.419 (–0.0238)	2.175 ± 0.272	5.40 ± 0.32	0.67	0.37	7.54 ± 0.29	8.27 ± 0.46
50 156	99 (59; 40) 7.00	–0.5450 ± 0.157 (–0.2851)	1.611 ± 0.335	5.83 ± 0.28	0.79	0.16	6.91 ± 0.14	7.11 ± 0.22
50 158	99 (62; 37) 7.00	–0.5380 ± 0.141 (–0.2897)	1.578 ± 0.316	5.89 ± 0.29	0.78	0.15	6.96 ± 0.16	7.16± 0.22

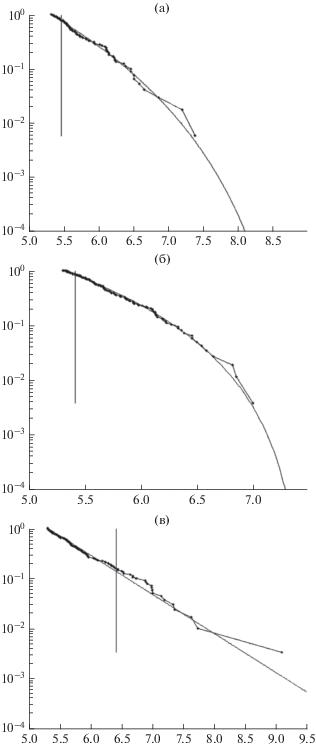
На рис 2а, 2б показаны примеры подгонки нашей модели к 2 субрегионам Курил. На рис. 2а качество подгонки высокое, расстояния Колмогорова равно 0.54. На рис. 2б подгонка хуже (но допустимая), расстояние Колмогорова равно 0.79.

Рис. 2.

Примеры аппроксимации составной моделью для субрегионов Курил: (а) – ячейка с центром (44°, 148°), 100 событий, KD = 0.54; (б) – ячейка с центром (50°, 156°), 99 событий, KD = 0.79. Круги радиусом 300 км. Вертикальная линия разделяет две ветви модели.

ДИСКУССИЯ И ВЫВОДЫ

По существу, мы предлагаем новую модель распределения магнитуд землетрясений во всем диапазоне представительной регистрации: это известный закон Гутенберга–Рихтера с конкретизацией на хвосте распределения в виде гладко подогнанного предельного закона Парето. Эта модель логически предпочтительнее ранее предлагавшихся, так как она теоретически (статистически) корректна и реализуемые в ее рамках расчеты дают, как правило, не только конечность величин сейсмической энергии, но и ограниченность распределения (что физически оправдано). Модель содержит 3 параметра. Параметр h характеризует положение условной, довольно неопределенной границы между законом распределения Гутенберга–Рихтера с самоподобным механизмом генерирования толчков в неограниченной среде и механизмом генерирования толчков экстремально большого размера в слое ограниченной толщины (земной коре). Количественно эта граница определяется не всегда определенно из-за плавного перехода одного механизма в другой. Наша модель требует непрерывности первой производной плотности магнитуд, из-за чего точное значение точки перехода становится также и теоретически довольно неопределенным. Расчеты подтверждают, что умеренные вариации величин параметра h слабо сказываются на качестве подгонки модели к реальным каталогам (качество подгонки контролируется расстоянием Колмогорова). Зато модель приобретает большую устойчивость и робастность.

Наглядный статистический смысл параметра ξ состоит в том, что величина –1/ξ характеризует остроту “клюва” плотности вероятности распределения магнитуд в крайней правой экстремальной области плотности распределения: чем ближе (отрицательное) значение ξ к нулю, тем острее этот клюв, тем больше возрастает максимально возможное значение распределения, M_max, а следовательно, и увеличивается значение квантиля Q_q(τ) (см. уравнения (17), (18)). Квантиль Q_q(τ) характеризует “вес клюва” интегральным образом, поэтому он, в отличие от параметра М_max, гораздо более устойчив, особенно при малых по абсолютной величине значениях ξ, представляющих особый интерес, т.к. они соответствуют регионам, где могут происходить (или уже произошли) самые большие события.

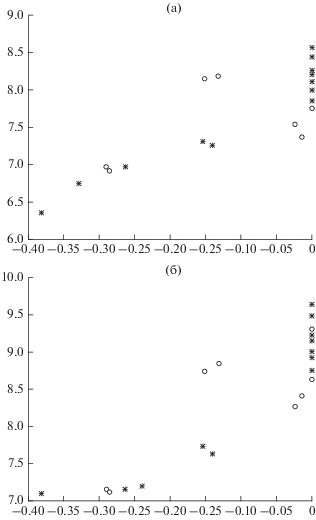
Отсюда естественно предположить тесную связь между важными в плане оценки сейсмической опасности значениями параметра ξ и величинами квантилей. Выше отмечалось, что она имеет место и между параметрами виртуальных каталогов, т.е., исходно присуща нашей модели. С другой стороны, она отражает различие сейсмического режима разных областей. На рис. 3а, 3б приведены соотношения расчетных величин ξ и квантилей Q_0.5(50) и Q_0.9(50) для субрегионов Японии и Курил. В обоих случаях видна четкая связь, с коэффициентом линейной корреляции ρ > 0.8, причем зависимость величин квантиля от значений параметра формы ξ ожидаемо становится сильнее и нелинейнее с ростом q (и τ).

Рис. 3.

Соотношение величин квантилей Q_0.5(50) (а) и Q_0.9(50) (б) и величин параметра формы ξ для субрегионов Японии (звездочки) и Курил (кружки).

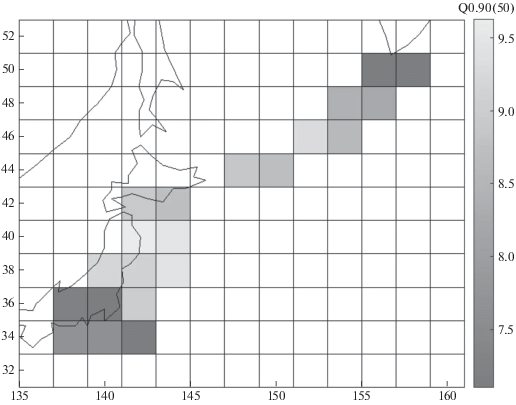
На рис. 4 представлена схема полученных величин квантиля Q_0.9(50). Видно, что пространственные вариации полученных значений квантилей отражают реальный сейсмический режим соответствующих участков зоны Беньофа, в частности, максимальные значения квантиля оказались приурочены к области реализации мегаземлетрясения Тохоку (2011 г.). Возможно, что значения квантиля Q_0.9(50), показанные на рис. 4, также оказались несколько завышенными (относительно осредненных на большом интервале времени) из-за реализации в рассмотренном интервале времени 1976–2016 гг. этого мегаземлетрясения.

Рис. 4.

Схема пространственного расположения полученных значений квантиля Q_0.9(50).

Один из аспектов полученных оценок параметров оказался несколько неожиданным. Оптимальное положение границы h в нашей составной модели по оценкам максимального правдоподобия иногда (см. рис. 1а, 1б) оказывалось сильно сдвинутым в область малых магнитуд. Можно предложить два возможных объяснения этого результата. Во-первых, мы уже отмечали выше неустойчивость определения h из-за самой конструкции нашей модели (ее гладкости в точке сопряжения ветвей). Соответственно, при передвижении h, один и тот же участок плотности может “благополучно” (почти с тем же правдоподобием) войти как в ветвь Гутенберга–Рихтера, так и в ветвь GPD (в логмасштабе это почти прямолинейный участок, что подходит как для Гутенберга–Рихтера, так и для GPD). Не исключено также, что представления о хорошей выполнимости линейности закона Гутенберга–Рихтера в широком диапазоне магнитуд завышены. Напомним, что в работах [Молчан и др., 1996; Molchan et al., 1997] уже были убедительно продемонстрированы значительные различия среднего угла наклона графика повторяемости в разных диапазонах магнитуд.

В целом, заключаем:

1. Предложена новая составная модель распределения магнитуд землетрясений, удовлетворительно описывающая как распределение в диапазоне слабых и умеренных землетрясений, так и в диапазоне сильнейших событий. В области событий меньшей магнитуды распределение описывается законом Гутенберга–Рихтера, а в области сильных землетрясений – обобщенным законом Парето, одним из предельных законов теории экстремальных значений. Условие сопряжения двух этих ветвей закона распределения позволяет уменьшить на единицу число подлежащих определению параметров, что ослабляет жесткие требования на число событий в анализируемых подборках данных. С физической точки зрения сопряжение двух ветвей закона распределения отвечает существованию связи между характером распределения редких сильнейших событий и часто повторяющихся событий меньшей магнитуды.

2. На примере Японии и Курил (по данным GCMT-каталога) показано, что модель хорошо описывает сейсмичность в кругах, содержащих не менее 80 основных событий в диапазоне уверенной регистрации m ≥ 5.3. Требование по числу событий задает статистическое ограничение на разрешающую способность предложенного метода. Для указанных регионов это ограничение привело к использованию единого радиуса круга 300 км по сетке 2 × 2°.

3. Использование указанной модели в разработанной нами ранее статистической методике оценки сейсмического риска (использование квантилей распределения максимальной магнитуды в заданный будущий период времени Q_q(τ)) дает возможность развить методику сейсмического районирования как в плане большей робастности (меньшей чувствительности результатов расчетов к случайной реализации редких сильнейших событий), так и в плане большей пространственной детальности, приближающейся к пространственному разрешению карт общего сейсмического районирования.

4. Несмотря на то, что значения параметра формы ξ предельного GPD распределения в подавляющем большинстве случаев оказывается отрицательным, что указывает на конечность значения максимально возможной магнитуды М_mаx, само значение М_mах может оказаться плохо определяемым и неробастным. В связи с этим авторы солидаризируются с мнением [Zoller et al., 2013], что представляют интерес значения М_mах(τ), реализующиеся с заданной вероятностью за некоторый будущий интервал времени τ.

Конечно, авторы отдают себе отчет в том, что для составления детальных, надежных карт общего сейсмического районирования нужны гораздо более представительные и длинные каталоги, чем каталог GCMT 1976–2016 гг., использованный в настоящей работе. Но, пользуясь этим каталогом, мы проиллюстрировали возможности новой, введенной нами, составной модели сейсмичности и показали ее возможности и перспективы применения.

Список литературы

Грачев А.Ф., Магницкий В.А., Мухамедиев С.А., Юнга С.Л. Определение максимальной, возможной магнитуды землетрясения на Восточно-Европейской платформе // Физика Земли. 1996. № 7. С. 3–20.
Молчан Г.М., Подгаецкая В.М. Параметры глобальной сейсмичности. Вычислительные и статистические методы интерпретации сейсмических данных // Вычислительная сейсмология. Вып. 6. 1973. С. 44–66.
Молчан Г.М., Кронрод Т.Л., Дмитриева О.Е., Некрасова А.К. Многомасштабная модель сейсмичности в задачах сейсмического риска: Италия. Современные проблемы сейсмичности и динамики Земли // Вычислительная сейсмология. Вып. 28. 1996. С. 193–224.
Писаренко В.Ф. О законе повторяемости землетрясений. Дискретные свойства геофизической среды. М.: Наука. 1989. С. 47–60.
Писаренко В.Ф. Статистическое оценивание максимальных возможных землетрясений // Физика Земли. 1991. № 9. С. 38–46.
Писаренко В.Ф. О Наилучшей статистической оценке максимальной возможной магнитуды землетрясения // Докл. РАН. 1995. Т. 344. № 2. С. 237–239.
Писаренко В.Ф., Лысенко В.Б. Распределение вероятностей максимального землетрясения, которое может произойти в заданный промежуток времени // Докл. РАН. 1997. Т. 347. № 2. С. 399–401.
Писаренко В.Ф., Родкин М.В. Распределения с тяжелыми хвостами: приложения к анализу катастроф // Вычислительная сейсмология. Вып. 38. 2007. М.: ГЕОС. 240 с.
Писаренко В.Ф., Родкин М.В. Неустойчивость параметра М_мах и альтернатива его применению // Физика Земли. 2009. № 9. С. 48–59.
Писаренко В.Ф., Родкин М.В., Рукавишникова Т.А. Оценка вероятности сильнейших сейсмических катастроф на основе теории экстремальных значений // Физика Земли. 2014. № 3. С. 89–103.
Baiesi M., Paczuski M. Scale-free networks of earthquakes and aftershocks // Phys. Rev. E. 2004. V. 69. P. 66–106.
Cosentino P., Ficara V., Luzio D. Truncated exponential frequency-magnitude relationship in the earthquake statistics // Bull Seism Soc Am. 1977. V. 67. P. 1615–1623.
Czechowski Z. The privilege as the cause of power distribution in geophysics // Geophys J. Int. 2003. V. 154. P. 754–766.
Dargahi-Noubary G.R. A procedure for estimation of the upper bound for earthquake magnitudes // Phys Earth Planet Inter. 1983. V. 33. P. 91–93.
Dargahi-Noubary G.R. Statistical methods for earthquake hazard assessment and risk analysis. Nova Science Publishers, Huntington, N.Y. 2000.
Embrechts P., Kluppelberg C., Mikosch T. Modelling extremal events. Berlin. Heidelberg, Springer-Verlag. 1997a. 645 p.
Epstein B.C., Lomnitz C. A model for the occurrence of large earthquakes // Nature. 1966. V. 211. P. 954–956.
Efron B. Bootstrap Methods: Another Look at the Jackknife // Ann. Statist. 1979. № 7. P. 1–26.
Golitsyn G.S. The place of the Gutemberg-Richter law among other statistical laws of nature // Comput Seismol. 2001. V. 32. P. 138–161.
Godano C., Pingue F. Is the seismic moment-frequency relation universal? // Geophys J. Int. 2000. V. 142. P. 193–198.
Gutenberg B., Richter C. Earthquake magnitude, intensity, energy and acceleration // Bull Seismol Soc Am. 1942. V. 32. P. 163–191.
Gutenberg B., Richter C. Seismicity of the Earth and associated phenomena. Princeton University Press, Princeton, N.Y. 1949.
Gutenberg B., Richter C. Earthquake magnitude, intensity, energy, and acceleration, part II // Bull Seism Soc Am. 1956. V. 46. P. 105–145.
Jarrard R.D. Relations among subduction parameters //Rev. Geophys. 1986. V. 24(2). P. 217–284.
Kagan Y.Y. Observational evidence for earthquakes as a non-linear dynamic process // Physica D. 1994. V. 77. P. 160–192.
Kagan Y.Y. Seismic moment-frequency relation for shallow earthquakes: Regional comparison. // J. Geophys Res. 1997a. V. 102. P. 2835–2852.
Kagan Y.Y. Earthquake size distribution and earthquake insurance // Commun Statist Stachastic Models. 1997b. V. 13(4). P. 775–797.
Kagan Y.Y. Universality of the seismic moment-frequency relation // Pure Appl Geophys. 1999. V. 155. P. 537–573.
Kagan Y.Y. Seismic moment distribution revisited: I Statistical results // Geophys J. Int. 2002a. V. 148. P. 520–541.
Kagan Y.Y. Seismic moment distribution revisited: II Moment conservation principle // Geophys J. Int. 2002b. V. 149. P. 731–754.
Kagan Y.Y. Statistics of characteristic earthquakes // Bull Seismol Soc Am. 1993. V. 83(1). P. 7–24.
Kagan Y.Y., Schoenberg F. Estimation of the upper cutoff parameter for the tapered distribution // J. Appl. Probab. 2001. V. 38A. P. 901–918.
Kijko A., Graham G. Parametric-historic procedure for probabilistic seismic hazard analysis, Part I, Estimation of Maximum Regional Magnitude M_max // Pure Appl Geophys. 1998. V. 152. P. 413–442.
Kijko A. Estimation of the maximum earthquake magnitude, M_max // Pure Appl Geophys. 2004. V. 161. P. 1–27.
Kijko A., Sellevol M.A. Estimation of earthquake hazard parameters from incomplete data files. Part I, Utilization of extreme and complete catalogues with different threshold magnitudes // Bull. Seism. Soc. Am. 1989. V. 79. P. 645–654.
Kijko A., Sellevol M.A. Estimation of earthquake hazard parameters from incomplete data files. Part II, Incorporation of magnitude heterogeneity // Bull. Seism. Soc. Am. 1992. V. 82. P. 120–134.
Molchan G., Kronrod T., Panza G.F. Multi-scale seismicity model for seismic risk // Bull Seism. Soc. Am. 1997. V. 87. P. 1220–1229.
Okal E.A., Romanowicz B.A. On variation of b-values with earthquake size // Phys. Earth Planet Interior. 1994. V. 87. P. 55–76.
Pacheco J.F., Scholz C., Sykes L. Changes in frequency-size relationship from small to large earthquakes // Nature. 1992. V. 355. P. 71–73.
Pisarenko V.F., Lyubushin A.A., Lysenko V.B., Golubeva T.V. Statistical estimation of seismic hazard parameters: maximum possible magnitude and related parameters // Bull. Seismol. Soc. Am. 1996. V. 86(3). P. 691–700.
Pisarenko V.F., Sornette D. Characterization of the Frequency of Extreme Earthquake Events by the Generalized Pareto Distribution // Pure Appl Geophys. 2003. V. 160. P. 2343–2364.
Pisarenko V.F., Sornette D. Statistical detection and characterization of a deviation from the Gutenberg-Richter distribution above magnitude 8. Pure Appl Geophys. 2004. V. 161. P. 839–864.
Pisarenko V.F., Sornette A., Sornette D., Rodkin M.V. New approach to the characterization of Mmax and of the tail of the distribution of earthquake magnitudes // Pure Appl Geophys. 2008. V. 165. P. 1–42.
Pisarenko V., Rodkin M. Heavy-Tailed Distributions in Disaster Analysis. Advances in Natural and Technological Hazards Research. Springer, Dordrecht–Heidelberg–London–N.Y. 2010. V. 30.
Pisarenko V.F., Sornette D., Rodkin M.V. Distribution of maximum earthquake magnitudes in future time intervals: application to the seismicity of Japan (1923–2007) // Earth Planets Space. 2010. V. 62. P. 567–578.
Pisarenko V., Rodkin M. Statistical Analysis of Natural Disasters and Related Losses. Springer Briefs in Earth Sciences. Springer, Dordrecht–Heidelberg–London–N.Y. 2013.
Pisarenko V.F., Sornette A., Sornette D., Rodkin M.V. Characterization of the Tail of the Distribution of Earthquake Magnitudes by Combining the GEV and GPD. Descriptions of Extreme Value Theory // Pure Appl. Geophys. 2014. V. 171. P. 1599–1624.
Romanovicz B., Rundle J.B. On scaling relation for large earthquakes // Bull. Seismol. Soc. Am. 1993. V. 83(4). P. 1294–1297.
Stephens M.A. EDF statistics for goodness of fit and some comparisons // J. Am Statist Ass. 1974. V. 68(347). P. 730–737.
Utsu T. Representation and analysis of the earthquake size distribution: A historical review and some new approaches // Pure Appl Geophys. 1999. V. 155. P. 509–535.
Ward S.N. More on M_max // Bull Seis Soc Am. 1997. V. 87(5). P. 1199–1208.
Wesnousky S.G. The Gutenberg-Richter or characteristic earthquake distribution, which is it? // Bull Seism Soc Am. 1994. V. 84. P. 1940–1959.
Wu Z.L. Frequency-size distribution of global seismicity seen from broad-band radiated energy // Geophys J. Int. 2000. V. 142. P. 59–66.
Zalyapin I., Ben-Zion Y. Earthquake clusters in Southern California I: Identification and stability. // J. Geophys. Res. 2013. V. 118. P. 2847–2864.
Zhuang J., Werner MJ, Hainzl S, Harte D., Zhou S. Basic models of seismicity: spatiotemporal models, Community Online Resource for Statistical Seismicity Analysis. 2011. https://doi.org/10.5078/corssa-07487583
Zoller G., Holschneider V., Hainzl H. The Maximum Earthquake Magnitude in a Time Horizon: Theory and Case Studies // BSSA. 2013. V. 103. 2A. P. 860–875.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал