Физика Земли, 2021, № 3, стр. 45-62
Определение тензора момента двойного диполя для землетрясений Камчатки по волновым формам региональных сейсмических станций
И. Р. Абубакиров 1, В. М. Павлов 1, *
1 Камчатский филиал Федерального исследовательского центра “Единая геофизическая служба РАН”
г. Петропавловск-Камчатский, Россия
* E-mail: pvm@emsd.ru
Поступила в редакцию 29.10.2020
После доработки 03.12.2020
Принята к публикации 16.12.2020
Аннотация
Развернутая в 2006–2010 гг. на Камчатке сеть цифровых сейсмических приборов создала принципиальную возможность для расчета тензора сейсмического момента (ТСМ) камчатских землетрясений по широкополосным волновым формам региональных станций. В статье описана методика расчета ТСМ типа двойной диполь без момента (ДД), опирающаяся на декомпозицию тензора ДД и проведение частичной линейной инверсии по двум (из четырех) переменным в явном виде. Это позволяет выразить целевую функцию метода наименьших квадратов через два угла, задающих ориентацию нулевой оси тензора ДД. Инверсия по углам проводится с использованием итерационного метода Левенберга–Марквардта. По описанной методике для 31 землетрясения Камчатки с моментной магнитудой Mw = 4.3–6.2 рассчитаны механизм очага, моментная магнитуда и глубина эквивалентного точечного источника и проведено сопоставление полученных оценок с данными каталога GCMT, которые имеются для 19 событий. Согласие оказалось вполне приемлемым. Значения угла K, характеризующего расхождение между механизмом двойного диполя, рассчитанного нами непосредственно по волновым формам, и механизмом наилучшего двойного диполя, сконструированного по тензору с нулевым следом из каталога GCMT, для 16 событий из 19 не превосходят 25 градусов. Моментные магнитуды недооценены относительно значений из каталога GCMT на величину ≈0.1 единиц магнитуды, а глубины занижены в среднем на 8 км.
ВВЕДЕНИЕ
Тензор сейсмического момента (ТСМ) является базовой характеристикой очага землетрясения в рамках модели точечного источника. ТСМ объединяет в себе характеристики очага в целом: а) его механизм – ориентацию плоскости очага и направление подвижки и б) его “силу” – скалярный сейсмический момент M0.
Тензор сейсмического момента был введен в первой половине 1970-х гг. в работах [Gilbert, 1970; Randall, 1971; Костров, 1970; 1974]. Дальнейшее развитие концепция тензора сейсмического момента получила в работах Дж. Бэкуса и М. Мулкахи [Backus, Mulcahy, 1976; Backus, 1977], в которых “обычный” тензор сейсмического момента фигурирует как тензор нулевого порядка.
Определение ТСМ по сейсмическим данным производится путем инверсии широкополосных волновых форм или их спектров с использованием синтетических сейсмограмм.
Рутинное определение ТСМ с использованием глобальной сети сейсмостанций, оснащенных широкополосными приборами, было начато в 1981 г. в работе [Dziewonski et al., 1981] с использованием метода CMT (Centroid Moment Tensor). В этом методе ТСМ определяется одновременно с пространственно-временным центроидом (см. также [Backus, 1977]) – векторной величиной, компонентами которой являются координаты эквивалентного точечного источника (широта, долгота, глубина) и время, соответствующее положению центра временной функции источника.
Затем в начале 1990-х гг. появились региональные методики в США [Pasyanos et al., 1996], в Японии [Kubo et al., 2002], Европе и Средиземноморье (см., например, обзор в работе [Cesca et al., 2010]) и в других сейсмоактивных регионах.
В СССР, а затем и в России работы по расчету тензора сейсмического момента велись как в теоретическом [Костров, 1970; 1974; 1975; Букчин, 1989; Фатьянов, 1991], так и в практическом плане [Абубакиров и др., 2015; Аптекман, Богданов, 1981; Букчин, 1989; Павлов, Абубакиров, 2012а; 2012б]. Методика Б.Г. Букчина [1989] была применена, в частности, для расчета ТСМ прибайкальских землетрясений [Середкина, Мельникова, 2013]. На Сахалине ТСМ рассчитывается [Сафонов и др., 2017] с помощью программного комплекса ISOLA [Sokos, Zahradnik, 2008]. В ближнем зарубежье также проводились расчеты ТСМ [Костюк, 2008; Сычева, 2016] с привлечением разработанных в ведущих мировых сейсмологических центрах программных комплексов.
В рамках проекта GCMT (The Global Centroid Moment Tensor) [Dziewonski et al., 1981; Ekström et al., 2012] ТСМ и параметры центроида систематически определяются для всех достаточно сильных землетрясений мира. При этом предполагается, что временная функция источника имеет форму прямоугольника или симметричного треугольника, а ее длительность задается по значению моментной магнитуды на основе эмпирической корреляционной формулы. Для расчета ТСМ и параметров центроида используются волновые формы трех типов: объемные волны с периодами более 40 c, “коровые” поверхностные волны с периодами более 40 c и “мантийные” поверхностные волны с периодами более 125 c. Результаты в режиме, близком к режиму реального времени, заносятся в каталог GCMT, размещенный на сайте проекта11. В этом каталоге приведены компоненты ТСМ и параметры центроида и для ряда камчатских землетрясений с моментной магнитудой Mw ≥ 4.8.
В Камчатском филиале ФИЦ ЕГС РАН проводились и продолжают проводиться в настоящее время работы по определению механизмов на основе знаков вступлений продольных волн [Иванова и др., 2011]. В настоящее время каталог механизмов по знакам первых вступлений22 насчитывает свыше 1400 событий Камчатки и Командорских островов периода 1964–2018 гг. с энергетическим классом по S-волне $K_{{S1,2}}^{{F68}}$ [Федотов, 1972] ≥ 11.5. До сих пор он остается наиболее полным однородным каталогом, характеризующим геометрию очагов камчатских землетрясений. Его основная проблема связана с достаточно часто возникающими ошибками в оценках полярности первых вступлений, которые ухудшают качество полученных индивидуальных решений; тем не менее, средние механизмы, построенные по группе событий, в большинстве случаев оказываются вполне приемлемыми и позволяют получить адекватное представление о сейсмотектонических процессах [Иванова и др., 2011].
Развернутая в 2006–2010 гг. на Камчатке сеть широкополосных цифровых приборов позволила получать оценки ТСМ по волновым формам смещений на основе разработанной в КФ ФИЦ ЕГС РАН методики [Абубакиров и др., 2015; Павлов, Абубакиров, 2012а; 2012б].
Эта методика имеет следующие основные черты: 1) модель Земли – плоскослоистое полупространство; 2) из характеристик центроида определяется только глубина; эпицентр не разыскивается – его положение фиксируется по каталогу; 3) время в очаге не определяется – перед началом инверсии синтетические и наблюденные сейсмограммы совмещаются по вступлению продольных волн. Кроме того, в отличие от GCMT длительность процесса в очаге не назначается по корреляционной зависимости, а рассчитывается перебором по критерию минимума невязки. Предусмотрены два варианта методики: 1) расчет тензора с нулевым следом (линейная задача) и 2) расчет тензора в предположении двойного диполя без момента (нелинейная задача). В последнем случае исходная нелинейная задача разбивается на линейную и собственно нелинейную части. Это возможно, так как любой тензор двойного диполя с фиксированной нулевой осью может быть представлен в виде суммы двух базисных тензоров с неизвестными коэффициентами. Линейная часть задачи заключается в нахождении этих коэффициентов, что удается сделать в аналитическом виде. После чего возникает нелинейная задача относительно углов, задающих ориентацию нулевой оси. Вычленение линейной части позволяет уменьшить число искомых нелинейных параметров до двух, что заметно облегчает поиск решения.
В статьях [Абубакиров и др., 2015; Павлов, Абубакиров, 2012а; 2012б] эта методика применена для сильных землетрясений c Mw ≥ 7.5. В данной работе методика адаптируется для землетрясений произвольной магнитуды. Будем ссылаться на эту методику с помощью аббревиатуры RSMT (Regional Seismic Moment Tensor).
В данной работе описана методика RSMT и приведены полученные с ее помощью оценки механизмов, глубин и моментных магнитуд камчатских землетрясений 2010–2012 гг. Оценки получены по широкополосным волновым формам, содержащим полное волновое поле, включающее как объемные, так и поверхностные волны. В качестве модели источника принимается “двойной диполь без момента”. Использованы, в основном, данные сейсмических станций Дальнего Востока России. Для 19 из 31 обработанных землетрясений имеются оценки в глобальном каталоге GCMT. Эти оценки использованы для проверки качества результатов, полученных по методике RSMT.
ПОСТАНОВКА ЗАДАЧИ
Для постановки задачи необходимо выбрать модели очага и среды, определить связь смещений грунта в точках среды с характеристиками очага и сформировать систему уравнений относительно искомых характеристик очага.
Модель очага
Длинноволновое сейсмическое излучение от протяженного очага землетрясения на расстояниях, значительно превышающих его размеры, можно промоделировать, используя эквивалентный точеный источник дипольного типа (см., например, [Костров, 1975]). Такой источник характеризуется симметричным тензором сейсмического момента M с компонентами Mij (i, j = 1, …, 3), временной функцией источника (ВФИ) $f(t)$, географическими координатами и глубиной he.
Тензор M определяет силу и диаграмму направленности сейсмического излучения (механизм), а безразмерная нормированная функция $f(t)$ моделирует временной ход излучения. Эта функция равна нулю до начала разрыва в очаге и единице после его завершения через промежуток времени τ. Величину τ будем называть длительностью источника. Для описания очага в терминах M и $f(t)$ в качестве основной модели мы используем двойной диполь без момента, который является точечным эквивалентом однонаправленной сдвиговой подвижки вдоль плоской площадки разрыва. Обозначим ТСМ двойного диполя через ${{{\mathbf{M}}}_{{DC}}}$, где “DC” – Double Couple, и допустим, что подвижка ${\mathbf{D}}({\mathbf{x}},t) = D({\mathbf{x}},t){\mathbf{d}}$ происходит по площадке Σ с нормалью n в направлении единичного вектора d. Тогда [Аки, Ричардс, 1983]:
(1)
${{{\mathbf{M}}}_{{DC}}} = {{M}_{0}}({\mathbf{n}}{{{\mathbf{d}}}^{{\text{T}}}} + {\mathbf{d}}{{{\mathbf{n}}}^{{\text{T}}}}),$(2)
$f(t) = \int\limits_\Sigma {D({\mathbf{x}},t)dS} {{\left( {\int\limits_\Sigma {D({\mathbf{x}},\tau )dS} } \right)}^{{ - 1}}}.$Из свойств тензора ${{{\mathbf{M}}}_{{DC}}}$ следует, что его след $tr\left( {{{{\mathbf{M}}}_{{DC}}}} \right)$ и определитель $\det \left( {{{{\mathbf{M}}}_{{DC}}}} \right)$ должны быть равны нулю:
Из условий (3) и (4) вытекает, что задача расчета ${{{\mathbf{M}}}_{{DC}}}$ по наблюдениям может быть поставлена как задача условной нелинейной оптимизации. Однако на практике обычно решают задачу безусловной оптимизации, используя параметрическое представление ${{{\mathbf{M}}}_{{DC}}}$ через четыре независимых параметра: углы простирания φ и падения δ площадки Σ, угол подвижки λ и сейсмический момент M0 [Аки, Ричардс, 1983]. Это представление является нелинейным относительно углов φ, δ и λ. Мы используем альтернативную параметризацию, описанную в Приложении. Она включает углы φ и $\theta $, определяющие ориентацию нулевой оси тензора (формула (А1)), и коэффициенты ${{x}_{1}},{\text{ }}{{x}_{2}}$ в разложении тензора ${{{\mathbf{M}}}_{{DC}}}$ (А3) по тензорам специального вида (А4). При таком подходе нелинейными являются лишь два параметра (φ и $\theta $), что существенно снижает вычислительную сложность расчета ${{{\mathbf{M}}}_{{DC}}}$.
Относительно ВФИ $f(t)$ мы предполагаем, что ее плотность $\dot {f}(t) \equiv \frac{d}{{dt}}f(t)$ имеет форму симметричного треугольника, и характеризуем свойства этой функции единственным параметром – ее длительностью τ.
Предполагается также, что географические координаты эквивалентного точечного источника известны заранее и совпадают с координатами эпицентра.
Таким образом, мы задаем эквивалентный точечный источник шестью параметрами, подлежащими определению: углами φ и $\theta $, коэффициентами ${{x}_{1}},{{x}_{2}}$, длительностью τ и глубиной he.
Модель среды
Принятая модель среды (табл . 1) состоит из 6 однородных слоев общей толщиной 660 км и подстилающего полупространства. Значения добротностей для P- и S-волн заданы постоянными: Qp = 600, Qs = 300. Скоростной разрез и профиль плотности построены на основе модели ak135 [Kennett et al., 1995]. В качестве границ раздела выбраны границы аk135 со скачками скорости. Параметры однородных слоев аk135 оставлены без изменений. Последовательности градиентных слоев преобразованы в однородные слои, которым приписаны значения скоростей P- и S-волн и плотности, полученные путем усреднения соответствующих величин на границах градиентных слоев. Параметры полупространства получены усреднением данных модели ak135 для глубин от 660 до 760 км.
Таблица 1.
Модель слоисто-однородной среды, использованная для расчета функций влияния
| Интревал глубин, км | Плотность ρ, г/см3 | Скорость P-волн, км/с | Скорость S-волн, км/с |
|---|---|---|---|
| 0–20 | 2.720 | 5.800 | 3.460 |
| 20–35 | 2.920 | 6.500 | 3.850 |
| 35–120 | 3.345 | 8.045 | 4.490 |
| 120–210 | 3.398 | 8.175 | 4.509 |
| 210–410 | 3.486 | 8.665 | 4.696 |
| 410–660 | 3.910 | 9.780 | 5.340 |
| 660–∞ | 4.416 | 10.990 | 6.150 |
Выражение смещений через характеристики источника
Смещения в точке наблюдения ${\mathbf{x}}$ в произвольный момент времени t от источника в точке ${{{\mathbf{x}}}_{0}}$ представляются в виде линейной комбинации компонент ТСМ [Аки, Ричардс, 1983]:
(5)
${{u}_{n}}({\mathbf{x}},t) = {{M}_{{ij}}}{{g}_{{nij}}}({\mathbf{x}},{{{\mathbf{x}}}_{0}},t),\,\,\,\,n,i,j{\text{ }} = {\text{ }}1, \ldots ,3,$(6)
${{g}_{{nij}}}({\mathbf{x}},{{{\mathbf{x}}}_{0}},t) = f(t){\text{*}}{{G}_{{ni,j}}} = \dot {f}(t){\text{*}}\int\limits_0^t {{{G}_{{ni,j}}}dt} ,$Система уравнений относительно компонент ТСМ
Обозначим через V вектор-столбец неизвестных компонент ТСМ:
(7)
${\mathbf{V}} = L\{ {\mathbf{M}}\} \equiv {{[{{M}_{{11}}},{{M}_{{12}}},{{M}_{{13}}},{{M}_{{22}}},{{M}_{{23}}},{{M}_{{33}}}]}^{{\text{T}}}},$При фиксированных значениях глубины he и длительности τ система уравнений относительно компонент ТСМ, составленная на основе дискретного аналога формулы (5), имеет вид:
где: B – вектор размерности N × 1, сформированный из выделенных для инверсии и профильтрованных в некоторой полосе частот сигналов реальных смещений; G – матрица размерности N × 6, построенная из функций влияния, которые выделяются и фильтруются точно так же, как и реальные данные.Формулировка задачи
Введем вектор неизвестных X, используя для этого матрицу T такую, что:
Вид и размерность этой матрицы зависят от ограничений, которые накладываются на компоненты ТСМ. Матрица T и вектор X будут конкретизированы в следующем разделе. В отсутствие ограничений T представляет собой единичную матрицу шестого порядка.
С учетом формулы (9), запишем систему (8) в виде:
гдеСистема (10), также как и (8), является переопределенной. Под ее решением будем понимать вектор ${\mathbf{X}} = {\mathbf{X}}{\text{*}}$, доставляющий минимум функции невязки $\varepsilon ({\mathbf{X}})$ – нормированной суммы квадратов разности наблюденных и модельных данных:
(12)
$\varepsilon ({\mathbf{X}}) = {{{{{\left\| {{\mathbf{B}} - {\mathbf{AX}}} \right\|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left\| {{\mathbf{B}} - {\mathbf{AX}}} \right\|}}^{2}}} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}}} \right. \kern-0em} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}},$Требуется для каждой пары пробных значений глубины hi ($i = 1,...,{{n}_{h}}$) и длительности τj ($j = 1,...,{{n}_{\tau }}$) найти вектор ${\mathbf{X}}{\text{*}}\left( {{{h}_{i}},{\text{ }}{{\tau }_{j}}} \right)$, доставляющий минимум функции (12), и само минимальное значение невязки $\varepsilon {\text{*}}\left( {{{h}_{i}},{\text{ }}{{\tau }_{j}}} \right) = \varepsilon \left( {{\mathbf{X}}{\text{*}}\left( {{{h}_{i}},{\text{ }}{{\tau }_{j}}} \right)} \right)$.
Минимум невязки $\varepsilon * = \varepsilon {\text{*}}\left( {h*,\tau {\text{*}}} \right)$ по глубине и длительности и доставляющие этот минимум оптимальные значения $h{\text{*}}$ и $\tau {\text{*}}$ определяются перебором по сетке (${{h}_{i}},{{\tau }_{j}}$).
Оптимальный тензор ${\mathbf{M}}{\text{*}}$ конструируется путем обращения оператора L{·}, заданного формулой (7):
где ${\mathbf{V}}* = {\mathbf{TX}}{\text{*}}\left( {h*,\tau {\text{*}}} \right)$.ТЕОРЕТИЧЕСКАЯ ОСНОВА РЕШЕНИЯ ЗАДАЧИ РАСЧЕТА ТСМ ПРИ ФИКСИРОВАННЫХ ЗНАЧЕНИЯХ ГЛУБИНЫ ЭКВИВАЛЕНТНОГО ТОЧЕЧНОГО ИСТОЧНИКА И ДЛИТЕЛЬНОСТИ ВРЕМЕННОЙ ФУНКЦИИ
Используемый нами метод расчета тензора двойного диполя предполагает этап предварительного определения тензора с нулевым следом. Рассмотрим сначала этот этап, а затем перейдем к случаю двойного диполя.
Решение при нулевом следе
Компоненты ТСМ удовлетворяют условию (3). Матрица T, входящая в формулы (9) и (11), представляет собой прямоугольную матрицу размерности 6 × 5, первые пять строк которой совпадают с единичной матрицей 5-го порядка, а 6-я строка задается вектором [–1, 0, 0, –1, 0]. Вектор неизвестных X и матрица A системы (10) имеют вид:
(14)
${\mathbf{X}} = {{[{{M}_{{11}}},{\text{ }}{{M}_{{12}}},{\text{ }}{{M}_{{13}}},{\text{ }}{{M}_{{22}}},{\text{ }}{{M}_{{23}}}]}^{{\text{T}}}},$(15)
${\mathbf{A}} = [{{{\mathbf{G}}}_{1}} - {{{\mathbf{G}}}_{6}},{{{\mathbf{G}}}_{2}},{{{\mathbf{G}}}_{3}},{{{\mathbf{G}}}_{4}} - {{{\mathbf{G}}}_{6}},{{{\mathbf{G}}}_{5}}],$Вектор ${\mathbf{X}} = {\mathbf{X}}{\text{*}}$, доставляющий минимум функции невязки (12), находится по формуле [Худсон, 1970]:
(16)
${\mathbf{X}}* = {{({{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{A}})}^{{ - 1}}}({{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{B}}),$Таким образом, для тензора с нулевым следом непосредственно в результате инверсии находятся пять компонент ТСМ. Шестая компонента определяется из условия нулевого следа (3) по формуле ${{M}_{{33}}} = - {\text{ }}({{M}_{{11}}} + {{M}_{{22}}})$.
Решение для двойного диполя без момента
Компоненты ТСМ удовлетворяют условиям (3) и (4). Воспользуемся описанной в приложении параметризацией тензора ДД. Напомним, что эта параметризация включает углы φ и $\theta $, задающие ориентацию нулевой оси, и компоненты вектора ${\mathbf{x}} = {{[{{x}_{1}},{{x}_{2}}]}^{{\text{T}}}}$ в представлении (А4). В этом случае матрица T размерности 6 × 2 зависит от углов φ и $\theta $:
(18)
${\mathbf{T}}(\varphi ,\theta ) = [L\{ {{{\mathbf{m}}}_{1}}(\varphi ,\theta )\} ,L\{ {{{\mathbf{m}}}_{2}}(\varphi ,\theta )\} ],$где матрицы ${{{\mathbf{m}}}_{1}},{{{\mathbf{m}}}_{2}}$ выражаются по формулам (А4), а оператор L определен формулой (7).
Значения параметров $\varphi ,\theta ,{\mathbf{x}}$ находятся в результате минимизации целевой функции:
(19)
$\varepsilon (\kappa ,\theta ,{\mathbf{x}}) = {{{{{\left\| {{\mathbf{B}} - {\mathbf{A}}(\varphi ,\theta ){\mathbf{x}}} \right\|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left\| {{\mathbf{B}} - {\mathbf{A}}(\varphi ,\theta ){\mathbf{x}}} \right\|}}^{2}}} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}}} \right. \kern-0em} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}},$Минимизация производится в два приема: сначала по x, а затем по углам φ и $\theta $.
Вектор ${\mathbf{x}} = {\mathbf{x}}{\text{*}}(\varphi ,\theta )$, доставляющий минимум функции невязки (19) при фиксированных значениях φ и $\theta ,$ находится из (10) стандартным способом:
(21)
${\mathbf{x}}{\text{*}}(\varphi ,\theta ) = {{({{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{A}})}^{{ - {\text{1}}}}}{{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{B}},$Заменяя в формуле (19) ${\mathbf{A}}(\varphi ,\theta )$ и ${\mathbf{x}} = {\mathbf{x}}{\text{*}}(\varphi ,\theta )$ с помощью формул (20) и (21) соответственно, получим выражение для целевой функции с аргументами φ и $\theta $:
(22)
$\varepsilon (\varphi ,\theta ) = {{{{{\left\| {{\mathbf{B}} - {\mathbf{GV}}(\varphi ,\theta )} \right\|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left\| {{\mathbf{B}} - {\mathbf{GV}}(\varphi ,\theta )} \right\|}}^{2}}} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}}} \right. \kern-0em} {{{{\left\| {\mathbf{B}} \right\|}}^{2}}}},$(23)
${\mathbf{V}}(\varphi ,\theta ) = {\mathbf{T}}{{({{{\mathbf{T}}}^{{\text{T}}}}{{{\mathbf{G}}}^{{\text{T}}}}{\mathbf{GT}})}^{{ - {\text{1}}}}}{{{\mathbf{T}}}^{{\text{T}}}}{{{\mathbf{G}}}^{{\text{T}}}}{\mathbf{B}},$Формула (22) позволяет свести задачу расчета тензора двойного диполя без момента к нелинейной задаче относительно двух неизвестных параметров φ и $\theta $, задающих ориентацию нулевой оси.
Остается найти среди нулевых осей ту, которая доставляет минимум целевой функции (22). Это можно сделать одним из методов нелинейной оптимизации. В данной работе мы воспользовались итерационным методом Левенберга–Марквардта [Press et al., 1986]. В качестве начального приближения выбирали промежуточную ось предварительно рассчитанного ТСМ с нулевым следом.
Обозначим значения углов φ и $\theta $, доставляющих минимум функции (22), через $\varphi {\text{*}}$ и $\theta {\kern 1pt} *$ соответственно. Используя выражение (23), получаем формулу для тензора оптимального двойного диполя без момента:
АЛГОРИТМ РАСЧЕТА ТСМ ПРИ ФИКСИРОВАННЫХ ЗНАЧЕНИЯХ ГЛУБИНЫ ЭКВИВАЛЕНТНОГО ТОЧЕЧНОГО ИСТОЧНИКА И ДЛИТЕЛЬНОСТИ ВРЕМЕННОЙ ФУНКЦИИ
Алгоритм расчета ТСМ состоит из трех шагов: 1) подготовка исходных данных; 2) начальная оценка ТСМ; 3) итерационное уточнение оценки ТСМ. Опишем подробнее каждый из этих шагов.
Шаг 1. Подготовка исходных данных.
1.1. Вычисление эпицентральных расстояний, азимутов из эпицентра на станции и обратных азимутов.
1.2. Расчет функций влияния (ФВ), заданных формулой (6), для каждой из станций и компонент (радиальной, поперечной и вертикальной).
1.3. Определение времен вступлений P-волн для исходных сейсмограмм и ФВ.
1.4. Расчет реальных волновых форм смещений грунта для радиальной, поперечной и вертикальной компонент (деконволюция и интегрирование исходных записей велосиграфов; поворот горизонтальных компонент).
1.5. Понижение частоты дискретизации (децимация) реальных волновых форм до значения, использованного при расчете ФВ.
1.6. Синхронизация времен вступления P-волн на волновых формах реальных смещений и на ФВ.
1.7. Полосовая фильтрация записей смещений и ФВ.
1.8. Выделение сегментов профильтрованных записей смещений и ФВ для расчета ТСМ.
1.9. Формирование исходной системы уравнений относительно компонент ТСМ по выделенным сегментам профильтрованных записей смещений и ФВ. При этом учитывается тип тензора.
Шаг 2. Начальная оценка ТСМ.
В случае тензора с нулевым следом начальные оценки для вектора ${\mathbf{X}}{\text{*}}$ и тензора ${{{\mathbf{M}}}_{{NT}}}$находятся по формулам (16) и (17) соответственно. Обозначим эти оценки через ${\mathbf{X}}_{*}^{{(0)}}$ и ${\mathbf{M}}_{{NT}}^{{(0)}}$. Минимальное значение невязки $\varepsilon ({\mathbf{X}}_{*}^{{(0)}})$ вычисляется по формуле (12).
Для тензора типа двойной диполь без момента начальная оценка ${\mathbf{M}}_{{{\text{DC}}}}^{{(0)}}$ строится следующим образом. Сначала рассчитывается оценка тензора ${\mathbf{M}}_{{NT}}^{{(0)}}$ в предположении нулевого следа. Затем тензор ${\mathbf{M}}_{{NT}}^{{(0)}}$ приводится к главным осям. Углы $\varphi _{0}^{{(0)}},\theta _{0}^{{(0)}}$, задающие ориентацию главной промежуточной оси, принимаются в качестве начального приближения для углов $\varphi _{*}^{{(0)}},\theta _{*}^{{(0)}}$, доставляющих минимум целевой функции (22). Оптимальные величины $\varphi _{*}^{{(0)}},\theta _{*}^{{(0)}}$ определяются с помощью итерационной процедуры Левенберга–Марквардта. Начальная оценка ${\mathbf{M}}_{{{\text{DC}}}}^{{(0)}}$ рассчитывается по значениям $\varphi _{*}^{{(0)}},\theta _{*}^{{(0)}}$ с использованием формул (23), (24). Минимальное значение целевой функции $\varepsilon _{*}^{{(0)}} = \varepsilon (\varphi _{*}^{{(0)}},\theta _{*}^{{(0)}})$, соответствующее этой оценке, вычисляется по формуле (22).
Шаг 3. Итерационное уточнение оценки ТСМ. Обозначим оптимальный тензор, рассчитанный на итерации с номером $k - 1,{\text{ }}(k \geqslant 1)$, через ${{{\mathbf{M}}}^{{(k - 1)}}}$ независимо от его типа. Очередное k-ое приближение ${{{\mathbf{M}}}^{{(k)}}}$ строится следующим образом. Сначала для всех станций и компонент синтезируются волновые формы от источника с тензором ${{{\mathbf{M}}}^{{(k - 1)}}}$. Далее для каждой станции по положению максимума функции взаимной корреляции определяются временные сдвиги, обеспечивающие наилучшее согласие между реальными и синтетическими волновыми формами. При этом величина сдвига ограничивается сверху общей для всех станций и компонент константой. Для радиальной и вертикальной компонент величина сдвига принята одинаковой и рассчитывается по взаимной корреляции сигналов, полученных путем склейки волновых форм на этих компонентах. Для поперечных компонент сдвиг оценивается независимо. Вычисленные значения сдвигов применяются к функциям влияния. Из сдвинутых функций влияния формируется k-ое приближение ${{{\mathbf{G}}}^{{\left( k \right)}}}$ для матрицы G, входящей в уравнения (15), (20), (22) и (23). После этого рассчитывается k-тое приближение ${{{\mathbf{M}}}^{{(k)}}}$ для ТСМ. Метод расчета зависит от типа тензора.
В случае тензора с нулевым следом сначала по матрице ${{{\mathbf{G}}}^{{\left( k \right)}}}$ рассчитывается k-ое приближение ${{{\mathbf{A}}}^{{\left( k \right)}}}$ для матрицы A. Для этого используется формула (15). Затем по формуле (16) при ${\mathbf{A}} = {{{\mathbf{A}}}^{{\left( k \right)}}}$ определяется k-ое приближение ${\mathbf{X}}_{*}^{{(k)}}$ для вектора ${\mathbf{X}}{\text{*}}$. Вектор ${\mathbf{X}}_{*}^{{(k)}}$ с учетом условия нулевого следа определяет k-ое приближение ${\mathbf{M}}_{{NT}}^{{(k)}}$ для тензора ${{{\mathbf{M}}}_{{NT}}}.$ Минимальное значение невязки $\varepsilon ({\mathbf{X}}_{*}^{{(k)}})$ вычисляется по формуле (12) при ${\mathbf{A}} = {{{\mathbf{A}}}^{{\left( k \right)}}}$.
Для тензора типа двойной диполь без момента в качестве начального приближения $\varphi _{0}^{{(k)}},\theta _{0}^{{(k)}}$ для углов $\varphi _{*}^{{(k)}},\theta _{*}^{{(k)}}$, доставляющих минимум целевой функции (22) при ${\mathbf{G}} = {{{\mathbf{G}}}^{{\left( k \right)}}}$, используются значения $\varphi _{0}^{{(k)}} = \varphi _{*}^{{(k - 1)}},$ $\theta _{0}^{{(k)}} = \theta _{*}^{{(k - 1)}}$. Сами оптимальные значения $\varphi _{*}^{{(k)}},\theta _{*}^{{(k)}}$, k-ое приближение ${\mathbf{M}}_{{DC}}^{{(k)}}$ для тензора ${{{\mathbf{M}}}_{{DC}}}$ и минимальное значение целевой функции $\varepsilon _{*}^{{(k)}} = \varepsilon (\varphi _{*}^{{(k)}},\theta _{*}^{{(k)}})$ рассчитываются так же как и на Шаге 2.
Итерационный процесс заканчивается, когда число итераций достигает заранее установленного максимально допустимого значения km. Искомая оптимальная оценка тензора и минимальная невязка в случае нулевого следа – ${\mathbf{M}}_{{NT}}^{*} = {\mathbf{M}}_{{NT}}^{{({{k}_{m}})}}$ и $\varepsilon _{*}^{{{\text{NT}}}} = \varepsilon ({\mathbf{X}}_{*}^{{({{k}_{m}})}})$ соответственно; в случае двойного диполя без момента – ${\mathbf{M}}_{{DC}}^{*} = {\mathbf{M}}_{{DC}}^{{({{k}_{m}})}}$ и $\varepsilon _{*}^{{{\text{DC}}}} = \varepsilon (\varphi _{*}^{{({{k}_{m}})}},\theta _{*}^{{({{k}_{m}})}})$.
Основанием для применения описанного итерационного алгоритма, опирающегося на сдвиги ФВ, можно считать, по крайней мере, два обстоятельства. Во-первых, положение эпицентра известно с ошибкой. В результате ФВ рассчитываются для эпицентральных расстояний, которые отличаются от истинных значений. Во-вторых, ошибки в расчетах ФВ неизбежно возникают из-за неполной адекватности принятой модели среды. Использование сдвигов позволяет частично скомпенсировать эти два типа ошибок и тем самым повысить качество оценок ТСМ.
На рис. 1 приведен пример расчета ТСМ в варианте двойной диполь без момента.
Рис. 1.
Пример применения алгоритма к землетрясению 2011/03/06 13:09:23 (№ 16 по табл. 2), Mw = 4.8. Приведены кривые невязки в зависимости от пробной глубины (а) и в зависимости от пробной длительности при оптимальной глубине (б). В случае (б) верхняя кривая – невязка для стартовой, а нижняя кривая – для заключительной итераций. Оптимальная длительность τ = 0 с. Показаны диаграммы механизма и значения Mw. На панели (в) дано сравнение наблюденных и синтетических сейсмограмм, рассчитанных для оптимальных значений. Сейсмограммы фильтрованы в полосе периодов 20–50 с. Приведены значения эпицентрального расстояния и азимута. Для станций APC (Апача) и OSS (Оссора) зашумленные компоненты не использованы и не приведены. 1 – наблюденная, 2 – синтетическая сейсмограммы; 3 – масштаб амплитуды; 4 – отметка начала и конца интервала подгонки; 5 – эпицентр; 6 – сейсмостанция.

ИСХОДНЫЕ ДАННЫЕ И ИХ ОБРАБОТКА
Исходная выборка из регионального каталога землетрясений Камчатки и Командорских островов33 включала события 2010–2012 гг. с эпицентрами в районе 52.0°–54.0° с.ш., 153.0°–170.0° в.д. и с энергетическим классом $K_{{S1,2}}^{{F68}}$ ≥ 11.5. Объем выборки составил 34 землетрясения. ТСМ, длительность τ и глубину he эквивалентного точечного источника удалось оценить для 31 события (табл. 2 ). Карта эпицентров этих толчков показана на рис . 2, гистограммы распределений по энергетическому классу $K_{{S1,2}}^{{F68}}$, по локальной магнитуде ML и по глубине гипоцентра h – на рис . 4. Отметим, что шкала ML, которая используется в КФ ФИЦ ГС РАН в качестве базовой, не имеет самостоятельной калибровки; значения ML определяются прямым пересчетом из KS по формуле [Гордеев и др., 2006]: ML = $K_{{S1,2}}^{{F68}}$/2 – 0.75. Корреляционная связь между ML и моментной магнитудой Mw для землетрясений вблизи восточного побережья Камчатки в диапазоне ML = 3.4–6.4 (Mw = 3.0–6.0) имеет вид: Mw = ML – 0.40 [Абубакиров и др., 2018].
Таблица 2.
Каталог механизмов и параметров очагов, рассчитанных для ТСМ типа двойной диполь без момента
| № | Время в очаге1) гггг/мм/дд чч:мм:сс.с |
Координаты гипоцентра1) | KS1) | Главные оси механизма | Механизм2) | he3), км | τ, с | M0, Н · м | Mw | K4), ° | η5), % | n6) | m7) | ε8) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lat° | lon° | h, км | T, ° | N, ° | P, ° | Пл. I, dI | Пл. II, dII | ||||||||||||
| az/pl | az/pl | az/pl | φ°/ δ°/ λ° | φ°/ δ°/ λ° | |||||||||||||||
| 1 | 2010/03/13 21:42:37.6 | 52.70 | 160.63 | 49 | 12.1 | 295/67 | 39/6 | 132/22 | 37/67/84 | 233/24/105 | 15 | 2 | 6.88e + 16 | 5.2 | 13 | 14 | 8 | 24 | 18.2 |
| 2 | 2010/07/15 20:28:04.0 | 52.22 | 161.04 | 45 | 11.7 | 23/67 | 221/22 | 129/7 | 57/55/117 | 196/43/57 | 15 | 4 | 8.94e + 15 | 4.6 | – | – | 6 | 13 | 20.2 |
| 3 | 2010/07/30 01:48:41.0 | 52.30 | 160.45 | 44 | 11.6 | 133/49 | 28/13 | 287/38 | 209/85/103 | 321/14/23 | 10 | 2 | 3.56e + 15 | 4.3 | – | – | 7 | 13 | 21.6 |
| 4 | 2010/07/30 03:56:10.5 | 52.22 | 160.45 | 38 | 14.1 | 283/82 | 31/2 | 121/7 | 29/52/87 | 214/38/94 | 20 | 4 | 2.61e + 18 | 6.2 | – | – | 10 | 29 | 16.5 |
| 5 | 2010/07/30 04:28:00.7 | 52.21 | 160.46 | 40 | 12.6 | 256/73 | 42/14 | 135/9 | 33/55/73 | 241/38/113 | 25 | 0 | 1.41e + 17 | 5.4 | 12 | 16 | 6 | 17 | 15.0 |
| 6 | 2010/08/15 02:10:35.6 | 53.25 | 160.74 | 56 | 12.9 | 306/81 | 36/0 | 126/9 | 36/54/90 | 217/36/90 | 45 | 0 | 2.10e + 17 | 5.5 | 10 | 42 | 5 | 15 | 10.3 |
| 7 | 2010/08/21 00:54:15.9 | 53.61 | 162.94 | 84 | 12.6 | 33/14 | 281/57 | 131/29 | 265/80/–148 | 169/59/–12 | 45 | 0 | 5.63e + 16 | 5.1 | 9 | –7 | 8 | 15 | 22.8 |
| 8 | 2010/09/03 04:13:15.4 | 52.84 | 155.34 | 528 | 12.4 | 14/6 | 281/25 | 117/64 | 263/56/–121 | 130/45/–53 | 520 | 2 | 9.29e + 15 | 4.6 | – | – | 3 | 6 | 25.7 |
| 9 | 2010/12/11 10:49:56.0 | 52.82 | 162.45 | 78 | 11.8 | 125/7 | 216/10 | 358/78 | 43/53/–78 | 204/39/–105 | 5 | 4 | 2.62e + 16 | 4.9 | 17 | –12 | 6 | 13 | 27.9 |
| 10 | 2010/12/15 14:38:49.6 | 53.66 | 158.71 | 210 | 11.5 | 114/57 | 15/6 | 282/32 | 196/78/96 | 352/14/66 | 200 | 0 | 1.61e + 16 | 4.7 | 22 | 16 | 5 | 14 | 19.7 |
| 11 | 2011/02/23 06:48:40.5 | 53.43 | 160.83 | 94 | 11.5 | 306/42 | 153/44 | 49/14 | 351/72/137 | 97/50/24 | 70 | 0 | 5.17e + 15 | 4.4 | – | – | 6 | 9 | 30.2 |
| 12 | 2011/02/28 09:36:21.4 | 52.51 | 160.18 | 45 | 11.5 | 265/62 | 40/21 | 137/18 | 30/66/67 | 256/33/131 | 40 | 0 | 5.59e + 15 | 4.4 | – | – | 7 | 11 | 26.0 |
| 13 | 2011/03/04 10:55:18.6 | 52.63 | 161.36 | 17 | 11.6 | 306/79 | 36/0 | 126/11 | 36/56/90 | 217/34/90 | 15 | 0 | 1.45e + 16 | 4.7 | – | – | 6 | 17 | 22.7 |
| 14 | 2011/03/05 00:31:04.9 | 52.63 | 161.29 | 16 | 11.6 | 312/68 | 212/4 | 120/22 | 33/67/94 | 202/24/80 | 10 | 0 | 1.86e + 16 | 4.8 | 22 | –11 | 6 | 14 | 23.4 |
| 15 | 2011/03/05 00:35:30.2 | 52.71 | 161.17 | 16 | 12.5 | 311/71 | 211/4 | 119/18 | 32/63/94 | 204/27/82 | 10 | 6 | 7.96e + 16 | 5.2 | 7 | 4 | 7 | 16 | 19.4 |
| 16 | 2011/03/06 13:09:23.8 | 52.53 | 161.35 | 16 | 11.8 | 334/74 | 214/8 | 122/14 | 39/59/99 | 201/32/75 | 15 | 0 | 1.98e + 16 | 4.8 | – | – | 6 | 15 | 29.9 |
| 17 | 2011/03/06 13:35:09.0 | 52.66 | 161.21 | 17 | 11.9 | 323/62 | 214/10 | 120/26 | 37/72/100 | 188/21/62 | 15 | 0 | 1.35e + 16 | 4.7 | – | – | 10 | 30 | 20.8 |
| 18 | 2011/03/08 10:46:21.8 | 52.61 | 161.14 | 16 | 11.7 | 315/79 | 216/2 | 125/11 | 37/56/92 | 213/34/87 | 15 | 0 | 1.54e + 16 | 4.7 | – | – | 9 | 27 | 16.7 |
| 19 | 2011/03/08 20:48:04.2 | 52.52 | 161.15 | 16 | 11.7 | 299/73 | 40/3 | 131/16 | 39/61/86 | 226/29/97 | 15 | 0 | 1.56e + 16 | 4.7 | – | – | 11 | 28 | 15.5 |
| 20 | 2011/03/08 22:42:33.3 | 52.52 | 161.30 | 15 | 12.0 | 313/70 | 215/3 | 124/20 | 36/65/93 | 209/25/83 | 10 | 2 | 1.01e + 17 | 5.3 | 4 | 9 | 13 | 31 | 17.0 |
| 21 | 2011/03/17 08:28:12.7 | 52.39 | 161.03 | 47 | 11.9 | 249/75 | 40/13 | 131/7 | 30/54/73 | 237/40/111 | 15 | 4 | 7.07e + 16 | 5.2 | 38 | 7 | 7 | 20 | 16.3 |
| 22 | 2011/03/27 12:15:09.2 | 53.67 | 160.89 | 54 | 11.6 | 269/35 | 13/19 | 127/49 | 196/83/–70 | 305/21/–159 | 45 | 0 | 6.96e + 15 | 4.5 | – | – | 10 | 19 | 16.5 |
| 23 | 2011/07/18 18:15:20.6 | 52.50 | 153.56 | 530 | 13.2 | 118/31 | 18/16 | 265/54 | 15/78/–106 | 249/20/–37 | 470 | 0 | 1.45e + 17 | 5.4 | 7 | 5 | 11 | 20 | 21.0 |
| 24 | 2011/07/26 06:17:36.3 | 52.72 | 160.12 | 25 | 12.4 | 282/69 | 46/12 | 140/17 | 40/63/76 | 248/30/115 | 35 | 0 | 1.63e + 17 | 5.4 | 15 | 2 | 8 | 22 | 16.5 |
| 25 | 2011/11/09 22:00:58.3 | 52.25 | 160.25 | 50 | 13.2 | 289/27 | 24/11 | 135/61 | 208/72/–79 | 354/21/–122 | 20 | 8 | 6.51e + 16 | 5.1 | 15 | 17 | 6 | 14 | 15.4 |
| 26 | 2012/01/14 06:11:39.8 | 52.55 | 160.11 | 40 | 11.9 | 252/73 | 37/14 | 130/9 | 27/56/73 | 236/38/114 | 50 | 0 | 2.48e + 16 | 4.9 | 25 | 11 | 4 | 11 | 13.3 |
| 27 | 2012/01/27 08:57:27.4 | 52.04 | 159.40 | 40 | 11.9 | 267/77 | 30/7 | 121/11 | 25/56/82 | 220/35/102 | 45 | 0 | 1.97e + 16 | 4.8 | 11 | –2 | 11 | 20 | 15.3 |
| 28 | 2012/03/02 12:18:35.4 | 52.57 | 160.61 | 40 | 12.0 | 345/79 | 220/7 | 129/9 | 45/55/98 | 211/36/79 | 25 | 0 | 1.14e + 16 | 4.6 | – | – | 13 | 24 | 16.6 |
| 29 | 2012/05/29 02:40:49.5 | 54.00 | 168.78 | 18 | 13.4 | 260/35 | 63/54 | 165/8 | 37/72/32 | 296/60/159 | 10 | 0 | 3.42e + 17 | 5.6 | 40 | –31 | 8 | 13 | 18.9 |
| 30 | 2012/06/13 10:31:45.9 | 53.58 | 159.27 | 140 | 11.6 | 104/31 | 217/33 | 342/41 | 41/84/–57 | 139/34/–170 | 110 | 4 | 1.78e + 16 | 4.8 | 7 | 5 | 7 | 14 | 15.9 |
| 31 | 2012/11/22 05:21:47.0 | 53.86 | 168.04 | 43 | 12.2 | 176/18 | 349/72 | 85/2 | 312/79/15 | 219/76/168 | 35 | 2 | 3.91e + 16 | 5.0 | 93 | –33 | 8 | 18 | 18.5 |
Рис. 2.
Сейсмические станции (1–6), эпицентры землетрясений (7) и диаграммы DC-механизмов (8). В 2010–2012 гг. сейсмические станции имели широкополосные каналы: STS-1 (1), STS-2 (2), CMG-3TB (3), KS2000 (4), CM3oc (5) и CMG-6TD (6). Диаграммы механизмов приведены в равноплощадной проекции нижней полусферы фокальной сферы (номера по табл. 2).
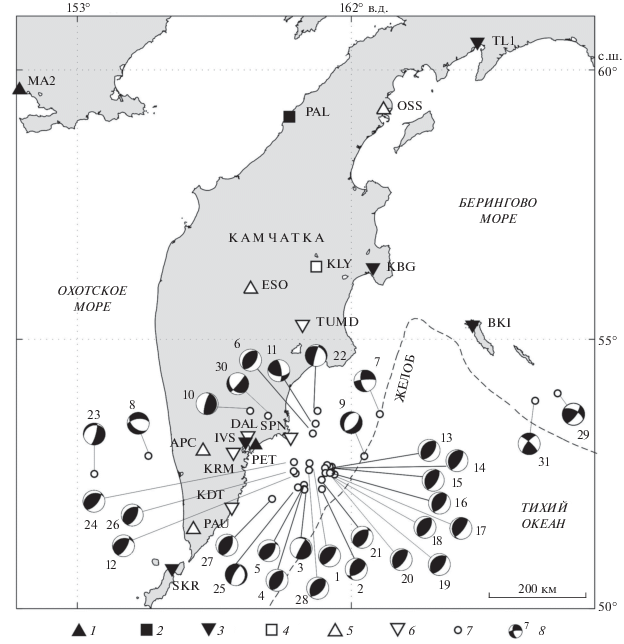
Рис. 3.
Форма амплитудно-частотной характеристики (по скорости) широкополосных приборов; по оси абсцисс – период. Номера указывают тип приборов: STS-1 (1), STS-2 (2), CMG-3TB (3), KS2000 (4), CM3-OC (5) и CMG-6TD (6). Показаны полосы фильтрации: 16–25 с (А), 20–50 с (Б), 40–90 с (В), 60–150 с (Г).

Для расчета ТСМ, he и τ были использованы трехкомпонентные волновые формы широкополосных станций, оборудованных велосиметрами: STS-1, STS-2 (Streckeisen, Швейцария); CMG-3ТВ, CMG-6TD (Güralp, Великобритания); KS-2000 (Geotech Instruments, США); СМ3-ОС (НПП “Геотех”, Россия). Форма амплитудных передаточных функций этих велосиметров в диапазоне периодов T = 10–1000 c приведена на рис . 3. Следует отметить, что собственный шум датчика CMG-6TD на периодах более 10 c превышает фоновый шум микросейсм [Шевченко, Яковенко, 2016], что в большинстве случаев не позволяет восстановить истинные движения грунта от землетрясений умеренной силы в представляющем интерес диапазоне периодов от 20 до 50 c. Поэтому записи этих велосиметров использовались в основном для деконволюции достаточно интенсивных сигналов в полосе периодов 16–25 c.
В общей сложности были задействованы материалы регистрации 26 сейсмических станций в диапазоне эпицентральных расстояний до 2500 км. Основная доля использованных записей приходится на 17 станций (рис. 2). Одна из них, а именно “Северо-Курильск” (SKR), входит в состав сейсмической подсистемы Службы предупреждения о цунами (СП СПЦ) на Дальнем Востоке России [Чебров и др., 2012]. Оставшиеся 16 станций – “Апача” (APC), “Беринг” (BKI), “Дальний” (DAL), “Эccо” (ESO), “Институт” (IVS), “Карымшина” (KRM), “Ключи” (KLY), “Крутоберегово” (KBG), “Оссора” (OSS), “Палана” (PAL), “Паужетка” (РAU), “Петропавловск” (РЕТ44), “Тиличики” (TL1), “Тумрок” (TUMD), “Ходутка” (KDT), “Шипунский” (SPN) – относятся к Камчатской системе сейсмологических наблюдений [Чебров и др., 2013]. Для наиболее сильных землетрясений к обработке дополнительно привлекались данные станций, входящих в состав: СП СПЦ – “Тымовское” (TYV), “Оха” (OKH), “Южно-Сахалинск” (SSH), “Шумшу” (SK3), “Малокурильское” (SHO); глобальной сейсмической сети GSN4 (Global Seismic Network) – “Магадан” (MA2), “Якутск” (YAK), “Matsushiro” (MAJO); сети Национального центра предупреждения о цунами США – “Shemya” (SMY)55.
Исходные волновые формы для всех станций, за исключением SMY, отбирали из цифрового архива региональных станций (ЦАРС) [Бахтиарова, 2010; Чемарев, Токарев, 2013]. Для хранения информации в ЦАРС используется формат miniSEED. Записи SMY в этом же формате, а также метаданные этой станции в формате dataless SEED получали через центр управления данными IRIS DMC66.
Предварительную обработку исходных сейсмограмм проводили с помощью программы DIMAS [Дрознин, Дрознина, 2010]. При работе с miniSEED-файлами эта программа извлекает необходимую дополнительную информацию о регистрирующей аппаратуре из собственной базы данных или из файлов dataless SEED, располагающихся в специально отведенной для этого директории. В ходе предварительной обработки волновые формы просматривали, проверяя их качество, и сохраняли в ASCII-файлах записи с ясно различимыми вступлениями P-волн, а также сопутствующие этим записям метаданные, содержащие необходимые для последующих расчетов сведения о станциях и о сейсмических каналах. Метаданные для каждой из трех компонент содержат, в частности, следующую информацию: дату и время первого отсчета; частоту дискретизации; число отсчетов в сигнале; передаточную функцию велосиметра, заданную в виде нулей и полюсов; коэффициенты цифровых фильтров; вертикальную и азимутальную ориентацию датчика и его чувствительность.
Подготовка данных для инверсии осуществлялась в соответствии с Шагом 1 раздела “АЛГОРИТМ РАСЧЕТА ТСМ …”.
При вычислении эпицентральных расстояний, азимутов из эпицентра на станции и обратных азимутов использовались координаты эпицентров из регионального каталога.
Функции влияния цилиндрических компонент ТСМ точечного мгновенного источника, зависящие от эпицентрального расстояния и глубины, но не зависящие от азимута, были рассчитаны заранее и сохранены в отдельной директории (“библиотеке”). ФВ рассчитывались с частотой дискретизации 1 Гц для диапазона глубин от 5 до 700 км (с шагом 5 км в интервале 5–100 км; с шагом 10 км – в интервале 100–700 км) в интервале эпицентральных расстояний от 100 до 4000 км (с шагом 10 км) и сохранялись в библиотеке в виде отдельных файлов на каждую глубину и эпицентральное расстояние. Функции Грина и их производные, необходимые для расчета ФВ, вычислялись по оригинальному алгоритму, изложенному в работе [Павлов, 2013; 2017].
Вступления P-волн с исходных широкополосных записей снимались вручную. Для ФВ вступления были рассчитаны заранее и сохранены в библиотеке вместе с ФВ.
Деконволюция проводилась в частотной области. Для полосовой фильтрации реальных волновых форм и функций влияния применялся фильтр Баттерворта 4-го порядка. Использовались 4 варианта полос периодов: 16–25; 20–50; 40–90; 60–150 с. Положение этих полос относительно амплитудных передаточных функций задействованных сейсмических датчиков приведено на рис. 3. На начальном этапе для всех землетрясений и станций принималась фиксированная полоса пропускания 20–50 с. Далее она выбиралась в зависимости от полученного значения моментной магнитуды: 40–90 с при 5.5 < Mw ≤ 6.0; 60–150 с при Mw > 6.0. В отдельных случаях, особенно при Mw < 5.0, выбиралась полоса периодов 16–25 с. Для некоторых станций вместо установленной по значению Mw полосы использовали ту, что позволяла уменьшить расхождение между реальными и теоретическими сейсмограммами и/или увеличить отношение сигнал/шум.
Рис. 4.
Гистограммы значений параметров землетрясений (табл. 2): класса $K_{{S1,2}}^{{F68}}$ (а), магнитуды ML (б) и глубины гипоцентра (в).
При расчете ТСМ допустимая величина временного сдвига для ФВ ограничивалась сверху 5 с, число итераций km принималось равным пяти.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Оценки ТСМ, глубины he эквивалентного точечного источника и длительности τ временной функции источника получены для 31 землетрясения в диапазоне $K_{{S1,2}}^{{F68}}$ = 11.5–14.1 (Mw = 4.3–6.2). Расчеты проводились для ТСМ типа двойной диполь без момента. По ТСМ определены параметры механизмов очагов, а также значения скалярного сейсмического момента ${{M}_{0}} = {{({{M}_{3}} - {{M}_{1}})} \mathord{\left/ {\vphantom {{({{M}_{3}} - {{M}_{1}})} 2}} \right. \kern-0em} 2}$, где М1 ≤ М2 ≤ М3 – главные значения ТСМ, и моментной магнитуды Mw = (2/3)(lg M0 [Н · м] – 9.1) [Kanamori, 1977]. Полученные оценки сведены в табл. 2 вместе с сопроводительной информацией. Для каждого события приведены следующие данные: характеристики гипоцентра по каталогу КФ ФИЦ ЕГС РАН (дата и время в очаге, координаты эпицентра и глубина гипоцентра, энергетический класс $K_{{S1,2}}^{{F68}}$); угол наклона и азимут главных осей ТСМ; углы, задающие ориентацию нодальных плоскостей и векторов подвижек; глубина эквивалентного точечного источника; длительность ВФИ; скалярный сейсмический момент; моментная магнитуда; число сейсмических станций и компонент, использованных в расчете; остаточная невязка. Кроме этого, для 19 событий, имеющих независимые решения GCMT, в табл. 2 дополнительно представлены значения коэффициента Лоде–Надаи $\eta = {{(2{{M}_{2}} - {{M}_{1}} - {{M}_{3}})} \mathord{\left/ {\vphantom {{(2{{M}_{2}} - {{M}_{1}} - {{M}_{3}})} {({{M}_{3}} - {{M}_{1}})}}} \right. \kern-0em} {({{M}_{3}} - {{M}_{1}})}}$, характеризующего отклонение решения GCMT от модели двойного диполя, и угла K (0° ≤ K ≤ 120°) [Kagan, 2007; Tape, Tape, 2012] между тройками главных осей тензоров RSMT и GCMT. Для трех землетрясений с $K_{{S1,2}}^{{F68}}$ = 11.5–11.6 (табл . 3) получить оценки параметров очагов не удалось из-за недостатка исходных данных с приемлемым отношением сигнал/шум.
Таблица 3.
Каталог землетрясений, для которых не удалось рассчитать параметры очагов
| № | Время в очаге1) гггг/мм/дд чч:мм:сс.с |
Координаты гипоцентра1) | KS1) | ||
|---|---|---|---|---|---|
| lat., ° | lon., ° | h, км | |||
| 1 | 2011/07/26 06:16:43.5 | 52.76 | 160.17 | 56 | 11.5 |
| 2 | 2011/12/15 13:18:30.4 | 52.52 | 159.90 | 54 | 11.6 |
| 3 | 2012/10/28 19:09:27.2 | 52.79 | 157.06 | 240 | 11.5 |
Примечание. 1) по каталогу [Камчатский филиал …, 2019].
На рис. 2 приведены диаграммы рассчитанных механизмов.
Качество полученных оценок моментных магнитуд, глубин и механизмов проверяли, сопоставляя их с аналогичными оценками из каталога GCMT. Для длительностей ВФИ такое сопоставление неинформативно по двум причинам. Во-первых, в методике GCMT длительность ВФИ не определяется непосредственно по волновым формам, а рассчитывается по корреляционной формуле τ(GCMT) = 2.1(M0[Н · м] × 10–17)1/3 [Ekström et al., 2012]. Во-вторых, в методике RSMT для слабых и умеренной силы землетрясений используются волновые формы с периодами в несколько десятков секунд, для которых форма и амплитуда синтетических сейсмограмм слабо зависят от очаговой длительности. В результате функция невязки оказывается малочувствительной к вариациям τ вблизи ожидаемого значения τ(GCMT), а сами оценки τ обладают низкой надежностью и их следует рассматривать как сугубо формальные.
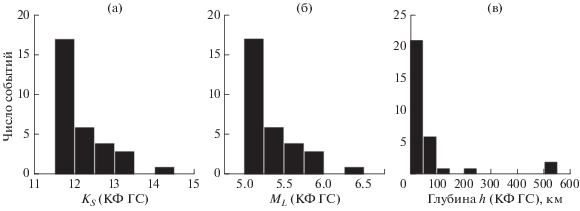
На рис . 5а–5в приведено сопоставление полученных оценок Mw с данными каталога GCMT. Максимальное абсолютное значение разности ∆Mw = Mw(RSMT) – Mw(GCMT) достигает 0.3 единиц магнитуды, а для большинства событий (в 17 случаях из 19) не превосходит 0.2. Среднее значение μ(∆Mw) = –0.09, стандартное отклонение σ(∆Mw) = 0.09. Рис. 5а–5в демонстрируют наличие устойчивой корреляции между парами величин Mw(RSMT) и Mw(GCMT), а также незначительную систематическую недооценку Mw(RSMT) относительно Mw(GCMT). Аналогичная тенденция к занижению региональных оценок Mw относительно Mw(GCMT) наблюдается во многих сейсмоактивных районах мира (см., например, [Bonita et al., 2015; Franco et al., 2020; Konstantinou, Rontogianni, 2011; Kubo et al., 2002; Nakano et al., 2010]). Систематические расхождения между самими региональными оценками Mw, полученными разными агентствами, могут достигать 0.2 единиц магнитуды (см., например, [Gasperini et al., 2012; Pondrelli et al., 2011; Serpetsidaki et al., 2016]). С учетом последнего обстоятельства, полученное нами расхождение ∆Mw ≈ –0.1 можно считать вполне приемлемым. Наблюдаемый дефицит Mw(RSMT) может быть обусловлен медленным ростом уровня очагового спектра c увеличением периода [Абубакиров и др., 2018]. Если предположить, что такой рост действительно имеет место в диапазоне периодов от десятка до сотен секунд, то среднепериодная оценка Mw(RSMT) всегда будет меньше более предпочтительной длиннопериодной оценки Mw(GCMT).
Рис. 5.
Сопоставление оценок моментной магнитуды Mw, приведенных в табл. 2 и глобальном каталоге GCMT (а)–(в); аналогично для оценок глубины эквивалентного точечного источника (г)–(е). На панелях (а), (г) сплошная линия отмечает точки, для которых соответствующие оценки совпадают; на (б), (д) нанесены разности, штриховые линии отмечают средние значения: 0.09 для разности магнитуд и 8.0 км для разности глубин (среднеквадратические отклонения составляют 0.09 и 11.0 соответственно). Панели (в) и (е) – гистограммы для зависимостей (б) и (д) соответственно.
На рис. 5г–5е приведено сопоставление оценок глубины he эквивалентного точечного источника с глубиной hс центроида GCMT. Максимальное абсолютное значение разности ∆h = he(RSMT) – ‒ hс(GCMT) достигает 30 км, а для большинства событий (в 14 случаях из 19) не превосходит 10 км. Среднее значение μ(∆h) = –8 км, стандартное отклонение σ(∆h) = 11 км. Схожие результаты получены в работе [Kubo et al., 2002] для землетрясений вблизи Японии. Наблюдаемое занижение глубин he(RSMT) относительно hс(GCMT) в случае поверхностных землетрясений может быть обусловлено принципиальными трудностями определения глубины по длиннопериодным волновым формам и связанным с ними ограничением в 12 км на минимально допустимую глубину в GCMT. В этом случае оценки he(RSMT), по-видимому, являются более реалистичными. Для глубоких землетрясений и землетрясений с промежуточной глубиной, напротив, предпочтение следует отдать оценкам hс(GCMT), т.к. они обеспечены исходными данными существенно большего объема и с более плотным азимутальным покрытием.
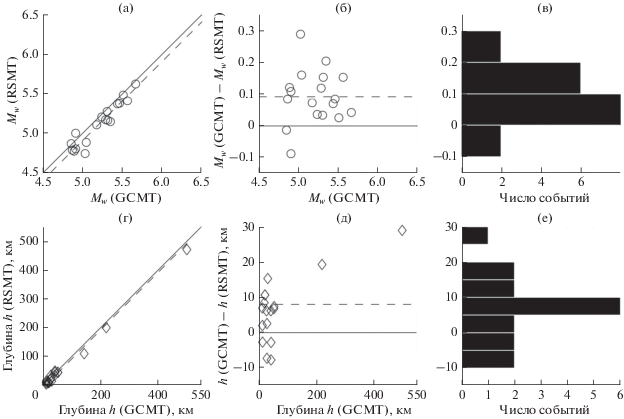
Сопоставление механизмов приведено на рис . 6, где показаны гистограмма и эмпирическая функция распределения угла K – наименьшего угла, на который нужно повернуть оси одного механизма, чтобы совместить их с соответствующими осями другого. Этот угол характеризует различие между механизмами двойных диполей, однако в методике GCMT непосредственно по волновым формам рассчитывается тензор MNT с нулевым следом, а уже затем по нему конструируется двойной диполь MВDC, который принято называть наилучшим двойным диполем [Ekström et al., 2012] и использовать для его обозначения аббревиатуру BDC (Best Double Couple):
(25)
${{{\mathbf{M}}}_{{{\text{BDC}}}}} = {{M}_{0}}({{{\mathbf{e}}}_{T}}{\mathbf{e}}_{T}^{{\text{T}}} - {{{\mathbf{e}}}_{P}}{\mathbf{e}}_{P}^{{\text{T}}}),$Рис. 6.
Гистограмма (а) и статистическая функция распределения (б) для угла K между тройками главных векторов тензоров ODC RSMT и GCMT.
В работе [Henry et al., 2002] показано, что в некоторых случаях MВDC может заметно отличаться от двойного диполя MDC, рассчитанного непосредственного по волновым формам. Такого различия можно ожидать, если тензор MNT, по которому конструируется MВDC, содержит существенную недипольную компоненту, или, другими словами, если коэффициент Лоде–Надаи для MNT сильно отклоняется от нуля. Примерами такого рода при сопоставлении наших оценок MDC с оценками MВDC из каталога GCMT являются события с номерами 29 и 31 в табл. 2, для которых K = 40°, η = −31% и K = 93°, η = −33% соответственно. К контрпримерам можно отнести землетрясения с номерами 6 (K = 42°, η = 10%) и 21 (K = 7°, η = 38%) . Таким образом, предположение о связи больших различий между MDC и MВDC с наличием большой недипольной компоненты по нашим данным не подтверждается. По-видимому, большие значения K следует воспринимать как индикатор низкой надежности наших оценок. Для событий 29 и 31, произошедших в районе Алеутской дуги, пониженное качество наших результатов вполне ожидаемо в силу удаленности эпицентров от основной массы станций камчатской сети и плохого азимутального покрытия. В целом, рис. 6 демонстрирует приемлемое согласие с данными каталога GCMT для большинства из рассчитанных механизмов (в 16 случаях из 19 величина К не превосходит 25°).
ЗАКЛЮЧЕНИЕ
Развернутая в 2006–2010 гг. на Камчатке сеть цифровых сейсмических приборов создала принципиальную возможность для массового расчета тензора сейсмического момента камчатских землетрясений по широкополосным волновым формам региональных станций. Ранее авторами была разработана и успешно опробована на примере нескольких событий Дальнего Востока России с Mw >7.5 методика расчета тензора сейсмического момента для сильных землетрясений [Абубакиров и др., 2015; Павлов, Абубакиров, 2012а; 2012б]. В данной работе вариант этой методики, предполагающий, что тензор имеет тип двойного диполя без момента, адаптирован для камчатских землетрясений умеренной силы.
Адаптированный вариант методики отработан на выборке из 34 землетрясений 2010–2012 гг. с $K_{{S1,2}}^{{F68}}$ ≥ 11.5, произошедших вблизи восточного побережья Камчатки в районе 52.0°–54.0° с.ш., 153.0°–170.0° в.д. Для 31 землетрясения с $K_{{S1,2}}^{{F68}}$ = = 11.5–14.1 (Mw = 4.3–6.2) рассчитаны механизм очага, моментная магнитуда и глубина эквивалентного точечного источника; для 3 землетрясений с $K_{{S1,2}}^{{F68}}$ = 11.5–11.6 получить оценки параметров очагов не удалось из-за недостатка волновых форм с приемлемым отношением сигнал/шум. Проверка качества полученных оценок проведена по выборке из 19 событий, входящих в каталог GCMT. Значения угла K, характеризующего расхождение между механизмом двойного диполя, рассчитанного нами непосредственно по волновым формам, и механизмом наилучшего двойного диполя, сконструированного по тензору с нулевым следом из каталога GCMT, для 84% событий находятся в интервале 0°–25°. Моментная магнитуда занижена относительно значений из каталога GCMT в среднем на 0.09 единиц. Глубина эквивалентного точечного источника меньше глубины центроида GCMT в среднем на 8 км. Наблюдаемые расхождения по всем параметрам вполне приемлемы.
Полученные результаты создают методическую основу для создания однородного каталога механизмов землетрясений Камчатки и Командорских островов с КS ≥ 11.5 по региональным широкополосным волновым формам как возможной альтернативы или дополнения к существующему каталогу механизмов по знакам первых вступлений.
Список литературы
Аки К., Ричардс П. Количественная сейсмология. Т. 1. М.: Мир. 1983. 520 с.
Абубакиров И.Р., Гусев А.А., Гусева Е.М., Павлов В.М., Скоркина А.А. Массовое определение моментных магнитуд Mw и установление связи между Mw и ML для умеренных и слабых камчатских землетрясений // Физика Земли. 2018. № 1. С. 37–51.
Абубакиров И.Р., Павлов В.М., Титков Н.Н. Механизм глубокого Охотоморского землетрясения 24.05.2013 г. по статическим смещениям и широкополосным сейсмограммам // Вулканология и сейсмология. 2015. № 4. С. 23–39.
Аптекман Ж.П., Богданов В.И. Определение тензора сейсмического момента из наблюдений // Изв. АН СССР. Сер. Физика Земли. 1981. № 10. С. 14–24.
Бахтиарова Г.М. Цифровой архив региональных станций Камчатского филиала ГС РАН. Геофизический мониторинг Камчатки. Материалы научно-технической конференции 17–18 января 2006 г. Петропавловск-Камчатский: КФ ГС РАН, 2006. С. 29–31.
Букчин Б.Г. Об определении параметров очага землетрясения по записям поверхностных волн в случае неточного задания характеристик среды // Изв. АН СССР. Сер. Физика Земли. 1989. № 9. С. 34–41.
Гордеев Е.И., Гусев А.А., Левина В.И., Леонов В.Л., Чебров В.Н. Мелкофокусные землетрясения п-ова Камчатка // Вулканология и сейсмология. 2006. № 3. С. 28–38.
Дрознин Д.В., Дрознина С.Я. Интерактивная программа обработки сейсмических сигналов DIMAS // Сейсмические приборы. 2010. Т. 46. № 3. С. 22–34.
Иванова Е.И., Ландер А.В., Токарев А.В., Чеброва А.Ю., Шевченко С.А. Каталог механизмов очагов землетрясений Камчатки и Командорских островов за период 1980–2007 гг. Труды конференции. Проблемы комплексного геофизического мониторинга Дальнего Востока России. Петропавловск-Камчатский. 2011. С. 74–79.
Камчатский филиал ФИЦ ЕГС РАН. Единая информационная система сейсмологических данных. URL: http://www.emsd.ru/sdis (дата обращения: 25.10.2020).
Костров Б.В. Теория очагов тектонического землетрясения // Изв. АН СССР. Сер. Физика Земли. 1970. № 4. С. 84–101.
Костров Б.В. Сейсмический момент, энергия землетрясения и сейсмическое течение горных масс // Изв. АН СССР. Сер. Физика Земли. 1974. № 1. С. 23–40.
Костров Б.В. Механика очага тектонического землетрясения. М.: Наука. 1975. 176 с.
Костюк А.Д. Механизмы очагов землетрясений средней силы на северном Тянь-Шане // Вестник КРСУ. Механика и физика. 2008. Т. 8. № 1. С. 100–105.
Павлов В.М. Алгоритм расчета синтетических сейсмограмм в слоистом полупространстве с применением матричного импеданса // Физика Земли. 2013. № 1. С. 26–35.
Павлов В.М. Алгоритмы расчета синтетических сейсмограмм от дипольного источника с использованием производных функций Грина // Физика Земли. 2017. № 4. С. 67–75.
Павлов В.М., Абубакиров И.Р. Создание и опробование алгоритма оценки тензора сейсмического момента сильных землетрясений по широкополосным записям региональных сейсмических станций. Сейсмологические и геофизические исследования на Камчатке. К 50-летию сейсмологических наблюдений / Под ред. Гордеева Е.И., Чеброва В.Н. Петропавловск-Камчатский: 2012а. С. 380–396.
Павлов В.М., Абубакиров И.Р. Алгоритм расчета тензора сейсмического момента сильных землетрясений по региональным широкополосным сейсмограммам объемных волн // Вестник КРАУНЦ. Науки о Земле. 2012б. № 2(20). С. 149–158.
Сафонов Д.А., Нагорных Т.В., Коновалов А.В., Степнов А.А. Тензор момента, механизмы очага землетрясения и напряженное состояние территории о. Сахалин // Вулканология и сейсмология. 2017. № 3. С. 59–70.
Середкина А.И. Мельникова В.И. Тензор сейсмического момента прибайкальских землетрясений по поверхностным волнам // Докл. РАН. 2013. Т. 451. № 1. С. 91–94.
Сычева Н.А. Применение метода волновой инверсии и сейсмотектонических деформаций для оценки напряженно-деформированного состояния территории Центрального Тянь-Шаня // Вестник КРСУ. Науки о Земле. 2016. Т. 16. № 1. С. 172–177.
Фатьянов А.Г. Прямые и обратные задачи для тензора сейсмического момента в слоистых средах // Докл. РАН. 1991. Т. 317. № 6. С. 1357–1361.
Федотов С.А. Энергетическая классификация Курило-Камчатских землетрясений и проблема магнитуд. М.: Наука. 1972. 117 с.
Худсон Д. Статистика для физиков. М.: МИР. 1970. 297 с.
Чебров В.Н., Гусев А.А., Дрознин Д.В., Мишаткин В.Н., Сергеев В.А., Синицын В.И., Шевченко Ю.В., Чебров Д.В. Развитие сейсмологических наблюдений на Дальнем Востоке России для Службы предупреждения о цунами // Сейсмологические и геофизические исследования на Камчатке. К 50-летию детальных сейсмологических наблюдений. Глава 3. Петропавловск-Камчатский: Холдинговая компания “Новая книга”. 2012. С. 70–104.
Чебров В.Н., Дрознин Д.В., Кугаенко Ю.А. и др. Система детальных сейсмологических наблюдений на Камчатке в 2011 г. // Вулканология и сейсмология. 2013. № 1. С. 18–40.
Чемарёв А.С., Токарев А.В. Подсистема ЕИС для формирования и хранения волновых форм землетрясений. Проблемы комплексного геофизического мониторинга Дальнего Востока России. Труды Четвертой научно-технической конференции. Петропавловск-Камчатский. 29 сентября–5 октября 2013 г. Обнинск: ГС РАН. 2013. С. 359–361.
Шевченко Ю.В., Яковенко В.В. Собственный шум сейсмометров на частотах от 0.01 до 0.1 Гц // Сейсмические приборы. 2016. Т. 52. № 2. С. 17–28.
Backus G.E. Interpreting the seismic glut moments of total degree two or less // Geophys. J. Int. 1977. V. 51. P. 1–25.
Backus G.E., Mulcahy M. Moment tensors and other phenomenological descriptions of seismic sources – I. Continuous displacements // Geophys. J. Int. 1976. V. 46. P. 341–361.
Bonita J.D., Kumagai H., Nakano M. Regional moment tensor analysis in the Philippines: CMT solutions in 2012–2013 // J. Disaster Research. 2015. V. 10. №. 1. P. 18–24.
Cesca S., Heimann S., Stammler K., Dahm T. Automated procedure for point and kinematic source inversion at regional distances // J. Geophys. Res., 2010. V. 115. B06304. P. 1–24. https://doi.org/10.1029/2009JB006450
Dziewonski A.M., Chou T.-A., Woodhouse J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity // J. Geophys. Res. 1981. V. 86. P. 2825–2852. https://doi.org/10.1029/JB086iB04p02825
Ekström G., Nettles M., Dziewonski A.M. The global CMT project 2004–2010: Centroid-moment tensors for 13 017 earthquakes // Phys. Earth Planet. Inter. 2012. V. 200–201. P. 1–9. https://doi.org/10.1016/j.pepi.2012.04.002
Franco S.I., Iglesias A., Fukuyama E. Moment tensor catalog for Mexican earthquakes: almost two decades of seismicity // Geofis. Int. 2020. V. 59. № 2. P. 54–82.
Gasperini P., Lolli B., Vannucci G., Boschi E. A comparison of moment magnitude estimates for the European–Mediterranean and Italian regions // Geophys. J. Int. 2012. V. 190. № 3. P. 1733–1745.
Gilbert F. Excitation of the Normal Modes of the Earth by Earthquake Sources // Geophys. J. R. Astron. Soc. 1970. V. 22. P. 223–226.
Henry C., Woodhouse J.H., Das S. Stability of earthquake moment tensor inversion: effect of the double-couple constraint // Tectonophysics. 2002. V. 356. №. 19. P. 115–124.
Kagan Y. Simplified algorithms for calculating double-couple rotation // Geophys. J. Int. 2007. V. 171. P. 411–418.
Kanamori H. The energy release in great earthquakes // J. Geophys. Res. 1977. V. 82. № 20. P. 2981–2987.
Kennett B.L.N., Engdahl E.R., Buland R. Constraints on seismic velocities in the Earth from traveltimes // Geophys. J. Int. 1995. V. 122. № 1. P. 108–124.
Konstantinou K.I., Rontogianni S. A comparison of teleseismic and regional seismic moment estimates in the European-Mediterranean region // Seismol. Res. Lett. 2011. V. 82. № 2. P. 188–200.
Kubo A., Fukuyama E., Kawai H., Nonomura K. NIED seismic moment tensor catalogue for regional earthquakes around Japan: quality test and application // Tectonophysics. 2002. V. 356. № 1–3. P. 23–48.
Nakano M., Yamashina T., Kumagai H., Inoue H. Centroid moment tensor catalogue for Indonesia // Phys. Earth Planet. Inter. 2010. V. 183. № 3–4. P. 456–467.
Pasyanos M.E., Dreger D.S., Romanowicz B. Towards real-time estimation of regional moment tensors // BSSA. 1996. V. 86. № 5. P. 1255–1269.
Pondrelli S., Salimbeni S., Morelli A., Ekström G., Postpischl L., Vannucci G., Boschi E. European–Mediterranean regional centroid moment tensor catalog: solutions for 2005–2008 // Phys. Earth Planet. Inter. 2011. V. 185. № 3–4. P. 74–81.
Press W.H., Flannery B.P., Teokolsky S.A., Vetterling W.T. Numerical recipes. Cambridge University Press, 1986. 823 p.
Randall, M.J. Elastic multipole theory and seismic moment // BSSA. 1971. V. 61. № 5. P. 1321–1326.
Serpetsidaki A., Sokos E., Tselentis G.A. A ten year moment tensor database for Western Greece // Phys. Chem. Earth, Parts A/B/C. 2016. V. 95. P. 2–9.
Sokos E. N., Zahradnik J. ISOLA a Fortran code and a Matlab GUI to perform multiple-point source inversion of seismic data // Comput. Geosci. 2008. V. 34. P. 967–977.
Tape W., Tape C. Angle between principal axis triples // Geophys. J. Int. 2012. V. 191. № 2. P. 813–831.
Дополнительные материалы отсутствуют.


