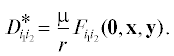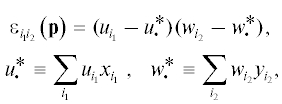Генетика, 2019, T. 55, № 5, стр. 593-603

Квазиравновесие по сцеплению при слабом двулокусном отборе по жизнеспособности. II. Локусы с множественными аллелями

В. П. Пасеков^*

Вычислительный центр им. А.А. Дородницына Федерального исследовательского центра “Информатика и управление” Российской академии наук
119991 Москва, Россия

^* E-mail: pass40@mail.ru

Поступила в редакцию 24.04.2018
После доработки 17.07.2018
Принята к публикации 23.07.2018

DOI: 10.1134/S001667581904012X

Полный текст (PDF)

Аннотация

Рассматривается модель слабого отбора по жизнеспособности по двум локусам с множественными аллелями в гаплоидной популяции. Предполагается, что скрещивание в популяции случайно, поколения не перекрываются, динамика генетической структуры моделируется обыкновенными дифференциальными уравнениями. Слабый отбор рассматривается как возмущение модели без отбора. Полученные ранее при диаллельных локусах оценки квазиравновесия для коэффициента неравновесности по сцеплению D обобщаются на случай множественных аллелей. При этом интерпретация оценок в терминах средних эффектов в количественной генетике оказалась независимой от числа аллелей. Первым приближением для квазиравновесия ${{D}_{{{{i}_{1}}{{i}_{2}}}}}$ будет $D_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}^{ * }$ = ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}(p)\frac{\mu }{r}{{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{2}}}}},$ где μ – интенсивность отбора; r – коэффициент рекомбинации; ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}(p)$ – коэффициент неаддитивности эпистаза для жизнеспособностей ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ гаплоидных генотипов i₁i₂; ${{x}_{{{{i}_{{\text{1}}}}}}},$ ${{y}_{{{{i}_{{\text{2}}}}}}}$ – частоты составляющих генотип аллелей с номерами i₁, i₂ первого и второго локуса соответственно. Специфика возмущенной модели в том, что в ней выделяются быстрые (неравновесности ${{D}_{{{{i}_{1}}{{i}_{{\text{2}}}}}}}$) и медленные (частоты аллелей) переменные, что характеризует модель как сингулярно возмущенную. Это позволяет без решения уравнений выделить в динамике два этапа. На первом быстрые переменные сходятся к квазиравновесным значениям, а на втором идет эволюция медленных переменных при условии квазиравновесия быстрых. Полученные дельта-методом уравнения относительно квазиравновесных значений ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ дают корректный результат с точки зрения разложения по степеням малого параметра решения сингулярно возмущенных уравнений. Обсуждаются проблемы измерения эпистаза и разложения коэффициента эпистаза на элементарные составляющие, а также анализируются двулокусные коэффициенты эпистаза как характеристики многолокусной модели. Кратко указано обобщение полученных результатов для гаплоидной популяции на диплоидный случай.

Ключевые слова: теоретическая популяционная генетика, математические модели, слабый двулокусный отбор по жизнеспособности, множественные аллели, квазиравновесие по сцеплению, сингулярные возмущения.

Рассмотрим модель динамики генетической структуры гаплоидной популяции с неперекрывающимися поколениями и случайным скрещиванием в непрерывном времени при учете отбора по жизнеспособности по двум локусам k и m (см. [1]). Напомним, что предполагается следующая последовательность стадий жизненного цикла:

замещение родительской популяции потомками → → отбор по жизнеспособности → рекомбинации → → появление потомков (нового поколения).

Генетическое состояние (структура) популяции описывается вектором p концентраций двулокусных гаплоидных генотипов:

${\mathbf{p}} = \{ {{p}_{{\mathbf{i}}}}\quad = {{p}_{{{{i}_{k}}{{i}_{m}}}}}\} ,\,\,\,\,\sum\limits_i {{{p}_{i}} = 1} ,\,\,\,\,1 \geqslant {{p}_{{\mathbf{i}}}} \geqslant 0,\,\,\,\,{\mathbf{i}} = ({{i}_{k}},{{i}_{m}}).$

Здесь i_k – номер аллеля k-го локуса, входящего в i-й генотип (короче, i_k обозначает соответствующий аллель); ${{p}_{{{{i}_{k}}{{i}_{m}}}}}$ – частота двулокусного гаплоидного генотипа с аллелями i_k, i_m. В дальнейшем состояние популяции будем относить к началу поколения (к “новорожденным”, заменяющим поколение родителей).

Покоординатно уравнения динамики генетического состояния популяции в модели имеют вид

${{d{{p}_{{{{i}_{k}}{{i}_{m}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{k}}{{i}_{m}}}}}} {dt}}} \right. \kern-0em} {dt}} = \mu \left( {{{\text{v}}_{{{{i}_{k}}{{i}_{m}}}}}\left( {\mathbf{p}} \right)--\text{v}\left( {\mathbf{p}} \right)} \right){{p}_{{{{i}_{k}}{{i}_{m}}}}}--r{{D}_{{{{i}_{k}}{{i}_{m}}}}}.$

Здесь t, ${{\text{v}}_{{{{i}_{k}}{{i}_{m}}}}}({\mathbf{p}})$ дают время и жизнеспособность генотипа i_ki_m соответственно, v(p) ≡ $\sum\nolimits_{{{i}_{k}},{{i}_{m}}} {{{\text{v}}_{{{{i}_{k}}{{i}_{m}}}}}{{{\mathbf{p}}}_{{{{i}_{k}}{{i}_{m}}}}}} $ – средняя жизнеспособность, μ и r обозначают параметры давления отбора и независимый от генотипа коэффициент рекомбинации.

Генетическое состояние популяции можно описывать не только частотами двулокусных гамет, но и частотами аллелей ${{x}_{{{{i}_{k}}}}}$ и ${{y}_{{{{i}_{m}}}}}$ и неравновесностями по сцеплению ${{D}_{{{{i}_{k}}{{i}_{m}}}}}{\text{:}}$

$\begin{gathered} {{x}_{{{{i}_{k}}}}} \equiv \sum\limits_{{{i}_{m}}} {{{p}_{{{{i}_{k}}{{i}_{m}}}}}} ,\,\,\,\,{\text{ }}{{y}_{{{{i}_{m}}}}} \equiv \sum\limits_{{{i}_{k}}} {{{p}_{{{{i}_{k}}{{i}_{m}}}}}} , \\ {{D}_{{{{i}_{k}}{{i}_{m}}}}} \equiv {{p}_{{{{i}_{k}}{{i}_{m}}}}}\quad--{\text{ }}{{x}_{{{{i}_{k}}}}}{{y}_{{{{i}_{m}}}}}\quad\quad\left( {{{p}_{{{{i}_{k}}{{i}_{m}}}}}\quad = {{D}_{{{{i}_{k}}{{i}_{m}}}}}\quad + \quad{\text{ }}{{x}_{{{{i}_{k}}}}}{{y}_{{{{i}_{m}}}}}} \right). \\ \end{gathered} $

Здесь допускаются множественные аллели.

Традиционной задачей исследования модели является анализ ее решения и в идеале получение явного выражения состояния популяции в зависимости от времени, начального состояния, жизнеспособностей и коэффициента рекомбинации. Когда такого явного выражения получить не удается, желательно определить качественную картину динамики: типы поведения, равновесия, циклы, их устойчивость и т.д. При этом важную роль могут играть методы приближенного анализа, в частности асимптотического анализа при различных соотношениях между параметрами.

При отсутствии отбора генетическое состояние популяции с течением времени приходит в результате процессов рекомбинации к равновесию по сцеплению, когда сочетания аллелей в генотипах особей независимы (и все коэффициенты неравновесности ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ равны нулю). Процесс перехода при произвольном числе аутосомных локусов для диплоидной популяции со случайным скрещиванием детально исследован Ю.И. Любичем [2, 3], получившим явное решение с использованием техники генетических алгебр. Качественно картина динамики перехода охарактеризована более простыми методами в [4]. Отбор способен препятствовать достижению такой независимости, и возникает проблема оценивания квазиравновесных значений коэффициентов ${{D}_{{{{i}_{k}}{{i}_{m}}}}}.$

Случай слабого давления отбора по жизнеспособности, зависящей от двух диаллельных локусов, исследовал М. Кимура [5], использовавший показатель неравновесности по сцеплению z ≡ ≡ p₁₁p₂₂/(p₁₂p₂₁). Предложенный им подход трудно перенести на другие сходные ситуации слабого давления систематических факторов микроэволюции, в частности на случай отбора по локусам с множественными аллелями. Здесь кажется привлекательным рассматривать слабый отбор как возмущение нейтральной модели без отбора и воспользоваться теорией возмущений в соответствии с логикой работы [1].

Изложение материала в настоящем сообщении придерживается следующей схемы. Сначала продемонстрировано, что слабый по сравнению с рекомбинациями отбор можно рассматривать как возмущение нейтральной модели. Далее дельта-методом находятся зависящие от отношения μ/r квазиравновесные значения коэффициентов ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ неравновесностей по сцеплению. Затем показано, что уравнения модели в терминах частот аллелей ${{x}_{{{{i}_{k}}}}}$ и ${{y}_{{{{i}_{m}}}}}$ и неравновесностей по сцеплению ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ имеют вид сингулярно возмущенных, где ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ являются быстрыми, а частоты аллелей ${{x}_{{{{i}_{k}}}}}$ и ${{y}_{{{{i}_{m}}}}}$ медленными переменными. Далее обосновывается вывод уравнения относительно квазиравновесного значения ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ и соответствующего коэффициента эпистаза с точки зрения разложения в ряд по степеням малого параметра решения сингулярно возмущенных систем уравнений. Затем обсуждаются проблемы измерения эпистаза и разложения коэффициента эпистаза на элементарные составляющие, а также анализируются двулокусные коэффициенты эпистаза как характеристики многолокусной модели. Кратко рассматривается обобщение полученных для гаплоидной популяции результатов на диплоидный случай. В заключение дано обсуждение результатов. В тексте векторы и матрицы набраны полужирным шрифтом. Получаемые выводы сформулированы как результаты и ремарки, конец доказательств отмечен символом ◀.

ЛОКУСЫ С МНОЖЕСТВЕННЫМИ АЛЛЕЛЯМИ

При изучении двух первых локусов (k = 1, m = 2) уравнения динамики частот гаплоидных генотипов ${{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ с учетом слабого отбора по жизнеспособности можно записать как

(1)

Напомним, что здесь r – коэффициент рекомбинации, ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {\mathbf{p}} \right)$ – жизнеспособность гаплоидной особи с генотипом i₁i₂ при генетическом состоянии популяции p.

Как и ранее [1], при диаллельности эти уравнения можно переписать в терминах неравновесностей по сцеплению и частот аллелей в векторном виде

(2)

$\begin{gathered} \frac{d}{{dt}}\left[ \begin{gathered} D \\ x \\ y \\ \end{gathered} \right] = \left[ \begin{gathered} - rD + \mu F \\ \mu O(1) \\ \mu O(1) \\ \end{gathered} \right] = - r\left[ \begin{gathered} D \\ 0 \\ 0 \\ \end{gathered} \right] + \mu \left[ \begin{gathered} F \\ O(1) \\ O(1) \\ \end{gathered} \right], \\ 0 < \mu \ll 1, \\ \end{gathered} $

где D, x, y обозначают векторы коэффициентов неравновесностей и частот аллелей первого и второго локуса соответственно, вектор-функция F описывает давление систематических факторов (в частности, отбора). Первое слагаемое в правой части соответствует нейтральной модели, а второе – ее возмущению давлением систематических факторов. При µ = 0 получаем невозмущенную модель, где в равновесии, очевидно, D = 0.

Результат 1. Пусть рассматривается модель (2) динамики генетической структуры гаплоидной популяции в отношении двух локусов с множественными аллелями при слабом давлении систематических факторов микроэволюции µF.

Тогда приближенным квазиравновесным значением коэффициента ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ будет

(3)

Доказательство следует схеме диаллельного случая в [1]. Будем анализировать модель в терминах неравновесностей и частот аллелей. Уточненная оценка квазиравновесного значения ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ отличается от нулевого приближения ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} = 0$ приращением $\Delta {{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}},$ и задача редуцируется к поиску $\Delta {{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}.$

А. Приращение $\Delta {{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ вызвано отклонением Δμ малого параметра μ (новым значением которого станет μ = Δμ) и векторами малых приращений Δx и Δy. Запишем ${{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ как $--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + \mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}({\mathbf{D}},{\mathbf{x}},{\mathbf{y}}),$ откуда в невозмущенном равновесии ${{\left. {\left( { - r{{D}_{{{{i}_{1}}{{i}_{2}}}}} + {{{\left. \mu \right|}}_{{{\mu = 0}}}}{{F}_{{{{i}_{1}}{{i}_{2}}}}}(D,x,y)} \right)} \right|}_{{D = 0}}} = 0.$ Аналогично в уточненном квазиравновесии возмущенной модели

$\begin{gathered} {{\left. { - r{{D}_{{{{i}_{1}}{{i}_{2}}}}}} \right|}_{{D = 0 + \Delta D}}} + {{\left. \mu \right|}_{{{\mu = 0 + }\Delta {\mu }}}}{{F}_{{{{i}_{1}}{{i}_{2}}}}}(D,x + \\ + \,\,{{\left. {\Delta x,y + \Delta y)} \right|}_{{D = 0 + \Delta D}}} = 0. \\ \end{gathered} $

При указанных приращениях аргументов функция $--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\quad + {\text{ }}\mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ не изменилась, т.е. приближенно ее приращение Δ можно записать как

$\begin{gathered} \Delta = \left( {\frac{\partial }{{\partial {\mathbf{D}}}}\left( {--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + \mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \right),\Delta {\mathbf{D}}} \right) + \\ + \,\,\left( {\frac{\partial }{{\partial x}}\left( {--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + \mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \right),\Delta x} \right) + \\ + \,\,\left( {\frac{\partial }{{\partial y}}\left( {--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + \mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \right),\Delta y} \right) + \\ + \,\,\frac{\partial }{{\partial \mu }}\left( {--r{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + \mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \right)\Delta \mu = 0,{\text{ }} \\ \end{gathered} $

где операция (,) означает скалярное умножение, производные ${{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ вычисляются при D = 0, при текущих значениях x, y и при μ = 0. Это уравнение отличается от полученного в диаллельном случае тем, что обычное умножение производных на приращения заменено на скалярное, производные по вектору понимаем как вектор-градиент.

Б. В результате приближенное значение $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ удовлетворяет уравнению

(4)

$\begin{gathered} {{\left. {--r\Delta D_{{{{i}_{1}}{{i}_{2}}}}^{{}} + \mu } \right|}_{{{\mu = 0}}}}\left( {\left( {\frac{\partial }{{\partial D}}{{F}_{{{{i}_{1}}{{i}_{2}}}}},\Delta {\mathbf{D}}} \right) + \left( {\frac{\partial }{{\partial x}}{{F}_{{{{i}_{1}}{{i}_{2}}}}},\Delta x} \right) + } \right. \\ \left. { + \,\,\left( {\frac{\partial }{{\partial y}}{{F}_{{{{i}_{1}}{{i}_{2}}}}},\Delta y} \right)} \right) + {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {{\mathbf{0}},{\mathbf{x}},{\mathbf{y}}} \right)\Delta \mu = --rD_{{{{i}_{1}}{{i}_{2}}}}^{ * } + \\ + \,\,{{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {{\mathbf{0}},{\mathbf{x}},{\mathbf{y}}} \right)\Delta \mu = 0. \\ \end{gathered} $

Отсюда видно, что значения отличных от ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ неравновесностей (с другими индексами) и их приращения, а также Δx, Δy не важны для вычисления $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ ($D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ обозначает уточненное значение квазиравновесия ${{D}_{{{{i}_{1}}{{i}_{2}}}}}$), поскольку от Δx, Δy зависит лишь коэффициент при нулевом μ. Кроме того, $\Delta {{D}_{{{{i}_{1}}{{i}_{2}}}}} = D_{{{{i}_{1}}{{i}_{2}}}}^{ * },$ так как приращение $\Delta {{D}_{{{{i}_{1}}{{i}_{2}}}}}$ отсчитывается от нуля до $D_{{{{i}_{1}}{{i}_{2}}}}^{ * },$ и аналогично Δμ = μ. В итоге искомым значением $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ будет $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ = = $\frac{\mu }{r}\quad{{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}({\mathbf{0}},{\mathbf{x}},{\mathbf{y}}).$ Тем самым и часть Б доказана. ◀

Следующая задача состоит в вычислении $D_{{{{i}_{1}}{{i}_{2}}}}^{ * },$ когда слабое давление систематических факторов микроэволюции соответствует слабому давлению отбора с соответствующим значением ${{F}_{{{{i}_{1}}{{i}_{2}}}}}$(D, x, y) при D = 0.

Результат 2. Пусть рассматривается модель гаплоидной популяции (1) со слабым отбором по жизнеспособности, зависящей от двух локусов с множественными аллелями.

Тогда приближенным значением квазиравновесия ${{D}_{{{{i}_{1}}{{i}_{2}}}}}$ для модели (1) будет

(5)

$\begin{gathered} D_{{{{i}_{1}}{{i}_{2}}}}^{ * } = {{\varepsilon }_{{{{i}_{1}}{{i}_{2}}}}}(p)\frac{\mu }{r}{{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{2}}}}} = \left( {\sum\limits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{1}}{{i}_{2}}{{j}_{1}}{{j}_{2}}}}}} {{x}_{{{{j}_{1}}}}}{{y}_{{{{j}_{2}}}}}} \right)\frac{\mu }{r}{{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{2}}}}}; \\ {{\varepsilon }_{{{{i}_{1}}{{i}_{2}}}}}(p) \equiv \left( {{{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}} - \text{v}_{{{{i}_{1}}\centerdot }}^{ * } - \text{v}_{{\centerdot {{i}_{2}}}}^{ * } + \text{v}{\text{*}}} \right) = \sum\limits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{1}}{{i}_{2}}{{j}_{1}}{{j}_{2}}}}}} {{x}_{{{{j}_{1}}}}}{{y}_{{{{j}_{2}}}}}, \\ {{\varepsilon }_{{{{i}_{1}}{{i}_{2}}{{j}_{1}}{{j}_{2}}}}} \equiv {{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}} - {{\text{v}}_{{{{i}_{1}}{{j}_{2}}}}} - {{\text{v}}_{{{{j}_{1}}{{i}_{2}}}}} + {{\text{v}}_{{{{j}_{1}}{{j}_{2}}}}}. \\ \end{gathered} $

Доказательство. Воспользуемся уравнением (1) динамики ${{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ (для краткости записи зависимость жизнеспособностей от генетической структуры p популяции опустим). Из определения частот аллелей следует, что

$\begin{gathered} {{d{{x}_{{{{i}_{1}}}}}} \mathord{\left/ {\vphantom {{d{{x}_{{{{i}_{1}}}}}} {dt}}} \right. \kern-0em} {dt}} \equiv \sum\limits_{{{i}_{2}}} {{{d{{p}_{{{{i}_{1}}{{i}_{2}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{1}}{{i}_{2}}}}}} {dt}}} \right. \kern-0em} {dt}}} = \\ = \sum\limits_{{{i}_{2}}} {\left( {\mu {{p}_{{{{i}_{1}}{{i}_{2}}}}}({{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}}(p) - \text{v}(p)) - r{{D}_{{{{i}_{1}}{{i}_{2}}}}}} \right)} = \\ = \sum\limits_{{{i}_{2}}} {\mu ({{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{2}}}}} + {{D}_{{{{i}_{1}}{{i}_{2}}}}})({{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}} - \text{v})} = \\ = \mu {{x}_{{{{i}_{1}}}}}\left( {\sum\limits_{{{i}_{2}}} {{{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}}{{y}_{{{{i}_{2}}}}} - \text{v}} } \right) + \mu G \equiv \mu {{x}_{{{{i}_{1}}}}}\left( {\text{v}_{{{{i}_{1}}\centerdot }}^{ * } - \text{v}} \right) + \mu G, \\ \end{gathered} $

где мы учли, что из определения неравновесности следует равенство $\sum\nolimits_{{{i}_{2}}} {r{{D}_{{{{i}_{1}}{{i}_{2}}}}}} = 0,$ и остаются только члены, содержащие произведения неравновесностей и жизнеспособностей. Их суммарное значение обозначено как G. Точный вид G для дальнейшего не имеет значения, важно лишь, что G обращается в нуль при равновесии по сцеплению, т.е. при D = 0 (будем сохранять обозначение G за разными функциями с данным свойством по аналогии с определением функции O). Жирной точкой обозначается индекс у ${{\text{v}}_{{{{i}_{1}}{{i}_{2}}}}},$ по которому произведено суммирование с весами, равными частотам аллелей соответствующего локуса. Значение $\text{v}_{{{{i}_{1}}\centerdot }}^{ * }$ дает среднюю (маргинальную) жизнеспособность аллеля первого локуса при равновесии по сцеплению. Аналогично находим, что

${{d{{y}_{{{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{y}_{{{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}} = \mu {{y}_{{{{i}_{{\text{2}}}}}}}(\text{v}--\text{v}) + \mu G.$

Как и в диаллельном случае, $\mu {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$(0, x, y) = = ${{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ при D = 0, а ${{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ = ${{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ – ‒ ${{d({{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}})} \mathord{\left/ {\vphantom {{d({{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}})} {dt}}} \right. \kern-0em} {dt}}$ согласно определению ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}.$ Вспомним, что при D = 0 (т.е. при G = 0 и v = v* ) ${{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ = = ${{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}$ (откуда ${{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ = $\mu {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}({{\text{v}}_{{{{i}_{1}}{{i}_{{\text{2}}}}}}}--\text{v}{\text{*}})),$ и найдем ${{d({{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}})} \mathord{\left/ {\vphantom {{d({{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}})} {dt}}} \right. \kern-0em} {dt}}{\text{:}}$

$\begin{gathered} {{d\left( {{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}} \right)} \mathord{\left/ {\vphantom {{d\left( {{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}} \right)} {dt}}} \right. \kern-0em} {dt}} = \mu {{x}_{{{{i}_{{\text{1}}}}}}}(\text{v}_{{{{i}_{{\text{l}}}}\centerdot }}^{ * }--\text{v}{\text{*}}){{y}_{{{{i}_{2}}}}} + \\ + \,\,\mu {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}(\text{v}_{{\centerdot {{i}_{{\text{2}}}}}}^{ * }--\text{v}{\text{*}}) = \mu {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}(\text{v}_{{{{i}_{{\text{l}}}}\centerdot }}^{ * } + \text{v}_{{\centerdot {{i}_{{\text{2}}}}}}^{ * }--{\text{2}}\text{v}{\text{*}}). \\ \end{gathered} $

Подставим в ${{\left. {{{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}} \right|}_{{D = 0}}}$ эти выражения. В результате после сокращения μ получим

$\begin{gathered} {{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {{\mathbf{0}},{\mathbf{x}},{\mathbf{y}}} \right) = {{\left. {({{{{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}--{\text{ }}d\left( {{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}} \right)} \mathord{\left/ {\vphantom {{{{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}--{\text{ }}d\left( {{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}} \right)} {dt}}} \right. \kern-0em} {dt}})} \right|}_{{{\mathbf{D}} = {\mathbf{0}}}}} = \\ = {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}\left( {{{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--\text{v}{\text{*}}} \right)--{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}(\text{v}_{{{{i}_{1}}\centerdot }}^{ * } + \text{v}_{{\centerdot {{i}_{2}}}}^{ * }--{\text{2}}\text{v}{\text{*}}) = \\ = {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}({{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--\text{v}_{{{{i}_{1}}\centerdot }}^{ * }--\text{v}_{{\centerdot {{i}_{2}}}}^{ * } + \text{v}{\text{*}}) = \\ = {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}\sum\limits_{{{j}_{1}},{{j}_{2}}} {\left( {{{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--{{\text{v}}_{{{{i}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}--{{\text{v}}_{{{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + {{\text{v}}_{{{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}} \right){{x}_{{{{j}_{{{\text{1}}\quad}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}}} \equiv \\ \equiv {{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{2}}}}}\sum\limits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}{{x}_{{{{j}_{{{\text{1}}\quad}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}} \equiv {{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}} . \\ \end{gathered} $

Здесь коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ ≡ ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--{{\text{v}}_{{{{i}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}--{{\text{v}}_{{{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + {{\text{v}}_{{{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ будем называть коэффициентом неаддитивности эпистаза для жизнеспособностей гаплоидных генотипов, образованных аллелями элементарного “генофонда”, состоящего из рассматриваемого генотипа i₁i₂ и случайно выбранного из популяции генотипа j₁j₂. При этом ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ интерпретируется как средний (маргинальный) эпистатический эффект генотипа i₁i₂. Итак, искомое значение ${{F}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$(0, x, y) будет равно ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}},$ а $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ имеет вид (5): $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ = ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {\mathbf{p}} \right)\frac{\mu }{r}{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}.$ ◀

Отметим, что ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ с точностью до множителя ${{x}_{{{{j}_{{\text{1}}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}}$ редуцируется к коэффициенту неаддитивности эпистаза в случае двух диаллельных локусов, рассмотренном в [1]. В форме (5) $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ формально совпадает с квазиравновесностью при диаллельных локусах, а коэффициенты эпистаза в диаллельном случае и при множественных аллелях одинаково интерпретируются в терминах средних эффектов аллелей:

$\begin{gathered} {{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {\mathbf{p}} \right) \equiv {{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--\text{v}_{{{{i}_{1}}\centerdot }}^{ * }--\text{v}_{{\centerdot {{i}_{2}}}}^{ * } + \text{v}{\text{*}} = \\ = \left( {{{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--\text{v}{\text{*}}} \right)--(\text{v}_{{{{i}_{1}}\centerdot }}^{ * }--\text{v}{\text{* }})--(\text{v}_{{\centerdot {{i}_{2}}}}^{ * }--\text{v}{\text{*}}) = \\ = {{\delta }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--\delta _{{{{i}_{1}}\centerdot }}^{ * }--\delta _{{\centerdot {{i}_{2}}}}^{ * }. \\ \end{gathered} $

Здесь $\delta _{{{{i}_{1}}\centerdot }}^{ * }$ имеет смысл (среднего) эффекта аллеля i₁ первого локуса, $\delta _{{\centerdot {{i}_{2}}}}^{ * }$ – эффект аллеля i₂ второго локуса, ${{\delta }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ – эффект генотипа i₁i₂, а ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}({\mathbf{p}})$ – эффект взаимодействия аллелей i₁, i₂, или эпистатическое отклонение (см., например, [6]). Такая интерпретация позволяет наглядно представить коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ как отклонение жизнеспособности ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ особи с генотипом i₁i₂ от средней жизнеспособности популяции v за вычетом вклада в отклонение аддитивного генотипа $\delta _{{{{i}_{1}}\centerdot }}^{ * } + \delta _{{\centerdot {{i}_{2}}}}^{ * }.$

Как и в диаллельном случае, при аддитивной детерминации жизнеспособности коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ равен нулю, а при мультипликативной

где ${{u}_{{{{i}_{{\text{1}}}}}}}$ и ${{w}_{{{{i}_{{\text{2}}}}}}}$ – мультипликативные компоненты жизнеспособности, соответствующие первому и второму локусам.

СЛАБЫЙ ОТБОР КАК СИНГУЛЯРНОЕ ВОЗМУЩЕНИЕ

Согласно изучению модели без отбора (см., например, [4]) частоты аллелей в ряду поколений остаются постоянными при динамике генетического состояния популяции. В ней уравнения, описывающие поведение во времени неравновесностей ${{D}_{{{{i}_{k}}{{i}_{m}}}}},$ отделяются, их можно изучать независимо. Каждая из неравновесностей сходится к нулю с относительной скоростью r. При слабом отборе частоты аллелей подобно диаллельному случаю будут медленными переменными (${{d{{x}_{{{{i}_{{\text{1}}}}}}}} \mathord{\left/ {\vphantom {{d{{x}_{{{{i}_{{\text{1}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ и ${{d{{y}_{{{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{y}_{{{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ порядка O(µ) согласно доказательству предыдущего результата), а неравновесности ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$ – быстрыми (${{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}}$ = O(r) согласно (2)), т.е. уравнения модели являются сингулярно возмущенными (см., например, [7]). В результате качественно динамика в случае множественных аллелей не отличается от наблюдаемой при диаллельных локусах. Согласно теории сингулярных возмущений на первом этапе все неравновесности по сцеплению быстро затухают с одной и той же относительной скоростью r (D = 0 является асимптотически устойчивым и устойчивым по первому приближению равновесием невозмущенной системы). После этого эволюция медленных частот аллелей приближенно идет при условии данного равновесия быстрых переменных – при многолокусных соотношениях Харди–Вайнберга. В результате, например, при постоянных жизнеспособностях эволюция протекает в направлении, соответствующем увеличению средней жизнеспособности популяции [8].

Разумеется, это лишь приближенное описание динамики. В точном решении уравнений динамики соотношения Харди–Вайнберга нарушаются в слабой степени и желательно оценить степень нарушения (величину отклонений от нуля неравновесностей ${{D}_{{{{i}_{k}}{{i}_{m}}}}}$). Такая оценка найдена выше путем, аналогичным предпринятому при изучении диаллельных локусов [1]. Обоснованием корректности полученных оценок квазиравновесия служит тот факт, что уравнения относительно $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ совпадают с соответствующей частью системы первого приближения асимптотического ряда для решения сингулярно возмущенных уравнений (см., например, [7]).

Ремарка 3. Построение модели динамики генетического состояния популяции под действием отбора и рекомбинаций мы начали с уравнений в терминах частот гамет (1). В ней сингулярный характер возмущений из-за слабого отбора не очевиден, и нужна некоторая изобретательность для отыскания замены переменных, приводящей уравнения модели к стандартному виду сингулярно возмущенной системы. Эта задача облегчается при наличии констант движения у невозмущенной системы. В [9] и, например, в [10] указано, что в таком случае при замене, в которой константы движения будут новыми переменными, последние являются медленными переменными.

В частности, у нас частоты аллелей являются константами движения невозмущенной модели динамики генетического состояния популяции под действием рекомбинаций при случайном скрещивании (см., например, [4]). Они же оказались медленными переменными при возмущении селективно нейтральной модели слабым отбором. Аналогична ситуация в многолокусном случае [8].

ОБ ОПРЕДЕЛЕНИИ ЭПИСТАЗА

Коснемся проблемы эпистаза подробнее. Общий случай отсутствия эпистаза в широком смысле при детерминации рассматриваемого признака многими локусами можно определить как такую ситуацию, когда значение признака находится каким-то образом по однолокусным характеристикам генотипов. Например, для такого признака как жизнеспособность эпистаза не будет в случае аддитивного (мультипликативного) отбора, когда для каждого многолокусного генотипа она определяется как сумма (произведение) однолокусных компонентов – характеристик жизнеспособности на уровне отдельных локусов. Аддитивная детерминация особо важна и выделяется среди прочих случаев эпистаза тем, что при наличии отклонений от нее именно аддитивная составляющая эффектов генов (аддитивный генотип) определяет среднее значение рассматриваемого признака у потомков. В связи с этим мы из различных определений эпистаза [11] предпочитаем вслед за Фишером [12] определять эпистаз как нарушения аддитивности вкладов генов в величину признака.

При наличии эпистаза возникает проблема его количественной характеризации. Поскольку в качестве точки отсчета мы выбрали простейший случай аддитивной по локусам детерминации признака, попытаемся измерить отклонение от аддитивности. При этом отклонения от аддитивности вкладов отдельных генов в признак различаются между генотипами, и появляется задача построения показателя, характеризующего такие отклонения в целом для всего рассматриваемого генофонда. Первое, что приходит в голову, это как-то усреднить отклонения по генотипам. Видимо, при этом следует принимать во внимание их распространенность (частоту) в популяции и определять подобные характеристики как соответствующие средние. Заметим, что общее усреднение дает неинформативное нулевое значение для отклонений, как показано ниже.

ЭЛЕМЕНТАРНЫЙ ГЕНОФОНД И КОЭФФИЦИЕНТ НЕАДДИТИВНОСТИ ЭПИСТАЗА

Очевидно, об эпистазе невозможно говорить по данным о величине признака только для одного генотипа. Показатель отклонения от аддитивности эпистаза для признака должен базироваться на генофонде, детерминирующем изменчивость величины признака v. В простейшей двулокусной диаллельной гаплоидной ситуации элементарный генофонд содержит по два аллеля в каждом из двух локусов с номерами i₁, i₂, j₁, j₂, нижний индекс дает номер локуса, а сама индексированная переменная – номер аллеля данного локуса. В этой ситуации имеются четыре гаплоидных генотипа, которые можно формально выписать как результат раскрытия скобок выражения

$\left( {{{i}_{1}} + {{j}_{1}}} \right)\left( {{{i}_{2}} + {{j}_{2}}} \right) = {{i}_{1}}{{i}_{2}} + {{i}_{1}}{{j}_{2}} + {{j}_{1}}{{i}_{2}} + {{j}_{1}}{{j}_{2}},$

где сложение символизирует включение в спектр возможных аллелей (и спектр генотипов, порождаемых данным набором аллелей для соответствующего генофонда).

Чтобы судить о нарушении аддитивности, надо сравнить значения признака ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ (для особи с генотипом i₁i₂) у разных генотипов. Поскольку соответствие i₁i₂ → ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ между генотипами и средними (генотипическими) значениями признака однозначно, спектру генотипов отвечает спектр генотипических значений признаков ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}},$ ${{\text{v}}_{{{{i}_{{\text{1}}}}{{j}_{{\text{2}}}}}}},$ ${{\text{v}}_{{{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}},$ ${{\text{v}}_{{{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}.$ Займемся построением показателя неаддитивности двулокусной детерминации признака v в гаплоидной популяции. Напомним, что в случае мультипликативной детерминации ε = (u₁ – u₂)(w₁ – – w₂), где ${{u}_{{{{i}_{{\text{1}}}}}}}$ и ${{w}_{{{{i}_{{\text{2}}}}}}}$ – мультипликативные компоненты жизнеспособности аллелей (с номерами i₁ и i₂, принимающими значения 1 и 2 как для первого, так и для второго локуса соответственно).

Рассмотрим произведение (i₁ – j₁)(i₂ – j₂). При формальном раскрытии скобок и замене получаемых произведений (символизирующих генотипы) соответствующими жизнеспособностями v_ij получим коэффициенты ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ неаддитивности эпистаза для элементарного генофонда (содержащего по два аллеля каждого из двух локусов с номерами i₁, i₂, j₁, j₂). Коэффициент

${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}\quad \equiv {{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--{{\text{v}}_{{{{i}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}--{{\text{v}}_{{{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\quad + \,{{\text{v}}_{{{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$

можно понимать как функцию гаплоидных генотипов i₁i₂ и j₁j₂. При аддитивной детерминации признака ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ обращается в нуль. Причина этого именно в аддитивности, а не в отсутствии эпистаза в широком смысле, так как при мультипликативной детерминации данный коэффициент отличен от нуля, хотя эпистаза нет.

Ремарка 4. Основными легко проверяемыми подстановкой в определение ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ свойствами коэффициента неаддитивности эпистаза при равновесии по сцеплению будут следующие.

1. При постоянных жизнеспособностях все коэффициенты ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ являются константами, характеризующими свойства генетической детерминации признака на организменном уровне (тонкие свойства эпистаза), тогда как коэффициент эпистаза ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ дает более грубый усредненный показатель.

2. Коэффициенты ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ не изменятся, если к всевозможным значениям признака v прибавить на одну и ту же константу или функцию состояния популяции.

3. При слабом отборе величина коэффициентов ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ как сумма разностей (относительных) жизнеспособностей имеет порядок O(μ), где μ характеризует давление отбора.

4. В случае аддитивной детерминации признака v все коэффициенты ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ равны нулю.

5. При мультипликативной детерминации признака v коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ равен $({{u}_{{{{i}_{{\text{1}}}}}}}--{{u}_{{{{j}_{{\text{1}}}}}}}) \times $ $ \times \,\,({{w}_{{{{i}_{{\text{2}}}}}}}--{{w}_{{{{j}_{{\text{2}}}}}}}),$ где ${{u}_{{{{j}_{{\text{1}}}}}}}$ и ${{w}_{{{{i}_{{\text{2}}}}}}}$ – соответствующие мультипликативные компоненты признака v, определяемого как ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} \equiv {{u}_{{{{i}_{{\text{1}}}}}}}{{w}_{{{{i}_{{\text{2}}}}}}}.$

6. Перестановка соответствующих одному и тому же локусу индексов у коэффициента неаддитивности не изменяет значения ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}.$

7. При совпадении у коэффициента ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ индексов, относящихся к одному и тому же локусу, значение коэффициента будет равно нулю. Это означает, что равенство значений индексов на первом и третьем и/или втором и четвертом местах определяет нулевое значение коэффициента.

8. В случае двух диаллельных локусов единственным ненулевым из коэффициентов ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ будет ε₁₁₂₂ – только у него нет совпадающих значений индексов, соответствущих одному и тому же локусу. Этот коэффициент равен показателю неаддитивности ε в диаллельном случае.

9. Сумма коэффициентов ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ по любому из пары индексов (относящихся к одному и тому же локусу) с весами, равными концентрациям соответствующих аллелей, равна нулю, так как получаемые в итоге маргинальные жизнеспособности сокращаются.

Отсюда следует, что взвешенная сумма коэффициентов ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ по любому из индексов i₁, i₂ равна нулю. Действительно, ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ получается взвешенным суммированием ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ по паре индексов разных локусов, а сумма еще по одному индексу означает, что произошло суммирование по двум индексам одного из локусов, сумма по которым даст нуль. Тем самым сумма по любому из индексов квазиравновесия $D_{{{{i}_{1}}{{i}_{2}}}}^{ * } = \left( {\sum\nolimits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{1}}{{i}_{2}}{{j}_{1}}{{j}_{2}}}}}{{x}_{{{{j}_{1}}}}}{{y}_{{{{j}_{2}}}}}} } \right)\frac{\mu }{r}{{x}_{{{{i}_{1}}}}}{{y}_{{{{i}_{2}}}}}$ равна нулю, как и в случае обычного коэффициента неравновесности ${{D}_{{{{i}_{{\text{1}}}}\quad{{i}_{{\text{2}}}}}}}.$

10. Коэффициент неаддитивности ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ также интерпретируется как оценка отклонения от аддитивности, получаемая при сравнении значений признака, порождаемых генотипами i₁i₂ и j₁i₂ двух особей (аллелями элементарного генофонда).

Согласно последнему свойству коэффициента ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ его можно интерпретировать как отвечающую генотипам двух особей характеристику, где генотип одной особи фиксирован, а вторая особь случайно выбрана из популяции. Такая постановка позволяет говорить о средней неаддитивности отдельного генотипа гаплоидной особи, скажем, i₁i₂ при усреднении по случайному выбору второй особи.

Пример. Продолжим измерение эпистаза в рамках концепций количественной генетики. Как уже говорилось, эффекты генотипов (и аллелей) находятся как средние отклонения величины признака у особей, несущих рассматриваемый аллель (соответственно генотип), от популяционного среднего. Средняя величина признака у таких особей вычисляется при условии, что учитываются только особи данного генотипа (или генотипа, содержащего данный аллель). Обозначим для элементарного генофонда со спектром значений признака v_AB, v_Ab, v_aB, v_ab средние эффекты аллелей A и B (первого и второго локуса соответственно) как δA и δB. При их вычислении учтем, что здесь частота каждого из аллелей (и генотипов) равна 1/2 (и 1/4), эффекты δ рассматриваем как условные средние.

Например, δA является отклонением средней жизнеспособности генотипа при условии, что он содержит аллель A. Поэтому при вычислении δA используются условные вероятности P(g|A) ≡ ≡ P(gA)/P(A), где g – событие наличия у особи генотипа g, gA обозначает, что данный генотип g содержит аллель A, P(A) – вероятность события обладания аллелем A. В рассматриваемой ситуации P(gA) = 1/4 как вероятность одного из четырех равновозможных генотипов, P(A) = 1/2 как вероятность одного из двух аллелей первого локуса (аналогично P(B) = 1/2). Отсюда P(g|A) = $\frac{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$ = = $\frac{1}{2},$ и δA (ожидаемое отклонение жизнеспособности особей-носителей A от популяционного среднего v) определяется как

(6)

$\begin{gathered} \delta A \equiv \sum\limits_{gA} {{{\text{v}}_{{gA}}}\frac{{{\text{P}}(gA)}}{{{\text{P}}(A)}} - \text{v}} {\text{ = }}\left( {{{\text{v}}_{{AB}}}\quad\frac{1}{2} + {{\text{v}}_{{Ab}}}\frac{1}{2}} \right)--\text{v} = \\ = \left( {{{\text{v}}_{{AB}}} + {{\text{v}}_{{Ab}}}--{\text{2}}\text{v}} \right)\frac{1}{2},\,\,\,\,\delta B \equiv \left( {{{\text{v}}_{{AB}}} + {{\text{v}}_{{aB}}}--{\text{2}}\text{v}} \right)\frac{1}{2}. \\ \end{gathered} $

При аддитивной детерминации признака v или при нарушении ε_AB аддитивности значения δ_AB записываются соответственно как

${{\delta }_{{AB}}} \equiv \delta A + \delta B,\,\,\,\,{{\delta }_{{AB}}} \equiv \delta A + \delta B + {{\varepsilon }_{{AB}}},$

где ε_AB – коэффициент взаимодействия аллелей разных локусов (эпистаза). Таким образом, показатель неаддитивности можно определить как

(7)

${{\varepsilon }_{{AB}}} \equiv {{\delta }_{{AB}}} - (\delta A + \delta B).$

Коэффициент ε_AB имеет ясный смысл отклонения значения признака от средней величины v (v = $\frac{1}{4}$ (v_AB + v_Ab + v_aB + v_ab)), вызванного эпистатическим взаимодействием аллелей. Таким образом, это отклонение дополняет отклонение аддитивного генотипа δA + δB. Вычислим ε_AB:

$\begin{gathered} {{\varepsilon }_{{AB}}} = {{\delta }_{{AB}}} - (\delta A + \delta B) = {{\text{v}}_{{AB}}} - \text{v} - (\delta A + \delta B) = \\ = {{\text{v}}_{{AB}}}--\text{v}--\frac{1}{2}(\left( {{{\text{v}}_{{AB}}} + {{\text{v}}_{{Ab}}}--{\text{2}}\text{v}} \right)-- \\ - \,\,\frac{1}{2}\left( {{{\text{v}}_{{AB}}} + {{\text{v}}_{{aB}}}--{\text{2}}\text{v}} \right)) = \\ = \frac{1}{2}\left( {{\text{2}}{{\text{v}}_{{AB}}}--{\text{2}}\text{v}--{\text{2}}{{\text{v}}_{{AB}}}{\text{ }}--{{\text{v}}_{{Ab}}}--{{\text{v}}_{{aB}}} + {\text{4}}\text{v}} \right) = \\ = \frac{1}{2}\left( {--{{\text{v}}_{{Ab}}}--{{\text{v}}_{{aB}}} + {\text{2}}\frac{1}{4}\left( {{{\text{v}}_{{AB}}} + {{\text{v}}_{{Ab}}} + {{\text{v}}_{{aB}}} + {{\text{v}}_{{ab}}}} \right)} \right) = \\ = \frac{1}{4}\left( {{{\text{v}}_{{AB}}}\quad--{\text{ }}{{\text{v}}_{{Ab}}}\quad--{\text{ }}{{\text{v}}_{{aB}}}\quad + {\text{ }}{{\text{v}}_{{ab}}}} \right) = \frac{1}{4}\varepsilon . \\ \end{gathered} $

Значение ε_AB можно также записать как $\frac{1}{4}$ε_ABab. Множитель $\frac{1}{4}$ равен произведению частот аллелей разных локусов генотипа AB.

КОЭФФИЦИЕНТ НЕАДДИТИВНОСТИ ЭПИСТАЗА НА ПОПУЛЯЦИОННОМ УРОВНЕ

Если в случае элементарного генофонда или двух диаллельных локусов можно при постоянных жизнеспособностях говорить о коэффициенте эпистаза ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ как о константе, характеризующей детерминацию признака на уровне организма, то средний коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ для популяции с множественными аллелями будет не константой, а одновременной характеристикой как организмов, так и популяции. Он служит общим и грубым показателем генетической детерминации жизнеспособности, тогда как элементарные коэффициенты ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ дают ее более детализированную структуру. При усреднении элементарных коэффициентов неаддитивности приходится учитывать концентрации генотипов в популяции, и не имеет смысла обсуждать средний эффект, скажем, генотипа без указания к какой популяции он относится.

Например, при условии многолокусных соотношений Харди–Вайнберга в гаплоидной популяции (при D = 0) такой средней неаддитивностью эпистаза для жизнеспособности генотипа i₁i₂ будет знакомый нам показатель ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ ≡ ≡ $\sum\nolimits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{1}}{{i}_{2}}{{j}_{1}}{{j}_{2}}}}}{{x}_{{{{j}_{1}}}}}{{y}_{{{{j}_{2}}}}}} .$ Здесь учтена вероятность ${{x}_{{{{j}_{{\text{1}}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}}$ случайно выбранной для сравнения жизнеспособностей особи иметь генотип j₁ j₂. Значит, в найденное в (5) квазиравновесное значение $D_{{{{i}_{1}}{{i}_{2}}}}^{ * }$ входит коэффициент эпистаза ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}},$ являющийся характеристикой популяционного уровня и имеющий в рамках стандартных концепций количественной генетики одну и ту же интерпретацию среднего эффекта неаддитивности и в случае двух, и множественных аллелей у пары локусов.

В простейшем случае аддитивной детерминации жизнеспособности коэффициент ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ равен нулю. При ее мультипликативной детерминации он равен $({{u}_{{{{i}_{{\text{1}}}}}}}--{{u}_{{\text{2}}}})({{w}_{{{{i}_{{\text{2}}}}}}}--{{w}_{{\text{2}}}}){\text{:}}$

$\begin{gathered} {{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} = \sum\limits_{{{j}_{1}},{{j}_{2}}} {{{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}{{x}_{{{{j}_{{\text{1}}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}}} = \\ = \sum\limits_{{{j}_{1}},{{j}_{2}}} {\left( {{{u}_{{{{i}_{{\text{1}}}}}}}\quad--{\text{ }}{{u}_{{{{j}_{{\text{1}}}}}}}} \right)\left( {{{w}_{{{{i}_{{\text{2}}}}}}}--{{w}_{{{{j}_{{\text{2}}}}}}}} \right){{x}_{{{{j}_{{\text{1}}}}}}}{{y}_{{{{j}_{{\text{2}}}}}}}\quad} = \\ = \left( {{{u}_{{{{i}_{{\text{1}}}}}}}--{{u}_{{\text{1}}}}} \right)\left( {{{w}_{{{{i}_{{\text{2}}}}}}}--{{w}_{{\text{2}}}}} \right), \\ \end{gathered} $

где u₁ и w₂ – взвешенные средние значения мультипликативных компонентов жизнеспособности первого и второго локусов.

Напомним, что общее среднее значение коэффициента неаддитивности ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ в популяции равно нулю, поскольку среднее для каждого члена в определении ${{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ ≡ ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}--{{\text{v}}_{{{{i}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}--{{\text{v}}_{{{{j}_{{\text{1}}}}{{i}_{{\text{2}}}}}}} + {{\text{v}}_{{{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}$ равно v. Следовательно, данная характеристика эпистаза неинформативна. Чтобы избежать подобного, можно использовать средний квадрат коэффициента неаддитивности (в силу нулевой средней для коэффициента он совпадает с его дисперсией). На этом пути можно двигаться далее и разложить дисперсию на компоненты, соответствующие типам эффектов.

ДВУЛОКУСНЫЕ КВАЗИРАВНОВЕСИЯ И МНОГОЛОКУСНЫЕ МОДЕЛИ

В реальных исследованиях природных популяций характер генетической детерминации жизнеспособности особей неизвестен в полном объеме, и нельзя гарантировать, что изучены все влияющие на нее локусы. Какой смысл в этом случае можно придать коэффициентам эпистаза, полученным при изучении лишь двулокусных генотипов и выражающимся в терминах жизнеспособностей и эффектов аллелей данных локусов? Очевидно, при оценивании жизнеспособности генотипов с помощью случайной выборки получаемые результаты характеризуют маргинальные жизнеспособности, усредненные по (пусть и неизвестным) многолокусным генотипам, содержащим в качестве своей части генотипы двух рассматриваемых локусов. Такое усреднение происходит неявно и автоматически при обработке случайной выборки данных по жизнеспособности.

Подобное неявное (без расшифровки генотипов особей в полном объеме) усреднение не означает чего-либо катастрофического. Фактически использованные при вычислении коэффициентов эпистаза эффекты аллелей являются средними для особей, генотипы которых содержат соответствующий аллель, и никак не используют информацию о прочем составе генотипа [13]. Значит, оценивание средних эффектов аллелей не требует дополнительных сведений о генотипе особей. Поэтому полученные оценки эпистаза для двух рассматриваемых локусов не опираются на дополнительные данные по другим локусам, а основываются на маргинальных жизнеспособностях, для вычисления которых нужно использовать сведения только по генотипам двух рассматриваемых локусов. При этом используемая ранее фраза о зависящей от двух локусов жизнеспособности не запрещает зависимости и от других локусов, лишь бы она не противоречила условию слабого отбора. Таким образом, двулокусные коэффициенты эпистаза следует понимать как маргинальные двулокусные характеристики многолокусных жизнеспособностей.

Это, например, подтверждается совпадением формул для коэффициентов квазиравновесия для заданного двулокусного генотипа при диаллельных локусах и при множественных (5) аллелях, поскольку они одинаково выражаются в терминах эффектов жизнеспособностей (генотипа и аллелей). Вычисление данных характеристик требует знания только соответствующей части генотипа особи и классификации особей лишь по аллелям этой части. В результате найденные коэффициенты эпистатического взаимодействия на уровне двух локусов можно использовать при оценивании эпистаза для трех локусов и т.д., последовательно повышая уровень по числу локусов. Как показали В. Юэнс и Г. Томсон [13] для модели с дискретным временем, все подсистемы полного множества локусов удовлетворяют соответствующим стандартным уравнениям динамики (и условиям равновесия), в которых используются маргинальные жизнеспособности. На этом пути рассмотренное оценивание эпистаза можно попытаться обобщить на случай нескольких локусов.

ДИПЛОИДНЫЕ ПОПУЛЯЦИИ

В диплоидной популяции со случайным скрещиванием уравнения динамики генетической структуры (на уровне гамет), рассматриваемой в отношении двух диаллельных аутосомных локусов, формально совпадают с уравнениями (1) для гаплоидного случая, но теперь жизнеспособность i-го гаплоидного генотипа (гаметы) будет условной средней:

(8)

$\begin{gathered} {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} \mathord{\left/ {\vphantom {{d{{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}} {dt}}} \right. \kern-0em} {dt}} = {{p}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}({{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\left( {\mathbf{p}} \right)--\text{v}\left( {\mathbf{p}} \right))--r{{\left( {--{\text{1}}} \right)}^{{{{i}_{{\text{1}}}} + {{i}_{{\text{2}}}}}}}D = \\ = {{p}_{{\mathbf{i}}}}({{\text{v}}_{{\mathbf{i}}}}\left( {\mathbf{p}} \right)--\text{v}\left( {\mathbf{p}} \right))--r{{\left( {--{\text{1}}} \right)}^{{{{i}_{{\text{1}}}} + {{i}_{{\text{2}}}}}}}D; \\ {{\text{v}}_{{\mathbf{i}}}}({\mathbf{p}}) = \sum\limits_{\mathbf{j}} {{{\text{v}}_{{{\mathbf{ij}}}}}({\mathbf{p}}){{p}_{{\mathbf{j}}}}} , \\ \text{v}({\mathbf{p}}) \equiv \sum\limits_{\mathbf{i}} {{{\text{v}}_{{\mathbf{i}}}}({\mathbf{p}}){{p}_{{{\mathbf{i}}\quad}}}} = \sum\limits_{{\mathbf{i}},{\mathbf{j}}} {{{\text{v}}_{{{\mathbf{ij}}}}}({\mathbf{p}}){{p}_{{{\mathbf{i}}\quad}}}{{p}_{{\mathbf{j}}}}} . \\ \end{gathered} $

Здесь p – вектор частот гаплоидных гамет, произведения которых (p_i на p_j) дают концентрации p_ij диплоидных генотипов ij при случайном скрещивании, (маргинальная) жизнеспособность i-й гаметы v_i(p) ≡ ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}({\mathbf{p}})$ определяется как средняя жизнеспособность диплоидных особей при условии, что их генотип порожден случайным слиянием в зиготе i-й гаметы и какой-либо еще. Напомним вычисление жизнеспособности v_i(p) i-й гаметы как условной средней при жизнеспособностях v_ij(p) ≡ ${{\text{v}}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}{{j}_{{\text{1}}}}{{j}_{{\text{2}}}}}}}({\mathbf{p}})$ генотипов ij:

$\begin{gathered} {{\text{v}}_{{\mathbf{i}}}}\left( {\mathbf{p}} \right) = \sum\limits_{\mathbf{j}} {{{\text{v}}_{{{\mathbf{ij}}}}}\left( {\mathbf{p}} \right){\text{P}}\left( {\left. {\mathbf{i}} \right|{\kern 1pt} {\mathbf{j}}} \right)} = \sum\limits_{\mathbf{j}} {{{\text{v}}_{{{\mathbf{ij}}}}}\left( {\mathbf{p}} \right)\frac{{{{p}_{{ij}}}}}{{{{p}_{i}}}}} = \\ = \sum\limits_{\mathbf{j}} {{{\text{v}}_{{{\mathbf{ij}}}}}\left( {\mathbf{p}} \right)\frac{{{{p}_{{ij}}}}}{{{{p}_{i}}}}} = \sum\limits_{\mathbf{j}} {{{\text{v}}_{{{\mathbf{ij}}}}}\left( {\mathbf{p}} \right){{p}_{{\mathbf{j}}}}} ; \\ {\mathbf{i}} = \left( {{{i}_{{\text{1}}}},{{i}_{{\text{2}}}}} \right),\,\,\,\,{\mathbf{j}} = \left( {{{j}_{{\text{1}}}},{{j}_{{\text{2}}}}} \right). \\ \end{gathered} $

Итак, уравнение динамики генетической структуры диплоидной популяции (8) согласуется с уравнением (1) для гаплоидного случая, однако теперь жизнеспособности гамет являются условными популяционными средними, т.е. даже при постоянных жизнеспособностях диплоидных особей они будут функциями генетического состояния p.

Тем не менее независимо от числа аллелей рассматриваемых локусов выводы для гаплоидного случая остаются верными, только в них жизнеспособности гамет следует понимать как указанные условные средние, а зависимости от v_i (например, в выражении для ε) – как зависимости от их определяемых генетическим состоянием p усредненных значений, поскольку все манипуляции над (1) для получения результатов допускали зависимость жизнеспособностей от p. Теперь при постоянных жизнеспособностях и диаллельных локусах в уравнениях динамики медленных частот аллелей в квазиградиентном виде (см., например, [1]) потенциалом будет не средняя жизнеспособность v, а $\frac{1}{2}\text{v}.$

Уравнения динамики при слабом отборе по-прежнему будут сингулярно возмущенными, качественная картина динамики сохраняется с теми же быстрыми и медленными переменными. Первое приближение для неравновесности по сцеплению, например, для двух диаллельных локусов записывается как

$D{\text{*}} = \bar {\varepsilon }\frac{\mu }{r}x({\text{1}}--x)y({\text{1}}--y),\,\,\,\,\quad\bar {\varepsilon } \equiv \overline {{{\text{v}}_{{11}}}} \quad--\,\,\overline {{{\text{v}}_{{21}}}} + \overline {{{\text{v}}_{{22}}}} ,$

где надчеркивание означает усреднение по отсутствующим в индексе символам второй гаметы диплоидного генотипа.

При этом медленная динамика частот аллелей (подчеркнем, что ее анализ лежит за рамками настоящей работы) теперь допускает при постоянных жизнеспособностях существование полиморфного равновесия – нового качественного свойства, отсутствующего в модели гаплоидной популяции.

ОБСУЖДЕНИЕ

В [8] показано, что качественно сходный характер динамики генетической структуры при слабом отборе присущ диплоидной популяции, рассматриваемой в отношении не двух, а произвольного числа аутосомных локусов с множественными аллелями. Причина сходства в том, что уравнения слабого отбора и здесь являются сингулярно возмущенными. При этом приближенно медленная эволюция частот аллелей происходит так, что средняя жизнеспособность v возрастает, если жизнеспособности генотипов постоянны и генетическая структура неравновесна. Более того, средняя жизнеспособность является потенциалом градиентного движения, что впервые показал для однолокусного случая Ю.М. Свирежев (см., например, [4, 14, 15]). И здесь средняя жизнеспособность определяется при условии квазиравновесного в нулевом приближении значения быстрых переменных, т.е. при нулевой неравновесности по сцеплению, соответствующей независимому комбинированию аллелей в гаметах.

Полученное уточненное значение квазиравновесия в модели с двумя диаллельными локусами означает малое отклонение от равновесия по сцеплению. На эволюционном этапе при текущих значениях частот аллелей x и y приближенным значением отклонения (коэффициента неравновесности) будет в нулевом приближении ${{D}_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}$ = 0 с точностью O(μ). Уточненным значением с точностью O(μ²) будет первое приближение $D_{{{{i}_{1}}{{i}_{2}}}}^{ * } = {{\varepsilon }_{{{{i}_{{\text{1}}}}{{i}_{{\text{2}}}}}}}\frac{\mu }{r}{{x}_{{{{i}_{{\text{1}}}}}}}{{y}_{{{{i}_{{\text{2}}}}}}}.{\text{ }}$

Настоящее исследование идейно мотивировано работой М. Кимуры [5], но отличается подходом и непрерывным временем модели. М. Кимура исследовал динамику генетического состояния популяции в отношении двух диаллельных локусов при слабом отборе в дискретном времени при неперекрывающихся поколениях. Проведенное им компьютерное моделирование, во многом подкрепленное аналитически, выявило качественную картину поведения, совпадающую с описанной для случая сингулярных возмущений. Из результатов изучения М. Кимурой [5, формула (14)] динамики показателя неравновесности по сцеплению z,

$z \equiv {{{{p}_{{11}}}{{p}_{{22}}}} \mathord{\left/ {\vphantom {{{{p}_{{11}}}{{p}_{{22}}}} {({{p}_{{12}}}{{p}_{{21}}})}}} \right. \kern-0em} {({{p}_{{12}}}{{p}_{{21}}})}} = 1 + {D \mathord{\left/ {\vphantom {D {({{p}_{{12}}}{{p}_{{21}}})}}} \right. \kern-0em} {({{p}_{{12}}}{{p}_{{21}}})}},$

можно вывести сходную с полученной нами ранее [1] количественную оценку квазиравновесия D*. Поскольку D и z выражаются одно через другое, между их динамикой должны были наблюдаться параллели. Неудивительно, что изученная в [5] динамика показателя неравновесности z оказалась соответствующей приведенной нами качественной картине сингулярного возмущения отбором модели динамики генетической структуры популяции в результате рекомбинаций и случайного скрещивания.

Отличие нашего подхода состоит в применении стандартных методов анализа, не требующих изобретения в конкретных случаях специальных приемов, а также в использовании в явном виде коэффициента степени давления отбора μ (показывающего будет отбор слабым или сильным). Коэффициент μ рассматривается в качестве малого параметра, r предполагается фиксированным и независящим от генотипа, откуда отношение μ к коэффициенту рекомбинации r также является малым параметром. Именно оно играет ведущую роль в возможности охарактеризовать динамику генетического состояния популяции как сингулярно возмущенную, а не отношение ε/r. Использование медленных и быстрых переменных позволяет без решения уравнений динамики представить качественные особенности поведения траекторий при слабом отборе.

Ремарка 5. Если μ и отношение μ/r малы, то мало и ε, но данное отношение может быть велико даже при нулевом значении ε. Например, при аддитивном по локусам отборе, когда эффекты отдельных локусов суммируются в общей жизнеспособности, коэффициент неаддитивности эпистаза ε равен нулю. Это выполняется как при слабой, так и при сильной (с большей величиной различий между жизнеспособностями) степени отбора μ, при которой μ/r уже невозможно рассматривать как малый параметр, а уравнения – как сингулярно возмущенные. То же самое остается верным и при слабом нарушении аддитивности жизнеспособности, когда скорость изменений частот аллелей может быть велика из-за давления отбора, на которое не наложено ограничений, а ε остается малым в силу почти аддитивной жизнеспособности. Таким образом ε может быть малым как при сильном, так и слабом отборе, но при условии слабого отбора ε может быть только малым. Действительно, при таком условии разности (относительных) жизнеспособностей генотипов малы, а отсюда следует малость ε как суммы двух таких разностей.

Разработанный М. Кимурой специфический прием анализа данного конкретного случая трудно обобщить для применений в других ситуациях и оценить точность получаемых результатов. Все это послужило дополнительным стимулом для применения в настоящей статье хорошо разработанной к настоящему времени теории малых возмущений с использованием стандартных уравнений для получения приближенного описания поведения модели генетической системы с заданной погрешностью. Кроме того, при этом достигается интерпретация результатов в терминах классической количественной генетики.

Обобщение анализа двулокусной модели на случай множественных аллелей показывает, что выражения для полученных показателей квазиравновесности в терминах эффектов генов идентичны. При записи коэффициентов квазиравновесности по сцеплению через средние эффекты аллелей и их взаимодействия на уровне популяции видно, что она не зависит от числа аллелей.

Список литературы

Пасеков В.П. Квазиравновесие по сцеплению при слабом двулокусном отборе по жизнеспособности. I. Гаплоидная популяция с диаллельными локусами // Генетика. 2019. Т. 55. № 4. С. 468–484.
Любич Ю.И. Основные понятия и теоремы эволюционной генетики свободных популяций // Успехи матем. наук. 1971. Т. 26. № 5. С. 51–116.
Любич Ю.И. Математические структуры в популяционной генетике. Киев: Наук. думка, 1983. 296 с.
Свирежев Ю.М., Пасеков В.П. Основы математической генетики. М.: Наука, 1982. 511 с.
Kimura M. Attainment of guasi linkage eguilibrium when gene freguencies are changing by natural selection // Genetics. 1965. V. 52. № 5. P. 875–890.
Фолконер Д.С. Введение в генетику количественных признаков. М.: Агропромиздат, 1985. 485 с.
Новожилов И.В. Методы разделения движений. Конспект лекций. М.: МЭИ, 1981. 48 с.
Пасеков В.П. Асимптотический анализ отбора в полилокусной полиаллельной популяции // Докл. АН СССР. Кибернетика и теория регулирования. 1984. Т. 277. № 6. С. 1338–1341.
Пасеков В.П. Математические модели эколого-генетических взаимодействий / Итоги науки и техники. Серия “Математическая биология и медицина”. Т. 2. М.: ВИНИТИ, 1988. С. 4–80.
Auger P.M. Hierarchically organized systems: The response to complexity // J. Sci. Industrial Res. 1992. V. 51. P. 725–735.
Cordell H.J. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans // Hum. Mol. Genet. 2002. V. 11. Issue 20. P. 2463–2468. doi 10.1093-hmg-11.20.2463
Fisher R.A. The correlation between relatives on the supposition of Mendelian inheritance // Trans. Roy. Soc. Edinburgh. 1918. V. 52. Part 2. P. 399–433.
Ewens W.J., Thomson G. Properties of equilibria in multi-locus genetic systems // Genetics. 1977. V. 87. № 4. P. 807–819.
Shahshahani S. A new mathematical framework for the study of linkage and selection // Memoirs Amer. Math. Soc. 1979. V. 7. № 211. 34 p.
Akin E. The Geometry of Population Genetics. Berlin e.a.: Springer, 1979. 205 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Генетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал