Геомагнетизм и аэрономия, 2019, T. 59, № 4, стр. 474-481
Статистические особенности временны́х рядов вариаций критических частот слоя F2
Н. П. Сергеенко *
Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
* E-mail: serg@izmiran.ru
Поступила в редакцию 30.11.2018
После доработки 14.12.2018
Принята к публикации 24.01.2019
Аннотация
На большом массиве экспериментальных данных изучены особенности временны́х рядов вариаций критических частот слоя F2 ионосферы. Проведена проверка стационарности выборок относительных вариаций критической частоты слоя F2 – δfoF2 с различным временны́м разрешением. На основании статистического анализа кривых распределения δfoF2, полученных по месячным выборкам данных семи станций за три года, показано, что закон распределения совокупности δfoF2 далек от нормального. Предложен способ интерпретации экспериментальных кривых функций плотности вероятности с помощью модели с эксцессом и асимметрией, построенной на базе пуассонова случайного процесса. Проведенный анализ позволил сделать вывод о применимости модели, построенной на базе пуассонового шума, для статистического описания и вероятностных оценок вариаций f0F2 как с часовыми, так и с пятиминутным разрешением, во время гелиосферных возмущений.
1 ВВЕДЕНИЕ
Как показали различные геофизические исследования, ионосферная плазма – статистически неоднородная среда, масштаб неоднородности ξ по сравнению с длиной волны l сигналов вертикального зондирования включает в себя набор от самых мелких (ξ $ \ll $ l) до самых крупных (ξ $ \gg $ l) [Альперт, 1972]. В различных ионосферных экспериментах выявляются неоднородности различных размеров в зависимости от того, какая частота рассеивается ими. Поэтому если речь идет об отражении декаметровых сигналов от ионосферы, то в зависимости от длины волны λ важно уметь правильно оценить размеры выборки принятого сигнала для изучения неоднородной структуры отражающей области методами теории флуктуации. При вертикальном зондировании ионосферы декаметровыми радиосигналами достаточно пятиминутных выборок сигнала для статистически полного анализа мелкомасштабной неоднородности (ξ ~ 100 м) [Ерухимов и др., 1980; Fejer and Kelley, 1980]. Для выявления крупномасштабной структуры необходимо брать более длинные выборки, поскольку период изменения поля сопоставляется с линейным размером отдельной неоднородности [Ерухимов и др., 1980; Иванов, 1991].
Одна из основных характеристик ионосферы – критическая частота слоя F2 – foF2, поэтому, изучая fоF2, мы можем получить представление о неоднородности ионосферы. Из всех параметров (полутолщина, высота) критическая частота больше всего подвержена изменчивости, а поскольку правильный прогноз необходим для служб, связанных с ионосферным распространением радиоволн, требуется детальное изучение статистических свойств критических частот.
2. ИСХОДНЫЕ ДАННЫЕ
Использованы данные вертикального зондирования ионосферы по мировой сети станций для разных уровней солнечной активности, спокойных и возмущенных гелиогеофизических условий.
Для исключения суточного и сезонного хода, а также резких отклонений, ведущих к нестационарности процесса, критические частоты слоя F2 пересчитаны в относительные отклонения критических частот от скользящего медианного значения
По рассчитанным δ foF2 для станций северного полушария, расположенных на различных широтах – от зоны полярных сияний до экваториальных, получены дифференциальные распределения δfoF2 за каждый месяц максимальной солнечной активности (1990 г.), минимальной – (1986 г.) и промежуточной – (1983 г.) для дневных (06–17 ч LТ) и ночных (18–05 ч) условий независимо. Генеральная совокупность статистических выборок данных для каждой станции составила 1.3 × 104 значений δfoF2. Рассматривались выборки из 360 значений для каждой отдельной станции, включающие дневные или ночные часы данного месяца, исходя из предположения о том, что дневные и ночные условия различны. По этим выборкам кроме функции плотности вероятности W(δ foF2) считались четыре начальных центральных момента: математическое ожидание m; стандартное отклонение $\sigma = \sqrt {{{m}_{2}}} ,$ σ2 – дисперсия; коэффициенты асимметрии А и эксцесса E.
Кроме того, статистические свойства рассматривались для нескольких выборок учащенных наблюдений foF2 продолжительностью 3–5 сут и временны́м разрешением 5 мин за 1971–1973 гг. по ст. Москва. По этим данным рассчитаны отклонения δfoF2, их дифференциальные распределения и моменты.
Выборки, полученные для различных условий, являются статистически независимыми, они дают возможность проследить за временны́ми изменениями статистических характеристик для каждой станции.
3. О СТАЦИОНАРНОСТИ ФЛУКТУАЦИЙ ЭЛЕКТРОННОЙ КОНЦЕНТРАЦИИ В МАКСИМУМЕ СЛОЯ F2
Во всех экспериментах, связанных с отражением радиоволн от ионосферы, одним из основных является вопрос о стационарности исследуемых случайных выборок отраженного сигнала. Решение этого вопроса вызывает необходимость решения другого немаловажного вопроса – о длительности выборок, при которых этот процесс можно считать стационарным. Использование данных относительных отклонений критических частот от скользящего медианного значения дает возможность исключать регулярные изменения критических частот, влияния крупных ионосферных образований. Однако такое утверждение является приближенным, и вопрос о стационарности выборок требует специального рассмотрения в каждом отдельном эксперименте [Алимов, 1974].
Случайный процесс называется стационарным в том случае, если его статистические характеристики – функции плотности вероятности и моменты – не зависят от сдвига по времени [Миддлтон, 1999]. Иными словами, данная реализация представляет собой выборку из стационарного случайного процесса тогда, когда она может быть разбита на статистически полные подвыборки, функции плотности вероятности которых и моменты остаются неизменными. Это условие является достаточно строгим и определяет стационарность в широком смысле.
Покажем, что исследуемые выборки δfoF2 с различным временны́м разрешением представляют собой квазистационарный процесс, на основании чего в исследованиях могут быть использованы стационарные статистические характеристики.
Прежде всего, следует решить вопрос о независимости выборок. Для этого необходимо, чтобы значения исследуемой величины для двух последовательных моментов времени были некоррелированными, т.е. tk + 1 – tk > 2τ0 [Гусев и др., 1972], где τ0 – радиус корреляции процесса. Отсюда необходимый объем выборки N = T/2τ0 (Т – интервал наблюдения). Для исследуемых выборок рассматривался радиус корреляции τ0 = τρ = 0.5.
Рассматривались две группы выборок {δfoF2} – с пятиминутным и часовым разрешениями, соответствующие мелкомасштабной и крупномасштабной ионосферной структуре. Записи для каждого сеанса пятиминутных наблюдений делились на ряд частей с нарастающими длительностями. По пятиминутным выборкам было обработано 10 сеансов учащенных ионосферных наблюдений. Длительность сеанса наблюдений составляла трое суток (за исключением 1–5.06.1971 г., когда сеанс продолжался пять суток). Специально для определения радиуса корреляции каждого сеанса считали функции автокорреляции, и был определен радиус корреляции процесса, который составлял в среднем ~1 ч 45 мин при ρ = 0.5. Таким образом, τ0 = τρ = 0.5 = 100 мин.
На основании этого был выбран минимальный допустимый объем некоррелированной выборки ~5 ч, т.е. в статистике участвовало 60 значений δfoF2. Таким образом, первый интервал содержал 60 значений δfoF2, следующий – 120 и т.д. Для каждой из этих частей вычислялись средние значения $\overline {\delta {\kern 1pt} foF2} $ = m и дисперсия σ. Согласно критерию Фишера [Худсон, 1970] была проверена случайность исследуемой величины с достоверностью не менее 0.9. Стационарными считались те выборки, различные значения среднего и дисперсии которых для соседних интервалов различались не более чем на 10% внутри доверительного интервала для m и σ соответственно. Из исследуемых 10 сеансов пятиминутных выборок 7 удовлетворяют условию стационарности в широком смысле и 3 сеанса не являются стационарными. На рисунке 1 приведен пример изменения m(t) и σ(t), представлены и доверительные интервалы (заштрихованная область).
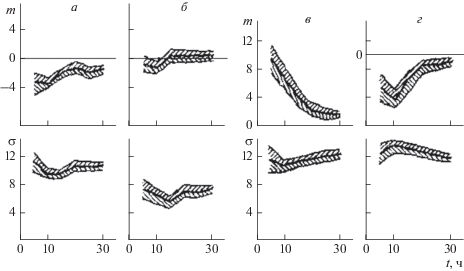
Рис. 1.
Изменения m(t) и σ(t) для выборок δ foF2 с пятиминутным разрешением 1–5.06.1971 г. (а) и 15–17.06.1971 г. (б). Заштрихованные области – доверительные интервалы.
Значение радиуса корреляции для ионосферных наблюдений с часовым разрешением равно 5–6 ч [Сергеенко, 2018]. Поскольку длительность периода наблюдений равняется месяцу, минимальный объем некоррелированной выборки должен составлять ~40 значений δfoF2, т.е. быть не менее четырех дней.
Мы взяли минимальную выборку из пяти дней, т.е. 60 значений δfoF2. Затем, увеличивая последовательно период наблюдения на пять дней, получили динамику соответствующих вероятностных статистических характеристик для всех последовательных интервалов для дневных и ночных часов отдельно по месяцам за 1990 и 1986 гг. по ст. Москва. Таким образом, исследовалось 48 случаев для определения стационарности этого процесса.
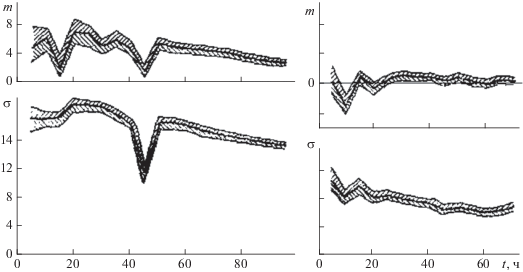
Рассмотрение всех случаев показало, что в 60% процесс является стационарным в широком смысле и в 40% наблюдений не является стационарным. Рисунок 2 иллюстрирует процесс установления стационарности для дневных часов декабря 1990 г. и июля 1986 г., ночных часов ноября 1990 г. и сентября 1986 г.
4. ОБ ОСОБЕННОСТЯХ КРИВЫХ РАСПРЕДЕЛЕНИЯ δ foF2
В ходе проведения экспериментов, контроля, испытаний и анализа полученных данных необходима проверка на нормальность выборок. Подробное изучение полученных дифференциальных распределений δfoF2 показало, что коэффициенты асимметрии и эксцесса отличны от 0, а это указывает на отличие распределений от нормального закона. Поскольку это утверждение не является строгим, то была предпринята проверка по критериям Крамера для совокупности δfoF2 [Крамер, 1975].
Всего было построено 72 функции плотности вероятности для каждой из семи станций мировой сети по трем годам, соответствующим различным фазам цикла солнечной активности и отдельно для дневных и ночных часов.
Покажем на основании имеющихся данных, что вероятностный закон распределения δfoF2 для каждой совокупности не описывается нормальным законом [Крамер, 1975]. Берем случайную выборку из n значений δfoF21, …, δfoF2n, имеющей некоторую функцию распределения F(δ foF2). Каждая статистическая характеристика выборки (распределения вероятности, моменты различного порядка) является случайной величиной с распределением, однозначно определяемым априорным F(δfoF2). Моменты выборки определятся как характеристики распределения выборки. И выборочные распределения, и соответствующие характеристики сходятся по вероятности к соответствующим распределениям для всей совокупности при п → ∞. Если предполагать распределение совокупности нормальным, то необходимо выяснить, в какой мере статистические характеристики выборочных распределений Fп соответствуют этому предположению.
С этой целью для всех 72 распределений по каждой станции были рассчитаны дифференциальные распределения и четыре центральных момента m, σ, A, E. для выборок из 360 точек для каждой станции. Общие свойства построенных выборочных функций плотности вероятности следующие: все кривые имеют т ≠ 0, |A| ≠ 0 и |E| ≠ 0, вероятности высоких уровней δfoF2 повышаются по сравнению с требуемыми значениями для нормального закона.
Далее были рассчитаны дифференциальные распределения и моменты для выборок характеристик распределений – m, σ, А, Е. Данные сведены в табл. 1.
Из всех характеристик (m, σ, A, E) для всех станций как для распределений δfoF2, так и для выборочных распределений только инварианты первого и второго порядка, т.е. т и σ имеют заметный суточный, широтный и сезонный ход. Для всех сезонов и уровней солнечной и геомагнитной активностей величина m наибольшая в высоких и на средних широтах и плавно уменьшается с понижением широты. Во время возмущений m(m) в высоких и на средних широтах смещены в отрицательную сторону, а на экваторе математическое ожидание m(m) положительно. При высокой солнечной активности хорошо проявляются сезонные различия: зимой и в равноденствия амплитуда эффекта заметно больше, чем летом; для лет минимума солнечной активности сезонные различия малы.
Все распределения характеристик унимодальные с ненулевыми коэффициентами асимметрии и эксцесса, причем коэффициенты асимметрии в распределении А достигают 3, а коэффициенты эксцесса Е достигают 6. Согласно же требованию для совокупности, распределенной нормально, средние значения и дисперсии нормальных выборок независимы, причем m должно быть распределено нормально, а дисперсия имеет распределение χ2 с п – 1 степенями свободы [Крамер, 1975]. Согласно этому были получены формулы для ${{(\sqrt {{{m}_{2}}} )}^{p}}$ и коэффициентов асимметрии и эксцесса для распределения стандартного отклонения
Таблица 1.
Моменты дифференциальных распределений для характеристик выборочных распределений δfoF2 – m1, σ1, А1, Е1
| Станции | День | Ночь | ||||||
|---|---|---|---|---|---|---|---|---|
| m1, % | σ1, % | А1 | Е1 | m1, % | σ1, % | А1 | Е1 | |
| m | ||||||||
| Салехард | –0.42 | 1.75 | 0.32 | 0.73 | –0.48 | 1.49 | –0.09 | –0.36 |
| Диксон | –0.76 | 1.79 | –0.48 | 0.12 | 0.98 | 1.70 | –0.39 | –0.49 |
| Горький | –0.56 | 1.55 | 0.18 | 0.57 | –0.66 | 1.42 | 0.36 | 0.16 |
| Москва | –0.21 | 1.66 | –0.45 | –0.13 | –0.12 | 1.54 | 0.25 | 1.51 |
| Алма-Ата | 0.02 | 1.14 | –0.61 | –0.28 | –0.16 | 1.43 | –0.48 | 1.08 |
| Бомбей | 0.35 | 1.03 | –0.36 | 2.54 | –0.54 | 1.57 | –0.48 | –0.46 |
| Уанкайо | 0.31 | 1.19 | 0.55 | –0.65 | –0.24 | 1.42 | –0.05 | –0.20 |
| σ | ||||||||
| Салехард | 16.12 | 4.61 | 0.02 | –1.33 | 15.7 | 4.26 | –0.31 | –1.05 |
| Диксон | 12.6 | 4.71 | 0.66 | –0.44 | 14.80 | 4.90 | 0.01 | –0.79 |
| Горький | 11.6 | 2.92 | –0.09 | 0.06 | 12.90 | 2.74 | –0.02 | 1.14 |
| Москва | 12.6 | 2.93 | 0.03 | –0.74 | 13.30 | 2.17 | –0.09 | –0.75 |
| Алма-Ата | 10.4 | 11.87 | 1.71 | –1.17 | 11.60 | 2.51 | –0.01 | –0.83 |
| Бомбей | 9.08 | 0.98 | –0.06 | 3.74 | 15.60 | 2.41 | –0.24 | –0.44 |
| Уанкайо | 9.72 | 1.31 | 0.08 | 0.08 | 15.00 | 1.92 | 0.13 | 0.79 |
| A | ||||||||
| Салехард | 0.12 | 0.92 | 3.23 | 6.60 | 0.15 | 0.57 | 1.01 | 1.00 |
| Диксон | 0.26 | 0.57 | 1.07 | 2.11 | 0.28 | 0.73 | 1.03 | 0.66 |
| Горький | 0.82 | 0.96 | 1.60 | 4.50 | –0.04 | 0.64 | 0.12 | –2.72 |
| Москва | 1.15 | 1.30 | 0.56 | 0.08 | 0.02 | 0.59 | 0.31 | –0.30 |
| Алма-Ата | 0.22 | 0.55 | 1.42 | –2.13 | 0.89 | 0.86 | 1.25 | 1.00 |
| Бомбей | 0.25 | 1.20 | 1.26 | –0.10 | 0.01 | 0.59 | 0.70 | 1.10 |
| Уанкайо | 0.40 | 0.63 | 2.92 | –2.33 | 0.13 | 0.67 | 0.04 | –2.75 |
| E | ||||||||
| Салехард | 0.18 | 0.72 | 2.03 | –1.23 | 0.21 | 0.54 | 1.56 | 2.50 |
| Диксон | 0.29 | 0.57 | 1.01 | 2.09 | 0.29 | 0.85 | 2.23 | 4.35 |
| Горький | 0.72 | 0.92 | 1.63 | 4.05 | 0.36 | 1.17 | 2.68 | 6.45 |
| Москва | 0.95 | 1.30 | 0.46 | 0.08 | 0.69 | 0.99 | 0.29 | 0.52 |
| Алма-Ата | 0.29 | 0.55 | 1.02 | –2.23 | 0.27 | 0.40 | 0.48 | –0.32 |
| Бомбей | 0.85 | 1.12 | 1.16 | –0.03 | 0.75 | 0.84 | 0.87 | 4.97 |
| Уанкайо | 1.60 | 1.16 | 0.31 | –0.65 | 0.98 | 0.65 | 0.78 | 0.28 |
Для характеристик распределений коэффициентов асимметрии и эксцесса выборок использовались критерии, приведенные в работе [Крамер, 1975] для среднего значения и дисперсии этих распределений при условии, что совокупность распределена нормально. Согласно этим критериям
Все изложенное с очевидностью приводит к выводу, что для совокупности одномерной случайной величины δfoF2 нормальный закон распределения неприменим.
4. ПРЕДЛОЖЕННАЯ МОДЕЛЬ
Для описания статистических характеристик совокупности δfoF2 необходимо привлечение асимметричной и эксцессивной модели, которая в пределе при A → 0 и E → 0 стремилась бы к нормальной. Для анализа данных используем представление о стационарном пуассоновском потоке точек, в соответствии с которым ставим моменты появления неоднородностей δfoF2. В основе этого представления лежат следующие соображения:
1) количество неоднородностей электронной концентрации внутри зоны Френеля, формирующей отраженный сигнал, конечно;
2) временны́е зависимости δfoF2(t) можно представить линейной совокупностью импульсов с амплитудой а и длительностью t: Х = Σхт(а, t), где т – конечно;
3) моменты появления отдельных импульсов в потоке статистически независимы, т.е. независимы моменты появления отдельных неоднородностей;
4) поток ординарен, т.е. в бесконечно малом интервале времени наблюдается одно воздействие.
Это дает возможность использовать для описания распределения δfоF2(t) статистическую модель, построенную на основе пуассонова случайного процесса. Такая модель может быть построена на базе характеристической функции, связанной преобразованием Фурье с функцией плотности вероятности процесса, рассматриваемого в работе [Сергеенко, 2017], но с экспоненциальным множителем, создающим асимметрию. Нормированная характеристическая функция несимметричного распределения имеет вид
где ${\beta }$ – параметр асимметрии; при $\beta \to 0$ функция f(λ) стремится к характеристической функции симметричного процесса.Фурье-преобразованием с характеристической функцией была получена функция плотности вероятности W(δfoF2) [Миддлтон, 1999]:
Условия существования этой функции распределения таковы: $E - \frac{4}{3}{{A}^{2}}$ > 0, $\frac{{Am}}{{3\sigma }}$ < 1. Для сопоставления экспериментальные и теоретические функции распределения для Алма-Аты приведены на рис. 3. Для сравнения там же нанесены кривые нормального распределения для соответствующих σ. Особенно хорошее согласие между теоретическими и экспериментальными кривыми видно в области отрицательных δfoF2, наиболее существенной для радиосвязи.
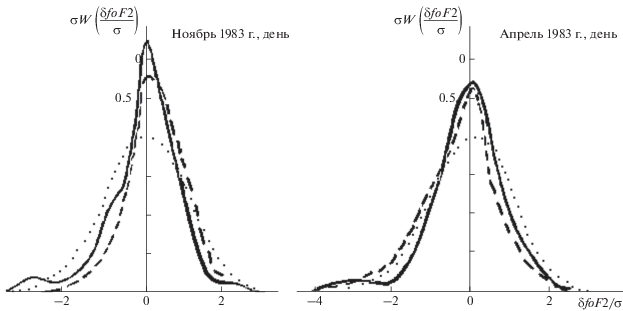
Рис. 3.
Экспериментальные распределения δ foF2 для выборок с 1-часовым разрешением для ст. Алма-Ата – сплошные линии; теоретические распределения – штриховые линии; точечные кривые – нормальный закон.
Эта модель была рассчитана для массива данных при разных гелиогеофизических ситуациях. Количественная оценка согласия ее с экспериментальными распределениями достаточно высока ~85–90%.
Представляет интерес провести подобный анализ для мелкомасштабной структуры ~102 м, для чего достаточно исследовать статистическую изменчивость 5-минутных выборок значений δfoF2. Рассматривались 6 продолжительных (3–5 сут) сеансов учащенных наблюдений δfoF2 (интервал наблюдений 5 мин) по ст. Москва, для которых рассчитаны дифференциальные распределения и моменты. В табл. 2 приведены периоды, для которых рассчитаны распределения, четыре центральных момента т, σ, А, Е и длина выборки К.
Таблица 2.
Периоды, центральные моменты т, σ, А, Е и длина выборки К для данных учащенных наблюдений δfoF2
| Дата | m, % | σ, % | А | Е | К |
|---|---|---|---|---|---|
| 15–17.06.1971 г. | 0.51 | 7.13 | 0.57 | 3.68 | 800 |
| 15–17.02.1972 г. | –0.86 | 12.62 | –0.62 | 2.16 | 864 |
| 1–5.06.1971 г. | 3.25 | 13.96 | 1.01 | 1.27 | 820 |
| 27–30.12.1971 г. | –0.22 | 11.91 | 0.13 | 1.19 | 856 |
| 12–14.01.1971 г. | 1.07 | 9.61 | 0.97 | 2.19 | 527 |
| 18–20.01.1972 г. | –1.01 | 14.40 | –0.68 | 2.97 | 852 |
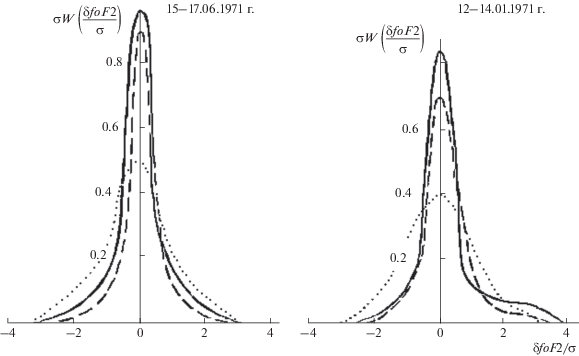
На рисунке 4 представлены экспериментальные распределения δfoF2 (сплошная кривая), штрихами нанесена теоретическая кривая, точками – нормальный закон. Очевидно, что модель более соответствует экспериментальным распределениям, чем нормальное распределение.
Рис. 4.
Экспериментальные распределения δ fоF2 для выборок с 5-минутным разрешением для ст. Москва (оплошная кривая); штриховая линия – теоретическая кривая; точки – нормальный закон.
Таким образом, можно утверждать, что модель, построенная на базе пуассонова случайного процесса, является адекватной для описания распределений δfоF2 не только для часовых выборок, соответствующих крупномасштабной неоднородной структуре слоя F2, но и для выборок, соответствующих мелкомасштабной структуре ионосферы.
4. ЗАКЛЮЧЕНИЕ
По данным сети ионосферных станций ВЗ, расположенных в различных широтных зонах, изучены статистические особенности относительных вариаций критических частот слоя F2. На основании статистического анализа кривых распределения δfoF2, полученных по месячным выборкам данных семи станций за три года, показано, что закон распределения совокупности δfoF2 далек от нормального. Предложен способ интерпретации экспериментальных кривых функций плотности вероятности с помощью модели с эксцессом и асимметрией, построенной на базе пуассонова случайного процесса для данных как с часовым разрешением, так и по учащенным пятиминутным наблюдениям.
Результаты приведенных исследований имеют прикладное значение. Полученные данные могут быть полезны для диагностики неоднородной структуры слоя F2. Неоднородности электронной плотности, находящиеся в непрерывном движении, существенно влияют на распространение радиоволн, используемых при наземной и космической связи.
Список литературы
– Альперт Я.Л. Распространение электромагнитных волн и ионосфера. М.: Наука. 563 с. 1972.
– Алимов В.А. О стационарности процесса рассеяния коротких радиоволн в ионосфере // Изв. вузов. Радиофизика. Т. 17. № 9. С. 1399–1401. 1974.
– Гусев В.Д., Казимировский Э.С., Кушнеревский Ю.В. Динамика неоднородностей ионизации в ионосфере // Ионосферные исслед. № 21. М.: Наука. С. 5–11. 1972.
– Ерухимов JI.M., Максименко О.И., Мясников Е.Н. О неоднородной структуре верхней ионосферы // Ионосферные исследования. № 30. М.: Наука. С. 27–48. 1980.
– Иванов В.Б. Формирование неоднородной структуры в области F среднеширотной ионосферы // Изв. вузов. Радиофизика. Т. 33. № 9. С. 1033–1037. 1991.
– Крамер Г. Математические методы статистики. М.: Мир. 648 с. 1975.
– Миддлтон Д. Модели негауссовского шума и обработка сигналов в телекоммуникациях – новые методы и результаты для моделей классов А и В // IEЕЕ Trans. Inf. Theory. V. 4. P. 1129–1140. 1999.
– Сергеенко Н.П. Статистическое описание негауссовых выборок в cлое F2 ионосферы во время гелиогеофизических возмущений // Геомагнетизм и аэрономия. Т. 57. № 6. С. 817–824. 2017.
– Сергеенко Н.П. Корреляционные свойства выборок вариаций критической частоты слоя F2 в различных гелиогеофизических условиях // Геомагнетизм и аэрономия. Т. 58. № 5. С. 662–668. 2018.
– Худсон Д. Статистика для физиков. М.: Мир, 296 с. 1970.
– Fejer B.G., Kelley M.C. Ionosphere irregularities // Rev. Geophys. Space Phys. V. 18. P. 401–454. 1980.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия