1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 60, № 2, 2020

Геомагнетизм и аэрономия, 2020, T. 60, № 2, стр. 164-172

Аналитическое описание околопланетной ударной волны на основе ГД- и МГД-моделирования для магнитного поля параллельного и перпендикулярного потоку плазмы

Г. А. Котова 1, *, М. И. Веригин 1, Т. Гомбоши 2, К. Кабин 3, В. В. Безруких 1

1 Институт космических исследований РАН (ИКИ РАН)
Москва, Россия

2 Университет Мичигана
Мичиган, Эн Арбор, США

3 Королевский военный колледж Канады
Онтарио, Кингстаун, Канада

* E-mail: kotova@iki.rssi.ru

Поступила в редакцию 10.07.2019
После доработки 06.09.2019
Принята к публикации 26.09.2019

Полный текст (PDF)

Аннотация

Продолжена разработка аналитической полуэмпирической модели ударной волны, основанной на теоретических МГД-расчетах, точных аналитических решениях и экспериментальных данных. Параметры модели имеют ясный физический смысл. Для случаев, когда магнитное поле солнечного ветра направлено вдоль его скорости или перпендикулярно вектору скорости, получены аналитические выражения, которые позволяют рассчитать параметры ударной волны – расстояние до подсолнечной точки, радиус кривизны и затупленность в подсолнечной точке – с использованием перенормировки ранее разработанной подробной газодинамической модели. Для случая, когда вектор магнитного поля перпендикулярен вектору скорости солнечного ветра, показано, что для аналитического описания поверхности ударной волны достаточно аппроксимировать ее параметры в 2-х перпендикулярных плоскостях.

1. ВВЕДЕНИЕ

Для исследования физических процессов в плазме вблизи планет часто требуется знание положения и формы околопланетной ударной волны. Современные теоретические МГД, кинетические модели и их совместное использование [см., например, обзор Ledvina et al., 2008; Wang et al., 2015; Chen et al., 2017] требуют значительного процессорного времени. Они составляют надежную базу для исследования ударных волн, но практически не могут быть применены для отслеживания перемещений этой границы в реальном времени. Поэтому в большинстве таких исследований использовались и используются эмпирические модели околопланетной ударной волны [Fairfield, 1971, 2001; Formisano, 1979; Slavin and Holzer, 1981; Nĕmeček and Šafránková, 1991; Peredo et al., 1995; Chao et al., 2002; Merka et al., 2003; Chapman et al., 2003; Jelínek et al., 2012; Meziane et al., 2014]. Однако такие модели применимы в области параметров солнечного ветра, использовавшихся при их построении, и ограничены в пространстве областью, в которой проводились измерения. При таком моделировании также не учитывается влияние показателя политропы γ на положение ударной волны.

В работах [Веригин и др., 1999; Verigin et al., 2001a, b; Verigin et al., 2003a, b; Веригин, 2004; Kotova et al., 2005] используется полуэмпирический подход, основанный на точных аналитических решениях, описывающих некоторые характерные свойства ударной волны, например, форму подсолнечной части фронта ударной волны при малых звуковых числах Маха Мs в газодинамическом приближении, асимптотический МГД конус Маха, свойства течения плазмы сразу же за разрывом. Параметры модели подбираются на основе детальных численных расчетов. При достаточно больших альвеновских числах Маха для моделирования околопланетных ударных волн можно использовать газодинамическое приближение. Газодинамическая аналитическая модель ударной волны для препятствий различной формы (от гиперболического до обрубленного цилиндра) представлена в работе [Verigin et al., 2003b].

Целью этой работы является построение аналитической МГД-модели околопланетной ударной волны, параметры которой имеют ясный физический смысл. Так как газодинамическая аналитическая модель ударной волны весьма точно описывает ее положение для препятствий различной формы [Verigin et al., 2003b], представляется целесообразным использовать сходные аналитические выражения для параметров, определяющих и МГД-ударную волну. Для этого нужно найти выражения, модифицирующие входные параметры ГД-модели для преобразования ее в МГД-модель. В настоящей работе рассмотрены случаи, когда межпланетное магнитное поле направлено параллельно потоку солнечного ветра и когда оно направлено перпендикулярно потоку.

2. СИСТЕМА КООРДИНАТ И ОБОЗНАЧЕНИЯ

Для описания ударной волны удобно использовать геоцентрическую систему координат, связанную с межпланетной средой GIPM (Geocentric Inter Planetary Medium). В этой системе координат ось X направлена противоположно направлению невозмущенного солнечного ветра. Ось Y направлена так, что вектор межпланетного магнитного поля лежит во втором – четвертом квадрантах плоскости (X, Y). Ось Z дополняет систему координат до правой. Эта система координат была впервые предложена Bieber & Stone [1979] для изучения истечения энергичных электронов из магнитосферы и позже использовалась Peredo et al. [1995] для анализа околоземной ударной волны.

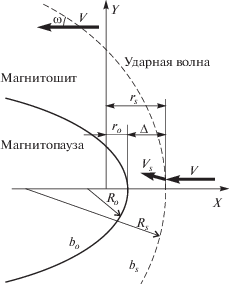
Обозначения, которые используются при построении аналитической модели околопланетной ударной волны показаны на рис. 1. Затупленность препятствия bo определяет его форму вблизи носовой части: bo = –1 – сфера, bo < –1 – “тупой” эллипсоид, –1 < bo < 0 – “вытянутый” эллипсоид, bo = 0 – параболоид, bo > 0 – гиперболоид. Угол ω определяет наклон ударной волны к направлению потока плазмы на больших расстояниях от планеты.

Рис. 1.

Обозначения пространственных переменных: ro, rs – расстояния до магнитопаузы (препятствие) и ударной волны, соответственно, Ro, Rs – радиусы кривизны носовых частей этих границ, bo, bs – затупленность магнитопаузы и ударной волны, соответственно, а Δ – отход ударной волны от подсолнечной магнитопаузы.

3. МГД-РАСЧЕТЫ ПОЛОЖЕНИЯ И ФОРМЫ УДАРНОЙ ВОЛНЫ

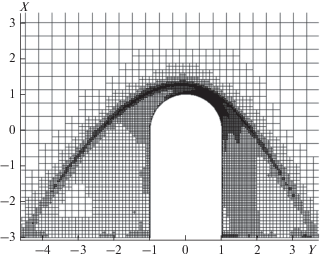
Для моделирования ударной волны, образующейся в сверхзвуковом и сверхальвеновском потоке набегающей плазмы около препятствий различной формы, использовались подробные магнитогазодинамические расчеты, выполненные в Мичиганском университете. Использовалась сетка с переменным адаптивным шагом с ~3 × 106 ячейками. Пример сетки в плоскости (x, y) для численных расчетов показан на рис. 2. Расчеты проводились для 2-х видов препятствия: полусфера с вытянутым цилиндрическим хвостом (рис. 2) и параболоид вращения. Все расчеты проводились в единицах ro.

Рис. 2.

Пример адаптивной сетки в плоскости (x, y) для численных расчетов положения и формы ударной волны около препятствия (ro = 1, Ro = 1, bo = –1, Ms = 6, Ma = 3, γ = 2.0).

4. УРАВНЕНИЕ, ОПИСЫВАЮЩЕЕ ФОРМУ И ПОЛОЖЕНИЕ УДАРНОЙ ВОЛНЫ

При построении газодинамической аналитической модели ударной волны для препятствий различной формы Веригин и др. [Verigin et al., 2003b] использовали следующее выражение для описания ее формы и положения:

(1)
${{y}^{2}}(x) = 2{{R}_{s}}({{r}_{s}} - x) + \frac{{{{{({{r}_{s}} - x)}}^{2}}}}{{{\text{M}}_{s}^{2} - 1}}\left( {1 + \frac{{{{b}_{s}}({\text{M}}_{s}^{2} - 1) - 1}}{{1 + {{d}_{s}}\frac{{{{r}_{s}} - x}}{{{{R}_{s}}}}}}} \right).$
Дополнительный параметр ds характеризует переход от доминирования параметров подсолнечной области ударной волны к области, где доминирующую роль играет асимптотический наклон ударной волны. Наклон ударной волны к направлению потока плазмы на больших расстояниях от планеты в газодинамике определяется звуковым числом Маха: tg2 ω = 1/(${\text{M}}_{s}^{2}$ – 1) и не зависит от часового угла $\varphi = \arccos ({y \mathord{\left/ {\vphantom {y \rho }} \right. \kern-0em} \rho })$, где $\rho = \sqrt {{{y}^{2}} + {{z}^{2}}} $. В магнитной газодинамике точное аналитическое решение для определения конуса Маха ωas(φ) при любом часовом угле φ получено в работе Verigin et al. [2003a]. Асимптотический конус Маха определяет асимптотическое число Маха Mas = 1/sin2ωas = 1/tg2ωas +1. Для описания МГД-ударной волны формулу (1) можно модифицировать, заменив Мs на Мas:
(2)
$\begin{gathered} {{\rho }^{2}}(x) = 2{{R}_{s}}({{r}_{s}} - x) + \\ + \,\,{\text{t}}{{{\text{g}}}^{2}}{{\omega }_{{as}}}{{({{r}_{s}} - x)}^{2}}\left( {1 + \frac{{\frac{{{{b}_{s}}}}{{{\text{t}}{{{\text{g}}}^{2}}{{\omega }_{{as}}}}} - 1}}{{1 + {{d}_{s}}\frac{{{{r}_{s}} - x}}{{{{R}_{s}}}}}}} \right). \\ \end{gathered} $
Выражение (2) можно непосредственно использовать для осесимметричного случая, когда межпланетное магнитное поле направлено параллельно набегающему потоку плазмы. Для всех остальных направлений магнитного поля необходимо принимать во внимание, что параметры Rs, bs, ωas и ds – зависят от часового угла φ.

5. АНАЛИТИЧЕСКАЯ АППРОКСИМАЦИЯ МГД РАСЧЕТОВ УДАРНОЙ ВОЛНЫ ДЛЯ МАГНИТНОГО ПОЛЯ ПАРАЛЛЕЛЬНОГО И ПЕРПЕНДИКУЛЯРНОГО ПОТОКУ ПЛАЗМЫ

На рисунке 3 для случаев, когда магнитное поле параллельно потоку плазмы, представлены 2 примера аппроксимации с помощью выражения (2) рассчитанных в МГД- приближении положения и формы ударной волны около различных препятствий. Видно, что указанное аналитическое выражение позволяет достаточно хорошо аппроксимировать осесимметричную поверхность ударной волны, которая образуется при магнитном поле параллельном потоку плазмы. Для препятствий с расстоянием до подсолнечной точки ro = 1 и радиусом кривизны в этой точке Ro = 1 и для потока солнечного ветра с параметрами Ms = 6, Ma = 3, γ = 5/3 получены следующие параметры аппроксимации: для параболического препятствия (слева) – rs = 1.2, Rs = 1.96, bs = 0.93, ds = 0.5, для сферического препятствия – rs = 1.18, Rs = 1.67, bs = 0.2, ds = 0.4.

Рис. 3.

Примеры положения и формы ударной волны, образующейся около двух различных препятствий, в набегающем потоке солнечного ветра с магнитным полем параллельным скорости. Точки – МГД-расчет, сплошные линии – аппроксимация с помощью выражения (2).

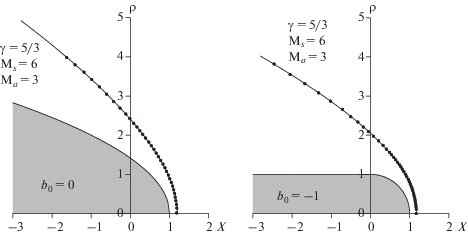
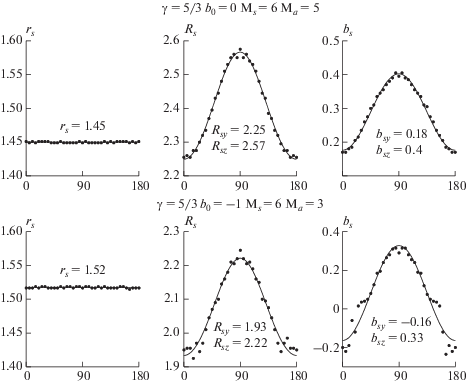
Рис. 4.

Примеры изменения параметров rs, Rs, bs в зависимости от угла φ при обтекании препятствий потоком солнечного ветра с магнитным полем перпендикулярным скорости. Точки – параметры аппроксимации МГД-расчетов в плоскостях φ = const с шагом по φ равным 5°, сплошные линия – аппроксимация с помощью выражений (3) и (4).

В случае, когда межпланетное магнитное поле перпендикулярно направлению скорости потока плазмы, носовая точка ударной волны по-прежнему лежит на оси x, но необходимо определить зависимость параметров нашей модели Rs, bs и ds от часового угла φ. Для этого рассчитанная в МГД-приближении трехмерная поверхность ударной волны аппроксимировалась с помощью выражения (2) в различных плоскостях φ = const с шагом по φ равным 5° в интервале 0 < φ < 180°. На рисунке 4 показаны полученные таким образом зависимости rs, Rs, bs от угла φ. Как и следовало ожидать, расстояние до подсолнечной точки ударной волны не зависит от φ. Зависимость радиуса кривизны в подсолнечной точке от φ хорошо описывается выражением:

(3)
${{R}_{s}} = \frac{{{{R}_{{sy}}}{{R}_{{sz}}}}}{{{{R}_{{sy}}}{{{\sin }}^{2}}\varphi + {{R}_{{sz}}}{{{\cos }}^{2}}\varphi }},$
где параметры Rsy и Rsz – радиусы кривизны поверхности ударной волны в плоскостях (x, y), т.е. при φ = 0°, и (x, z), т.е. при φ = 90°, соответственно. Аналогично, зависимость затупленности в подсолнечной точке от φ хорошо описывается выражением:
(4)
${{b}_{s}} = {{b}_{{sz}}}{{\sin }^{2}}\varphi + {{b}_{{sy}}}{{\cos }^{2}}\varphi $
с параметрами bsy, bsz, соответствующих затупленностям поверхности ударной волны в подсолнечной точке в плоскостях (x, y) и (x, z).

Таким образом, формулы (3) и (4) позволяют использовать выражение (2) для аппроксимации трехмерной поверхности ударной волны. Зависимость ds(φ) выявить не удалось, поэтому при аппроксимации будем считать, ds(φ) = const = ds. На рисунке 5 для случая, когда магнитное поле направлено перпендикулярно потоку плазмы, показан пример аппроксимации положения и формы отошедшей ударной волны с помощью выражений (2‒4). При этом определены 6 свободных параметров: rs, Rsy, Rsz, bsy, bsz, ds.

Рис. 5.

Примеры положения и формы ударной волны в плоскости (x, y) (нижние кривые (а)) и плоскости (x, z) (верхние кривые (б)), образующиеся около двух различных препятствий, в набегающем потоке солнечного ветра с магнитным полем перпендикулярным скорости. Точки – МГД-расчеты, сплошные линии – аппроксимация с помощью выражения (2) с учетом (3) и (4).

6. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МГД-АППРОКСИМАЦИИ УДАРНОЙ ВОЛНЫ ПО ГД-РАСЧЕТАМ

В случае газодинамического течения относительный темп расширения поперечного сечения S центральной трубки тока за ударной волной [например, Biermann et al., 1967; Wallis, 1973]:

(5)
$\frac{1}{S}\frac{{dS}}{{dx}} = - \frac{2}{{{{R}_{s}}}}\frac{{1 - \varepsilon }}{\varepsilon },$
где ε – величина обратная наибольшему скачку плотности газа на фронте ударной волны. В случае магнитной газодинамики ε = ε(γ, Ma, Ms, αvn, ϑbn), где αvn и ϑbn – углы между нормалью к ударной волне и направлением потока плазмы или магнитного поля, соответственно. Кубическое уравнение для определения ε получено в работе [Petrinec and Russell, 1997, уравнение 12].

Для магнитно-газодинамического течения относительный темп расширения поперечного сечения S центральной трубки тока за осесимметричной или имеющей две плоскости симметрии ударной волной (магнитное поле параллельно или перпендикулярно набегающему потоку плазмы, αvn = 0) определяется выражением:

(6)
$\frac{1}{S}\frac{{dS}}{{dx}} = - \frac{{{{R}_{{sy}}} + {{R}_{{sz}}}}}{{{{R}_{{sy}}}{{R}_{{sz}}}}}\frac{{1 - \varepsilon }}{\varepsilon }\left[ {\frac{{\varepsilon {\text{M}}_{a}^{2}}}{{\varepsilon {\text{M}}_{a}^{2} - {{{\cos }}^{2}}{{\vartheta }_{{bn}}}}}} \right],$
где ${{R}_{{sy}}} < {{R}_{{sz}}}$ – радиусы кривизны в направлениях параллельном и перпендикулярном магнитному полю, соответственно.

В случае, когда межпланетное магнитное поле параллельно скорости солнечного ветра ${{R}_{{sy}}} = {{R}_{{sz}}} = {{R}_{s}}$:

(7)
$\frac{1}{S}\frac{{dS}}{{dx}} = - \frac{2}{{{{R}_{s}}\varepsilon {\text{*}}\Gamma }},$
где ε* = ε/(1 – ε), скачок плотности на ударной волне ε совпадает с его значением в газовой динамике $\varepsilon = \frac{{\gamma - 1}}{{\gamma + 1}} + \frac{2}{{{\text{M}}_{s}^{2}(\gamma + 1)}},$ но по сравнению с выражением (5) появляется новый фактор Г = Гpar = = 1 – ${1 \mathord{\left/ {\vphantom {1 {\varepsilon {\text{{\rm M}}}_{a}^{2}}}} \right. \kern-0em} {\varepsilon {\text{{\rm M}}}_{a}^{2}}}.$

В случае, когда межпланетное магнитное поле перпендикулярно скорости солнечного ветра

(8)
$\frac{1}{S}\frac{{dS}}{{dx}} = - \frac{{{{R}_{{sy}}} + {{R}_{{sz}}}}}{{{{R}_{{sy}}}{{R}_{{sz}}}}}\frac{{1 - \varepsilon }}{\varepsilon } = \frac{2}{{\left\langle {{{R}_{s}}} \right\rangle }}\frac{{1 - \varepsilon }}{\varepsilon }.$
Скачок плотности на ударной волне в этом случае также можно рассчитать аналитически ε = $ = \frac{{\gamma - 1}}{{2(\gamma + 1)}}$ + $\frac{\gamma }{{2{\text{M}}_{a}^{2}(\gamma + 1)}}$ + $\frac{1}{{2{\text{M}}_{a}^{2}(\gamma + 1)}}$ × × $\sqrt {{{{((\gamma - 1){\text{M}}_{a}^{2} - \gamma )}}^{2}} + 8{\text{M}}_{a}^{2}} .$ Фактор Г = Гper здесь неявно входит в величины Rsy(Гper) и Rsz(Гper).

МГД фактор Γ и значения Mаs можно использовать для перенормировки газодинамических параметров rs, Rs, bs, ds и определения МГД-параметров (Verigin et al., 2001a). Газодинамические параметры rs = ro + Δ(ε*, γ, Ro, bo), Rs(ε*, γ, Ro, bo), bs(γ, bo, Ms), ds(bo) рассчитываются с помощью выражений (34)‒(38) и (39)‒(43) из работы (Verigin et al., 2003b) (в выражении (36) имеется опечатка, исправленная в обзоре Веригина (2004), перед вторым слагаемым должен быть знак +, а не –).

Для учета межпланетного магнитного поля в потоке плазмы солнечного ветра в случае, когда оно направлено параллельно скорости плазмы, МГД-параметры rs, Rs, bs выражения (2) можно получить по тем же формулам (34)–(43) из [Verigin et al., 2003b], но с рассчитанным в МГД-приближении параметром сжатия ε и заменой ε* на ε*Гpar и Ms на Mas, а также введением дополнительного фактора, зависящего от Гpar:

(9)
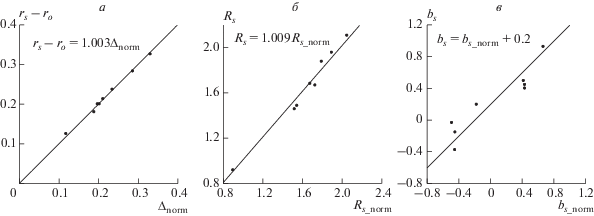
$\begin{gathered} {{\Delta }_{{{\text{norm}}}}} = {{r}_{{s\_{\text{norm}}}}}--{{r}_{o}},\,\,\,\, = \Gamma _{{{\text{par}}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}\Delta (\varepsilon {\text{*}}{{\Gamma }_{{{\text{par}}}}},\gamma ,{{R}_{o}},{{b}_{o}}), \\ {{R}_{{s\_{\text{norm}}}}} = \Gamma _{{{\text{par}}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}{{R}_{s}}(\varepsilon {\text{*}}{{\Gamma }_{{{\text{par}}}}},\gamma ,{{R}_{o}},{{b}_{o}}), \\ {{b}_{{s\_{\text{norm}}}}} = {{b}_{s}}(\gamma ,{{b}_{o}},{{{\text{M}}}_{{as}}}). \\ \end{gathered} $

На рисунке 6 перенормированные параметры (9) сравниваются с параметрами, полученными при аппроксимации МГД-расчетов положения и формы ударной волны. Видно, что согласие между rs_norm и rs, Rs_norm и Rs очень хорошее (панели а, б), а для bs_norm и bs несколько хуже (панель в), и для аппроксимации затупленности ударной волны в носовой точке мы использовали величину bs_norm + + βpar, где βpar = 0.2. Газодинамический параметр ds зависит только от затупленности (формы) препятствия bo, поэтому изменять его пока не будем, несмотря на то, что аппроксимированные МГД-параметры и параметры, рассчитанные по ГД-формулам существенно различаются.

Рис. 6.

Сравнение параметров модели ударной волны (2), аппроксимирующих МГД- расчеты, с параметрами, рассчитанными по ГД-модели [Verigin et al., 2001a], для набегающего потока солнечного ветра с магнитным полем параллельным скорости потока. Сплошные линии на панелях (а, б, в) – аппроксимирующие зависимости.

На рисунке 7 показаны 2 примера положения и формы ударной волны перед различными препятствиями, определенные с помощью перенормированных газодинамических формул.

Рис. 7.

Примеры положения и формы ударной волны, образующейся около двух различных препятствий, в набегающем потоке солнечного ветра с магнитным полем параллельным скорости. Точки – МГД-расчет, сплошные линии – аппроксимация с помощью газодинамических расчетов и выражений (9).

Теперь рассмотрим образование ударной волны в потоке солнечного ветра с магнитным полем, направленным перпендикулярно направлению скорости потока плазмы. Как было показано выше для расчета положения и формы околопланетной ударной волны в таком случае достаточно определить параметры выражения (2) в плоскостях (x, y) и (x, z). Для определения параметров rs, Rsу, bsz можно использовать выражения аналогичные формулам (9), но с параметром Г = Гper = = 1/(1 – ${1 \mathord{\left/ {\vphantom {1 {\varepsilon {\text{{\rm M}}}_{a}^{2}}}} \right. \kern-0em} {\varepsilon {\text{{\rm M}}}_{a}^{2}}}$). Кроме того, асимптотический наклон ударной волны на бесконечности зависит от часового угла, поэтому для расчета параметров кроме величины Гper введем отношение асимптотических чисел Маха в направлениях y (Mas(0)) и z (Mas(90)):

(10)
$\begin{gathered} {{\Delta }_{{{\text{norm}}}}} = {{r}_{{s\_{\text{norm}}}}} - {{r}_{o}} = \Gamma _{{{\text{per}}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}\Delta (\varepsilon {\text{*}}{{\Gamma }_{{{\text{per}}}}},\gamma ,{{R}_{o}},{{b}_{o}}), \\ {{R}_{{sy\_{\text{norm}}}}} = \Gamma _{{{\text{per}}}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}{{R}_{s}}(\varepsilon {\text{*}}{{\Gamma }_{{{\text{per}}}}},\gamma ,{{R}_{o}},{{b}_{o}}) \times \\ \times \,\,{{[{{{{{\text{M}}}_{{as}}}(0)} \mathord{\left/ {\vphantom {{{{{\text{M}}}_{{as}}}(0)} {{{{\text{M}}}_{{as}}}(90)}}} \right. \kern-0em} {{{{\text{M}}}_{{as}}}(90)}}]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{b}_{{sz\_{\text{norm}}}}} = ({{b}_{s}}(\gamma ,{{b}_{o}},{{{\text{M}}}_{{as}}}(90)) + {{\beta }_{{{\text{par}}}}}) \times \\ \times \,\,{{[{{{{{\text{M}}}_{{as}}}(0)} \mathord{\left/ {\vphantom {{{{{\text{M}}}_{{as}}}(0)} {{{{\text{M}}}_{{as}}}(90)}}} \right. \kern-0em} {{{{\text{M}}}_{{as}}}(90)}}]}^{{ - 2}}}. \\ \end{gathered} $

На рисунке 8 перенормированные параметры (10) Δnorm (а) и Rsy_norm (б) сравниваются с параметрами rs – ro, и Rsy, полученными при аппроксимации МГД-расчетов положения и формы ударной волны. Кроме того, сравниваются между собой аппроксимированные в плоскостях (x, y) и (x, z) радиусы кривизны подсолнечной области ударной волны (в).

Рис. 8.

Сравнение параметров модели ударной волны (2), аппроксимирующих МГД- расчеты, с параметрами, рассчитанными по ГД-модели [Verigin et al., 2001a], для набегающего потока солнечного ветра с магнитным полем перпендикулярным скорости потока. Сплошные линии на панелях – аппроксимирующие зависимости.

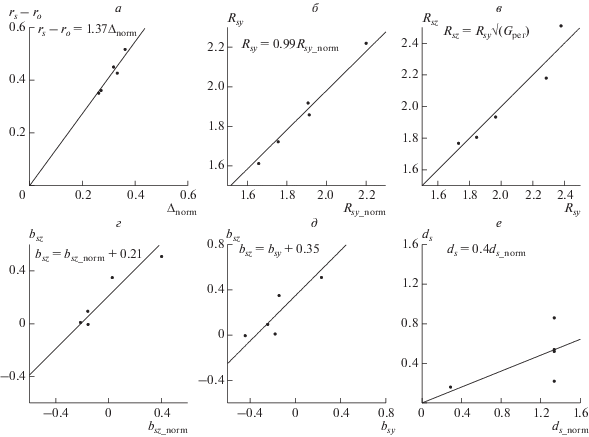
Из рисунка 8 видно, что для определения отхода ударной волны в потоке солнечного ветра с магнитным полем, направленным перпендикулярно направлению скорости потока плазмы, нужно ввести дополнительный параметр χ(ϑbv) ~ 1.4. Этот параметр, очевидно, зависит от направления магнитного поля и равен 1 при угле между направлениями скорости солнечного ветра и магнитного поля ϑbv = 0 (9). Величина Rsу хорошо коррелирует с Rsy_norm (рис. 8б). Взаимозависимость радиусов кривизны в плоскостях (x, y) и (x, z): Rsz = $\Gamma _{{{\text{per}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{R}_{{sy}}}$ (рис. 8в) позволяет, зная Rsy_norm, рассчитать Rsz_norm.

Затупленность в плоскости (x, z) bsz (рис. 8г) неплохо аппроксимируется величиной bsz_norm + + 0.21, рассчитанной с использованием соответствующего выражения (10). Затупленность же в плоскости (x, y) bsy (рис. 8д) можно рассчитать по dsz_norm. Газодинамический параметр ds_norm зависит только от формы препятствия bo, но параметр ds, аппроксимирующий МГД расчеты (рис. 8е) в среднем существенно меньше газодинамического ds = 0.4ds_norm.

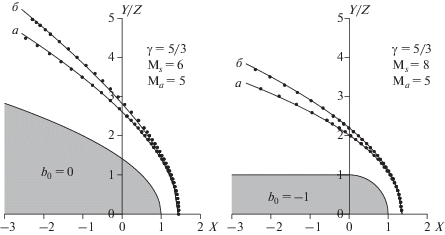
На рисунке 9 показаны 2 примера положения и формы ударной волны определенные с помощью перенормированных газодинамических формул, для потока солнечного ветра с магнитным полем, направленным перпендикулярно вектору скорости потока, набегающего на различные препятствия.

Рис. 9.

Примеры положения и формы ударной волны в плоскости (x, y) (нижние кривые (а)) и плоскости (x, z) (верхние кривые (б)), образующиеся около двух различных препятствий, в набегающем потоке солнечного ветра с магнитным полем перпендикулярным скорости. Точки – МГД-расчет, сплошные линии – аппроксимация с помощью газодинамических расчетов, выражений (10) и поправок в соответствии с рис. 8.

7. ВЫВОДЫ

В настоящей работе рассмотрены случаи образования ударной волны перед препятствиями различной формы в случаях, когда межпланетное магнитное поле направлено параллельно потоку солнечного ветра и когда оно направлено перпендикулярно потоку.

Показано, что для аппроксимации поверхности околопланетной ударной волны можно использовать рациональную функцию, применявшуюся ранее в газодинамическом приближении.

В случае, когда вектор магнитного поля параллелен вектору скорости потока, достаточно определить 4 свободных параметра: расстояние до носовой точки, радиус кривизны и затупленность в носовой точке и параметр перехода к асимптотическому углу наклона. Эти параметры удается аппроксимировать по газодинамическим расчетам.

Показано, что в случае, когда вектор магнитного поля перпендикулярен вектору скорости потока плазмы, поверхность околопланетной ударной волны можно аппроксимировать с помощью 6 свободных параметров: расстояние до носовой точки, радиусы кривизны и затупленности в носовой точке в плоскостях (x, y) и (x, z) и параметр перехода к асимптотическому углу наклона. Получены соотношения для пересчета этих параметров по газодинамическим расчетам.

В дальнейшем предполагается определить параметры, позволяющие описать околопланетную ударную волну аналитической рациональной функцией при произвольном направлении межпланетного магнитного поля, и аппроксимировать эти параметры также исходя из газодинамических расчетов.

Список литературы

  1. ‒ Веригин М.И., Котова Г.А., Ремизов А.П.и др. Форма и положение околопланетных ударных волн // Космич. исслед. Т. 37. № 1. С. 38‒43. 1999.

  2. ‒ Веригин М.И. Положение и форма околопланетных ударных волн: газодинамические и МГД аспекты / Солнечно-земные связи и электромагнитные предвестники землетрясений. Сб. докладов III Международной конференции 16‒21 августа 2004 г. ИКИР ДВО РАН, Петропавловск-Камчатский. С. 49‒69. 2004.

  3. ‒ Bieber J.W., Stone E.C. Energetic electron bursts in the magnetopause electron layer and in interplanetary space / Magnetospheric Boundary Layers – A Sydney Chapman Conference / ESA SP-148. P. 131. 1979.

  4. ‒ Chao J.K., Wu D.J., Lin C.-H., Yang Y.-H., Wang X.Y., Kessel M., Chen S.H., Lepping R.P. Models for the size and shape of the Earth’s magnetopause and bow shock / Space Weather Study Using Multipoint Techniques, Ed. L.-H. Lyu, Pergamon Press. P. 360–368. 2002.

  5. ‒ Chapman J.F., Cairns I.H. Three-dimensional modeling of Earth’s bow shock: Shock shape as a function of Alfvén Mach number // J. Geophys. Res. V. 108. № A051174. 2003.https://doi.org/10.1029/2002JA009569

  6. ‒ Chen Y., Tóth G., Cassak P., Jia X., Gombosi T.I., Slavin J.A., Markidis S., Peng I.B., Jordanova V.K., Henderson, M.G. Global three-dimensional simulation of Earth’s dayside reconnection using a two-way coupled magnetohydrodynamics with embedded particle-in-cell model: Initial results // J. Geophys. Res. V. 122, P.10.318–10.335. 2017.https://doi.org/10.1002/2017JA024186

  7. ‒ Fairfield D.H. Average and unusual locations of the Earth’s magnetopause and bow shock // J. Geophys. Res. V. 76. № 28. P. 6700‒6716. 1971.

  8. ‒ Fairfield D.H., Cairns I.H., Desch M.D., Szabo A., Lazarus A.J., Aellig M.R. The location of low Mach number bow shocks at Earth // J. Geophys. Res. V. 106. № A11. P. 25 361‒25 376. 2001.

  9. ‒ Formisano V. Orientation and shape of the Earth’s bow shock in three dimensions // Planet. Space Sci. V. 27. P. 1151. 1979.

  10. ‒ Jelínek K., Němeček Z., Šafránková J. A new approach to magnetopause and bow shock modeling based on automated region identification // J. Geophys. Res. V. 117. № A05208. 2012.https://doi.org/10.1029/2011JA017252

  11. ‒ Kotova G., Verigin M., Zastenker G., Nikolaeva N., Smolkin B., Slavin J., Szabo A., Merka J., Nemechek Z., Safrankova J. Bow shock observations by Prognoz–Prognoz 11 data: analysis and model comparison // Adv. Space. Res. V. 36. P. 1958‒1963. 2005.

  12. ‒ Ledvina S.A., Ma Y.-J., Kallio E. Modeling and simulating flowing plasmas and related phenomena // Space Sci. Rev. V. 139. P. 143–189. 2008.https://doi.org/10.1007/s11214-008-9384-6

  13. ‒ Merka J., Szabo A., Narock T.W., King J.H., Paularena K.I., Richardson J.D. A comparison of IMP 8 observed bow shock positions with model predictions // J. Geophys. Res. V. 108. № A021077. 2003.https://doi.org/10.1029/2002JA009384

  14. ‒Meziane K., Alrefay T.Y., Hamza A. On the shape and motion of the earth’s bow shock // Planet. Space Sci. V. 93‒94. P. 1‒9. 2014.

  15. ‒ N$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{e} $meček Z., Šafránková J. The Earth’s bow shock and magnetopause position as a result of solar wind-magnetosphere interaction // J. Atmos. Terr. Phys. V. 53. P. 1049‒ 1054. 1991.

  16. ‒ Peredo M., Slavin J.A., Mazur E., Curtis S.A. Three-dimensional position and shape of the bow shock and their variation with Alfvénic, sonic and magnetosonic Mach numbers and interplanetary magnetic field orientation // J. Geophys. Res. V. 100. № A5. P. 7907‒7916. 1995.

  17. ‒ Petrinec S.M., Russell C.T. Hydrodynamic and MHD equations across the bow shock and along the surfaces of planetary obstacles // Space Sci. Rev. V. 79. P. 757‒791. 1997.

  18. ‒ Slavin J.A., Holzer R.E., Solar wind flow about the terrestrial planets, 1, Modeling bow shock position and shape // J. Geophys. Res. V. 86. № A13. P. 11401‒11418. 1981.

  19. ‒ Verigin M.I., Kotova G.A., Remizov A.P. et al. Studies of the Martian bow shock response to the variation of the magnetosphere dimensions according to TAUS and MAGMA meaurements aboard the PHOBOS 2 orbiter // Adv. Space Res. V. 20. № 2. P. 155‒158. 1997.

  20. ‒ Verigin M., Kotova G., Szabo A., Slavin J., Gombosi T., Kabin K., Shugaev F., Kalinchenko A. WIND observations of the terrestrial bow shock 3-d shape and motion // Earth Planets Space. V. 53. № 10. P. 1001‒1009. 2001a.

  21. ‒ Verigin M.I., Kotova G.A., Slavin J. et al. Analysis of the 3-D shape of the terrestrial bow shock by Interball/Magion 4 observations // Adv. Space Res. V. 28. № 6. P. 857‒862. 2001b.

  22. ‒ Verigin M., Slavin J., Szabo A., Kotova G., Gombosi T. Planetary bow shocks: Asymptotic MHD Mach cones // Earth Planets Space. V. 55. P. 33‒38. 2003a.

  23. ‒ Verigin M., Slavin J., Szabo A., Gombosi T., Kotova G., Plochova O., Szegö K., Tatrallyay M., Kabin K., Shugaev F. Planetary bow shocks: Gasdynamic analytic approach // J. Geophys. Res. V. 108. No. A081323. 2003b.https://doi.org/10.1029/2002JA009711

  24. ‒ Wang M., Lu J.Y., Yuan H.Z., Kabin K., Liu Z.Q., Zhao M.X., G. Li. The dipole tilt angle dependence of the bow shock for southward IMF: MHD results // Planet. Space Sci. V. 106. P. 99‒107. 2015.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал