Геомагнетизм и аэрономия, 2020, T. 60, № 4, стр. 463-468

1. ВВЕДЕНИЕ

В настоящее время считается, что за высокую температуру короны Солнца могут быть ответственны магнитогидродинамические (МГД) волны, генерируемые в фотосфере Солнца конвективными движениями плазмы [см., например, обзор Sakurai, 2017]. Гипотеза об определяющем вкладе мелкомасштабных процессов вспышечного энерговыделения в нагрев корональных петель также остается популярной [Klimchuk, 2015]. Однако этот подход по мере совершенствования наблюдательных возможностей вызывает все больше вопросов [Aschwanden et al., 2018].

Альвеновские волны являются наиболее вероятными МГД-модами, ответственными за нагрев солнечной атмосферы [Srivastava et al., 2017; Soler et al., 2019]. Между тем особенности их распространения хорошо изучены лишь для наиболее простых моделей атмосфер. Например, в случае неизотермической среды требуются довольно сложные численные расчеты [Murawski and Musielak, 2010; Wójcik et al., 2017]. При этом интерпретация результатов и соответственно тестирование программ сталкивается с трудностями. В связи с этим Musielak et al. [2006] разработали аналитический метод, основанный на анализе осцилляционных теорем [Мышкис, 1971; Пушкарь, 2007], благодаря применению которых можно находить так называемые точки поворота (turning points), характеризующие, по мнению авторов, частоту отсечки. Однако такой поход, как станет ясно из дальнейшего изложения, представляется не до конца обоснованным. Это связано как с недостаточно корректной трактовкой осцилляционных теорем, так и со слишком упрощенными представлениями о физической сущности переноса волновой энергии квазипериодическими возмущениями в стратифицированной атмосфере. Обсуждению этих аспектов и посвящена настоящая работа.

2. КРИТЕРИЙ КНЕЗЕРА И ПЕРЕНОС ЭНЕРГИИ АЛЬВЕНОВСКИМИ ВОЛНАМИ

Основная идея методики, разработанной Musieak et al. [2006] (см. также Schmitz and Fleck [1998]) заключается в сведении с помощью замены переменных волнового уравнения к частному случаю уравнения Клейна–Гордона и последующим исследованием его свойств на основе так называемых осцилляционных теорем. Прежде чем приступить к изучению особенностей распространения линейных альвеновских волн рассмотрим эти теоремы и их следствия более детально.

Из теоремы сравнения [Мышкис, 1971; Пушкарь, 2007] вытекает следующее важное следствие. Если функция y(x) есть решение уравнения

причем $Q{\text{(}}x{\text{)}} < {\text{0}}$ на интервале (a, b), где a и b – действительные числа, таком что $ - \infty < a \leqslant b < {\text{ + }}\infty ,$ то y(x) имеет не более одного нуля (решение неосциллирующего типа). Если же y(x) есть решение уравнения (1) на полубесконечном интервале ${\text{[}}{{x}_{{\text{0}}}}{\text{,}} + {\kern 1pt} \infty {\text{)}}$ и $Q{\text{(}}x{\text{)}} > {{a}^{{\text{2}}}} > {\text{0}},$ то решение имеет бесконечно много нулей (решение осциллирующего типа).

Требование положительной или отрицательной определенности функции Q(x) является слишком сильным. Вследствие этого для разделения решений на осциллирующие и неосцилирующие разумнее обратиться к так называемой теореме (критерию) Кнезера [Пушкарь, 2007], который формулируется следующим образом. Если в дифференциальном уравнении (1) на полубесконечном интервале ${\text{[}}{{x}_{{\text{0}}}}{\text{,}} + {\kern 1pt} \infty {\text{)}}$ (${{{x}_{{\text{0}}}}}$ > 0) коэффициент $Q{\text{(}}x{\text{)}} < {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{\text{4}}{{x}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{4}}{{x}^{{\text{2}}}}}}$ то его решение y(x) имеет не более одного нуля (не осциллирует). Если $Q{\text{(}}x{\text{)}} > {{{\text{(1}} + \varepsilon {\text{)}}} \mathord{\left/ {\vphantom {{{\text{(1}} + \varepsilon {\text{)}}} {{\text{4}}{{x}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{4}}{{x}^{{\text{2}}}}}},$ где ε > 0, то y(x) содержит бесконечно много нулей (осциллирует).

Критерий Кнезера следует из свойств решения дифференциального уравнения Эйлера

которое имеет периодические решения при С > 1 и соответственно апериодические при С < 1 [Мышкис, 1971]. Отметим, в общем случае вместо уравнения Эйлера можно использовать любое другое уравнение, которое содержит как осциллирующие, так и неосциллирующие решения.

Musielak et al. [2006] с помощью уравнения (1) и критерия Кнезера, проигнорировав ограничения, накладываемые на x, сформулировали “теорему” о точках поворота x_tn, удовлетворяющих равенству: $Q{\text{(}}{{x}_{{tn}}}{\text{)}} = {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{\text{4}}x_{{tn}}^{{\text{2}}}}}} \right. \kern-0em} {{\text{4}}x_{{tn}}^{{\text{2}}}}}.$ По мнению авторов, точки x_tn позволяют отделить осциллирующие решения от неосциллирующих (монотонных). При этом частоту, соответствующую x_tn на определенной высоте, можно рассматривать как аналог акустической частоты отсечки Лэмба, характеризующей переход от распространяющихся волн к нераспространяющимся. Следовательно, в стратифицированной атмосфере точки поворота будут соответствовать высотам, начиная с которых перенос волновой энергии на заданной частоте становится малоэффективным (см. также Routh et al. [2007]). Учитывая следствия из теоремы сравнения, Perera et al. [2015] определили также переходные точки x_tr (transition points), описывающие переход от осциллирующих решений уравнения (1) при Q(x) > 0 к монотонным при Q(x) < 0. По мнению авторов, они также могут быть использованы для характеристики переноса волновой энергии по аналогии с точками поворота.

Изложенный выше подход, на наш взгляд, нельзя считать обоснованным. Дело в том, что критерий Кнезера должен выполняться на полубесконечных интервалах ${\text{[}}{{x}_{{\text{0}}}}{\text{,}} + {\kern 1pt} \infty {\text{)}},$ поэтому отсутствие нулей в решении y(x) на ограниченном промежутке значений x совсем не означает, что функция y(x) будет оставаться монотонной на бóльших интервалах. Например, функция Бесселя (можно также взять любую гармоническую функцию) первого порядка J₁(x) лишь при малых значениях положительного аргумента $x \ll {\text{1}}$ ведет себя монотонным образом $\left( {{{J}_{{\text{1}}}}{\text{(}}x{\text{)}} \approx {x \mathord{\left/ {\vphantom {x {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right),$ пересекая ось X только один раз. Пренебрежение этим важным обстоятельством может приводить к некорректным выводам. Кроме того, метод Musieak et al. [2006] основывается на ошибочном предположении, что только осциллирующие в пространстве решения уравнения (1) способны переносить волновую энергию. Рассмотрим данный вопрос более обстоятельно.

Вектор Умова–Пойнтинга, характеризующий плотность потока энергии F, можно представить следующим образом

Откуда с учетом условия “вмороженности” магнитных силовых линий в плазму для потока электромагнитной энергии вдоль магнитного поля получим В случае возбуждения гармоничных по времени альвеновских возмущений мы можем представить векторы возмущения скорости и магнитного поля в виде где δV(r) и δB(r) в общем случае могут быть комплексными величинами. Из уравнений (2) и (3) следует, что усредненный по времени продольный относительно B₀ волновой поток равен где Δφ – разность фаз между δV(r) и δB(r). В ходе получения последнего выражения мы учли, что процедура усреднения по времени для комплексных величин в рассматриваемом случае сводится к умножению соответствующего выражения на 1/2.

Таким образом, согласно (4) волновой поток 〈F〉 может быть и не равен нулю, если возмущенные по пространству величины δV(r) и δB(r) являются монотонными функциями радиус-вектора r.

3. АЛЬВЕНОВСКИЕ ВОЗМУЩЕНИЯ СКОРОСТИ И МАГНИТНОГО ПОЛЯ В СТРАТИФИЦИРОВАННОЙ АТМОСФЕРЕ

Волновое уравнение, описывающее распространение альвеновских мод вдоль вертикальной оси Z с постоянным магнитным полем B₀ = (0, 0, B₀), в стандартных обозначениях имеет вид [Hollweg, 1984; Tsap, 2012]

где δV – поперечная компонента возмущения скорости по отношению к оси Z, а альвеновская скорость Считая атмосферу изотермической с характерной шкалой высот H, т.е., полагая плотность плазмы ρ(z) = ρ₀exp(–z/H) и δV(t, η) ∝ exp(–iωt)δV(η), из (5) получим уравнение, решение которого выражается через функции Ханкеля [Hollweg, 1984; Tsap, 2006] Здесь С₁ и С₂ – произвольные константы, которые, как показывает анализ, соответствуют членам, описывающим распространение альвеновских мод в противоположных направлениях [Hollweg, 1984; Цап и др., 2007]. Используя линеаризованное уравнение индукции с учетом (6) получим Откуда для усредненного по времени потока энергии альвеновских волн вдоль оси Z согласно (4) находим [Hollweg, 1984] Как следует из уравнения (8), поток волн 〈F〉 не зависит от осциллирующего или монотонного характера поведения возмущений скорости δV(η)и магнитного поля δB(η) в пространстве.

Для того чтобы лучше понять физическую сущность переноса энергии, исследуем сначала зависимость разности фаз Δφ между возмущениями Re[δV] и Re[δB] от аргумента η, который, в свою очередь, зависит от относительной высоты z/H и частоты волн (η ∝ exp(–z/H)). Выделяя действительную и мнимую часть в правой части уравнений (6) и (7), используя формулу Эйлера и считая для простоты здесь и в дальнейшем С₁ = 0, нетрудно получить следующее выражение

где J_n и Y_n – соответственно функции Бесселя и Неймана первого рода.

Как видно из рис. 1, значение Δφ с высотой z увеличивается и стремится к π/2, что должно приводить как к уменьшению эффективности переноса энергии (см. формулу (4)), так и ухудшению обмена энергией между возмущениями скорости и магнитного поля. В результате, несмотря на рост амплитуды скорости Re[δV] с высотой из-за уменьшения плотности ρ(z), амплитуда Re[δB] уменьшается, что подтверждают численные расчеты (рис. 2).

На первый взгляд, из формулы (8) следует, что волновую энергию могут одинаково эффективно переносить как высокочастотные, так и низкочастотные моды. Однако эффективность передачи механической энергии от нижних слоев атмосферы к верхним характеризуется групповой скоростью V_GA, которую согласно теореме Леонтовича–Лайтхилла можно оценить из соотношения [Рабинович и Трубецков, 1984]

где усредненная плотность энергии волн [Цап и Копылова, 2001] Откуда с учетом (6) и (7) следует функциональная зависимость представленная на рис. 3. Видно, что при $\eta \ll 1$ перенос энергии альвеновскими волнами становится малоэффективным, тогда как для $\eta \gg 1$ групповая скорость V_GA стремится к альвеновской V_A. При этом даже когда цилиндрические функции J_n(η) и Y_n(η) ведут себя монотонным образом (η < 1), перенос волновой энергии может происходить достаточно эффективно, однако в любом случае высокочастотные моды для этого лучше приспособлены (η ∝ ω).

4. ВЫВОДЫ

В представленной работе мы провели анализ метода, предложенного Musielak et al. [2006], для исследования особенностей распространения линейных МГД-волн в неоднородной солнечной атмосфере. Показано, что, несмотря на свою привлекательность, он не позволяет адекватно характеризовать эффективность переноса волновой энергии в атмосферах Солнца и звезд, поскольку Musielak et al. [2006] не приняли во внимание ограничения, содержащиеся в критерии Кнезера. Кроме того, уравнение Эйлера является далеко не единственным дифференциальным уравнением, у которого можно выделить осциллирующие и неосциллирующие решения, поэтому теорема сравнения предполагает возможность существования большого числа несвязанных между собой точек поворота. Необходимо также учесть, что вид функции Q(x), входящей в уравнение (1), благодаря замене переменных может варьироваться в широких пределах [Perera et al., 2015].

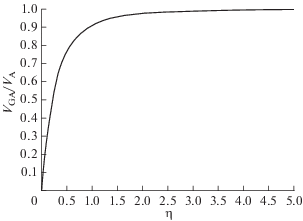
Как следует из полученных результатов, если не принимать во внимание диссипативные процессы, альвеновские моды с меньшими периодами лучше переносят волновую энергию из фотосферы в хромосферу Солнца. В значительной мере это объясняется зависимостью фазовых соотношений между возмущениями от высоты, что может существенным образом сказаться как на их амплитуде, так и потоке волновой энергии. Интересно также отметить, поскольку η ∝ ∝ exp(–z/H), то относительная групповая скорость альвеновских мод V_GA/V_A с высотой должна уменьшаться (рис. 3).

Нами было также показано, что осциллирующий или монотонный характер поведения возмущений в пространстве не является надежным критерием эффективности переноса энергии альвеновскими волнами. Этот вывод хорошо согласуется с результатами работы [Chae and Litvinenko, 2018], в которой рассматривались акустические моды. Еще раз подчеркнем, что поток электромагнитной энергии непосредственно связан с разностью фаз между возмущенными величинами, поскольку от этого зависит обмен энергией между возмущениями скорости и магнитного поля и соответственно поведение амплитуд возмущений с высотой (рис. 2). Более детально этот вопрос мы надеемся рассмотреть в нашей следующей работе.