Известия РАН. Энергетика, 2021, № 4, стр. 140-160
Сопряженная задача “испарение – гиперболическое уравнение теплопроводности”
Ю. Б. Зудин 1, *, Д. С. Уртенов 1, В. С. Устинов 1
1 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: yzudin@gmail.com
Поступила в редакцию 28.02.2021
После доработки 23.04.2021
Принята к публикации 26.04.2021
Аннотация
Проведено аналитическое исследование сопряженной задачи “испарение-теплопроводность” с учетом конечной скорости распространения тепла. Для расчета потока испарения использованы результаты линейной кинетической теории. Методом интегрального преобразования Лапласа получено аналитическое решение краевой задачи для гиперболического уравнения теплопроводности в случае нестационарных граничных условий первого и второго рода. Построено обобщенное аналитическое решение сопряженной задачи, учитывающее влияние параметра релаксации на развитие процесса теплопереноса во времени. Проведен анализ влияния коэффициента конденсации на интенсивность испарения. Выполнена двухзонная аппроксимация решения, позволившая выделить характерные параметры сопряженной задачи.
ВВЕДЕНИЕ
Настоящая работа, выполненная в продолжение работы [1], посвящена аналитическому исследованию сопряженной задачи “испарение–теплопроводность” с учетом конечной скорости распространения тепла.
Как известно, большинство задач гидродинамики и теплообмена описываются дифференциальными уравнениями в частных производных. Так, уравнения Навье-Стокса и уравнение энергии представляют собой квазилинейные дифференциальные уравнения, решение которых для практических приложений выполняется с помощью численных методов. Однако прямые численные методы являются эффективными далеко не во всех случаях. В частности, численные алгоритмы не дают возможности обобщить полученное частное решение на широкий диапазон параметров. Это наиболее заметно проявляется при исследовании многопараметрических задач, к которым относится большинство прикладных проблем. Поэтому в настоящее время продолжают играть важную роль аналитические решения задач гидродинамики и теплообмена, которые обладают следующими преимуществами.
• Аналитические решения имеют общий характер, позволяющий проводить параметрические исследования путем варьирование начальных и краевых условий задачи.
• Для тестирования численных решений полных уравнений необходимы базовые аналитические решения упрощенных уравнений.
• Аналитические решения используются для проверки корректности постановки и валидации результатов численных исследований.
• Ярким примером достоинств аналитического подхода служат монографии [2–4], где представлен широкий спектр аналитических решений задач теория теплопроводности и термоупругости.
В работе [1] проведен анализ сопряженной задачи, состоящей из двух взаимосвязанных частей: а) краевой задачи для классического уравнения теплопроводности в твердом теле (мишени); б) молекулярно-кинетической модели испарения с поверхности мишени. В настоящей работе развитый в [1] подход обобщается на случай конечной скорости распространения тепла в облучаемой мишени. Для этого осуществляется переход от параболической модели теплопроводности к более общей гиперболической модели, учитывающей инерционность теплового потока [3, 4].
В технических приложениях задача теплопроводности, как правило, является сопряженной с некоторой внешней задачей: краевой задачей термоупругости, обратной задачей теплопроводности, задачей оптимального управления. Практически важная сопряженная задача возникает при взаимодействии лазерного излучения с мишенью. При этом осуществляется “лазерная абляция” – совокупность сложных физико-химических процессов, результатом которых является удаление вещества с поверхности раздела фаз. Лазерное облучение мишени сопровождается интенсивным процессом испарения на поверхности, взаимосвязанным с внешним газодинамическим течением. Описанию физического механизма и многочисленных практических приложений лазерной абляции посвящены тысячи журнальных публикаций и многие международные конференции. Результатом первого периода этих исследований стала тепловая модель лазерного испарения, в рамках которой мишень и сублимированный материал находятся в локальном термодинамическом равновесии. Исчерпывающее описание процесса лазерной абляции представлено, в частности, в монографии [5] и обзоре [6].
Настоящая работа базируется на тепловой модели, описывающей основные физические черты процесса испарения и в своей основе сохранившейся до настоящего времени. При этом не учитываются экстремальные явления – образование лазерной плазмы, ее взаимодействие с излучением, механизм взрывного кипения. Тем не менее, даже в таких (сравнительно простых) условиях к настоящему времени не прояснены некоторые важные особенности наносекундной лазерной абляции. В частности, в различных работах неоднозначно анализируется испарение с поверхности мишени – как определяемые испарением граничные условия (ГУ), так и характерное время его развития [5, 6].
ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
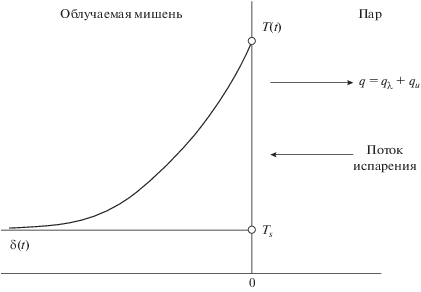
Сопряженная задача. Базовым условием сопряженной задачи “теплопроводность – испарение” является баланс теплового потока на поверхности мишени, включающий две составляющие (рис. 1) – поток теплопроводности ${{q}_{{{\lambda }}}},$ идущий на нагрев тела, и поток испарения с его поверхности ${{q}_{u}}{\text{:}}$
Основная цель настоящего анализа состоит в определении развития во времени интенсивности испарения после начала облучения поверхности. Важно отметить, что в процессе лазерной абляции происходит облучение мишени короткими периодическими импульсами. Физически это означает, что происходящие в мишени процессы нагревания/охлаждения будут развиваться в тонком поверхностном слое твердого тела. Это позволяет использовать для расчета ${{q}_{{{\lambda }}}}$ нестационарное одномерное уравнение теплопроводности в полуограниченном теле $\left( {0 \leqslant x < \infty } \right){\text{:}}$
(2)
$\frac{{\partial \vartheta }}{{\partial t}} = a\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{x}^{2}}}}.$В начальный момент времени в твердом теле задается однородное распределение температур: $\vartheta = 0$ при $t = 0~\left( {0 \leqslant y < \infty } \right).$ ГУ для уравнения (2) в общем виде имеет вид: $\vartheta = \vartheta \left( t \right)$ при $y = 0~\left( {t > 0} \right).$ Уравнение (2) представляет собой классическое параболическое уравнение теплопроводности (ПУТ). В соответствие с [1] будем использовать интегральный метод решения, основанный на концепции теплового слоя. В рамках этого метода дифференциальное уравнение теплопроводности заменяется на интеграл теплового баланса для слоя толщиной $\delta \left( t \right),$ монотонно продвигающегося от поверхности вглубь твердого тела [2–4]. Использование такого подхода приводит к аналитическим решениям, которые точно удовлетворяют начальному и граничным условиям и приближенно – исходному дифференциальному уравнению. При этом поток теплопроводности может быть записан в виде:
где $\lambda $ – коэффициент теплопроводности твердого тела.После ряда элементарных преобразований, подробно изложенных в [1], из (2), (3) выводится линейное неоднородное дифференциальное уравнение первого порядка относительно $\delta \left( t \right).$ Его общее решение имеет вид:
(4)
${{\delta }^{2}} = \frac{{12a}}{{{\text{\;}}{{\vartheta }^{2}}}}\int\limits_0^t {{{\vartheta }^{2}}dt} .$Вычисление квадратуры (4) для классических ГУ дает: $\delta = \sqrt {12at} $ – для ГУ первого рода $\left( {\vartheta = {\text{const}}} \right);$ $\delta = \sqrt {6at} $ – для ГУ второго рода $\left( {q = {\text{const}}} \right).$
Параметр испарения. Согласно линейной кинетической теории [7] поток испарения ${{q}_{u}}$ и разность температур $\vartheta $ связаны соотношением:
(5)
$\vartheta = \sqrt {2\pi } {{\left( {\frac{{1 - 0.4\beta }}{\beta }} \right)}^{2}}\frac{{R_{g}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}T_{s}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}{{{{\rho }_{{\text{v}}}}{{r}^{2}}}}{{q}_{u}}.$При выводе соотношения (5) использовалось также уравнение Клапейрона–Клаузиуса, связывающее температуру и давление пара на линии насыщения [7]. В последующих выкладках используются следующие величины:
• “параметр испарения”
обозначающий долю падающего на мишень лучистого потока, которая идет на парообразование;• масштаб времени
(7)
${{t}_{0}} = \frac{{2\pi }}{3}\frac{{1 - 0.4\beta }}{\beta }\frac{{a{{R}_{g}}c_{p}^{2}T_{s}^{3}}}{{{{r}^{4}}}};$Опуская промежуточные выкладки, запишем полученное в работе [1] аналитическое решение параболической сопряженной задачи (рис. 2):
(8)
$\tau = \frac{{\psi \left( {2 - \psi } \right)}}{{2{{{\left( {1 - \psi } \right)}}^{2}}}} + {\text{ln}}\left( {1 - \psi } \right).$Рис. 2.
Зависимость параметра испарения от безразмерного времени для параболического уравнения теплопроводности.
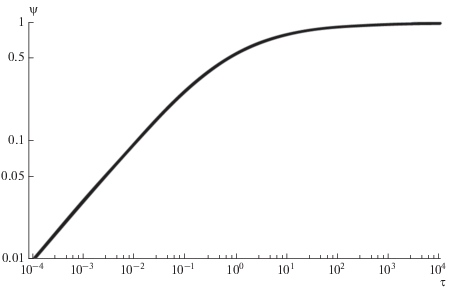
Рассмотрим асимптотики решения (8). В начальный момент доля теплового потока, идущего на испарение, является пренебрежимо малой, и практически весь теплоподвод к твердому телу идет на его нагрев:
Устремляя время облучения к бесконечности, приходим ко второму предельному случаю. Мишень полностью прогревается, весь подводимый к поверхности тепловой поток расходуется на испарение:
При этом в соответствии с (5) температура поверхности будет стремиться к своему постоянному максимальному значению:
Коэффициент теплоотдачи. Представим поток теплопроводности в виде: ${{q}_{{{\lambda }}}} = \alpha \vartheta ,$ где $\alpha $ – коэффициент теплоотдачи. Из теории теплопроводности [2] известно, что коэффициент теплоотдачи для полуограниченного тела может изменяться
в диапазоне ${{\alpha }_{\vartheta }} \leqslant \alpha \leqslant {{\alpha }_{q}}.$ Здесь нижние индексы обозначают соответствующие термические ГУ:  – первого рода $\left( {\vartheta = {\text{const}}} \right);$
– первого рода $\left( {\vartheta = {\text{const}}} \right);$ 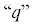 – второго рода $\left( {q = {\text{const}}} \right).$ Для дальнейшего анализа целесообразно ввести безразмерные коэффициенты теплоотдачи,
определяемые соотношениями:
– второго рода $\left( {q = {\text{const}}} \right).$ Для дальнейшего анализа целесообразно ввести безразмерные коэффициенты теплоотдачи,
определяемые соотношениями:
(9)
$\tilde {\alpha } = \alpha \sqrt {\frac{{{{t}_{0}}}}{{\lambda c\rho }}} ,\,\,\,\,{{\tilde {\alpha }}_{\vartheta }} = {{\alpha }_{\vartheta }}\sqrt {\frac{{{{t}_{0}}}}{{\lambda c\rho }}} ,\,\,\,\,{{\tilde {\alpha }}_{q}} = {{\alpha }_{q}}\sqrt {\frac{{{{t}_{0}}}}{{\lambda c\rho }}} .$При этом выполняется двойное неравенство: ${1 \mathord{\left/ {\vphantom {1 {\sqrt {3\tau } }}} \right. \kern-0em} {\sqrt {3\tau } }} \leqslant \tilde {\alpha } \leqslant \sqrt {{3 \mathord{\left/ {\vphantom {3 {\left( {4\tau } \right)}}} \right. \kern-0em} {\left( {4\tau } \right)}}} .$ С учетом (9) формулу (6) для параметра испарения можно представить в виде:
Как показывает анализ асимптотик решения (8), в процессе облучения твердого тела термическое состояние его поверхности будет эволюционировать между двумя предельными вариантами – от $q = {\text{const}}$ к $\vartheta = {\text{const}}{\text{.}}$ Согласно (9), для указанных случаев будем иметь следующие асимптотики:
С учетом этого решение (8) можно представить в виде:
(10)
$\psi = {{\left\{ {1 + \left[ {\sqrt 3 {{{\tilde {\alpha }}}_{\vartheta }} + \left( {\sqrt {8{\text{/}}3} {{{\tilde {\alpha }}}_{q}} - \sqrt 3 {{{\tilde {\alpha }}}_{\vartheta }}} \right)\varphi } \right]} \right\}}^{{ - 1}}}.$Соотношение (10) представляет собой явную форму записи решения (8) для параметра испарения. Здесь
Для эталонного случая ПУТ выражение (10) принимает вид:
(11)
$\psi = 1 + {{\tau }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\left[ {1 + \left( {\sqrt 2 - 1} \right){{{\left( {1 + {{\tau }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} \right].$ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Гипотеза теплопроводности Фурье. Аналитическая теория теплопроводности берет свое начало от доклада Фурье (Fourier) “О распространении тепла в твердом теле”, с которым он выступил в Париже в 1807 г. В законченном виде Фурье представил свою теорию в 1822 г. в работе “Аналитическая теория тепла (Théorie analytique de la chaleur), которую Кельвин (Kelvin) назвал "великой математической поэмой”. Фундаментальный результат, который носит имя закона Фурье (или гипотезы теплопроводности Фурье), гласит, что поток тепла $q$ пропорционален градиенту температуры11:
(12)
$q\left( {x,t} \right) = - \lambda {\text{\;}}\frac{{\partial \vartheta \left( {x,t} \right)}}{{\partial x}}.$Для полного описания процесса распространения тепла в неподвижной среде необходимо привлечь также закон сохранения энергии:
Отсюда следует параболическое уравнение (2). Рассмотрим принадлежащее Кельвину классическое решение ПУТ о точечном тепловом источнике. Пусть в момент $t = 0$ в точке x $~ = 0$ мгновенно выделяется количества тепла $Q.$ Решением уравнения (2) с начальным условием $\vartheta \left( {x,0} \right) = 0$ при $ - \infty < x < \infty $ будет:
Решение Кельвина описывает затухающую во времени тепловую диффузию и характеризуется мгновенным распространением теплового сигнала:
Эта свойство ПУТ наглядно иллюстрирует известный “парадокс Фурье”: тепловое возмущение в какой-либо точке тела приводит к мгновенному изменению температуры во всех других его точках. Исследуя парадокс Фурье, Риман (Riemann) показал, что различным видам изотермических поверхностей соответствуют различные дифференциальные операторы теплопроводности (в частности, линейный оператор параболического типа). Следовательно, гипотеза Фурье является неполной, так как она не содержит параметров, ограничивающих скорость распространения тепла. Необходимость введения таких параметров обусловлена механизмом переноса тепла элементарными частицами вещества – электронами, молекулами, ионными решетками. Поэтому результат теплопереноса – формирование поля температур в твердом теле – также должен определяться процессами, связанными с периодическими колебаниями этих частиц. Отсюда следует, что закон распространения тепла должен иметь волновой характер, определяемый параметрами движения частиц (скоростью, длиной и временем свободного пробега, взаимодействием при соударении).
Традиционно полагается, что для большинства задач теплопроводности влияние конечной скорости распространения тепла пренебрежимо мало. Поэтому для описания теплопереноса в твердом теле практически всегда используется ПУТ. Конечная скорость распространения тепловых возмущений учитывается лишь при исследовании процессов с экстремальными тепловыми воздействиями и со сверхбыстрым изменением температурных полей. Характерным примером таких явлений служит воздействие на поверхность мишени мощных импульсных тепловых потоков при лазерной обработке материалов, время протекания которых составляет нано- или фемтосекунды. К числу других относятся процессы, связанные с нагреванием при трении с аномально высокой скоростью, а также при “тепловом ударе”.
Гипотеза теплопроводности Каттанео–Вернотте. В 1958 г. Каттанео (Cattaneo) [8] и Вернотте (Vernotte) [9] независимо предложили обобщение классического закона теплопроводности путем учета в соотношении (12) времени тепловой релаксации ${{t}_{r}}{\text{:}}$
(13)
$q\left( {x,t + {{t}_{r}}} \right) = - \lambda {\text{\;}}\frac{{\partial \vartheta \left( {x,t} \right)}}{{\partial x}}.$Раскладывая левую часть (13) в ряд Тейлора по ${{t}_{r}},$ получаем в нулевом приближении – гипотезу Фурье (12), в первом приближении – гипотезу Каттанео–Вернотте:
(14)
$q\left( {x,t} \right) + {{t}_{r}}\frac{{\partial q\left( {x,t} \right)}}{{\partial t}} = - \lambda ~\frac{{\partial \vartheta \left( {x,t} \right)}}{{\partial x}}.$Использование формулы (14) в уравнении сохранения энергии приводит к гиперболическому уравнению теплопроводности (ГУТ):
(15)
$\frac{{\partial \vartheta }}{{\partial t}} + {{t}_{r}}\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{t}^{2}}}} = a\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{x}^{2}}}}.$Уравнение (15) учитывает запаздывание реакции неравновесной системы на термическое возмущение. Этот эффект является следствием инерционности теплового потока, который откликается на изменение температурного градиента не мгновенно (как в равновесной системе), а через конечное время ${{t}_{r}}.$ При ${{t}_{r}} \to 0$ уравнение (15) сводится к классическому параболическому уравнению (2).
Важные задачи нестационарной теплопроводности для гиперболической моделей переноса детально рассмотрены в работах Карташова [10–12]. В них развит аналитический подход, приводящий к новым интегральным соотношениям, которые могут непосредственно использоваться для проведения численных расчетов. Автор [10–12] дал исчерпывающе описание волнового механизма нестационарной теплопроводности с учетом конечной скорости распространения тепла. В работе [13] получено точное аналитическое решение ГУТ для бесконечной пластины при ГУ первого рода. Показано, что прогрев (охлаждение) твердого тела может быть описан как движение теплового слоя, на границе которого имеет место скачок температуры.
Пространственно-неоднородные структуры. В большинстве исследований полагается, что скорость переноса тепла по порядку величины совпадает со скоростью звука $w$. Это означает, что время релаксации является характеристикой вещества, которую можно оценить как ${{t}_{r}}{\text{\;}} \approx {a \mathord{\left/ {\vphantom {a {{{w}^{2}}}}} \right. \kern-0em} {{{w}^{2}}}}.$ Для твердых тел, жидкостей и газов это дает диапазон величин: ${{t}_{r}} \approx {{10}^{{ - 12}}} \ldots {{10}^{{ - 8}}}$ с. Отсюда делается вывод о пренебрежимо малой роли тепловой релаксации в подавляющем числе практических задач.
В резкое противоречие с такими оценками вступили результаты экспериментов [14] по измерению нестационарной температурной функции в засыпках (мокрый песок, пищевая сода, стеклянные шарики) в воздушной сплошной среде. Обработка опытных данных [14] дала огромные (по сравнению с общепринятыми) времена релаксации в диапазоне от 10 до 54 с. Сопоставимые с этими значения (${{t}_{r}} \approx $ 15 с) были получены также в опытах [15] по измерению нестационарного поля температур при контакте двух образцов биологической ткани. С другой стороны, в экспериментах [16, 17] с засыпкой из песка и биологической ткани не был зарегистрирован сколь-нибудь заметный эффект запаздывания теплового потока. Авторы [16, 17] описывали свои опытные данные с помощью классического ПУТ.
Сравнительный анализ методик проведения эксперимента и обработки опытных данных [14–17], выполненный в работе [18], привел к следующим выводам.
• Автор [14] при определении коэффициента эффективной температуропроводности сыпучей среды ${{a}_{e}}$ применял решение параболического уравнения (2). Это значение далее использовалось для расчета времени релаксации, входящего в гиперболическое уравнение (15), что является некорректным. Кроме того, при описании экспериментальных данных в [14] допущена терминологическая путаница (связанная с определением коэффициентов теплопроводности и температуропроводности), ставящая под сомнение достоверность полученных результатов.
• В работе [15] с высокой точностью измерялось поле температур в образце, а также проводились тарировочные опыты с нагревом алюминиевой пластины. К недостаткам методики [15] следует отнести измерение каждого теплофизических параметров среды (теплопроводности ${{\lambda }_{e}},$ теплоемкости ${{c}_{e}}$ и плотности ${{\rho }_{e}}$) в отдельных независимых опытах. Это могло повлечь за собой существенные погрешности определения эффективного коэффициента температуропроводности ${{a}_{e}} = {{{{\lambda }_{e}}} \mathord{\left/ {\vphantom {{{{\lambda }_{e}}} {\left( {{{c}_{e}}{{\rho }_{e}}} \right)}}} \right. \kern-0em} {\left( {{{c}_{e}}{{\rho }_{e}}} \right)}}$ и как следствие – времени релаксации.
• В экспериментах [16] с засыпкой из мокрого песка методически спорно проводилось определение ${{a}_{e}}.$ Кроме того, подвод тепла к образцу осуществлялся путем электрообогрева, что соответствует ГУ второго рода. При этом температура поверхности определялась как средняя за период нагрева, что существенно снижает точность полученных результатов.
• Также, как и в работах [14, 16], применяемая в работе [17] методика определения ${{a}_{e}}$ представляется спорной. Кроме того, используемый в опытах [17] способ обогрева образца за счет циркуляции теплоносителя соответствует ГУ третьего рода. Наконец, измерение нестационарного поля температур в образце с опросом одной термопары в секунду не позволяло корректно оценивать время релаксации.
С целью разрешения противоречий, возникших при систематизации опытных данных [14–17], авторы [18] провели специальные опыты, в ходе которых одновременно измерялись эффективная температуропроводность среды ${{a}_{e}}$ и время релаксации ${{t}_{r}}.$ Использовались различные виды засыпки: искусственный песок; порошок (гидроксида натрия и оксида алюминия); свинцовые шарики с медным покрытием. Для воспроизведения условий экспериментов [15, 17] исследовалась также биологическая ткань.
Рабочим телом в экспериментах [18] служила цилиндрическая засыпка диаметром 40 мм и высотой 80 мм. В качестве газового наполнителя использовались воздух, гелий, азот, аргон. Опыты проводились для различных значений давления и температуры газового наполнителя. Гармонические пульсации температуры генерировались на поверхности образца с помощью элемента Пельтье. Распределение температур по оси образца измерялось шестью термопарами, расположенными с шагом 10 мм. Измерявшиеся в опытах фазовый сдвиг пульсаций и декремент затухания их амплитуды использовались совместно с результатами аналитического решения ГУТ для полуограниченного тела. Найденные таким образом значения ${{a}_{e}},{{t}_{r}}$ сопоставлялись с результатами работ [14–17] (табл. 1). Как видно из таблицы, полученные в [18] значения ${{t}_{r}}$ оказались примерно на порядок меньшими, чем в работах [14, 15]. Была также установлена сильная зависимость ${{t}_{r}}$ от характерного размера частиц в засыпке и от температуры среды.
Таблица 1.
Сопоставление значений эффективной температуропроводности ${{a}_{e}}$ и времени релаксации ${{t}_{r}},$ измеренных в экспериментах [14–18]
| Материал | ${{a}_{e}} \times {{10}^{6}}$, м2/с | ${{t}_{r}}$, с | Источник |
|---|---|---|---|
| Песок | 0.226 | 2.26 | [18] |
| Песок | 0.408 | 20 | [14] |
| Песок | 0.218 | 0 | [16] |
| Песок | 0.169 | 0 | [17] |
| Пищевая сода | 0.185 | 0.66 | [18] |
| Пищевая сода | 0.310 | 28.7 | [14] |
| Биологическая ткань | 0.132 | 1.77 | [18] |
| Биологическая ткань | 0.140 | 15.5 | [15] |
| Биологическая ткань | 0.130 | 0 | [17] |
Оценка времени релаксации. Проведем оценку времени тепловой релаксации в телах с пространственно-неоднородной структурой на основе приведенных в [18] экспериментальных данных. Логично предполагать, что причиной сильного запаздывания теплового сигнала в сыпучих средах является их ячеистая структура, препятствующая распространению тепла. Механизм теплопроводность здесь затруднен в силу точечного контакта соприкасающихся частиц, поэтому теплоперенос будет осуществляться путем свободной конвекции в газовом наполнителе. Следовательно, эффективная теплопроводность образца должна зависеть от размера частиц, характера их упаковки в засыпке, а также от рода используемого газа и его температуры. Так, в серии экспериментов [18] для засыпки из свинцовых шариков диаметром 4.4 мм с газовым наполнителем из смеси аргона и азота было получено: ${{a}_{e}}$ ≈ 8 × 10–6 м2/с; ${{t}_{r}}$ ≈ 14 с.
Для проведения оценок воспользуемся аналитическим решением [19] задачи о скачке температур на поверхности шара, полученным с помощью интегрального метода теплового баланса:
Здесь $\Delta = {{\left( {{{\vartheta }_{s}} - {{\vartheta }_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\vartheta }_{s}} - {{\vartheta }_{0}}} \right)} {{{\vartheta }_{s}}}}} \right. \kern-0em} {{{\vartheta }_{s}}}};$ ${{\vartheta }_{s}} = {\text{const}}~$ – температура поверхности; ${{\vartheta }_{0}}\left( t \right)$ – температура в центре шара; ${{d}_{0}}$ – диаметр шара. Сделаем следующие допущения.• Диаметр условной ячейки засыпки (включающей собственно шарик и окружающий его газ) равен удвоенному диаметру шарика в засыпке ${{d}_{0}}$ = 8.8 мм.
• Время релаксации равно промежутку времени, в течении которого центр шара прогреется на 95%: ${{\vartheta }_{0}} = 0.95{{\vartheta }_{s}};$ $\Delta $ = 0.05.
Заменяя температуропроводность шара $a$ на ее эффективное значение ${{a}_{e}}$ для ячейки неоднородной среды, будем иметь: ${{t}_{r}} \approx {{0.107d_{0}^{2}} \mathord{\left/ {\vphantom {{0.107d_{0}^{2}} {{{a}_{e}}}}} \right. \kern-0em} {{{a}_{e}}}}.$ Для приведенных выше условий опытов [18] отсюда получаем близкую к измеренной величину: ${{t}_{r}}$ ≈ 10.4 с. Проведенные оценки свидетельствуют в пользу корректности полученных в эксперименте [18] значений времени релаксации.
Другим ярким примером проявления существенной тепловой релаксации в среде являются результаты работы [20], полученные при экспериментальном исследовании переходного термического процесса в пластине из полиметилметакрилата. Было установлено, что при внезапном погружении в горячую дистиллированную воду температура в центре пластины в течение определенного времени остается неизменной. Затем пластина начинает нагреваться со скоростью, значительно меньшей, чем это предсказывает решение ГУП с ГУ третьего рода. Для обработки экспериментальных данных авторы [20] использовали уравнение теплопроводности, выведенное Лыковым [21] из системы дифференциальных уравнений Онзагера. В отличие от стандартного ГУТ это уравнение содержит дополнительный член со смешанной третьей производной от температуры (по времени и по поперечной координате), а также новую физическую константу ${{t}_{T}}$ – “время демпфирования температуры”22. В итоге авторы [20] получили: ${{t}_{r}} = 3.5$ с, ${{t}_{T}} = 2.45$ с. Для настоящего анализа важно, что рассчитанное в [20] значение ${{t}_{r}}$ весьма близко к полученным в [18] значениям для случаев песка и биологической ткани.
ПОСТРОЕНИЕ АНАЛИТИЧЕСКОГО РЕШЕНИЯ
Интегральное преобразование Лапласа. Как известно [10–12], основным инструментом нахождения аналитических решений краевых задач нестационарной теплопроводности в областях канонического типа (пластина, цилиндр, шар) является операционный метод. В его основе лежит процедура интегральных преобразований Лапласа и Фурье, позволяющая перевести дифференциальные уравнения в частных производных в класс обыкновенных дифференциальных уравнений. Последние, в свою очередь, сводятся к алгебраическим (операторным) уравнениям. Важно отметить, что операционный метод применим только для линейных уравнений теплопроводности с постоянными коэффициентами и линейными граничными условиями. Как известно [10–12], преобразование Лапласа переводит оригинал $f\left( {x,t} \right)$ в изображение $F\left( {p,t} \right)$ путем интегрирования с весовой функцией:
Ниже мы будем символически обозначать эту процедуру как $f\left( {x,t} \right) \Rightarrow F\left( {p,t} \right).$Автор [10, 11] подчеркивает особенность краевых задач гиперболической модели теплопроводности: несмотря на свое сравнительно простое математическое описание они в большинстве случаев не позволяют получить замкнутое аналитическое решение. Это делает нахождение точных решений задач для ГУТ существенно более трудоемким по сравнению с параболическим случаем. Использование операционных методов приводит в этом случае к сложным функциональным конструкциям в пространстве изображений (по Фурье или по Лапласу). Вследствие этого справочники по операционному исчислению [12, 23] содержат сравнительно небольшую часть оригиналов исследованных к настоящему времени конструкций. В подавляющем большинстве случаев эти оригиналы не могут быть найдены в аналитическом виде, поэтому решение записывается в виде весьма сложных квадратур. Тем большую ценность приобретают в этой связи те немногочисленные случаи, которые допускают аналитическое решение.
Граничное условие первого рода. В работе [24] было получено аналитическое решение ГУТ со стационарным ГУ первого рода для полуограниченного тела с помощью интегрального преобразования Лапласа:
Ниже приводится обобщение решения [24] на случай, когда температура поверхности тела является произвольной функцией времени: ${{\vartheta }_{0}}\left( t \right).$ Зададим однородные начальные условия в виде:
На бесконечности должно выполняться условие затухания температурных возмущений:
Для этого случая интегрирование уравнения (15) с учетом гипотезы Каттанео–Вернотте (14) дает выражение для теплового потока в следующем виде:
По этой квадратуре при известной температурной функции $\vartheta \left( {x,t} \right)$ можно рассчитать тепловой поток в любой точке тела в произвольный момент времени.
Для преобразований Лапласа температуры и граничного условия будем писать:
Решением в области изображений будет:
Обращаясь к таблицам [12, 23], восстанавливаем оригинал и находим решение исследуемой краевой задачи в виде:
Здесь введены следующие обозначения:
Граничное условие второго рода. По аналогии с полученным выше решением будем использовать операционный метод для случая нестационарного ГУ второго рода:
где ${{q}_{0}}\left( t \right)$ – произвольная функция времени. На бесконечности должно выполняться условие затухания градиента температур:Это условие можно заменить на эквивалентное условие:
Преобразования Лапласа для рассматриваемого случая пишем в виде:
Будем иметь следующее решение в области изображений:
Возвращаясь к таблицам оригиналов [12, 23], получаем:
Здесь величина ${{J}_{2}}$ обозначает следующий интеграл:
Относительные коэффициенты теплоотдачи. Введем коэффициент теплоотдачи, связывающий тепловой поток и температуру на поверхности твердого тела:
Из полученных выше аналитических решений следует:
(16)
$\left. {\begin{array}{*{20}{c}} {{{\alpha }_{\vartheta }} = \sqrt {\frac{{\rho \lambda {{c}_{p}}}}{{{{t}_{r}}}}} \exp \left( { - \tilde {t}} \right){{I}_{0}}\left( {\tilde {t}} \right),} \\ {{{\alpha }_{q}} = \sqrt {\frac{{\rho \lambda {{c}_{p}}}}{{{{t}_{r}}}}} exp\left( {\tilde {t}} \right){{{\left\{ {{{I}_{0}}\left( {\tilde {t}} \right) + 2\tilde {t}\left[ {{{I}_{0}}\left( {\tilde {t}} \right) + {{I}_{1}}\left( {\tilde {t}} \right)} \right]} \right\}}}^{{ - 1}}}.} \end{array}} \right\}$Если время релаксации пренебрежимо мало $\left( {{{t}_{r}} \to 0} \right),$ будем иметь $\tilde {t} \to \infty ,$ и формулы (16) будут описывать коэффициент теплоотдачи для параболического случая:
(17)
$\left. {\begin{array}{*{20}{c}} {{{\alpha }_{{\vartheta *}}} = \sqrt {\frac{{\rho \lambda {{c}_{p}}}}{{\pi t}}} ,} \\ {{{\alpha }_{{q*}}} = \frac{{\sqrt \pi }}{2}\sqrt {\frac{{\rho \lambda {{c}_{p}}}}{t}} .} \end{array}} \right\}$Опираясь на эталонные значения (17), введем относительные коэффициенты теплоотдачи, позволяющие выразить влияние конечной скорости передачи тепла:
Для ГУ первого и второго рода из (16), (17) получаем:
(18)
$\left. {\begin{array}{*{20}{c}} {{{\Psi }_{\vartheta }} = \sqrt {2\pi \tilde {t}} ~{\text{exp}}\left( { - \tilde {t}} \right){{I}_{0}}\left( {\tilde {t}} \right),} \\ {{{\Psi }_{q}} = \sqrt {\left( {8{\text{/}}\pi } \right)\tilde {t}} ~{\text{exp}}\left( {\tilde {t}} \right){{{\left\{ {{{I}_{0}}\left( {\tilde {t}} \right) + 2\tilde {t}\left[ {{{I}_{0}}\left( {\tilde {t}} \right) + {{I}_{1}}\left( {\tilde {t}} \right)} \right]} \right\}}}^{{ - 1}}}.} \end{array}} \right\}$Рассмотрим асимптотики (18). При ${{t}_{r}} \to 0$ оба выражения (18) сводятся к эталонному параболическому случаю:
При ${{t}_{r}} \to \infty $ будем иметь случай максимального влияния гиперболичности:
Рис. 3.
Относительный коэффициент теплоотдачи: 1 – граничное условие первого рода; 2 – граничное условие второго рода.
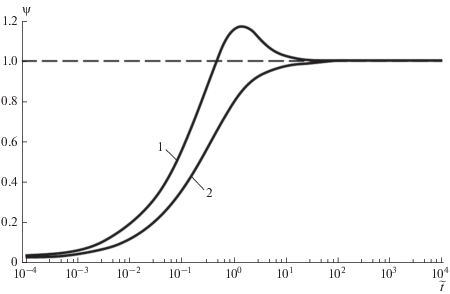
Как видно из рисунка, при увеличении $\tilde {t}$ функция$~{{\Psi }_{q}}$ монотонно возрастает от 0 до 1. В то же время зависимость ${{\Psi }_{\vartheta }}$ обнаруживает локальный максимум с координатами: $\tilde {t} = 1.58,$ ${{\Psi }_{\vartheta }} = 1.175.$ Из (16) следует, что в начальный момент времени коэффициенты теплоотдачи для обоих ГУ описываются соотношением:
Сопоставление этой асимптотики с эталонными значениями (17) демонстрирует радикальное различие параболической и гиперболической моделей теплопроводности.
• $\vartheta = {\text{const}}{\text{.}}$ В параболическом случае начальный тепловой поток принимает бесконечно большое значение, в гиперболическом случае – остается конечным.
• $q = {\text{const}}{\text{.}}$ В начале обогрева перепад температур на поверхности для ПУТ равен нулю, а для ГУТ – скачкообразно возрастает до некоторого фиксированного значения.
ОБОБЩЕННОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
Безразмерные коэффициенты теплоотдачи. Введем безразмерное время релаксации: ${{\tau }_{r}} = {{{{t}_{r}}} \mathord{\left/ {\vphantom {{{{t}_{r}}} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}$ и перейдем в (16) к безразмерным коэффициентам теплоотдачи, определяемым формулой (9):
(19)
$\left. {\begin{array}{*{20}{c}} {{{{\tilde {\alpha }}}_{\vartheta }} = \tau _{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}{\text{exp}}\left( { - \tilde {t}} \right){{I}_{0}}\left( {\tilde {t}} \right),} \\ {{{{\tilde {\alpha }}}_{q}} = \tau _{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}{\text{exp}}\left( {\tilde {t}} \right){{{\left\{ {{{I}_{0}}\left( {\tilde {t}} \right) + 2\tilde {t}\left[ {{{I}_{0}}\left( {\tilde {t}} \right) + {{I}_{1}}\left( {\tilde {t}} \right)} \right]} \right\}}}^{{ - 1}}}.} \end{array}} \right\}$Соотношения (19) содержат два различных безразмерных времени – $\tau = {t \mathord{\left/ {\vphantom {t {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},\tilde {t} = {t \mathord{\left/ {\vphantom {t {2{{t}_{r}}}}} \right. \kern-0em} {2{{t}_{r}}}}$ – и поэтому неудобны для последующего анализа. С погрешностью менее 1% их можно аппроксимировать формулами:
(20)
$\left. {\begin{array}{*{20}{c}} {{{{\tilde {\alpha }}}_{\vartheta }} = {{{\left( {\frac{{3{{\tau }_{r}} + \tau }}{{3\tau _{r}^{2} + 4{{\tau }_{r}}\tau + 3{{\tau }^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},} \\ {{{{\tilde {\alpha }}}_{q}} = {{{\left( {\frac{{3\left( {3{{\tau }_{r}} + \tau } \right)}}{{9\tau _{r}^{2} + 12{{\tau }_{r}}\tau + 4{{\tau }^{2}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.} \end{array}} \right\}$В свою очередь, в “гиперболическом пределе” $t \to 0$ эти величины определяются только временем релаксации:
Запишем конструкцию аналитического решения сопряженной задачи, обобщающее эталонный параболический вариант (10):
(21)
${{\psi }_{*}} = {{\left\{ {1 + \left[ {\sqrt 3 {{{\tilde {\alpha }}}_{\vartheta }} + \left( {\sqrt {{\text{8/}}3} {{{\tilde {\alpha }}}_{q}} - \sqrt 3 {{{\tilde {\alpha }}}_{\vartheta }}} \right){{\varphi }_{*}}} \right]} \right\}}^{{ - 1}}}.$В (21) входит переходная функция:
(22)
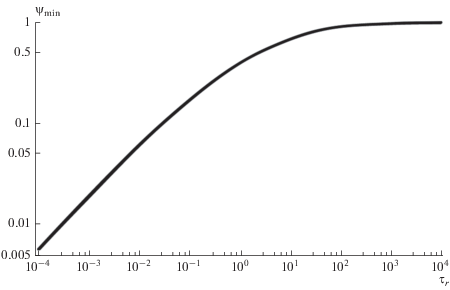
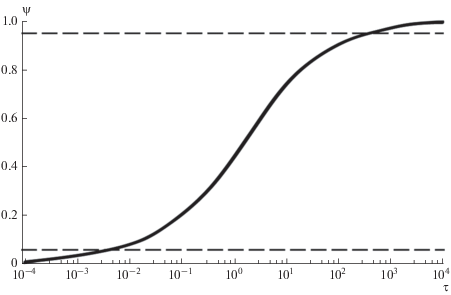
${{\varphi }_{*}} = {{3}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{\left( {\frac{{{{{\tilde {\alpha }}}_{\vartheta }}}}{{1 + \sqrt 3 {{{\tilde {\alpha }}}_{\vartheta }}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$Соотношения (19)–(22) представляют собой приближенное аналитическое решение сопряженной задачи “теплопроводность – испарение” для общего случая конечной скорости распространения тепла. На рис. 4 представлены функции ${{\psi }_{*}}\left( \tau \right)$ для различных значений ${{\tau }_{r}}.$ Как видно из рисунка, обобщенные зависимости представляют собой протяженные пологие участки в окрестности $\tau = 0,$ плавно переходящие в эталонную зависимость (8) для случая ${{t}_{r}} = 0$ (рис. 2). Важной особенностью общего решения для ГУТ является выход величины ${{\psi }_{*}}$ при $\tau = 0$ на фиксированную “гиперболическую полку”:
(23)
${{\psi }_{{*{\text{min}}}}} = {{\left( {1 + \sqrt {\frac{3}{{{{\tau }_{r}}}}} } \right)}^{{ - 1}}}.$Рис. 4.
Зависимость параметра испарения от времени для различных значений времени релаксации: 1 – ${{\tau }_{r}} = 0;$ 2 – ${{\tau }_{r}} = {{10}^{{ - 3}}};$ 3 – ${{\tau }_{r}} = {{10}^{{ - 2}}};$ 4 – ${{\tau }_{r}} = {{10}^{{ - 1}}};$ 5 – ${{\tau }_{r}} = {{10}^{0}}.$
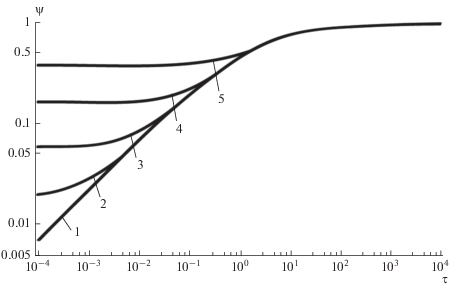
На рис. 5 приведена зависимость ${{\psi }_{{*{\text{min}}}}}\left( {{{\tau }_{r}}} \right).$ При ${{\tau }_{r}} = 0$ имеем предельный случай, описываемый ПУТ: ${{\psi }_{{*{\text{min}}}}} = 0.$ При увеличении времени релаксации ${{\psi }_{{*{\text{min}}}}}$ монотонно возрастает и при ${{\tau }_{r}} \to \infty $ достигает предельного значения: ${{\psi }_{{*{\text{min}}}}} = 1.$ Эта асимптотика соответствует полному выключению механизма теплопроводности: ${{\psi }_{*}} = {{\psi }_{{*{\text{min}}}}} = 1.$ Физически это означает, что во всем интервале $0 < \tau < \infty $ излучаемый тепловой поток полностью затрачивается на испарение: ${{q}_{u}} \to q = {\text{const}}{\text{.}}$
Двухзонная аппроксимация решения. Для проведения прикладных расчетов, а также приближенных физических оценок целесообразно использовать приближенную аппроксимацию решения (21). Для этого заменим пологие участки на рис. 3 на горизонтальные участки (“полки”) в интервале $0 \leqslant \tau \leqslant {{\tau }_{0}},$ ширина которых равна (рис. 6):
(24)
${{\tau }_{0}} = \frac{{2{{\tau }_{r}}\left( {5 + 3\sqrt {{{\tau }_{r}}} } \right)}}{{15\left( {1 + \sqrt {{{\tau }_{r}}} } \right)}}.$Рис. 6.
Двухзонная аппроксимация решения (21): 1 – ${{\tau }_{r}} = 0;$ 2 – ${{\tau }_{r}} = {{10}^{{ - 3}}};$ 3 – ${{\tau }_{r}} = {{10}^{{ - 2}}};$ 4 – ${{\tau }_{r}} = {{10}^{{ - 1}}};$ 5 – ${{\tau }_{r}} = {{10}^{0}}.$
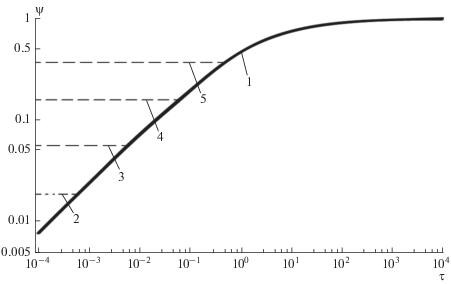
Как видно из формулы (24), время запаздывания ${{\tau }_{0}}$ оказывается пропорциональным времени релаксации: ${{\tau }_{0}} = 2{\text{/}}3{{\tau }_{r}}$ при ${{\tau }_{r}} = 0;$ ${{\tau }_{0}} = 2{\text{/}}5{{\tau }_{r}}$ при ${{\tau }_{r}} \to \infty .$ Согласно (23), высота “гиперболической полки” зависимости ${{\psi }_{*}}\left( \tau \right)$ однозначно определяется параметром релаксации:
В итоге можно записать двухзонную аппроксимацию аналитического решения:
(25)
$\psi = \left\{ {\begin{array}{*{20}{c}} {{{\psi }_{{*{\text{min}}}}},\,\,\,\,0 < \tau < {{\tau }_{0}}} \\ {\psi \left( \tau \right),\,\,\,\,{{\tau }_{0}} \leqslant \tau < \infty } \end{array}} \right..$Двухзонная аппроксимация дает наглядную картину влияния параметра релаксации на интенсивность испарения. Как видно из рис. 6, учет конечной скорости распространения тепла отсекает от предельной параболической кривой, описываемой формулой (8), “гиперболическую зону” протяженностью ${{\tau }_{0}}.$ Физически это означает, что в тепловом балансе (1) поток испарения при $\tau = 0$ скачкообразно возрастает от нуля до значения ${{q}_{u}} = {{\psi }_{{*{\text{min}}}}}q.$ Далее на протяжении гиперболической зоны $\left( {0 < \tau < {{\tau }_{0}}} \right)$ составляющие теплового баланса остаются неизменными. Начиная с момента $\tau = {{\tau }_{0}},$ реализуется “параболическая зона”, подчиняющаяся соотношению (8). С увеличением времени релаксации высота гиперболической полки увеличивается.
Приведенная двухзонная аппроксимация качественно подтверждает отмеченную в работах [10–13] тенденцию вырождения влияния времени релаксации на теплоперенос. На рис. 7 приведены предельные ситуации двухзонной аппроксимации. Так, значению ${{\psi }_{{*{\text{min}}}}} = 0.05$ соответствует время запаздывания ${{\tau }_{0}} \approx 5.5 \times {{10}^{{ - 3}}}.$ Здесь мы имеем протяженную параболическую зону, в течение которой происходит нарастание потока испарения. Значению ${{\psi }_{{*{\text{min}}}}} = 0.95$ отвечает ${{\tau }_{0}} \approx 400.$ При этом процесс теплопроводности практически перестает влиять на теплоперенос, так что на протяжении всей гиперболической зоны происходит рост потока испарения лишь на 5%.
Рис. 7.
Двухзонная аппроксимация решения (30): 1 – ${{\tau }_{r}} = 0;$ 2 – ${{\tau }_{r}} = {{10}^{{ - 3}}};$ 3 – ${{\tau }_{r}} = {{10}^{{ - 2}}};$ 4 – ${{\tau }_{r}} = {{10}^{{ - 1}}};$ 5 – ${{\tau }_{r}} = {{10}^{0}}.$
Влияние коэффициента конденсации. Полученное выше решение (19)–(22) является компактным и удобным для проведения расчетов. Однако для наглядного выявления влияние коэффициента конденсации на параметр испарения целесообразно представить решение в параметрическом виде. Введем для этого вместо соотношения (7) новый масштаб времени:
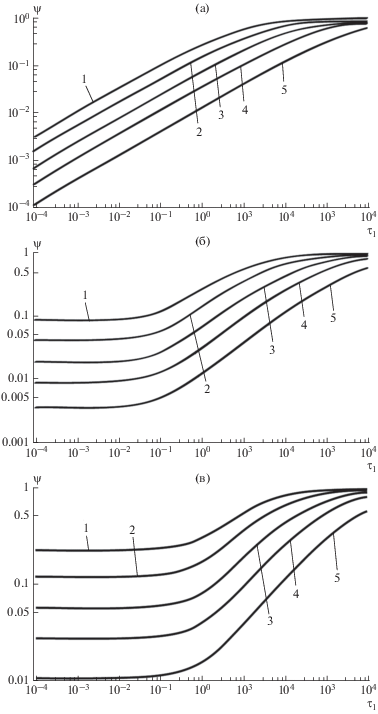
С учетом (26) будут переопределены также параметр релаксации $\left( {{{\tau }_{{r1}}} = {{{{t}_{r}}} \mathord{\left/ {\vphantom {{{{t}_{r}}} {{{t}_{{1~}}}}}} \right. \kern-0em} {{{t}_{{1~}}}}}} \right)$ и безразмерное время $\left( {{{\tau }_{1}} = {{{{t}_{1}}} \mathord{\left/ {\vphantom {{{{t}_{1}}} {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}} \right).$ В результате в задаче возникает дополнительный параметр $\beta .$ Как видно из рис. 8, при том же значении параметра релаксации при уменьшении $\beta $ кривые ${{\psi }_{*}}\left( \tau \right)$ смещаются вниз и вправо. Физически это означает две взаимосвязанные тенденции: перевод сопряженной задачи из гиперболической в параболическую; затягивание процесса испарения.
Рис. 8.
Влияние коэффициента конденсации на параметр испарения: 1 – $\beta = 1;$ 2 – $\beta = 0.6;$ 3 – $\beta = 0.3;$ 4 – $\beta = 0.15;$ 5 – $\beta = 0.06;$ а – ${{\tau }_{r}} = {{10}^{{ - 2}}};$ б – ${{\tau }_{r}} = {{10}^{{ - 1}}};$ в – ${{\tau }_{r}} = {{10}^{0}}.$
Дальнейшие рекомендации. Полученные в [14–18] экспериментальные и теоретические результаты являются дискуссионными и требуют проведения специальных исследований, которые выходят за пределы настоящей статьи. Перспективной представляется направление, намеченное в работе [26]. Было построено решение кинетического уравнения Больцмана для случая многомасштабной функции распределения молекул по скоростям. С помощью обобщенного метода Энскога–Чепмена авторы [26] получили, что в уравнениях переноса молекулярных потоков импульса и энергии появляются дополнительные члены, описывающие релаксационные эффекты. Их учет приводит к появлению добавочных слагаемых в выражениях для тензора вязких напряжений и вектора потока тепла.
Представленные результаты показывают важность учета эффекта релаксации теплового потока, являющегося составной частью механизма нестационарной теплопроводности. Полученное общее аналитическое решение позволяет проследить тенденции влияния физических факторов на параметр испарения и провести корректный анализ предельных вариантов.
ЗАКЛЮЧЕНИЕ
Проведено аналитическое исследование сопряженной задачи “испарение – теплопроводность” с учетом конечной скорости распространения тепла. Базовым условием является баланс теплового потока на поверхности облучаемого твердого тела (мишени), включающее две составляющие: поток теплопроводности и поток испарения. Для решения одномерного нестационарного параболического уравнения теплопроводности в полуограниченном теле применяется интегральный метод теплового слоя. Для расчета искомого параметра испарения используются результаты линейной кинетической теории. На основе анализа имеющихся экспериментальных и теоретических данных проведена оценка времени релаксации теплового потока в среде с пространственно-неоднородной структурой. Методом интегрального преобразования Лапласа получено аналитическое решение краевой задачи для гиперболического уравнения теплопроводности в случае нестационарных граничных условий первого и второго рода. Построено обобщенное аналитическое решение сопряженной задачи, учитывающее влияние параметра релаксации на развитие процесса теплопереноса во времени. Проведен анализ влияния коэффициента конденсации на интенсивность испарения. Выполнена двухзонная аппроксимация аналитического решения, позволяющая выделить характерные параметры сопряженной задачи: время запаздывания, высота гиперболической полки, гиперболическая и параболическая зоны процесса испарения.
ОБОЗНАЧЕНИЯ
$a$ – коэффициент температуропроводности; $c$ – удельная теплоемкость; $q$ – тепловой поток; ${{q}_{\lambda }}$ – поток теплопроводности; ${{q}_{u}}$ – поток испарения; $t$ – время; ${{t}_{0}}~$– масштаб времени; ${{t}_{r}}$ – время тепловой релаксации; $\alpha $ – коэффициент теплоотдачи; $\tilde {\alpha }$ – безразмерный коэффициент теплоотдачи; $\delta $ – толщина теплового слоя; $\vartheta $ – температура; $\lambda $ – коэффициент теплопроводности; $\psi $ – параметр испарения; ${{\psi }_{*}}$ – обобщенный параметр испарения; $\Psi $ – относительный коэффициент теплоотдачи; $\rho $ – плотность, $\tau $ – безразмерное время.
Список литературы
Зудин Ю.Б., Уртенов Д.С., Устинов В.С. Анализ сопряженной задачи испарение–теплопроводность. Изв. РАН. Энергетика. 2020. № 1 С. 138–158.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М. Высшая школа, 2001. 540 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М. URSS. 2012. 653 с.
Карташов Э.М., Кудинов В.А. Аналитические методы теории теплопроводности и ее приложений. М.: URSS. 2018. 1080 с.
Bäuerle D.W. Laser Processing and Chemistry. Springer. 2011. 851 p.
Анисимов С.И., Лукьянчук Б.С. Избранные задачи теории лазерной абляции. УФН. 2002. 172:3. С. 301–333.
Муратова Т.М., Лабунцов Д.А. Кинетический анализ процессов испарения и конденсации // ТВТ. 1969. Т. 7. № 5. С. 959–967.
Cattaneo C.A. Form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compt. Rend. 1958. V. 247. P. 431–433.
Vernotte P. Les paradoxes de la théorie continue de i’equation de la chaleur. Compt. Rend. 1958. V. 246. P. 3154–3155.
Карташов Э.М. Краевые задачи для гиперболических моделей переноса. Вестн. МИТХТ. 2008. Т. 3. № 3. С. 20–22.
Карташов Э.М. Аналитические решения гиперболических моделей нестационарной теплопроводности. Тонкие химические технологии. 2018. Т. 13. № 2. С. 81–90.
Карташов Э.М. Оригиналы операционных изображений для обобщенных задач нестационарной теплопроводности. Тонкие химические технологии. 2019. Т. 14. № 4. С. 77–86
Кудинов В.А., Кудинов И.В. Получение и анализ точного аналитического решения гиперболического уравнения теплопроводности для плоской стенки. ТВТ. 2012. Т. 50. Вып. 1. С. 118–125.
Kaminski W. Hyperbolic heat conduction equation for materials with a non-homogeneous inner structure. ASME J. Heat Transfer. 1990. V. 112. P. 555–560.
Mitra K., Kumar S., Vedavarz A., Moallemi M.K. Experimental evidence of hyperbolic heat conduction in processed meat. J. Heat Transfer, Trans. ASME. 1995. V. 117. P. 568–573.
Graßmann A., Peters F. Experimental investigation of heat conduction in wet sand. Heat Mass Transfer. 1999. V. 35. P. 289–294.
Herwig H., Beckert K. Experimental evidence about controversy concerning Fourier or non-Fourier heat conduction in materials with nonhomogeneus inner structure. Heat Mass Transfer. 2000. V. 36. P. 387–392.
Roetzel W., Putra N., Das S.K. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int J Thermal Sci. 2005. V. 42. P. 541–552.
Антимонов М.С., Кудинов В.А., Стефанюк Е.В. Аналитические решения задач теплопроводности для цилиндра и шара на основе определения фронта температурного возмущения”. Журн. вычисл. матем. и матем. физ. 2008. Т. 48. № 4. С. 681–692.
Кирсанов, Ю. А. Кирсанов А.Ю., Юдахин А. Е. Измерение времени тепловой релаксации и демпфирования температуры в твердом теле. ТВТ. 2017. Т. 55. № 1. С. 122–128.
Лыков А.В. Применение методов термодинамики необратимых процессов к исследованию тепло- и массообмена. ИФЖ. 1965. Т. 9. № 3. С. 287–304.
Кудинов В.А., Кудинов И.В. Исследование теплопроводности с учетом конечной скорости распространения теплоты. ТВТ. 2013. Т. 51. № 2. С. 301–310.
Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Том 1. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. 344 с.
Баумейстер К., Хамилл Т. Гиперболическое уравнение теплопроводности. Решение задачи о полубесконечном теле. Теплопередача. 1969. № 4. С. 112–119.
Бейтмен Г., Эрдейи А. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. Т. 2. Высшие трансцендентные функции. М.: Наука, 1974. 296 с.
Синкевич О.А., Семенов А.М. Решение уравнения Больцмана методом разложения функции распределения в ряд Энскога по параметру Кнудсена в случае наличия нескольких масштабов зависимости функции распределения от времени и координат. ЖТФ. 2003. Т. 73. № 10. С. 1–5.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика