Известия РАН. Энергетика, 2022, № 4, стр. 25-42

Моделирование водородной пожар-струи с помощью методики КАБАРЕ

В. Ю. Глотов^1, *, А. А. Канаев¹, А. В. Данилин¹, В. Г. Кондаков¹

¹ Институт безопасного развития атомной энергетики РАН
Москва, Россия

Поступила в редакцию 16.02.2022
После доработки 14.04.2022
Принята к публикации 18.04.2022

EDN: PIRDIC
DOI: 10.31857/S0002331022040069

Аннотация

В настоящей работе проведено численное моделирование водородной пожар-струи в вихреразрешающем приближении с помощью беспараметрической методики КАБАРЕ. В статье представлено описание математических моделей термического излучения и реакций горения водородной пожар-струи, предложен способ аппроксимации уравнений переноса излучения. Получено хорошее соответствие результатов расчета с экспериментом по основным характеристикам пожар-струи (видимая длина пламени, доля излучаемого тепла, профиль радиационного теплового потока).

Ключевые слова: методика КАБАРЕ, пожар струя, тепловое излучение, диффузионное горение

1. ВВЕДЕНИЕ

Водородная энергетика (ВЭ) представляется перспективным альтернативным направлением развития топливно-энергетического комплекса России вследствие экологичности используемого топлива и продукта реакции горения в воздухе, а также широкого распространения этого химического элемента. В России в августе 2021 г. утверждена Концепция развития ВЭ, предполагающая использование водородных энергоносителей на внутреннем рынке уже к 2021–2024 гг. Технологии транспортировки и хранения водорода рассматриваются как один из наиболее значимых сдерживающих факторов развития ВЭ. Поскольку водород является воспламеняемым газом, а высокая удельная теплота сгорания водорода в воздухе обусловливает высокие поражающие характеристики при его взрывах, то задачи обоснования водородной безопасности являются неотъемлемой частью развития данных технологий. В настоящее время в России расчетные средства для обоснования водородной взрывобезопасности технологий транспортировки и хранения водорода и водородной энергетики в целом отсутствуют. Разработка перспективных моделей и инструментов на основе CFD и их валидация на современных экспериментальных данных позволит проводить анализ гипотетических аварий на качественно новом уровне.

В ИБРАЭ РАН для проведения численного анализа задач водородной безопасноcти разрабатывается программа для ЭВМ (ПрЭВМ) CABARET-SC1. Схема аппроксимации уравнений гидродинамики в ПрЭВМ CABARET-SC1 основана на методике КАБАР-Е [7], позволяющей проводить расчеты турбулентных течений в вихреразрешающем приближении на сетках с неполным разрешением масштабов турбулентности без использования настроечных параметров. Применение вихреразрешающих подходов к моделированию турбулентности для обоснования безопасности ВЭ позволяет устранить неопределенности, возникающие при использовании полуэмпирических RANS-моделей турбулентности, основанных на решении осредненных по времени уравнений Навье-Стокса, и за счет этого повысить прогнозные возможности в части распространения водорода.

Существенной угрозой и уязвимостью объектов инфраструктуры водородной энергетики при авариях является возгорание водорода при его истечении из резервуаров высокого давления с образованием турбулентного газового факела (пожар-струи). Горение пожар-струй обладает рядом существенных отличий от горения перемешанных горючих смесей, поэтому для его моделирования требуется применение специальных методов. Определение безопасных расстояний от водородной пожар-струи требует анализа процессов термического излучения пожар-струи. Таким образом, для выполнения расчетного анализа горения пожар-струи с помощью основанного на методике КАБАРЕ вихреразрешающего подхода к моделированию турбулентности требуется адаптация расчетной модели термического излучения и реакций диффузионного горения.

В настоящей работе представлено описание математических моделей термического излучения и реакций горения водородной пожар-струи, реализованных в ПрЭВМ CABARET-SC1, а также приведены результаты верификации программы на эксперименте по изучению характеристик турбулентного диффузионного водородного пламени, проведенного сотрудниками Национальной лаборатории Сандия [8].

2. МОДЕЛЬ ДИФФУЗИОННОГО ГОРЕНИЯ ВОДОРОДНОЙ ПОЖАР-СТРУИ

Диффузионное горение, частным примером которого является горение затопленных струй, имеет значительные отличия от горения перемешанных горючих смесей. В частности, в диффузионном горении топливо и окислитель поступают в зону горения отдельно друг от друга, при этом химические реакции преимущественно происходят вблизи поверхности, образуемой газовой смесью со стехиометрическим концентрационным соотношением топлива и окислителя. Диффузионное горение не может существовать в неподвижной среде, поскольку для его поддержания требуется постоянный отток продуктов реакции, накопление которых привело бы к погасанию пламени. Диффузионное горение, в отличие от горения перемешанных смесей, не имеет характерной скорости распространения. Диффузионное горение не имеет характерной толщины фронта горения. Фактически, данная толщина зависит от степени возмущенности поля скорости. Описанные выше свойства показывают серьезные отличия горения перемешанных смесей от диффузионного горения, что говорит о необходимости применения специальных методов для моделирования последних.

Одним из распространенных подходов к моделированию турбулентных диффузионных пламен является модель диссипации вихрей (eddy dissipation model, EDM), предложенная в 1977 году в работе [1]. В этой модели скорость расхода топлива и окислителя, кг/(м³ с), не зависит от кинетики химических реакций, а определяется скоростью турбулентного перемешивания реагентов по формуле:

(1)

${{\dot {r}}_{F}} = - A{{\rho \tau }}_{t}^{{ - 1}}\min \left( {{{Y}_{F}},{{{{Y}_{O}}} \mathord{\left/ {\vphantom {{{{Y}_{O}}} s}} \right. \kern-0em} s},{{B{{Y}_{P}}} \mathord{\left/ {\vphantom {{B{{Y}_{P}}} {\left( {1 + s} \right)}}} \right. \kern-0em} {\left( {1 + s} \right)}}} \right),$

где $A$, $B$ – модельные константы; ${{Y}_{F}}$, ${{Y}_{O}}$, ${{Y}_{P}}$ – массовые доли топлива, окислителя и продуктов горения; $s$ – стехиометрический коэффициент реакции; ${{\tau }_{t}}$ – временной масштаб турбулентного смешения, с.

Типичные значения модельных констант составляют $A = 4$, $B = 0.5$ [1].

Изначально данная модель разрабатывалась для моделирования турбулентного горения в рамках RANS подходов, где характерный временной масштаб, с, оценивается по формуле:

(2)

${{\tau }_{t}} = {k \mathord{\left/ {\vphantom {k \varepsilon }} \right. \kern-0em} \varepsilon },$

где k – кинетическая энергия турбулентности, Дж/м³; ε – скорость диссипации кинетической энергии турбулентности, Дж/м³/с.

Для применения рассматриваемой модели горения в LES подходах (в том числе в методике КАБАРЕ) временной масштаб турбулентных пульсаций, с, можно оценить по формуле:

(3)

${{\tau }_{t}} = {{\left( {\sqrt {2{{S}_{{ij}}}{{S}_{{ij}}}} } \right)}^{{ - 1}}},$

где ${{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)$ – тензор сдвиговых скоростей, с^–1.

3. МОДЕЛЬ ТЕРМИЧЕСКОГО ИЗЛУЧЕНИЯ ВОДОРОДНОЙ ПОЖАР-СТРУИ

3.1. Уравнения динамики излучающего газа

Для описания динамики излучающего газа уравнения Навье-Стокса дополняются интегро-дифференциальным уравнением переноса излучения [2]

(4)

$\frac{1}{c}\frac{{\partial {{I}_{\nu }}}}{{\partial t}} + \left( {\vec {s},\vec {\nabla }{{I}_{\nu }}} \right) = - \left( {{{\chi }_{\nu }} + {{\sigma }_{s}}} \right){{I}_{\nu }}{\text{ + }}{{\chi }_{\nu }}{{I}_{{\nu p}}} + \frac{{{{\sigma }_{s}}}}{{4\pi }}\int\limits_{4\pi } {{{I}_{\nu }}\left( {\vec {r},\vec {s}{\kern 1pt} '} \right){{\Phi }_{\nu }}\left( {\vec {s}{\kern 1pt} ',\vec {s}} \right)d\Omega {\kern 1pt} '} ,$

где ${{I}_{\nu }}$ – спектральная интенсивность излучения и направления движения фотонов $\vec {s}$ и частоты фотонов $\nu $, Вт/(м²Гц); ${{I}_{{\nu p}}} = {{2h{{v}^{3}}} \mathord{\left/ {\vphantom {{2h{{v}^{3}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}{{\left( {\exp \left\{ {\frac{{h\nu }}{{kT}}} \right\} - 1} \right)}^{{ - 1}}}$ – спектральная интенсивность равновесного излучения при температуре $T$ (формула Планка), Вт/(м² Гц); ${{\chi }_{\nu }}$, ${{\sigma }_{s}}$ – спектральные коэффициенты поглощения и рассеяния среды, м^–1.

При низких температурах (<0.5 кэВ) излучение влияет только на перераспределение энергии в веществе [2]. В этом случае в правую часть уравнении закона сохранения энергии добавляется плотность потока энергии излучения $\vec {W}$:

(5)

$\frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + {\text{div}}\left( {\left( {\rho E + P} \right)\vec {u}} \right) = - {\text{div}}\left( {\vec {q} + \vec {W}} \right),$

где $\vec {W} = \int_0^{4\pi } {\left( {\int_0^\infty {{{I}_{\nu }}} d\nu } \right)\vec {s}d\Omega } $, Вт/м².

Для задач радиационной газовой динамики характерна исключительная трудоемкость решаемых уравнений, вызванная многомерностью уравнения переноса излучения. Интенсивность излучения ${{I}_{\nu }} = {{I}_{\nu }}\left( {\vec {r},\vec {s},\nu ,t} \right)$ зависит не только от пространственных переменных $\vec {r}$ и времени t, но и от направления движения фотонов $\vec {s}$ и их частоты ν. На практике обычно используются различные приближения, позволяющие существенно упростить математическую модель. Например, для достаточно широкого класса задач можно пренебречь рассеянием фотонов, т.к. оно становится сопоставимым с поглощением либо при высоких температурах (>1 кэВ) и низких плотностях среды, либо при прохождении света через замутненные среды [2], в которых рассеяние фотонов происходит на оптических неоднородностях (аэрозолях).

Другим приближением является упрощенное моделирование спектра поглощения газа. Общее число линий в спектре поглощения может достигать десятки и сотни тысяч, поэтому для решения прикладных задач прямая модель, разрешающая отдельные спектральные линии (line-by-line model), не применима. В расчетах обычно используются интегральные модели, в которых коэффициенты поглощения усредняются по всему спектру. Одной из наиболее простых интегральных моделей, но и наименее точной, является модель “серого” газа. В ней используются планковские средние коэффициенты поглощения, полученные экспериментальным путем или теоретически на основе баз данных HITRAN, HITEMP со спектрами поглощения высокого разрешения [3]. Более точной интегральной моделью расчета поглощательной способности газов является модель взвешенной суммы “серых” газов (WSGG), предложенная Хоттелем [4]. В модели WSGG реальный газ представляется в виде совокупности небольшого количества эффективных “серых” газов с постоянным коэффициентом поглощения. Для каждого “серого” газа расчет переноса энергии излучения выполняется независимо, после чего интенсивность и радиационные потоки для исходного газа вычисляются путем суммирования вкладов каждого “серого” газа с надлежащими весовыми коэффициентами [5]. Недостатком модели WSGG, очевидно, является пропорциональное увеличение вычислительной сложности задачи от количества “серых” газов в модели.

В настоящей работе рассматривается упрощенная модель переноса излучения в приближении “серого” газа и при отсутствии рассеяния фотонов. В этом случае уравнение переноса излучения (4) примет вид

(6)

$\frac{1}{c}\frac{{\partial I}}{{\partial t}} + \left( {\vec {s},\vec {\nabla }I} \right) = \chi \left( {{{I}_{p}} - I} \right),$

где $I = \int_0^\infty {{{I}_{\nu }}d\nu } $ – интегральная интенсивность излучения, Вт/м²; ${{I}_{p}} = \frac{\sigma }{\pi }{{T}^{4}}$ – интегральная интенсивность равновесного излучения при температуре $T$, Вт/м²; $\chi $ – средний коэффициент поглощения газа, м^–1.

Вычисление среднего коэффициента поглощения газовой смеси производится по формуле

(7)

$\chi = \sum\limits_i {{{a}_{i}}{{P}_{i}}} ,$

где ${{a}_{i}}$ – осредненный по Планку коэффициент поглощения i-ой компоненты, бар^—1 м^–1; ${{P}_{i}}$ – парциальное давление i-ой компоненты, бар.

Для аппроксимации температурной зависимости осредненных по Планку коэффициентов поглощения газов используются полиномы высокой степени [6]. В водородной пожар-струе единственной оптически непрозрачной компонентной является водяной пар, образующийся при сгорании водорода в окружающем воздухе. Для водяного пара полином имеет вид [6]

(8)

${{a}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = - 0.23093 - 1.1239\theta + 9.4153{{\theta }^{2}} - 2.9988{{\theta }^{3}} + 0.51382{{\theta }^{4}} - 1.8684 \times {{10}^{{ - 5}}}{{\theta }^{5}},$

где $\theta = {{1000} \mathord{\left/ {\vphantom {{1000} T}} \right. \kern-0em} T}$; $T$ – температура в Кельвинах.

3.2. Метод дискретных ординат

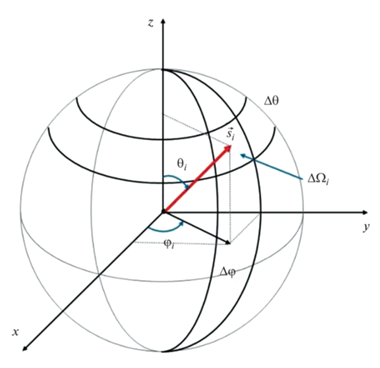
Решение уравнения (6) будем искать с помощью конечно-объемного метода дискретных ординат (FVDOM) [5]. В методах дискретных ординат все угловое пространство разбивается на ряд дискретных телесных углов $\Delta {{\Omega }_{i}}$, в каждом из которых интенсивность излучения равна среднему значению по этому углу ${{I}_{i}}$. Наиболее простым способом дискретизации углового пространства является прямоугольная сетка с постоянным шагом по углам $\varphi $ и $\theta $ (рис. 1).

Рис. 1.

Сфера направлений.

Внутри i-го телесного угла $\Delta {{\Omega }_{i}}$ вектор направлений может принимать значения

(9)

$\vec {s} = \left( {\cos {\kern 1pt} \varphi \sin {\kern 1pt} \theta ,\sin {\kern 1pt} \varphi \sin {\kern 1pt} \theta ,\cos {\kern 1pt} \theta } \right),$

где $\varphi \in \left( {{{\varphi }_{i}} - {{\Delta \varphi } \mathord{\left/ {\vphantom {{\Delta \varphi } {2,{{\varphi }_{i}} + {{\Delta \varphi } \mathord{\left/ {\vphantom {{\Delta \varphi } 2}} \right. \kern-0em} 2}}}} \right. \kern-0em} {2,{{\varphi }_{i}} + {{\Delta \varphi } \mathord{\left/ {\vphantom {{\Delta \varphi } 2}} \right. \kern-0em} 2}}}} \right)$, $\theta \in \left( {{{\theta }_{i}} - {{\Delta \theta } \mathord{\left/ {\vphantom {{\Delta \theta } {2,{{\theta }_{i}} + {{\Delta \theta } \mathord{\left/ {\vphantom {{\Delta \theta } 2}} \right. \kern-0em} 2}}}} \right. \kern-0em} {2,{{\theta }_{i}} + {{\Delta \theta } \mathord{\left/ {\vphantom {{\Delta \theta } 2}} \right. \kern-0em} 2}}}} \right)$, углы ${{\varphi }_{i}}$ и ${{\theta }_{i}}$ определяют положение центра ${{\vec {s}}_{i}}$ телесного угла $\Delta {{\Omega }_{i}}$.

Для дискретизации уравнение переноса излучения (6) на сфере направлений проинтегрируем его по контрольному телесному углу $\Delta {{\Omega }_{i}}$. Получим

(10)

$\frac{1}{c}\frac{{\partial {{I}_{i}}}}{{\partial t}} + \frac{1}{{\Delta {{\Omega }_{i}}}}{\text{div}}\left( {{{I}_{i}}{{{\vec {S}}}_{i}}} \right) = \chi \left( {{{I}_{p}} - {{I}_{i}}} \right),$

где геометрические коэффициенты ${{\vec {S}}_{i}}$ и $\Delta {{\Omega }_{i}}$ определяются по формулам

(11)

${{\vec {S}}_{i}} = \int\limits_{\Delta {{\Omega }_{i}}} {\vec {s}d\Omega } = \int\limits_{\Delta \theta } {\int\limits_{\Delta \varphi } {\vec {s}} } \sin {\kern 1pt} \theta d\theta d\varphi = \left( {\begin{array}{*{20}{c}} {\cos {\kern 1pt} {{\varphi }_{i}}\sin \left( {{{\Delta \varphi } \mathord{\left/ {\vphantom {{\Delta \varphi } 2}} \right. \kern-0em} 2}} \right)\left( {\Delta \theta - \cos \left( {2{{\theta }_{i}}} \right)\sin {\kern 1pt} \Delta \theta } \right)} \\ {\sin {\kern 1pt} {{\varphi }_{i}}\sin \left( {{{\Delta \varphi } \mathord{\left/ {\vphantom {{\Delta \varphi } 2}} \right. \kern-0em} 2}} \right)\left( {\Delta \theta - \cos \left( {2{{\theta }_{i}}} \right)\sin {\kern 1pt} \Delta \theta } \right)} \\ {0.5\Delta \varphi {\kern 1pt} \sin \left( {2{{\theta }_{i}}} \right)\sin {\kern 1pt} \Delta \theta } \end{array}} \right),$

(12)

$\Delta {{\Omega }_{i}} = \int\limits_{\Delta \theta } {\int\limits_{\Delta \varphi } {\sin {\kern 1pt} \theta d\theta d\varphi } } = 2\sin \left( {{{\theta }_{i}}} \right)\sin \left( {{{\Delta \theta } \mathord{\left/ {\vphantom {{\Delta \theta } 2}} \right. \kern-0em} 2}} \right)\Delta \varphi .$

В качестве граничных условий обычно используются диффузионные отражающие и испускающие поверхности. Излучение от границы в этом случае является изотропным.

(13)

$I\left( {\vec {s}} \right) = \varepsilon {{I}_{p}} + \frac{{1 - \varepsilon }}{\pi }\int\limits_{\left( {\vec {s}{\kern 1pt} ',\vec {n}} \right) > 0} {I\left( {\vec {s}{\kern 1pt} '} \right)\left( {\vec {s}{\kern 1pt} ',\vec {n}} \right)d\Omega } ,\,\,\,\,\left( {\vec {s},\vec {n}} \right) < 0,$

где $\varepsilon $ – степень черноты стенки.

При аппроксимации уравнения (13) из-за несогласованного задания сеток в физическом пространстве и в пространстве направлений возникает т.н. проблема перекрытия дискретных телесных углов с границей области. Проблема перекрытия приводит к нарушению закона сохранения энергии.

Рассмотрим плотность потока энергии, Вт/м², падающего ${{E}^{{\left( + \right)}}}$ и испускаемого излучения ${{E}^{{\left( - \right)}}}$ на границе области (рис. 2)

(14)

$\begin{gathered} {{E}^{{\left( + \right)}}} = \int\limits_{\left( {\vec {s},\vec {n}} \right) > 0} {{{I}^{{\left( + \right)}}}\left( {\vec {s},\vec {n}} \right)d\Omega } = {{{\bar {I}}}^{{\left( + \right)}}}\int\limits_{\left( {\vec {s},\vec {n}} \right) > 0} {\left( {\vec {s},\vec {n}} \right)d\Omega } = \pi {{{\bar {I}}}^{{\left( + \right)}}}, \hfill \\ {{E}^{{\left( - \right)}}} = \int\limits_{\left( {\vec {s},\vec {n}} \right) < 0} {{{I}^{{\left( - \right)}}}\left( {\vec {s},\vec {n}} \right)d\Omega } = {{I}^{{\left( - \right)}}}\int\limits_{\left( {\vec {s},\vec {n}} \right) < 0} {\left( {\vec {s},\vec {n}} \right)d\Omega } = \pi {{I}^{{\left( - \right)}}}, \hfill \\ \end{gathered} $

где ${{\bar {I}}^{{\left( + \right)}}}$ – средняя проекция на нормаль интенсивность падающего излучения ${{I}^{{\left( + \right)}}}$; для испускаемого излучения в силу его изотропности справедливо ${{\bar {I}}^{{\left( - \right)}}} \equiv {{I}^{{\left( - \right)}}}$.

Рис. 2.

Падающие и испускаемые лучи на границе области (слева) и перекрытие телесного угла с границей (справа).

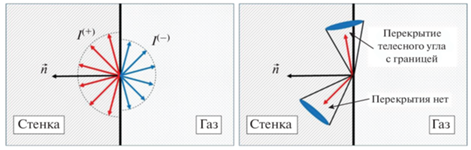
На дискретном уровне соотношения (14) не выполняются. Действительно, для контрольных углов с $\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0$, но пересекающих границу области, интегрирование $\int_{\left( {\vec {s},\vec {n}} \right) > 0} {\left( {\vec {s},\vec {n}} \right)d\Omega } $ должно проводится только по части контрольного телесного угла, для которой выполняется соотношение $\left( {\vec {s},\vec {n}} \right) > 0$, иначе ${{\left[ {\int\limits_{\left( {\vec {s},\vec {n}} \right) > 0} {\left( {\vec {s},\vec {n}} \right)d\Omega } } \right]}_{h}} = \sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} \ne \pi $.

Для устранения проблемы перекрытия контрольных углов на границе области будем аппроксимировать плотности потоков энергии по формулам

(15)

$\begin{gathered} E_{h}^{{\left( + \right)}} = \pi \bar {I}_{h}^{{( + )}} = \pi {{\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {I_{i}^{{\left( + \right)}}\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {I_{i}^{{\left( + \right)}}\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} } {\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} }}} \right. \kern-0em} {\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} }}, \\ E_{h}^{{\left( - \right)}} = \pi I_{h}^{{( - )}} = \pi {{\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {I_{i}^{{( - )}}\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {I_{i}^{{( - )}}\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} } {\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} }}} \right. \kern-0em} {\sum\limits_{i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{i}},\vec {n}} \right)} }} = \pi I_{i}^{{( - )}}. \\ \end{gathered} $

Тогда аппроксимация уравнения (13) будет иметь вид

(16)

$I_{i}^{{\left( - \right)}} = \varepsilon {{I}_{p}} + \left( {1 - \varepsilon } \right){{\sum\limits_{j:\left( {{{{\vec {S}}}_{j}},\vec {n}} \right) > 0} {I_{j}^{{( + )}}\left( {{{{\vec {S}}}_{j}},\vec {n}} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{j:\left( {{{{\vec {S}}}_{j}},\vec {n}} \right) > 0} {I_{j}^{{( + )}}\left( {{{{\vec {S}}}_{j}},\vec {n}} \right)} } {\sum\limits_{j:\left( {{{{\vec {S}}}_{j}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{j}},\vec {n}} \right)} }}} \right. \kern-0em} {\sum\limits_{j:\left( {{{{\vec {S}}}_{j}},\vec {n}} \right) > 0} {\left( {{{{\vec {S}}}_{j}},\vec {n}} \right)} }},\,\,\,\,i:\left( {{{{\vec {S}}}_{i}},\vec {n}} \right) \leqslant 0.$

3.3. Применение методики КАБАРЕ для решения уравнения переноса излучения

Уравнения переноса излучения (10) относится к уравнениям гиперболического типа, поэтому для их аппроксимации можно воспользоваться методикой КАБАРЕ [7]. Однако, из-за явной аппроксимации уравнений по времени, интегрирование должно проводится с чрезвычайно малым шагом по времени $\tau \sim {{с}^{{ - 1}}}$ (где $с \approx 3 \times {{10}^{8}}{\text{ м/с}}$ – скорость распространения света). Поэтому для применения методики КАБАРЕ потребуется использовать искусственную скорость распространения света ${{c}_{a}} \ll с$. Искусственная скорость света должна выбираться из условия, чтобы время установления радиационного теплового потока было много меньше характерного времени в задаче. Например, в газовой динамике изменение полей температуры и концентрации компонент смеси определяется конвективными потоками, следовательно критерием выбора для искусственной скорости света будет ${{c}_{a}} \gg {{u}_{{\max }}}$, где ${{u}_{{\max }}}$ – максимальная скорость течения газа.

В схеме КАБАРЕ используются два типа переменных – консервативные переменные в центрах контрольных объемов и потоковые переменные в центрах граней. Для вычисления консервативных переменных используется дивергентная форма уравнений (10)

(17)

$\frac{{\partial {{I}_{i}}}}{{\partial t}} + {\text{div}}\left( {{{I}_{i}}{{{\vec {v}}}_{i}}} \right) = {{Q}_{i}}{\text{, }}i = 1 - N,$

где ${{\vec {v}}_{i}} = \frac{{{{с}_{a}}}}{{\Delta {{\Omega }_{i}}}}{{\vec {S}}_{i}}$ – потоковая скорость, м/с; ${{Q}_{i}} = {{c}_{a}}\chi \left( {{{I}_{p}} - {{I}_{i}}} \right)$ – источник в правой части уравнения, Вт/(м² с).

Для вычисления потоковых переменных уравнение (10) записывается в форме переноса инвариантов Римана по характеристическим направлениям

(18)

$\frac{{\partial {{I}_{i}}}}{{\partial t}} + {{\lambda }_{i}}\frac{{\partial {{I}_{i}}}}{{\partial n}} = {{F}_{i}},$

где ${{\lambda }_{i}}{\text{ = }}\left( {{{{\vec {v}}}_{i}},\vec {n}} \right)$ – характеристическая скорость, м/с; $\vec {n}$ – нормаль к грани, направленная из задней ячейки в переднюю; ${{F}_{i}}$ – правая часть, не используется в явном виде.

Алгоритм схемы КАБАРЕ можно разбить на три фазы. На первой фазе вычисляются консервативные переменные на промежуточном (полуцелом) временном слое ${{\tilde {\varphi }}_{C}}$. На второй фазе вычисляются потоковые переменные на новом слое по времени ${{\hat {\varphi }}_{S}}$. На третьей фазе вычисляются консервативные переменные на новом слое по времени ${{\hat {\varphi }}_{C}}$.

Фаза 1.

Для вычисления консервативных переменных в ячейках на полуцелом временном слое ${{\tilde {\varphi }}_{C}}$ записывается аппроксимация дивергентной формы уравнений с первым порядком точности по времени и со вторым по пространству:

(19)

$\Delta V\frac{{{{{\tilde {I}}}_{С}} - {{I}_{С}}}}{{{\tau \mathord{\left/ {\vphantom {\tau 2}} \right. \kern-0em} 2}}} + \sum\limits_f {{{I}_{f}}\left( {{{{\vec {v}}}_{f}},{{{\vec {n}}}_{f}}} \right){{S}_{f}}} = Q.$

Здесь $\Delta V$ – объем ячейки; ${{S}_{f}}$ – площадь грани; ${{\vec {n}}_{f}}$ – внешней к ячейке вектор нормали к грани. Индекс i опущен.

Введем обозначения $\Phi = \sum\nolimits_f {{{I}_{f}}\left( {{{{\vec {v}}}_{f}},{{{\vec {n}}}_{f}}} \right){{S}_{f}}} $ и $d = {\tau \mathord{\left/ {\vphantom {\tau {\Delta V}}} \right. \kern-0em} {\Delta V}}$, тогда уравнение (19) примет компактный вид:

(20)

${{\tilde {I}}_{С}} = {{I}_{С}} - 0.5d\left( {\Phi - Q} \right).$

Фаза 3.

Пусть потоковые переменные на новом временном слое ${{\hat {\varphi }}_{S}}$ вычислены. Для вычисления консервативных переменных в ячейках на новом временном слое ${{\hat {\varphi }}_{C}}$ записывается аппроксимация дивергентной формы уравнений со вторым порядком по времени и пространству:

(21)

${{\hat {I}}_{С}} = {{I}_{С}} - d\left( {\bar {\Phi } - \tilde {Q}} \right),$

где $\bar {\Phi } = {{\left( {\hat {\Phi } + \Phi } \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\Phi } + \Phi } \right)} 2}} \right. \kern-0em} 2}$.

Фаза 2.

На первом шаге (предиктор) инварианты Римана экстраполируются со вторым порядком точности по значениям в ячейке, из которой приходит характеристика

(22)

${{\hat {I}}_{f}} = 2{{\tilde {I}}_{C}} - {{I}_{{OP}}},$

где индекс OP указывает на противоположную грань к грани f в ячейке C.

На втором шаге (корректор) производится нелинейная коррекция инвариантов Римана по принципу максимума [7], необходимая для монотонизации решения

(23)

${{\hat {I}}_{f}} = \min \left( {{{I}_{{\max }}},\max \left( {{{I}_{{\min }}},{{{\hat {I}}}_{f}}} \right)} \right) + \tau F,$

где ${{I}_{{\max }}} = \max \left( {{{I}_{f}},{{I}_{C}},{{I}_{{OP}}}} \right)$ и ${{I}_{{\min }}} = \min \left( {{{I}_{f}},{{I}_{C}},{{I}_{{OP}}}} \right)$ – оценки для минимального и максимального значения инварианта Римана в ячейке C на старом временном слое.

Величина $F$в уравнении (23) – это аппроксимация правой части уравнения (18)

(24)

$F = \frac{{{{{\tilde {I}}}_{C}} - {{I}_{C}}}}{{{\tau \mathord{\left/ {\vphantom {\tau 2}} \right. \kern-0em} 2}}} + {{\tilde {\lambda }}_{С}}\frac{{{{I}_{f}} - {{I}_{{OP}}}}}{{\left| {{{{\vec {r}}}_{f}} - {{{\vec {r}}}_{{OP}}}} \right|}}.$

На границе области по формулам (22), (23) и (24) вычисляется интенсивность падающего излучения на новом слое по времени ${{\hat {I}}^{{\left( + \right)}}}$. Интенсивность испускаемого излучения на новом слое по времени ${{\hat {I}}^{{\left( - \right)}}}$ определяется по формуле (16).

Условие устойчивости схемы КАБАРЕ записывается в виде

(25)

$\tau = CFL\frac{{{{h}_{{\min }}}}}{{{{\lambda }_{{\max }}}}} \sim \frac{{{{h}_{{\min }}}}}{{{{с}_{a}}}},$

где $CFL < 0.5$ – число Куранта; ${{h}_{{\min }}}$ – минимальный размер ячеек в сеточной модели; ${{\lambda }_{{\max }}}$ – максимальная характеристическая скорость по всем дискретным направлениям.

3.4. Источник тепла от излучения

Выражение для источника тепла от излучения ${{Q}_{{rad}}} = - {\text{div}}\vec {W}$ в уравнении (5) можно получить из уравнения (10)

(26)

$\begin{gathered} {{Q}_{{rad}}} = - {\text{div}}\left( {\sum\limits_i {{{I}_{i}}{{{\vec {S}}}_{i}}} } \right) = - \sum\limits_i {\chi \left( {{{I}_{p}} - {{I}_{i}}} \right)\Delta {{\Omega }_{i}}} + \frac{1}{c}\frac{\partial }{{\partial t}}\sum\limits_i {{{I}_{i}}\Delta {{\Omega }_{i}}} = \\ = - 4\chi \sigma {{T}^{4}} + \left( {\chi + \frac{1}{c}\frac{\partial }{{\partial t}}} \right)\sum\limits_i {{{I}_{i}}\Delta {{\Omega }_{i}}} . \\ \end{gathered} $

Из уравнения (26) следует интересный факт, что даже в оптически прозрачной среде ($\chi = 0$) источник тепла может отличаться от нуля на величину $Q_{{rad}}^{0} = \frac{1}{c}\frac{\partial }{{\partial t}}\sum\nolimits_i {{{I}_{i}}\Delta {{\Omega }_{i}}} $. Однако из-за высокой скорости распространения света величина $Q_{{rad}}^{0}$ мала и проявляется лишь на временах $\delta t \sim {L \mathord{\left/ {\vphantom {L c}} \right. \kern-0em} c} \sim {{10}^{{ - 8}}}c$ ($L$ – размер области), поэтому обычно данной составляющей пренебрегают, полагая, что скорость света бесконечно большая. Тогда уравнение для источника тепла примет вид

(27)

${{Q}_{{rad}}} = \chi \left( {\sum\limits_i {{{I}_{i}}\Delta {{\Omega }_{i}}} - 4\sigma {{T}^{4}}} \right).$

В модели с конечной искусственной скоростью света ${{c}_{a}} \ll с$ применение формулы (27) в нестационарных задачах может приводить к ошибкам $ \sim O\left( {{L \mathord{\left/ {\vphantom {L {{{c}_{a}}}}} \right. \kern-0em} {{{c}_{a}}}}} \right)$, тогда как применение формулы (26) может привести к существенным “паразитным” флуктуациям температуры даже для оптически прозрачных газов. Для достижения заданной точности необходимо использовать дополнительные ограничения при выборе параметра ${{c}_{a}}$.

4. ОПИСАНИЕ ВЕРИФИКАЦИОННОГО ЭКСПЕРИМЕНТА

Для верификации расчетной модели термического излучения и реакций диффузионного горения с использованием основанного на методике КАБАРЕ вихреразрешающего подхода к моделированию турбулентности были использованы данные эксперимента [8], в котором исследовались водородные струйные пламена, образующиеся при нестационарном истечении водорода из двух напорных резервуаров под давлением 431 бар через сопло диаметра 5.08 мм. Объем каждого резервуара составлял 617 л.

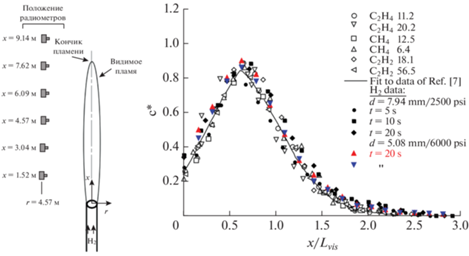
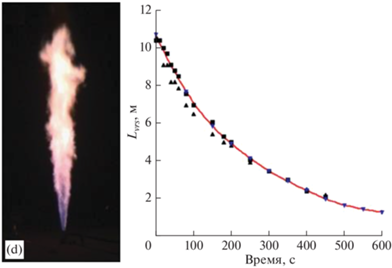
Для получения информации о структуре и длине пламени проводилась цифровая видеосъемка пламени. Из-за относительно слабой светимости водородного пламени все эксперименты проводились ночью, чтобы устранить фоновый свет и улучшить видимость пламени. Длина пламени ${{L}_{{vis}}}$, основанная на видеоизображениях видимого пламени, использовалась для определения усредненной по времени длины пламени (рис. 3). Средняя длина пламени уменьшается со временем вследствие уменьшения массового расхода по мере снижения давления в резервуаре.

Рис. 3.

Фотография видимой светимости пламени (слева) и длина видимого пламени в различные моменты времени (справа) [8].

Измерение потока лучистого тепла от пожар-струи производилось в момент времени 20 секунд с помощью радиометров, расположенных по вертикали на расстоянии ${{{{L}_{{vis}}}} \mathord{\left/ {\vphantom {{{{L}_{{vis}}}} 2}} \right. \kern-0em} 2}$ от оси струи (рис. 4). Доля тепла, излучаемого зоной горения пожар-струи ${{X}_{{rad}}}$ определяется как отношение общего лучистого тепла, выделяемого ${{Q}_{{rad}}}$ струйным пламенем, к общей скорости тепловыделения $Q$, равной произведению массового расхода топлива $\dot {m}$ на энтальпию реакции горения топлива $\Delta H$

(28)

${{X}_{{rad}}} = {{{{Q}_{{rad}}}} \mathord{\left/ {\vphantom {{{{Q}_{{rad}}}} {\left( {\dot {m}\Delta H} \right)}}} \right. \kern-0em} {\left( {\dot {m}\Delta H} \right)}}.$

Рис. 4.

Система координат (x,r) и расположение радиометров в эксперименте [8] (слева) и профили нормированного лучистого теплового потока для турбулентных пожар-струй (справа). Сплошные треугольники соответствуют данным эксперимента [8].

В работе [9] авторы предложили определять лучистый поток тепла ${{q}_{{rad}}}$ от пожар-струи, приходящий в точку $(x,R)$, расположенной на фиксированном расстоянии от оси струи $R = {{{{L}_{{vis}}}} \mathord{\left/ {\vphantom {{{{L}_{{vis}}}} 2}} \right. \kern-0em} 2}$, как ${{q}_{{rad}}}(x,R) = {{C{\kern 1pt} *{{Q}_{{rad}}}} \mathord{\left/ {\vphantom {{C{\kern 1pt} *{{Q}_{{rad}}}} {4\pi {{R}^{2}}}}} \right. \kern-0em} {4\pi {{R}^{2}}}}$, где $C{\kern 1pt} * = С{\kern 1pt} *\left( {{x \mathord{\left/ {\vphantom {x {{{L}_{{vis}}}}}} \right. \kern-0em} {{{L}_{{vis}}}}}} \right)$ – универсальный для всех пожар-струй профиль нормированного лучистого теплового потока. Экспериментальные исследования вертикальных турбулентных водородных пожар-струй, проведенных в Национальной лаборатории Сандия [8], [10], подтвердили выводы о том, что графики значений безразмерной величины

(29)

$C{\kern 1pt} {\kern 1pt} * = \frac{{4\pi {{R}^{2}}{{q}_{{rad}}}(x{\text{/}}{{L}_{{vis}}},R{\text{/}}{{L}_{{vis}}})}}{{{{Q}_{{rad}}}}},$

относительно нормированной на длину факела координаты x/L_vis для разных газов и условий истечения ложатся на одну кривую (рис. 4).

Формулы (28) и (29) позволяют определить долю излучаемого тепла ${{X}_{{rad}}}$ по результатам измерений лучистого потока тепла в точке $\left( {x,R} \right) = \left( {{{{{L}_{{vis}}}} \mathord{\left/ {\vphantom {{{{L}_{{vis}}}} 2}} \right. \kern-0em} 2},{{{{L}_{{vis}}}} \mathord{\left/ {\vphantom {{{{L}_{{vis}}}} 2}} \right. \kern-0em} 2}} \right)$

(30)

${{X}_{{rad}}} = \frac{{4\pi {{R}^{2}}{{q}_{{rad}}}({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{{C{\kern 1pt} *\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)\dot {m}\Delta H}}.$

Анализ экспериментальных данных [11] показал, что величина ${{X}_{{rad}}}$ коррелирует с т.н. временем жизни пламени ${{\tau }_{f}}$

(31)

${{X}_{{rad}}} = a{\kern 1pt} {{\log }_{{10}}}\left( {{{\tau }_{f}}} \right) - b,$

где ${{\tau }_{f}} = {{f}_{s}}{{{{\rho }_{f}}{{V}_{f}}} \mathord{\left/ {\vphantom {{{{\rho }_{f}}{{V}_{f}}} {\dot {m}}}} \right. \kern-0em} {\dot {m}}}$ – время жизни пламени, с; ${{V}_{f}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}W_{{vis}}^{2}{{L}_{{vis}}}$ – объем видимой части пламени (в модели конуса), м³; ${{W}_{{vis}}} \approx 0.17{{L}_{{vis}}}$ – видимая ширина пламени, м; ${{\rho }_{f}} = {{{{P}_{a}}{{M}_{{mix}}}} \mathord{\left/ {\vphantom {{{{P}_{a}}{{M}_{{mix}}}} {R{{T}_{{ad}}}}}} \right. \kern-0em} {R{{T}_{{ad}}}}}$ – плотность стехиометрической смеси в пламени, кг/м³; ${{f}_{s}}$ – массовая доля топлива в стехиометрической смеси; $a$ и $b$ – константы, зависящие от газа.

Экспериментальные данные для водородных струй в воздухе хорошо ложатся на прямую [8]

(32)

${{X}_{{rad}}} = 0.07105{{\log }_{{10}}}\left( {{{\tau }_{f}}} \right) - 0.06049.$

5. ПОСТАНОВКА ЗАДАЧИ

5.1. Начальные и граничные условия

По аналогии с работой [12] для моделирования квазистационарного факела были выбраны условия в момент времени 93 секунды от начала эксперимента. Давление и температура водорода в баллоне в данный момент времени составляют P = 104.8 бар и T = 231.4 K. Давление и температура в окружающей среде составляют P_a = 1 бар и T = 293 K.

Для моделирования начального ударно-волнового участка недорасширенной струи в работе [12] использовалась модель эффективного сечения Birch (1987) [13] с уравнением состояния реального газа Abel-Noble [14]. Без учета уравнения состояния реального газа авторы статьи наблюдали завышение видимой длины пламени на 50% по сравнению с экспериментом. Параметры в эффективном сечении приведены в табл. 1. В настоящей работе эти параметры были использованы для моделирования эффективного сечения.

Таблица 1.

Параметры в эффективном сечении, полученные с помощью модели Birch (1987) с уравнением состояния реального газа Abel-Noble [12]

Давление, бар	Температура, К	Диаметр, мм	Скорость, м/с
1	231.4	31.5	1795

5.2. Геометрия и сетка

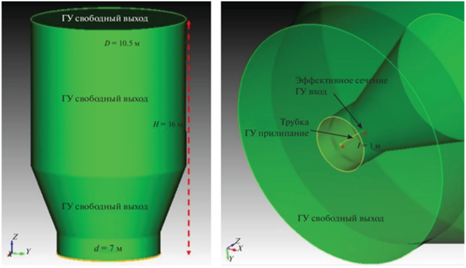
Геометрия расчетной области представляет собой цилиндр высотой 16 м переменного диаметра от 7 м в нижней части до 10.5 м на высоте больше 6 м (рис. 5). В нижней части диаметр цилиндра меньше для уменьшения аспектного отношения ячеек в области сгущения сетки. На нижнем торце цилиндра по центру располагается инжекционная трубка длиной 1 м и диаметром, равным диаметру эффективного сечения. На стенках трубки задаются условия прилипания. На верхнем торце трубки граничное условие входа (поток газа через трубку не моделируется). На внешних границах расчетной области задается условие свободного выхода.

Рис. 5.

Геометрия расчетной области.

В расчетной модели используется блочно-структурированная гексаэдральная сетка (рис. 6). Размер сеточной модели составляет 109 3496 ячеек. Число ячеек на входе составляет 12 с характерным линейным размером около 7.875 мм. В окрестности входа сетка близка к равномерной. При отдалении от входа сетка растягивается по всем направлениям. На правом торце характерные размеры ячеек составляют 5–30 см.

Рис. 6.

Сеточная модель.

6. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

6.1. Лучевой эффект

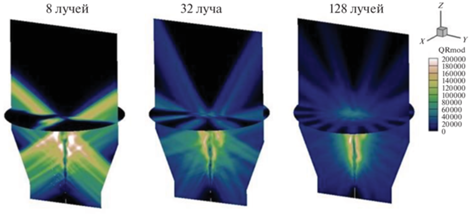
Главным недостатком метода дискретных ординат является т.н. эффект луча (ray effect), который заключается в сильной пространственной неоднородности расчетного радиационного потока на большом расстоянии от источника [5]. Лучевой эффект особенно сильно выражен, если размер источника излучения меньше расстояния, на котором определяется радиационный поток. Действительно, поскольку число дискретных направлений (лучей) в методе DOM конечно, расстояние между лучами увеличивается по мере удаления от источника. Излучение диффузионного пламени также существенно неоднородно распределено в пространстве. На рис. 7 показаны поля модуля теплового потока в расчетах с числом лучей 8, 32 и 128. Лучевой эффект ослабевает при увеличении дискретных направлений, однако при этом сильно снижается вычислительная эффективность кода.

Рис. 7.

Модуль теплового потока излучения в центральных сечениях расчетной области в момент времени 0.2 с в расчетах с излучением с числом лучей 8, 32 и 128.

6.2. Проверка закона сохранения энергии

Другим недостатком метода дискретных ординат являются проблемы с выполнением закона сохранения энергии из-за перекрытия контрольных углов с гранями контрольных объемов [5]. В методе конечных объемов данная проблема решается специальной процедурой согласования пространственной и угловой дискретизации. В схеме КАБАРЕ используется дивергентная форма уравнений переноса излучения, а потоковые переменные на гранях являются независимыми, поэтому проблемы с консервативностью алгоритма исключены.

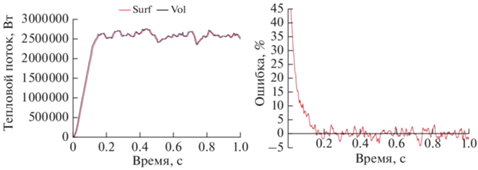
Однако, для исключения паразитных осцилляций температуры (из-за введения искусственной скорости света) источник тепла в ячейках вычислялся по формуле (27). Для проверки закона сохранения энергии вычислим суммарный поток лучистой энергии, Вт, двумя способами

(33)

$Q_{{rad}}^{{\left( {Vol} \right)}} \triangleq \int\limits_V {{{Q}_{{rad}}}dV} = - \int\limits_V {{\text{div}}\left( {\vec {q}} \right)dV} = - \int\limits_S {\left( {\vec {q},\vec {n}} \right)dS} \triangleq Q_{{rad}}^{{\left( {Surf} \right)}}.$

На рис. 8 слева приведены графики суммарных тепловых потоков, вычисленных двумя способами. Как видно, обе кривые практически совпадают друг с другом, отклонения связаны с конечной скоростью распространения света. Относительная ошибка $\varepsilon = \left( {1 - {{Q_{{rad}}^{{\left( {Surf} \right)}}} \mathord{\left/ {\vphantom {{Q_{{rad}}^{{\left( {Surf} \right)}}} {Q_{{rad}}^{{\left( {Vol} \right)}}}}} \right. \kern-0em} {Q_{{rad}}^{{\left( {Vol} \right)}}}}} \right) \times 100\% $ показана на рис. 8 справа.

Рис. 8.

Суммарный радиационный тепловой поток, вычисленный двумя способами, (слева) и относительная ошибка (справа).

6.3. Видимая длина пламени

В работе [12] для определения видимой длины пламени в CFD расчете используется формула

(34)

${{L}_{{vis}}} = {{\left. {\max \left( {{{Z}_{{cell}}}} \right)} \right|}_{{\Delta Y \geqslant 0}}},\,\,\,\,\Delta Y = {{Y}_{F}} - {{{{Y}_{O}}} \mathord{\left/ {\vphantom {{{{Y}_{O}}} s}} \right. \kern-0em} s},$

где ${{Z}_{{cell}}}$ – координата центра ячейки по оси Z, м; ${{Y}_{F}}$ – массовая доля топлива; ${{Y}_{O}}$ – массовая доля окислителя; $s$ – массовый стехиометрический коэффициент ($s = 8$ для водородной струи).

Условие $\Delta Y = {{Y}_{F}} - {{{{Y}_{O}}} \mathord{\left/ {\vphantom {{{{Y}_{O}}} s}} \right. \kern-0em} s} = 0$ выполняется на фронте горения, поэтому критерий (34) определяет границу фронта горения.

В работе [15] видимая длина пламени определялась по температуре смеси. Основываясь на экспериментальных данных [16], для определения видимой длины пламени в водородной струе использовался интервал температур от 1300 К до 1500 К. Очевидно, на фронте горения температура смеси выше 1500 К, поэтому первый способ будет давать более низкие значения видимой длины пламени по сравнению со вторым.

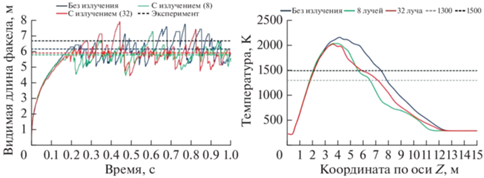
На рис. 9 слева представлены результаты расчета видимой длины пламени по формуле (34), а справа осредненный по времени (от 0.4 с до 0.9 с) профиль температуры вдоль оси симметрии струи в расчетах без излучения и с излучением с числом лучей 8 и 32. В табл. 2 приведены средние значения видимой длины пламени в интервале, вычисленные двумя способами. Экспериментальное значение составляет 6.7 м [12] (рис. 3). Как видно из таблицы, второй способ дает близкие значения видимой длины пламени к измеренному значению, тогда как первый способ приводит к занижению данной величины на 8–13%.

Рис. 9.

Видимая длина факела по границе фронта горения (слева) и профиль температуры вдоль оси X (справа).

Таблица 2.

Видимая длина пламени

Число лучей	1 способ	2 способ
0	6.17 м	7.4–7.9 м
8	5.80 м	5.6–6.6 м
32	5.92 м	5.9–7.2 м

6.4. Доля излучаемой энергии

Доля энергии, рассеиваемой за счет излучения (radiant fraction), вычисляется по формуле

(35)

${{X}_{{rad}}} = \frac{{\int\limits_V {{\text{div}}\left( {{{{\vec {q}}}_{{rad}}}} \right)dV} }}{{\int\limits_V {{{{\dot {r}}}_{{{{{\text{H}}}_{{\text{2}}}}}}}\Delta HdV} }},$

где ${{\dot {r}}_{{{{{\text{H}}}_{{\text{2}}}}}}}$ – скорость сгорания топлива, кг/с.

В формуле (35) учитывается не только излучение от фронта горения пламени, но и от горячего шлейфа продуктов горения, поднимающегося над факелом. В работе [12] при вычислении коэффициента ${{X}_{{rad}}}$ использовалось дополнительное ограничение $\Delta Y = {{Y}_{F}} - {{{{Y}_{O}}} \mathord{\left/ {\vphantom {{{{Y}_{O}}} s}} \right. \kern-0em} s} \geqslant 0$ на концентрацию топлива и окислителя в ячейках, позволяющее исключить излучение шлейфа:

(36)

${{\tilde {X}}_{{rad}}} = {{\left( {\frac{{\int\limits_V {{\text{div}}\left( {{{{\vec {q}}}_{{rad}}}} \right)dV} }}{{\int\limits_V {{{{\dot {r}}}_{{{{{\text{H}}}_{{\text{2}}}}}}}\Delta HdV} }}} \right)}_{{\Delta Y \geqslant 0}}} = \frac{{\int\limits_V {{\text{div}}\left( {{{{\vec {q}}}_{{rad}}}} \right)\theta \left( {\Delta Y} \right)dV} }}{{\int\limits_V {{{{\dot {r}}}_{{{{{\text{H}}}_{{\text{2}}}}}}}\Delta H\theta \left( {\Delta Y} \right)dV} }},$

где $\theta \left( x \right)$ – функция Хевисайда.

На рис. 10 представлены результаты вычисления коэффициента ${{X}_{{rad}}}$ в расчетах с числом лучей 8 и 32. Синяя и зеленая кривая соответствуют расчету коэффициента ${{X}_{{rad}}}$ по формуле (35), красная кривая – по формуле (36). В табл. 3 приведены осредненные значения коэффициента ${{X}_{{rad}}}$ по интервалу от 0.2 до 1 с. Как видно из таблицы, при расчете по формуле (35) осредненные значения коэффициента оказываются выше эмпирической корреляции (9.5% в работе [12] или 9.8% по формуле (32)) на 6–7% (по абсолютной величине), а при расчете ${{X}_{{rad}}}$ без учета излучения шлейфа (формула (36)) результаты близки к эмпирическому значению.

Рис. 10.

Доля излучаемого факелом тепла от выделяемого тепла при сгорании водорода (radiant fraction) в зависимости от времени в расчетах с числом лучей 8 и 32.

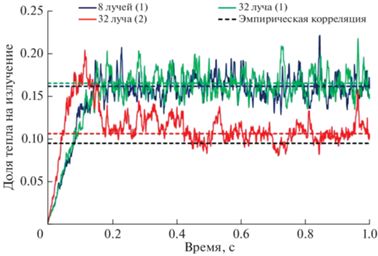
Таблица 3.

Доля излучаемого факелом тепла от выделяемого тепла при сгорании водорода (radiant fraction) (осредненное значение по интервалу 0.4–1с) в сравнении с эмпирической корреляцией

Число лучей	Расчет X_rad, %	Эмпирическая корреляция X_rad, %	Отклонение расчета от эксперимента, %
8 лучей (1)	16.21	9.5/9.8	70.63/65.41
32 луча (1)	16.54	9.5/9.8	74.11/68.78
32 луча (2)	10.65	9.5/9.8	12.11/8.67

6.5. Профиль радиационного теплового потока

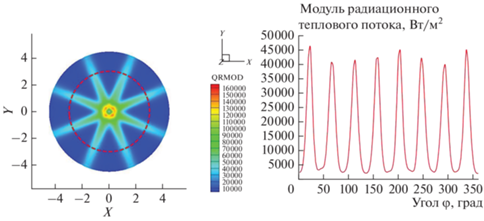
Из-за лучевого эффекта в методе дискретных ординат распределение радиационного потока тепла в пространстве на некотором отдалении от факела существенно неоднородно. На рис. 11 приведен график зависимости радиационного потока от угла φ на высоте Z = 3 м от сопла в расчете с числом лучей 32. В точках, попадающих в лучи значения радиационного теплового потока завышены, а в областях между лучами, наоборот, занижены. Среднее по углу значение радиационного потока на расстоянии R от оси струи и на высоте Z от сопла характеризует реальный тепловой поток в точке (R, Z).

Рис. 11.

Распределение радиационного теплового потока по углу на высоте Z = 3 м от сопла в расчете с числом лучей 32.

На рис. 12 показан безразмерный профиль радиационного теплового потока С* (29) в зависимости от безразмерной координаты Z/L_vis в расчетах с числом лучей 8 и 32. Результаты расчетов сравниваются с эмпирической зависимостью для С* (черная пунктирная линия) и экспериментальными данными (маркеры).

Рис. 12.

Безразмерный профиль радиационного теплового потока в зависимости от безразмерной координаты Z/L_vis.

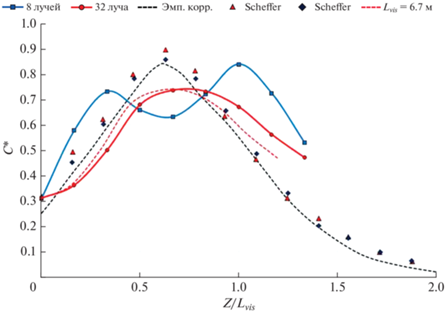
В расчете с 8-ю лучами кривая для С* (синяя линия) имеет минимум в окрестности Z/L_vis ≈ 0.5, где располагается область с наиболее интенсивным горением водорода. Это связано с тем, что лучи из данной области расходятся под углом 45° к горизонтальной плоскости и не попадают в исследуемую зону (R = L_vis/2, Z/L_vis ≈ 0.5). В расчете с 32‑мя лучами (красная линия) лучевой эффект выражен заметно меньше. Из-за расхождения лучей от «горячей» области факела значения С* в центре кривой занижены.

В обоих расчетах профиль кривой С* шире, чем в экспериментах. Это напрямую связано с выбором значения для видимой длины факела (L_vis= 6 м). По всей видимости, это значение характеризует верхнюю границу фронта горения, а не видимую длину факела. Если по оси абсцисс подставить обезразмеренную на экспериментальное значение L_vis = 6.7 м координату, то профиль С* будет заметно лучше соответствовать эмпирической кривой (красная пунктирная линия).

7. ЗАКЛЮЧЕНИЕ

Проведена верификация расчетных моделей термического излучения и реакций горения для водородной пожар-струи в открытом пространстве при использовании вихреразрешающей методики КАБАРЕ. Для верификации модели были использованы данные эксперимента по изучению характеристик турбулентного диффузионного водородного пламени, проведенного сотрудниками Национальной лаборатории Сандия. Эти данные релевантны относительно сценария непреднамеренной утечки водорода из напорного резервуара хранения под высоким давлением. В результате верификации получено хорошее соответствие результатов расчета с экспериментальными данными и эмпирическими корреляциями по видимой длине факела, доли тепла, рассеиваемой излучением, профилю нормированного теплового потока.

Верификация моделей может быть продолжена как на экспериментах по исследованию теплопереноса излучением (из проекта OECD\NEA HYMERES-2), так и на экспериментах с пожар-струями (эксперименты Studer, Ekoto, Schefer).

Список литературы

Magnussen B.F., Hjertager Bjørn. (1977). On Mathematical Modeling of Turbulent Combustion With Special Emphasis on Soot Formation and Combustion. Symposium (International) on Combustion. 16. 719–729. https://doi.org/10.1016/S0082-0784(77)80366-4.
Четверушкин Б.Н. Математическое моделирование задач динамики излучающего газа. – М: Наука. Главная редакция физико-математической литературы, 1985. – 304с.
Chmielewski M., Gieras M. Planck Mean Absorption Coefficients of H₂O, CO₂, CO and NO for radiation numerical modeling in combusting flows. Journal of Power Technologies, 95 (2) – 2015 – 97–104.
Hottel H.C., Sarofim A.F. Radiative Transfer. – McGraw-Hill, New York, 1967. – 520 p.
Снегирёв А.Ю. Тепловое излучение. Основы теории и методы расчета: учеб. пособие / А. Ю. Снегирев. – Спб. : ПОЛИТЕХ-ПРЕСС, 2021. – 177с.
International Workshop on Measurement and Computation of Turbulent Flames. (https:// t-nfworkshop.org/radiation/).
Головизнин В.М., Зайцев М.А., Карабасов С.А. и др. Новые алгоритмы вычислительной гидродинамики для многопроцессорных вычислительных комплексов. М.: Из-во МГУ им. М.В. Ломоносова, 2013, 472 с.
Schefer R.W., Houf W.G., Williams T.C., Bourne B., Colton J. Characterization of high-pressure, underexpanded hydrogen-jet flame // Int. J. Hydrog. Energy. 2007. V. 32. P. 2081–2093.
Sivathanu Y.R., Gore J.P. Total radiative heat loss in jet flames from single point radiative flux measurements. Combust Flame 94:265–270, 1993.
Houf W.G., Schefer R. Predicting radiative heat fluxes and flammability envelopes from unintended releases of hydrogen. International Journal of Hydrogen Energy, 2007 – INT J HYDROGEN ENERG. 32. 136–151. https://doi.org/10.1016/j.ijhydene.2006.04.009
Turns S.R., Myhr F.H. Oxides of nitrogen emissions from turbulent jet flames: Part II-Fuel effects and flame radiation. Combust Flame 1991; 87:319e35.
Wang C.J., Wen J.X., Chen Z.B., Dembele S. Predicting radiative characteristics of hydrogen and hydrogen/methane jet fires using FireFOAM // International Journal of Hydrogen Energy 39 – (2014) 20560–20569.
Birch A.D., Hughes D.J., Swaffield F. Velocity decay of high pressure jets. Combust Sci Technol 1987;52:161e71.
Molkov V. Fundamentals of hydrogen safety engineering I. – 2012, – 216 p.
Brennan S.L., Makarov D.V., Molkov V. LES of high pressure hydrogen jet fire // Journal of Loss Prevention in the Process Industries 22, 2009 – 353–359.
Schefer R., Houf B., Colton J. Experimental measurements to characterize the thermal and radiation properties of an open-flame hydrogen plume // In Proceedings of the 15th annual hydrogen conference and hydrogen expo, 26–30 April 2004 Los Angeles, CA, USA.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал