Известия РАН. Энергетика, 2023, № 1, стр. 51-56

Тела цилиндрической формы относятся к наиболее часто встречающимся конструктивным элементам в технике и инженерной практике [1]. При тепловой обработке таких изделий, как правило, различают две основные стадии процесса, начальную и упорядоченную (регулярную). Для анализа распределения температуры во времени и по сечению такого тела необходимо осуществить исследование следующей математической задачи, представленной в безразмерном виде, являющимся более предпочтительным, а именно [2]

Здесь ${\text{Bi}}$ безразмерное число подобия Био, характеризующее интенсивность теплообмена на наружной поверхности тела. Используя классический метод математической физики разделения переменных, решение задачи (1)–(4) удается получить в форме бесконечного ряда [1–3] где ${{J}_{0}}\left( {{{\mu }_{n}}\psi } \right)$ – подробно изученная функция Бесселя первого рода нулевого порядка [4–12].

Собственные числа ${{\mu }_{n}}$ данной зависимости являются корнями характеристического уравнения

в котором ${{J}_{1}}\left( \mu \right)$ – функция Бесселя первого рода первого порядка, также всесторонне исследована и протабулирована [3–6, 10, 13]. Коэффициенты ряда (5) ${{A}_{n}}$ определяются по соотношению

Значения первых шести корней ${{\mu }_{n}}$ уравнения (6) и коэффициентов ${{A}_{n}}$ выражения (7) приведены в широко известной монографии [1] для некоторых конкретных величин чисел ${\text{Bi}}$ в форме таблиц.

При сравнительно больших числах Фурье ${\text{Fo}} \geqslant 0.3$ ряд (5) будет быстросходящимся, и тогда все его члены, за исключением первого, становятся пренебрежимо малыми. Для такой стадии процесса, называемой регулярной, аналитическое решение (5) существенно упрощается

Это относительно несложное математическое выражение может быть использовано в дальнейшем для изучения различных других процессов, например, для определения термических напряжений в конструкциях [8]. При этом для нахождения первого собственного числа ${{\mu }_{1}}$ для любого значения ${\text{Bi}}$ может быть применена простая аналитическая формула

полученная авторами данной работы на основе разложения функций ${{J}_{0}}\left( \mu \right)$ и ${{J}_{1}}\left( \mu \right)$ в полиномы ограниченных порядков. Выражение (9) обладает высокой точностью, если ${\text{Bi}} < {\text{2}}$. Так, в частности, при ${\text{Bi}} = {\text{1}}$ расчет по (9) дает результат т.е. ${{\mu }_{1}} = 1.2547$, а соответствующая табличная величина [1] ${{\mu }_{1}} = 1.2558$. Следовательно невязка в данном случае составляет менее $0.1\% $. При этом с уменьшением ${\text{Bi}}$ она становится еще ниже. Причем нужно заметить, что для тел цилиндрической формы безразмерный теплотехнический параметр ${\text{Bi}}$, являющийся весьма важным показателем, на практике сравнительно редко превышает значение 1. Кроме этого, следует также иметь ввиду, что при проведении реальных инженерных расчетов используется исходная величина ${\text{Bi}}$ известная неизбежно с некоторой погрешностью. К особенностям рекомендуемой зависимости (9) относится также то, что она дает оценку ${{\mu }_{1}}$ несколько заниженную на всем интервале чисел ${\text{Bi}}$. Так, для ${\text{Bi}} = {\text{2}}$ согласно (9) получим ${{\mu }_{1}} = 1.5925$, а табличная величина [1] ${{\mu }_{1}} = 1.5994$.

Для расчета температурного поля на начальной стадии нагрева необходимо в решении (5) учитывать большое число слагаемых ряда и с уменьшением числа ${\text{Fo}}$ приходится принимать во внимание все возрастающее количество членов бесконечной суммы (5). Для этого необходимо знать несколько первых корней характеристического уравнения (6). При этом важно знать предельные значения ${{\mu }_{n}}$. В табл. 1 указаны эти значения для случая, когда $2 \leqslant n \leqslant 6$.

Данная таблица может быть легко продолжена до необходимых еще больших порядковых номеров $n$. Для определения указанных корней при ${\text{0}} < {\text{Bi}} < \infty $ целесообразно записать характеристическое уравнение (6), по аналогии с элементарными функциями [17], через обратную функцию, т.е. принять, что

В табл. 2 приведены численные величины обратной функции отношения ${{J}_{0}}\left( \mu \right)$ и ${{J}_{1}}\left( \mu \right)$, принадлежащей также к классу специальных функций, в зависимости от аргумента $\mu $. Для сокращения объема таблицы шаг по оси ${\text{arc}}\frac{{{{J}_{0}}\left( \mu \right)}}{{{{J}_{1}}\left( \mu \right)}}$ принят $0.1$ на интервале 0–1 и увеличен до 0.2 в дальнейшем. Использование табл. 2 позволяет оперативно вычислять искомые значения ${{\mu }_{n}}$ с помощью несложного быстросходящегося итерационного процесса.

Предположим, что надо найти ${{\mu }_{2}}$ в случае, когда ${\text{Bi}} = {\text{2}}$. На первом шаге последовательных приближений задаемся $\frac{{{{\mu }_{{2\,\min }}}}}{{{\text{Bi}}}} = \frac{{3.8713}}{2} = 1.9159$. Из табл. 2 следует, что для ${\text{arc}}\frac{{{{J}_{0}}\left( {{{\mu }_{{2\,\max }}}} \right)}}{{{{J}_{1}}\left( {{{\mu }_{{2\,\max }}}} \right)}} = 1.9159$ ${{\mu }_{{2\,\max }}} = 4.34$. Таким образом, можно утверждать, что искомый корень ${{\mu }_{2}}$ находится в интервале $3.8317 < {{\mu }_{2}} < 4.34$. Далее, принимая за основу ${{\mu }_{{2\,\max }}} = 4.34$ и учитывая, что $\frac{{{{\mu }_{{2\,\max }}}}}{{{\text{Bi}}}} = \frac{{4.34}}{2} = 2.17$, снова на основе табл. 2 находим по величине $arc\frac{{{{J}_{0}}\left( {{{\mu }_{{2\,\min }}}} \right)}}{{{{J}_{1}}\left( {{{\mu }_{{2\,\min }}}} \right)}}$ новое значение снизу для ${{\mu }_{2}}$, а именно $\mu _{{2\,\min }}^{'} = 4.2862$, т.е. вторая “вилка” оказывается существенно меньше первой, а именно $4.2862 < {{\mu }_{2}} < 4.34$. Табличное значение ${{\mu }_{2}}$ согласно [1] для ${\text{Bi}} = {\text{2}}$ равно $\mu = 4.2910$. Если за основу взять $\mu {{_{{2\,\min }}^{'}}_{{}}} = 4.2862$, то из условия $arc\frac{{{{J}_{0}}\left( {\mu _{{2\,\max }}^{'}} \right)}}{{{{J}_{1}}\left( {\mu _{{2\,\max }}^{'}} \right)}} = 2.1431$ следует 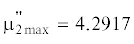. Таким образом, получим величину 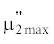практически совпадающую с действительной. Подобный подход применим и ко всем последующим числам ${{\mu }_{n}}$. Так, например, требуется вычислить ${{\mu }_{6}}$ при ${\text{Bi}} = {\text{2}}$. Естественно, что нужно за исходное значение принять согласно данным табл. 1 $\mu _{{6\,\min }}^{'} = 16.4706$. Тогда, исходя из условия $\frac{{\mu _{{6\,\min }}^{'}}}{{{\text{Bi}}}} = 8.2353$, т.е. зная $arc\frac{{{{J}_{0}}\left( {{{\mu }_{{6\,\max }}}} \right)}}{{{{J}_{1}}\left( {{{\mu }_{{6\,\max }}}} \right)}} = 8.2353$, получим на основе табл. 2 ${{\mu }_{{6\,\max }}} = 16.5920$. Отсюда следует, что имеет место “вилка” $16.4706 < {{\mu }_{6}} < 16.5920$. Если итерацию повторить, т.е. принять, что 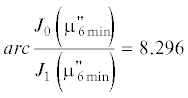, то нижняя граница ${{\mu }_{{6\,\min }}} = 16.591$. Отсюда имеем очень узкий интервал $16.591 < {{\mu }_{6}} < 16.592$. Табличное значение ${{\mu }_{6}}$ при ${\text{Bi}} = {\text{2}}$, согласно данным [1], равно ${{\mu }_{6}} = 16.5910$.

Итак, предложенный итерационный экспресс-способ позволяет весьма быстро и сравнительно просто вычислить любой корень ${{\mu }_{n}}$ уравнения (6) с высокой степенью точности. Имея в распоряжении необходимое количество собственных чисел ${{\mu }_{n}}$, можно провести расчет нестационарного температурного поля в цилиндрическом теле при малых величинах ${\text{Fo}}$, т.е. может быть выполнено исследование теплового процесса на начальной его стадии. В работе [16] предложено инженерное аналитическое решение аналогичных задач для тел плоской и сферической конфигураций. Следует добавить, что с помощью рекомендуемого метода может быть на основе аналитического решения (9) для первого собственного значения ${{\mu }_{1}}$ несложно получить также очень близкое его верхнее значение.

В заключение следует отметить, что введение в расчетную практику некоторых обратных специальных функций позволяет существенно расширить возможности эффективного решения многих важных теплофизических задач.