Известия РАН. Серия физическая, 2019, T. 83, № 1, стр. 83-86
Восстановление трехмерного строения среды по данным о временах пробега объемных волн от внутренних источниковД. В. Лиходеев, Д. А. Преснов, Л. Б. Славина
Д. В. Лиходеев 1, *, Д. А. Преснов 1, Л. Б. Славина 1
1 Институт физики Земли имени О.Ю. Шмидта Российской академии наук
Москва, Россия
* E-mail: dmitry@ifz.ru
Аннотация
Представлены основные положения метода “обратимой волны” и новый алгоритм обработки экспериментальных данных, разработанный на основе этого метода. Предложено несколько тестовых моделей трехмерно-неоднородной среды, в рамках которых в лучевом приближении определены синтетические входные данные и опробован новый алгоритм. Приводятся результаты восстановления строения земной коры на примере Азербайджана.
ВВЕДЕНИЕ
Наиболее эффективные методы изучения строения крайне недородной земной коры основаны на использовании сейсмических волн, которые могут быть как естественного, так и искусственного происхождения. Задача восстановления свойств среды по данным о наблюдаемых параметрах волн, прошедших через заданную область среды, является примером типичной обратной задачи. За последние несколько десятков лет интенсивное развитие и широкое распространение получили томографические методы изучения строения Земли на масштабах от нескольких десятков до тысяч км, в основе которых лежит информация о временах вступлений продольных (P) и поперечных (S) волн, вызванных землетрясениями [1]. Главный принцип лучевой сейсмической томографии заключается в параметризации модели среды набором базисных функций, параметры которых выбираются таким образом, чтобы время пробега волны вдоль рассчитанного в рамках модели луча удовлетворяло экспериментально наблюденному времени. Таким образом, выполнение локальных исследований с целью изучения достаточно мелких особенностей среды в томографическом подходе возможно лишь в сейсмически активных регионах земного шара, среди которых особый интерес представляют вулканические области [2]. При этом наиболее сложно устроенные объекты, в которых возникают сами сейсмические события, обычно расположены на границе изучаемой области и остаются слабо покрытыми лучами, а значит информация, получаемая об их строении, является либо слишком сглаженной, либо недостаточно достоверной.
МЕТОД ОБРАТИМОЙ ВОЛНЫ
В настоящей работе представлен новый алгоритм инверсии данных о временах пробега объемных сейсмических волн в трехмерно-неоднородной среде, основанный на предложенном ранее методе “обратимой волны” [3]. Этот метод применялся для изучения строения земной коры и фокальных зон землетрясений на Камчатке [4]. В отличие от томографии, где восстанавливается распределение скоростей во всем регионе, через который проходят сейсмические лучи, в развиваемом методе рассматривается только небольшая сферическая область вблизи источника.
Пусть время пробега волны от источника до приемника в неоднородной среде описывается функцией координат $\Psi \left( {x,y,z} \right) = t - {{t}_{0}},$ где $t$ – время прихода волны на станцию, ${{t}_{0}}$ – время начала излучения. Раскладывая $\Psi \left( {x,y,z} \right)$ в ряд Тейлора вблизи точки $\left( {{{x}_{0}},{{y}_{0}},{{z}_{0}}} \right)$ и оставляя только первый член разложения, получим касательную к фронту волны плоскость. Таким образом, выбирая достаточно малую сферическую область, в которой фронт волны действительно можно считать плоским, а скорость постоянной, и используя попадающие в эту область источники, необходимо найти такой вектор нормали, при плоском распространении вдоль которого невязка времен пробега обратимой волны от приемника до различных источников будет минимальной. Задача состоит в поиске приближенного решения несовместной системы уравнений:
(1)
$A\left( {{{x}_{i}} - {{x}_{0}}} \right) + B\left( {{{y}_{i}} - {{y}_{0}}} \right) + C\left( {{{z}_{i}} - {{z}_{0}}} \right) = {{t}_{i}} - {{t}_{0}},$В рамках настоящей работы разработан программный комплекс среды Matlab, использующий, в качестве исходных, данные из каталога сейсмических событий, включающие в себя координаты эпицентра и глубину землетрясения, время в очаге землетрясения, а также время прихода волн типа P или S на соответствующую приемную станцию. Для каждой станции алгоритм автоматически выбирает все сфероидальные области, ограниченные внутренним ${{R}_{{min}}}$ и внешним ${{R}_{{max}}}$ радиусами, в которые попадает, по меньшей мере i = 4 сейсмических события. Используя координаты события в центре сферы и координаты i-го события, а также времена пробега волны одного типа от этих источников, составляем систему из i уравнений (1) с тремя неизвестными A, B, C, на основе которой строится квадратичный функционал, который минимизируются алгоритмом Нелдера–Мида при помощи встроенной функции Matlab. Заметим, что при построении функционала может быть учтено условие гладкости восстанавливаемого распределения скоростей в среде путем добавления регуляризующего слагаемого вида: $\alpha i{{\left( {{{{{V}_{0}} - 1} \mathord{\left/ {\vphantom {{{{V}_{0}} - 1} {\sqrt {{{A}^{2}} + {{B}^{2}} + {{C}^{2}}} }}} \right. \kern-0em} {\sqrt {{{A}^{2}} + {{B}^{2}} + {{C}^{2}}} }}} \right)}^{2}},$ где коэффициент регуляризации α определяет меру близости восстанавливаемого значения скорости и фоновой априорно известной скорости в среде ${{V}_{0}}.$
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Апробация метода была выполнена на синтетических трехмерных моделях. По заданным координатам источника и распределению скоростей в различных пространственных точках модели среды решалась прямая задача, и рассчитывалось время прихода волны на приемник в лучевом приближении. Лучевое трассирование выполнялось с учетом принципа наименьшего действия путем численного решения уравнения эйконала на основе явной конечно-разностной схемы и метода “расширяющегося волнового фронта” [6]. На первом этапе исследований была задана трехмерная модель среды с неоднородностью в горизонтальной плоскости в виде шахматной доски (такой тип часто используется при оценке разрешающей способности сейсмической томографии) с размером клетки 26 × 26 км, значение скорости от клетки к клетке изменяется скачком на 1 км ⋅ с–1; по вертикали задан линейный градиент скорости от 4 км ⋅ с–1 на поверхности до 7 км ⋅ с–1 на глубине. В качестве источников волнового сигнала при моделировании использовались координаты более 5000 гипоцентров землетрясений, зарегистрированных в Азербайджане за период с 2006 по 2014 гг. (отмечены кружками на рис. 1) по данным того же каталога землетрясений, что использовался в работе [7]. Рассчитывалось время пробега волны от каждого источника до каждого приемника – станции сейсмологической службы Национальной академии наук Азербайджана (отмечены треугольниками на рис. 1). Размер области, в которой выполнялась инверсия, задавался двумя параметрами ${{R}_{{min}}} = $ 5 км, ${{R}_{{max}}} = $ 15 км.
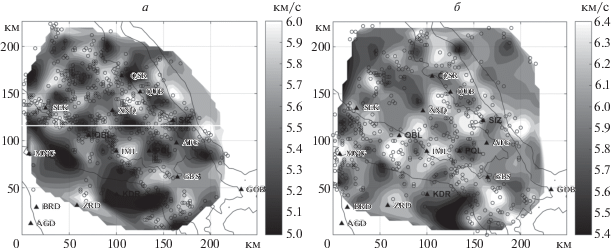
Рис. 1.
Результат восстановления скоростных параметров среды для синтетической модели в виде шахматной доски на примере сети приемников в Азербайджане – горизонтальный срез на глубине 10 (а) и 25 км (б).
Необходимо учитывать, что реальные экспериментальные данные всегда содержат ошибки, связанные как с недостаточной точностью определения гипоцентра по причине того, что реальное строение коры отличается от принятой расчетной модели, так и с другими причинами случайного характера. При моделировании нами также вносились случайно распределенные ошибки в координаты землетрясений с среднеквадратическим отклонением ${{\sigma }_{r}}$ = 2 км и во времена пробега волн с ${{\sigma }_{t}}$ = 0.2 с.
В результате решения обратной задачи была восстановлена заданная трехмерная модель. В качестве примера на рис. 1 представлены результаты восстановления в виде двух горизонтальных срезов. Контурами на рис. 1 нанесены изолинии рельефа. Можно сделать вывод, что исходная модель восстановлена достаточно точно в местах с плотным заполнением источниками, что свидетельствует о достоверности и высокой разрешающей способности метода.
РЕЗУЛЬТАТЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Результаты численного моделирования подтвердили работоспособность разработанного алгоритма, что позволило перейти к обработке реальных экспериментальных данных, полученных сейсмологической службой Азербайджана. Здесь использовались те же сейсмические события, что и ранее. В результате работы было восстановлено трехмерное распределение скоростей сейсмических волн в регионе. На рис. 2 (масштабы осей не совпадают) для примера приведен вертикальный разрез, полученный при анализе времен пробега продольных (P) волн. Этот разрез соответствует линейному профилю вдоль ординаты со значением 120 км, отмеченному на рис. 1а белым цветом. Как можно видеть, геофизический разрез характеризуется слоистой структурой, с возрастающей с глубиной скоростью. Полученный результат находится в согласии с материалами последних работ по интерпретации данных глубинного сейсмического зондирования с использованием мощных детерминированных источников на Кавказе [8].
Рис. 2.
Пример вертикального разреза вдоль линейного профиля, показанного белым цветом на рис. 1а. Результат обработки реальных экспериментальных данных.

Таким образом, на основе численного моделирования и обработки экспериментальных данных, в работе показана работоспособность алгоритма восстановления трехмерного строения среды по данным о временах пробега объемных волн от внутренних источников. Показано, что размер сферической области и разрешение метода определяются плотностью распределения источников в объеме среды, что затрудняет его применение на границах региона. Путем внесения случайных ошибок в исходные данные доказана устойчивость решения обратной задачи. Дальнейшее развитие работы связано с использованием итерационных процедур для последовательного уточнения координат гипоцентров землетрясений, с учетом восстанавливаемой скоростной модели среды.
Детальный анализ, полученных в настоящей работе данных позволит перейти к выделению и изучению локальных флюидопроводящих структур в земной коре восточного Кавказа, насыщенного грязевыми вулканами и месторождениями полезных ископаемых. Отметим также, что использование метода “обратимой волны” совместно с томографическими методами [9] позволит значительно повысить точность скоростных моделей в сейсмоактивных районах Земли.
Работа выполнена при финансовой поддержке гранта Президента Российской федерации для поддержки научных школ № НШ-5545.2018.5, а также в рамках гос. задания ИФЗ РАН.
Список литературы
Nolet G. A Breviary of seismic tomography. Cambridge Univ. Press. 2008. 360 p.
Koulakov I., Shapiro N. Seismic Tomography of Volcanoes. Berlin, Heidelberg: Springer, 2014.
Slavina L.B., Pivovarova N.B. // Phys. of the Earth and Planetary Interiors. 1992. V. 75. № 1. P. 77.
Славина Л.Б., Пивоварова Н.Б., Сенюков С.Л. // Вулканология и сейсмология. 2012. № 2. С. 39; Slavina L.B., Pivovarova N.B., Senyukov S.L. // J. Volcanology and Seism. 2012. V. 6. № 2. P. 100.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория Волн. М.: Наука, 1990.
Schuster G. Seismic Inversion. Society of Exploration Geophysicists. 2017. 377 p.
Славина Л.Б., Кучай М.С., Лиходеев Д.В., Абдуллаева Р.Р. // Вопросы инж. сейсм. 2017. Т. 44. № 1. С. 31.
Павленкова Г.А. // Физика Земли. 2012. № 5. С. 16; Pavlenkova G.A. // Izv. Physics of the Solid Earth. 2012. V. 48. № 5. P. 375.
Жостков Р.А., Преснов Д.А., Шуруп А.С., Собисевич А.Л. // Изв. РАН. Сер. физ. 2017. Т. 81. № 1. С. 72; Zhostkov R.A., Presnov D.A., Shurup A.S., Sobisevich A.L. // Bull. Russ. Acad. Sci.: Physics. 2017. V. 81. № 1. P. 64.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


