Известия РАН. Серия физическая, 2019, T. 83, № 1, стр. 76-82
Кодировка зондирующих сигналов при томографировании акустических нелинейных параметровЕ. А. Котельников, Р. В. Крюков, В. А. Буров, К. В. Дмитриев, О. Д. Румянцева
Е. А. Котельников 1, Р. В. Крюков 1, В. А. Буров 1, К. В. Дмитриев 1, **, О. Д. Румянцева 1, *
1 Московский государственный университет имени М.В. Ломоносова, физический факультет
Москва, Россия
** E-mail: kdmitrie@aesc.msu.ru
* E-mail: burov@phys.msu.ru
Аннотация
Сопоставляются разные способы кодировки излучаемых сигналов, зондирующих томографируемый объект типа жидкой среды с целью восстановления пространственного распределения акустических нелинейных параметров с помощью малого количества преобразователей. Обсуждаются результаты восстановления модельных нелинейных рассеивателей и анализируется область пространственных частот, доступных для восстановления.
ВВЕДЕНИЕ
Возникновение и степень проявления нелинейных эффектов при распространении акустических волн зависит от нелинейных свойств среды (объекта), исследуемой в процессе томографирования. Количественными характеристиками, отвечающими за нелинейные свойства (до третьего порядка, включительно) жидкой среды, являются акустические нелинейные параметры второго порядка ${{\varepsilon }_{2}}(\vec {r})$ и третьего порядка ${{\varepsilon }_{3}}(\vec {r}).$ Их можно ввести при разложении уравнения состояния $P = P(\rho )$ в ряд по малым отклонениям $\rho {\text{'}}(\vec {r},t)$ плотности среды $\rho (\vec {r},t) \equiv {{\rho }_{0}} + \rho {\text{'}}(\vec {r},t)$ от ее постоянного невозмущенного значения ${{\rho }_{0}}.$ Здесь $P(\vec {r},t) \equiv {{P}_{0}} + p(\vec {r},t)$ – полное давление, ${{P}_{0}}$ – его постоянное невозмущенное значение, $p(\vec {r},t)$ – акустическое давление. С точностью до величин третьего порядка малости (включительно) этот ряд имеет вид:
Знание акустических нелинейных параметров среды представляет большой интерес для задач медицинской диагностики. Такие параметры обладают более высоким относительным контрастом в патологически измененной биоткани (по сравнению со здоровой), чем линейные параметры – скорость звука, плотность биоткани и поглощение в ней [1].
ТРУДНОСТИ ВОССТАНОВЛЕНИЯ НЕЛИНЕЙНЫХ ПАРАМЕТРОВ
Восстановление нелинейных параметров возможно с помощью малого количества преобразователей за счет эффекта рассеяния звука на звуке при неколлинеарном взаимодействии кодированных первичных волн, зондирующих томографируемый объект [2–4]. Кодировка зондирующих сигналов может использоваться при томографировании линейных характеристик среды, например, скорости звука [5]. В рассматриваемой схеме нелинейного томографирования привлечение кодировки позволяет восстановить пространственное распределение в виде комбинации ${{\varepsilon }_{2}}(\vec {r})$ и ${{\varepsilon }_{3}}(\vec {r}),$ имея всего три излучателя (которые одновременно посылают первичные сигналы, нелинейно взаимодействующие в области томографирования) и один приемник [3, 4], регистрирующий нелинейно рассеянные сигналы на комбинационных частотах третьего порядка [6, 7]. Однако задача получения томограмм отдельно для ${{\varepsilon }_{2}}(\vec {r})$ и отдельно для ${{\varepsilon }_{3}}(\vec {r})$ усложняется тем, что регистрируемый комбинационный сигнал третьего порядка формируется за счет двух конкурирующих процессов, происходящих при нелинейном взаимодействии трех первичных волн. Это, во-первых, взаимодействие чисто третьего порядка и, во-вторых, двукратное взаимодействие второго порядка [6, 8].
Первый процесс представляет собой локальное (т.е. происходящее в одной и той же точке среды $\vec {r}$) взаимодействие трех зондирующих волн с образованием результирующего нелинейно рассеянного сигнала на комбинационных частотах третьего порядка. В силу локальности процесса такой комбинационный сигнал несет информацию о нелинейных параметрах ${{\varepsilon }_{2}}(\vec {r})$ и ${{\varepsilon }_{3}}(\vec {r})$ именно в данной точке. Значения ${{\varepsilon }_{3}}(\vec {r})$ для биотканей в настоящее время исследованы весьма слабо и поэтому представляют наибольший интерес при нелинейном томографировании третьего порядка. Именно в той части упомянутого комбинационного сигнала, которая соответствует так называемым физическим нелинейным вторичным источникам [6], представлена информация о ${{\varepsilon }_{3}}(\vec {r})$ в виде комбинированного нелинейного параметра $\varepsilon _{3}^{'}(\vec {r}) \equiv 2{{\left( {{{\varepsilon }_{2}}(\vec {r}) - 1} \right)}^{2}} - {{\varepsilon }_{3}}(\vec {r}).$
Второй процесс – нелокальный, поскольку он состоит из двух последовательных актов нелинейного взаимодействия второго порядка, которые могут происходить в различных точках среды. Поэтому в соответствующем нелинейно рассеянном сигнале третьего порядка содержится информация о ${{\varepsilon }_{2}}(\vec {r}\,{\text{'}})$ в различных точках $\vec {r}{\kern 1pt} {\text{'}},$ что чрезвычайно усложняет возможность определения значения ${{\varepsilon }_{2}}(\vec {r})$ в конкретной точке $\vec {r}.$ В то же время информация о ${{\varepsilon }_{3}}(\vec {r})$ в нем вообще отсутствует. Тем самым, вклад в поле на приемнике, обусловленный данным процессом, является мешающим.
Разделение вклада от упомянутых конкурирующих процессов в получаемую итоговую томограмму представляет одну из основных трудностей в задачах акустической нелинейной томографии третьего порядка [8]. Тем не менее кодирование всех трех первичных сигналов позволяет сделать второй конкурирующий процесс – двукратное взаимодействие второго порядка – квазилокальным и, как следствие, говорить о возможности получения томограмм отдельно для ${{\varepsilon }_{2}}(\vec {r})$ и ${{\varepsilon }_{3}}(\vec {r})$ [7, 8].
СПОСОБЫ КОДИРОВКИ СИГНАЛОВ И РЕЗУЛЬТАТЫ ОБРАБОТКИ
Было исследовано несколько способов кодировки зондирующих сигналов. Дело в том, что регистрируемый информативный сигнал третьего порядка имеет весьма малую амплитуду, по сравнению с первичными сигналами и даже с нелинейно рассеянными сигналами второго порядка. Это приводит к необходимости жесткого ограничения ширины частотной полосы спектра зондирующих сигналов, причем максимальная возможная ширина $\Delta f$ для каждого зондирующего сигнала определяется параметрами томографической схемы [4]. Тем самым, нужно выбрать наиболее подходящий способ кодировки, как с точки зрения практической реализации зондирующего сигнала с учетом требования жесткой локализации спектра в полосе $\Delta f,$ так и с точки зрения качества получаемого изображения.
Первый исследованный и использованный в экспериментах [2, 4] способ кодировки – фазоманипулированный сигнал. Для его формирования монохроматический сигнал исходно кодируется псевдослучайной последовательностью, которая задается произвольным количеством элементов. Каждый элемент последовательности принимает одно из двух значений (“1” либо “–1”), и ему сопоставляется кодовый интервал с длительностью ${{\tau }^{{code}}}.$ При наступлении каждого нового кодового интервала, фаза исходного монохроматического сигнала либо не изменяется (в случае значения кодирующей последовательности “1”), либо изменяется на π (в случае значения “–1”). Спектр сигнала, кодированного таким способом, не имеет изначально хорошей локализации (рис. 1а), и поэтому при формировании излучаемого сигнала такой спектр необходимо предварительно профильтровать, оставив компоненты лишь в заданной частотной полосе $\Delta f.$
Рис. 1.
Абсолютное значение спектра фазоманипулированного (а) и sinc-модулированного (б) сигналов; толстыми вертикальными линиями показана частотная полоса, в которой фильтруется сигнал.
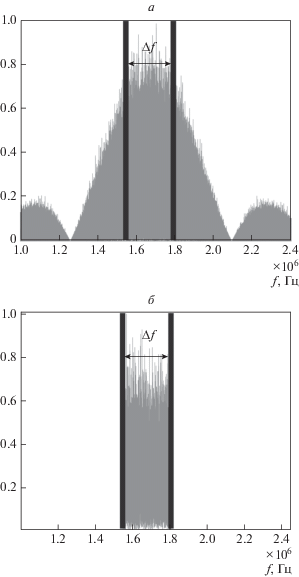
Поэтому встает вопрос об оптимальной длительности кодового интервала ${{\tau }^{{code}}}$ для исходного фазоманипулированного сигнала до фильтрации. Другими словами, требуется определить, какое количество периодов n на центральной частоте сигнала ${{f}_{0}}$ должно укладываться на протяжении кодового интервала при заданном максимально допустимом значении $\Delta f,$ т.е. $n \equiv {{\tau }^{{code}}}{{f}_{0}}.$ Так, с одной стороны, увеличение длительности кодового интервала ${{\tau }^{{code}}}$ приводит к сужению ширины спектра исходного фазоманипулированного сигнала, и можно добиться, чтобы существенная часть этого спектра лежала внутри заданной полосы $\Delta f.$
Например, количество периодов, при котором ширина центрального “лепестка” спектра фазоманипулированного сигнала практически совпадает с шириной $\Delta f,$ определяемой параметрами схемы, составляет $n = {{2{{f}_{0}}} \mathord{\left/ {\vphantom {{2{{f}_{0}}} {\Delta f}}} \right. \kern-0em} {\Delta f}}.$ Однако, чем длиннее кодовый интервал ${{\tau }^{{code}}},$ тем меньше при фиксированной длительности излучения сложность излучаемого зондирующего сигнала (т.е. полное количество элементов в последовательности, кодирующей излучаемый сигнал); как следствие, ухудшается разрешающая способность итоговой томограммы [4]. С другой стороны, если, наоборот, уменьшать ${{\tau }^{{code}}},$ то ширина центрального “лепестка” спектра исходного сигнала будет увеличиваться. Тогда фильтрация этого спектра прямоугольным “окном” (края “окна” сглаживаются) с заданной шириной $\Delta f,$ – фильтрация выполняется для формирования излучаемого сигнала, – будет приводить к потере тем большей части кодовой информации, чем меньше ${{\tau }^{{code}}}.$ Следовательно, нужен компромиссный вариант для значения ${{\tau }^{{code}}},$ при котором обеспечивается приемлемая разрешающая способность.
Численным моделированием было найдено, что наиболее подходящим является количество периодов $n \approx {{{{f}_{0}}} \mathord{\left/ {\vphantom {{{{f}_{0}}} {(1.5\Delta f)}}} \right. \kern-0em} {(1.5\Delta f)}}$ (n округляется до целого значения), как наиболее сбалансированное (рис. 1а). Это значение n, эквивалентное длительности кодового интервала ${{\tau }^{{{\text{code}}}}} \approx {1 \mathord{\left/ {\vphantom {1 {(1.5\Delta f)}}} \right. \kern-0em} {(1.5\Delta f)}},$ индивидуально для каждого излучаемого сигнала как зависящее от параметров данного сигнала ${{f}_{0}}$ и $\Delta f.$
В рассмотренном выше случае исходного фазоманипулированного сигнала фильтрация приводит к отсечению периферийной части спектра этого сигнала (рис. 1а) и, следовательно, к потере определенной части кодовой информации. Кроме того, необходимо обеспечить это отсечение с высокой степенью точности; в противном случае остатки компонент спектра, которые, в идеале, должны быть отфильтрованы, могут порождать сильные мешающие сигналы в рабочей полосе принимаемого сигнала третьего порядка. Данное обстоятельство предъявляет повышенные требования к практической реализации процедуры фильтрации, особенно с помощью аналоговых устройств. Более целесообразно использовать тот способ кодировки исходного сигнала, который изначально дает хорошо локализованный спектр. Ниже рассматриваются два таких способа: формирование исходного сигнала, во-первых, в виде суммы модулированных по фазе сигналов с sinc-образной огибающей и, во-вторых, в виде случайного шума, спектр которого программно фильтруется в заданной полосе $\Delta f.$
Исходный sinc-модулированный сигнал формируется как функция времени t в виде $\sum\nolimits_{m = 1}^M {{{Z}_{m}}{\text{sinc}}} \left\{ {\pi \Delta f(t - {{\tau }^{{code}}}m)} \right\}\exp \left\{ { - i2\pi {{f}_{0}}(t - {{\tau }^{{code}}}m)} \right\},$ где m – порядковый номер текущего кодового интервала, M – общее количество кодовых интервалов в последовательности, ${{Z}_{m}}$ – значение (“1” либо “–1”) текущего элемента псевдослучайной последовательности. Каждому новому кодированному интервалу сопоставляется центральный пик отдельной sinc-образной огибающей. Значение ${{Z}_{m}}$ элемента псевдослучайной последовательности определяет фазу (0 при ${{Z}_{m}} = 1;$ π при ${{Z}_{m}} = - 1$), которая сопоставляется текущей sinc-образной огибающей. Спектр такого сигнала четко локализован именно в той полосе частот от $\left( {{{f}_{0}} - {{\Delta f} \mathord{\left/ {\vphantom {{\Delta f} 2}} \right. \kern-0em} 2}} \right)$ до $\left( {{{f}_{0}} + {{\Delta f} \mathord{\left/ {\vphantom {{\Delta f} 2}} \right. \kern-0em} 2}} \right),$ в которой может присутствовать спектр зондирующего сигнала (рис. 1б).
В случае использования шумового сигнала исходно генерируется случайная последовательность как функция времени. Далее ее спектр программно фильтруется прямоугольным “окном” со сглаженными краями и шириной $\Delta f$ (внешний вид такого профильтрованного спектра аналогичен рис. 1б), после чего делается обратный переход во временное представление.
При численном моделировании использовались параметры реальной томографической схемы [7, 9]. Так, спектры трех кодированных зондирующих волн были представлены частотами ${{f}_{1}},{{f}_{2}} \in (1.55 - 1.8)$ МГц, ${{f}_{3}} \in (2.075 - 2.325)$ МГц; углы между акустической осью приемника (ее положение соответствует углу 0°) и акустическими осями трех излучателей составляли соответственно ${{\beta }_{1}} = 33^\circ ,$ ${{\beta }_{2}} = - 104^\circ ,$ ${{\beta }_{3}} = - 19^\circ .$ Длительность кодового интервала определялась количеством периодов $n = 4,4,5$ для соответствующих зондирующих сигналов. Приемником с центром в точке $\vec {y}$ регистрировался сигнал $p(\vec {y},t)$ на суммарно-разностных комбинационных частотах ${{f}_{{ + \, - }}} = {{f}_{1}} + {{f}_{2}} - {{f}_{3}},$ где ${{f}_{{ + \, - }}} \in (0.9 - 1.4)$ МГц. Надо заметить, что в имеющейся экспериментальной установке используются излучатели и приемник цилиндрической формы. Однако благодаря специально разработанной системе акустических конических зеркал [4, 10] излучаемые цилиндрические волны превращаются в области томографирования в плоские волны с волновыми векторами ${{\vec {k}}_{1}},$ ${{\vec {k}}_{2}},$ ${{\vec {k}}_{3}}.$ Фиксированные направления этих векторов описываются соответствующими углами $(180^\circ + {{\beta }_{1}}),$ $(180^\circ + {{\beta }_{2}}),$ $(180^\circ + {{\beta }_{3}}).$ Сигнал, идущий из области томографирования, проходит через ту же систему зеркал и попадает на цилиндрический приемник.
Для сравнения трех способов кодировки излучаемых зондирующих сигналов – фазоманипулированного, sinc-модулированного и фильтрованного шумового – были выбраны модели двумерных нелинейных рассеивателей в виде одиночного точечного рассеивателя (рис. 2, 3) и в виде различно ориентированных полос (рис. 4). Фиксировалась реализация случайной последовательности, и на ее основе формировался исходный сигнал, соответствующий каждому из рассмотренных способов кодировки. Далее численно моделировался сигнал третьего порядка на приемнике $p(\vec {y},t),$ причем учитывался только один вид нелинейных вторичных источников – физические источники чисто третьего порядка [6]. Тогда корреляционная обработка (типа согласованной фильтрации) принимаемого сигнала дает оценку $\hat {\varepsilon }_{3}^{'}(\vec {r})$ комбинированного нелинейного параметра $\varepsilon _{3}^{'}(\vec {r})\,:$
(1)
$\hat {\varepsilon }_{3}^{'}(\vec {r}) = \frac{{\int {p_{{ + \, - \,\,\delta ({\text{C}})}}^{ * }(\vec {y}\left| {\vec {r}} \right.;t){{p}_{{({\text{C}})}}}(\vec {y},t)dt} }}{{\int {p_{{ + \, - \,\,\delta ({\text{C}})}}^{ * }(\vec {y}\left| {\vec {r}} \right.;t){{p}_{{ + \, - \,\,\delta ({\text{C}})}}}(\vec {y}\left| {\vec {r}} \right.;t)} dt}},$Рис. 2.
Случай трех кодированных первичных волн. Оценка одиночного точечного нелинейного рассеивателя (а) и пространственный спектр этой оценки (б); область локализации и плотность восстанавливаемой части пространственного спектра нелинейного рассеивателя в предположении одинаковой амплитуды всех спектральных составляющих первичных волн (в).
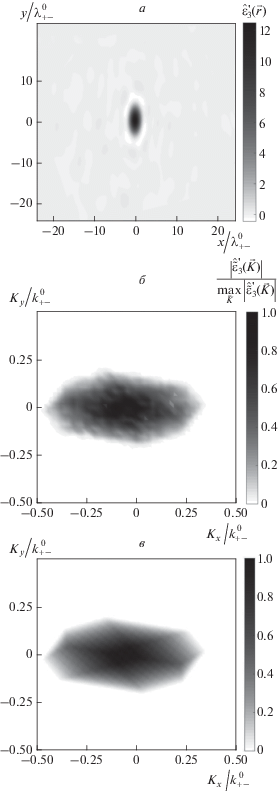
Рис. 3.
Случай двух кодированных и одной монохроматической первичных волн. Подпись аналогична рисунку 2.

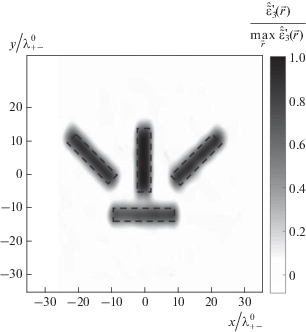
Рис. 4.
Восстановленное нормированное пространственное распределение акустического нелинейного рассеивателя третьего порядка в виде четырех полос, расположенных на фоне с $\varepsilon _{3}^{'} \equiv 0;$ контуры модельных полос изображены штриховыми линиями.
Рассматривались различные реализации случайных последовательностей, на основе которых формировались кодированные зондирующие сигналы. Оказалось, что томограммы, получаемые в результате обработки (1), не имеют сколько-нибудь принципиальных различий при рассмотренных трех способах кодировки. Тем самым, на практике можно использовать тот вид кодировки, который удобнее реализовать с помощью имеющейся аппаратуры. Ниже обсуждаются характерные особенности томограмм, и приводятся их изображения (рис. 2–4) для способа формирования кодированных первичных сигналов в виде фильтрованного шума при фиксированной длительности сигнала на приемнике 0.06 с. Шаг пространственной дискретизации при решении прямой и обратной задач составлял ${{\lambda _{{ + \, - }}^{0}} \mathord{\left/ {\vphantom {{\lambda _{{ + \, - }}^{0}} 5}} \right. \kern-0em} 5},$ где $\lambda _{{ + \, - }}^{0}$ – длина волны, соответствующая центральной частоте $f_{{ + \, - }}^{0}$ в рабочем диапазоне принимаемых частот ${{f}_{{ + \, - }}} = {{f}_{1}} + {{f}_{2}} - {{f}_{3}}.$
Одиночному точечному нелинейному рассеивателю, помещенному в начало координат, сопоставлялось значение комбинированного нелинейного параметра $\varepsilon _{3}^{'} = 12.$ Откликом (1) на этот рассеиватель является томограмма в виде ограниченного “пятна” (рис. 2а), размеры которого определяют разрешающую способность томографической системы в соответствующем направлении. Надо обратить внимание, что на рис. 2а (и далее на рис. 3а и 4) в качестве оценки изображена, на самом деле, действительная часть $\operatorname{Re} \hat {\varepsilon }{{_{3}^{'}}_{3}}(\vec {r}),$ поскольку априори известно, что восстанавливаемые акустические нелинейные параметры являются действительными величинами. В рассматриваемом случае точечного нелинейного рассеивателя и трех кодированных зондирующих волн получилось ${{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }_{3}^{'}(\vec {r})} \right|} \mathord{\left/ {\vphantom {{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }_{3}^{'}(\vec {r})} \right|} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}}} \right. \kern-0em} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}} \approx 0.22$ при упомянутой длительности обрабатываемого сигнала для всех способов кодировки и всех реализациях случайных последовательностей.
Для сравнения на рис. 3а приведен отклик на тот же рассеиватель, для случая, когда среди трех первичных волн две кодированы (с прежними частотными полосами), а третья – монохроматическая (с частотой $f_{3}^{0} = 2.\,2$ МГц, равной центральной частоте кодированной третьей волны в предшествующем случае); ${{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|} \mathord{\left/ {\vphantom {{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}}} \right. \kern-0em} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}} \approx 0.27.$ Из сравнения рис. 2а и рис. 3а видны преимущества замены третьей монохроматической волны на кодированную: “пятно” отклика становится более четко локализованным, нежелательные отрицательные флуктуации этого отклика уменьшаются, и ${{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|} \mathord{\left/ {\vphantom {{{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Im} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}}} \right. \kern-0em} {{{{\max }}_{{\vec {r}}}}\left| {\operatorname{Re} \hat {\varepsilon }{{{_{3}^{'}}}_{3}}(\vec {r})} \right|}}$ также уменьшается.
“Пятно” отклика на рис. 2а и 3а вытянуто вдоль оси $Oy$, т.е. разрешающая способность в этом направлении хуже. Это взаимнооднозначно связано с той областью компонент пространственного спектра $\tilde {\varepsilon }_{3}^{'}(\vec {K})$ рассеивателя $\varepsilon _{3}^{'}(\vec {r}),$ которая доступна для восстановления в данном томографическом эксперименте, т.е. при заданных угловых позициях приемного и излучающих преобразователей и при заданных рабочих частотных полосах излучаемых и принимаемого сигналов. Так, область локализации и плотность для векторов $\vec {K}$ восстанавливаемой части пространственного спектра, в предположении одинаковой амплитуды всех спектральных составляющих первичных волн, получается перебором частот излучаемых волн (${{f}_{1}},$ ${{f}_{2}},$ ${{f}_{3}}$) с учетом рабочей полосы информативных принимаемых частот ${{f}_{{ + \, - }}} = {{f}_{1}} + {{f}_{2}} - {{f}_{3}}$ при фиксировании направлений волновых векторов первичных волн (${{\vec {k}}_{1}},$ ${{\vec {k}}_{2}},$ ${{\vec {k}}_{3}}$) и принимаемого сигнала ${{\vec {k}}_{{ + \, - }}}.$ Здесь $\vec {K} = {{\vec {K}}_{{ + \, - }}}$ ≡ ${{\vec {k}}_{{ + \, - }}} - ({{\vec {k}}_{1}} + {{\vec {k}}_{2}} - {{\vec {k}}_{3}}),$ где $\left| {{{{\vec {k}}}_{1}}} \right| = {{2\pi {{f}_{1}}} \mathord{\left/ {\vphantom {{2\pi {{f}_{1}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ $\left| {{{{\vec {k}}}_{2}}} \right| = {{2\pi {{f}_{2}}} \mathord{\left/ {\vphantom {{2\pi {{f}_{2}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ $\left| {{{{\vec {k}}}_{3}}} \right| = {{2\pi {{f}_{3}}} \mathord{\left/ {\vphantom {{2\pi {{f}_{3}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ $\left| {{{{\vec {k}}}_{{ + \, - }}}} \right| = {{2\pi {{f}_{{ + \, - }}}} \mathord{\left/ {\vphantom {{2\pi {{f}_{{ + \, - }}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}};$ ${{c}_{0}}$ – скорость звука [3].
Шкала на рис. 2в и 3в отражает нормированное (на свое максимальное значение) количество реализаций, формирующих фиксированный вектор пространственной частоты ${{\vec {K}}_{{ + \, - }}}.$ Пространственно-спектральная плотность векторов $\vec {K}$ внутри такой области неоднородна в случае трех кодированных первичных волн (рис. 2в; волновое число $k_{{ + \, - }}^{0}$ соответствует центральной частоте $f_{{ + \, - }}^{0}$). В то же время в случае третьей монохроматической первичной волны эта плотность будет одинаковой (рис. 3в), причем при любых (не обязательно совпадающих) центральных частотах и ширинах рабочих частотных полос двух первичных кодированных волн. Пространственный спектр $\hat {\tilde {\varepsilon }}_{3}^{'}(\vec {K})$ оценки $\hat {\varepsilon }_{3}^{'}(\vec {r})$ точечного нелинейного рассеивателя с учетом реального спектра излучаемых сигналов представлен на рис. 2б и 3б.
Другой нелинейный рассеиватель задавался в виде четырех полос с постоянным значением $\varepsilon _{3}^{'} = 12$ внутри них. Полосы располагались на фоне с $\varepsilon _{3}^{'} \equiv 0$ под углами 0°, 45°, 90° и 135° по отношению к направлению приема; ширина и длина каждой полосы составляли $4.2\lambda _{{ + \, - }}^{0}$ и $20.2\lambda _{{ + \, - }}^{0},$ соответственно (рис. 4, штриховые линии). Данная модель позволяет проиллюстрировать качество восстановления различно ориентированных деталей нелинейного рассеивателя в случае трех кодированных первичных волн (см. рис. 4, на котором приведенная оценка $\hat {\varepsilon }_{3}^{'}$ пронормирована на свое максимальное значение). Для обеспечения более точных значений оценки нужна пространственная фильтрация полученной функции $\hat {\varepsilon }_{3}^{'}(\vec {r}),$ предполагающая нормировку компонент ее пространственного спектра $\hat {\tilde {\varepsilon }}{{_{3}^{'}}_{3}}(\vec {K})$ с помощью пространственного спектра оценки одиночного рассеивателя (рис. 2б).
ЗАКЛЮЧЕНИЕ
Итак, целесообразность выбора того или иного способа кодировки определяется, в первую очередь, имеющимися техническими возможностями излучения и приема сигналов в заданных частотных полосах с заданной точностью [4, 7, 10]. Так, к преимуществам использования фазоманипулированного сигнала относится, во-первых, возможность его генерации на основе обычного генератора гармонического сигнала и программируемой логики. Во-вторых, для вычисления сигнала сравнения в процессе обработки (1) достаточно иметь лишь малый объем информации о кодирующей М-последовательности, а передавать в ЭВМ непосредственно весь излучаемый сигнал излишне. Недостатком же является необходимость аналоговой фильтрации спектра сигнала. В то же время преимуществом sinc-модулированного сигнала и сигнала в виде профильтрованного случайного шума является уже изначально ограниченный спектр. К недостаткам относится использование относительно дорогого генератора сигнала произвольной формы, а также необходимость формировать и запоминать излучаемый сигнал целиком в памяти компьютера. Имеющаяся в настоящее время экспериментальная установка [7, 9] позволяет, в принципе, реализовать любой из упомянутых способов кодировки, причем использование фильтрованного шумового сигнала представляется наиболее удобным.
Работа поддержана грантом РФФИ № 16-29-02097 офи_м.
Список литературы
Duck F.A. Phys. Properties of Tissue. London: Academic Press, 1990.
Береза С.А., Буров В.А., Евтухов С.Н. // Акуст. журн. 2008. Т. 54. № 4. С. 522.
Буров В.А., Шмелев А.А. // Акуст. журн. 2009. Т. 55. № 4–5. С. 466.
Буров В.А., Шмелев А.А., Зотов Д.И. // Акуст. журн. 2013. Т. 59. № 1. С. 31.
Wang K., Matthews T., Anis F. et al. // IEEE Transact. on Ultrasonics, Ferroelectrics, and Frequency Control. 2015. V. 62. № 3. P. 475.
Буров В.А., Шмелев А.А., Крюков Р.В., Румянцева О.Д. // Акуст. журн. 2015. Т. 61. № 6. С. 669.
Дмитриев К.В., Зотов Д.И., Румянцева О.Д. // Изв. РАН. Сер. физ. 2017. Т. 81. № 8. С. 1014.
Буров В.А., Крюков Р.В., Румянцева О.Д. // Изв. РАН. Сер. физ. 2015. Т. 79. № 12. С. 1676.
Дмитриев К.В., Котельников Е.А., Зотов Д.И., Румянцева О.Д. // Уч. записки физ. ф-та МГУ. 2017. № 5. С. 1750713.
Буров В.А., Шмелев А.А., Евтухов С.Н. и др. Патент на изобретение RU 2530659 C2. Приоритет от 08.08.2012. Москва, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


