Известия РАН. Серия физическая, 2019, T. 83, № 3, стр. 420-423

ВВЕДЕНИЕ

Криптография ‒ одна из старейших прикладных наук о контроле секретных свойств информации, история которой насчитывает несколько тысяч лет. Именно в ней понятие “полезной случайности” постепенно выросло в отдельное научное направление, связанное с фундаментальным изучением понятий хаоса и предсказуемости. На данный момент в мире существует огромное количество разных подходов к количественному определению хаотических и случайных явлений, многие из которых в своем корне опираются на меру сравнения набора из данных друг относительно друга. Именно здесь кроются проблемы окончательного осмысления таких важных понятий как “измерение”, “повторяемость” и “закон природы”, заложенных математиками-механиками в физику около 300 лет назад. Несмотря на видимые значительные успехи в техническом развитии цивилизации за эти века, сами основы анализа и обработки данных в прикладных естественных науках не получили достаточного внимания со стороны исследователей-экспериментаторов. В этой работе мы хотим продемонстрировать читателю применение новых прикладных методов анализа физических данных, кардинально меняющих взгляд на проблему измерения, случайности и хаоса в естественных науках.

Наше исследование посвящено изучению случайности в рамках высокоскоростной квантовой криптографии на непрерывных переменных [1–4], где требуется большой расход случайных чисел. По сути, системы квантовой криптографии представляют собой распределенную систему согласования двух независимых случайных последовательностей на передающей и приемной сторонах при помощи квантовых состояний. Сами случайные последовательности реализуются с помощью генераторов случайных чисел (ГСЧ). При разработке ГСЧ для квантовой криптографии недостаточно того, что тесты на случайность по некоторому критерию были пройдены, что является лишь необходимым условием. Принципиально важен источник первичной случайности [1], который используется для получения равнораспределенной последовательности 0 и 1 и который был бы источником случайности по другим физическим соображениям [4], не зависящим от тестов. Многие псевдослучайные ГСЧ проходят тесты, но не являются, очевидно, истинно случайными. Все ГСЧ можно разделить на два класса. Первый класс ‒ физические генераторы, когда случайная последовательность извлекается из некоторого физического процесса. Второй класс ‒ математические ГСЧ, когда случайная последовательность получается как результат математического преобразования, как правило, рекуррентного, некоторого затравочного числа. Любой математический генератор выдает псевдослучайную последовательность, которая полностью предсказуема, если известны исходные затравочные числа.

Поэтому процесс генерации случайных чисел на основе результатов измерений физических величин (физический ГСЧ) на существующий момент является единственным источником случайности, который признан научным миром надежным для использования в квантовых коммуникациях. Этот процесс разделяется на 2 стадии: измерение (вместе с получением цифровых данных) и затем экстракция битовой последовательности. Экстракция конечной битовой последовательности, которая будет проходить известные тесты на случайность, достаточно хорошо изучена, и многочисленные эффективные алгоритмы экстракции присутствуют в огромном количестве в свободной печати [5, 6].

В этой работе мы делаем акцент на изучении первой стадии, то есть на изучении качества исходных сырых данных, полученных в ходе измерений физической системы. Нами выявлены новые дискретно-интегральные характеристики шумов и предложена робастная оценка меры случайности на основе метода ранжированных амплитуд, дополняющая традиционный энтропийный анализ Шеннона–Реньи в криптографии. Сделан анализ качества случайности исходных данных для квантового ГСЧ на основе гомодинного детектирования.

ФИЗИЧЕСКИЙ ГСЧ И ИДЕЯ ЕГО АНАЛИЗА

Основным вопросом, решаемым в рамках построения физического ГСЧ на стадии измерения, остается количественный вопрос о “качестве” исходных цифровых данных, полученных с аналого-цифрового преобразователя (АЦП) устройства. Статистические меры “качества” в криптографии, стеганографии и анализе временных рядов сильно различаются. Однако обеспечение физической случайности ГСЧ на первой стадии связано в первую очередь с мерой совпадения экспериментальных данных с теоретически предсказуемыми в пространстве состояний АЦП или его расширенном пространстве (случай более идеального АЦП). Такое сравнение невозможно на уровне стандартных энтропийных мер Шеннона–Реньи, к которым прибегают все известные авторам методы реализации физических ГСЧ.

Поэтому мы предлагаем использовать более естественную меру случайности, основанную на статистике дробных моментов, построенных на основе последовательности ранжированных амплитуд (ПРА) [7–9]. Метод ПРА, называемый в математической литературе порядковыми статистиками, является основным промежуточным звеном трансформации данных, которое включает в себя всю исходную статистическую информацию без потерь (неинвазивность). ПРА-выборки {s_k} ‒ это ее упорядоченная выборка SRA[{s_k}] = {x_k}, где x_k ≥ x_k + 1. Для случайных последовательностей самой широкой природы, не имеющих явно выраженного тренда и заранее известной физически или математически детерминированной природы, ПРА-анализ является единственно возможным достоверным статистическим методом гладкого анализа дискретной случайности.

КАЧЕСТВО ГСЧ И ИНТЕГРАЛЬНАЯ СТАТИСТИКА

Дискретное интегрирование и центрирование (вычитание среднего) известны в дискретной статистике как одни из немногих методов локального неинвазивного анализа, позволяющих эффективно отобразить хаотический ряд чисел во множество с уникальным трендом. В математике многократное интегрирование и дифференцирование исходных функций системы позволяют построить ее расширенное фазовое пространство (теория струй), где “законы” (дифференциальные уравнения) приобретают максимально простой вид. На этом пути были достигнуты значительные успехи, связанные с построением формальных решений дифференциальных уравнений, что в корне изменило возможности анализа теоретической физики. Дискретным аналогом такой схемы является изучение рекуррентных соотношений. На уровне прикладной статистики интересным становится изучение трендов многократных дискретных интегралов от данных с целью их идентификации.

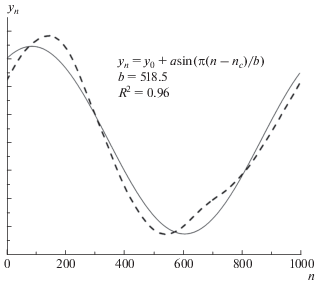
Для экспериментальных данных, полученных на основе гомодинного детектирования лазерного излучения, мы построили несколько выборок и задались целью их сравнить. Мы взяли 2 подряд идущих подвыборки и вычли их друг из друга. Для полученной разницы, которая номинально также должна быть случайной величиной, мы 3 раза провели обратимую операцию дискретного интегрирования и центрирования. В результате мы получили кривую y_n, показанную на рис. 1, имеющую явный синусоидальный тренд. Этот факт говорит об отсутствии полной случайности и наличии не выявленных пока сложных закономерностях. Эти тренды интегральных кривых допускают количественную параметризацию, являющуюся уникальным идентификатором физического ГСЧ [8]. Дискретно-интегральные характеристики шумов также могут быть использованы в качестве аналогов хэш-функций для первичных данных физических ГСЧ.

Рис. 1.

Типичный результат тройного дискретного интегрирования y_n разницы двух коротких выборок (масштаб для наглядности опущен): штриховая линия ‒ эксперимент, сплошная линия ‒ явно выраженный синусоидальный тренд.

ПРА-МЕРА КАЧЕСТВА ДАННЫХ

По сравнению с общеизвестными информационными энтропийными мерами Шеннона–Реньи, предложенные техники работают на естественном фазовом пространстве физической измеряемой системы для набора дискретных данных. При увеличении разрядности АЦП и качества установки вид и форма ПРА-кривых останутся практически неизменными, в отличие от энтропии Шеннона–Реньи, которая больше подходит для определения качества затравочной случайности абстрактных чисел (не привязанных к фазовому пространству физической системы) в схемах с каскадной генерацией случайных чисел.

Самым простым и прозрачным методом сравнения для ПРА-кривых [9] может служить коэффициент детерминации R², определяющий точность совпадения двух кривых (или точность фитинга при сравнении эксперимента с гипотезой, отвечающей некоторой модельной функции с параметрами). По изложенной выше схеме мы получили ПРА исходных данных с АЦП (целые числа от –75 до 75) для квантового генератора случайных чисел на основе гомодинного детектирования. Предполагалось, что ПРА-распределение данных с АЦП имело пуассоновский характер [10, 11], то есть x_n = a – b*ln(n + 1).

В результате фитинга ПРА [3, 4] пуассоновским распределением (сравнение с пуассоновской статистикой) для N = 1000 точек мы получили R² = 0.82, что определяет в нашем случае меру качества экспериментальных данных по отношению к идеальным для ГСЧ данным (см. рис. 2). То есть около 82% сырых данных с АЦП могут считаться “хорошими” (надежными) для конвертации в конечную битовую последовательность, что говорит о достаточно хорошем качестве квантового ГСЧ, основанного на гомодинном детектировании.

Рис. 2.

ПРА данных с АЦП после гомодинного детектора: кружками отмечены экспериментальные данные, прямая линия ‒ теория (отвечает распределению Пуассона). Качество данных, определяемое коэффициентом детерминации R², составляет 0.82.

ЗАКЛЮЧЕНИЕ

ПРА-анализ и многократное дискретное интегрирование являются удобными робастными инструментами для быстрого прикладного анализа качества первичной случайности, заложенной в физический ГСЧ. По сравнению с известными информационными энтропийными мерами Шеннона–Реньи, предложенные техники работают на естественном фазовом пространстве физической измеряемой системы для набора дискретных данных и являются гладкими функциями. Более того, тренды ПРА и интегральных кривых допускают количественную параметризацию, являющуюся уникальным идентификатором физического ГСЧ.

При анализе экспериментальных данных для квантового ГСЧ на основе гомодинного детектирования нами выявлены новые дискретно-интегральные характеристики шумов, показывающие наличие уникальных трендов, что может быть использовано в качестве аналогов хэш-функций для первичных данных физических ГСЧ. Предложена робастная оценка качества случайности на основе сравнения ПРА-кривой с идеальной ПРА-кривой для пуассоновского процесса, которая дополняет известные оценки качества случайности. Изученные методы также могут быть использованы в квантовых коммуникациях в целях мониторинга и для обеспечения большей безопасности.

Работа поддержана грантом молодых ученых РТ № 06-36-ц-Г 2018 “Безопасность оптических и квантовых коммуникаций” (рук. Перминов Н.С.) (основная идея и численное моделирование), а также грантом Правительства Российской Федерации, проект № 14.Z50.31.0040, 17 февраля 2017 года (эксперимент).