Известия РАН. Серия физическая, 2019, T. 83, № 4, стр. 544-549

О двойных спиновых асимметриях в упругом рассеянии электронов на протонах

М. Я. Сафин^*

Федеральное государственное бюджетное учреждение высшего образования “Российский университет дружбы народов”
Москва, Россия

^* E-mail: misafin@gmail.com

Поступила в редакцию 01.10.2018
После доработки 15.10.2018
Принята к публикации 19.11.2018

DOI: 10.1134/S0367676519040227

Полный текст (PDF)

Аннотация

На основе полученных дифференциальных сечений рассеяния продольно поляризованных электронов с учетом поляризации протонной мишени или продольной поляризации протонов отдачи исследованы одинарные спиновые асимметрии: нарушающая T-четность асимметрия по спину протона мишени ${{A}^{{( \bot )}}}$ и степень продольной поляризации протонов отдачи ${{P}_{p}}.$ Получены и проанализированы также двойные спиновые асимметрии: асимметрия по корреляции спиральности падающего электрона и спина протона мишени ${{A}_{{ep}}}$ и право-левая асимметрия степени продольной поляризации протона отдачи ${{D}_{p}}.$ Показано, что указанные асимметрии дают возможность измерения отношений формфакторов протона ${{{{G}_{{Ep}}}} \mathord{\left/ {\vphantom {{{{G}_{{Ep}}}} {{{G}_{{Mp}}}}}} \right. \kern-0em} {{{G}_{{Mp}}}}}$ и ${{{{G}_{{Mp}}}} \mathord{\left/ {\vphantom {{{{G}_{{Mp}}}} {{{G}_{{1p}}}}}} \right. \kern-0em} {{{G}_{{1p}}}}}.$

ВВЕДЕНИЕ

Применение поляризационных методов играет существенную роль при изучении структуры ядер и нуклонов, а также фундаментальных свойств элементарных частиц [1, 2]. Недавние поляризационные эксперименты [3, 4] по электрон-нуклонному рассеянию значительно расширили наше понимание нуклонных электромагнитных формфакторов (наблюдение быстрого уменьшения отношения электрического и магнитного формфакторов протона ${{G_{E}^{p}} \mathord{\left/ {\vphantom {{G_{E}^{p}} {G_{M}^{p}}}} \right. \kern-0em} {G_{M}^{p}}}$ в области квадрата переданного импульса ${{Q}^{2}} \geqslant 1$ ГэВ²).

Исследуемые экспериментально спиновые асимметрии могут быть разделены на две группы: одинарные спиновые асимметрии (ОСА) и двойные спиновые асимметрии (ДСА).

В качестве примера изучения асимметрии первого типа можно привести эксперименты по рассеянию продольно поляризованных пучков электронов на протонной мишени для исследования эффектов нарушения пространственной четности за счет интерференции электромагнитного и слабого взаимодействий. В этом случае ОСА представляет собой хорошо известную право-левую асимметрию A_RL.

В работе [5] исследован ряд продольных и поперечных ОСА $A_{{p,RL}}^{{(\parallel , \bot )}}.$ В работе [6] исследована ДСА – право-левая асимметрия $D_{p}^{{(M)}}$ зеркальной асимметрии $A_{p}^{{(M)}}$ при вылете в правую или левую полусферу относительно плоскости $\left( {\vec {s},\vec {n}} \right),$ а в работе [7] – двойная “зеркальная” асимметрия $P_{e}^{{( \bot )}}$ степени продольной поляризации рассеянного электрона.

Здесь мы рассмотрим два типа ДСА в упругом рассеянии продольно поляризованных (спиральность $\zeta = \pm 1$) электронов: 1) на поляризованной $\left( {\vec {s}} \right)$ протонной мишени без учета поляризации протонов отдачи и рассеянных электронов и 2) на неполяризованной протонной мишени с учетом продольной поляризации (спиральность $h = \pm 1$) протонов отдачи и без учета поляризации рассеянных электронов.

В разделе 1 кратко описана эффективная амплитуда ${{M}_{{eff}}}$ рассматриваемого процесса. В разделе 2 приведены дифференциальные сечения упругого рассеяния продольно поляризованных электронов со спиральностью $\zeta {\text{:}}$ ${{d\sigma \left( {\omega ,\tau ;\,\,\vec {s},\zeta } \right)} \mathord{\left/ {\vphantom {{d\sigma \left( {\omega ,\tau ;\,\,\vec {s},\zeta } \right)} {d\Omega }}} \right. \kern-0em} {d\Omega }}$ – угловое распределение рассеянных электронов с учетом поляризации $\vec {s}$ протона мишени и ${{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h} \right)} \mathord{\left/ {\vphantom {{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h} \right)} {d{{\Omega }_{p}}}}} \right. \kern-0em} {d{{\Omega }_{p}}}}$ – угловое распределение протонов отдачи с учетом их спиральности $h.$ В разделе 3 рассмотрены асимметрии: ОСА по спину протона мишени ${{A}^{{( \bot )}}}\left( {\omega ,\tau ;\,\,\zeta } \right),$ связанная с нарушением Т-четности, и ДСА ${{A}_{{ep}}}\left( {\omega ,\tau } \right)$ – аналогичная той, что экспериментально исследовалась в [4] для измерения отношения электрического и магнитного формфакторов протона G_Ep/G_Mp. В разделе 4 рассмотрена ОСА ${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ – степень продольной поляризации протона отдачи при рассеянии электрона спиральности $\zeta $ и ДСА ${{D}_{p}}\left( {\omega ,\tau } \right)$ – право-левая асимметрия степени продольной поляризации протона отдачи по спиральности падающего электрона, которая в пренебрежении слабым взаимодействием определяется отношением магнитного и анапольного формфакторов ${{{{G}_{{Mp}}}} \mathord{\left/ {\vphantom {{{{G}_{{Mp}}}} {{{G}_{{1p}}}}}} \right. \kern-0em} {{{G}_{{1p}}}}}$ протона.

ЭФФЕКТИВНАЯ АМПЛИТУДА РАССЕЯНИЯ

Рассматриваемые процессы

(1a)

${{e}^{ - }}\left( {k,\zeta } \right) + p\left( {p,\vec {s}} \right) \to {{e}^{ - }}\left( {k{\text{'}}} \right) + p\left( {p{\text{'}}} \right),$

(1b)

${{e}^{ - }}\left( {k,\zeta } \right) + p\left( p \right) \to {{e}^{ - }}\left( {k{\text{'}}} \right) + p\left( {p{\text{'}},h} \right)$

описываются суммой амплитуд рассеяния за счет электромагнитного взаимодействия и взаимодействия слабых нейтральных токов. Эту амплитуду в случае продольно поляризованных налетающих электронов высокой энергии можно представить в виде [7]:

(2)

${{M}_{{eff}}} = \frac{{4\pi Z\alpha }}{{{{q}^{2}}}}{{m}_{{eff}}},\,\,\,\,{{m}_{{eff}}} = {{j}_{{\left( {em} \right){\mu }}}}J_{{eff}}^{{\mu }},$

где ${{j}_{{\left( {em} \right){\mu }}}}$ – электромагнитный ток электрона, а эффективный нуклонный ток имеет вид

(3)

$J_{{eff}}^{{\mu }} = J_{{em}}^{{\mu }} - {{\delta }_{{\zeta }}}J_{{weak}}^{{\mu }}.$

Параметр ${{\delta }_{{\zeta }}}$ определяет относительную интенсивность электромагнитного и слабого взаимодействий:

(4)

$\begin{gathered} {{\delta }_{{\zeta }}} = {{\delta }_{{0p}}}\tau \left( {{{g}_{{Ve}}} - \zeta {{g}_{{Ae}}}} \right),\,\,\,\,{{\delta }_{{0p}}} = \frac{{{{G}_{F}}m_{p}^{2}}}{{\pi \alpha \sqrt 2 }} \approx 3.14 \cdot {{10}^{{ - 4}}}, \\ \tau = - \frac{{{{q}^{2}}}}{{4m_{p}^{2}}}, \\ \end{gathered} $

${{g}_{{Ve}}} = - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} + 2{{\sin }^{2}}{{\theta }_{W}} \approx - 0.04$ и ${{g}_{{Ae}}} = - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ – векторная и аксиально-векторная константы слабого нейтрального тока электрона.

Вершины электромагнитного тока нуклона с учетом вкладов анапольного и электрического дипольного моментов, а также слабого нейтрального тока, имеют вид:

(5a)

$\Gamma _{{em}}^{{\mu }} = {{{\gamma }}^{{\mu }}}\left( {{{G}_{{Mp}}} + \frac{{{{q}^{2}}}}{{m_{p}^{2}}}{{G}_{{1p}}}{{{\gamma }}_{5}}} \right) - \frac{{{{P}^{{\mu }}}}}{{2{{m}_{p}}}}\left( {{{F}_{{2p}}} - i{{G}_{{2p}}}{{{\gamma }}_{5}}} \right),$

(5b)

$\Gamma _{{weak}}^{{\mu }} = {{{\gamma }}^{{\mu }}}\left( {{{g}_{{Mp}}} + {{g}_{{Ap}}}{{{\gamma }}^{5}}} \right) - \frac{{{{P}^{{\mu }}}}}{{2{{m}_{p}}}}{{f}_{{Vp}}}.$

Здесь $P = p + p{\text{'}}$ – сумма 4-импульсов начального и конечного протона, ${{G}_{{Ep}}}$ и ${{G}_{{Mp}}}$ – электрический и магнитный саксовские формфакторы протона; ${{G}_{{1p}}}$ и ${{G}_{{2p}}}$ – формфакторы анапольного момента и электрического дипольного момента (ЭДМ) протона; ${{g}_{{Ep}}}$ и ${{g}_{{Mp}}}$ – слабые аналоги электромагнитных саксовских формфакторов протона, которые определяются соотношениями ${{F}_{{1p}}}$ = = ${{\left( {{{G}_{{Ep}}} + \tau {{G}_{{Mp}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{G}_{{Ep}}} + \tau {{G}_{{Mp}}}} \right)} {\left( {1 + \tau } \right)}}} \right. \kern-0em} {\left( {1 + \tau } \right)}},$ ${{F}_{{2p}}}$ =${{\left( {{{G}_{{Mp}}} - {{G}_{{Ep}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{G}_{{Mp}}} - {{G}_{{Ep}}}} \right)} {\left( {1 + \tau } \right)}}} \right. \kern-0em} {\left( {1 + \tau } \right)}},$ g_Vp = ${{\left( {{{g}_{{Ep}}} + \tau {{g}_{{Mp}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{g}_{{Ep}}} + \tau {{g}_{{Mp}}}} \right)} {\left( {1 + \tau } \right)}}} \right. \kern-0em} {\left( {1 + \tau } \right)}},$ ${{f}_{{Vp}}}$ = ${{\left( {{{g}_{{Mp}}} - {{g}_{{Ep}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{g}_{{Mp}}} - {{g}_{{Ep}}}} \right)} {\left( {1 + \tau } \right)}}} \right. \kern-0em} {\left( {1 + \tau } \right)}}.$

Таким образом, эффективная вершина нуклонного тока в случае рассеяния продольно поляризованных электронов может быть представлена в виде:

(6)

$\begin{gathered} \Gamma _{{eff}}^{{\mu }} = \Gamma _{{em}}^{{\mu }} - {{\delta }_{{\zeta }}}\Gamma _{{weak}}^{{\mu }} = \\ = {{{\gamma }}^{{\mu }}}\left( {{{G}_{{M(eff)}}} + \frac{{{{q}^{2}}}}{{m_{p}^{2}}}{{G}_{{1(eff)}}}{{{\gamma }}_{5}}} \right) - \\ - \,\,\frac{{{{P}^{{\mu }}}}}{{2{{m}_{p}}}}\left( {{{F}_{{2(eff)}}} - i{{G}_{{2(eff)}}}{{{\gamma }}_{5}}} \right). \\ \end{gathered} $

Здесь и далее

(6a)

$\begin{gathered} {{G}_{{M(eff)}}} = {{G}_{{Mp}}} - {{\delta }_{{\zeta }}}{{g}_{{Mp}}},\,\,\,\,{{G}_{{E(eff)}}} = {{G}_{{Ep}}} - {{\delta }_{{\zeta }}}{{g}_{{Ep}}}, \\ {{F}_{{2(eff)}}} = {{F}_{{2p}}} - {{\delta }_{{\zeta }}}{{f}_{{Vp}}}, \\ \end{gathered} $

(6b)

${{G}_{{1(eff)}}} = {{G}_{{1p}}} + \frac{1}{{4\tau }}{{\delta }_{{\zeta }}}{{g}_{{Ap}}},\,\,\,\,{{G}_{{2(eff)}}} = {{G}_{{2p}}}.$

ДИФФЕРЕНЦИАЛЬНЫЕ СЕЧЕНИЯ РАССЕЯНИЯ

Дифференциальное сечение, описывающее угловое распределение рассеянных электронов, дается выражением

(7)

$\frac{{d\sigma }}{{d\Omega }} = {{\sigma }_{{Mott}}}\frac{{{{{\left| {{{m}_{{(eff)}}}} \right|}}^{2}}}}{{16{{\omega }^{2}}m_{p}^{4}}}\frac{1}{{{{f}_{ - }}\left( {\omega ,\tau } \right)}},$

где

(8)

${{\sigma }_{{Mott}}} = {{\left( {\frac{\alpha }{{2\omega }}} \right)}^{2}}\frac{1}{{m_{p}^{2}}}\frac{{{{{\cos }}^{2}}\frac{\theta }{2}}}{{{{{\sin }}^{4}}\frac{\theta }{2}}}\frac{1}{{1 + 2\omega {{{\sin }}^{2}}\frac{\theta }{2}}},$

кинематические функции ${{f}_{ \mp }}\left( {\omega ,\tau } \right)$ определены, например, в [7] (см. формулы (14)), $\omega = {E \mathord{\left/ {\vphantom {E {{{m}_{p}}}}} \right. \kern-0em} {{{m}_{p}}}}$– энергия налетающих электронов в единицах массы протона, $\theta $ – угол рассеяния электрона.

Разложим это дифференциальное сечение по спин-импульсным корреляциям:

(9)

$\begin{gathered} \frac{{d\sigma }}{{d\Omega }}\left( {\omega ,\tau ;\,\,\vec {s},\zeta } \right) = \frac{{{{\sigma }_{{Mott}}}}}{{\left( {1 + \tau } \right){{f}_{ - }}\left( {\omega ,\tau } \right)}}\left\{ {a\left( {\omega ,\tau ;\,\,\zeta } \right) + } \right. \\ + \,\,b\left( {\omega ,\tau ;\,\,\zeta } \right)\left( {\vec {s}\vec {n}} \right) + c\left( {\omega ,\tau ;\,\,\zeta } \right)\left( {\vec {s}\vec {m}} \right) + \\ \left. { + \,\,d\left( {\omega ,\tau ;\,\,\zeta } \right)\left( {\vec {s}\left[ {\vec {n}\vec {m}} \right]} \right)} \right\}. \\ \end{gathered} $

Здесь $\vec {n} = {{\vec {k}} \mathord{\left/ {\vphantom {{\vec {k}} {\left| {\vec {k}} \right|}}} \right. \kern-0em} {\left| {\vec {k}} \right|}}$ и $\vec {m} = {{\vec {k}{\text{'}}} \mathord{\left/ {\vphantom {{\vec {k}{\text{'}}} {\left| {\vec {k}{\text{'}}} \right|}}} \right. \kern-0em} {\left| {\vec {k}{\text{'}}} \right|}}$ – единичные векторы в направлении импульсов падающего и рассеянного электронов соответственно. Для корреляционных функций $a,b,c,d$ найдем следующие выражения

(9a)

$\begin{gathered} a\left( {\omega ,\tau ;\,\,\zeta } \right) = {{f}_{ - }}\left( {\omega ,\tau } \right)\left[ {G_{{E(eff)}}^{2} + \tau \left( {1 + \tau } \right)G_{{2(eff)}}^{2}} \right] + \\ + \,\,\tau {{f}_{ + }}\left( {\omega ,\tau } \right)\left[ {G_{{M(eff)}}^{2} + 16\tau \left( {1 + \tau } \right)G_{{1(eff)}}^{2}} \right] + \\ + \,\,16\zeta \tau \frac{\tau }{\omega }{{f}_{0}}\left( {\omega ,\tau } \right){{G}_{{1\left( {eff} \right)}}}{{G}_{{M\left( {eff} \right)}}}, \\ \end{gathered} $

(9b)

$\begin{gathered} b\left( {\omega ,\tau ;\,\,\zeta } \right) = 4\omega \tau \left[ {\left( {1 - \frac{\tau }{\omega }} \right){{f}_{1}}\left( {\omega ,\tau } \right){{G}_{{E(eff)}}} - } \right. \\ \left. { - \,\,{{f}_{ + }}\left( {\omega ,\tau } \right){{G}_{{M(eff)}}}} \right]{{G}_{{1(eff)}}} + \zeta \tau \left[ {\left( {{{f}_{1}}\left( {\omega ,\tau } \right){{G}_{{E(eff)}}} - } \right.} \right. \\ \left. {\left. { - \,\,\left( {1 - \frac{\tau }{\omega }} \right){{G}_{{M(eff)}}}} \right){{G}_{{M(eff)}}} - 16\tau {{f}_{0}}\left( {\omega ,\tau } \right)G_{{1(eff)}}^{2}} \right], \\ \end{gathered} $

(9c)

$\begin{gathered} c\left( {\omega ,\tau ;\,\,\zeta } \right) = \left( {1 - 2\frac{\tau }{\omega }} \right)\left\{ { - 4\omega \tau \left[ {\left( {1 - \frac{\tau }{\omega }} \right){{\omega }_{0}}{{G}_{{E(eff)}}} - } \right.} \right. \\ - \,\,\left. {{{f}_{ + }}\left( {\omega ,\tau } \right){{G}_{{M(eff)}}}} \right]{{G}_{{1(eff)}}} - \zeta \tau \left[ {\left( {{{\omega }_{0}}{{G}_{{E(eff)}}} - } \right.} \right. \\ - \,\,\left. {\left. {\left. {\left( {1 - \frac{\tau }{\omega }} \right){{G}_{{M(eff)}}}} \right){{G}_{{M(eff)}}} - 16\tau {{f}_{0}}\left( {\omega ,\tau } \right)G_{{1(eff)}}^{2}} \right]} \right\}, \\ \end{gathered} $

(9d)

$\begin{gathered} d\left( {\omega ,\tau ;\,\,\zeta } \right) = \\ = {{f}_{2}}\left( {\omega ,\tau } \right)\left[ {4\omega \tau \left( {1 - \frac{\tau }{\omega }} \right){{G}_{{1(eff)}}} + \zeta \tau {{G}_{{M(eff)}}}} \right]{{G}_{{2(eff)}}}. \\ \end{gathered} $

Кинематические функции ${{f}_{0}}\left( {\omega ,\tau } \right),$ ${{f}_{1}}\left( {\omega ,\tau } \right)$ и ${{f}_{2}}\left( {\omega ,\tau } \right)$ определены в [7].

Дифференциальное сечение, описывающее угловое распределение протонов отдачи, дается выражением

(10)

$\frac{{d\sigma }}{{d{{\Omega }_{p}}}} = \frac{{{{\alpha }^{2}}}}{{m_{p}^{2}}}\frac{1}{{{{\omega }_{0}}\tau }}\sqrt {\frac{{1 + \tau }}{\tau }} \frac{{1 + \tau }}{{16{{\omega }^{2}}m_{p}^{4}}}{{\left| {{{m}_{{(eff)}}}} \right|}^{2}}.$

В случае продольно поляризованных падающих электронов и протонов отдачи это сечение раскладывается по корреляциям спиральностей $\zeta $ и $h{\text{:}}$

(11)

$\begin{gathered} \frac{{d\sigma }}{{d{{\Omega }_{p}}}}\left( {\omega ,\tau ;\,\,\zeta ,h} \right) = \frac{{{{\alpha }^{2}}}}{{2m_{p}^{2}}}\frac{1}{{{{\omega }_{0}}\tau }}\sqrt {\frac{{1 + \tau }}{\tau }} \times \\ \times \,\,\left\{ {a{\text{'}}\left( {\omega ,\tau } \right) + \zeta b{\text{'}}\left( {\omega ,\tau } \right) + hc{\text{'}}\left( {\omega ,\tau } \right) + \zeta hd{\text{'}}\left( {\omega ,\tau } \right)} \right\}. \\ \end{gathered} $

Здесь

(11a)

$\begin{gathered} a{\text{'}}\left( {\omega ,\tau } \right) = {{f}_{ - }}\left( {\omega ,\tau } \right)\left[ {G_{{E(eff)}}^{2} + \tau \left( {1 + \tau } \right)G_{{2(eff)}}^{2}} \right] + \\ + \,\,\tau {{f}_{ + }}\left( {\omega ,\tau } \right)\left[ {G_{{M(eff)}}^{2} + 16\tau \left( {1 + \tau } \right)G_{{1(eff)}}^{2}} \right], \\ \end{gathered} $

(11b)

$b{\text{'}}\left( {\omega ,\tau } \right) = 16\frac{{{{\tau }^{2}}}}{\omega }{{f}_{0}}\left( {\omega ,\tau } \right){{G}_{{M(eff)}}}{{G}_{{1(eff)}}},$

(11c)

$c{\text{'}}\left( {\omega ,\tau } \right) = 8\tau \sqrt {\tau \left( {1 + \tau } \right)} {{f}_{ + }}\left( {\omega ,\tau } \right){{G}_{{M(eff)}}}{{G}_{{1(eff)}}},$

(11d)

$\begin{gathered} d{\text{'}}\left( {\omega ,\tau } \right) = 2\frac{\tau }{\omega }\sqrt {\frac{\tau }{{1 + \tau }}} {{f}_{0}}\left( {\omega ,\tau } \right) \times \\ \times \,\,\left[ {G_{{M(eff)}}^{2} + 16\tau \left( {1 + \tau } \right)G_{{1(eff)}}^{2}} \right]. \\ \end{gathered} $

АСИММЕТРИИ ПО СПИНУ ПРОТОНА МИШЕНИ

Рассмотрим сначала поперечную асимметрию, обусловленную тройной спин-импульсной корреляцией $\left( {\vec {s}\left[ {\vec {n}\vec {m}} \right]} \right){\text{:}}$

(12)

$\begin{gathered} {{A}^{{( \bot )}}}\left( {\omega ,\tau ;\,\,\zeta } \right) = \\ = \frac{{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,\vec {s} \uparrow \uparrow \left[ {\vec {n}\vec {m}} \right]} \right) - d\sigma \left( {\omega ,\tau ;\,\,\zeta ,\vec {s} \downarrow \uparrow \left[ {\vec {n}\vec {m}} \right]} \right)}}{{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,\vec {s} \uparrow \uparrow \left[ {\vec {n}\vec {m}} \right]} \right) + d\sigma \left( {\omega ,\tau ;\,\,\zeta ,\vec {s} \downarrow \uparrow \left[ {\vec {n}\vec {m}} \right]} \right)}}. \\ \end{gathered} $

Из (9) после подстановки эффективных формфакторов в пренебрежении вкладами, пропорциональными $G_{{2p}}^{2},$ $G_{{1p}}^{2}$, $\delta _{{0p}}^{2}$ и ${{\delta }_{{0p}}}{{G}_{{1p}}}$ (ожидаемое значение ${{G}_{{1p}}}\sim {{G}_{F}}m_{p}^{2}$ имеет тот же порядок величины, что и ${{\delta }_{{0p}}}$ [8]), а также с учетом ${{g}_{{Ve}}} \ll {{g}_{{Ae}}},$ получим

(13)

${{A}^{{( \bot )}}}\left( {\omega ,\tau ;\,\,\zeta } \right) = \sin \left( \theta \right)\frac{{{{d}_{{eff}}}\left( {\omega ,\tau ;\,\,\zeta } \right)}}{{{{a}_{{eff}}}\left( {\omega ,\tau ;\,\,\zeta } \right)}},$

где

(13a)

$\begin{gathered} {{a}_{{eff}}}\left( {\omega ,\tau ;\,\,\zeta } \right) = {{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2} + \\ + \,\,16\zeta \tau \frac{\tau }{\omega }{{f}_{0}}{{G}_{{1p}}}{{G}_{{Mp}}} - 2\tau {{\delta }_{{0p}}}{{g}_{{Ae}}} \times \\ \times \,\,\left[ {2\frac{\tau }{\omega }{{f}_{0}}{{g}_{{Ap}}}{{G}_{{Mp}}} - \zeta \left( {{{f}_{ - }}{{g}_{{Ep}}}{{G}_{{Ep}}} + \tau {{f}_{ + }}{{g}_{{Mp}}}{{G}_{{Mp}}}} \right)} \right], \\ \end{gathered} $

(13b)

$\begin{gathered} {{d}_{{eff}}}\left( {\omega ,\tau ;\,\,\zeta } \right) = \omega \tau {{f}_{2}}{{G}_{{2p}}}\left[ {4\left( {1 - \frac{\tau }{\omega }} \right){{G}_{{1p}}} + } \right. \\ \left. { + \,\,\zeta \frac{1}{\omega }{{G}_{{Mp}}} + {{\delta }_{{0p}}}{{g}_{{Ae}}}\left( {\frac{\tau }{\omega }{{g}_{{Mp}}} - \zeta \left( {1 - \frac{\tau }{\omega }} \right){{g}_{{Ap}}}} \right)} \right]. \\ \end{gathered} $

Нарушающая T-четность асимметрия (13) пропорциональна формфактору протона ${{G}_{{2p}}}$ (см. также [5]) и должна быть весьма малой в силу имеющихся экспериментальных ограничений на величину ЭДМ протона ${{d}_{p}} < 7.9 \cdot {{10}^{{ - 25}}}$ e · см [9].

Определим двойную поляризационную асимметрию:

(14)

${{A}_{{ep}}}\left( {\omega ,\tau } \right) = \frac{{d{{\sigma }^{{( + )}}}\left( {\omega ,\tau } \right) - d{{\sigma }^{{( - )}}}\left( {\omega ,\tau } \right)}}{{d{{\sigma }^{{( + )}}}\left( {\omega ,\tau } \right) + d{{\sigma }^{{( - )}}}\left( {\omega ,\tau } \right)}},$

где

(14a)

$\begin{gathered} d{{\sigma }^{{( + )}}}\left( {\omega ,\tau } \right) = d\sigma \left( {\omega ,\tau ;\,\,\zeta = + 1,\vec {s} \uparrow \uparrow \vec {n}} \right) + \\ + \,\,d\sigma \left( {\omega ,\tau ;\,\,\zeta = - 1,\vec {s} \downarrow \downarrow \vec {n}} \right), \\ \end{gathered} $

(14b)

$\begin{gathered} d{{\sigma }^{{( - )}}}\left( {\omega ,\tau } \right) = d\sigma \left( {\omega ,\tau ;\,\,\zeta = + 1,\vec {s} \downarrow \downarrow \vec {n}} \right) + \\ + \,\,d\sigma \left( {\omega ,\tau ;\,\,\zeta = - 1,\vec {s} \uparrow \uparrow \vec {n}} \right). \\ \end{gathered} $

Легко видеть, что спин-импульсные корреляции в (9) при $\vec {s} \uparrow \uparrow \vec {n}$ и $\vec {s} \downarrow \downarrow \vec {n}$ принимают значения $\left( {\vec {s}\vec {n}} \right) = + 1,$ $\left( {\vec {s}\vec {m}} \right) = + \cos \left( \theta \right),$ $\left( {\vec {s}\left[ {\vec {n}\vec {m}} \right]} \right) = 0$ и $\left( {\vec {s}\vec {n}} \right) = - 1,$ $\left( {\vec {s}\vec {m}} \right) = - \cos \left( \theta \right),$ $\left( {\vec {s}\left[ {\vec {n}\vec {m}} \right]} \right) = 0$ соответственно.

В том же приближении, что и (13), найдем

(15)

${{A}_{{ep}}}\left( {\omega ,\tau } \right) = \omega \tau \frac{{\frac{1}{\omega }{{G}_{{Mp}}}\left( {{{f}_{4}}{{G}_{{Ep}}} - \left( {1 - \frac{\tau }{\omega }} \right){{f}_{3}}{{G}_{{Mp}}}} \right) + {{\delta }_{{0p}}}{{g}_{{Ae}}}{{g}_{{Ap}}}\left( {{{f}_{3}}{{f}_{ + }}{{G}_{{Mp}}} - \left( {1 - \frac{\tau }{\omega }} \right){{f}_{4}}{{G}_{{Ep}}}} \right)}}{{{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2} - 4\tau \frac{\tau }{\omega }{{\delta }_{{0p}}}{{g}_{{Ae}}}{{g}_{{Ap}}}{{f}_{0}}{{G}_{{Mp}}}}},$

где дополнительные кинематические функции ${{f}_{3}}$ и ${{f}_{4}}$ определены в [7] (формулы (24)). Заметим, что эта асимметрия не содержит вкладов от анапольного момента протона ${{G}_{{1p}}}.$

В случае чисто электромагнитного взаимодействия (т.е. при ${{\delta }_{{0p}}} = 0$) получим формулу

(16)

$A_{{ep}}^{{(em)}}\left( {\omega ,\tau } \right) = \tau {{G}_{{Mp}}}\frac{{{{f}_{4}}{{G}_{{Ep}}} - \left( {1 - \frac{\tau }{\omega }} \right){{f}_{3}}{{G}_{{Mp}}}}}{{{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2}}},$

которая позволяет в экспериментах, подобных экспериментам Jefferson Lab [10], измерить отношение электрического и магнитного формфакторов протона ${{{{G}_{{Ep}}}} \mathord{\left/ {\vphantom {{{{G}_{{Ep}}}} {{{G}_{{Mp}}}}}} \right. \kern-0em} {{{G}_{{Mp}}}}}$ [4].

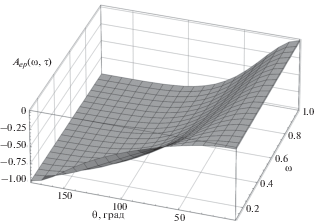
На рис. 1 показана зависимость асимметрии ${{A}_{{ep}}}\left( {\omega ,\tau } \right)$ от энергии налетающих электронов $\omega $ и угла их рассеяния $\theta $. Эта асимметрия практически совпадает с асимметрией $A_{{ep}}^{{(em)}}\left( {\omega ,\tau } \right),$ поскольку, как показывает расчет, в рассматриваемом интервале энергий слабые поправки пренебрежимо малы: $\left| {{{A}_{{ep}}}\left( {\omega ,\tau } \right) - A_{{ep}}^{{(em)}}\left( {\omega ,\tau } \right)} \right| \leqslant 1.5 \cdot {{10}^{{ - 6}}}.$

Рис. 1.

Двойная поляризационная асимметрия ${{A}_{{ep}}}\left( {\omega ,\tau } \right)$ в упругом рассеянии продольно поляризованных электронов на поляризованной протонной мишени в зависимости от энергии налетающего электрона $\omega $ и угла его рассеяния $\theta .$

СТЕПЕНЬ ПРОДОЛЬНОЙ ПОЛЯРИЗАЦИИ ПРОТОНА ОТДАЧИ

Определим степень продольной поляризации протона отдачи при рассеянии электрона спиральности $\zeta $

(17)

$\begin{gathered} {{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right) = \\ = \frac{{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h = + 1} \right) - d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h = - 1} \right)}}{{d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h = + 1} \right) + d\sigma \left( {\omega ,\tau ;\,\,\zeta ,h = - 1} \right)}}. \\ \end{gathered} $

Отсюда с учетом (11) получим

(18)

${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right) = \frac{{c{\text{'}}\left( {\omega ,\tau } \right) + \zeta d{\text{'}}\left( {\omega ,\tau } \right)}}{{a{\text{'}}\left( {\omega ,\tau } \right) + \zeta b{\text{'}}\left( {\omega ,\tau } \right)}}.$

Воспользовавшись формулами (11a)–(11d), (4) и (6a)–(6b), в линейном по ${{\delta }_{{0p}}},$ ${{G}_{{1p}}},$ ${{G}_{{2p}}}$ приближении, а также с учетом ${{g}_{{Ve}}} \ll {{g}_{{Ae}}},$ найдем

(19)

$\begin{gathered} {{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right) = 2\tau \sqrt {\frac{\tau }{{1 + \tau }}} {{G}_{{Mp}}}\left\{ {\left( {4\left( {1 + \tau } \right){{f}_{ + }}{{G}_{{1p}}} + \zeta \frac{{{{f}_{0}}}}{\omega }{{G}_{{Mp}}}} \right) + {{\delta }_{{0p}}}{{g}_{{Ae}}}\left[ {2\frac{\tau }{\omega }{{f}_{0}}{{g}_{{Mp}}} - \zeta \left( {1 + \tau } \right){{f}_{ + }}{{g}_{{Ap}}}} \right]} \right\} \times \\ \times \,\,{{\left. {\left\{ {{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2} + 16\zeta \tau \frac{\tau }{\omega }{{f}_{0}}{{G}_{{1p}}}{{G}_{{Mp}}} + 2\tau {{\delta }_{{0p}}}{{g}_{{Ae}}}\left[ { - 2\frac{\tau }{\omega }{{f}_{0}}{{g}_{{Ap}}}{{G}_{{Mp}}} + \zeta \left( {{{f}_{ - }}{{g}_{{Ep}}}{{G}_{{Ep}}} + \tau {{f}_{ + }}{{g}_{{Mp}}}{{G}_{{Mp}}}} \right)} \right]} \right.} \right\}}^{{ - 1}}}. \\ \end{gathered} $

В случае неполяризованного падающего электрона протон отдачи приобретет продольную поляризацию за счет нарушающих пространственную четность эффектов:

(20)

$\begin{gathered} P_{p}^{{(0)}}\left( {\omega ,\tau } \right) = 4\tau \sqrt {\frac{\tau }{{1 + \tau }}} {{G}_{{Mp}}} \times \\ \times \,\,\frac{{2\left( {1 + \tau } \right){{f}_{ + }}{{G}_{{1p}}} + {{\delta }_{{0p}}}\frac{\tau }{\omega }{{f}_{0}}{{g}_{{Ae}}}{{g}_{{Mp}}}}}{{{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2} - 4{{\delta }_{{0p}}}\frac{{{{\tau }^{2}}}}{\omega }{{f}_{0}}{{g}_{{Ae}}}{{g}_{{Ap}}}{{G}_{{Mp}}}}}. \\ \end{gathered} $

Определим двойную поляризационную асимметрию – право-левую асимметрию степени продольной поляризации протона отдачи по спиральности падающего электрона:

(21)

${{D}_{p}}\left( {\omega ,\tau } \right) = \frac{{{{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta = + 1} \right) - {{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta = - 1} \right)}}{{{{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta = + 1} \right) + {{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta = - 1} \right)}}.$

В принятом выше приближении получим

(22)

${{D}_{p}}\left( {\omega ,\tau } \right) = \frac{1}{{2{{f}_{ - }}}}\frac{{\left( {{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2}} \right)\left[ {{{f}_{0}}{{G}_{{Mp}}} - {{\delta }_{{0p}}}{{g}_{{Ae}}}{{g}_{{Ap}}}\omega \left( {1 + \tau } \right){{f}_{ + }}} \right] - 4{{\delta }_{{0p}}}{{g}_{{Ae}}}{{g}_{{Ap}}}\frac{{{{\tau }^{2}}}}{\omega }f_{0}^{2}G_{{Mp}}^{2}}}{{2\omega \left( {1 + \tau } \right)\left( {{{f}_{ + }}G_{{Ep}}^{2} + \tau {{f}_{ - }}G_{{Mp}}^{2}} \right){{G}_{{1p}}} + {{\delta }_{{0p}}}{{g}_{{Ae}}}{{G}_{{Ep}}}\tau {{f}_{0}}\left( {{{g}_{{Mp}}}{{G}_{{Ep}}} - {{g}_{{Ep}}}{{G}_{{Mp}}}} \right)}}.$

Отсюда без учета вклада слабого взаимодействия для этой двойной асимметрии найдем

(23)

$D_{p}^{{(em)}}\left( {\omega ,\tau } \right) = \frac{{{{f}_{0}}{{G}_{{Mp}}}\left( {{{f}_{ - }}G_{{Ep}}^{2} + \tau {{f}_{ + }}G_{{Mp}}^{2}} \right)}}{{4\omega \left( {1 + \tau } \right){{f}_{ - }}{{G}_{{1p}}}\left( {{{f}_{ + }}G_{{Ep}}^{2} + \tau {{f}_{ - }}G_{{Mp}}^{2}} \right)}}.$

Очевидно, что измерение этой асимметрии позволило бы непосредственно определить отношение магнитного и анапольного формфакторов ${{{{G}_{{Mp}}}} \mathord{\left/ {\vphantom {{{{G}_{{Mp}}}} {{{G}_{{1p}}}}}} \right. \kern-0em} {{{G}_{{1p}}}}}$ протона.

На рис. 2 показана зависимость асимметрии ${{D}_{p}}\left( {\omega ,\tau } \right)$ от энергии налетающих электронов в области малых углов вылета ${{\theta }_{p}}$ протонов отдачи при различных значениях анапольного момента ${{G}_{{1p}}}\left( 0 \right).$ Видно, что ее величина растет с уменьшением ${{G}_{{1p}}}\left( 0 \right)$ и угла ${{\theta }_{p}}.$ На рис. 3 показана зависимость степени продольной поляризации ${{P}_{p}}\left( {\omega ,\tau ;\;\zeta } \right)$ протонов отдачи от угла их вылета и энергии налетающих электронов при разных значениях спиральности падающих электронов. Видно, что передача спиральности рассеивающегося электрона протону отдачи усиливается при уменьшении угла вылета протона отдачи. Рисунок 4 иллюстрирует поведение приобретаемой степени продольной поляризации $P_{p}^{{(0)}}\left( {\omega ,\tau } \right)$ протоном отдачи при рассеянии неполяризованных электронов на неполяризованном протоне, обусловленной анапольным моментом протона и взаимодействием слабых нейтральных токов.

Рис. 2.

Право-левая асимметрия ${{D}_{p}}\left( {\omega ,\tau } \right)$ степени продольной поляризации ${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ протона отдачи по спиральности падающего электрона $\zeta $ в зависимости от энергии налетающего электрона $\omega $ и угла вылета ${{\theta }_{p}}$ протона отдачи: 1 – ${{G}_{{1p}}}\left( 0 \right) = 0.4{{\delta }_{{0p}}},$ 2 – ${{G}_{{1p}}}\left( 0 \right) = 0.7{{\delta }_{{0p}}},$ 3 – ${{G}_{{1p}}}\left( 0 \right) = {{\delta }_{{0p}}}.$

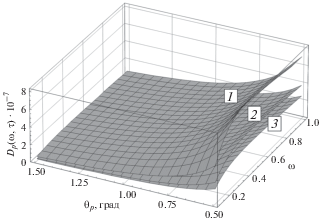
Рис. 3.

Степень продольной поляризации ${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ протонов отдачи в зависимости от энергии налетающего электрона $\omega $ и угла вылета ${{\theta }_{p}}$ протона отдачи при ${{G}_{{1p}}}\left( 0 \right) = {{\delta }_{{0p}}}{\text{:}}$ 1 – $\zeta = + 1,$ 2 – $\zeta = - 1,$ 3 – налетающий электрон не поляризован.

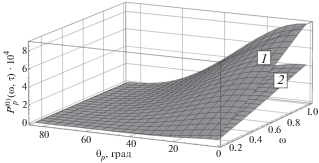
Рис. 4.

Приобретенная продольная поляризация $P_{p}^{{(0)}}\left( {\omega ,\tau } \right)$ протонов отдачи при рассеянии неполяризованных электронов на неполяризованной протонной мишени в зависимости от энергии налетающего электрона $\omega $ и угла вылета ${{\theta }_{p}}$ протона отдачи: 1 – ${{G}_{{1p}}}\left( 0 \right) = {{\delta }_{{0p}}},$ 2 – ${{G}_{{1p}}}\left( 0 \right) = 0.5{{\delta }_{{0p}}}.$

ЗАКЛЮЧЕНИЕ

В рамках формализма эффективного тока найдены аналитические выражения для дифференциальных сечений рассеяния продольно поляризованных электронов с учетом поляризации протона мишени или продольной поляризации протона отдачи, а также формфакторов анапольного ${{G}_{{1p}}}$ и электрического дипольного ${{G}_{{2p}}}$ моментов протона и формфакторов слабого нейтрального нуклонного тока.

Получены и исследованы одинарные и двойные спиновые асимметрии ${{A}^{{( \bot )}}}\left( {\omega ,\tau ;\,\,\zeta } \right),$ ${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ и ${{A}_{{ep}}}\left( {\omega ,\tau } \right),$ ${{D}_{p}}\left( {\omega ,\tau } \right)$ в минимальном линейном приближении по ${{G}_{{1p}}},$ ${{G}_{{2p}}}$ и параметру относительной интенсивности слабого и электромагнитного взаимодействий ${{\delta }_{{0p}}}.$

Показано, что асимметрия ${{A}^{{( \bot )}}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ пропорциональна нарушающему T-четность формфактору ${{G}_{{2p}}},$ а двойная асимметрия ${{A}_{{ep}}}\left( {\omega ,\tau } \right)$ вполне может использоваться для измерения отношения электромагнитных формфакторов протона ${{{{G}_{{Ep}}}} \mathord{\left/ {\vphantom {{{{G}_{{Ep}}}} {{{G}_{{Mp}}}}}} \right. \kern-0em} {{{G}_{{Mp}}}}}.$ Показано также, что двойная асимметрия ${{D}_{p}}\left( {\omega ,\tau } \right)$ существенно зависит от анапольного момента протона ${{G}_{{1p}}},$ и становится значительной при малых углах вылета протона отдачи. Угловая зависимость ${{P}_{p}}\left( {\omega ,\tau ;\,\,\zeta } \right)$ свидетельствует, что спиральность рассеивающегося электрона практически полностью передается протонам отдачи при малых углах их вылета. При рассеянии неполяризованных электронов протоны отдачи приобретают небольшую продольную поляризацию за счет анапольного момента протона и взаимодействия слабых нейтральных токов.

Публикация подготовлена при поддержке Программы РУДН “5-100”.

Список литературы

Crawford C.B., Sindile A., Akdogan T. et al. // arXiv: nucl-ex/0609007v1 7 Sep 3006.
Pacetti S., Ferroli R.B. // Phys. Rep. 2015. V. 550–551. P. 1.
Puckett A.J.R., Brash E.J., Jones M.K. et al. // arXiv: 1707.08587v1 [nucl-ex] 26 Jul 2017.
Liyanage A., Armstrong W., Kang H. et al. // arXiv: 1806.11156v1 [nucl-ex] 28 Jun 2018.
Сафин М.Я. // Изв. РАН. Сер. физ. 2015. Т. 79. С. 1053; Safin M.Ya. // Bull. Russ. Acad. Sci. Phys. 2015. V. 79. P. 940.
Сафин М.Я. // Изв РАН Сер. физ. 2016. Т. 80. С. 664; Safin M.Ya. // Bull. Russ. Acad. Sci. Phys. 2016. V. 80. P. 603.
Сафин М.Я. // Изв РАН Сер. физ. 2018. Т. 82. С. 836; Safin M.Ya. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. P. 752.
Beck D.H., McKeown R.D. // Ann. Rev. Nucl. Part. Sci. 2001. V. 51. P. 189.
Griffith W.C., Swallows M.D., Loftus T.H. et al. // Phys. Rev. Lett. 2009. V. 102. Art. no . 101601.
Gilfoyle G. // EPJ Web Conf. 2018. V. 172. Art. no. 02004.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал