Известия РАН. Серия физическая, 2019, T. 83, № 5, стр. 614-617

ВВЕДЕНИЕ

Глобальным гелиосферным токовым слоем (ГГТС) мы называем единственный гелиосферный токовый слой (ГТС), соединяющий все долготы и существующий примерно 70–80% времени в эпохи средней и низкой пятнообразовательной активности Солнца [1, 2]. Важность ГГТС для распространения ГКЛ обусловлена двумя его свойствами: 1) ГГТС разделяет гелиосферу на два униполярных полушария по направлению гелиосферного магнитного поля (ГМП) и 2) cкорость солнечного ветра (СВ) сильно зависит от углового расстояния от ГГТС [3, 4].

Стандартные модели распространения ГКЛ в гелиосфере [5] учитывают два эффекта, связанные с ГГТС: 1) магнитный дрейф частиц в униполярных полушариях и на самом ГГТС и 2) существенное изменение скорости СВ и, как следствие, характеристик ГМП и скорости дрейфа частиц с расстоянием от ГГТС. В осесимметричных моделях распространения ГКЛ, разрабатываемых нашей группой [6–8], учитываются еще два эффекта, связанные с ГГТС: 3) разный спектр флуктуаций ГМП в зоне секторной структуры и вне ее и 4) источник ГКЛ, возникающий при переходе от трехмерного по пространственным переменным (3D) транспортного уравнения для характеристик ГКЛ к усредненному по долготе (2D) уравнению.

Гелиосферные эффекты, обсуждаемые в этой статье, обусловлены влиянием ГГТС на пространственное поведение скорости СВ. Этим влиянием определяется как широтный, так и долготный градиенты скорости СВ, причем последний приводит к образованию коротирующих областей взаимодействия разноскоростных потоков СВ [9], изменяет спектр флуктуаций ГМП [10] и т.д. Рассмотрены подходы к построению 3D моделей СВ для использования при теоретическом изучении модуляции ГКЛ и предлагается еще одна такая модель. Затем обсуждается выбор для описания поведения ГКЛ (модели распространения ГКЛ), адекватной ситуации в период низкой и средней пятнообразовательной активности Солнца.

ГЛОБАЛЬНЫЙ ГЕЛИОСФЕРНЫЙ ТОКОВЫЙ СЛОЙ И СКОРОСТЬ СВ

В середине 1970-х годов сложилась концепция ГТС, разделяющего гелиосферу на два полушария с униполярным ГМП в каждом, и простая модель т.н. “наклонного” ГТС (НГТС) и скорости СВ относительно него [3]. В этой модели ГТС считается большим кругом, наклоненным к плоскости гелиоэкватора на угол ${{\alpha }_{t}}$ (тилт). При этом скорость СВ остается радиальной и зависит только от магнитной широты 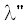(угла, отсчитываемого от плоскости ГТС как “магнитного экватора”), т.е., где $\overrightarrow {{{r}_{0}}} $ – единичный вектор в радиальном направлении от Солнца.

Если перейти от исходной гелиоцентрической системы координат {r, θ, φ} с осью вращения Солнца 0Z к системе координат {r, θ'', φ''} с осью 0Z  '', образующей с 0Z угол α_t, то

Если в (1) положить θ'' = π/2, получим выражение (2) для формы ГТС θ^cs(φ; α_t) в исходной системе координат как большого круга, наклоненного к экватору на угол α_t:

Теперь рассмотрим, что известно о форме ГГТС и насколько хорошо она описывается моделями НГТС. Общее представление о форме ГГТС позволяют получить модели СМП в слое между фотосферой и т.н. поверхностью источника (внутренней поверхностью гелиосферы), например, модель потенциального СМП [11]. Пользуясь этой моделью, можно рассчитать форму изолиний $B\left( {\theta ,\varphi } \right) = 0\quad$ или нейтральных линий на поверхности источника (НЛПИ). Многочисленные измерения ГМП в первом приближении согласуются с представлением о ГТС как вытянутой в гелиосферу солнечным ветром поверхностью, опирающейся на соответствующую НЛПИ [4]. В работе [12] было подробно рассмотрено, насколько форма расчетных НЛПИ, рассчитанных по модели [11], соответствует модели НГТС и показано, что обычно форма НЛПИ намного сложнее, чем ожидаемая по модели НГТС. Тем не менее модели ГМП и СВ, основанные на модели НГТС, широко используются, особенно при моделировании поведения в гелиосфере ГКЛ [5]. Рассмотрим еще одну такую модель.

Зададим зависимость скорости СВ от в N‑полушарии основания гелиосферы в виде:

где V^pol и V^cs – скорость СВ на полюсе (θ'' = 0) и на токовом слое (θ'' = π/2) соответственно, а θ_1/2 и Δθ определяют положение и ширину переходной области с естественным обобщением для S-полушария. Теперь, пользуясь выражением (1), можно получить зависимость скорости от направления в исходной системе координат. На левой панели (а) рис. 1 показана скорость СВ как функция широты в наклонной системе координат при некоторых параметрах {V ^pol, V ^cs, θ_1/2, Δθ}, а на правой панели (б) – карта распределения скорости СВ в исходной системе координат. Ясно, что параметры {V ^pol, V  ^cs, θ_1/2, Δθ} и их возможная зависимость от фазы солнечного цикла должны быть оценены из наблюдений.

ОБ АДЕКВАТНОМ ОПИСАНИИ ДОЛГОВРЕМЕННЫХ ВАРИАЦИЙ ГКЛ

Поскольку скорость СВ, а значит и другие характеристики гелиосферы могут зависеть как от широты, так и от долготы, исходное транспортное уравнение для распространения ГКЛ [13–15] должно зависеть от трех пространственных переменных {$r,\vartheta ,\varphi $}, т.е., быть трехмерным (3D). Обычно это уравнение формулируется для функции распределения $U,$ связанной с интенсивностью J выражением $U(r,\theta ,\varphi ,p) = J(r,\vartheta ,\varphi ,T){\text{/}}{{p}^{2}},$ где T и p – кинетическая энергия и импульс ГКЛ соответственно:

где $K{\text{,}}\;V,\;{{V}_{d}}$ – зависящие от всех трех пространственных координат тензор диффузии частиц, скорости СВ и магнитного дрейфа частиц соответственно. При исследовании долговременных вариаций интенсивности ГКЛ кажется естественным использовать двумерное по пространственным переменным (2D) транспортное уравнение для усредненной по долготе функции распределения $\bar {U}{\text{:}}$где черта над символом означает усреднение по долготе, а S – источник, образующийся при получении этого уравнения усреднением по долготе соответствующего однородного 3D транспортного уравнения [16]. В работе [16] было показано, что член источника S имеет структуру суммы сверток: где δq_i– долготные вариации i-го члена модулирующего оператора в 3D-уравнении (например, скоростей СВ и магнитного дрейфа частиц ГКЛ во втором и третьем членах уравнения (4)), а δu_i – долготные вариации i-го члена соответствующего оператора от функции распределения ГКЛ (градиента в первых трех членах 3D-уравнения (4)).

Ясно, что все усредненные по долготе коэффициенты уравнения (6) сильно зависят от использованной 3D модели скорости СВ. Более того, как видно из рис. 1б, широтная область секторной структуры ГМП, занятая ГГТС, отличается наличием гелиодолготного градиента скорости, постепенно уменьшающего к внешней границе области. Разноскоростные потоки образуются в окрестностях ГГТС вблизи Солнца, с увеличением расстояния высокоскоростные потоки догоняют низкоскоростные, и они взаимодействуют с образованием т.н. коротирующих областей взаимодействия (CIR) (например, [9] и ссылки в ней).

Если пренебречь указанным взаимодействием разноскоростных потоков СВ, то краевая задача, основанная на 2D-уравнении (5), может быть решена [6], причем в источник (6) даст вклад только дрейфовый член уравнения (4). Естественно, используя 3D-модель скорости СВ (3), можно легко определить усредненную по долготе скорость СВ, показанную на рис. 2а и не сильно отличающуюся от использованной в [5]. Более того, предположив, что широтная зависимость усредненного по долготе результата взаимодействия разноскоростных потоков СВ (характеристик спектра неоднородностей ГМП и т.п.) η(λ) определяется, например, величиной среднего по долготе модуля долготного градиента скорости СВ, можно определить η_n(λ), нормированную на экваторе на единицу и показанную на рис. 2б. Тогда для некоторого параметра P этого спектра его зависимость от гелиошироты можно определить как

где ${{P}^{{eq}}}$ и ${{P}^{{pol}}}$ – значения P на экваторе и полюсе соответственно. В качестве параметров P можно рассматривать, например, мощность спектра неоднородностей ГМП на заданной частоте P₀ и показатель частотного спектра мощностей γ. Конечно выбор зависимости результата взаимодействия разноскоростных потоков СВ от деталей поля скорости, фазы солнечного цикла и т.д. требует дальнейшего исследования.

Таким образом, отказавшись от рассмотрения разноскоростных потоков СВ и их взаимодействия (например, считая скорость СВ независящей от долготы, [6–8]), вполне можно численно исследовать модуляцию ГКЛ, пользуясь 2D-моделями. Однако согласно расчетам (например, [17]), взаимодействие разноскоростных потоков СВ существенно искажает с увеличением расстояния от основания гелиосферы исходную форму ГГТС, ГМП и поле скорости СВ, а оценить эти искажения можно лишь путем 3D-моделирования СВ и ГМП (например, используя магнитогидродинамический подход [17]). Поэтому мы склоняемся к предположению, что в основном для периодов средней пятнообразовательной активности Солнца, когда степень изогнутости ГГТС не очень мала и слабо изменяется, решение 3D‑уравнения (4) с коэффициентами, определенными заранее путем 3D-моделирования СВ и ГМП, является подходом к расчету долговременных вариаций характеристик ГКЛ, более адекватным, чем решение 2D-уравнения (5) с коэффициентами, определенными без указанного моделирования характеристик гелиосферы.

ЗАКЛЮЧЕНИЕ

1. Предложена 4-х параметрическая модель скорости солнечного ветра, опирающаяся на модель наклонного гелиосферного слоя. После оценки по данным наблюдений параметров модели и их возможной зависимости от фазы солнечного цикла модель может быть полезна для изучения вариаций интенсивности ГКЛ.

2. Для периодов средней пятнообразовательной активности Солнца решение трехмерных уравнений для характеристик гелиосферы и распространения ГКЛ является более адекватным подходом к расчету долговременных вариаций характеристик ГКЛ, чем решение двумерных уравнений.

Работа выполнена при частичной поддержке РФФИ (гранты №№ 17-02-00584_а, 18-02-00582_а).